单项式与多项式
第二章 第一节 单项式和多项式
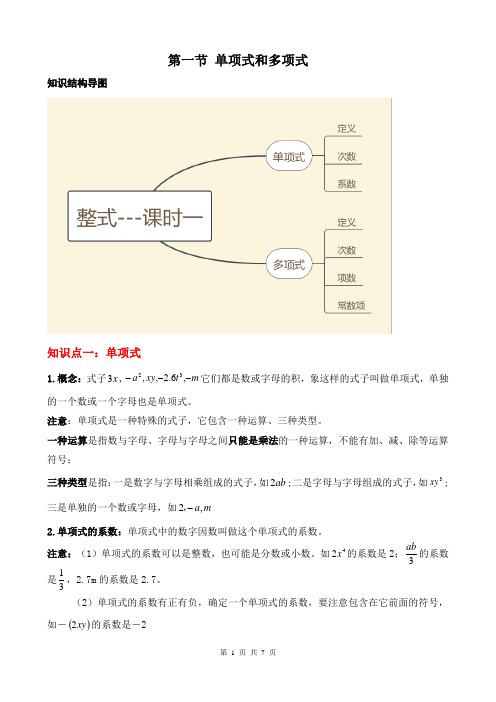
第一节 单项式和多项式知识结构导图知识点一:单项式1.概念:式子x 3,m t xy a ---,6.2,,32它们都是数或字母的积,象这样的式子叫做单项式,单独的一个数或一个字母也是单项式。
注意:单项式是一种特殊的式子,它包含一种运算、三种类型。
一种运算是指数与字母、字母与字母之间只能是乘法的一种运算,不能有加、减、除等运算符号;三种类型是指:一是数字与字母相乘组成的式子,如ab 2;二是字母与字母组成的式子,如3xy ;三是单独的一个数或字母,如m a ,2-,2.单项式的系数:单项式中的数字因数叫做这个单项式的系数。
注意:(1)单项式的系数可以是整数,也可能是分数或小数。
如42x 的系数是2;3ab 的系数是31,2.7m 的系数是2.7。
(2)单项式的系数有正有负,确定一个单项式的系数,要注意包含在它前面的符号,如-()xy 2的系数是-2(3)对于只含有字母因素的单项式,其系数是1或-1,不能认为是0,如-2xy 的系数是-1;2xy 的系数是1。
(4)表示圆周率的π,在数学中是一个固定的常数,当它出现在单项式中时,应将其作为系数的一部分,而不能当成字母。
如2πxy 的系数就是2π3单项式的次数:一个单项式中,所有字母的指数和叫做这个单项式的次数。
注意:(1)计算单项式的次数时,应注意是所有字母的指数和,不要漏掉字母指数是1的情况。
如单项式z y x 342的次数是字母z y x ,,的指数和,即4+3+1=8,而不是7次,应注意字母Z 的指数是1而不是0.(2)单项式是一个单独字母时,它的指数是1,如单项式m 的指数是1,单项式是单独的一个常数时,一般不讨论它的次数。
(3)单项式的指数只和字母的指数有关,与系数的指数无关。
如单项式-43242z y x 的次数是2+3+4=9而不是13次。
(4)单项式通常根据单项式的次数进行命名。
如x 6是一次单项式,xyz 2是三次单项式。
例题:下列说法正确的是( )A .单项式23x -的系数是3-B .单项式3242π2ab -的次数是7 C .1x是单项式 D .单项式可能不含有字母检测:1、判断下列各代数式是不是单项式?若是,写出它的系数与次数。
单项式与多项式ppt

05
单项式与多项式的例子
单项式的例子
总结词
单项式是由一个字母表示的数学表达式,如2x,3y等。
详细描述
单项式在数学中有着广泛的应用,它是代数、几何等数学领域的基础。单项 式是由一个字母表示的数学表达式,其系数和次数都非常重要。例如,2x表 示x的系数为2,次数为1的单项式。
多项式的例子
总结词
多项式是由多个单项式组成的数学表达式,如2x+3y,4x^2-5xy+6y^2等。
展望单项式与多项式未来的发展
拓展单项式与多项式的应用领域
随着科学技术的发展,单项式与多项式的应用领域将不断拓展,例如在人工智能、大数据 、金融等领域的应用。
完善单项式与多项式的理论体系
随着数学和其他学科的发展,将不断完善单项式与多项式的理论体系,例如对高阶多项式 的研究和应用。
发展新的数学工具和方法
《单项式与多项式ppt》
xx年xx月xx日
目录
• 单项式概述 • 多项式概述 • 单项式与多项式的应用 • 单项式与多项式的运算 • 单项式与多项式的例子 • 总结与展望
01
单项式概述
单项式的定义
定义
单项式是由数字与字母的积组成的代数式,如:2x,3y等。
示例
2x^3表示一个单项式,因为它是由数字2与字母x的三次方组 成的。
经济学
03
经济学中经常使用单项式与多项式来建立模型,例如成本函数
、收益函数、价格函数等。
04
单项式与多项式的运算
单项式的加减法运算
定义
单项式的加减法运算是指将同类单项式进行合并的过程。
运算法则
单项式的加减法运算法则基于合并同类项的规则,即系数相加,字母及指数 不变。例如,2x^2 + 3x^2 = (2+3)x^2 = 5x^2。
单项式和多项式区分

页眉内容
单项式:
a,-5,1X,2XY都是单项式,而0.5m+n不是单项式
单项式是指只含乘法的式子,单独的字母或数字也是单项式。
这个名词是清代数学家李善兰译书时根据原词概念汉化的。
1,单项式中只含有乘法和乘方运算,不能含有加减运算;
2,单项式中可以含有除以数的运算,但不能含有除未知数的运算。
多项式:
若干个单项式的代数和组成的式子。
多项式中每个单项式叫做多项式的项,这些单项式中的最高次数,就是这个多项式的次数。
不含字母的项叫做常数项。
只含一个变元的多项式叫做一元多项式,含两个(或两个以上)变元的多项式叫做多元多项式。
整式:
单项式和多项式统称为整式。
代数式中的一种有理式.不含除法运算或分数,以及虽有除法运算及分数,但除式或分母中不含变数者,则称为整式。
页脚内容1。
单项式和多项式课件

01
在单项式之间进行加减法时,只需对系数进行加减运算,变量
保持不变。
运算优先级
02
在进行单项式之间的加减法时,应遵循数学中的运算优先级规
则,先进行乘除运算,再进行加减运算。
括号的作用
03
当单项式中包含括号时,应先计算括号内的内容,再进行加减
法运算。
多项式之间的加减法
逐项相加减
多项式之间的加减法需要逐项进 行,即对每个单项式分别进行加
单项式和多项式课件
• 单项式的定义和性质 • 多项式的定义和性质 • 单项式和多项式的加减法 • 单项式和多项式的乘除法 • 单项式和多项式的因式分解 • 单项式和多项式的应用
01
单项式的定义和性质
单项式的定义
单项式是数学中一个基本的代数 概念,它是由数字、字母通过有
限次乘法运算得到的代数式。
十字相乘法
适用于二次多项式的因式分解,通过十字相乘法 找到两个数,它们的和等于一次项系数,它们的 积等于常数项,从而将二次多项式分解为两个一 次多项式的乘积。
06
单项式和多项式的应用
在代数方程中的应用
单项式和多项式是代数方程的基 础,可以用来表示方程中的未知
数和已知数。
通过合并同类项,可以将代数方 程化简为更简单的形式,便于求
在实际生活中的应用
单项式和多项式可以用来描述实际生活中的各种现象,如时间、速度、距离等之间的关系。
在物理学中,单项式和多项式可以用来描述物理量之间的关系,如力、质量、加速度等。
在经济学中,单项式和多项式可以用来描述成本、收益、利润等之间的关系,以及建立经济 模型。
THANKS
感谢观看
多项式的定义和性质
多项式的定义
单项式和多项式

2
-6+x
x 7
a
-xy
x 2x 1 4
-1
哪些是多项式?如果是单项式,它的系数又 是多少? a+b+c -3 b
2
想一想:下列代数式中哪些是单项式?
2-6+x源自x 7a-xy
书 P.86
x 2x 1 4
6
-1
(1).小军100m赛跑时用了 t s,那么小军跑完
100m的平均速度是多少? 解:小军跑完100m的平均速度是
我想说
这节课的收获是……
如果一个单项式只含有字母因数,它的系数就是1 或者-1, 注:单项式的系数要 例如ab就是1· ab,系数是1 连同其前面的符号 再如-n就是-1· n,系数是-1
单项 式 8x
2a bc xy t
2
2
2
b 5 2 xy vt 7 3
系数
5 8 -2 1 -1 7
2 3
1
次数
x y 像a b, 这样的式子叫做多项式 5
定义:几个单项式的和叫做多项式 其中每个单项式叫做多项式的项 例:a+b这个多项式由两项组成,它的项是 a,b 2x-3y这个多项式的项是2x,-3y
注:
在说多项式的项的时候要连同前面的符号 次数最高项的次数,叫做这个多项式的次数.
单项式和多项式统称整式 下列代数式中哪些是单项式? 哪些是
多项式?如果是单项式,它的系数又是多少? a+b+c -3 b
a b 像0.9a,0.8b, 2a,15 15%m, 2a , , 等都是 2 数与字母的乘积, 这样的代数式叫 单项式
2
注:单独一个数或一个字母也是单项式 单项式中的数字因数叫做这个单项式的系数 1 2 1 2 2 例 : 单项式4x,-7xy , a b 的系数分别是4, 7, 3 3 单项式中所有字母的指数的和叫做这个单项 式的次数.
《单项式与多项式》

单项式与多项式的区别
形式不同
单项式是由数字与字母的乘积 组成的代数式,而多项式是由 若干个单项式按照加减法组合
而成。
运算性质不同
单项式在进行四则运算时,只 能直接进行乘除运算,而多项 式在加减运算时需要遵循分配
律和结合律。
表达式形式不同
单项式通常可以写成简单的商 的形式,而多项式则是由若干 个单项式按照加减法组合而成
03
单项式与多项式的异同点
异同点概述
定义不同
单项式是由数字与字母的乘积 组成的代数式,而多项式是由 若干个单项式组成的代数式。
表达式形式不同
单项式通常可以写成简单的商的 形式,而多项式则是由若干个单 项式按照加减法组合而成。
运算性质不同
单项式在进行四则运算时,只能直 接进行乘除运算,而多项式在加减 运算时需要遵循分配律和结合律。
《单项式与多项式》
2023-11-05
目 录
• 单项式 • 多项式 • 单项式与多项式的异同点 • 单项式与多项式的应用 •
定义:单项式是由数字与字母 的积组成的代数式,如3x,-2y
,4z等。
数字与字母的积:单项式中的 数字称为系数,字母称为未知 数,如3x^2的系数为3,未知
多项式的项和次数
项
在多项式中,每个单项式称为多项式的项。例如,在多项式2x^3 + 3x^2 4x + 5中,2x^3、3x^2、-4x和5都是它的项。
次数
多项式中次数最高的项的次数叫做多项式的次数。例如,在多项式2x^3 + 3x^2 - 4x + 5中,它的次数是3,因为它的最高次项是2x^3,次数为3。
数据拟合
在数据拟合中,单项式和多项式也经常被一起使用,比如用单项式来拟合数据的趋势,用多项式来拟合数据的 波动情况。
单项式多项式概念讲解

单项式多项式概念讲解单项式与多项式的概念1、单项式的有关概念(1)单项式:由数与字母或字母与字母相乘组成的代数式。
单独的一个数或字母.........也叫做单项式。
例如:a x abx n m a ,9,4,,,332- 注意:单项式不含加减运算,只含字母与字母或字母的乘法(包括乘方)运算(2)单项式的系数:单项式中数字因数叫做这个单项式的系数。
例如:单项式227,21xy y x -的系数分别是7,21-,当单项式系数是1或-1时,“1”通常省略不写,如ab 就是ab ⋅1,系数是1;n -就是n ⋅-1,系数是-1.(3)单项式的次数(指数):一个单项式中,所有字母的指数的和叫做这个单项式的次数。
如x 4的次数是1,z y x 323的次数是2+3+1=6;数学的次数是0,如3,-9等可以当作0次单项式。
一个单项式的次数是几就叫做几次单项式,如2231b a 中,a 与b 的指数和为4,则2231b a 是四次单项式。
之,则称为升幂排列。
例 2 、已知多项式y x xy 514322--,试按下列要求将其重新排列(1)按字母x 作降幂排列;(2)按字母y 作升幂排列3、整式的概念单项式与多项式统称为整式判断一个式子是不是整式应注意几点(1)分母不含字母;(2)根号里面不含字母①单项式②多项式4、几种约定俗成的读与写 (1)字母与数字相乘,或字母与字母相乘,乘号不用“⨯”,而是用“⋅”,或省略不写,如“a 4乘以b ”可写成“b a ⋅4”或“ab 4”。
但数字与数字相乘一般用“⨯”,且不得省略,如“34⨯”不能简写成“43”或“34⋅”(2)字母与数字相乘,一般数字写在字母之前,如“n m 235”不要写成“352n m ”;系数为带分数的,一般写成假分数,如“213与2x 的积”写成“227x ”而不写成“2213x ”,以免造成混淆。
(3)多项式中,“a 与b 的差”是指“b a -”,而不是“a b -”“a 、b 的平方和”是指“22b a+”,而不是“2b a +” “a 与b 的平方的差”是指“2b a -”,而不是“22b a -”“a 与b 的差的立方”是指“3)(b a -”,而不是“3b a -”例1:指出下列各式中,哪些是单项式,哪些是多项式,哪些是整式?π2222222,5,52,71,19,3,,r R x x x x n m xy b a x y x -+--++-+例2、多项式5)13(72++-+x n kx xm 是关于x 的三次三项式,并且一次项系数为-7,求m+n-k 的值变式:已知多项式63512212--+-+x xy y x m 是六次四项式,单项式m n y x -523与该多项式的次数相同,那么m 、n 的值分别为( )A 、5,3B 、3,2C 、2,1D 、0,21例3、(1)某班共有x 个学生,其中女生人数占45%,用代数式表示该班的男生人数是(2)某商品的原价为100元,如果经过两次降价,且每次降价的百分率都是m ,那么该商品现在的价格是 元(结果用含m 的代数式表示)课堂训练1、多项式134223--y x x是几次几项式;并说出最高次项和常数项是什么?2、把多项式3322543y x xy y x -+-重新排列;(1)按y 的降幂排列;(2)按x 的升幂排列。
初一下册数学单项式与多项式的性质

初一下册数学单项式与多项式的性质1. 单项式①由数与字母的积组成的代数式叫做单项式。
单独一个数或字母也是单项式。
②单项式的系数是这个单项式的数字因数,作为单项式的系数,必须连同数字前面的性质符号,如果一个单项式只是字母的积,并非没有系数.③一个单项式中,所有字母的指数和叫做这个单项式的次数.2.多项式①几个单项式的和叫做多项式.在多项式中,每个单项式叫做多项式的项.其中,不含字母的项叫做常数项.一个多项式中,次数最高项的次数,叫做这个多项式的次数.②单项式和多项式都有次数,含有字母的单项式有系数,多项式没有系数.多项式的每一项都是单项式,一个多项式的项数就是这个多项式作为加数的单项式的个数.多项式中每一项都有它们各自的次数,但是它们的次数不可能都作是为这个多项式的次数,一个多项式的次数只有一个,它是所含各项的次数中最高的那一项次数.3.整式单项式和多项式统称为整式.4. 整式的加减实质上就是去括号后,合并同类项,运算结果是一个多项式或是单项式.5. 括号前面是“-”号,去括号时,括号内各项要变号,一个数与多项式相乘时,这个数与括号内各项都要相乘.6.同底数幂的乘法法则: (m,n都是正数)是幂的运算中最基本的法则,在应用法则运算时,要注意以下几点:①法则使用的前提条件是:幂的底数相同而且是相乘时,底数a可以是一个具体的数字式字母,也可以是一个单项或多项式;②指数是1时,不要误以为没有指数;③不要将同底数幂的乘法与整式的加法相混淆,对乘法,只要底数相同指数就可以相加;而对于加法,不仅底数相同,还要求指数相同才能相加;④当三个或三个以上同底数幂相乘时,法则可推广为 (其中m、n、p均为正数); ⑤公式还可以逆用: (m、n均为正整数)7. 幂的乘方法则: (m,n都是正数)是幂的乘法法则为基础推导出来的,但两者不能混淆.8底数有负号时,运算时要注意,底数是a与(-a)时不是同底,但可以利用乘方法则化成同底,如将(-a)3化成-a39.底数有时形式不同,但可以化成相同。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
单项式与多项式3一、选择题 1.在下列代数式:21ab ,2b a +,ab 2+b+1,x3+y2,x 3+ x 2-3中,多项式有( )A .2个B .3个C .4个 D5个2.多项式-23m 2-n 2是( )A .二次二项式B .三次二项式C .四次二项式D 五次二项式 3.下列说法正确的是( )A .3 x 2―2x+5的项是3x 2,2x ,5 B .3x -3y 与2 x 2―2x y -5都是多项式C .多项式-2x 2+4x y 的次数是3D .一个多项式的次数是6,则这个多项式中只有一项的次数是6 4.下列说法正确的是( ) A .整式abc 没有系数 B .2x +3y +4z 不是整式C .-2不是整式D .整式2x+1是一次二项式 5.下列代数式中,不是整式的是( )A 、23x -B 、745b a - C 、xa 523+ D 、-20056.下列多项式中,是二次多项式的是( )A 、132+xB 、23xC 、3xy -1D 、253-x 7.x 减去y 的平方的差,用代数式表示正确的是( )A 、2)(y x -B 、22y x -C 、y x -2D 、2y x -8.某同学爬一楼梯,从楼下爬到楼顶后立刻返回楼下。
已知该楼梯长S 米,同学上楼速度是a 米/分,下楼速度是b 米/分,则他的平均速度是( )米/分。
A 、2b a + B 、ba s + C 、bs as +D 、bs ass +2 9.下列单项式次数为3的是( )A.3abcB.2×3×4C.41x 3yD.52x10.下列代数式中整式有( )x1, 2x +y ,31a 2b ,πyx -,xy 45, 0.5 , a A.4个 B.5个 C.6个D.7个11.下列整式中,单项式是( )A.3a +1B.2x -yC.0.1D.21+x12.下列各项式中,次数不是3的是( )A .xyz +1B .x 2+y +1C .x 2y -xy 2D .x 3-x 2+x -1 13.下列说法正确的是( ) A .x(x +a)是单项式 B .π12+x 不是整式 C .0是单项式 D .单项式-31x 2y 的系数是3114.在多项式x 3-xy 2+25中,最高次项是( )A .x 3B .x 3,xy 2C .x 3,-xy 2D .2515.在代数式yy y n x y x 1),12(31,8)1(7,4322++++中,多项式的个数是( )A .1B .2C .3D .416.单项式-232xy 的系数与次数分别是( ) A .-3,3B .-21,3 C .-23,2 D .-23,317.下列说法正确的是( )A .x 的指数是0B .x 的系数是0C .-10是一次单项式D .-10是单项式 18.已知:32y x m -与n xy 5是同类项,则代数式n m 2-的值是( )A 、6-B 、5-C 、2-D 、5 19.系数为-21且只含有x 、y 的二次单项式,可以写出( ) A .1个B .2个C .3个D .4个20.多项式212x y -+的次数是( )A 、1B 、 2C 、-1D 、-221.下列说法中,正确的是…………………………………………………………( ) A .22x y 的系数是2; B .32x 的系数是3;C .多项式23x y -+的系数为3;D .32x 的系数是2.22.下列多项式中是二次三项式的是………………………………………( ). (A )3x xy y +-; (B )23x ; (C )23x y +-; (D )231x y y --. 23.x 与y 的和的倒数,可以用代数式表示为………………………………( ). (A )11x y+; (B )1x y+; (C )1y x+; (D )1x y+.24.字母表达式223y x -的意义为…………………………………………( )A. x 与3y 的平方差B. x 的平方减3的差乘以y 的平方C. x 与3y 的差的平方D. x 的平方与y 的平方的3倍的差 25.下列代数式中的整式的个数为……………………………………( )3x y z-+,4xy ,1a,22m n,21x x x ++,0,212x x -,m ,52.0110-⨯(A) 9 (B) 8 (C) 7 (D) 626.某品牌电脑降价%15后,每台售价a 元,则这种电脑的原价为每台( )。
(A )a 85.0元;(B )a 15.0元;(C )15.0a 元;(D )85.0a元二、填空题1.当a =-1时,34a = ; 2.单项式: 3234y x -的系数是 ,次数是 ;3.多项式:y y x xy x +-+3223534是 次 项式;4.220053xy 是 次单项式;5.y x 342-的一次项系数是 ,常数项是 ;6._____和_____统称整式. 7.单项式21xy 2z 是_____次单项式.8.多项式a 2-21ab 2-b 2有_____项,其中-21ab 2的次数是 . 9.整式①21,②3x -y 2,③23x 2y ,④a ,⑤πx +21y ,⑥522a π,⑦x +1中,单项式有 ,多项式有10.x+2xy +y 是 次 项式. 11.42234263y y x y x x --+-的次数是 ; 12.当x =2,y =-1时,代数式||||x xy -的值是 ; 13.当t = 时,31t t +-的值等于1;14.当y = 时,代数式3y -2与43+y 的值相等;15.-23ab 的系数是 ,次数是 次. 16.在x 2,21 (x +y),π1,-3中,单项式是 ,多项式是 ,整式是 .17.单项式7532c ab 的系数是____________,次数是____________.18.多项式x 2y +xy -xy 2-53中的三次项是____________. 19.当a=____________时,整式x 2+a -1是单项式. 20.多项式xy -1是____________次____________项式. 21.当x =-3时,多项式-x 3+x 2-1的值等于____________.22.如果整式(m -2n)x 2y m+n-5是关于x 和y 的五次单项式,则m+n23.系数是-3,且只含有字母x 和y 的四次单项式共有 个,分别是. 24.指出下列各式中哪些是单项式,哪些是多项式,哪些是整式?22222112,,,10,61,,,25,37a b x y x xy m n x x x x x++-+--+单项式:_____________________________ 多项式:_____________________________ 整式:________________________________ 25.已知单项式632211037a x y x yπ+--与的次数相同,则a=___________.26.若(k-5)x |k-2|y 3是关于x 、y 的6次单项式,则k 的值是__________. 27.如果多项式2221m a b x π-+-是一个四次三项式,那么m=_________ . 28.如果2x n +(m-1)x+1是关于x 的三次二项式,则n=_____,m=______. 29.多项式223431723x y x y x y-+--+是______次______项式,最高次项是_____________.30.如果2|3|(24)0y x -+-=,那么2x y -的值是____________________. 31.将代数式2322431111,,,,20,,,5,372222a am n xy a x m n y kx----+-+中是单项式的是___________________________________,是多项式的是_________________________. 32. 多项式32(1)n m a a --++是关于a 的三次二项式,则m=_______,n=_________. 33.已知,a b 表示的数在数轴上如图,那么||2||a b a b --++=___________34.用代数式表示:x 的一半与y 的平方的差 ;35.当2-=a 时,代数式2)1(2+a a 的值等于 ;36.请你写出一个只含字母a 和b ,系数为3-且次数为4的单项式 ;37.将多项式按x 的降幂排列=-+-x x x 13242 ; 38.一个正方形的边长是4a -,用含有a 的式子表示它的面积为 . 39.多项式2233243x y xy x y --+++按x 降幂排列得到 . 40.多项式43622+-a a的常数项是 .41.多项式2234a a -+是a 的 次 项式.45.把多项式2233324xy x y y x --+按字母y 的降幂排列是: .46.单项式45x y -的次数是 .47.将多项式332364xy x x y ++-按字母x 降幂排列是___________________________. 48.若代数式同时满足条件:①含字母a 、b ;②含有关于字母a 、b 的加、减、乘和乘方运算;③当3,1=-=b a 时,该代数式的值为7-.请写出一个这样的代数式 .49.已知:4a b +=,2ab =,求代数式22a b ab +的值=50.当2a =,12b =时,代数式2ab 的值是 .51.单项式3x -的系数是 .52.多项式225a a -+中的一次项是 .53.把多项式223321xy x y x -+-按字母x 的降幂排列: . 54.代数式3322a b a b+1-34是几次几项式?______ ______,三次项是__ ___。
