《弹性波动力学》第二章第四次作业评析 111023
《弹性力学》第十一章 弹性波

15
由于 e 0 ,故不计体力的运动微分方程,简化后得等
容波的波动方程:
2u 2 2 c u 2 2 t
2 2 2 c 2 2 t
2w 2 2 c w 2 2 t
E 其中 c2 2(1 )
v E
得
30
v钢 5130 m / s , v混凝土 3500 m/ s
31
c2 就是等容波在无限大弹性体中的传播速度。
16
对于无旋波和等容波,我们不加证明地给出如下结论:
在弹性体中,形变、应力以及质点速度,都将和位移以相
同的方式与速度进行传播。
17
§11-3 纵波与横波
一、纵波 [定义] 弹性体的质点运动方向平行弹性波的传播方向(图示)
纵波的传播形式
18
将x轴取为波的传播方向,则弹性体内任取一点的位 移分量都有:
11
[证]:在弹性体的任一点处,该点对z 轴的旋转量
u z x y u 将 代入,可得: y x
z 0
同理
x 0
y 0
即弹性体的任一点对三个坐标的旋转量都等于零。 [得证]
12
在无旋位移状态下
u w e 2 x y z
然后介绍弹性波的几个概念,针对不同的弹性波,对运 动微分方程进行简化,最后给出波在无限大弹性体中传 播速度公式。
3
§11-1 弹性体的运动微分方程
本章仍然采用如下假设:
(1) 弹性体为理想弹性体。 (2) 假定位移和形变都是微小的。
上述两条假设,完全等同于讨论静力问题的基本假 设。因此,在静力问题中给出的物理方程和几何方程, 以及把应力分量用位移分量表示的弹性方程,仍然适用
[工学]08无限弹性介质中的弹性波
![[工学]08无限弹性介质中的弹性波](https://img.taocdn.com/s3/m/352670da4b73f242326c5f48.png)
VS
x t
33
4
振动在空间的传播过程称为波动,简称为波。
在弹性动力学中,把所研究的弹性体称为弹性介质。当外力 很小且作用时间很短时,自然界大部分固体都可以近似地看成为 理想弹性介质。
实践证明:弹性介质受到外力作用时,并非在弹性介质的所 有各部分都立即引起位移、应变和应力,而是在作用开始时,距 离外力作用处较远的部分保持不受干扰。
df1(x Vpt) (x Vpt) d
d (x Vpt) x
d
f1( )
x Vpt
28
其余的应变分量都等于零,说明弹性介质的每一个点都 始终处于方向的简单拉压状态。
由物理方程求应力分量:
x
t
2 x
(
2) x
(1
E(1 )(1
)
2
)
x
y
t
2 y
x
E (1 )(1
2) x
z
t
2w t 2
(
)
t
z
2w
Z
32
2w t 2
2w x2
VS 2
2w x2
VS 2
此为平面横波的波动方程。
解此偏微分方程;(二阶线形偏微分方程),其通解为:
w w1 w2 f1(x VSt) f2 (x VSt)
w1 f1(x VSt) 表示一个沿x方向传播的横波。
它的传播速度就是
• 变形物体受突加载荷作用后,将产生变形。这种变 形和与之伴随而生的应力并不能立即传递到物体的 其它部分。在开始时刻,物体的变形仅仅在加载区 域的临近区域产生,而这个邻域以外的部分则仍处 于未扰动状态。其后,物体的变形和应力便以波的 形式向远处传播。
罗益民大学物理答案第二章

2.第二章 质点动力学2-1 (1)对木箱,由牛顿第二定律,在木箱将要被推动的情况下如图所示,x 向:0cos max min =-f F θ y 向:0sin min =--Mg F N θ 还有 N f s max μ=解以上三式可得要推动木箱所需力F 的最小值为θμθμsin cos s s min -=MgF在木箱做匀速运动情况下,如上类似分析可得所需力F 的大小为θμθμsin cos k k min -=MgF(2)在上面min F 的表示式中,如果0sin cos s →-θμθ,则∞→min F ,这意味着用任何有限大小的力都不可能推动木箱,不能推动木箱的条件是0sin cos s ≤-θμθ由此得θ的最小值为s1arctan μθ=2-2 (1)对小球,由牛顿第二定律x 向:ma N T =-θθsin cosy 向:0cos sin =-+mg N T θθ 联立解此二式,可得N)(32.3)30sin 8.930cos 2(5.0)sin cos (=︒+︒⨯⨯=+=ααg a m T N)(74.3)30sin 230cos 8.9(5.0)sin cos (=︒-︒⨯⨯=+=ααa g m N由牛顿第三定律,小球对斜面的压力N)(74.3=='N N(2)小球刚要脱离斜面时N =0,则上面牛顿第二定律方程为mg T ma T ==θθsin ,cos习题2-1图习题2-2图由此二式可解得2m/s 0.1730tan /8.9tan /=︒==θg a2-3 要使物体A 与小车间无相对滑动,三物体必有同一加速度a ,且挂吊B 的绳应向后倾斜。
作此时的隔离体受力图如图所示三物体只有水平方向的运动,只须列出水平方向的牛顿方程及相关方程:)4(:)3(0cos )2(sin :)1(:322211MaN F M g m T a m T m am T m =-⎩⎨⎧=-==水平αα水平3N 为绳中的雨拉力在水平向的合力)5(sin 3αT T N +=水平联立(1),(2),(3),(4),(5)解得)N (78480)(2221212==-++=g m m g m m m m F(因为三个物体有同一加速度a ,且在水平方向只受外力F 的作同,所以,可将三个物体看作一个物体:a M m m F )(21++=再与(1),(2),(3)式联立求解即可。
《固体物理学》房晓勇-思考题02第二章 晶体的结合和弹性

第二章 晶体的结合和弹性2.1 是否有库仑力无关的晶体结合类型?解答:(参考王矜奉2.1.1,中南大学2.1.1)共价结合中,电子虽然不能脱离电负性大的原子,但靠近的两个电负性大的原子可以各出一个电子,形成电子共享的形式,即这一对电子的主要活动范围处于两个原子之间,通过库仑力,把两个原子连接起来。
离子晶体中,正离子与负离子的吸引力就是库仑力。
金属结合中,原子实依靠原子实与电子云之间的库仑力紧紧地吸引着。
分子结合中,是电偶极矩把原本分离的原子结合成了晶体。
电偶极矩的作用力实际就是库仑力。
氢键结合中,氢先与电负性大的原子形成共价结合后,氢核与负电中心不在重合,迫使它通过库仑力再与另一个电负性大的原子结合。
可见,所有晶体结合类型都与库仑力有关。
2.2 如何理解库仑力是原子结合的动力?解答:(参考王矜奉2.1.2,中南大学2.1.2)晶体结合中, 原子间的排斥力是短程力, 在原子吸引靠近的过程中, 把原本分离的原子拉近的动力只能是长程力, 这个长程吸引力就是库仑力. 所以, 库仑力是原子结合的动力.2.3 为什么组成晶体的粒子(分子、原子或离子)间的相互作用力除吸引力还要有排斥力?排斥力的来源是什么?解答:(参考王矜奉2.1.4,中南大学2.1.4)邻的原子靠得很近, 以至于它们内层闭合壳层的电子云发生重叠时, 相邻的原子间便产生巨大排斥力. 也就是说, 原子间的排斥作用来自相邻原子内层闭合壳层电子云的重叠.2.4 晶体的结合能、内能、以及原子间的相互作用势能有何区别?解答:(参考王矜奉2.1.3,中南大学2.1.3)自由粒子结合成晶体过程中释放出的能量, 或者把晶体拆散成一个个自由粒子所需要的能量, 称为晶体的结合能.原子的动能与原子间的相互作用势能之和为晶体的内能.在0K 时, 原子还存在零点振动能. 但零点振动能与原子间的相互作用势能的绝对值相比小得多. 所以, 在0K 时原子间的相互作用势能的绝对值近似等于晶体的结合能.2.5 试述范德瓦耳斯力的起源和特点。
《弹性波动力学》习题

第二层 介质
h
界面3
图 4.21 (a)
图 4.21(b)
3
6) 7)
2
忽略体力作用,试推导弹性细杆中的一维波动方程。 设均匀弹性固体中声标势为φ,声矢势只存在 y 方向分量ψ y ,所有的量与 y 无关, 试用φ和 ψ y 表示虎克 定律(即把各应力用φ和 ψ y 的导数表示出来).
8) 试叙述固体中弹性波波动方程建立的思路。 9) 试分析声波在多层介质中反射和透射时影响反射系数和透射系数的各种可能因素。 10) 试分析声波传播过程中引起声波幅度变化的各种可能原因。
P θi θ r I ΙΙຫໍສະໝຸດ P z θ tT θ tL S
P
x
图 4.12
x
θ tl P 流体 固体 P θ i θ rt θ rl
图 4.18
z
S
P
o
1.0 0.8 0.6 Amplitude 0.4 0.2
界面1
VP = 2500m / s 第一层介质
1000m
界面2
0.0 -0.2 0.00
VP = 3000m / s
按关系式设均匀弹性固体中声标势为声矢势只存在y方向分量所有的量与y无关试用和表示虎克定律即把各应力用和试分析声波在多层介质中反射和透射时影响反射系数和透射系数的各种可能因素
《弹性波动力学》习题
―――标记*者为选作,其它为必作――― 第一章机械振动
1) *试证明,当单质点系统发生速度共振时,简谐力在一个周期内对系统所做的功最大. 2) *有一质点振动系统,被外力所策动,试证明当系统发生速度共振时, 系统每周期的损耗能量与总的振动能 量之比等于
运动弹性机构动力学分析v2012-2013-11-12

弹性机构动力学分析方法(运动弹性机械动力学)第一章 概论1.1 弹性机构动力学的产生与发展亦称:运动弹性机构动力学/ 机械弹性动力学1.1.1机械动力学分析的两类问题1) 逆动力学 已知机构运动状态和阻力,求解主动力(输入扭矩)和各运动副反力及变化规律。
2) 正动力学 给定输入扭矩和工作阻力变化规律,求运动。
1.1.2机械动力学的不同分析方法不同水平的四种方法[1,4]1) 静力分析(Static Analysis) 忽略惯性力,用静力学方法分析力和运动副中的反作用力,适用于低速机械。
2) 动态静力分析(Kineto-static Analysis) 达朗贝尔原理方法又称动静法。
先进行运动分析,求出惯性力,再加惯性力计入静力平衡方程,求反作用力。
运动分析时,假定理想化的“驱动构件等速回转”或按某一理想运动规律运动。
3) 动力分析(Dynamic Analysis) 不用理想化的“驱动构件等速回转”假定,求解外力作用下机械的真实运动,也称为机械系统动力学。
4) 弹性动力学(Elasto-dynamic Analysis) 抛弃以上将构件视为刚性体的假定,计入构件弹性动力学分析方法。
●动力学分析方法的发展趋势不考虑惯性(静力学分析)→考虑惯性(动力学分析)→不考虑变形(刚体动力学分析)→考虑变形(柔性/弹性动力学分析,KES,KED,Multibody Dynsmic Analysis)简化的动力学分析方法(线性假设,简化模型,KED)→更精确的动力学分析方法(考虑更多非线性项,更准确的模型,Multibody Dynsmic Analysis)1.1.3运动弹性机构动力学的发展背景●高速化>>> 惯性力变大●精密化>>> 要求误差小、变形小●轻量化>>> 弹性变形变大●大型化(大功率)1.1.4运动弹性机构动力学的发展历史简介1)高速转轴的振动——转子动力学。
(完整word版)弹性力学简明教程(第四版)_第二章_课后作业题答案
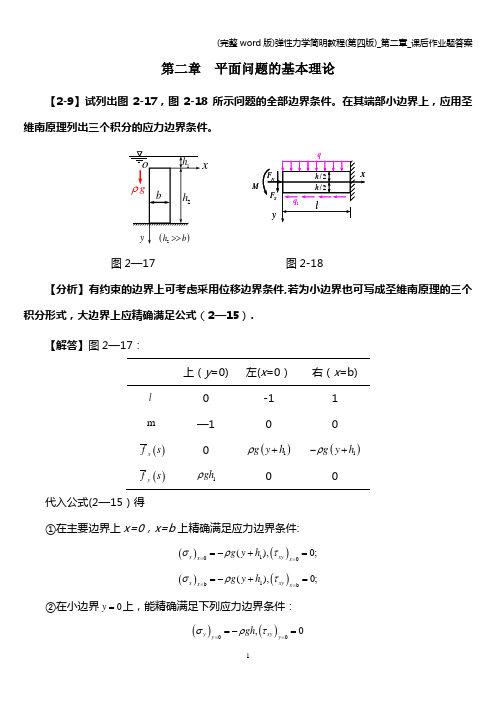
第二章 平面问题的基本理论【2-9】试列出图2-17,图2-18所示问题的全部边界条件。
在其端部小边界上,应用圣维南原理列出三个积分的应力边界条件。
xM图2—17图2-18【分析】有约束的边界上可考虑采用位移边界条件,若为小边界也可写成圣维南原理的三个积分形式,大边界上应精确满足公式(2—15).【解答】图2—17:上(y =0)左(x =0)右(x =b)l 0 -1 1 m—1() x f s0 ()1g y h ρ+()1g y h ρ-+() yfs 1gh ρ代入公式(2—15)得①在主要边界上x=0,x=b 上精确满足应力边界条件:()()100(),0;===-+=x xy x x g y h σρτ ()()1b b (),0;===-+=x xy x x g y h σρτ②在小边界0y =上,能精确满足下列应力边界条件:()(),0yxy y y gh σρτ===-=③在小边界2y h =上,能精确满足下列位移边界条件:()()220,0====y hy h u v这两个位移边界条件可以应用圣维南原理,改用三个积分的应力边界条件来代替,当板厚=1δ时,可求得固定端约束反力分别为:10,,0s N F F ghb M ρ==-=由于2y h =为正面,故应力分量与面力分量同号,则有:()()()222100000b y y h by y h bxy y h dx gh b xdx dx σρστ===⎧=-⎪⎪⎪=⎨⎪⎪=⎪⎩⎰⎰⎰ ⑵图2-18①上下主要边界y=-h/2,y=h/2上,应精确满足公式(2—15)lmx f (s )y f (s ) 2h y =-0 —1 0 q2h y =1-1q-/2()y y h q σ==-,-/2()0yx y h τ==,/2()0y y h σ==,/21()yx y h q τ==-②在x =0的小边界上,应用圣维南原理,列出三个积分的应力边界条件:负面上应力与面力符号相反,有/20/2/20/2/20/2()()()h xy x Sh h x x N h h x x h dx Fdx F ydx M τσσ=-=-=-⎧=-⎪⎪=-⎨⎪⎪=-⎩⎰⎰⎰③在x=l 的小边界上,可应用位移边界条件0,0====l x l x v u 这两个位移边界条件也可改用三个积分的应力边界条件来代替。
弹性力学(10)讲义版

r r r u = u1 + u 2
没有转动的位移 (无旋 没有体积变化的位移 (等体 r r r r r 的)∇ × u 1 = 0 , u 1 = ∇ Φ 的)θ = ∇ g u 2 = 0 , u 2 = ∇ × Ψ
r r u = ∇Φ + ∇ × Ψ
位移矢量的Stokes分解式
一、无限弹性介质中的无旋波
•当两波通过之后, 又恢复初始的形状 (拉)σ 和大小继续传播。 质点速度v
σ (拉
n
质点速度v
讨论 Ø入射的应力波 经固定端反射得 到同号的应
力波, 固定端处的应力将加 倍。
波速c (拉)σ 质点速度v 波速c (拉)σ 质点速度v n n m m •在两波相遇的整 个期间,中间 截 面mn处的位移及 速度始终为零。 •这种波的 传播及 叠加过程相当于 应力波在固定端 反射的情况。 •入射的应力波 经 固定端反射得 到 同号的应力波, 固定端处的应力 将加倍。 波速c σ (拉) 质点速度v 波速c σ (拉) 质点速度v
质点速度v缩波在自由端反射成 拉伸波,拉伸波反射
•在两波相遇的整 个期间,中间 截 质点速度v 面mn处的应力始 终为零。 (压)σ •这种波的 传播及 波速c 叠加过程相当于 应力波在自由端 波速c 反射的情况。 (拉)σ •压缩波在自由端 反射成拉伸波, 质点速度v 拉伸波反射成压 缩波,自由端截 面处的质点速度 加倍。 m 波速c σ (拉) 质点速度v
&
波动方程的 达朗伯解
函数f与g由边界条件 和初始条件确定 。
解的物理意义:考虑f (x-ct) 这一部分。 Ø取以速度 c沿x正方向移动的 坐标轴 η,η=x- ct ; Ø f (x-ct) = f (η) ,在动坐标系中, 函数值只取决于 坐标η,而与时间 t无关,即函数的图形相对于动坐标 系保持不变; Øf (x-ct)表示一个以速度 c沿x正方向移动 且保持其形 状及大 小不变的行波。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0~2kHz , f max = 2000 Hz , 根 据
可 以 算 出 , f10 = 860 ( Hz ) , f 01 = 1720 ( Hz ) ,
f11 = 1923 ( Hz ) , f 20 = 1720 ( Hz ) 因此,当声源的频率范围为 0~2kHz 时,波导管中存在主波、(1,0)波、(0,1) 波、(1,1)波和(2,0)波。 (4) (nx , n y ) 次的简正波的相速度和群速度的表达式分别为 相速度 cz = 1− c0 π c nx 2 n y 2 [( ) + ( ) ] ω lx ly
2
2
故只传播主波的条件为声源的频率低于 860Hz. (2) f 30 = 3 f10 = 3co 344 × 3 = = 2580 ( Hz ) 2lx 2 × 0.2
故声源的频率高于 2580Hz 时可以在此波导中传播(3,0)波. (3) 声 源 的 频 率 范 围 为 f nx ,ny c n n = o x + y 2 lx ly
相速度cz 群速度cg
Velocity(m/s)
1200 1000 800 600 400 200 0 0 2 4 6 8 10
(1,1)次波
(2,1)次波
Frequency(kHz)
点评:主要存在以下问题 (1) 注意区分 ω 和 w 的书写; (2) 计算截止频率时, 若 lx > l y ,则 f10 < f 01 ,所以 f c = f10 ;反之,则 f c = f 01 ; (3) 计算第三问时,应当按照一定顺序计算。 一、当给出的频率较小时,可以用枚举的方法求解: A. 设频率小于 f max 时,可以传播 (m, n) 次波; B. 首先令 m = 0 , n = 0,1, 2,... ,求出满足要求的最大 n 为止; C. 然后令 m = 1 , n = 0,1, 2,... ,重复 B 步骤;每算完一组 n ,将 m 加 1, 依次求出满足要求的最大 m , 则,以上求得的都是可以满足要求的波动 模式。 很多同学不按照顺序计算,导致求出的结果中会丢失一部分波动模式。 二、当给出的频率较小时,枚举的方法计算量过大,也可用直接求解的办 法: A .首先令 m = 0 , f c = f max ,可以 求 出 一个 nmax , 然后对 nmax 向 下 取整 N = floor (nmax ) ,则当 m = 0 时, n = 0,..., N 的模式可以传播, B.依次将 m 加 1,就可以求出所有的波动模式。 (4)绘制第(4)问图像时,要列出必要的公式、要说明坐标轴的名称和单位。
2 2 0 2 2 n π 2 c0 n [( x ) 2 + ( y )2 ] 2 ω lx ly
群速度 cg = c0 1 −
于是, 由上式可以得到(1,1)模式波和(2,1)模式波的相速度和群速度随频率变化的 曲线,如下图所示。
2000 1800 1600 1400
(1,1)次波
(2,1)次波
《弹性波动力学》第二章第四次作业评析 111023 作业:第二章(15) 应交作业 104 份,实际收到 97 份,其中 95 份为本次作业,缺交率 8.6%。
第二章流体中的声传播规律
15) 已知刚性壁矩形波导管内充满空气,其两个边长分别为 lx = 0.2m 和 l y = 0.1m , 若在其中(1)只传播主波(2)传播(3,0 0~2kHz,则可在此波导管中激发起哪些模式波?(4)试绘出(1,1)模式 波和(2,1)模式波的相速度和群速度随频率变化的曲线。 答案:矩形波导的简正频率的表达式为 f nx ,ny 由题意知: lx = 0.2m , l y = 0.1m (1) 由于 f c = f10 = co 344 = = 860 ( Hz ) 2lx 2 × 0.2 c n n = o x + y 2 lx ly
