第三章 拱桥计算
合集下载
第三章第三节拱桥计算2

平力大小相等,方向相反,即可抵消弹性压缩及混凝土收缩在拱顶拱脚产 生的弯矩值。
悬链线拱轴线与三铰拱压力线存在近似波形的自然偏离, 据此道理,三铰拱压力线基础上根据实际情况再叠加一个正弦 波形调整拱轴线,用逐次逼近法使弹压砼收缩产生的不利弯矩 为最小。
九、考虑几何非线性的拱桥计算简介
➢ 在线弹性条件下,一般拱桥内力与变形计算结果 和实际不会产生太大误差,随着拱桥跨度增大, 这种由于非线性引起的误差会增大;
(1)假载法调整内力 (2)用临时铰调整内力 (3)改变拱轴线调整内力
(1)假载法调整内力
所谓假载法调整内力,就是在计算跨径、 计算矢高和拱圈厚度保持不变的情况下,通 过改变拱轴系数的数值来改变拱轴线形状, m调整幅度一般为半级或一级。
( y1/4 相差0.01为一级) f
(1)假载法调整内力
实腹拱的内力调整
八、主拱内力调整
• 悬链线无铰拱在最不利荷载组合时,常常 出现拱脚负弯矩或拱顶正弯矩过大的情况, 为了减小它们,可从设计、施工方面采取 措施调整拱圈内力。
(1)假载法调整内力 (2)用临时铰调整内力 (3)改变拱轴线调整内力
八、主拱内力调整
• 悬链线无铰拱在最不利荷载组合时,常常 出现拱脚负弯矩或拱顶正弯矩过大的情况, 为了减小它们,可从设计、施工方面采取 措施调整拱圈内力。
三、拱桥内力计算
(一)手算法计算拱桥内力 1、等截面悬链线拱恒载内力计算 2、等截面悬链线拱活载内力计算 3、等截面悬链线拱其它内力计算
(二)有限元法计算简介 (三)拱在横向力及偏心荷载作用下的计算 (四)拱上建筑计算 (五)内力调整 (六)考虑几何非线性的拱桥计算简介
四、拱在横向水平力及偏心荷载作用下的计算
• 调整前:
悬链线拱轴线与三铰拱压力线存在近似波形的自然偏离, 据此道理,三铰拱压力线基础上根据实际情况再叠加一个正弦 波形调整拱轴线,用逐次逼近法使弹压砼收缩产生的不利弯矩 为最小。
九、考虑几何非线性的拱桥计算简介
➢ 在线弹性条件下,一般拱桥内力与变形计算结果 和实际不会产生太大误差,随着拱桥跨度增大, 这种由于非线性引起的误差会增大;
(1)假载法调整内力 (2)用临时铰调整内力 (3)改变拱轴线调整内力
(1)假载法调整内力
所谓假载法调整内力,就是在计算跨径、 计算矢高和拱圈厚度保持不变的情况下,通 过改变拱轴系数的数值来改变拱轴线形状, m调整幅度一般为半级或一级。
( y1/4 相差0.01为一级) f
(1)假载法调整内力
实腹拱的内力调整
八、主拱内力调整
• 悬链线无铰拱在最不利荷载组合时,常常 出现拱脚负弯矩或拱顶正弯矩过大的情况, 为了减小它们,可从设计、施工方面采取 措施调整拱圈内力。
(1)假载法调整内力 (2)用临时铰调整内力 (3)改变拱轴线调整内力
八、主拱内力调整
• 悬链线无铰拱在最不利荷载组合时,常常 出现拱脚负弯矩或拱顶正弯矩过大的情况, 为了减小它们,可从设计、施工方面采取 措施调整拱圈内力。
三、拱桥内力计算
(一)手算法计算拱桥内力 1、等截面悬链线拱恒载内力计算 2、等截面悬链线拱活载内力计算 3、等截面悬链线拱其它内力计算
(二)有限元法计算简介 (三)拱在横向力及偏心荷载作用下的计算 (四)拱上建筑计算 (五)内力调整 (六)考虑几何非线性的拱桥计算简介
四、拱在横向水平力及偏心荷载作用下的计算
• 调整前:
结构力学第三章静定结构组合结构及拱

0 FNJ 右 FQJ 右 sin FH cos (7.5) (0.447) 10 0.894
3.35 8.94 12.29kN (压)
二、三较拱的压力线
如果三铰拱某截面D以左(或以右)所有外力的 合力FRD已经确定,则该截面的弯矩、剪力、轴 力可按下式计算:
15kN K右
Fº =-2.5kN QK右
0 0 (FH 10kN , FQK左 12.5kN , FQK右 2.5kN )
(sin 0.447, cos 0.894)
0 FQK 左 FQK 左 cos FH sin 12.5 0.894 10 0.447
67.5kN
50
A F C G E
B
30
D
M图
kN.m
求AC杆和BC杆剪力
F
FQAC
y
0, FQAC 7.5kN
22.5kN 7.5 32.5 10kN/m FNAD
FAy
+ _
15
+
7.15 67.5kN 35 FQ图 kN
作业
3-20
§3-6 三铰拱受力分析
拱 (arch)
FN DE 135kN ,
FNDF FN EG =-67.5kN
FAy
D
FCx 135kN , FCy 15kN
FNDA
FNDF
D
FN DA FN EB= kN 151
FNDE
2m
F
50kN.m
求AC杆和BC杆弯矩
22.5kN 5kN.m
20kN.m 10kN/m
30kN.m
MD FRD
3.35 8.94 12.29kN (压)
二、三较拱的压力线
如果三铰拱某截面D以左(或以右)所有外力的 合力FRD已经确定,则该截面的弯矩、剪力、轴 力可按下式计算:
15kN K右
Fº =-2.5kN QK右
0 0 (FH 10kN , FQK左 12.5kN , FQK右 2.5kN )
(sin 0.447, cos 0.894)
0 FQK 左 FQK 左 cos FH sin 12.5 0.894 10 0.447
67.5kN
50
A F C G E
B
30
D
M图
kN.m
求AC杆和BC杆剪力
F
FQAC
y
0, FQAC 7.5kN
22.5kN 7.5 32.5 10kN/m FNAD
FAy
+ _
15
+
7.15 67.5kN 35 FQ图 kN
作业
3-20
§3-6 三铰拱受力分析
拱 (arch)
FN DE 135kN ,
FNDF FN EG =-67.5kN
FAy
D
FCx 135kN , FCy 15kN
FNDA
FNDF
D
FN DA FN EB= kN 151
FNDE
2m
F
50kN.m
求AC杆和BC杆弯矩
22.5kN 5kN.m
20kN.m 10kN/m
30kN.m
MD FRD
第三章第三~七节 整体型拱桥计算

➢(4)对于变截面拱,一般拱肋截面惯性矩变化
规律取
Id为拱肋顶部的惯性矩
整理版ppt
34
六、拱式组合体系桥梁计算
1、拱式组合体系桥梁的受力特点与计算模式
(2)刚性系杆柔性拱
➢刚性系杆柔性拱组合体系中, 拱
的推力传给刚性系杆承受,属 外部
静定体系。
➢拱肋与系杆的刚 度比相对小很多,
形成刚性的系 杆和纤细的拱肋。因
第四节 中下承式拱桥计算
第五节 钢管混凝土拱桥计算
第六节 拱式组合体系拱桥计算
第七节整理版墩ppt 台计算
19
五、钢管混凝土拱桥计算
1、设计理论概述
➢采用它作为主拱承压用的结构材料。它既可以被 应用到上承式拱桥上,但比较多地被用在中、下 承式地拱桥上。 ➢钢管混凝土拱桥内力计算与施工过程密切相关。 ➢钢管混凝土作为一种钢-混凝土组合材料,一般 采用叠加法(合成法)确定钢管混凝土的基本性能。 ➢我国应用钢管混凝土拱桥全是超静定结构,对于 温度变化、混凝土收缩和徐变产生的次内力尚缺 乏系统的试验和理论研究。
整理版ppt
22
五、钢管混凝土拱桥计算
2、主拱承载力及变形影响因素分析
➢钢管混凝土拱桥采用自架设施工方法,主拱圈逐 步形成,强度验算有应力叠加法和内力叠加法两 种。在施工 过程中,采用应力叠加法验算钢拱架 的强度与稳定性,并用容许应力法进行验算。当 管内混凝土达到设计强度后,采用内力叠加法计 算内力,并采用极限状态法。 ➢对于钢管混凝土构件,混凝土的裂缝开展受到钢 管 的约束而较迟出现且不发育,弹、塑性性能均 强于钢筋混凝土结构,而且其含筋率较高,因此 可以不考虑折减。
整理版ppt
3
三、桁架拱的计算要点
第三章第三~七节 整体型拱桥计算 ppt课件

11
第一节 概述
第二节 普通型拱桥计算
第三节 整体型拱桥计算
第四节 中下承式拱桥计算
第五节 钢管混凝土拱桥计算
第六节 拱式组合体系拱桥计算
2020/10/28
第七节 墩台计算
12
四、中、下承式钢筋混凝土拱桥计算
中、下承式钢筋混凝土拱桥计算的主要内容有:
➢主拱内力计算及截面强度验算; ➢主拱纵、横向稳定性验算; ➢吊杆计算; ➢桥面系计算等。
(二)刚架拱
刚架拱一般采用电算,无条件时也可采用手算法, 计算图式可简化为一次超静定的两铰拱,但拱轴线 并非光滑。仍以拱脚水平推力为赘余力计算。
2020/10/28
10
三、刚架拱的计算要点
(二)刚架拱
2、结构计算
刚架拱:属高次超静定结构,各构件均为压弯构 件,用有限元法计算内力。
2020/10/28
16
四、中、下承式钢筋混凝土拱桥计算
2、拱肋横向稳定性验算 ➢刚性吊杆铰支承失稳的拱肋临界力为:
2020/10/28
17
四、中、下承式钢筋混凝土拱桥计算
3、吊杆计算
➢通常分为柔性吊杆和刚性吊杆。
➢柔性吊杆只承受轴向拉力,而不承受弯矩,按轴 向受拉构件计算;刚性吊杆与拱肋及横梁的联结
一般是刚性联结,吊杆兼受轴力和和弯矩,故按
2020/10/28
15
四、中、下承式钢筋混凝土拱桥计算
2、拱肋横向稳定性验算
➢对无风撑的中下承式拱桥需要考虑吊杆拉力的 非保向力效应;
➢假定吊杆是不可拉伸
但无拉弯刚度的受拉构
件,吊杆将以其张力的
水 平分力施加到拱肋上,
从 而增强了拱肋的侧向
稳定 性,这个效应被称
第4篇第3章 拱桥的计算
5
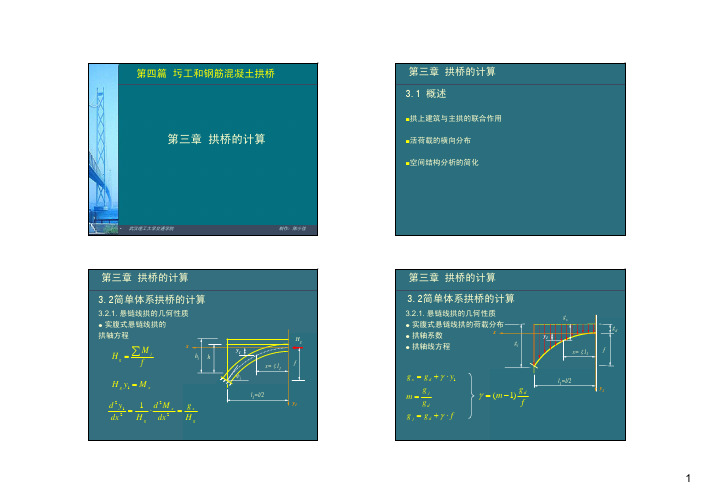
第三章 拱桥的计算 3.3 恒载作用下拱的内力计算
3.3.2. 考虑弹性压缩引起的内力 在恒载产生的压力作用下,拱沿轴线方向会产生弹性压 缩。由此将在超静定结构上产生内力。水平赘余力为:
第三章 拱桥的计算 3.3 恒载作用下拱的内力计算
3.3.3.恒载作用下拱圈各截面的总内力 符号规定
x
φj
Q N M
g x = g d + γ ⋅ y1
y1
m=
gj gd
g γ = (m − 1) d f
l1=l/2
y1
g j = gd + γ ⋅ f
1
第三章 拱桥的计算 3.2简单体系拱桥的计算
3.2.1. 悬链线拱的几何性质 z 实腹式悬链线拱的荷载分布 x z 拱轴系数 z 拱轴线方程
gx y1 x=ξl1 f gd
s
弹性中心
y1
第三章 拱桥的计算 3.3 恒载作用下拱的内力计算
3.3.1. 不考虑弹性压缩的恒载内力 实腹式悬链线拱的恒载内力
第三章 拱桥的计算 3.3 恒载作用下拱的内力计算
3.3.1. 不考虑弹性压缩的恒载内力 空腹式悬链线无铰拱的恒载内力: 直接根据静力平衡条 件写出:
g l2 H g = kg d f
( H g + ∆X 2 ) sin ϕ ± ∆X 2 sin ϕ
6
第三章 拱桥的计算 3.3 恒载作用下拱的内力计算
3.3.4. 计算实例
如图所示无铰拱, 计算跨径l=80m,主拱圈及拱上建筑恒载见图,主 拱圈截面面积A=5.0m2,截面惯性矩I=1.0m4,容重γ=25kN/m3 。试应用 “五点重合法”,
②
确定拱桥拱轴系数m 计算
第三节拱桥计算

(1)不考虑弹性压缩旳恒载内力--实腹式拱
以为实腹式拱轴线与压力线完全重叠,拱圈
中只有轴力而无弯矩,按纯压拱计算:
恒载水平推力: H g
m 1 4k 2
gdl2 f
kg
gdl2 f
(0.128 ~ 0.18)
gdl2 f
拱脚竖向反力为半拱恒载重力:
Vg
l1 0
g x dx
m2 2 ln(m
3、活载横向分布:活载作用在桥面上使主拱 截面应力不均匀旳现象。在板拱情况下经常 不计荷载横向分布,以为主拱圈全宽均匀承 担荷载。 4、计算措施:手算和程序计算。
第三节 拱桥计算
一、拱轴线旳选择与拟定 二、拟定拱轴系数 三、主拱圈弹性中心及弹性压缩系数计算 四、主拱圈截面内力计算 五、主拱圈正截面强度验算 六、主拱圈稳定性验算 七、主拱圈裸拱强度和稳定性验算 八、主拱圈应力调整
第三节 拱桥计算 一、拱轴线旳选择与拟定 二、拟定拱轴系数 三、主拱圈弹性中心及弹性压缩系数计算 四、主拱圈截面内力计算 五、主拱圈正截面强度验算 六、主拱圈稳定性验算 七、主拱圈裸拱强度和稳定性验算 八、主拱圈应力调整
2.3.3 主拱圈弹性中心及弹性压缩系数计算
1 悬链线无铰拱旳弹性中心
采用恒载压力线作为拱轴线,在恒载作用下不 考虑拱圈变形旳影响时,拱圈各截面均只有轴向压 力,此时拱圈处于纯压状态。但是拱圈材料有弹性, 它在恒载产生旳轴向压力作用下会产生弹性压缩, 使拱轴长度缩短,这种现象称为拱旳弹性压缩。因 为无铰拱是超静定构造,弹性压缩引起拱轴旳缩短, 会在拱中产生内力,在设计中为了计算以便将恒载 压力分为两个部分,即:不考虑弹性压缩引起旳内 力与弹性压缩引起旳内力。两者相加,得到恒载作 用下旳总内力。
拱桥的计算

gd o
y1
第三章 拱桥的计算
3.1.2. 空腹式悬链线拱 五点重合法
三铰拱的情形
M A 0 H g
Mj f
M B 0 H g
Ml 4 yl 4
yl 4
Ml 4
f Mj
B
A l1=l/4
Δy l1=l/4
Hg y1/4
f
y1 4 f
1
2m 1 2
3.1.1. 实腹式悬链线拱 实腹式悬链线拱轴系数的确定
φj
φj
d
hj h d /cosφj
d /cosφj
r1 r2 r
hd
d
x=ξl1
f
φj
l1=l/2
第三章 拱桥的计算
3.1.1. 实腹式悬链线拱 拱轴系数与悬链线线 形的关系
m gj
gj
gd
y1 4 f
1
2m 1 2
x
yl 4
Ml 4
f Mj
2
m
1 2
f yl
4
2
1
第三章 拱桥的计算
3.1.2. 空腹式悬链线拱 五点重合法 三铰拱的实际压力线与按五点重合法 确定的悬链线的差异
Δy B
压力线与拱轴线偏离在拱中产生 附加内力
A l1=l/4
l1=l/4
A Mp=ΔyHg B
Hg y1/4
d 2M dx2
x
gd Hg
1 (m 1)
y1 f
x=ξl1 dx=l1dξl1
d 2 y1
d 2
l12 gd Hg
4-2拱桥设计计算

PDF 文件使用 "pdfFactory Pro" 试用版本创建
2、悬链线
n
(b)
实腹式拱桥的恒载集度,从拱顶向拱脚是均匀增加的,这种荷 载分布图式的拱圈的压力线是一条悬链线。因此,实腹式拱桥 采用悬链线作拱轴线,在恒载作用下,当不计拱圈由恒载弹性 压缩产生的影响时,拱圈截面将只承受中心压力而无弯矩。 对于空腹式拱桥,由于拱上建筑的形式发生了变化,恒载集度 从拱顶到拱脚不再是均匀增大的,相应的恒载压力线也不再是 悬链线,甚至也不是一条光滑的曲线。如仍用相应的悬链线作 拱轴线,恒载压力线与拱轴线将有偏离。但理论分析证明,这 种偏离对拱圈控制截面的内力是有利的。同时,用悬链线作拱 轴线,对各种空腹型式的拱上建筑的适应性较强,并且已有现 成的完备的计算图表可供利用,为了设计的方便起见,空腹式 拱桥也广泛采用悬链线作为拱轴线。因此,悬链线是目前我国 大、中跨径拱桥采用最普遍的拱轴线型。
PDF 文件使用 "pdfFactory Pro" 试用版本创建
n
事实上理想的拱轴线是不可能获得的,因为除恒载外,拱圈 还要受到活载、温度变化和材料弹塑性变形等因素的作用。 当拱轴线与恒载压力线吻合时,在活载作用下就不再吻合。 而且即便在恒载作用下,拱轴线也将因材料的弹性压缩而变 形,致使拱圈的实际压力线与设计所采用的拱轴线产生偏离。 因此在拱桥设计时,要选择一条能够使恒载作用下的截面弯 矩都为零的拱轴线,也是不可能的。尽管如此,对于拱桥还 有一个有利条件,即拱桥的恒载在全部荷载中所占的比重较 大,而活载所占的比重较小。以30m跨径的双车道公路拱桥为 例,活载大约只是恒载的20%,而且随着跨径的增大,恒载所 占的比重还将进一步增大。因此,一般情况下以恒载压力线 作为设计拱轴线,可以认为是适宜的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1-2-19)
将上式代入式(1-2-14),并引参数:
x l1
可得:
则:
dx l1d
d 2 y1 l12 g d y1 1 (m 1) f 2 d Hg l12 g d k (m 1) Hg f
2
令
(1-2-20)
则
d 2 y1 l12 g d k 2 y1 d 2 Hg
d)比较mi和mi+1,如两者相符,即假定的mi为真实值;如两者相差较大, 则以计算出的mi+1作为假设值,重新计算,直到两者相等
(2)空腹式拱拱轴系数的确定 空腹式拱桥中,桥跨结构的恒载由两部 分组成,即主拱圈承受由实腹段自重的分布 力和空腹部分通过腹孔墩传下的集中力(如 左图)。由于集中力的存在,拱的压力线为 在集中力作用点处有转折的曲线。但实际设 计拱桥时,由于悬链线的受力情况较好,故 多用悬链线作为拱轴线。 为了使悬链线与其恒载压力线重和, 一般采用“ 五点重和法”确定悬链线的m 值。即要求拱轴线在全拱(拱定、两1/4l点 和两拱脚)与其三铰拱的压力线重和。其 相应的拱轴系数确定如下
其中:y以弹性中心为原点(向上为正)的拱轴坐标。
拱顶、拱脚处:Mp=0 拱顶: M d X1 X 2 ys 0 拱脚: M j X1 X 2 ( f ys ) 0 其中,ys弹性中心至拱顶的距离。 (5)拱轴系数初值的选定
m gj gd
坦拱:m值选用较小 陡拱:m值选用较大
d 2 y1 1 d 2M gx 2 2 dx H g dx Hg
(1-1-14)
由上式可知,为了计算拱轴线(压力线)的一般方程,需首先知道恒载 的分布规律,对于实腹式拱,其任意截面的恒载可以用下式表示:
g x gd y1 gd
拱顶处恒载强度;
(1-2-15)
拱上材料的容重。
l12 g d k2 (m 1) Hg f
恒载水平推力Hg :利用上式有
(1-2-20)
l1 l / 2
gd l 2 m 1 gd l Hg kg 2 4k f f
2
(1-2-42)
其中:
kg
m 1 4k 2
(1-2-23)
k ch1m ln(m m2 1)
弯矩 Md=0
剪力Qd=0 恒载推力为Hg
对拱脚截面取矩,有:
Hg
M
f
(1-2-12)
M
半拱恒载对拱脚的弯矩。
对任意截面取矩,有:
Mx y1 Hg
y1以拱顶为原点,拱轴线上任意点的坐标;
(1-2-13)
M 任意截面以右的全部恒载对该截面的弯矩值。 对式(1-2-13)两边对x取两次导数,可得:
空腹式拱桥的恒载从拱顶到拱脚不再是连续分布的(如下图),其 恒载压力线是一条不光滑的曲线,难于用连续函数来表达。目前最 普遍的还是采用悬连线作为空腹拱的拱轴线,仅需拱轴线在拱顶、 跨径的四分之一点和拱脚初与压力线重合。
1、拱轴方程的建立(实腹拱压力线) 如下图所示,设拱轴线为恒载压力线,则拱顶截面的内力为:
dy1 fk shk d m 1 dy dy 2dy1 2 fkshk tg 1 1 shk dx l1d ld l (m 1)
其中
2kf l (m 1)
k可由式(1-2-23)计算
代=1,如上式,即可求得:
tg j shk
c)根据计算出的 j 计算出gj后,即可求得mi+1
拱脚的竖向反力:拱脚的竖向反力为半拱的恒载重力,即
Vg g x dx g xl1d
0 0
l1
1
代
y1 g x g d y1 g d 1 (m 1) f
Vg m2 1 2[ln(m m 1)]
2 ' gd l kg gd l
chk m
通常m为已知,则可以用下式计算k值:
k ch1m ln(m m2 1)
反双曲余弦函数对数表示
(1-2-23)
当m=1时 gx=gj,可以证明,在均布荷载作用下的压力线为二次抛 物线,其方程变为:
f 2 y1 f 2 x l
2
由悬链线方程可以看出,当拱的跨度和失高确定后,拱轴线各点的坐 标取 确于拱轴系数m。其线线形可用l/4点纵坐标y1/4的大小表示: 当
(二)抛物线拱
在竖向均布荷载作用下,拱的合理拱轴线是二次抛物线。对于 恒载集度比较接近均布的拱桥(如矢跨比较小的空腹式钢筋混 凝土拱桥,或钢筋混凝土桁架拱和刚架拱等轻型拱桥),往往 可以采用抛物线拱。其拱轴线方程为:
y1
4f 2 x 2 l
(三)、悬链线桥
实腹式拱桥的恒载集度从拱顶到拱脚均匀增加,其压力线是一条悬 链线(如下图)。一般采用恒载压力线作为实腹式拱桥的拱轴线
拱定处弯矩Md=0;剪力Qd=0。对拱脚取距,由有: 对拱脚取距,由
M
Hg
A
0 有:
j
M
f
(1-2-26)
对l/4截面取距,由 M B 0 有:
H g y1/ 4 M 1/ 4 0 Hg
M
y1/ 4 f
1/ 4
y1/ 4
代上式到式(1-2-26),可得:
拱顶填料、拱圈及拱腹填料的容重
拱顶填料厚度 拱圈厚度
d
j 拱脚处拱轴线的水平倾角
d d h f 2 2 cos j
由上计算m值的公式可以看出,除 j 为未知数外,其余均为已知; 在具体计算m值时可采用试算法,具体做法如下: a) 先假设mi b)根据悬链线方程(1-2-22)求 j ; 将式(1-2-22)两边取导数,有:
对于无铰拱,由于其是超静定结构, 偏离弯矩将引起次内力,其计算过程 如下: 取左图所示的基本结构,赘余力X1, X2作用在弹性中心,则有:
M1 1 M p H g y
s EI s X 1 1 p I ds M12 ds 11
s
M 1M p ds
13 31 0 23 32 0
但任有 12 21 0 达到。
为了使 12 21=0 ,可以按下图引用“ 刚臂 ”的办法
12 21 0
y1ds s EI 时, =0 可以证明当 ys 12 21 ds s EI
设想沿拱轴线作宽度等于1/EI的图形,则ds/EI就代表此图的面积,而上 式就是计算这个图形的形心公式,其形心称为弹性中心。
到上式,并积分,有
(1-2-43)
其中
Vg
m2 1 2[ln(m m 2 1)]
拱圈各截面的轴力N:由于不考虑弹性压缩时恒载弯矩和剪力为零,有
N
Hg cos
(1-2-44)
2)空腹拱 在计算空腹式悬链线不考虑弹性压缩的恒载内力时,可分为两部分, 即先不考虑拱轴线与压力线偏离的影响,假设恒载压力线与拱轴线 完全重和,然后再考虑偏离的影响,计算由偏离引起的恒载内力, 二者叠加。 不考虑偏离的影响:此时拱的恒载推力Hg,拱脚的竖向反力Vg和 拱任意截面的轴力可由静力平衡条件得到
由上式,取y1=f,可得拱脚处恒载强度 g j 为:
g j gd f mgd
m gj gd
(1-2-16)
其中:
称为拱轴系数。
这样gx可变换为:
g j gd f mgd
y1 g x g d y1 g d 1 (m 1) f
(m 1) gd / f
1 2
时, y1
y1/ 4 ;代
1 2
到悬链线方程(1-2-22)有:
半元公式
chk m
y1/ 4 1 k (ch 1) f m 1 2 ch k chk 1 2 2 m 1 1 2 m 1 m 1 2 1 2( m 1) 2
y1/ 4 f
第三章 拱桥的计算
第一节 上承式拱桥的计算
一、概述
拱轴线的选择与确定
拱 桥 的 计 算
恒载内力 活载内力 温度、收缩徐变 拱脚变位 内力调整 拱上建筑的计算
成桥状态的内力分析和强度、刚度、 稳定验算
施工阶段的内力分析和稳定验算
二、拱轴线的选择与确定
拱轴线的形状直接影响主截面的内力分布与大小, 选择拱轴线的原则,是要尽可能降低荷载产生的弯 矩。最理想的拱轴线是与拱上各种荷载作用下的压 力线相吻合,使拱圈截面只受压力,而无弯矩及剪 力的作用,截面应力均匀,能充分利用圬工材料的 抗压性能。实际上由于活载、主拱圈弹性压缩以及 温度、收缩等因素的作用,实际上得不到理想的拱 轴线。一般以恒载压力线作为设计拱轴线。
M M
1/ 4 j
(1-2-27)
M
1/ 4
自拱定至拱跨1/4点的恒载对l/4截面的力距。
求得 y1/ 4 后,即可求得m值:
f
y1/ 4 1 f 2(m 1) 2
(1-2-28)
1 f m ( 2) 2 1 2 y1/ 4
空腹拱的m值,任需采用试算法计算(逐次渐近法)。 (3)悬链线无铰拱的弹性中心 无铰拱是三次超静定结构。对称无铰 拱若从拱定切开取基本结构,多余力 X1(弯矩),X2 (轴力)为对称, 而X3(剪力)是反对称的,故知副系 数
y1ds
s
ds
s
f 0 m 1
1
(chk 1) 1 2 sh 2 k d
1
0
1 2 sh 2 k d
(4)空腹式无铰拱压力线与拱轴线偏离产生的附加内力 对于静定三铰拱,各截面的偏离弯矩 值Mp可以按下式计算:
M p H g y
将上式代入式(1-2-14),并引参数:
x l1
可得:
则:
dx l1d
d 2 y1 l12 g d y1 1 (m 1) f 2 d Hg l12 g d k (m 1) Hg f
2
令
(1-2-20)
则
d 2 y1 l12 g d k 2 y1 d 2 Hg
d)比较mi和mi+1,如两者相符,即假定的mi为真实值;如两者相差较大, 则以计算出的mi+1作为假设值,重新计算,直到两者相等
(2)空腹式拱拱轴系数的确定 空腹式拱桥中,桥跨结构的恒载由两部 分组成,即主拱圈承受由实腹段自重的分布 力和空腹部分通过腹孔墩传下的集中力(如 左图)。由于集中力的存在,拱的压力线为 在集中力作用点处有转折的曲线。但实际设 计拱桥时,由于悬链线的受力情况较好,故 多用悬链线作为拱轴线。 为了使悬链线与其恒载压力线重和, 一般采用“ 五点重和法”确定悬链线的m 值。即要求拱轴线在全拱(拱定、两1/4l点 和两拱脚)与其三铰拱的压力线重和。其 相应的拱轴系数确定如下
其中:y以弹性中心为原点(向上为正)的拱轴坐标。
拱顶、拱脚处:Mp=0 拱顶: M d X1 X 2 ys 0 拱脚: M j X1 X 2 ( f ys ) 0 其中,ys弹性中心至拱顶的距离。 (5)拱轴系数初值的选定
m gj gd
坦拱:m值选用较小 陡拱:m值选用较大
d 2 y1 1 d 2M gx 2 2 dx H g dx Hg
(1-1-14)
由上式可知,为了计算拱轴线(压力线)的一般方程,需首先知道恒载 的分布规律,对于实腹式拱,其任意截面的恒载可以用下式表示:
g x gd y1 gd
拱顶处恒载强度;
(1-2-15)
拱上材料的容重。
l12 g d k2 (m 1) Hg f
恒载水平推力Hg :利用上式有
(1-2-20)
l1 l / 2
gd l 2 m 1 gd l Hg kg 2 4k f f
2
(1-2-42)
其中:
kg
m 1 4k 2
(1-2-23)
k ch1m ln(m m2 1)
弯矩 Md=0
剪力Qd=0 恒载推力为Hg
对拱脚截面取矩,有:
Hg
M
f
(1-2-12)
M
半拱恒载对拱脚的弯矩。
对任意截面取矩,有:
Mx y1 Hg
y1以拱顶为原点,拱轴线上任意点的坐标;
(1-2-13)
M 任意截面以右的全部恒载对该截面的弯矩值。 对式(1-2-13)两边对x取两次导数,可得:
空腹式拱桥的恒载从拱顶到拱脚不再是连续分布的(如下图),其 恒载压力线是一条不光滑的曲线,难于用连续函数来表达。目前最 普遍的还是采用悬连线作为空腹拱的拱轴线,仅需拱轴线在拱顶、 跨径的四分之一点和拱脚初与压力线重合。
1、拱轴方程的建立(实腹拱压力线) 如下图所示,设拱轴线为恒载压力线,则拱顶截面的内力为:
dy1 fk shk d m 1 dy dy 2dy1 2 fkshk tg 1 1 shk dx l1d ld l (m 1)
其中
2kf l (m 1)
k可由式(1-2-23)计算
代=1,如上式,即可求得:
tg j shk
c)根据计算出的 j 计算出gj后,即可求得mi+1
拱脚的竖向反力:拱脚的竖向反力为半拱的恒载重力,即
Vg g x dx g xl1d
0 0
l1
1
代
y1 g x g d y1 g d 1 (m 1) f
Vg m2 1 2[ln(m m 1)]
2 ' gd l kg gd l
chk m
通常m为已知,则可以用下式计算k值:
k ch1m ln(m m2 1)
反双曲余弦函数对数表示
(1-2-23)
当m=1时 gx=gj,可以证明,在均布荷载作用下的压力线为二次抛 物线,其方程变为:
f 2 y1 f 2 x l
2
由悬链线方程可以看出,当拱的跨度和失高确定后,拱轴线各点的坐 标取 确于拱轴系数m。其线线形可用l/4点纵坐标y1/4的大小表示: 当
(二)抛物线拱
在竖向均布荷载作用下,拱的合理拱轴线是二次抛物线。对于 恒载集度比较接近均布的拱桥(如矢跨比较小的空腹式钢筋混 凝土拱桥,或钢筋混凝土桁架拱和刚架拱等轻型拱桥),往往 可以采用抛物线拱。其拱轴线方程为:
y1
4f 2 x 2 l
(三)、悬链线桥
实腹式拱桥的恒载集度从拱顶到拱脚均匀增加,其压力线是一条悬 链线(如下图)。一般采用恒载压力线作为实腹式拱桥的拱轴线
拱定处弯矩Md=0;剪力Qd=0。对拱脚取距,由有: 对拱脚取距,由
M
Hg
A
0 有:
j
M
f
(1-2-26)
对l/4截面取距,由 M B 0 有:
H g y1/ 4 M 1/ 4 0 Hg
M
y1/ 4 f
1/ 4
y1/ 4
代上式到式(1-2-26),可得:
拱顶填料、拱圈及拱腹填料的容重
拱顶填料厚度 拱圈厚度
d
j 拱脚处拱轴线的水平倾角
d d h f 2 2 cos j
由上计算m值的公式可以看出,除 j 为未知数外,其余均为已知; 在具体计算m值时可采用试算法,具体做法如下: a) 先假设mi b)根据悬链线方程(1-2-22)求 j ; 将式(1-2-22)两边取导数,有:
对于无铰拱,由于其是超静定结构, 偏离弯矩将引起次内力,其计算过程 如下: 取左图所示的基本结构,赘余力X1, X2作用在弹性中心,则有:
M1 1 M p H g y
s EI s X 1 1 p I ds M12 ds 11
s
M 1M p ds
13 31 0 23 32 0
但任有 12 21 0 达到。
为了使 12 21=0 ,可以按下图引用“ 刚臂 ”的办法
12 21 0
y1ds s EI 时, =0 可以证明当 ys 12 21 ds s EI
设想沿拱轴线作宽度等于1/EI的图形,则ds/EI就代表此图的面积,而上 式就是计算这个图形的形心公式,其形心称为弹性中心。
到上式,并积分,有
(1-2-43)
其中
Vg
m2 1 2[ln(m m 2 1)]
拱圈各截面的轴力N:由于不考虑弹性压缩时恒载弯矩和剪力为零,有
N
Hg cos
(1-2-44)
2)空腹拱 在计算空腹式悬链线不考虑弹性压缩的恒载内力时,可分为两部分, 即先不考虑拱轴线与压力线偏离的影响,假设恒载压力线与拱轴线 完全重和,然后再考虑偏离的影响,计算由偏离引起的恒载内力, 二者叠加。 不考虑偏离的影响:此时拱的恒载推力Hg,拱脚的竖向反力Vg和 拱任意截面的轴力可由静力平衡条件得到
由上式,取y1=f,可得拱脚处恒载强度 g j 为:
g j gd f mgd
m gj gd
(1-2-16)
其中:
称为拱轴系数。
这样gx可变换为:
g j gd f mgd
y1 g x g d y1 g d 1 (m 1) f
(m 1) gd / f
1 2
时, y1
y1/ 4 ;代
1 2
到悬链线方程(1-2-22)有:
半元公式
chk m
y1/ 4 1 k (ch 1) f m 1 2 ch k chk 1 2 2 m 1 1 2 m 1 m 1 2 1 2( m 1) 2
y1/ 4 f
第三章 拱桥的计算
第一节 上承式拱桥的计算
一、概述
拱轴线的选择与确定
拱 桥 的 计 算
恒载内力 活载内力 温度、收缩徐变 拱脚变位 内力调整 拱上建筑的计算
成桥状态的内力分析和强度、刚度、 稳定验算
施工阶段的内力分析和稳定验算
二、拱轴线的选择与确定
拱轴线的形状直接影响主截面的内力分布与大小, 选择拱轴线的原则,是要尽可能降低荷载产生的弯 矩。最理想的拱轴线是与拱上各种荷载作用下的压 力线相吻合,使拱圈截面只受压力,而无弯矩及剪 力的作用,截面应力均匀,能充分利用圬工材料的 抗压性能。实际上由于活载、主拱圈弹性压缩以及 温度、收缩等因素的作用,实际上得不到理想的拱 轴线。一般以恒载压力线作为设计拱轴线。
M M
1/ 4 j
(1-2-27)
M
1/ 4
自拱定至拱跨1/4点的恒载对l/4截面的力距。
求得 y1/ 4 后,即可求得m值:
f
y1/ 4 1 f 2(m 1) 2
(1-2-28)
1 f m ( 2) 2 1 2 y1/ 4
空腹拱的m值,任需采用试算法计算(逐次渐近法)。 (3)悬链线无铰拱的弹性中心 无铰拱是三次超静定结构。对称无铰 拱若从拱定切开取基本结构,多余力 X1(弯矩),X2 (轴力)为对称, 而X3(剪力)是反对称的,故知副系 数
y1ds
s
ds
s
f 0 m 1
1
(chk 1) 1 2 sh 2 k d
1
0
1 2 sh 2 k d
(4)空腹式无铰拱压力线与拱轴线偏离产生的附加内力 对于静定三铰拱,各截面的偏离弯矩 值Mp可以按下式计算:
M p H g y
