第七章离散信号与系统的复频域分析(2)L23_CH7.
信号与系统8.离散时间信号的复频域分析
常用单边序列的z变换
Z {ku[k ]}
z 1
z
2
2
1 z 1 z 1
za
证明：
Z { k u [ k ] } k z k ?
k0
1
Z {u[k ]}
z 1 即
1 z 1
zk
1
k0
1 z 1
两边对z 求导 -1
k
s域到z域的映射关系：z esT
P4
江西财经大学
Jiangxi University of Finance and Economics
单边z变换的定义
z变换的定义
双边z变换
X (z)
x[k ]z k
k
z反变换
1
x[k ]
X (z )z k1dz
P8
江西财经大学
Jiangxi University of Finance and Economics
z变换的定义
常用单边序列的z变换
P9
江西财经大学
Jiangxi University of Finance and Economics
常用单边序列的z变换
Z { [k ]} 1, z 0
单边z变换的反变换
幂级数展开和长除法
由X(z)的定义，将其展开为幂级数
X ( z )
x [ k ] z k x [ 0 ] x [1 ] z 1 x [ 2 ] z 2 ....
k0
展开式中 z-k 项的系数即为x[k]。当X(z)是有
理函数时，可以通过长除的方法将其展开为
信号与系统的频域分析
三、Ｆourier级数系数的对称性质：
• 1、偶函数：f(t) ＝f(－t)
4 a n f t cos(n1 t )dt T bn 0 an 2 Fn f t cos(n1 t )dt 2 T
T 2 0
T 2 0
2、奇函数：f(t) ＝－f(－t)
an 0 4 b n f t sin(n1 t )dt T T jb n 2 2 Fn j f t sin(n1 t )dt 2 T 0
xt g t dt 0
i
• （i为任意正整数），则此函数集称为完备正 交函数集。
四、信号的分解
Y
• A=c1x+c2y+c3z • X,y,z,为单位向量 若{ ri(t) }为n维正 交函数集
y x
z Z
A
X
.f(t)=c1.r1(t)+ c2.r2(t)+ c3.r3(t)+…..+ cn.rn(t)
§３－１
信号的正交分解
f1 t cf 2 t
• 一、正交函数：
若
t1 , t 2
•确定使方均误差最小的系数C：
2 t2 1 2 t t1 f1 t cf 2 t dt t 2 t1 2 t2 d2 d 1 t1 f1 t cf 2 t dt dc dc t 2 t 1
二、奇异信号：
1. t 1
重要推论：
•
２、常数１
e
j xy
dy 2 x
1 2
３、符号函数：（sign function）
1 t 0 sgnt 1 t 0 2 j F 0 0 0
离散时间信号与系统的频域分析2
一、序列的傅里叶变换的定义
连续时间信号x(t)的傅里叶变换:
X (j )F T [x(t)]x(t)ej td t
而X(jΩ)的傅里叶反变换定义为
x (t)F 1 [T X (j ) ]1X (j )ej td 2
离散时间信号x(n)的傅里叶变换（DTFT）：
X(ej) x(n)ejn
n
n
式中的级数才是绝对收敛的，或x(n)的傅里叶变换存在 。
二、常用序列的傅里叶变换
1.单位脉冲序列 (n)
其傅里叶变换为
=1
含义是什么
这就是用单 位脉冲响应能够 表征线性时不变 系统的原因。
单位脉冲信
号包含了所有频
率分量，而且这
T[(n)]h(n) 些分量的幅度和 相位都相同。
2.矩形序列
反变换
n
x(n)21
X(ej)ejnd
X(ej) x(n)ejn n
在物理意义上，X(ejω)表示序列x(n)的频谱，ω为数字域 频率。 X(ejω)一般为复数。
但是右边的级数并不总是收敛的，即并不是任何序列 x(n)的傅里叶变换都是存在的。
只有当序列x(n)绝对可和
|x(n)ejn| |x(n)|
X (ej) X e(ej) X o (ej)
2）DTFT的对称特性（同学们自己证明）
D DT T[[F FjR IT Tm xe(xn [([)n]) ]] ]XX e(oe(je)j) D DT T[[F Fxxoe(T T (n n))]] R jIem X[X (e[(jej)])] 若x(n)为实序列，则 X(ej)X*(ej) ReX[(ej)]ReX[(ej)] ImX[(ej)]ImX[(ej)] X(ej) X(ej) argX[(ej)]argX[(ej)]
离散时间信号与系统的复频域分析
六,单边z反变换 单边z
1 k 1 x[k ] = ∫c X ( z ) z dz 2 πj
C为X(z) 的ROC中的一闭合曲线. 计算方法: 幂级数展开和长除法 部分分式展开 留数计算法
2 z 0 .5 k = z z 1
z = 0.5
= (0.5) k
x[k] = Res[ X (z)zk1]z=1 + Res[ X (z)zk1]z=0.5 =[1+(-0.5)k]u[k]
1) z变换与拉普拉斯变换的关系. 2) 双,单边z变换的定义与适用范围: 双边适用于离散系统综合设计 单边大多用于离散系统的分析 3) z域分析与其他域分析方法相同, z变换的 性质类似于其他变换.
A = (1 2 z ) G ( z ) z = 2
1 2
G(z)
2 = = 2 1 1 4z
z =2
1 d[G ( z )(1 2 z 1 ) 2 ] B= (2) dz 1
1 d 2 = z =2 2 dz 1 1 4 z 1
= 4
1 8 z 1 + 20 z 2 16 z 3 例 : X (z) = (1 2 z 1 ) 2 (1 4 z 1 )
离散时间系统响应的z 离散时间系统响应的z域分析
解差分方程
时域差分方程
变 换 z z
时域响应y 时域响应y[k]
反 变 换 z z z z
z域
方程
解 方程
z域响应Y(z) 域响应Y
二阶系统响应的z 二阶系统响应的z域求解
清华大学信号与系统课件第七章离散系统的时域分析
2020/4/4
课件
10
二、离散系统的数学模型
• 输入是离散序列及其时移函数
x(n)x ,(n1)x ,(n2),....
• 输出是离散序列及其时移函数
y(n)y ,(n1)y ,(n2),....
• 系统模型是输入输出的线性组合
系数乘，相加，延时单元
N
M
y(n) aky(nk) brx(nr)
a0
1 E
a1
b1
1 E
a2
b2
2020/4/4
课件
20
§7.3常系数差分方程的求解
• 迭代法 • 时域经典法 • 离散卷积法：利用齐次解得零输入
解，再利用卷积和求零状态解。 • 变换域法（Z变换法） • 状态变量分析法
2020/4/4
课件
21
一、迭代法
• 当差分方程阶次较低时常用此法
y(n) ay(n 1) x(n) x(n) (n)
M
yi(n)
i0
M
ai yi (n)
i0
• 时不变性 xi(nm)
2020/4/4
课件
yi(nm)
9
连续系统的数学模型
C0ddnr(ntt)C1ddn1nrt(1t)..C.n1dd(rt)tCnr(t) E0ddmem (tt)E1ddm1m te(1t)..E.m1dd(et)tEme(t)
网络结构图：
x(n)
1 a
1 E
y(n)1y(n1)x(n) a
2020/4/4
课件
16
1 x(n1)
E
b1
y(n)a1y(n1) b0x(n)b1x(n1)
数字信号处理-离散时间信号和系统的频域分析共28页文档
数字信号处理-离散时间信号和系统的 频域分析
1、纪律是管理关系的形式。——阿法 纳西耶 夫 2、改革如果不讲纪律，就难以成功。
3、道德行为训练，不是通过语言影响 ，而是 让儿童 练习良 好道德 行为， 克服懒 惰、轻 率、不 守纪律 、颓废 等不良 行为。 4、学校没有纪律便如磨房里没有水。 ——夸 美纽斯
5、教导儿童服从真理、服从集体，养 成儿童 自觉的 纪律性 ，这是 儿童道 德教育 最重要 的部分 。—— 陈鹤琴
Байду номын сангаас
66、节制使快乐增加并使享受加强。 ——德 谟克利 特 67、今天应做的事没有做，明天再早也 是耽误 了。——裴斯 泰洛齐 68、决定一个人的一生，以及整个命运 的，只 是一瞬 之间。 ——歌 德 69、懒人无法享受休息之乐。——拉布 克 70、浪费时间是一桩大罪过。——卢梭
《信号与系统》离散信号的频域分析实验报告
信息科学与工程学院《信号与系统》实验报告四专业班级电信 09－班姓名学号实验时间 2011 年月日指导教师陈华丽成绩实验名称离散信号的频域分析实验目的1. 掌握离散信号谱分析的方法：序列的傅里叶变换、离散傅里叶级数、离散傅里叶变换、快速傅里叶变换，进一步理解这些变换之间的关系；2. 掌握序列的傅里叶变换、离散傅里叶级数、离散傅里叶变换、快速傅里叶变换的Matlab实现；3. 熟悉FFT算法原理和FFT子程序的应用。
4. 学习用FFT对连续信号和离散信号进行谱分析的方法，了解可能出现的分析误差及其原因，以便在实际中正确应用FFT。
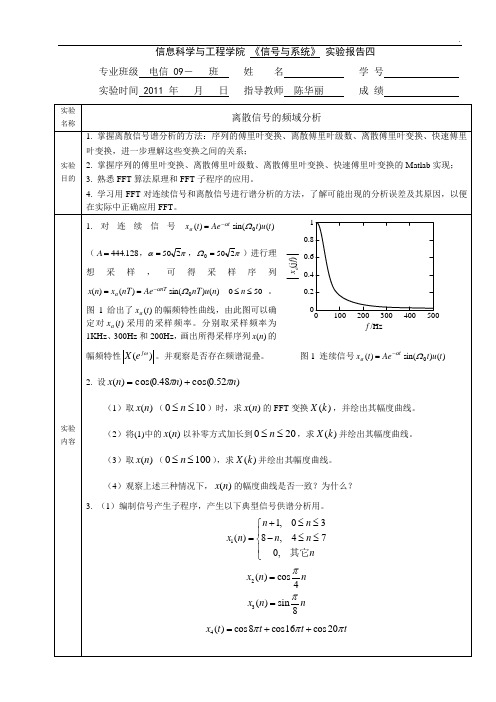
实验内容1.对连续信号)()sin()(0tutAetx taΩα-=（128.444=A，πα250=，πΩ250=）进行理想采样，可得采样序列50)()sin()()(0≤≤==-nnunTAenTxnx nTaΩα。
图1给出了)(txa的幅频特性曲线，由此图可以确定对)(txa采用的采样频率。
分别取采样频率为1KHz、300Hz和200Hz，画出所得采样序列)(nx的幅频特性)(ωj eX。
并观察是否存在频谱混叠。
图1 连续信号)()sin()(0tutAetx taΩα-=2. 设)52.0cos()48.0cos()(nnnxππ+=（1）取)(nx（100≤≤n）时，求)(nx的FFT变换)(kX，并绘出其幅度曲线。
（2）将(1)中的)(nx以补零方式加长到200≤≤n，求)(kX并绘出其幅度曲线。
（3）取)(nx（1000≤≤n），求)(kX并绘出其幅度曲线。
（4）观察上述三种情况下，)(nx的幅度曲线是否一致？为什么？3. （1）编制信号产生子程序，产生以下典型信号供谱分析用。
11,03()8,470,n nx n n nn+≤≤⎧⎪=-≤≤⎨⎪⎩其它2()cos4x n nπ=3()sin8x n nπ=4()cos8cos16cos20x t t t tπππ=++10.80.60.40.20100200300400500xa(jf)f /Hz（2）对信号1()x n ，2()x n ，3()x n 进行两次谱分析，FFT 的变换区间N 分别取8和16，观察两次的结果是否一致？为什么？（3）连续信号4()x n 的采样频率64s f Hz =，16,32,64N =。
离散信号的频域分析
时频变换的基本概念：时频变换是信号处理 中的一种重要方法，它能够将信号的时域和 频域信息相互转换。
添加 标题
离散信号的频域与时域的关系：离散信号的 频域与时域之间存在密切的关系。通过时频 变换，可以分析离散信号在不同时间点的频 率特征，从而更好地理解信号的特性和行为。
添加 标题
时频变换的不变性：时频变换具有一些重要 的性质，其中最重要的是时频变换的不变性。 这意味着通过时频变换得到的信号的时域和 频域特征在变换前后保持不变。
数字调制解调的 优势：抗干扰能 力强、传输距离 远等
数字音频信号 的频域分析
音频压缩与编 码
数字滤波器设 计
音频特效处理
图像压缩：离散信号的频域分析有助于图像压缩，减少存储空间和传输带宽。
图像增强：通过频域处理，可以增强图像的细节和对比度，提高图像质量。
图像识别：利用离散信号的频域特征，可以实现图像识别和分类，应用于人脸识别、物体检测等 领域。
时频变换的应用：时频变换在信号处理、 通信、雷达、声呐等领域有着广泛的应用。 通过时频变换，可以实现对信号的快速、 准确的分析和处理，从而提高信号处理的 效率和精度。
时频变换的基本原理
离散信号的频域与时域的关 系
离散信号的频域分析方法
时频变换在信号处理中的应 用
汇报人：XX
时频变换的对称性：离散信号的频域与时域之间存在对称性，即频域和时域的变换具有相互对 应的关系。
离散信号的时频分析：利用时频变换的方法，将离散信号表示为时频平面上的分布，以便同时 分析其时间和频率特性。
时频变换的物理意义：离散信号的时频变换具有物理意义，可以揭示信号在不同时间和频率下 的表现和特征。
添加 标题
离散性：离散信号的频谱是离散的，即只有某些特定的频率分量存在。
第7章 信号与系统控制的复频域分析
⑽ 初值和终值定理 初值定理：若 f (t ) 中不包含冲激函数 (t ) 及其各阶导数，并且
f (t ) F (s) ( Re[ s] 0 ) ， f (t ) 的初值为 f (0 ) lim f (t ) lim s F ( s ) 则 。
频域分析法揭示了信号的频谱特性和系统的频域特性，但频域分 析法有两个局限性：一是某些信号的傅立叶变换不存在，给信号 与系统的分析带来了很大的不便；另一个最大的局限性就是只能 求解系统的零状态响应。
复频域分析法则是能够有效克服频域分析法局限性：不仅能够避 免出现信号分析的死区，全面解决信号的复频域分析问题；而且 能够求解系统的零状态响应与零输入响应问题，即可以求解系统 的完全响应，使信号与系统的分析更为完整、简洁。
f
( n)
(t ) s n F ( s) s n1i f
i 0
n 1
(i )
(0 )
( Re[ s] 0 )
时域微分性质中包含了信号的初始状态，因此在求解系统 的微分方程时，不仅能求解零状态响应，而且还能求解零输入 响应，所以单边拉氏变换的时域微分性质非常重要。 若 f (t ) 为因果信号，则有 f ( n) (0 ) 0 (n 0,1,2,) 此时，时域 微分性质可简化为 f ( n) (t ) s n F ( s) (n 1， ， , Re[ s] ) 2
7.1.2 复频域分析法的主要特点
在连续信号与系统的分析中，复频域分析 法的主要特点是在频域分析法的基础上引 e t ，使傅立叶正变换中的e j t 入衰减因子 e s t ；使原来频域分析中的基本虚指数 变成 信号 e j t 扩展为复频域分析中的基本复指数 st 信号 e ，其中 s j ( ， 为实数 ) 即为 复频率；同时也使傅立叶变换成为了拉普拉 斯变换。
离散时间系统频域分析
离散时间系统频域分析离散时间系统的频域分析是研究离散时间信号在频域上的性质和行为的方法。
在离散时间系统频域分析中，使用离散时间傅里叶变换（Discrete Fourier Transform，DFT），来将离散时间信号从时域转换到频域。
通过分析信号在频域上的频谱分布和频谱特性，可以得到离散时间系统的频率响应和频域特性，对信号的频域分布和频率区间进行评估和分析。
离散时间傅里叶变换是时域信号分析的重要工具，它可以将离散时间信号从时域转换到频域。
离散时间傅里叶变换的定义可以表示为：X(k) = Σ[x(n) * exp(-j*2πkn/N)]其中，X(k)是离散时间信号在频域的频谱，x(n)是离散时间信号，N是信号的长度，k是频谱的索引。
离散时间傅里叶变换将时域信号分解成多个频率成分，通过频谱的幅度和相位信息，可以得到信号在频域上的分布情况。
通过离散时间傅里叶变换可以得到离散时间信号的频谱，进而分析信号在频域上的频率响应和频域特性。
频谱可以反映信号在不同频率上的能量分布情况，通过观察频谱的幅度和相位，可以得到信号的频率成分、频带宽度和频率特性等信息。
在离散时间系统频域分析中，常用的分析工具有频谱图、功率谱密度、频率响应等。
频谱图可以将信号的频谱以图形形式展示出来，通过观察频谱图的形状和分布，可以得到信号在频域上的特点。
功率谱密度是指信号在不同频率上的功率分布情况，可以评估信号在不同频率上的能量分布情况。
频率响应是指系统对不同频率信号的响应情况，可以评估系统对不同频率信号的滤波和增益特性。
离散时间系统频域分析的应用包括信号处理、通信系统、控制系统等领域。
在信号处理中，通过频域分析可以对信号进行滤波、去噪、频域变换等操作，提高信号的质量和分析能力。
在通信系统中，通过频域分析可以评估信号传输和接收的性能，并对系统进行优化和改进。
在控制系统中，通过频域分析可以评估系统的稳定性和控制特性，提高系统的响应速度和稳定性。
离散信号的频域分析
DFS
⊗为周期卷积的符号，两周期序列x(n)和h(n)的周期卷积定义为： x(n) ⊗ h(n)=h(n) ⊗ x(n) = ∑ x(k )h(n − k )
k =0 N −1
周期卷积和线性卷积的惟一区别在于周期卷积时仅仅在单个 周期内求和，而线性卷积则是对所有k值求和。
k=1,-1 其余
−1 0 1 2 3 4 5 6 7 k
X (kω 0 )
⋯
−1 0 1 2 3 4 5 6
⋯
k
X1(kΩ01)
其频谱图为：
⋯
−5
−1 0 1 2 3 4 5
⋯
7 11 13
13
π − jk n 1 7 X 2 (k Ω02 ) = ∑ x(n)e 4 8 n =0
频谱如图：
X 2 ( k Ω 02 )
（2）泄露 泄露误差是由于截取波形的时间长度不恰当造成的。 从原来比较集中的谱线由于截取信号长度不当，出现了分散的 扩展谱线的现象，称之为频谱泄露或者功率泄露。
二、非周期信号的频域分析 （DTFT Discrete Time Fourier Transformation） 1、定义 序列x(n)的离散时间傅里叶变换定义为：
因此：
X(kΩ0)
1 X (k Ω0 ) = 2 0 k=1,5 k=0,2,3,4
1 2
0 12 34 5 6
x(n)
2π π Ω0 = = 解：基本频率： N 3
1
⋯
−1 0 1
⋯
n
周期信号的频谱为：
π − jk n 1 5 X (kΩ0 ) = ∑ x(n)e 3 6 n=0 π 5π − jk − jk 1 = [ x(0) + x(1)e 3 + x(5)e 3 ] 6 π π − jk jk 1 1 πk 3 3 = [1+ e + e ] = [1+ 2cos ] 6 6 3
离散系统的复频域分析
离散系统的复频域分析专题研讨【目的】(1) 了解系统函数的零、极点分布与系统特性的关系； (2) 培养学生分析与解决实际问题的能力。
【知识点】离散时间线性时不变系统的系统函数与系统特性、系统响应分析【研讨内容】我国市电是电压为220V 、频率为50Hz 的交流电，电气设备经常受到市电以耦合的方式干扰。
在不影响有用信号的情况下，如何去除信号中混入的工频信号(50Hz)干扰？情况1：信号x 1 (t )=s 1(t )+n (t )中有用信号频率为f 1=20Hz 的正弦信号s 1(t )=sin(2πf 1t )，混入频率为50Hz 的工频信号n (t )=0.2sin(100πt )。
现经过采样率f s =500Hz 模数转换器(ADC)通过设计系统H (z )的零极点的方法，滤除50Hz 工频干扰信号n (t )。
情况2：如果x 2(t )=s 1(t )+s 2(t )+n (t )，其中f 2=100Hz 的正弦信号s 2(t )=sin(2πf 2t )，又如何设计零极点滤除工频干扰？1. (*)信号x (t )经过模数转换(A/D)后变成离散信号x [k ]，x [k ]的表达式是什么？编写matlab程序产生信号x 1[k ]和x 2[k ]。
[]()k x k x Fs= ()Fs 为抽样频率1[]sin(2*20*)0.2sin(2*50*)x k k k ππ=+2[]sin(2*20*)sin(2*100*)0.2sin(2*50*)x k k k k πππ=++产生信号源程序f1=20;f2=100;Fs=500;k=0:1:Fs; s1=sin(2*pi*f1*k/Fs); s2=sin(2*pi*f2*k/Fs); n=0.2*sin(100*pi*k/Fs); x1=s1+n; x2=s1+s2+n; X1=fft(x1); X2=fft(x2);subplot(2,2,1); stem(k,x1); title('x1ʱÓòͼ') subplot(2,2,3);plot(-250:250,fftshift(abs(X1))) title('x1ƵÓòͼ')subplot(2,2,2); stem(k,x2); title('x2ʱÓòͼ') subplot(2,2,4);plot(-250:250,fftshift(abs(X2))) title('x2ƵÓòͼ')2. (*)离散LTI 系统的零极点与系统函数的关系是什么？11()()()mjj nii z z H z Kz p ==-=-∏∏ 其中z j 为零点，p i 为极点其中||jjj j j j j z z z z eN eψψ-=-=||i i j j i i i z p z p e D e θθ-=-=()()j i j jiN H z Ke Dψθ+∑∑=∏∏|()|jiN H z KD=∏∏由上式可见，当z 接近于零点z j 时，N j 趋向于0，系统函数幅值趋向于0。
离散信号与系统的时域和频域分析
h(k n) an1h(k n 1) an2h(k n 2) ... a0h(k ) 0 K>0时， n 齐次差分方程解： k
h(k ) [ ci ( ) ] (k )
离散信号与系统分析
开始
下一页
结束
本章说明
与连续信号与系统相比较，离散系统的数学描述是激励响应的差分方 程，其系统分析求响应实质是求解描述离散系统的差分方程。离散系 统的零状态响应可以用卷积和来求取。 时域分析： 1.掌握离散信号与系统的基本概念。 2.熟悉并掌握常用基本信号的描述、特性、运算与变换。 3.深刻理解采样定理的意义、内容及应用。 4.掌握离散系统的数学描述方法—差分方程及模拟图 5.掌握离散系统的时域分析—经典法求零输入响应、零状态响应。 6.熟悉卷积和法及其主要性质并会应用卷积和法求零状态响应。
4、图解法卷积
①变量代换 f1(n) 变成f1(k) f2(n) 变成f2( ②反折其中之一信号 ③将反折信号移位 m f2(-k) f2(m-k) 以k代n
④e将平移后的f2(m-k)与对应的f1(k)相乘 ⑤将各乘积值相加可画出全部y(m) ⑥重复步骤③到⑤可画出全部y(n) 5、系统零状态响应为
5、序列的运算
④差分：离散信号的差分运算 f (k ) f (k 1) f (k ) 前向差分： f (k ) f (k ) f (k 1) 后向差分： ⑤反折：将离散信号以纵轴为对称轴反折（转） ⑥压扩：将离散信号中f（k）的自变量k置换为ak得到的过程称为信号的尺 度变换 注意：不存在非整数ak的值！ ⑦求和：离散信号的求和运算是对某一离散信号进行历史推演的求和过程。
离散时间信号和系统的频域分析
离散时间信号和系统的频域分析离散时间信号与系统是研究数字信号与系统的频域分析，其中离散时间信号是对连续时间信号进行采样得到的，而离散时间系统是对连续时间系统进行离散化得到的。
频域分析是对信号与系统在频率域上的特性进行研究和分析。
对于离散时间信号，其离散化的过程是将连续时间信号在时间轴上进行均匀采样，得到指定的采样间隔，得到离散时间序列。
在频域上，其频谱是周期性的，并且频谱是以单位圆为单位周期的。
频域分析的目的是研究离散时间信号在频率域上的特性，包括频谱范围、频率分辨率、功率谱密度等。
离散时间信号的频域分析可以通过离散时间傅里叶变换（DTFT）来实现。
DTFT是信号在频域上的完全变换，将一个离散时间信号映射到一个连续的频率域函数。
DTFT是一个复数函数，表示信号在不同频率上的振幅和相位。
频谱的振幅可以表示信号在该频率上的能量大小，相位可以表示信号在该频率上的相对位置。
除了DTFT之外，还可以使用离散傅里叶变换（DFT）进行频域分析。
DFT是DTFT的一种计算方法，可以将离散时间信号转换为有限的频域信号。
DFT的计算是通过对离散时间信号进行有限长的时间窗口进行采样，并进行频域变换得到的。
DFT的结果是一个离散的频域信号，也称为频谱。
DFT通常使用快速傅里叶变换（FFT）算法来快速计算。
离散时间系统的频域分析主要是通过系统的频率响应函数来实现。
频率响应函数是系统在不同频率上对信号的响应情况的描述。
对于线性时不变系统，其频率响应函数是系统的传递函数的傅里叶变换。
频率响应函数拥有类似信号的频谱特性，可以描述系统对不同频率的信号的增益和相位。
频域分析在离散时间信号与系统中有着广泛的应用。
首先，频域分析可以帮助我们理解信号的频率构成和能量分布情况，有助于对信号进行合理的处理和分析。
其次，频域分析可以快速计算离散时间系统的响应，能够有效地评估系统的性能和稳定性。
此外，频域分析还可以进行滤波器设计、信号压缩、信号重构等应用。
信号与系统王明泉第七章习题解答
第7章离散时间系统的Z域分析7.1 学习要求（1）深刻理解z变换的定义、收敛域及基本性质，会根据z变换的定义和性质求解一些常用序列的z变换，能求解z反变换，深刻理解z变换与拉普拉斯变换得关系；（2）正确理解z变换的应用条件；（3）能用z域分析分析系统，求离散系统的零状态响应、零输入响应、完全响应、单位样值响应；（4）深刻理解系统的单位样值响应与系统函数H(z)之间的关系，并能用系统函数H(z)求解频率响应函数，能用系统函数的分析系统的稳定性、因果性。
7.2 本章重点（1）z变换（定义、收敛域、性质、反变换、应用）；（2）z域分析（求解分析系统）；（3）系统的频率响应函数。
7.3 本章的知识结构7.4 本章的内容摘要7.4.1 Z变换（1）定义∑∞-∞=-=n nzn x z X )()( 表示为：)()]([z X n x Z =。
（2）收敛域 1.有限长序列12(),()0,x n n n n x n n ≤≤⎧=⎨⎩其他 （1）当0,021>>n n 时，n 始终为正，收敛条件为0>z ； （2）当0,021<<n n 时，n 始终为负，收敛条件为∞<z ；（3）当0,021><n n 时，n 既取正值，又取负值，收敛条件为∞<<z 0。
2.右边序列11(),()0,x n n n x n n n ≥⎧=⎨<⎩ （1）当01>n 时，n 始终为正，由阿贝尔定理可知，其收敛域为1x R z >，1x R 为最小收敛半径；（2）当01<n 时，)(z X 分解为两项级数的和，第一项为有限长序列，其收敛域为∞<z ；第二项为z 的负幂次级数，由阿贝尔定理可知，其收敛域为1x R z >；取其交集得到该右边序列的收敛域为∞<<z R x 1。
3．左边序列2(),()0,x n n n x n n ≤⎧=⎨⎩其他（1）当02<n ，n 始终为负，收敛域为2x R z <，2x R 为最大收敛半径； （2）当02>n ，)(z X 可分解为两项级数的和，第一项为z 的正幂次级数，根据阿贝尔定理,其收敛域为2x R z <，2x R 为最大收敛半径；第二项为有限长序列，其收敛域为0>z ；取其交集，该左边序列的收敛域为20x R z <<。
第7章离散信号与系统的Z域分析
k
z za
k
|z|>|a|
F ( z)
k
[a (k 1)]z
z za
|z|<|a|
第 7 章 离散信号与系统的Z域分析
7.2 双边Z变换的性质
1. 线性
若
f1 (k ) F1 ( z ) f 2 (k ) F2 ( z )
a1 z 1 a2 z 2
f ( n) z
m k
( n m )
z
f ( n) z
n
z F ( z)
m
第 7 章 离散信号与系统的Z域分析 例 7.2-2 已知f(k)=3k［ε(k+1)-ε(k-2)］，求f(k)的双边Z
变换及其收敛域。
解 f(k)可以表示为
f (k ) 3 (k 1) 3 (k 2)
第 7 章 离散信号与系统的Z域分析
第 7 章 离散信号与系统的Z域分析
7.1 Z变换 7.2 双边Z变换的性质 7.3 Z逆变换 7.4 单边Z变换 7.5 离散系统的Z域分析
7.6 离散系统差分方程的Z域解
7.7 离散系统的表示和模拟
7.8 系统函数与系统特性
第 7 章 离散信号与系统的Z域分析
f (k ) z
k
k
第 7 章 离散信号与系统的Z域分析
1 s 1nz T ze
sT
1 k 1 f (k ) C F ( z) z dz 2j
第 7 章 离散信号与系统的Z域分析
7.1.2 双边Z变换的定义和收敛域
1. 双边Z变换的定义 对于离散序列f(k)(k=0, ±1, ±2, …)， 函数(z的幂级数)
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Signals and Systems
普通高等教育“十一五”国家级规划教材 《信号与系统》
陈后金，胡健，薛健 高等教育出版社， 2007年
离散时间信号与系统的复频域分析
离散时间信号的复频域分析 离散时间LTI系统的复频域分析 离散时间系统函数与系统特性 离散时间系统的模拟
离散时间信号的复频域分析
z 4, 求x[k ]
解： m=n，由多项式除法可得
X
(z)
1
(1
2z
2 1 ) 21
4z
1
G(z)
G(z)
A (1 2z 1)2
B 1 2z 1
C 1 4z 1
A
(1 2z1)2 G(z)
z2
2 1 4z1
2
B
1 (2)
d[G(z)(1 2z 1)2 ] dz 1
解：
X
(
z
)
1
(
1 z/
a)
2
X
1
(
z)
1
1 z
2
x1[k
]
s
in
[π 2
(k
1)]u[k
]
由指数加权性质
x[k] ak cos(π k)u[k] 2
例：X (z)
1 (1 2z1)(1 z1 z2 ) ,
z
0
求x[k]。
解：
A
Bz 1 C
X (z) 1 2z1 1 z1 z2
B, C用待定系数法求
1 z 1 z 2 1 2 cos(π / 3)z 1 z 2
A=4/3, B=2/3, C= 1/3;
x[k ]
{4
(2)k
2sin(
π 3
k)
sin[
π 3
(k
1)] }u[k ]
3
3sin(π / 3) 3sin(π / 3)
六、单例:
X (z)
2z 2 0.5z z 2 0.5z 0.5
z 1, 求x[k]
解： 将X(z)化为z的负幂，可得
X
(
z)
1
2 0.5z
0.5 z 1 1 0.5
z
2
1
A z
1
1
B 0.5z
1
A
(1
z 1)
X
(z)
z 1
部分分式法
X
(z)
B(z) A(z)
b0 b1z1 bm zm 1 a1z1 an zn
1. m<n，分母多项式无重根
n
X (z)
i 1
ri 1 pi z 1
各部分分式的系数为
ri (1 pi z1) X (z) z pi
六、单边z反变换
C (1 4z1)G(z) z4 8
X (z)
1
2 (1 2z1)2
1
4 2
z
1
1
8 4
z
1
进行z反变换，得
x[k] [k] [2(k 1)2k 4 2k 8 4k ]u[k]
例：X (z)
z2 z2 a2
,
z
a, 求x[k]
解：
X(z)有一对共轭复根，复根时部分分式展开, 可以直接利用
sin(0k
)u[k
]Z
1
sin 0 z 1 2z 1 cos 0
z
2
sin[0 (k
1)]u[k]Z 1
sin 0 2z1 cos 0
z 2
例：X (z)
z2 z2 a2
,
z
a, 求x[k]
Res[X (z)zk1]z1 (z 1)X (z)zk1 z1
2z 0.5 z k z 0.5
1
z 1
Res[
X
(
z)z
k
]1 z0.5
2 0.5z1 1 0.5z1
z1 1
B
(1
0.5z1) X (z)
z 0.5
2 0.5z1 1 z1
z0.5 1
将X(z)进行z反变换，可得
x[k] Z 1{X (z)} u[k] (0.5)k u[k]
例
:
X
(z)
1
8z 1 20 z 2 16 z 3 (1 2z 1)2 (1 4z 1)
部分分式法
X
(z)
B(z) A(z)
b0 b1z1 bm zm 1 a1z1 an zn
2. m<n，分母多项式在z=u处有l阶重极点
nl
X (z)
i 1
1
ri pi z 1
l 1 i0
qi (1 uz1)li
1
di
qi (u)i i! d(z1)i
(1 uz1)l X (z)
zu ,
i 0,l 1
六、单边z反变换
部分分式法
X
(z)
B(z) A(z)
b0 b1z1 bm zm 1 a1z1 an zn
3. mn
mn
X (z)
i 1
ki zi
B1(z 1) A(z 1)
多项式
Re s[ X z p
( z ) z k 1 ]
(n
1 dn1(z p)n
1)!
dz n1
X
(z) z p
例：X (z)
2z2 0.5z z2 0.5z 0.5 ,
z
1,用留数法求x[k]。
解：
X(z)z k1在z=1, z=0.5有两个一阶极点，其留数为
留数法
x[k] 1
n
X (z)zk1dz Re s[ X (z)zk1]
2πj c
i1 z pi
若X(z)z k1在z = pi处有一阶极点，则该极点的留数为
Re s[ X (z)zk1]
z pi
(z
zi ) X (z)zk1
z zi
若X(z)z k1在z = p处有一阶极点，则该极点的留数为
z2
1 2
d dz 1
1
2 4 z 1
z2 4
例
:
X
(z)
1
8z 1 20 z 2 16 z 3 (1 2z 1)2 (1 4z 1)
z 4, 求x[k ]
解：
G(z)
A (1 2z 1)2
B 1 2z 1
C 1 4z 1
所以
由离散时间Fourier变换到z变换
单边z变换及其收敛域 常用单边序列的z变换 单边z变换的性质 单边z反变换
六、单边z反变换
x[k] 1 X (z)zk1dz
2πj c
C为X(z) 的ROC中的一闭合曲线。
计算方法： 幂级数展开和长除法 部分分式展开 留数计算法
六、单边z反变换