“隐圆”最值问题习题
专题18 隐形圆及最值问题
AB是 O 的直径，
ACB 90．
ABC 45 ， AC 5 ，
ABC 45 ，
AB AC 5 5 2 ， sin 45 2 2
MN最大
52 2
．
故答案为： 5 2 ．
6．如图，在平面直角坐标系中，已知 C(3, 4) ，以点 C 为圆心的圆与 y 轴相切．点 A 、 B 在 x 轴上，且 OA OB ．点 P 为 C 上的动点， APB 90 ，则 AB 长度的最大值为 ．
1．如图，等边 ABC 的边长为 2， A 的半径为 1，D 是 BC 上的动点，DE 与 A 相切于 E ， DE 的最小值是 ( )
A．1
B． 2
C． 3
D．2
【分析】连接 AE ， AD ，作 AH BC 于 H ，因为 DE 与 A 相切于 E ，所以 AE DE ， 可得 DE AD2 AE2 AD2 1 ，当 D 与 H 重合时， AD 最小，此时 DE 最小，求出 AH 的长，即可得出 DE 的最小值． 【解答】解：如图，连接 AE ， AD ，作 AH BC 于 H ，
若平面上 A、B、C、D 四个点满足 ABC ADC ， 则 A、B、C、D 四点共圆． 证明条件：1．四边形对角互补； 2．四边形外角等于内对角．
两条线段被一点分成（内分或外分）两段长的乘积相等，则这两条线段的四个端点共圆．
D
C
H
O
A
B
四边形 ABCD 的对角线 AC、BD 交于 H， 若 AH CH BH DH ，则 A、B、C、D 四点共圆.
作 AM⊥BP 于 M．当点 P 从点 C 运动到点 A 时，线段 BM 的中点 N 运动的路径长为（
）
A． 2 π 2
2020年九年级数学中考专题复习：隐形圆求最值问题(含答案)
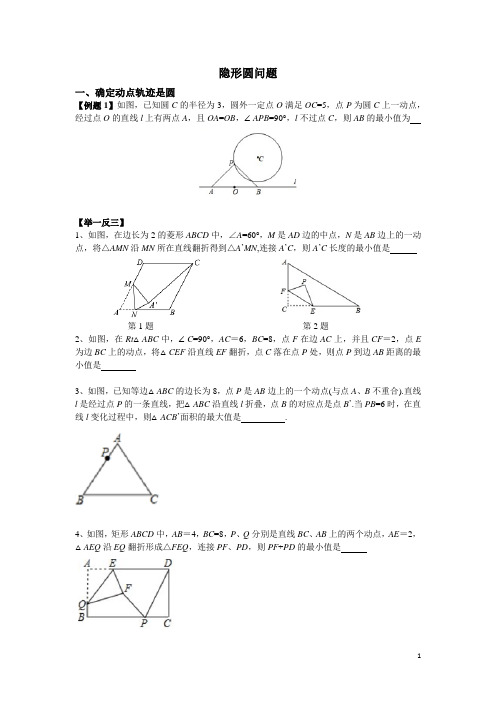
隐形圆问题一、确定动点轨迹是圆【例题1】如图，已知圆C的半径为3，圆外一定点O满足OC=5，点P为圆C上一动点，经过点O的直线l上有两点A，且OA=OB，∠APB=90°，l不过点C，则AB的最小值为【举一反三】1、如图，在边长为2的菱形ABCD中，∠A=60°，M是AD边的中点，N是AB边上的一动点，将△AMN沿MN所在直线翻折得到△A’MN,连接A’C，则A’C长度的最小值是第1题第2题2、如图，在Rt△ABC中，∠C=90°，AC＝6，BC=8，点F在边AC上，并且CF＝2，点E 为边BC上的动点，将△CEF沿直线EF翻折，点C落在点P处，则点P到边AB距离的最小值是3、如图，已知等边△ABC的边长为8，点P是AB边上的一个动点(与点A、B不重合).直线l是经过点P的一条直线，把△ABC沿直线l折叠，点B的对应点是点B’.当PB=6时，在直线l变化过程中，则△ACB’面积的最大值是.4、如图，矩形ABCD中，AB＝4，BC=8，P、Q分別是直线BC、AB上的两个动点，AE＝2，△AEQ沿EQ翻折形成△FEQ，连接PF、PD，则PF+PD的最小值是二、定边对直角知识回顾:直径所对的圆周角是直角构造思路:一条定边所对的角始终为直角，则直角顶点轨迹是以定边为直径的圆或圆弧.图形释义:若AB是一条定线段，且∠APB-90°，则P点轨迹是以AB为直径的圆【例题1】已知正方形ABCD边长为2，E、F分别是BC、CD上的动点，且满足BE＝CF，连接AE、BF，交点为P点，则PC的最小值为【举一反三】1、如图，E、F是正方形ABCD的边AD上的两个动点，满足AE＝DF，连接CF交BD于点G，连接BE交AG于点H，若正方形边长为2，则线段DH长度的最小值是2、如图，Rt△ABC中，AB⊥BC，AB=6，BC＝4，P是△ABC内部的一个动点，且满足∠P AB ＝∠PBC，则线段CP长的最小值是3、如图，AB是半圆O的直径，点C在半圆O上，AB＝5，AC＝4.D是弧BC上的一个动点，连接AD，过点C作CE⊥AD于E，连接BE.在点D移动的过程中，BE的最小值为4、如图，在Rt△ABC中，∠BAC=90°，AC＝12，AB＝10，点D是AC上的一个动点，以AD为直径作圆O，连接BD交圆O于点E，则AE的最小值为5、如图，正方形ABCD的边长为4，动点E、F分別从点A、C同时出发，以相同的速度分别沿AB、CD向终点B、D移动，当点E到达点B时，运动停止，过点B作直线EF的垂线BG，垂足为点G，连接AG，则AG长的最小值为【辅助圆+将军饮马】如图，正方形ABCD的边长是4，点E是AD边上一动点，连接BE，过点A作AF⊥BE于点F，点P是AD边上另一动点，则PC+PF的最小值为【辅助圆+相切】如图，在Rt△ABC中，∠ACB=90°，∠B=30°，AB＝4，D是BC上一动点，CE⊥AD于E，EF⊥AB交BC于点F，则CF的最大值是三、定边对定角在“定边对直角”问题中，依据“直径所对的圆周角是直角”，关键性在于寻找定边、直角，而根据圆周角定理:同圆或等圆中，同弧或等弧所対的圆周角都相.定边必不可少，而直角则可一般为定角.例如，AB为定值，∠P为定角，则P点轨迹是一个圆.当然，∠P度数也是特殊角，比如30°、45°、60°、120°，下面分别作对应的轨迹圆若∠P＝30°，以AB为边，同侧构造等边三角形AOB，O即为圆心若∠P＝45°，以AB为斜边，同侧构造等腰直角三角形AOB，O即为圆心.若∠P＝60°，以AB为底，同侧构造顶角为120°的等腰三角形AOB，O即为圆心.若∠P＝120°，以AB为底，异侧为边构造顶角为120°的等腰三角形AOB，O即为圆心.【例题1】如图，等边△ABC边长为2，E、F分別是BC、CA上两个动点，且BE=CF，连接AE、BF，交点为P点，则CP的最小值为【举一反三】1、如图，△ABC为等边三角形，AB=3，若P为△ABC内一动点，且满足∠P AB＝∠ACP，则线段PB长度的最小值为2、在△ABC中，AB＝4，∠C＝60°，∠A>∠B，则BC的长的取值范围是3、如图，AB是圆O的直径，M、N是弧AB(异于A、B)上两点，C是弧MN上一动点，∠ACB 的角平分线交圆O于点D，∠BAC的平分线交CD于点E，当点C从点M运动到点N时，则C、E两点的运动路径长的比是。
专题03 隐圆(辅助圆)最值模型
专题03 隐圆类最值问题题型一 滑梯类1．如图，ABC ∆中，90C ∠=︒，10AC =，8BC =，线段DE 的两个端点D 、E 分别在边AC ，BC 上滑动，且6DE =，若点M 、N 分别是DE 、AB 的中点，则MN 的最小值为( )A ．10B 3-C ．6D ．32．如图，矩形ABCD ，1AB =，2BC =，点A 在x 轴正半轴上，点D 在y 轴正半轴上．当点A 在x 轴上运动时，点D 也随之在y 轴上运动，在这个运动过程中，点C 到原点O 的最大距离为 ．3．已知边长为a 的正方形ABCD ，两顶点A 、B 分别在平面直角坐标系的x 轴、y 轴的正半轴上滑动，点C 点D 在第一象限，点E 为正方形ABCD 的对称中心，连接OE ，则OE 的长的最大值是 ．4．已知边长为a 的正三角形ABC ，两顶点A 、B 分别在平面直角坐标系的x 轴、y 轴的正半轴上滑动，点C在第一象限，连接OC，则OC的长的最大值是．5．如图，矩形ABCD中，20AD=，点E，F分别是AB，BC边上的两个动点，且10EF=，AB=，30点G为EF的中点，点H为AD边上一动点，连接CH、GH，则GH CH+的最小值为．题型二定点定长6．如图，在矩形ABCD中，4∆沿AB=，6AD=，E是AB边的中点，F是线段BC边上的动点，将EBF EF所在直线折叠得到△EB F'，连接B D'，则B D'的最小值是．7．如图，在边长为4的菱形ABCD中，60∠=︒，M是AD边的中点，点N是AB边上一动点，将AMN∆A沿MN所在的直线翻折得到△A MN'，连接A C'，则线段A C'长度的最小值是．8．如图，四边形ABCD中，AB AC AD∠=度．∠=︒，则CBDCAD==，若769．如图，在Rt ABCBC=，点F在边AC上，并且2CF=，点E为边BC上的AC=，8∠=︒，6C∆中，90动点，将CEF∆沿直线EF翻折，点C落在点P处，则点P到边AB距离的最小值是()A．1.5B．1.2C．2.4D．以上都不对10．如图，在平行四边形ABCD中，30BC=，CD=M是AD边的中点，N是AB边上BCD∠=︒，4的一动点，将AMN'，连接A C'，则A C'长度的最小值是．∆沿MN所在直线翻折得到△A MN题型三直角所对的是直径11．如图，在圆O中，半径OA弦10⊥，BC=，点Q是劣弧AC上的一个动点，连接BQ，作CP BQ垂足为P．在点Q移动的过程中，线段AP的最小值是()A．6B．7C．8D．912．如图，在ABCAB=，12BC=，D为AC边上的一个动点，连接BD，E为BD ∠=︒，8ABC∆中，90上的一个动点，连接AE，CE，当ABD BCE∠=∠时，线段AE的最小值是()A ．3B ．4C ．5D ．613．如图，Rt ABC ∆中，AB BC ⊥，12AB =，8BC =，P 是ABC ∆内部的一个动点，且满足PAB PBC ∠=∠，连接PC ，则线段CP 长的最小值为 ．14．如图，已知C 的半径为3，圆外一定点O 满足5OC =，点P 为C 上一动点，经过点O 的直线l 上有两点A 、B ，且OA OB =，90APB ∠=︒，l 不经过点C ，则AB 的最小值为 ．15．如图，E 、F 是正方形ABCD 的边AD 上两个动点，满足AE DF =，连接CF 交BD 于G ，连接BE 交AG 于点H ，若正方形的边长为3，则线段DH 长度的最小值是 ．题型四 定边对定角16．如图，在边长为6的等边ABC ∆中，点E ，F 分别是边AC ，BC 上的动点，且AE CF =，连接BE ，AF 交于点P ，连接CP ，则CP 的最小值为 ．第16题 第19题 17．在锐角三角形ABC 中，30A ∠=︒，2BC =，设BC 边上的高为h ，则h 的取值范围是 ．18．在ABC ∆中，90ABC ∠=︒，2AB =，3BC =．点D 为平面上一个动点，45ADB ∠=︒，则线段CD 长度的最小值为 ．19．如图，ABC ∆为等边三角形，2AB =．若P 为ABC ∆内一动点，且满足PAB ACP ∠=∠，则线段PB 长度的最小值为 ．20．【问题情境】（1）点A 是O 外一点，点P 是O 上一动点．若O 的半径为2，且5OA =，则点P 到点A 的最短距离为 ．【直接运用】（2）如图1，在Rt ABC ∆中，90ACB ∠=︒，2AC BC ==，以BC 为直径的半圆交AB 于D ，P 是弧CD 上的一个动点，连接AP ，则AP 的最小值是 ．【构造运用】（3）如图2ABCD 的边长为6，点M 、N 分别从点B 、C 同时出发，以相同的速度沿边BC 、CD 方向向终点C 和D 运动，连接AM 和BN 交于点P ，则点P 到点C 的最短距离，并说明理由．【灵活运用】（4）如图3，O 的半径为4，弦4AB =，点C 为优弧AB 上一动点，AM AC ⊥交直线CB 于点M ，则ABM ∆的面积最大值是 ．21．（1）如图1，已知ABC ∆中，30ABC ∠=︒，1AB AC ==，则ABC S ∆= ．（2）如图2，在平面直角坐标系xOy 中，点A 在y 轴上运动，点B 在x 轴上运动，且4AB =，求AOB ∆面积的最大值．（3）如图3，O的半径为2，弦AB=C为优弧AmB上一动点，AM AC⊥交射线CB于点M，请问，ABM∆的周长存在最大值还是最小值？若存在，求出相应的最值；若不存在，说明理由．22．如图，在平面直角坐标系中，抛物线289=--的图象经过点(0,3)y ax ax aC，交x轴于点A、(B A点在B点左侧），顶点为D．（1）求抛物线的解析式及点A、B的坐标；∠=∠？若存在，求出点P的坐标；若不（2）抛物线的对称轴上是否存在点P，使BPC BAC存在，请说明理由．23．如图，在平面直角坐标系中，二次函数2y ax bx c =++的图象交x 轴于A 、B 两点，交y 轴于C 点，P为y 轴上的一个动点，已知(2,0)A -、(0,C -，且抛物线的对称轴是直线1x =．（1）求此二次函数的解析式；（2）连接PA 、PB ，P 点运动到何处时，使得60APB ∠=︒，请求出P 点坐标．24．如图，顶点为M 的抛物线23y ax bx =++与x 轴交于(3,0)A ，(1,0)B -两点，与y 轴交于点C ．（1）求这条抛物线对应的函数表达式；（2）若在第一象限的抛物线下方有一动点D ，满足DA OA =，过D 作DG x ⊥轴于点G ，设ADG ∆的内心为I ，试求CI 的最小值．题型五 定角定高25．如图，在矩形ABCD 中，1AB =，AD =，E 为BC 边上一动点，F 、G 为AD 边上两个动点，45FEG ∠=︒，则线段FG 的长度最大值为 ．26．辅助圆之定角定高求解探究（1）如图①，已知线段AB ，以AB 为斜边，在图中画出一个直角三角形；（2）如图②，在ABC ∆中，60ACB ∠=︒，CD 为AB 边上的高，若4CD =，试判断AB 是否存在最小值，若存在，请求出AB 最小值；若不存在，请说明理由；（3）如图③，某园林单位要设计把四边形花园划分为几个区域种植不同花草，在四边形ABCD 中，45A ∠=︒，90B D ∠=∠=︒，CB CD ==点E 、F 分别为AB 、AD 上的点，若保持CE CF ⊥，那么四边形AECF 的面积是否存在最大值，若存在，请求出面积的最大值，若不存在，请说明理由．27．问题研究（1）若等边ABC ∆边长为4，则ABC ∆的面积为 ；（2）如图1，在ABC ∆中，60ACB ∠=︒，CD 为AB 边上的高，若4CD =，试判断ABC ∆的面积是否存在最小值．若存在，求出这个最小值；若不存在，请说明理由．问题解决（3）如图2，四边形ABCD 中，AB AD ==，45B ∠=︒，60C ∠=︒，135D ∠=︒，点E 、F 分别为边AB 、BC 上的动点，且EAF C ∠=∠，求四边形AECF 面积的最大值．28．（1）如图1，已知AC 、BC 为O 的两条弦，点D 为O 外一点，则ACB ∠ ADB ∠（请用“<”“ >”或“=”填空）（2）①如图2，若等边ABC ∆内接于O ，4AB =，CD 为O 的切线，则ABD ∆的面积为 ． ②如图3，在ABC ∆中，60ACB ∠=︒，CD 为AB 边上的高．若4CD =，试判断ABC ∆的面积是否存在最小值，若存在，求出这个最小值；若不存在，请说明理由．（3）如图4，正方形ABCD 的边长为4，点E 、F 分别为边AB 、BC 上的动点，且45EDF ∠=︒，求四边形DEBF 面积的最大值．29．问题探究（1）如图1．在ABC ∆中，8BC =，D 为BC 上一点，6AD =．则ABC ∆面积的最大值是 ．（2）如图2，在ABC ∆中，60BAC ∠=︒，AG 为BC 边上的高，O 为ABC ∆的外接圆，若3AG =，试判断BC 是否存在最小值？若存在，请求出最小值；若不存在，请说明理由．问题解决：如图3，王老先生有一块矩形地ABCD ，6212AB =+，626BC =+，现在他想利用这块地建一个四边形鱼塘AMFN ，且满足点E 在CD 上，AD DE =，点F 在BC 上，且6CF =，点M 在AE 上，点N 在AB 上，90MFN ∠=︒，这个四边形AMFN 的面积是否存在最大值？若存在，求出面积的最大值；若不存在，请说明理由．30．如图，平面直角坐标系中，O为原点，点A、B分别在y轴、x轴的正半轴上．AOB∆的两条外角平分线交于点P，P在反比例函数9yx=的图象上．PA的延长线交x轴于点C，PB的延长线交y轴于点D，连接CD．（1）求P∠的度数及点P的坐标；（2）求OCD∆的面积；（3）AOB∆的面积是否存在最大值？若存在，求出最大面积；若不存在，请说明理由．专题03 隐圆（辅助圆）最值模型题型一 滑梯类模型1．如图，ABC ∆中，90C ∠=︒，10AC =，8BC =，线段DE 的两个端点D 、E 分别在边AC ，BC 上滑动，且6DE =，若点M 、N 分别是DE 、AB 的中点，则MN 的最小值为( )A ．10B 3-C ．6D ．3【解答】解：ABC ∆中，90C ∠=︒，10AC =，8BC =，AB ∴==，6DE =，点M 、N 分别是DE 、AB 的中点，12CN AB ∴==，132CM DE ==， 当C 、M 、N 在同一直线上时，取最小值，MN ∴3，故选：B ．2．如图，矩形ABCD ，1AB =，2BC =，点A 在x 轴正半轴上，点D 在y 轴正半轴上．当点A 在x 轴上运动时，点D 也随之在y 轴上运动，在这个运动过程中，点C 到原点O 的最大距离为 1 ．【解答】解：如图，取AD 的中点H ，连接CH ，OH ，矩形ABCD ，1AB =，2BC =，1CD AB ∴==，2AD BC ==，点H 是AD 的中点，1AH DH ∴==，CH ∴===90AOD ∠=︒，点H 是AD 的中点，112OH AD ∴==， 在OCH ∆中，CO OH CH <+，当点H 在OC 上时，CO OH CH =+，CO ∴的最大值为1OH CH +=，1．3．已知边长为a 的正方形ABCD ，两顶点A 、B 分别在平面直角坐标系的x 轴、y 轴的正半轴上滑动，点C 点D 在第一象限，点E 为正方形ABCD 的对称中心，连接OE ，则OE 的长的最大值是 a ．【解答】解：取AB 中点F ，连OF ，EF ，有OE OF FC +，当O 、E 、F 共线时，OE 有最大值，最大值是OF EF +．四边形ABCD 为正方形，90BEA ∴∠=︒，且F 为AB 中点，1122EF OF AB a ∴===， OE ∴的最大值为1122OF EF a a a +=+=， 故答案为：a ．4．已知边长为a 的正三角形ABC ，两顶点A 、B 分别在平面直角坐标系的x 轴、y 轴的正半轴上滑动，点C 在第一象限，连接OC ，则OC 的长的最大值是 ．【解答】解：取AB 中点D ，连OD ，DC ，有OC OD DC +，当O 、D 、C 共线时，OC 有最大值，最大值是OD CD +．ABC ∆为等边三角形，AB BC AC a ∴===，根据三角形的性质可知：12OD a =，CD ==．OC ∴．5．如图，矩形ABCD 中，20AB =，30AD =，点E ，F 分别是AB ，BC 边上的两个动点，且10EF =，点G 为EF 的中点，点H 为AD 边上一动点，连接CH 、GH ，则GH CH +的最小值为 45 ．【解答】解：由已知，点G 在以B 圆心，5为半径的圆在与长方形重合的弧上运动． 作C 关于AD 的对称点C '，连接C B '，交AD 于H ，交以B 为圆心，以5为半径的圆于G 由两点之间线段最短，此时C B '50==，则GH CH +的最小值50545=-=，故答案为：45．题型二 定点定长模型6．如图，在矩形ABCD中，4∆沿AB=，6AD=，E是AB边的中点，F是线段BC边上的动点，将EBFEF所在直线折叠得到△EB F'，连接B D'，则B D'的最小值是2．【解答】解：如图所示点B'在以E为圆心EA为半径的圆上运动，当D、B'、E共线时，此时B D'的值最小，根据折叠的性质，EBF∆≅△EB F'，∴'⊥'，EB B F∴'=，EB EBAB=，E是AB边的中点，4∴='=，2AE EBAD=，6∴=DE2∴'=．B D7．如图，在边长为4的菱形ABCD中，60∆A∠=︒，M是AD边的中点，点N是AB边上一动点，将AMN沿MN所在的直线翻折得到△A MN'，连接A C'，则线段A C'长度的最小值是2．【解答】解：如图所示：在N的运动过程中A'在以M为圆心，MA的长为半径的圆上，∴'是定值，A C'长度取最小值时，即A'在MC上时，MA过点M作MF DC⊥于点F，在边长为4的菱形ABCD 中，60A ∠=︒，M 为AD 中点，2MD ∴=，60FDM ∠=︒，30FMD ∴∠=︒，112FD MD ∴==，cos30FM DM ∴=⨯︒=，MC ∴=2A C MC MA ∴'=-'=．故答案为：2．8．如图，四边形ABCD 中，AB AC AD ==，若76CAD ∠=︒，则CBD ∠= 38 度．【解答】解：AB AC AD ==，∴点B ，C ，D 可以看成是以点A 为圆心，AB 为半径的圆上的三个点，CBD ∴∠是弧CD 对的圆周角，CAD ∠是弧CD 对的圆心角；76CAD ∠=︒，11763822CBD CAD ∴∠=∠=⨯︒=︒． 9．如图，在Rt ABC ∆中，90C ∠=︒，6AC =，8BC =，点F 在边AC 上，并且2CF =，点E 为边BC 上的动点，将CEF ∆沿直线EF 翻折，点C 落在点P 处，则点P 到边AB 距离的最小值是( )A ．1.5B ．1.2C ．2.4D ．以上都不对【解答】解：以F 为圆心，CF 为半径作F ，过点F 作FH AB ⊥于点H 交F 于点G ，则点P 到AB 的距离的最小值FH FP FH FG =-=-．由翻折的性质可知，2PF CF ==，∴点P 在F 上，6AC =，8BC =，10AB ∴=，由AHF ACB ∆∆∽， ∴AF FH AB BC =， ∴4108FH =， 3.2FH ∴=，∴点P 到AB 的距离的最小值 3.22 1.2FH FG =-=-=．故选：B ．10．如图，在平行四边形ABCD 中，30BCD ∠=︒，4BC =，CD =M 是AD 边的中点，N 是AB 边上的一动点，将AMN ∆沿MN A MN '，连接A C '，则A C '长度的最小值是 5 ．【解答】解：如图，连接MC ；过点M 作ME CD ⊥，交CD 的延长线于点E ；四边形ABCD 为平行四边形，//AD BC ∴，4AD BC ==，点M 为AD 的中点，30BCD ∠=︒，2DM MA ∴==，30MDE BCD ∠=∠=︒，112ME DM ∴==，DE ，CE CD DE ∴=+=222CM ME CE =+，7CM ∴=；由翻折变换的性质得：2MA MA '==，显然，当折线MA C '与线段MC 重合时，线段A C '的长度最短，此时725AC '=-=，故答案为5．题型三 直角所对的是直径11．如图，在圆O 中，半径OA 弦10BC =，点Q 是劣弧AC 上的一个动点，连接BQ ，作CP BQ ⊥，垂足为P ．在点Q 移动的过程中，线段AP 的最小值是( )A ．6B ．7C ．8D ．9【解答】解：如图，连接AC ，取BC 的中点K ，连接PK ，AKAB 是直径，90ACB ∴∠=︒，12AC ∴=，5CK BK ==，13AK ∴==，CP BQ ⊥，152PK BC ∴==， PA AK PK -，1358PA ∴-=，PA ∴的最小值为8．故选：C ．12．如图，在ABC ∆中，90ABC ∠=︒，8AB =，12BC =，D 为AC 边上的一个动点，连接BD ，E 为BD 上的一个动点，连接AE ，CE ，当ABD BCE ∠=∠时，线段AE 的最小值是( )A ．3B ．4C ．5D ．6【解答】解：如图，取BC 的中点T ，连接AT ，ET ．90ABC ∠=︒，90ABD CBD ∴∠+∠=︒，ABD BCE ∠=∠，90CBD BCE ∴∠+∠=︒，90CEB ∴∠=︒，6CT TB ==，162ET BC ∴==，10AT ==， AE AT ET -，4AE ∴，AE ∴的最小值为4，故选：B ．13．如图，Rt ABC ∆中，AB BC ⊥，12AB =，8BC =，P 是ABC ∆内部的一个动点，且满足PAB PBC ∠=∠，连接PC ，则线段CP 长的最小值为 4 ．【解答】解：90ABC ∠=︒，90ABP PBC ∴∠+∠=︒，PAB PBC ∠=∠，90BAP ABP ∴∠+∠=︒，90APB ∴∠=︒，∴点P 在以AB 为直径的O 上，连接OC 交O 于点P ，此时PC 最小，在Rt BCO ∆中，90OBC ∠=︒，8BC =，6OB =，10OC ∴==，1064PC OC OP ∴=-=-=．PC ∴最小值为4．故答案为：4．14．如图，已知C 的半径为3，圆外一定点O 满足5OC =，点P 为C 上一动点，经过点O 的直线l 上有两点A 、B ，且OA OB =，90APB ∠=︒，l 不经过点C ，则AB 的最小值为 4 ．【解答】解：如图，连接OP ，PC ，OC ，OP PC OC +，5OC =，3PC =，∴当点O ，P ，C 三点共线时，OP 最短，如图，OA OB =，90APB ∠=︒，2AB OP ∴=，当O ，P ，C 三点共线时，5OC =，3CP =，532OP ∴=-=，24AB OP ∴==，故答案为：4．15．如图，E 、F 是正方形ABCD 的边AD 上两个动点，满足AE DF =，连接CF 交BD 于G ，连接BE 交AG 于点H ，若正方形的边长为3，则线段DH 长度的最小值是 31)2- ．【解答】解：在正方形ABCD 中，AB AD CD ==，BAD CDA ∠=∠，ADG CDG ∠=∠， 在ABE ∆和DCF ∆中，AB CDBAD CDA AE DF=⎧⎪∠=∠⎨⎪=⎩，()ABE DCF SAS ∴∆≅∆，12∴∠=∠，在ADG ∆和CDG ∆中，AD CDADG CDG DG DG=⎧⎪∠=∠⎨⎪=⎩，()ADG CDG SAS ∴∆≅∆，23∴∠=∠，13∴∠=∠，390BAH BAD ∠+∠=∠=︒，190BAH ∴∠+∠=︒，1809090AHB ∴∠=︒-︒=︒，取AB 的中点O ，连接OH 、OD ， 则1322OH AO AB ===，在Rt AOD ∆中，OD根据三角形的三边关系，OH DH OD +>，∴当O 、D 、H 三点共线时，DH 的长度最小，最小值31)2OD OH =-=．故答案为：31)2．题型四 定边对定角模型16．如图，在边长为6的等边ABC ∆中，点E ，F 分别是边AC ，BC 上的动点，且AE CF =，连接BE ，AF 交于点P ，连接CP ，则CP 的最小值为【解答】解：ABC ∆是等边三角形，AB AC BC ∴==，60CAB ACB ∠=∠=︒，在ABE ∆和CAF ∆中，AB AC BAC ACB AE CF =⎧⎪∠=∠⎨⎪=⎩，()ABE CAF SAS ∴∆≅∆，ABE CAF ∴∠=∠，60BPF PAB ABP CAP BAP ∴∠=∠+∠=∠+∠=︒，120APB ∴∠=︒，如图，过点A ，点P ，点B 作O ，连接CO ，PO ，∴点P 在AB 上运动，AO OP OB ==，OAP OPA ∴∠=∠，OPB OBP ∠=∠，OAB OBA ∠=∠，360120AOB OAP OPA OPB OBP ∴∠=︒-∠-∠-∠-∠=︒，30OAB ∴∠=︒，90CAO ∴∠=︒，AC BC =，OA OB =，CO ∴垂直平分AB ，30ACO ∴∠=︒，cos AC ACO CO ∴∠==2CO AO =，CO ∴=AO ∴=，在CPO ∆中，CP CO OP -，∴当点P 在CO 上时，CP 有最小值，CP ∴的最小值=故答案为17．在锐角三角形ABC 中，30A ∠=︒，2BC =，设BC 边上的高为h ，则h 的取值范围是 23h <+ 【解答】解：如图，BC 为O 的弦，2OB OC ==，2BC =，OB OC BC ∴==，OBC ∴∆为等边三角形，60BOC ∴∠=︒，1302BAC BOC ∴∠=∠=︒， 作直径BD 、CE ，连接BE 、CD ，则90DCB EBC ∠=∠=︒，∴当点A 在DE 上（不含D 、E 点）时，ABC ∆为锐角三角形，在Rt BCD ∆中，30D BAC ∠=∠=︒，CD ∴==当A 点为DE 的中点时，A 点到BC 的距离最大，即h 最大，延长AO 交BC 于H ，如图， A 点为DE 的中点，∴AB AC =，AH BC ∴⊥，1BH CH ∴==，OH ∴==2AH OA OH ∴=+=+h ∴的范围为23h +．故答案为23h +．18．在ABC ∆中，90ABC ∠=︒，2AB =，3BC =．点D 为平面上一个动点，45ADB ∠=︒，则线段CD 长度的最小值为 【解答】解：如图所示．45ADB ∠=︒，2AB =，作ABD ∆的外接圆O （因求CD 最小值，故圆心O 在AB 的右侧），连接OC ， 当O 、D 、C 三点共线时，CD 的值最小．90AOB ∴∠=︒，AOB ∴∆为等腰直角三角形，sin 45AO BO AB ∴==︒⨯=45OBA ∠=︒，90ABC ∠=︒，45OBE ∴∠=︒，作OE BC ⊥于点E ，OBE ∴∆为等腰直角三角形．sin451OE BE OB ∴==︒⋅=，312CE BC BE ∴=-=-=，在Rt OEC ∆中，OC ==当O 、D 、C 三点共线时，CD 最小为CD OC OD =-．19．如图，ABC ∆为等边三角形，2AB =．若P 为ABC ∆内一动点，且满足PAB ACP ∠=∠，则线段PB 长度的最小值为 ．【解答】解：ABC ∆是等边三角形，60ABC BAC ∴∠=∠=︒，2AC AB ==，PAB ACP ∠=∠，60PAC ACP ∴∠+∠=︒，∴点P的运动轨迹是AC，当O、P、B共线时，PB长度最小，设OB交AC于D，如图所示：此时PA PC=，OB AC⊥，则112AD CD AC===，30PAC ACP∠=∠=︒，1302ABD ABC∠=∠=︒，tan30PD AD AD∴=⋅︒==，BDPB BD PD∴=-==20．【问题情境】（1）点A是O外一点，点P是O上一动点．若O的半径为2，且5OA=，则点P到点A的最短距离为3．【直接运用】（2）如图1，在Rt ABC∆中，90ACB∠=︒，2AC BC==，以BC为直径的半圆交AB于D，P是弧CD上的一个动点，连接AP AP的最小值是．【构造运用】（3）如图2，已知正方形ABCD的边长为6，点M、N分别从点B、C同时出发，以相同的速度沿边BC、CD方向向终点C和D运动，连接AM和BN交于点P，则点P到点C的最短距离，并说明理由．【灵活运用】（4）如图3，O的半径为4，弦4AB=，点C为优弧AB上一动点，AM AC⊥交直线CB于点M，则ABM∆的面积最大值是．【解答】解：（1）连接AP、OP，如图4所示：O 的半径为2，2OP ∴=，523OA OP ∴-=-=，PA OA OP ∴-，3PA ∴，∴当点P 在OA 上时，PA 最短，最小值为3，故答案为：3；（2）连接OA ，交半圆于P '，连接OP ，如图1所示：2AC BC ==，BC 为半圆的直径，112OP OC BC ∴===，90ACB ∠=︒，OA ∴==AP OA OP -， 51AP ∴-，∴当点P 在OA 上时，AP1-，1；（3）点P 到点C 的最短距离为3，理由如下：取AB 中点O ，连接OP 、OC 、PC ，如图2所示：点M 、N 分别从点B 、C 同时出发，以相同的速度沿边BC 、CD 方向向终点C 和D 运动， BM CN ∴=，四边形ABCD 是正方形，6AB BC ∴==，90ABM BCN ∠=∠=︒，在ABM ∆和BCN ∆中，BM CNABM BCN AB BC=⎧⎪∠=∠⎨⎪=⎩，()ABM BCN SAS ∴∆≅∆，BAM CBN ∴∠=∠，90CBN ABN ∠+∠=︒， 90BAM ABN ∴∠+∠=︒， 90APB ∴∠=︒， ∴点P 在以AB 为直径的O 上运动， 132OP OA OB AB ====，OC =又PC OC OP -， 353PC ∴-，PC ∴的最小值为3；（4）连接OA 、OB ，如图3所示： 4OA OB AB ===， AOB ∴∆是等边三角形， 60AOB ∴∠=︒， 11603022ACB AOB ∴∠=∠=⨯︒=︒，AM AC ⊥， 60M ∴∠=︒， ∴点M 在以120ADB ∠=︒的D 上， 4AB =，ABM S ∆最大，则点M 的距离最大， ∴当AM BM =时点M 到AB 的距离最大， ABM ∴∆是等边三角形，114422ABM S AB AB ∆∴==⨯=故答案为：21．（1）如图1，已知ABC ∆中，30ABC ∠=︒，1AB AC ==，则ABC S ∆= ． （2）如图2，在平面直角坐标系xOy 中，点A 在y 轴上运动，点B 在x 轴上运动，且4AB =，求AOB ∆面积的最大值．（3）如图3，O 的半径为2，弦AB =C 为优弧AmB 上一动点，AM AC ⊥交射线CB 于点M ，请问，ABM ∆的周长存在最大值还是最小值？若存在，求出相应的最值；若不存在，说明理由．【解答】解：（1）如图1中，作AH BC ⊥于H ．AB AC =，AH BC ⊥，BH CH ∴=，1AB =，30B ∠=︒，1122AH AB ∴==，2BC BH ==1122ABC S ∆∴==．（2）如图2中，取AB 的中点E ，连接OE ，作OH AB ⊥于H ．90AOB ∠=︒，AE EB =，122OE AB ∴==，OH AB ⊥，OH OE ∴，即2OH ，OH ∴的最大值为2，AOB ∴∆的面积的最大值12442=⨯⨯=．（3）如图3中，连接OA ，OB ，作OH AB ⊥于H ．OH AB ⊥，OA OB =，AH BH ∴==AOH BOH ∠=∠，sin AOH ∴∠，60AOH ∴∠=︒，2120AOB AOH ∠=∠=︒，1602ACB AOB ∴∠=∠=︒， MA AC ⊥，90MAC ∴∠=︒30M ∴∠=︒，如图31-中，ABM ∆中，AB =30AMB ∠=︒，ABM ∆的周长存在最大值，理由如下；作ABM ∆的外接圆，取优弧AB 的中点O ，连接OA ，OB ，以O 为圆心，OA 为半径作O ，延长AM 交O 于F ，连接BF ．30AOB AMB ∠=∠=︒，1152AFB AOB ∴∠=∠=︒， 30AMB F MBF ∠=∠+∠=︒，F MBF ∴∠=∠，MF MB ∴=，MA MB MA MF AF ∴+=+=，∴当AF 的值最大时，MA MB +的值最大，此时MAB ∆的周长最大，延长AO 交O 于E ，连接BE 交ABM ∆的外接圆于D ，连接AD ，OD ． 易知：90ABD AOD ∠=∠=︒，OD AE ∴⊥，OA OE =，DA DE ∴=，15E EAD ∴∠=∠=︒，151530ADB ∴∠=︒+︒=︒，2AD DE AB ∴===6BD =，6BE ∴=，AE ∴当AF 与AE 重合时，AF 的值最大，AF ∴的最大值为ABM ∴∆的周长的最大值为22．如图， 在平面直角坐标系中， 抛物线289y ax ax a =--的图象经过点(0,3)C ，交x 轴于点A 、(B A 点在B 点左侧） ，顶点为D ．（1） 求抛物线的解析式及点A 、B 的坐标；（2）抛物线的对称轴上是否存在点P ，使BPC BAC ∠=∠？若存在， 求出点P 的坐标；若不存在， 请说明理由 ．【解答】解： （1）把(0,3)C 代入289y ax ax a =--得93a -=，解得13a =-， ∴所以抛物线的解析式为182333y x x =-++． 令0y =得：1823033x x -++=，解得：11x =-，29x =， (1,0)A ∴-，(9,0)B ．（2）分两种情况：①如图 2 ，以AB 为直径作M ，M 交抛物线的对称轴于(P BC 的下方） ．42b x a=-=， ∴点P 的横坐标为 4 ．由圆周角定理得CPB CAB ∠=∠，(1,0)A -，(9,0)B ，10AB ∴=．152MP AB ∴==． (4,5)P ∴-．②如图 3 所示： 以A B '为直径作M '，M '交抛物线的对称轴于P '，过点M '作M E P F '⊥'，垂足为E ，连接P M ''．点A '与点A 关于BC 对称，10AB A B ∴='=，A A ∠=∠'．CP B CA B ∠'=∠'，CP B A ∴∠'=∠．(1,6)A '，(9,0)B(5,3)M ∴'．1M E ∴'=．152M P A B ''='=，P E ∴'=∴点P '的坐标为(4，3)．综上所述， 点P 的坐标为(4,5)P -或(4，3)．23．如图，在平面直角坐标系中，二次函数2y ax bx c =++的图象交x 轴于A 、B 两点，交y 轴于C 点，P 为y 轴上的一个动点，已知(2,0)A -、(0,C -，且抛物线的对称轴是直线1x =．（1）求此二次函数的解析式；（2）连接PA 、PB ，P 点运动到何处时，使得60APB ∠=︒，请求出P 点坐标．【解答】解：（1）将A ，C 点坐标代入函数解析式，及对称轴，得42012a b c c b a⎧-+=⎪⎪=-⎨⎪⎪-=⎩，解得a b c ⎧=⎪⎪⎪⎪=⎨⎪⎪=-⎪⎪⎩，抛物线的解析式为2y x -，（2）以AB 为边作等边ABM ∆，作ABM ∆的外接圆O '，交y 轴负半轴于P ，作O E AB '⊥于E ，连接BO '，O P '．设(0,)P m ． 易知：(1,3)O '-，23BO O P '='=，21(3)12m ∴++=，113m ∴=--或113-（舍弃）， (0,311)P ∴--，根据对称性可知(0,311)P '+也符合条件．24．如图，顶点为M 的抛物线23y ax bx =++与x 轴交于(3,0)A ，(1,0)B -两点，与y 轴交于点C ．（1）求这条抛物线对应的函数表达式；（2）若在第一象限的抛物线下方有一动点D ，满足DA OA =，过D 作DG x ⊥轴于点G ，设ADG ∆的内心为I ，试求CI 的最小值．【解答】解：（1）抛物线23y ax bx =++过点(3,0)A ，(1,0)B -，∴933030a b a b ++=⎧⎨-+=⎩ 解得：12a b =-⎧⎨=⎩， ∴这条抛物线对应的函数表达式为223y x x =-++．（2）解法一：如图，连接IO ，ID ，IA ，I 是ADG ∆的内心，IA ∴平分DAG ∠，ID 平分ADG ∠，12IAD DAG ∴∠=∠，12ADI ADG ∠=∠．90DAG ADG ∠+∠=︒，45IAD ADI ∴∠+∠=︒，135AID ∴∠=︒．在ADI ∆和AOI ∆中，AD AODAI OAI AI AI=⎧⎪∠=∠⎨⎪=⎩，()ADI AOI SAS ∴∆≅∆．135AID AIO ∴∠=∠=︒． OA 为定线段，OIA ∠恒等于135︒，∴点I 在以OA 为弦，所含的圆周角等于135︒的圆弧上，设该圆的圆心为E ，连接EO ，EA ，135OIA ∠=︒，90OEA ∴∠=︒．EO EA =，EOA ∴∆为等腰直角三角形．过点E 作EH OA ⊥于点H ， 则1322AH OH OA ===．OE ∴=．∴圆心E 的坐标为3(2，3)2，E ． 当点I 在线段CE 上时，CI 的值最小，CI 的最小值CE OE =-==．题型五 定角定高模型25．如图，在矩形ABCD 中，1AB =，AD =，E 为BC 边上一动点，F 、G 为AD 边上两个动点，45FEG ∠=︒，则线段FG 的长度最大值为 2 ．【解答】解：如图，作EFG ∆的外接圆O ，连接OA ，OE ，OG ，过点O 作OH AD ⊥于H ，过点E 作EQ AD ⊥于Q ，连接AC ．四边形ABCD 是矩形，90B ∴∠=︒，1AB CD ==，AD BC ==2AC ∴=，45FEG ∠=︒，290FOG FEG ∴∠=∠=︒，12EFG EOG ∠=∠， 290EOF FOG EOG EFG ∴∠=∠+∠=∠+︒，1112221cos cos(45)cos(90)2EF EF EF OF OE OEF EFG EOF ====∠︒-∠︒-∠， ∴当EF 最大，且EFG ∠最小时，OF 的值最大，则FG 的值最大， 1sin 2EQEQ EFG FQ AC ∠==， ∴当点E 与C 重合，F与A 重合时，“=”号成立，12cos(4530)AC OF OE ∴==-︒-︒FG ∴的最大值2==．故答案为2．26．辅助圆之定角定高求解探究（1）如图①，已知线段AB ，以AB 为斜边，在图中画出一个直角三角形；（2）如图②，在ABC ∆中，60ACB ∠=︒，CD 为AB 边上的高，若4CD =，试判断AB 是否存在最小值，若存在，请求出AB 最小值；若不存在，请说明理由；（3）如图③，某园林单位要设计把四边形花园划分为几个区域种植不同花草，在四边形ABCD 中，45A∠=︒，90B D ∠=∠=︒，CB CD ==点E 、F 分别为AB 、AD 上的点，若保持CE CF⊥，那么四边形AECF【解答】解：（1）如图①中，ABC ∆即为所求．（2）如图②中，作ABC ∆的外接圆O ，连接OA ，OB ，OC ，作OE AB ⊥于E ．设2OA OC x ==．2120AOB ACB ∠=∠=︒，OA OB =，OE AB ⊥，AE EB ∴=，60AOE BOE ∠=∠=︒， 12OE OA x ∴==，AE =，OC OE CD +，34x ∴， 43x∴， x ∴的最小值为43，2AB =，AB ∴． （3）如图③中，连接AC ，延长BC 交AD 的延长线于G ，将CDF ∆顺时针旋转得到CBH ∆，作CEH ∆的外接圆O ．90ADC ABC ∠=∠=︒，AC AC =，CD CB =，Rt ACD Rt ACB(HL)∴∆≅∆， ACD ACB S S ∆∆∴=，45DAB ∠=︒，135DCB ∴∠=︒， 45DCG ∴∠=︒， 90CDG ∠=︒，CD DG ∴==12CG ∴==，12AB GB ∴==+由（2）可知，当CEH ∆的外接圆的圆心O 在线段BC 上时，ECH ∆的面积最小，此时四边形AFCE 的面积最大，设OC OE r ==，易知2OB EB ==，r ∴=r ∴=，12(2EH ∴=，∴四边形AFCE 的面积的最大值112(1212(214422=⨯⨯+⨯⨯⨯． 27．问题研究（1）若等边ABC ∆边长为4，则ABC ∆的面积为（2）如图1，在ABC ∆中，60ACB ∠=︒，CD 为AB 边上的高，若4CD =，试判断ABC ∆的面积是否存在最小值．若存在，求出这个最小值；若不存在，请说明理由． 问题解决（3）如图2，四边形ABCD 中，AB AD ==，45B ∠=︒，60C ∠=︒，135D ∠=︒，点E 、F 分别为边AB 、BC 上的动点，且EAF C ∠=∠，求四边形AECF 面积的最大值．【解答】解：（1）过点C 作CD AB ⊥于D ，等边ABC ∆边长为4，114222AD BD AB ∴===⨯=， 在Rt ACD ∆中，由勾股定理得22AC AD CD =+，即22242CD =+，解得：CD =，11422ABC S AB CD ∆∴=-=⨯⨯故答案为：（2）CD 为AB 边上的高，若4CD =，设AB c =，AC b =，BC a =，过A 作AE BC ⊥于E ，111sin60222ABC S AB CD AE BC BC AC ∆∴=⨯=⨯=⨯⨯︒，4c ∴=，又sin 60AE AC =⋅︒=，1cos602CE AC b =⋅︒=， 12BE BC EC a b =-=-，在Rt ABE ∆中，由勾股定理得222AB AE BE =+，即2221)()2c a b =+-， 2222c a b ab ab ab ab ∴=+--=，仅当a b =时取等号，即ABC ∆为等边三角形时， 283c c ∴，833c∴，11422ABC S AB CD ∆∴=⋅==最小 （3）45B ∠=︒，60C ∠=︒，135ADC ∠=︒，3603604560135120BAD B C D ∴∠=︒-∠-∠-∠=︒-︒-︒-︒=︒，将ABE ∆逆时针旋转120︒得ADG ∆， 45ADG B ∠=∠=︒，AE AG =， 45135180ADG ADC ∴∠+∠=︒+︒=︒， C ∴、D 、G 三点共线，60EAF C ∠=∠=︒，12060BAE FAD EAF ∠+∠=︒-∠=︒， 60GAD FAD BAE FAD ∴∠+∠=∠+∠=︒，在EAF ∆和GAF ∆中，AE AGEAF GAF AF AF =⎧⎪∠=∠⎨⎪=⎩， ()EAF GAF SAS ∴∆≅∆， EF GF ∴=，ABE ADF AGF AECF ABCD ABCD S S S S S S ∆∆∆=--=-四边形四边形四边形，∴当AGF S ∆最小时，AECF S 四边形最大，过A 作AH CG ⊥于H ，4AD =45ADH ∠='，sin454AH DH AD ∴==⋅︒=， 60FAG ∠=︒，11sin 6022AGF S AF AG AG AH GF ∆∴=--︒⋅=-， 由（2）知AG AF =时，AFG ∆面积最小，由点F 在CD 上运动，达不到AFG ∆是等边三角形，当向D 运动时，AFG ∆面积逐渐减小，∴点F 到点D 时，AFG ∆面积最小，此时ABE AFG AFE ∆≅∆≅∆，45ABE AFE AFG HAF ∴∠=∠=∠=∠=︒，6BAE FAE AG O ∠=∠=∠=︒，AB AF AD ===在_AH 上取点M 使30HGM ∠=︒， 604515HAG FAG FAH ∠=∠-∠=︒-︒=︒，9075AGH GAH '∴∠=-∠=︒，75(9030)15AGM AGH MGH HAG ∴∠=∠-∠=︒-︒-︒=︒=∠，设GH x =，2MG x =，由勾股定理MH =，24AH AM MH x ∴=+=+=，4(2x ∴=-，44(212GF ∴=+=-，14(12242AEF AGF S S ∆∆==⨯⨯-=-12EF GF ==-1354590EFC ADC ADE ∠=∠-∠=︒-︒=︒，60C ∠=︒，2111tan (1248222CEF S EF FC EF EF FEC ∆∴=⋅=⋅⋅∠=⨯-=，244824AEF CEF AECF S S S ∆∆∴=+=-=四边形．∴四边形AECF 面积的最大值为24．28．（1）如图1，已知AC 、BC 为O 的两条弦，点D 为O 外一点，则ACB ∠ > ADB ∠（请用“<”“ >”或“=”填空）（2）①如图2，若等边ABC ∆内接于O ，4AB =，CD 为O 的切线，则ABD ∆的面积为 ． ②如图3，在ABC ∆中，60ACB ∠=︒，CD 为AB 边上的高．若4CD =，试判断ABC ∆的面积是否存在最小值，若存在，求出这个最小值；若不存在，请说明理由．（3）如图4，正方形ABCD 的边长为4，点E 、F 分别为边AB 、BC 上的动点，且45EDF ∠=︒，求四边形DEBF 面积的最大值．【解答】解：（1）如图1，设AD 与O 交于E ，连接BE ， 则C AEB ∠=∠，AEB D ∠>∠，ACB ADB ∴∠>∠；故答案为：>；（2）①如图2，连接CO 并延长交AB 于E ， ABC ∆是等边三角形， AC CB ∴=，∴AC BC =，CE AB ∴⊥，2AE BE ==，CE ∴=CD 为O 的切线，CE CD ∴⊥， //CD AB ∴，ABD ∴∆的面积11422AB CE =⋅=⨯=故答案为：②如图3中，作ABC ∆的外接圆O ，连接OA ，OB ，OC ，作OE AB ⊥于E ．设2OA OC x ==． 2120AOB ACB ∠=∠=︒，OA OB =，OE AB ⊥，AE EB ∴=，60AOE BOE ∠=∠=︒， 12OE OA x ∴==，AE =，OC OE CD +， 34x ∴， 43x∴， x ∴的最小值为43，2AB =，AB ∴； ABC ∴∆的面积的最小值142=⨯； （3）四边形DEBF 面积ADE CDF ABCD S S S ∆∆=--正方形，∴当ADE CDF S S ∆∆+DEBF 的面积有最大值，如图4，将DAE ∆逆时针旋转90︒得到DCM ∆， 180FCM FCD DCM ∴∠=∠+∠=︒，AE CM =，F ∴、C 、M 三点共线， DE DM ∴=，90EDM ∠=︒，90EDF FDM ∴∠+∠=︒， 45EDF ∠=︒，45FDM EDF ∴∠=∠=︒，在DEF ∆和DMF ∆中，DE DMEDF MDF DF DF =⎧⎪∠=∠⎨⎪=⎩， ()DEF DMF SAS ∴∆≅∆，EF MF ∴=，EF CF AE ∴=+；DEF ∆的面积DFM =∆的面积122ADE DCF S S EF CD EF ∆∆=+=⨯=，DEF ∴∆面积2EF =．EF AE CF =+，4AE BE AB +==，4BF CF BC +==， 8EF BE BF AB BC ∴++=+=， 8BE BF EF ∴+=-，22222(8)6416BE BF BE BF EF EF EF ∴⋅++=-=+-，且222BE FB EF +=， 328BE BF EF ∴⋅=-，2()0BE BF -， 222BE BF BE BF ∴+⋅， 26416EF EF ∴-2(8)128EF ∴+，828EF ∴-，或828EF --（舍去），EF ∴的最小值为8-，DEF ∴∆面积的最小值为，∴四边形DEBF 面积的最大值441632=⨯-=-29．问题探究（1）如图1．在ABC ∆中，8BC =，D 为BC 上一点，6AD =．则ABC ∆面积的最大值是 24 ． （2）如图2，在ABC ∆中，60BAC ∠=︒，AG 为BC 边上的高，O 为ABC ∆的外接圆，若3AG =，试判断BC 是否存在最小值？若存在，请求出最小值；若不存在，请说明理由．问题解决：如图3，王老先生有一块矩形地ABCD ，12AB =，6BC =，现在他想利用这块地建一个四边形鱼塘AMFN ，且满足点E 在CD 上，AD DE =，点F 在BC 上，且6CF =，点M 在AE 上，点N 在AB 上，90MFN ∠=︒，这个四边形AMFN 的面积是否存在最大值？若存在，求出面积的最大值；若不存在，请说明理由．【解答】解：（1）当AD BC ⊥时，ABC ∆面积的最大，则ABC ∆面积的最大值是11862422BC AD ⋅=⨯⨯=，故答案为：24；（2）如图2中，连接OA ，OB ，OC ，作OE BC ⊥于E ．设2OA OC x ==，2120COB CAB ∠=∠=︒，OC OB =，OE CB ⊥， CE EB ∴=，60COE BOE ∠=∠=︒，12OE OB x ∴==，BE ，OA OE AG +，33x ∴， 1x ∴，x ∴的最小值为1，2BC =，BC ∴的最小值为（3）如图3中，连接AF ，EF ，延长BC 交AE 的延长线于G ，90D ∠=︒，6AD DE ==，45DAE AED ∴∠=∠=︒，12CD AB ==，6CE CF ∴==，45CEF CFE ∴∠=∠=︒， 90AEF ∴∠=︒，EF BF ∴=，将EFM ∆顺时针旋转得到FBH ∆，作FHN ∆的外接圆O 交AB 于N ， 连接ON ，90AEF ABF ∠=∠=︒，AF AF =，EF BF =，Rt AEF Rt ABF(HL)∴∆≅∆， AEF ABF S S ∆∆∴=，。
初中数学,隐圆与极值问题经典题型.doc
初中数学，隐圆与极值问题经典题型有关隐圆比较经典的极值题型总结，分享如下：1、矩形ABCD，M为边AB上一动点，沿着DM翻折△MDA得到△MDA1，则BA1的最小值是2、如图，E，F是正方形ABCD的边AD上两个动点，满足AE=DF．连接CF交BD于点G，连接BE交AG于点H．若正方形的边长为2，则线段DH长度的最小值是3、如图，边长为3的等边△ABC，D、E分别为边BC、AC上的点，且BD＝CE，AD、BE交于P点，则CP的最小值为4、如图，Rt△ABC中，AB⊥BC，AB=2，BC=3，P是△ABC 内部的一个动点，且满足∠PAB=∠PBC，则线段CP长的最小值为．5、如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，D 为AB边上一点，过点D作CD的垂线交直线BC于点E，则线段CE长度的最小值是6、Rt△ABC中, ∠C＝90°, ∠ABC＝30°,AB＝6, D在AB 边上, 点E是BC边上一点(不与点B、C重合), 且DA＝DE,则AD的最小值是7、如图，∠xOy=45°，把线段的两个顶点A,B分别在Ox，Oy上移动，其中AB=10，点O到AB的距离的最大值为8、如图4，在边长为2的菱形ABCD中，∠A=60°，M 是AD边的中点，N是AB边上一动点，将△AMN沿直线MN翻折得到△A1MN,连接CA1,BA1.（1）A1B长度的最小值是（2）A1C长度的最小值是9、四边形ABCD中，AD∥BC，∠A=90,AD=1，AB=2,BC=3,P是线段AD上一动点，将△ABP沿BP所在直线翻折得到△QBP，则△CQD的面积最小值为10、如图，半圆O的半径为1，AC⊥AB，BD⊥AB，且AC=1，BD=3，P是半圆上任意一点，则封闭图形ABDPC 面积的最大值是11、如图，P为圆O内一个定点，A为圆O上一个动点，射线AP,AO分别与圆O交于B，C两点，若圆O的半径为3，OP=，则弦BC的最大值为________12、已知A（2，0），B（5，0），点P为圆A上一动点，圆A半径为2，以PB为边作等边△PMB，求线段AM的取值范围。
专题09巧用隐圆妙解最值(原卷版)
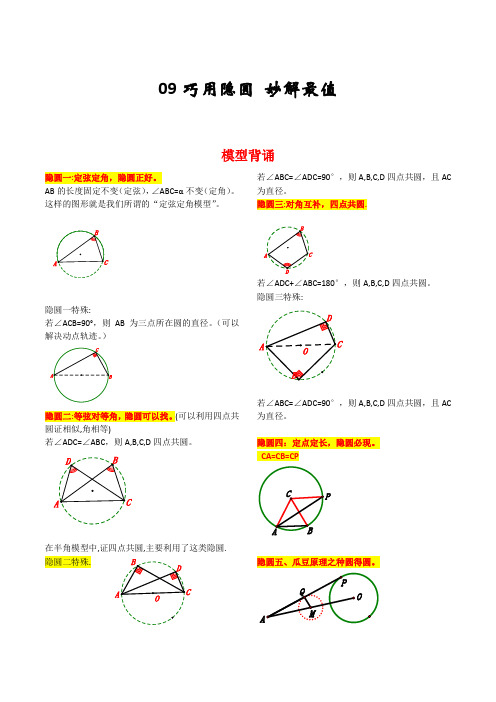
A09巧用隐圆 妙解最值模型背诵隐圆一:定弦定角，隐圆正好。
AB 的长度固定不变（定弦），∠ABC=α不变（定角）。
这样的图形就是我们所谓的“定弦定角模型”。
隐圆一特殊:若∠ACB=90°，则AB 为三点所在圆的直径。
（可以解决动点轨迹。
）隐圆二:等弦对等角，隐圆可以找。
(可以利用四点共圆证相似,角相等)若∠ADC=∠ABC ，则A,B,C,D 四点共圆。
在半角模型中,证四点共圆,主要利用了这类隐圆.隐圆二特殊.若∠ABC=∠ADC=90°，则A,B,C,D 四点共圆，且AC 为直径。
隐圆三:对角互补，四点共圆.若∠ADC+∠ABC=180°，则A,B,C,D 四点共圆。
隐圆三特殊:若∠ABC=∠ADC=90°，则A,B,C,D 四点共圆，且AC为直径。
隐圆四：定点定长，隐圆必现。
CA=CB=CP隐圆五、瓜豆原理之种圆得圆。
若Q为AP的中点，当P沿⊙O运动一周，则Q的运动轨迹为以 AO 中点M为圆心的圆。
（P为“主动点”，点Q为“从动点。
）典例分析如图11，点P（3,4），圆P半径为2，A（2.8,0），B（5.6,0），点M是圆P上的动点，点C是MB的中点，则AC的最小值是_______．【点睛】图12，M点为主动点，C点为从动点，B点为定点．考虑C是BM中点，可知C点轨迹：取BP 中点O，以O为圆心，OC为半径作圆，即为点C轨迹．图13：当A、C、O三点共线且点C在线段OA上时，AC取到最小值，根据B、P坐标求O，利用两点间距离公式求得OA，再减去OC即可．实战训练一．选择题（共8小题）1．如图，在Rt△ABC中，∠C＝90°且AB＝10，点P为△ABC的内心，点O为AB边中点，将BO绕点B 顺时针旋转90°得到线段BD，连接DP，则DP长的最小值为（）A．5√5−5√2B．52C．3√5−3√2D．5√2−522．已知抛物线y=−316(x−1)(x−9)与x轴交于A，B两点，对称轴与x轴交于点D，点C为抛物线的顶OyxA BCMPOOyxA BCMPOPMCBA xyO图11图12图13点，以C 点为圆心的⊙C 半径为2，点G 为⊙C 上一动点，点P 为AG 的中点，则DP 的最大值与最小值和为（ ）A ．72B ．2√3C ．√412D ．53．如图，矩形ABCD 中，AB ＝4，BC ＝6，点P 是矩形ABCD 内一点，连接P A ，PC ，PD ，若P A ⊥PD ，则PC 的最小值为（ ）A ．2√13−4B ．2√10−3C ．2D ．44．如图，在矩形ABCD 中，已知AB ＝3，BC ＝4，点P 是BC 边上一动点（点P 不与B ，C 重合），连接AP ，作点B 关于直线AP 的对称点M ，则线段MC 的最小值为（ ）A ．2B ．52C ．3D ．√105．如图，AB 为⊙O 的直径，C 为⊙O 上一点，其中AB ＝4，∠AOC ＝120°，P 为⊙O 上的动点，连接AP ，取AP 中点Q ，连接CQ ，则线段CQ 的最大值为（ ）A ．3B ．1+√6C ．1+3√2D ．1+√76．如图，在△ABC 中，∠ACB ＝90°，AC ＝BC ，AB ＝4cm ，CD 是中线，点E 、F 同时从点D 出发，以相同的速度分别沿DC 、DB 方向移动，当点E 到达点C 时，运动停止，直线AE 分别与CF 、BC 相交于G 、H ，则在点E 、F 移动过程中，点G 移动路线的长度为（ ）A ．2B ．πC ．2πD ．√22π 7．如图，在△ABC 中，∠ABC ＝90°，AB ＝8，BC ＝12，D 为AC 边上的一个动点，连接BD ，E 为BD 上的一个动点，连接AE ，CE ，当∠ABD ＝∠BCE 时，线段AE 的最小值是（ ）A ．3B ．4C ．5D ．68．如图，已知在矩形ABCD 中，AB ＝1，BC =√3，点P 是AD 边上的一个动点，连接BP ，点C 关于直线BP 的对称点为C 1，当点P 运动时，点C 1也随之运动．若点P 从点A 运动到点D ，则线段CC 1扫过的区域的面积是（ ）A ．πB ．π+3√34C ．3√32D ．2π二．填空题（共12小题）9．如图，等边三角形ABC 和等边三角形ADE ，点N ，点M 分别为BC ，DE 的中点，AB ＝6，AD ＝4，△ADE 绕点A 旋转过程中，MN 的最大值为 ．10．如图，正方形ABCD中，AB＝4，动点E从点A出发向点D运动，同时动点F从点D出发向点C运动，点E、F运动的速度相同，当它们到达各自终点时停止运动，运动过程中线段AF、BE相交于点P，M是线段BC上任意一点，则MD+MP的最小值为√．11．如图，在锐角三角形ABC中，BC＝8，sin A=45，BN⊥AC于点N，CM⊥AB于点M，连接MN，则△AMN面积的最大值是．12．在△ABC中，AB＝4，∠C＝45°，则√2AC+BC的最大值为．13．如图，四边形ABCD中，AB＝AC＝AD，∠CBD＝15°，BD=√3AB，则∠BDC＝．14．如图，等边△ABC中，AB＝6，点D、点E分别在BC和AC上，且BD＝CE，连接AD、BE交于点F，则CF的最小值为．15．如图，正方形ABCD中，AB＝2，动点E从点A出发向点D运动，同时动点F从点D出发向点C运动，点E、F运动的速度相同，当它们到达各自终点时停止运动，运动过程中线段AF、BE相交于点P，M是线段BC上任意一点，则MD+MP的最小值为．16．如图，Rt△ABC中，∠ACB＝90°，∠CAB＝60°，AB＝4，点P是BC边上的动点，过点C作直线AP的垂线，垂足为Q，当点P从点C运动到点B时，点Q的运动路径长为．17．如图，在平面直角坐标系中，有一条长为10的线段AB，其端点A、点B分别在y轴、x轴上滑动，点C为以AB为直径的⊙D上一点（C始终在第一象限），且tan∠BAC=12．则当点A从A0（0，10）滑动到O（0，0），B从O（0，0）滑动到B0（10，0）的过程中，点C运动的路径长为．18．如图，等边△ABC的边长为6，D为BC边上的中点，P为直线BC上方的一个动点，且满足∠P AD＝∠PDB，则线段CP长的最大值为．19．在△ABC中，∠ABC＝90°，AB＝2，BC＝3．点D为平面上一个动点，∠ADB＝45°，则线段CD长度的最小值为．20．如图，在矩形ABCD中，AB＝1，AD=√3，P为AD上一个动点，连接BP，线段BA与线段BQ关于BP所在的直线对称，连接PQ，当点P从点A运动到点D时，线段PQ在平面内扫过的面积为．三．解答题（共3小题）21．圆的定义：在同一平面内，到定点的距离等于定长的所有点所组成的图形．（1）已知：如图1，OA＝OB＝OC，请利用圆规画出过A、B．C三点的圆．若∠AOB＝70°，则∠ACB ＝．如图，Rt△ABC中，∠ABC＝90°，∠BCA＝30°，AB＝2．（2）已知，如图2．点P为AC边的中点，将AC沿BA方向平移2个单位长度，点A、P、C的对应点分别为点D、E、F，求四边形BDFC的面积和∠BEA的大小．（3）如图3，将AC边沿BC方向平移a个单位至DF，是否存在这样的a，使得直线DF上有一点Q，满足∠BQA＝45°且此时四边形BADF的面积最大？若存在，求出四边形BADF面积的最大值及平移距离a，若不存在，说明理由．22．阅读下列材料，回答问题．材料：求圆外一定点到圆上距离最小值是安徽省中考数学较为常见的一种题型，此类题型试题有时出题者将圆隐藏，故又称为“隐圆问题”．解决这类问题，关键是要找到动点的运动轨迹，即该动点是绕哪一个定点旋转，且能保持旋转半径不变．从而找到动点所在的隐藏圆，进而转换成圆外一点到圆心的距离减半径，求得最小值．解决问题：（1）如图①，圆O的半径为1，圆外一点A到圆心的距离为3，圆上一动点B，当A、O、B满足条件时，AB有最小值为．（2）如图②，等腰△ABC两腰长为5，底边长为6，以A为圆心，2为半径作圆，圆上动点P到BC的距离最小值为．（3）如图③，OA⊥OB，P、Q分别是射线OA、OB上两个动点，C是线段PQ的中点，且PQ＝4，则在线段PQ滑动的过程中，求点C运动形成的路径长，并说明理由．（4）如图④，在矩形ABCD中，AB＝4，AD＝8，点E是AB中点，点F是BC上一点，把△BEF沿着EF翻折，点B落在点B'处，求DB'的最小值，并说明理由．（5）如图⑤，在△ABC中，AB＝10，AC＝8，BC＝6，以边AB中点O为圆心，作半圆与AC相切，点P，Q分别是边BC和半圆上的动点，连接PQ，求PQ长的最小值，并说明理由．23．在矩形ABCD中，BC=√3CD，点E、F分别是边AD、BC上的动点，且AE＝CF，连接EF，将矩形ABCD沿EF折叠，点C落在点G处，点D落在点H处．（1）如图1，当EH与线段BC交于点P时，求证：PE＝PF；（2）如图2，当点P在线段CB的延长线上时，GH交AB于点M，求证：点M在线段EF的垂直平分线上；（3）当AB＝5时，在点E由点A移动到AD中点的过程中，计算出点G运动的路线长．。
隐圆问题 最值问题 7种题型 知识点+例题+练习(非常好 分类全面)
4、90o的圆周角所对的弦为直径
（动态问题中一般会出现多个直角，往往会有一个直角所对斜边是固定不变的，选取该斜边中点为圆心，斜边中线为半径）
7、寻找特殊点和线段两端点形成特殊角
例1：如图， 为正三角形，做 的外接圆
（1）D为优弧 上一点，则 =
（2）已知线段 和直线 ，请用尺规作图在直线 上找一点 ，使得 .（可改成 ， ）
练习：1、如图， 为正三角形，做 的外接圆
（1）D为劣弧 上一点，则 =
（2）若三角形的3个内角均小于120°，三角形存在一点P，使得PA、PB、PC的夹角均为120°，我们称点P为 的费马点。
A．1B． C． D．5
3、如图，已知△ABC为等腰直角三角形，∠BAC=90∘，AC=2，以点C为圆心，1为半径作圆，点P为⊙C上一动点，连结AP，并绕点A顺时针旋转90∘得到AP′，连结CP′，则CP′的取值范围是____________.
4、如图，在Rt△ABC中，∠ACB=90∘，AC=4，BC=3，点D是平面内的一个动点，且AD=2，M为BD的中点，在D点运动过程中，线段CM长度的取值范围是_________.
例2、平面内有四个点A、O、B、C，其中∠AOB=120°，∠ACB=60°，AO=BO=2，则满足题意的OC长度为整数的值可以是___________
练习、如图，AB为直径，AB=4，C、D为圆上两个动点，N为CD中点，CM⊥AB于M，当C、D在圆上运动时保持∠CMN=30°，则CD的长（ ）
隐形圆中求最值
利用隐形圆求最值定线+定角1.依据：与一条定线的两端夹角一定的动点路径是以定线为弦，定角为圆周角的弧。
1.如图，△ABC中，∠ABC＝90°，AB＝6，BC＝8，O为AC的中点，过O作OE⊥OF，OE、OF分别交射线AB、BC于E、F，则EF的最小值为．2在Rt△ABC中，∠A CB＝90°，AC＝12，BC＝5,点D是边BC上一个动点，连接AD,作CE⊥AD于点E,再连接BE,求BE的最小值是_______________3.如图，Rt△ABC中，AB⊥BC，AB＝6，BC＝4，P是△ABC内部的一个动点，且满足∠PAB+∠PBA＝90°，则线段CP长的最小值为．4.在正方形ABCD中，点E，F分别从D，C两点同时出发，以相同的速度在直线DC，CB上移动，连接AE和DF交于点P，由于点E，F的移动，使得点P也随之运动，若AD＝4，试求出线段CP的最小值．5.直线y＝x+4分别与x轴、y轴相交于点M，N，边长为2的正方形OABC一个顶点O在坐标系的原点，直线AN与MC相交于点P，若正方形绕着点O旋转一周，则点P到点（0，2）长度的最小值是（）定点+定长1.依据：到定点的距离等于定长的点的集合是以定点为圆心定长为半径的圆。
6．如图，在Rt△ABC中，∠C＝90°，AC＝6，BC＝8，点F在边AC上，并且CF＝2，点E为边BC上的动点，将△CEF沿直线EF翻折，点C落在点P处，则点P到边AB距离的最小值是（）7如图，直线y＝﹣x+3与x轴、y轴分别交于A、B两点，点P是以C（﹣1，0）为圆心，1为半径的圆上一点，连接PA，PB，则△PAB面积的最小值是（）8如图，四边形ABCD中，AB＝AC＝AD，若∠CAD＝76°，则∠CBD＝度．9.如图，在△ABC中，∠B＝75°，∠C＝45°，BC＝6﹣2，点P是BC上一动点，PD⊥AC于D，PE⊥AB于E．无论P的位置如何变化，线段DE的最小值为（）10.如图，矩形ABCD中，AB＝2，AD＝3，点E、F分别为AD、DC边上的点，且EF＝2，点G为EF的中点，点P为BC上一动点，则PA+PG的最小值为（）11．如图，△ABC为等边三角形，AB＝2．若P为△ABC内一动点，且满足∠PAB＝∠ACP，则线段PB长度的最小值为．12.如图，Rt△ABC中，∠C＝90°，∠ABC＝30°，AB＝6．点D在AB边上，点E是BC边上一点（不与点B、C重合），且DA＝DE，则AD的取值范围是．13如图，在平行四边形ABCD中，∠BCD＝30°，BC＝4，CD＝3，M是AD边的中点，N是AB边上的一动点，将△AMN沿MN所在直线翻折得到△A′MN，连接A′C，则A′C长度的最小值是．14.在矩形ABCD中，AB=10,AD=4,点P是CD上的动点，当∠APB＝90°J ,则DP的长是_15在锐角三角形ABC中，AB=2,AC=6, ∠ACB＝45°, 点D是平面内一点，且∠ADB＝45°，则线段CD的最小值是___________16.如图，在边长为的等边△ABC中，动点D，E分别在BC，AC边上，且保持AE＝CD，连接BE，AD，相交于点P，则CP的最小值为．17.边长为2的等边△ABC的顶点A在x轴的正半轴上移动，顶点B在射线OD上移动，∠AOD＝45°，则顶点C到原点O的最大距离为．18.如图，正方形ABCD中，AB＝2，E是BC中点，CD上有一动点M，连接EM、BM，将△BEM沿着BM翻折得到△BFM．连接DF、CF，则DF+FC的最小值为．19.如图，点A是直线y＝﹣x上的动点，点B是x轴上的动点，若AB＝2，则△AOB面积的最大值为__________20.如图，正方形OABC的边长为2，以O为圆心，EF为直径的半圆经过点A，连接AE，CF相交于点P，将正方形OABC从OA与OF重合的位置开始，绕着点O逆时针旋转90°，交点P运动的路径长是．21如图，在矩形纸片ABCD中，已知AB＝1，BC＝，点E在边CD上移动，连接AE，将多边形ABCE沿直线AE翻折，得到多边形AB′C′E，点B、C的对应点分别为点B′、C′．（1）当B′C′恰好经过点D时（如图1），求线段CE的长；（2）若B′C′分别交边AD，CD于点F，G，且∠DAE＝22.5°（如图2），求△DFG的面积；（3）在点E从点C移动到点D的过程中，求点C′运动的路径长．22如图，△ABC为等边三角形，D、E分别是边AB、BC所在直线上的两个动点，且满足AD＝BE，连接AE、CD，直线AE、CD交于点P．如图（1），当点D、E在线段AB、BC上时，求∠APC的度数；如图（2），当点D、E分别是AB、BC延长线上的两个动点，连接AE、CD，DC的延长线与AE交于点P，求∠APC的度数；若等边三角形边长为2，当D、E在运动的过程中，连接BP，直接写出线段BP的最小值和最大值．21．（1）如图①，已知正方形ABCD的边长为4．点M和N分别是边BC、CD上两点，且BM＝CN，连接AM和BN，交于点P．猜想AM与BN的位置关系，并证明你的结论．（2）如图②，已知正方形ABCD的边长为4．点M和N分别从点B、C同时出发，以相同的速度沿BC、CD方向向终点C和D运动．连接AM和BN，交于点P，求△APB 周长的最大值；问题解决（3）如图③，AC为边长为2的菱形ABCD的对角线，∠ABC＝60°．点M和N分别从点B、C同时出发，以相同的速度沿BC、CA向终点C和A运动．连接AM和BN，交于点P．求△APB周长的最大值．。
隐圆、路径最值问题
隐圆、路径、最值问题1. 如图，以G(0，1)为圆心，半径为2的圆与x轴交于A、B两点，与y轴交于C、D两点，点E 为⊙G上一动点，CF⊥AE于F．若点E从在圆周上运动一周，则点F所经过的路径长为___2. 如图，在弓形ABC中，∠BAC＝60°，BC＝32，若点P在优弧BAC上由B点向C点移动，设△PBC的内心为I，点I随点P的移动所经过的路程为m，则m的最大值为_________3. 如图1，在边长为4的正方形ABCD中，点E. F分别是边CD、AD上的动点，连接BE、CF交于点P，若始终保持CE=DF.①线段BE和CF的关系是BE=CF，且BE⊥CF，说明理由；当点E从点C运动到点D时，求点P 运动的路径长；(2)在边长为6的等边三角形ABC中,点E. F分别是边AC、BC上的动点,连接AF、BE,交于点P,若始终保持AE=CF,当点E从点A运动到点C时,直接写出点P运动的路径长是_______.4. 如图，RT⊿ABC中，AC＝BC＝2，P为边AC上的一动点，CQ⊥BP，垂足为Q点，则线段AQ长度的最小值是．5. 如图，在等腰Rt△ABC中，∠BAC＝90°，AB＝AC，BC＝24，点D是AC边上一动点，连接BD，以AD为直径的圆交BD于E，则线段CE长度的最小值为______6. 如图，点O为坐标原点，⊙O的半径为1，点A（2，0）．动点B在⊙O上，连结AB，作等边△ABC（A，B，C为顺时针顺序），求求OC的最大值与最小值．OyxACB7、如图，ABC ∆中，4=BC ，︒=∠45BAC ，以24为半径，过C B 、两点作O ⊙，连接OA ，则线段OA 的最大值为8. 如图：△ABC 中，AB=2，BC=4，△ACD 是等边△，则△BCD 的面积的最大值是。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
B
M
C D A
E
F
D C
B
A
B
D
C
F A
“隐圆”最值问题
重难点：分析题目条件发现题目中的隐藏圆，并利用一般的几何最值求解方法来解决问题
【例1】在平面直角坐标系中，直线y = - x + 6分别与x 轴、y 轴交于点A 、B 两点，点C 在y 轴的左边，且∠ACB = 90°，则点C 的横坐标x C 的取值范围是__________．
分析：在构造圆的前提下 考虑90°如何使用。
直角对直径所以以AB 为直径画圆。
使用垂径定理即可得到3-20c x ≤<3
【练】（2013-2014·六中周练·16）如图，已知Rt △ABC 中，∠ACB = 90°，AC = 3，BC = 4，点D 是AB 的中点，E 、F 分别是直线AC 、BC 上的动点，∠EDF = 90°，则EF 长度的最小值是__________．
分析：过D 点作DE 垂直AB 交AC 于点M 可证△FBD ∽△ECD 即可 求出最小值
【例2】如图，在Rt △ABC 中，∠ACB = 90°，D 是AC 的中点，
M 是BD 的中点，将线段AD 绕A 点任意旋转（旋转过程中始 终保持点M 是BD 的中点），若AC = 4，BC = 3，那么在旋转 过程中，线段CM 长度的取值范围是_______________．
分析：将线段AD 绕A 点任意旋转隐藏着以A 为圆心AD 为半径的圆构造 出来。
接下来考虑重点M 的用途即可。
中点的用法可尝试下倍长和中位线。
此题使用中位线。
答案是
3722
c x ≤≤
【练】已知△ABC 和△ADE 都是等腰直角三角形，∠ACB =∠ADE = 90°，AC 2，AD = 1，F 是BE 的中点，若将△ADE 绕点A
旋转一周，则线段AF 4242
22
AC -+≤≤ 分析：同例题
【例3】如图，已知边长为2的等边△ABC ，两顶点A 、B 分别在平面直角
坐标系的x轴、y轴的正半轴上滑动，点C在第一象限，连接OC，则OC
长的最大值是（）
A．2 B．1 C．3D．3
分析：取AB中点M连接OM、CM。
因为OM=1，3，所以
3
【练1】如图，在矩形ABCD中，AB = 2，BC3，两顶点A、B分别在平面
直角坐标系的x轴、y轴的正半轴上滑动，点C在第一象限，连接OC，则OC
长的最大值为_______3___．
分析：取AB中点M，方法同例题
【练2】如图，E、F是正方形ABCD的边AD上两个动点，
满足AE = DF，连接CF交BD于点G，连接BE交AG于点H，若正方形的边
长为2，则线段DH长度的最小值是51____．
分析：取AB中点M，方法同例题
【例4】如图，∠XOY = 45°，一把直角三角尺ABC的两个顶点A、B分别在
OX、OY上移动，其中AB = 10，那么点O到AB的距离的最大值为__________．
分析：构造△ABO的外接圆。
点O可以在圆上任意动，利用垂径定理即可得到
+
O到AB的最大距离为：552
【练1】已知线段AB = 4，在线段AB上取一点P，在AB的同侧作等边△APC和等边△BPD，则线段CD的最小值为____2______．
分析：可构造一个以CD为斜边的水平的直角三角形，快速得到当AP=BP时最小，CD最小
【练2】如果满足∠ABC = 60°，AC = 12，BC = k的△ABC恰有一个，那么k的取值范围是
A
D
C
B
O
y x
N
M
B
Q
C
P
A
____012k <≤______．
分析：画出△ABC 的外接圆，观察动点B 在弧上面的运动即可
【例5】已知A （2，0），B （4，0）是x 轴上的两点，点C 是y 轴上的动点，当∠ACB 最大时，则点C 的坐标为__________．
分析：画出△ABC 的外接圆M 。
要保证∠ACB 最大，即圆周角最大，只要圆心角最大即可。
所以在等腰△MAB 中只要半径最小即可，半径什么时候最小呢？只要圆与Y 轴相切即可所以得答案为：(0,2)±
【练】当你站在博物馆的展厅中时，你知道站在何处观赏最理想吗？ 如图，设墙壁上的展品最高点P 距底面2.5米，最低点Q 距底面 2米，观察者的眼睛E 距底面1.6米，当视角∠PEQ 最大时，站 在此处观赏最理想，则此时E 到墙壁的距离为（ B ）
A ．1米
B ．0.6米
C ．0.5米
D ．0.4米
分析：只要△PQE 的外接圆与人眼所在的水平线相切即可，通过垂径定理可得答案是B
【提升】
1．如图，Rt △ABC 中，∠C = 90°，∠ABC = 30°，AB = 6， 点D 在AB 边上，点E 是BC 边上一点（不与点B 、C 重合），且DA = DE ，则AD 的取值范围是（ ）
A ．2 < AD < 3
B ．2 ≤ AD < 3
C ．2 ≤ A
D ≤ 3 D ．1 ≤ AD < 2 2．（2012·济南）如图，矩形ABCD 中，AB = 2，AD = 1，当A 、B 两点 分别在x 轴正半轴和y 轴正半轴上移动时，矩形ABCD 的形状不变，则 OD 的最大值为（ ）
A 2+ 1
B 5
C 145
D ．5
2
3．（2013-2014·黄陂区九上期中·10）在△ABC 中，∠ACB = 90°，∠ABC = 30°，将△ABC 绕顶点C 顺时针旋转，旋转角为θ（0° < θ < 180° ），得 到△MNC ，P 、Q 分别是AC 、MN 的中点，AC = 2t ，连接PQ ，则旋转时 PQ 长度的最大值是（ ）
A ．6
B ．3t
C 6
D ．3t
4．已知点A 、B 的坐标分别是（0，1）、（0，3），点C 是x 轴正半轴上一动点，当∠ACB 最大时，点C 的坐标为__________．。