(完整word版)“隐圆”最值问题习题
专题18 隐形圆及最值问题
AB是 O 的直径，
ACB 90．
ABC 45 ， AC 5 ，
ABC 45 ，
AB AC 5 5 2 ， sin 45 2 2
MN最大
52 2
．
故答案为： 5 2 ．
6．如图，在平面直角坐标系中，已知 C(3, 4) ，以点 C 为圆心的圆与 y 轴相切．点 A 、 B 在 x 轴上，且 OA OB ．点 P 为 C 上的动点， APB 90 ，则 AB 长度的最大值为 ．
1．如图，等边 ABC 的边长为 2， A 的半径为 1，D 是 BC 上的动点，DE 与 A 相切于 E ， DE 的最小值是 ( )
A．1
B． 2
C． 3
D．2
【分析】连接 AE ， AD ，作 AH BC 于 H ，因为 DE 与 A 相切于 E ，所以 AE DE ， 可得 DE AD2 AE2 AD2 1 ，当 D 与 H 重合时， AD 最小，此时 DE 最小，求出 AH 的长，即可得出 DE 的最小值． 【解答】解：如图，连接 AE ， AD ，作 AH BC 于 H ，
若平面上 A、B、C、D 四个点满足 ABC ADC ， 则 A、B、C、D 四点共圆． 证明条件：1．四边形对角互补； 2．四边形外角等于内对角．
两条线段被一点分成（内分或外分）两段长的乘积相等，则这两条线段的四个端点共圆．
D
C
H
O
A
B
四边形 ABCD 的对角线 AC、BD 交于 H， 若 AH CH BH DH ，则 A、B、C、D 四点共圆.
作 AM⊥BP 于 M．当点 P 从点 C 运动到点 A 时，线段 BM 的中点 N 运动的路径长为（
）
A． 2 π 2
新高考数学人教版必修2课件第2章 习题课 与圆有关的最值问题
内容索引
一、与距离有关的最值问题 二、与面积相关的最值问题 三、利用数学式的几何意义解圆的最值问题
随堂演练
课时对点练
一、与距离有关的最值问题
1.圆外一点到圆上任意一点距离的最小值＝ d－r ，最大 值＝ d＋r .
2.直线与圆相离，圆上任意一点到直线距离的最小值＝ d-r ，最大值＝ d＋r .
解析 圆C：x2＋y2－2y＝0的圆心为C(0,1)，半径r＝1， 由圆的性质可知，四边形的面积S＝2S△PBC， 又四边形PACB的最小面积是2， 则 S△PBC 的最小值为 S＝1＝12r|PB|min＝12|PB|min， 则|PB|min＝2，因为|PB|＝ |PC|2－r2＝ |PC|2－1，
解析 设点A(3,1)，易知圆心C(2,2)，半径r＝2. 当弦过点A(3,1)且与CA垂直时为最短弦， |CA|＝ 2－32＋2－12＝ 2. ∴半弦长＝ r2－|CA|2＝ 4－2＝ 2. ∴最短弦长为 2 2.
二、与面积相关的最值问题
例2 已知点O(0,0)，A(0,2)，点M是圆(x－3)2＋(y＋1)2＝4上的动点，则
√C. (－∞，－ 3]∪[ 3，＋∞) D. [－ 3， 3]
解析 将yx看作圆上动点(x，y)与原点 O(0,0)连线的斜率， 如图，可得 k≥ 3或 k≤－ 3.
1234
4.已知圆C1：x2＋y2＋4x－4y＝0，动点P在圆C2：x2＋y2－4x－12＝0上， 则△PC1C2面积的最大值为_4___5_. 解析 因为C1(－2,2)，r1＝2，C2(2,0)，r2＝4， 所以|C1C2|＝ －2－22＋22＝2 5， 当 PC2⊥C1C2 时，△PC1C2 的面积最大，其最大值为12×2 5×4＝4 5.
2023年中考数学一轮复习专题利用隐形圆求圆的最值课件
8
方法总结：利用隐圆解决线圆最值问题时， 第一：变化中寻找不变，找到隐圆； 第二：“一线穿心”--过圆心向定线段作垂直 找到圆上目标最值点，求得最值。
坚持用每一天的进步书写人生的辉煌
9
变式训练2：如图，在矩形ABCD中，AB＝3，BC＝4， O为矩形ABCD的中心，以D为圆心，1为半径作⊙D， P为⊙D上的一个动点，连接AP、OP、AO，则△AOP 面积的最大，延长AO至C点，过点D作 DF⊥AC于点F，延长FD交⊙D于点P′， 连接AP′，OP′，要使△AOP面积最大， 则只需AO边上的高最大，此时P′满足条 件，即P′F为最大的高，
坚持用每一天的进步书写人生的辉煌
11
拓展：定弦定角型
如图1⊙O中，A、B为定点，则AB为定弦，点C为优弧上 任一点，在C点运动过程中则∠ACB的度数不变⇒逆运用⇒ 如图2、点A、B为定点，点C为线段AB外一点，且 ∠ACB=θ（θ为固定值）⇒点C在以AB为弦的圆上运动（ 不与A、B重合）
是_______．
D
C
M A
AN
B
坚持用每一天的进步书写人生的辉煌
方法总结：利用隐圆解决点圆最值问题时， 第一：变化中寻找不变，找到隐圆； 第二：“一线穿心”--连接圆心和定点找到 圆上目标最值点，求得最值。
坚持用每一天的进步书写人生的辉煌
6
变式训练1： 如图，在Rt△ABC中，∠ABC＝90°， ∠C＝30°，AB＝1，点D在AC边上运动，点E为AC的 中点，将△BCD沿BD翻折，点C的对应点为点F，则 在点D从C到A的运动过程中，线段EF的最小值为___.
1
上的一点，且AM＝ AD，N是AB边上3 的一动点，将△AMN沿MN
所在直线翻折得到△A′MN，连接A′C，则A′C长度的最小值
2020年九年级数学中考专题复习：隐形圆求最值问题(含答案)
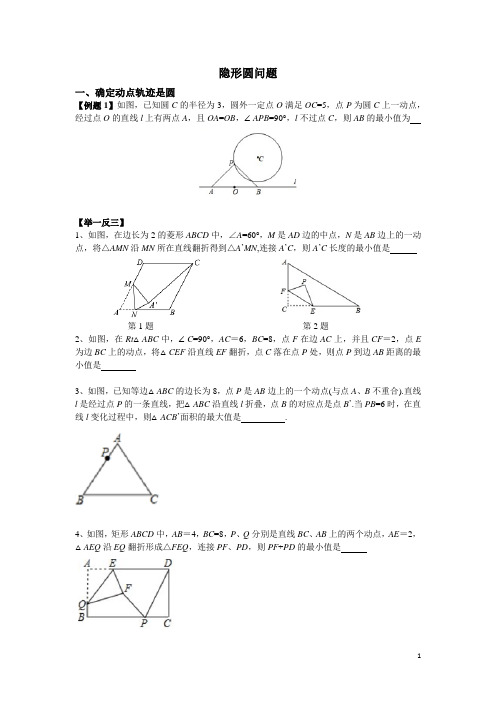
隐形圆问题一、确定动点轨迹是圆【例题1】如图，已知圆C的半径为3，圆外一定点O满足OC=5，点P为圆C上一动点，经过点O的直线l上有两点A，且OA=OB，∠APB=90°，l不过点C，则AB的最小值为【举一反三】1、如图，在边长为2的菱形ABCD中，∠A=60°，M是AD边的中点，N是AB边上的一动点，将△AMN沿MN所在直线翻折得到△A’MN,连接A’C，则A’C长度的最小值是第1题第2题2、如图，在Rt△ABC中，∠C=90°，AC＝6，BC=8，点F在边AC上，并且CF＝2，点E 为边BC上的动点，将△CEF沿直线EF翻折，点C落在点P处，则点P到边AB距离的最小值是3、如图，已知等边△ABC的边长为8，点P是AB边上的一个动点(与点A、B不重合).直线l是经过点P的一条直线，把△ABC沿直线l折叠，点B的对应点是点B’.当PB=6时，在直线l变化过程中，则△ACB’面积的最大值是.4、如图，矩形ABCD中，AB＝4，BC=8，P、Q分別是直线BC、AB上的两个动点，AE＝2，△AEQ沿EQ翻折形成△FEQ，连接PF、PD，则PF+PD的最小值是二、定边对直角知识回顾:直径所对的圆周角是直角构造思路:一条定边所对的角始终为直角，则直角顶点轨迹是以定边为直径的圆或圆弧.图形释义:若AB是一条定线段，且∠APB-90°，则P点轨迹是以AB为直径的圆【例题1】已知正方形ABCD边长为2，E、F分别是BC、CD上的动点，且满足BE＝CF，连接AE、BF，交点为P点，则PC的最小值为【举一反三】1、如图，E、F是正方形ABCD的边AD上的两个动点，满足AE＝DF，连接CF交BD于点G，连接BE交AG于点H，若正方形边长为2，则线段DH长度的最小值是2、如图，Rt△ABC中，AB⊥BC，AB=6，BC＝4，P是△ABC内部的一个动点，且满足∠P AB ＝∠PBC，则线段CP长的最小值是3、如图，AB是半圆O的直径，点C在半圆O上，AB＝5，AC＝4.D是弧BC上的一个动点，连接AD，过点C作CE⊥AD于E，连接BE.在点D移动的过程中，BE的最小值为4、如图，在Rt△ABC中，∠BAC=90°，AC＝12，AB＝10，点D是AC上的一个动点，以AD为直径作圆O，连接BD交圆O于点E，则AE的最小值为5、如图，正方形ABCD的边长为4，动点E、F分別从点A、C同时出发，以相同的速度分别沿AB、CD向终点B、D移动，当点E到达点B时，运动停止，过点B作直线EF的垂线BG，垂足为点G，连接AG，则AG长的最小值为【辅助圆+将军饮马】如图，正方形ABCD的边长是4，点E是AD边上一动点，连接BE，过点A作AF⊥BE于点F，点P是AD边上另一动点，则PC+PF的最小值为【辅助圆+相切】如图，在Rt△ABC中，∠ACB=90°，∠B=30°，AB＝4，D是BC上一动点，CE⊥AD于E，EF⊥AB交BC于点F，则CF的最大值是三、定边对定角在“定边对直角”问题中，依据“直径所对的圆周角是直角”，关键性在于寻找定边、直角，而根据圆周角定理:同圆或等圆中，同弧或等弧所対的圆周角都相.定边必不可少，而直角则可一般为定角.例如，AB为定值，∠P为定角，则P点轨迹是一个圆.当然，∠P度数也是特殊角，比如30°、45°、60°、120°，下面分别作对应的轨迹圆若∠P＝30°，以AB为边，同侧构造等边三角形AOB，O即为圆心若∠P＝45°，以AB为斜边，同侧构造等腰直角三角形AOB，O即为圆心.若∠P＝60°，以AB为底，同侧构造顶角为120°的等腰三角形AOB，O即为圆心.若∠P＝120°，以AB为底，异侧为边构造顶角为120°的等腰三角形AOB，O即为圆心.【例题1】如图，等边△ABC边长为2，E、F分別是BC、CA上两个动点，且BE=CF，连接AE、BF，交点为P点，则CP的最小值为【举一反三】1、如图，△ABC为等边三角形，AB=3，若P为△ABC内一动点，且满足∠P AB＝∠ACP，则线段PB长度的最小值为2、在△ABC中，AB＝4，∠C＝60°，∠A>∠B，则BC的长的取值范围是3、如图，AB是圆O的直径，M、N是弧AB(异于A、B)上两点，C是弧MN上一动点，∠ACB 的角平分线交圆O于点D，∠BAC的平分线交CD于点E，当点C从点M运动到点N时，则C、E两点的运动路径长的比是。
专题03 隐圆(辅助圆)最值模型
专题03 隐圆类最值问题题型一 滑梯类1．如图，ABC ∆中，90C ∠=︒，10AC =，8BC =，线段DE 的两个端点D 、E 分别在边AC ，BC 上滑动，且6DE =，若点M 、N 分别是DE 、AB 的中点，则MN 的最小值为( )A ．10B 3-C ．6D ．32．如图，矩形ABCD ，1AB =，2BC =，点A 在x 轴正半轴上，点D 在y 轴正半轴上．当点A 在x 轴上运动时，点D 也随之在y 轴上运动，在这个运动过程中，点C 到原点O 的最大距离为 ．3．已知边长为a 的正方形ABCD ，两顶点A 、B 分别在平面直角坐标系的x 轴、y 轴的正半轴上滑动，点C 点D 在第一象限，点E 为正方形ABCD 的对称中心，连接OE ，则OE 的长的最大值是 ．4．已知边长为a 的正三角形ABC ，两顶点A 、B 分别在平面直角坐标系的x 轴、y 轴的正半轴上滑动，点C在第一象限，连接OC，则OC的长的最大值是．5．如图，矩形ABCD中，20AD=，点E，F分别是AB，BC边上的两个动点，且10EF=，AB=，30点G为EF的中点，点H为AD边上一动点，连接CH、GH，则GH CH+的最小值为．题型二定点定长6．如图，在矩形ABCD中，4∆沿AB=，6AD=，E是AB边的中点，F是线段BC边上的动点，将EBF EF所在直线折叠得到△EB F'，连接B D'，则B D'的最小值是．7．如图，在边长为4的菱形ABCD中，60∠=︒，M是AD边的中点，点N是AB边上一动点，将AMN∆A沿MN所在的直线翻折得到△A MN'，连接A C'，则线段A C'长度的最小值是．8．如图，四边形ABCD中，AB AC AD∠=度．∠=︒，则CBDCAD==，若769．如图，在Rt ABCBC=，点F在边AC上，并且2CF=，点E为边BC上的AC=，8∠=︒，6C∆中，90动点，将CEF∆沿直线EF翻折，点C落在点P处，则点P到边AB距离的最小值是()A．1.5B．1.2C．2.4D．以上都不对10．如图，在平行四边形ABCD中，30BC=，CD=M是AD边的中点，N是AB边上BCD∠=︒，4的一动点，将AMN'，连接A C'，则A C'长度的最小值是．∆沿MN所在直线翻折得到△A MN题型三直角所对的是直径11．如图，在圆O中，半径OA弦10⊥，BC=，点Q是劣弧AC上的一个动点，连接BQ，作CP BQ垂足为P．在点Q移动的过程中，线段AP的最小值是()A．6B．7C．8D．912．如图，在ABCAB=，12BC=，D为AC边上的一个动点，连接BD，E为BD ∠=︒，8ABC∆中，90上的一个动点，连接AE，CE，当ABD BCE∠=∠时，线段AE的最小值是()A ．3B ．4C ．5D ．613．如图，Rt ABC ∆中，AB BC ⊥，12AB =，8BC =，P 是ABC ∆内部的一个动点，且满足PAB PBC ∠=∠，连接PC ，则线段CP 长的最小值为 ．14．如图，已知C 的半径为3，圆外一定点O 满足5OC =，点P 为C 上一动点，经过点O 的直线l 上有两点A 、B ，且OA OB =，90APB ∠=︒，l 不经过点C ，则AB 的最小值为 ．15．如图，E 、F 是正方形ABCD 的边AD 上两个动点，满足AE DF =，连接CF 交BD 于G ，连接BE 交AG 于点H ，若正方形的边长为3，则线段DH 长度的最小值是 ．题型四 定边对定角16．如图，在边长为6的等边ABC ∆中，点E ，F 分别是边AC ，BC 上的动点，且AE CF =，连接BE ，AF 交于点P ，连接CP ，则CP 的最小值为 ．第16题 第19题 17．在锐角三角形ABC 中，30A ∠=︒，2BC =，设BC 边上的高为h ，则h 的取值范围是 ．18．在ABC ∆中，90ABC ∠=︒，2AB =，3BC =．点D 为平面上一个动点，45ADB ∠=︒，则线段CD 长度的最小值为 ．19．如图，ABC ∆为等边三角形，2AB =．若P 为ABC ∆内一动点，且满足PAB ACP ∠=∠，则线段PB 长度的最小值为 ．20．【问题情境】（1）点A 是O 外一点，点P 是O 上一动点．若O 的半径为2，且5OA =，则点P 到点A 的最短距离为 ．【直接运用】（2）如图1，在Rt ABC ∆中，90ACB ∠=︒，2AC BC ==，以BC 为直径的半圆交AB 于D ，P 是弧CD 上的一个动点，连接AP ，则AP 的最小值是 ．【构造运用】（3）如图2ABCD 的边长为6，点M 、N 分别从点B 、C 同时出发，以相同的速度沿边BC 、CD 方向向终点C 和D 运动，连接AM 和BN 交于点P ，则点P 到点C 的最短距离，并说明理由．【灵活运用】（4）如图3，O 的半径为4，弦4AB =，点C 为优弧AB 上一动点，AM AC ⊥交直线CB 于点M ，则ABM ∆的面积最大值是 ．21．（1）如图1，已知ABC ∆中，30ABC ∠=︒，1AB AC ==，则ABC S ∆= ．（2）如图2，在平面直角坐标系xOy 中，点A 在y 轴上运动，点B 在x 轴上运动，且4AB =，求AOB ∆面积的最大值．（3）如图3，O的半径为2，弦AB=C为优弧AmB上一动点，AM AC⊥交射线CB于点M，请问，ABM∆的周长存在最大值还是最小值？若存在，求出相应的最值；若不存在，说明理由．22．如图，在平面直角坐标系中，抛物线289=--的图象经过点(0,3)y ax ax aC，交x轴于点A、(B A点在B点左侧），顶点为D．（1）求抛物线的解析式及点A、B的坐标；∠=∠？若存在，求出点P的坐标；若不（2）抛物线的对称轴上是否存在点P，使BPC BAC存在，请说明理由．23．如图，在平面直角坐标系中，二次函数2y ax bx c =++的图象交x 轴于A 、B 两点，交y 轴于C 点，P为y 轴上的一个动点，已知(2,0)A -、(0,C -，且抛物线的对称轴是直线1x =．（1）求此二次函数的解析式；（2）连接PA 、PB ，P 点运动到何处时，使得60APB ∠=︒，请求出P 点坐标．24．如图，顶点为M 的抛物线23y ax bx =++与x 轴交于(3,0)A ，(1,0)B -两点，与y 轴交于点C ．（1）求这条抛物线对应的函数表达式；（2）若在第一象限的抛物线下方有一动点D ，满足DA OA =，过D 作DG x ⊥轴于点G ，设ADG ∆的内心为I ，试求CI 的最小值．题型五 定角定高25．如图，在矩形ABCD 中，1AB =，AD =，E 为BC 边上一动点，F 、G 为AD 边上两个动点，45FEG ∠=︒，则线段FG 的长度最大值为 ．26．辅助圆之定角定高求解探究（1）如图①，已知线段AB ，以AB 为斜边，在图中画出一个直角三角形；（2）如图②，在ABC ∆中，60ACB ∠=︒，CD 为AB 边上的高，若4CD =，试判断AB 是否存在最小值，若存在，请求出AB 最小值；若不存在，请说明理由；（3）如图③，某园林单位要设计把四边形花园划分为几个区域种植不同花草，在四边形ABCD 中，45A ∠=︒，90B D ∠=∠=︒，CB CD ==点E 、F 分别为AB 、AD 上的点，若保持CE CF ⊥，那么四边形AECF 的面积是否存在最大值，若存在，请求出面积的最大值，若不存在，请说明理由．27．问题研究（1）若等边ABC ∆边长为4，则ABC ∆的面积为 ；（2）如图1，在ABC ∆中，60ACB ∠=︒，CD 为AB 边上的高，若4CD =，试判断ABC ∆的面积是否存在最小值．若存在，求出这个最小值；若不存在，请说明理由．问题解决（3）如图2，四边形ABCD 中，AB AD ==，45B ∠=︒，60C ∠=︒，135D ∠=︒，点E 、F 分别为边AB 、BC 上的动点，且EAF C ∠=∠，求四边形AECF 面积的最大值．28．（1）如图1，已知AC 、BC 为O 的两条弦，点D 为O 外一点，则ACB ∠ ADB ∠（请用“<”“ >”或“=”填空）（2）①如图2，若等边ABC ∆内接于O ，4AB =，CD 为O 的切线，则ABD ∆的面积为 ． ②如图3，在ABC ∆中，60ACB ∠=︒，CD 为AB 边上的高．若4CD =，试判断ABC ∆的面积是否存在最小值，若存在，求出这个最小值；若不存在，请说明理由．（3）如图4，正方形ABCD 的边长为4，点E 、F 分别为边AB 、BC 上的动点，且45EDF ∠=︒，求四边形DEBF 面积的最大值．29．问题探究（1）如图1．在ABC ∆中，8BC =，D 为BC 上一点，6AD =．则ABC ∆面积的最大值是 ．（2）如图2，在ABC ∆中，60BAC ∠=︒，AG 为BC 边上的高，O 为ABC ∆的外接圆，若3AG =，试判断BC 是否存在最小值？若存在，请求出最小值；若不存在，请说明理由．问题解决：如图3，王老先生有一块矩形地ABCD ，6212AB =+，626BC =+，现在他想利用这块地建一个四边形鱼塘AMFN ，且满足点E 在CD 上，AD DE =，点F 在BC 上，且6CF =，点M 在AE 上，点N 在AB 上，90MFN ∠=︒，这个四边形AMFN 的面积是否存在最大值？若存在，求出面积的最大值；若不存在，请说明理由．30．如图，平面直角坐标系中，O为原点，点A、B分别在y轴、x轴的正半轴上．AOB∆的两条外角平分线交于点P，P在反比例函数9yx=的图象上．PA的延长线交x轴于点C，PB的延长线交y轴于点D，连接CD．（1）求P∠的度数及点P的坐标；（2）求OCD∆的面积；（3）AOB∆的面积是否存在最大值？若存在，求出最大面积；若不存在，请说明理由．专题03 隐圆（辅助圆）最值模型题型一 滑梯类模型1．如图，ABC ∆中，90C ∠=︒，10AC =，8BC =，线段DE 的两个端点D 、E 分别在边AC ，BC 上滑动，且6DE =，若点M 、N 分别是DE 、AB 的中点，则MN 的最小值为( )A ．10B 3-C ．6D ．3【解答】解：ABC ∆中，90C ∠=︒，10AC =，8BC =，AB ∴==，6DE =，点M 、N 分别是DE 、AB 的中点，12CN AB ∴==，132CM DE ==， 当C 、M 、N 在同一直线上时，取最小值，MN ∴3，故选：B ．2．如图，矩形ABCD ，1AB =，2BC =，点A 在x 轴正半轴上，点D 在y 轴正半轴上．当点A 在x 轴上运动时，点D 也随之在y 轴上运动，在这个运动过程中，点C 到原点O 的最大距离为 1 ．【解答】解：如图，取AD 的中点H ，连接CH ，OH ，矩形ABCD ，1AB =，2BC =，1CD AB ∴==，2AD BC ==，点H 是AD 的中点，1AH DH ∴==，CH ∴===90AOD ∠=︒，点H 是AD 的中点，112OH AD ∴==， 在OCH ∆中，CO OH CH <+，当点H 在OC 上时，CO OH CH =+，CO ∴的最大值为1OH CH +=，1．3．已知边长为a 的正方形ABCD ，两顶点A 、B 分别在平面直角坐标系的x 轴、y 轴的正半轴上滑动，点C 点D 在第一象限，点E 为正方形ABCD 的对称中心，连接OE ，则OE 的长的最大值是 a ．【解答】解：取AB 中点F ，连OF ，EF ，有OE OF FC +，当O 、E 、F 共线时，OE 有最大值，最大值是OF EF +．四边形ABCD 为正方形，90BEA ∴∠=︒，且F 为AB 中点，1122EF OF AB a ∴===， OE ∴的最大值为1122OF EF a a a +=+=， 故答案为：a ．4．已知边长为a 的正三角形ABC ，两顶点A 、B 分别在平面直角坐标系的x 轴、y 轴的正半轴上滑动，点C 在第一象限，连接OC ，则OC 的长的最大值是 ．【解答】解：取AB 中点D ，连OD ，DC ，有OC OD DC +，当O 、D 、C 共线时，OC 有最大值，最大值是OD CD +．ABC ∆为等边三角形，AB BC AC a ∴===，根据三角形的性质可知：12OD a =，CD ==．OC ∴．5．如图，矩形ABCD 中，20AB =，30AD =，点E ，F 分别是AB ，BC 边上的两个动点，且10EF =，点G 为EF 的中点，点H 为AD 边上一动点，连接CH 、GH ，则GH CH +的最小值为 45 ．【解答】解：由已知，点G 在以B 圆心，5为半径的圆在与长方形重合的弧上运动． 作C 关于AD 的对称点C '，连接C B '，交AD 于H ，交以B 为圆心，以5为半径的圆于G 由两点之间线段最短，此时C B '50==，则GH CH +的最小值50545=-=，故答案为：45．题型二 定点定长模型6．如图，在矩形ABCD中，4∆沿AB=，6AD=，E是AB边的中点，F是线段BC边上的动点，将EBFEF所在直线折叠得到△EB F'，连接B D'，则B D'的最小值是2．【解答】解：如图所示点B'在以E为圆心EA为半径的圆上运动，当D、B'、E共线时，此时B D'的值最小，根据折叠的性质，EBF∆≅△EB F'，∴'⊥'，EB B F∴'=，EB EBAB=，E是AB边的中点，4∴='=，2AE EBAD=，6∴=DE2∴'=．B D7．如图，在边长为4的菱形ABCD中，60∆A∠=︒，M是AD边的中点，点N是AB边上一动点，将AMN沿MN所在的直线翻折得到△A MN'，连接A C'，则线段A C'长度的最小值是2．【解答】解：如图所示：在N的运动过程中A'在以M为圆心，MA的长为半径的圆上，∴'是定值，A C'长度取最小值时，即A'在MC上时，MA过点M作MF DC⊥于点F，在边长为4的菱形ABCD 中，60A ∠=︒，M 为AD 中点，2MD ∴=，60FDM ∠=︒，30FMD ∴∠=︒，112FD MD ∴==，cos30FM DM ∴=⨯︒=，MC ∴=2A C MC MA ∴'=-'=．故答案为：2．8．如图，四边形ABCD 中，AB AC AD ==，若76CAD ∠=︒，则CBD ∠= 38 度．【解答】解：AB AC AD ==，∴点B ，C ，D 可以看成是以点A 为圆心，AB 为半径的圆上的三个点，CBD ∴∠是弧CD 对的圆周角，CAD ∠是弧CD 对的圆心角；76CAD ∠=︒，11763822CBD CAD ∴∠=∠=⨯︒=︒． 9．如图，在Rt ABC ∆中，90C ∠=︒，6AC =，8BC =，点F 在边AC 上，并且2CF =，点E 为边BC 上的动点，将CEF ∆沿直线EF 翻折，点C 落在点P 处，则点P 到边AB 距离的最小值是( )A ．1.5B ．1.2C ．2.4D ．以上都不对【解答】解：以F 为圆心，CF 为半径作F ，过点F 作FH AB ⊥于点H 交F 于点G ，则点P 到AB 的距离的最小值FH FP FH FG =-=-．由翻折的性质可知，2PF CF ==，∴点P 在F 上，6AC =，8BC =，10AB ∴=，由AHF ACB ∆∆∽， ∴AF FH AB BC =， ∴4108FH =， 3.2FH ∴=，∴点P 到AB 的距离的最小值 3.22 1.2FH FG =-=-=．故选：B ．10．如图，在平行四边形ABCD 中，30BCD ∠=︒，4BC =，CD =M 是AD 边的中点，N 是AB 边上的一动点，将AMN ∆沿MN A MN '，连接A C '，则A C '长度的最小值是 5 ．【解答】解：如图，连接MC ；过点M 作ME CD ⊥，交CD 的延长线于点E ；四边形ABCD 为平行四边形，//AD BC ∴，4AD BC ==，点M 为AD 的中点，30BCD ∠=︒，2DM MA ∴==，30MDE BCD ∠=∠=︒，112ME DM ∴==，DE ，CE CD DE ∴=+=222CM ME CE =+，7CM ∴=；由翻折变换的性质得：2MA MA '==，显然，当折线MA C '与线段MC 重合时，线段A C '的长度最短，此时725AC '=-=，故答案为5．题型三 直角所对的是直径11．如图，在圆O 中，半径OA 弦10BC =，点Q 是劣弧AC 上的一个动点，连接BQ ，作CP BQ ⊥，垂足为P ．在点Q 移动的过程中，线段AP 的最小值是( )A ．6B ．7C ．8D ．9【解答】解：如图，连接AC ，取BC 的中点K ，连接PK ，AKAB 是直径，90ACB ∴∠=︒，12AC ∴=，5CK BK ==，13AK ∴==，CP BQ ⊥，152PK BC ∴==， PA AK PK -，1358PA ∴-=，PA ∴的最小值为8．故选：C ．12．如图，在ABC ∆中，90ABC ∠=︒，8AB =，12BC =，D 为AC 边上的一个动点，连接BD ，E 为BD 上的一个动点，连接AE ，CE ，当ABD BCE ∠=∠时，线段AE 的最小值是( )A ．3B ．4C ．5D ．6【解答】解：如图，取BC 的中点T ，连接AT ，ET ．90ABC ∠=︒，90ABD CBD ∴∠+∠=︒，ABD BCE ∠=∠，90CBD BCE ∴∠+∠=︒，90CEB ∴∠=︒，6CT TB ==，162ET BC ∴==，10AT ==， AE AT ET -，4AE ∴，AE ∴的最小值为4，故选：B ．13．如图，Rt ABC ∆中，AB BC ⊥，12AB =，8BC =，P 是ABC ∆内部的一个动点，且满足PAB PBC ∠=∠，连接PC ，则线段CP 长的最小值为 4 ．【解答】解：90ABC ∠=︒，90ABP PBC ∴∠+∠=︒，PAB PBC ∠=∠，90BAP ABP ∴∠+∠=︒，90APB ∴∠=︒，∴点P 在以AB 为直径的O 上，连接OC 交O 于点P ，此时PC 最小，在Rt BCO ∆中，90OBC ∠=︒，8BC =，6OB =，10OC ∴==，1064PC OC OP ∴=-=-=．PC ∴最小值为4．故答案为：4．14．如图，已知C 的半径为3，圆外一定点O 满足5OC =，点P 为C 上一动点，经过点O 的直线l 上有两点A 、B ，且OA OB =，90APB ∠=︒，l 不经过点C ，则AB 的最小值为 4 ．【解答】解：如图，连接OP ，PC ，OC ，OP PC OC +，5OC =，3PC =，∴当点O ，P ，C 三点共线时，OP 最短，如图，OA OB =，90APB ∠=︒，2AB OP ∴=，当O ，P ，C 三点共线时，5OC =，3CP =，532OP ∴=-=，24AB OP ∴==，故答案为：4．15．如图，E 、F 是正方形ABCD 的边AD 上两个动点，满足AE DF =，连接CF 交BD 于G ，连接BE 交AG 于点H ，若正方形的边长为3，则线段DH 长度的最小值是 31)2- ．【解答】解：在正方形ABCD 中，AB AD CD ==，BAD CDA ∠=∠，ADG CDG ∠=∠， 在ABE ∆和DCF ∆中，AB CDBAD CDA AE DF=⎧⎪∠=∠⎨⎪=⎩，()ABE DCF SAS ∴∆≅∆，12∴∠=∠，在ADG ∆和CDG ∆中，AD CDADG CDG DG DG=⎧⎪∠=∠⎨⎪=⎩，()ADG CDG SAS ∴∆≅∆，23∴∠=∠，13∴∠=∠，390BAH BAD ∠+∠=∠=︒，190BAH ∴∠+∠=︒，1809090AHB ∴∠=︒-︒=︒，取AB 的中点O ，连接OH 、OD ， 则1322OH AO AB ===，在Rt AOD ∆中，OD根据三角形的三边关系，OH DH OD +>，∴当O 、D 、H 三点共线时，DH 的长度最小，最小值31)2OD OH =-=．故答案为：31)2．题型四 定边对定角模型16．如图，在边长为6的等边ABC ∆中，点E ，F 分别是边AC ，BC 上的动点，且AE CF =，连接BE ，AF 交于点P ，连接CP ，则CP 的最小值为【解答】解：ABC ∆是等边三角形，AB AC BC ∴==，60CAB ACB ∠=∠=︒，在ABE ∆和CAF ∆中，AB AC BAC ACB AE CF =⎧⎪∠=∠⎨⎪=⎩，()ABE CAF SAS ∴∆≅∆，ABE CAF ∴∠=∠，60BPF PAB ABP CAP BAP ∴∠=∠+∠=∠+∠=︒，120APB ∴∠=︒，如图，过点A ，点P ，点B 作O ，连接CO ，PO ，∴点P 在AB 上运动，AO OP OB ==，OAP OPA ∴∠=∠，OPB OBP ∠=∠，OAB OBA ∠=∠，360120AOB OAP OPA OPB OBP ∴∠=︒-∠-∠-∠-∠=︒，30OAB ∴∠=︒，90CAO ∴∠=︒，AC BC =，OA OB =，CO ∴垂直平分AB ，30ACO ∴∠=︒，cos AC ACO CO ∴∠==2CO AO =，CO ∴=AO ∴=，在CPO ∆中，CP CO OP -，∴当点P 在CO 上时，CP 有最小值，CP ∴的最小值=故答案为17．在锐角三角形ABC 中，30A ∠=︒，2BC =，设BC 边上的高为h ，则h 的取值范围是 23h <+ 【解答】解：如图，BC 为O 的弦，2OB OC ==，2BC =，OB OC BC ∴==，OBC ∴∆为等边三角形，60BOC ∴∠=︒，1302BAC BOC ∴∠=∠=︒， 作直径BD 、CE ，连接BE 、CD ，则90DCB EBC ∠=∠=︒，∴当点A 在DE 上（不含D 、E 点）时，ABC ∆为锐角三角形，在Rt BCD ∆中，30D BAC ∠=∠=︒，CD ∴==当A 点为DE 的中点时，A 点到BC 的距离最大，即h 最大，延长AO 交BC 于H ，如图， A 点为DE 的中点，∴AB AC =，AH BC ∴⊥，1BH CH ∴==，OH ∴==2AH OA OH ∴=+=+h ∴的范围为23h +．故答案为23h +．18．在ABC ∆中，90ABC ∠=︒，2AB =，3BC =．点D 为平面上一个动点，45ADB ∠=︒，则线段CD 长度的最小值为 【解答】解：如图所示．45ADB ∠=︒，2AB =，作ABD ∆的外接圆O （因求CD 最小值，故圆心O 在AB 的右侧），连接OC ， 当O 、D 、C 三点共线时，CD 的值最小．90AOB ∴∠=︒，AOB ∴∆为等腰直角三角形，sin 45AO BO AB ∴==︒⨯=45OBA ∠=︒，90ABC ∠=︒，45OBE ∴∠=︒，作OE BC ⊥于点E ，OBE ∴∆为等腰直角三角形．sin451OE BE OB ∴==︒⋅=，312CE BC BE ∴=-=-=，在Rt OEC ∆中，OC ==当O 、D 、C 三点共线时，CD 最小为CD OC OD =-．19．如图，ABC ∆为等边三角形，2AB =．若P 为ABC ∆内一动点，且满足PAB ACP ∠=∠，则线段PB 长度的最小值为 ．【解答】解：ABC ∆是等边三角形，60ABC BAC ∴∠=∠=︒，2AC AB ==，PAB ACP ∠=∠，60PAC ACP ∴∠+∠=︒，∴点P的运动轨迹是AC，当O、P、B共线时，PB长度最小，设OB交AC于D，如图所示：此时PA PC=，OB AC⊥，则112AD CD AC===，30PAC ACP∠=∠=︒，1302ABD ABC∠=∠=︒，tan30PD AD AD∴=⋅︒==，BDPB BD PD∴=-==20．【问题情境】（1）点A是O外一点，点P是O上一动点．若O的半径为2，且5OA=，则点P到点A的最短距离为3．【直接运用】（2）如图1，在Rt ABC∆中，90ACB∠=︒，2AC BC==，以BC为直径的半圆交AB于D，P是弧CD上的一个动点，连接AP AP的最小值是．【构造运用】（3）如图2，已知正方形ABCD的边长为6，点M、N分别从点B、C同时出发，以相同的速度沿边BC、CD方向向终点C和D运动，连接AM和BN交于点P，则点P到点C的最短距离，并说明理由．【灵活运用】（4）如图3，O的半径为4，弦4AB=，点C为优弧AB上一动点，AM AC⊥交直线CB于点M，则ABM∆的面积最大值是．【解答】解：（1）连接AP、OP，如图4所示：O 的半径为2，2OP ∴=，523OA OP ∴-=-=，PA OA OP ∴-，3PA ∴，∴当点P 在OA 上时，PA 最短，最小值为3，故答案为：3；（2）连接OA ，交半圆于P '，连接OP ，如图1所示：2AC BC ==，BC 为半圆的直径，112OP OC BC ∴===，90ACB ∠=︒，OA ∴==AP OA OP -， 51AP ∴-，∴当点P 在OA 上时，AP1-，1；（3）点P 到点C 的最短距离为3，理由如下：取AB 中点O ，连接OP 、OC 、PC ，如图2所示：点M 、N 分别从点B 、C 同时出发，以相同的速度沿边BC 、CD 方向向终点C 和D 运动， BM CN ∴=，四边形ABCD 是正方形，6AB BC ∴==，90ABM BCN ∠=∠=︒，在ABM ∆和BCN ∆中，BM CNABM BCN AB BC=⎧⎪∠=∠⎨⎪=⎩，()ABM BCN SAS ∴∆≅∆，BAM CBN ∴∠=∠，90CBN ABN ∠+∠=︒， 90BAM ABN ∴∠+∠=︒， 90APB ∴∠=︒， ∴点P 在以AB 为直径的O 上运动， 132OP OA OB AB ====，OC =又PC OC OP -， 353PC ∴-，PC ∴的最小值为3；（4）连接OA 、OB ，如图3所示： 4OA OB AB ===， AOB ∴∆是等边三角形， 60AOB ∴∠=︒， 11603022ACB AOB ∴∠=∠=⨯︒=︒，AM AC ⊥， 60M ∴∠=︒， ∴点M 在以120ADB ∠=︒的D 上， 4AB =，ABM S ∆最大，则点M 的距离最大， ∴当AM BM =时点M 到AB 的距离最大， ABM ∴∆是等边三角形，114422ABM S AB AB ∆∴==⨯=故答案为：21．（1）如图1，已知ABC ∆中，30ABC ∠=︒，1AB AC ==，则ABC S ∆= ． （2）如图2，在平面直角坐标系xOy 中，点A 在y 轴上运动，点B 在x 轴上运动，且4AB =，求AOB ∆面积的最大值．（3）如图3，O 的半径为2，弦AB =C 为优弧AmB 上一动点，AM AC ⊥交射线CB 于点M ，请问，ABM ∆的周长存在最大值还是最小值？若存在，求出相应的最值；若不存在，说明理由．【解答】解：（1）如图1中，作AH BC ⊥于H ．AB AC =，AH BC ⊥，BH CH ∴=，1AB =，30B ∠=︒，1122AH AB ∴==，2BC BH ==1122ABC S ∆∴==．（2）如图2中，取AB 的中点E ，连接OE ，作OH AB ⊥于H ．90AOB ∠=︒，AE EB =，122OE AB ∴==，OH AB ⊥，OH OE ∴，即2OH ，OH ∴的最大值为2，AOB ∴∆的面积的最大值12442=⨯⨯=．（3）如图3中，连接OA ，OB ，作OH AB ⊥于H ．OH AB ⊥，OA OB =，AH BH ∴==AOH BOH ∠=∠，sin AOH ∴∠，60AOH ∴∠=︒，2120AOB AOH ∠=∠=︒，1602ACB AOB ∴∠=∠=︒， MA AC ⊥，90MAC ∴∠=︒30M ∴∠=︒，如图31-中，ABM ∆中，AB =30AMB ∠=︒，ABM ∆的周长存在最大值，理由如下；作ABM ∆的外接圆，取优弧AB 的中点O ，连接OA ，OB ，以O 为圆心，OA 为半径作O ，延长AM 交O 于F ，连接BF ．30AOB AMB ∠=∠=︒，1152AFB AOB ∴∠=∠=︒， 30AMB F MBF ∠=∠+∠=︒，F MBF ∴∠=∠，MF MB ∴=，MA MB MA MF AF ∴+=+=，∴当AF 的值最大时，MA MB +的值最大，此时MAB ∆的周长最大，延长AO 交O 于E ，连接BE 交ABM ∆的外接圆于D ，连接AD ，OD ． 易知：90ABD AOD ∠=∠=︒，OD AE ∴⊥，OA OE =，DA DE ∴=，15E EAD ∴∠=∠=︒，151530ADB ∴∠=︒+︒=︒，2AD DE AB ∴===6BD =，6BE ∴=，AE ∴当AF 与AE 重合时，AF 的值最大，AF ∴的最大值为ABM ∴∆的周长的最大值为22．如图， 在平面直角坐标系中， 抛物线289y ax ax a =--的图象经过点(0,3)C ，交x 轴于点A 、(B A 点在B 点左侧） ，顶点为D ．（1） 求抛物线的解析式及点A 、B 的坐标；（2）抛物线的对称轴上是否存在点P ，使BPC BAC ∠=∠？若存在， 求出点P 的坐标；若不存在， 请说明理由 ．【解答】解： （1）把(0,3)C 代入289y ax ax a =--得93a -=，解得13a =-， ∴所以抛物线的解析式为182333y x x =-++． 令0y =得：1823033x x -++=，解得：11x =-，29x =， (1,0)A ∴-，(9,0)B ．（2）分两种情况：①如图 2 ，以AB 为直径作M ，M 交抛物线的对称轴于(P BC 的下方） ．42b x a=-=， ∴点P 的横坐标为 4 ．由圆周角定理得CPB CAB ∠=∠，(1,0)A -，(9,0)B ，10AB ∴=．152MP AB ∴==． (4,5)P ∴-．②如图 3 所示： 以A B '为直径作M '，M '交抛物线的对称轴于P '，过点M '作M E P F '⊥'，垂足为E ，连接P M ''．点A '与点A 关于BC 对称，10AB A B ∴='=，A A ∠=∠'．CP B CA B ∠'=∠'，CP B A ∴∠'=∠．(1,6)A '，(9,0)B(5,3)M ∴'．1M E ∴'=．152M P A B ''='=，P E ∴'=∴点P '的坐标为(4，3)．综上所述， 点P 的坐标为(4,5)P -或(4，3)．23．如图，在平面直角坐标系中，二次函数2y ax bx c =++的图象交x 轴于A 、B 两点，交y 轴于C 点，P 为y 轴上的一个动点，已知(2,0)A -、(0,C -，且抛物线的对称轴是直线1x =．（1）求此二次函数的解析式；（2）连接PA 、PB ，P 点运动到何处时，使得60APB ∠=︒，请求出P 点坐标．【解答】解：（1）将A ，C 点坐标代入函数解析式，及对称轴，得42012a b c c b a⎧-+=⎪⎪=-⎨⎪⎪-=⎩，解得a b c ⎧=⎪⎪⎪⎪=⎨⎪⎪=-⎪⎪⎩，抛物线的解析式为2y x -，（2）以AB 为边作等边ABM ∆，作ABM ∆的外接圆O '，交y 轴负半轴于P ，作O E AB '⊥于E ，连接BO '，O P '．设(0,)P m ． 易知：(1,3)O '-，23BO O P '='=，21(3)12m ∴++=，113m ∴=--或113-（舍弃）， (0,311)P ∴--，根据对称性可知(0,311)P '+也符合条件．24．如图，顶点为M 的抛物线23y ax bx =++与x 轴交于(3,0)A ，(1,0)B -两点，与y 轴交于点C ．（1）求这条抛物线对应的函数表达式；（2）若在第一象限的抛物线下方有一动点D ，满足DA OA =，过D 作DG x ⊥轴于点G ，设ADG ∆的内心为I ，试求CI 的最小值．【解答】解：（1）抛物线23y ax bx =++过点(3,0)A ，(1,0)B -，∴933030a b a b ++=⎧⎨-+=⎩ 解得：12a b =-⎧⎨=⎩， ∴这条抛物线对应的函数表达式为223y x x =-++．（2）解法一：如图，连接IO ，ID ，IA ，I 是ADG ∆的内心，IA ∴平分DAG ∠，ID 平分ADG ∠，12IAD DAG ∴∠=∠，12ADI ADG ∠=∠．90DAG ADG ∠+∠=︒，45IAD ADI ∴∠+∠=︒，135AID ∴∠=︒．在ADI ∆和AOI ∆中，AD AODAI OAI AI AI=⎧⎪∠=∠⎨⎪=⎩，()ADI AOI SAS ∴∆≅∆．135AID AIO ∴∠=∠=︒． OA 为定线段，OIA ∠恒等于135︒，∴点I 在以OA 为弦，所含的圆周角等于135︒的圆弧上，设该圆的圆心为E ，连接EO ，EA ，135OIA ∠=︒，90OEA ∴∠=︒．EO EA =，EOA ∴∆为等腰直角三角形．过点E 作EH OA ⊥于点H ， 则1322AH OH OA ===．OE ∴=．∴圆心E 的坐标为3(2，3)2，E ． 当点I 在线段CE 上时，CI 的值最小，CI 的最小值CE OE =-==．题型五 定角定高模型25．如图，在矩形ABCD 中，1AB =，AD =，E 为BC 边上一动点，F 、G 为AD 边上两个动点，45FEG ∠=︒，则线段FG 的长度最大值为 2 ．【解答】解：如图，作EFG ∆的外接圆O ，连接OA ，OE ，OG ，过点O 作OH AD ⊥于H ，过点E 作EQ AD ⊥于Q ，连接AC ．四边形ABCD 是矩形，90B ∴∠=︒，1AB CD ==，AD BC ==2AC ∴=，45FEG ∠=︒，290FOG FEG ∴∠=∠=︒，12EFG EOG ∠=∠， 290EOF FOG EOG EFG ∴∠=∠+∠=∠+︒，1112221cos cos(45)cos(90)2EF EF EF OF OE OEF EFG EOF ====∠︒-∠︒-∠， ∴当EF 最大，且EFG ∠最小时，OF 的值最大，则FG 的值最大， 1sin 2EQEQ EFG FQ AC ∠==， ∴当点E 与C 重合，F与A 重合时，“=”号成立，12cos(4530)AC OF OE ∴==-︒-︒FG ∴的最大值2==．故答案为2．26．辅助圆之定角定高求解探究（1）如图①，已知线段AB ，以AB 为斜边，在图中画出一个直角三角形；（2）如图②，在ABC ∆中，60ACB ∠=︒，CD 为AB 边上的高，若4CD =，试判断AB 是否存在最小值，若存在，请求出AB 最小值；若不存在，请说明理由；（3）如图③，某园林单位要设计把四边形花园划分为几个区域种植不同花草，在四边形ABCD 中，45A∠=︒，90B D ∠=∠=︒，CB CD ==点E 、F 分别为AB 、AD 上的点，若保持CE CF⊥，那么四边形AECF【解答】解：（1）如图①中，ABC ∆即为所求．（2）如图②中，作ABC ∆的外接圆O ，连接OA ，OB ，OC ，作OE AB ⊥于E ．设2OA OC x ==．2120AOB ACB ∠=∠=︒，OA OB =，OE AB ⊥，AE EB ∴=，60AOE BOE ∠=∠=︒， 12OE OA x ∴==，AE =，OC OE CD +，34x ∴， 43x∴， x ∴的最小值为43，2AB =，AB ∴． （3）如图③中，连接AC ，延长BC 交AD 的延长线于G ，将CDF ∆顺时针旋转得到CBH ∆，作CEH ∆的外接圆O ．90ADC ABC ∠=∠=︒，AC AC =，CD CB =，Rt ACD Rt ACB(HL)∴∆≅∆， ACD ACB S S ∆∆∴=，45DAB ∠=︒，135DCB ∴∠=︒， 45DCG ∴∠=︒， 90CDG ∠=︒，CD DG ∴==12CG ∴==，12AB GB ∴==+由（2）可知，当CEH ∆的外接圆的圆心O 在线段BC 上时，ECH ∆的面积最小，此时四边形AFCE 的面积最大，设OC OE r ==，易知2OB EB ==，r ∴=r ∴=，12(2EH ∴=，∴四边形AFCE 的面积的最大值112(1212(214422=⨯⨯+⨯⨯⨯． 27．问题研究（1）若等边ABC ∆边长为4，则ABC ∆的面积为（2）如图1，在ABC ∆中，60ACB ∠=︒，CD 为AB 边上的高，若4CD =，试判断ABC ∆的面积是否存在最小值．若存在，求出这个最小值；若不存在，请说明理由． 问题解决（3）如图2，四边形ABCD 中，AB AD ==，45B ∠=︒，60C ∠=︒，135D ∠=︒，点E 、F 分别为边AB 、BC 上的动点，且EAF C ∠=∠，求四边形AECF 面积的最大值．【解答】解：（1）过点C 作CD AB ⊥于D ，等边ABC ∆边长为4，114222AD BD AB ∴===⨯=， 在Rt ACD ∆中，由勾股定理得22AC AD CD =+，即22242CD =+，解得：CD =，11422ABC S AB CD ∆∴=-=⨯⨯故答案为：（2）CD 为AB 边上的高，若4CD =，设AB c =，AC b =，BC a =，过A 作AE BC ⊥于E ，111sin60222ABC S AB CD AE BC BC AC ∆∴=⨯=⨯=⨯⨯︒，4c ∴=，又sin 60AE AC =⋅︒=，1cos602CE AC b =⋅︒=， 12BE BC EC a b =-=-，在Rt ABE ∆中，由勾股定理得222AB AE BE =+，即2221)()2c a b =+-， 2222c a b ab ab ab ab ∴=+--=，仅当a b =时取等号，即ABC ∆为等边三角形时， 283c c ∴，833c∴，11422ABC S AB CD ∆∴=⋅==最小 （3）45B ∠=︒，60C ∠=︒，135ADC ∠=︒，3603604560135120BAD B C D ∴∠=︒-∠-∠-∠=︒-︒-︒-︒=︒，将ABE ∆逆时针旋转120︒得ADG ∆， 45ADG B ∠=∠=︒，AE AG =， 45135180ADG ADC ∴∠+∠=︒+︒=︒， C ∴、D 、G 三点共线，60EAF C ∠=∠=︒，12060BAE FAD EAF ∠+∠=︒-∠=︒， 60GAD FAD BAE FAD ∴∠+∠=∠+∠=︒，在EAF ∆和GAF ∆中，AE AGEAF GAF AF AF =⎧⎪∠=∠⎨⎪=⎩， ()EAF GAF SAS ∴∆≅∆， EF GF ∴=，ABE ADF AGF AECF ABCD ABCD S S S S S S ∆∆∆=--=-四边形四边形四边形，∴当AGF S ∆最小时，AECF S 四边形最大，过A 作AH CG ⊥于H ，4AD =45ADH ∠='，sin454AH DH AD ∴==⋅︒=， 60FAG ∠=︒，11sin 6022AGF S AF AG AG AH GF ∆∴=--︒⋅=-， 由（2）知AG AF =时，AFG ∆面积最小，由点F 在CD 上运动，达不到AFG ∆是等边三角形，当向D 运动时，AFG ∆面积逐渐减小，∴点F 到点D 时，AFG ∆面积最小，此时ABE AFG AFE ∆≅∆≅∆，45ABE AFE AFG HAF ∴∠=∠=∠=∠=︒，6BAE FAE AG O ∠=∠=∠=︒，AB AF AD ===在_AH 上取点M 使30HGM ∠=︒， 604515HAG FAG FAH ∠=∠-∠=︒-︒=︒，9075AGH GAH '∴∠=-∠=︒，75(9030)15AGM AGH MGH HAG ∴∠=∠-∠=︒-︒-︒=︒=∠，设GH x =，2MG x =，由勾股定理MH =，24AH AM MH x ∴=+=+=，4(2x ∴=-，44(212GF ∴=+=-，14(12242AEF AGF S S ∆∆==⨯⨯-=-12EF GF ==-1354590EFC ADC ADE ∠=∠-∠=︒-︒=︒，60C ∠=︒，2111tan (1248222CEF S EF FC EF EF FEC ∆∴=⋅=⋅⋅∠=⨯-=，244824AEF CEF AECF S S S ∆∆∴=+=-=四边形．∴四边形AECF 面积的最大值为24．28．（1）如图1，已知AC 、BC 为O 的两条弦，点D 为O 外一点，则ACB ∠ > ADB ∠（请用“<”“ >”或“=”填空）（2）①如图2，若等边ABC ∆内接于O ，4AB =，CD 为O 的切线，则ABD ∆的面积为 ． ②如图3，在ABC ∆中，60ACB ∠=︒，CD 为AB 边上的高．若4CD =，试判断ABC ∆的面积是否存在最小值，若存在，求出这个最小值；若不存在，请说明理由．（3）如图4，正方形ABCD 的边长为4，点E 、F 分别为边AB 、BC 上的动点，且45EDF ∠=︒，求四边形DEBF 面积的最大值．【解答】解：（1）如图1，设AD 与O 交于E ，连接BE ， 则C AEB ∠=∠，AEB D ∠>∠，ACB ADB ∴∠>∠；故答案为：>；（2）①如图2，连接CO 并延长交AB 于E ， ABC ∆是等边三角形， AC CB ∴=，∴AC BC =，CE AB ∴⊥，2AE BE ==，CE ∴=CD 为O 的切线，CE CD ∴⊥， //CD AB ∴，ABD ∴∆的面积11422AB CE =⋅=⨯=故答案为：②如图3中，作ABC ∆的外接圆O ，连接OA ，OB ，OC ，作OE AB ⊥于E ．设2OA OC x ==． 2120AOB ACB ∠=∠=︒，OA OB =，OE AB ⊥，AE EB ∴=，60AOE BOE ∠=∠=︒， 12OE OA x ∴==，AE =，OC OE CD +， 34x ∴， 43x∴， x ∴的最小值为43，2AB =，AB ∴； ABC ∴∆的面积的最小值142=⨯； （3）四边形DEBF 面积ADE CDF ABCD S S S ∆∆=--正方形，∴当ADE CDF S S ∆∆+DEBF 的面积有最大值，如图4，将DAE ∆逆时针旋转90︒得到DCM ∆， 180FCM FCD DCM ∴∠=∠+∠=︒，AE CM =，F ∴、C 、M 三点共线， DE DM ∴=，90EDM ∠=︒，90EDF FDM ∴∠+∠=︒， 45EDF ∠=︒，45FDM EDF ∴∠=∠=︒，在DEF ∆和DMF ∆中，DE DMEDF MDF DF DF =⎧⎪∠=∠⎨⎪=⎩， ()DEF DMF SAS ∴∆≅∆，EF MF ∴=，EF CF AE ∴=+；DEF ∆的面积DFM =∆的面积122ADE DCF S S EF CD EF ∆∆=+=⨯=，DEF ∴∆面积2EF =．EF AE CF =+，4AE BE AB +==，4BF CF BC +==， 8EF BE BF AB BC ∴++=+=， 8BE BF EF ∴+=-，22222(8)6416BE BF BE BF EF EF EF ∴⋅++=-=+-，且222BE FB EF +=， 328BE BF EF ∴⋅=-，2()0BE BF -， 222BE BF BE BF ∴+⋅， 26416EF EF ∴-2(8)128EF ∴+，828EF ∴-，或828EF --（舍去），EF ∴的最小值为8-，DEF ∴∆面积的最小值为，∴四边形DEBF 面积的最大值441632=⨯-=-29．问题探究（1）如图1．在ABC ∆中，8BC =，D 为BC 上一点，6AD =．则ABC ∆面积的最大值是 24 ． （2）如图2，在ABC ∆中，60BAC ∠=︒，AG 为BC 边上的高，O 为ABC ∆的外接圆，若3AG =，试判断BC 是否存在最小值？若存在，请求出最小值；若不存在，请说明理由．问题解决：如图3，王老先生有一块矩形地ABCD ，12AB =，6BC =，现在他想利用这块地建一个四边形鱼塘AMFN ，且满足点E 在CD 上，AD DE =，点F 在BC 上，且6CF =，点M 在AE 上，点N 在AB 上，90MFN ∠=︒，这个四边形AMFN 的面积是否存在最大值？若存在，求出面积的最大值；若不存在，请说明理由．【解答】解：（1）当AD BC ⊥时，ABC ∆面积的最大，则ABC ∆面积的最大值是11862422BC AD ⋅=⨯⨯=，故答案为：24；（2）如图2中，连接OA ，OB ，OC ，作OE BC ⊥于E ．设2OA OC x ==，2120COB CAB ∠=∠=︒，OC OB =，OE CB ⊥， CE EB ∴=，60COE BOE ∠=∠=︒，12OE OB x ∴==，BE ，OA OE AG +，33x ∴， 1x ∴，x ∴的最小值为1，2BC =，BC ∴的最小值为（3）如图3中，连接AF ，EF ，延长BC 交AE 的延长线于G ，90D ∠=︒，6AD DE ==，45DAE AED ∴∠=∠=︒，12CD AB ==，6CE CF ∴==，45CEF CFE ∴∠=∠=︒， 90AEF ∴∠=︒，EF BF ∴=，将EFM ∆顺时针旋转得到FBH ∆，作FHN ∆的外接圆O 交AB 于N ， 连接ON ，90AEF ABF ∠=∠=︒，AF AF =，EF BF =，Rt AEF Rt ABF(HL)∴∆≅∆， AEF ABF S S ∆∆∴=，。
专题4 阿波罗尼斯圆与隐性圆问题-2017-2018学年江苏高一下学期数学期末复习备考(必修2) Word版含解析
专题4 阿波罗尼斯圆与隐性圆问题-2017-2018学年江苏高一下学期数学期末复习备考（必修2）一、 填空题1.如果圆(x －2a )2＋(y －3a －3)2＝4上总存在两个点到原点的距离为1，则实数a 的取值范围是________． 解析：原问题可转化为：圆(x －2a )2＋(y －a －3)2＝4和圆x 2＋y 2＝1相交，可得两圆圆心之间的距离d ＝＝，由两圆相交可得2－1<＜2＋1，解得－56<a <0.2.(2017·南通二模)在平面直角坐标系xOy 中，已知B ，C 为圆x 2＋y 2＝4上两点，点A (1,1)，且AB ⊥AC ，则线段BC 的长的取值范围是________．又BC 2＝4(4－OP 2)，OP ∈2，则BC ∈ [4，4]＝[－，＋]．法二：设BC 的中点为M (x ，y )，因为OB 2＝OM 2＋BM 2＝OM 2＋AM 2，有4＝x 2＋y 2＋(x －1)2＋(y －1)2，化简得21＋(y －21)2＝23，所以点M 的轨迹是以21为圆心，22为半径的圆，所以AM 的取值范围是2，所以BC 的取值范围是[－，＋]．3.已知x ，y 满足0≤x ≤，则x －3y －2的取值范围是________．解析：由已知得x 2＋y 2≤4(x ≥0)，则点(x ，y )在以(0,0)为圆心，2为半径的右半圆内，x －3y －2＝2表示点(x ，y )和点(3,2)连线的斜率，设切线方程为y －2＝k (x －3)，即kx －y ＋2－3k ＝0，则k2＋1|2－3k|＝2，解得k ＝0或k＝512，故x －3y －2的取值范围是512.4.在平面直角坐标系xOy 中，圆C 1：x 2＋y 2＝4，圆C 2：x 2＋y 2＝16，点M (1,0)，动点P ，Q 分别在圆C 1和圆C 2上，满足MP ⊥MQ ，则线段PQ 的取值范围是________．解析：设P (x 1，y 1)，Q (x 2，y 2)，则x22＋y22＝16x12＋y12＝4，设PQ 的中点N (x ，y )，即N 2y1＋y2，则x 2＋y 2＝x1x2＋y1y2＝5＋21(x 1x 2＋y 1y 2)，由MP ⊥MQ ，得x 1x 2＋y 1y 2＝x 1＋x 2－1＝2x －1，所以x 2＋y 2＝5＋x －21，即21＋y 2＝419.因为PQ ＝2MN ，MN ∈2＋1，所以PQ ∈[－1，＋1]5.已知圆O ：x 2＋y 2＝1.若圆O 上存在两点A ，B ，直线y ＝2上存在点M ，满足λ＝(λ>0)，则λ的取值范围是________．6. (2017·江苏高考)在平面直角坐标系xOy 中，A (－12,0)，B (0,6)，点P 在圆O ：x 2＋y 2＝50上，若·≤20，则点P 的横坐标的取值范围是________．解析：设P (x ，y )，由·≤20，易得2x －y ＋5≤0，由x2＋y2＝502x －y ＋5＝0，可得A ：y ＝－5x ＝－5或B ：y ＝7x ＝1，由2x －y＋5≤0得P 点在圆左边弧上，结合限制条件－5≤x ≤5，可得点P 横坐标的取值范围为[－5，1]．7.已知变量a ，θ∈R ，则(a －2cos θ)2＋(a －5－2sin θ)2的最小值为________．解析：(a ，a －5)在直线x －y －5＝0上，点(2cos θ，2sin θ)在圆x 2＋y 2＝4上，圆心到直线x －y －5＝0距离的为5，则圆上点到直线距离最小值为3，故所求为9.8.已知点A ，B ，C 在圆x 2＋y 2＝1上运动，且AB ⊥BC .若点P (2,0)，则|＋＋|的最大值________．9.已知直线l ：x ＋3y ＋1＝0，圆C ：x 2＋y 2－2ax －2ay ＝1－2a 2(a >0)，过原点的直线l 1与直线l 垂直，l 1与圆C 交于M ，N 两点，则当△CMN 的面积最大时，圆心C 的坐标为________．解析：圆C ：(x －a )2＋(y －a )2＝1，直线l 1：3x －y ＝0，当CM ⊥CN 时，△CMN 的面积最大，此时C 到l 1的距离为22，则10|3a －a|＝22，a ＝25，圆心C (25，25)．二、解答题10.过A (4,0)的直线l 交抛物线D ：y 2＝4x 于M 、N 两点．是否存在垂直于x 轴的直线m 被以MA 为直径的圆E 所截得的弦长为定值？如果存在，求出m 的方程；如果不存在，说明理由．解析：假设存在直线m ：x ＝a 满足题意，设M (x 1，y 1)，则M (2x1＋4，2y1)，过M 作直线x ＝a 的垂线，垂足为E ，设直线m 与圆M 的一个交点为G .可得EG 2＝MG 2－ME 2，即EG 2＝MA 2－ME 2＝1－－a x1＋4 ＝41y 12＋4x1＋42＋a (x 1＋4)－a 2＝x 1－4x 1＋a (x 1＋4)－a 2＝(a －3)x 1＋4a －a 2.当a ＝3时，EG 2＝3，此时直线m 被以AP 为直径的圆M 所截得的弦长恒为定值2.因此存在直线m ：x ＝3满足题意．11.如图，在平面直角坐标系xOy 中，已知F 1(－4,0)，F 2(4,0)，A (0,8)，直线y ＝t (0<t <8)与线段AF 1，AF 2分别交于点P 、Q 过点Q 作直线QR ∥AF 1交F 1F 2于点R ，记△PRF 1的外接圆为圆C .(1)求证：圆心C 在定直线7x ＋4y ＋8＝0上；(2)圆C 是否恒过异于点F 1的一个定点？若过，求出该点的坐标；若不过，请说明理由．解析：(1)法一：易得直线AF 1：y ＝2x ＋8；AF 2：y ＝－2x ＋8，所以可得P ，t t －8，Q ，t 8－t ，再由QR ∥AF 1，得R (4－t,0)，则线段F 1R 的中垂线方程为x ＝－2t ，线段PF 1的中垂线方程为y ＝－21x ＋85t －16，由2t 得△PRF 1的外接圆的圆心坐标为－27t ，经验证，该圆心在定直线7x ＋4y ＋8＝0上．所以圆心坐标为(－2t ，87t －2)，经验证，该圆心在定直线7x ＋4y ＋8＝0上．②由①可得圆C 的方程为x 2＋y 2＋tx ＋(4－47t )y ＋4t －16＝0， 该方程可整理为(x 2＋y 2＋2y －16)＋t (x －47y ＋4)＝0， 则由y ＋4＝07 解得1332或y ＝0x ＝－4，所以圆C 恒过异于点F 1的一个定点，该点坐标为1332.12.如图，已知以点A (－1,2)为圆心的圆与直线l 1：x ＋2y ＋7＝0相切．过点B (－2,0)的动直线l 与圆A 相交于M ，N 两点，Q 是MN 的中点，直线l 与l 1相交于点P .·是否为定值？如果是，求出其定值；如果不是，请说明理由．解析：因为AQ ⊥BP ，所以·＝0，所以·＝(＋)·＝·＋·＝·.当直线l 与x 轴垂直时，得P (－2，－25)．则＝(0，－25)，又＝(1,2)，所以·＝·＝－5.当直线l 的斜率存在时，设直线l 的方程为y ＝k (x ＋2)．由x ＋2y ＋7＝0，x ＋2，解得P 1＋2k －5k.所以＝1＋2k －5k .所以·＝·＝1＋2k －5－1＋2k 10k ＝－5.综上所述，·是定值，且·＝－5.。
八种隐圆类最值问题,圆来如此简单(原卷版)
八种隐圆类最值问题，圆来如此简单在中考数学中，有一类高频率考题，几乎每年各地都会出现，明明图形中没有出现“圆”，但是解题中必须用到“圆”的知识点，像这样的题我们称之为“隐圆模型”。
正所谓：有“圆”千里来相会，无“圆”对面不相逢。
“隐圆模型”的题的关键突破口就在于能否看出这个“隐藏圆”。
一旦“圆”形毕露，则答案手到擒来！知识点梳理题型一定点定长得圆2023年湖北省鄂州市中考数学真题2023·邵阳市中考真题2023·广西南宁市二模2022·辽宁抚顺·中考真题2022·长春·中考真题题型二直角的对边是直径2023·菏泽市中考真题2022·通辽·中考真题2023·汕头市金平区一模2023·广州市天河区三模2022·成都市成华区二诊题型三对角互补得圆2023年·广元市一模题型四定弦定角得圆2023·成都市新都区二模2023·成都市金牛区二模2023·达州·中考真题题型五四点共圆题型六相切时取到最值2023·随州市中考真题2022·江苏无锡·中考真题2022扬州中考真题题型七定角定高面积最小、周长最小问题题型八米勒角（最大张角）模型徐州中考知识点梳理一、定点定长得圆在几何图形中，通过折叠、旋转，滑梯模型得到动点的轨迹为绕定点等于定长的圆，从而画出动点轨迹，并进行计算二、直角的对边是直径前世：在⊙O中，AB为直径，则始终有AB所对的∠C=90°今生：若有AB是固定线段，且总有∠ACB＝90°，则C在以AB为直径径的圆上．(此类型本来属于定弦定角，但是因为比较特殊，故单独分为一类)xB三、对角互补前世：在⊙O 上任意四点A ，B ，C ，D 所围成的四边形对角互补 今生：若四边形ABCD 对角互补，则A ，B ，C ，D 四点共圆四、定弦定角模型定角模型是直角模型的一种变形形式，其依据是已知定角，则根据“同弧所对的圆周角相等”得到动点的轨迹为圆弧，再画出对应图形进行计算．前世：在⊙O 中，若弦AB 长度固定则弦AB 所对的圆周角都相等(注意：弦AB 在劣弧AB 上也有圆周角，需要根据题目灵活运用)今生：若有一固定线段AB 及线段AB 所对的∠C 大小固定，根据圆的知识可知C 点并不是唯一固定的点，C 在⊙O 的优弧ACB 上均可(至于是优弧还是劣弧取决于∠C 的大小，小于90°，则C 在优弧上运动；等于90°，则C 在半圆上运动；大于90°则C 在劣弧运动)五、四点共圆模型前世:在⊙O 中，ABCD 是圆的内接四边形，则有∠1=∠2，∠3=∠4，△BPC~△APD(同理△BPA~△CPD) 今生:若四边形ABCD 中有∠1=∠2(通常情况下∠5=∠6对顶角相等，故不需要∠3=∠4，实际应用中长用∠1=∠2，∠5=∠6)则ABCD 四点(某些不能直接使用四点共圆的地区，可以通过证明两次三角形相似也可)，选填题可以直接使用六、定角定高（探照灯模型）什么叫定角定高，如右图，直线BC 外一点A ，A 到直线BC 距离为定值（定高），∠BAC 为定角。
专题复习三(与圆有关的最值问题)
问题2：利用几何意义求与圆有关的最值
例：已知实数x, y满足方程x 2 y 2 4 x 1 0 求下列各式的最大值与 最小值： y (1) ； x (2) y x；
涉及与圆有关的最值问 题， 利用数形结合与几何意 义求解 y b 形如u 转化为直线斜率 xa 形如t ax by 转化为直线截距
专题复习三
与圆有关的最值问题
问题1：定点、定直线到圆的最大（小）距离
定点与圆上的点的距离 的最大值与最小值
y D P A
O
•
定直线与圆上点的距离 的最大值与最小值yCຫໍສະໝຸດ DC P BE
A
x
B
x
O
|AB|最短、|AC|最长
|AB|最短、|AC|最 长
问题1：练习题
1.直线y x 1上的点到圆x 2 y 2 4 x 2 y 4 0 的最近距离是__________ __ 变式：圆x 2 y 2 4 x 2 y 4 0上到直线y x 1 距离最近的点的坐标是 __________ __ 2.圆x 2 y 2 4 x 4 y 10 0上的点到直线 x y 14 0 的最大距离与最小距离 的差是 __________ _ 3.点M在圆C1 : x 2 y 2 6 x 2 y 1 0上，点N 在圆C2 : x 2 y 2 2 x 4 y 1 0上，求 MN 的最大值.
(3) x 2 y 2； y 1 ( 4) ； x4 含有x 2与y 2的 转化为两点间距离 (5) x 2 10x y 2 14 y；
问题2：基础训练
1 1. 已知x, y满足( x 1) y , 分别求x 2 y 2、 4 y x y、 的最值. x 2.若x, y满足( x 1) 2 ( y 2) 2 4, 求S 2 x y的最大值与最小值 . y 1 2 2 3.实数x, y满足x y 4 x 2 y 0, 求 和x y的取值范围 . x 1 4.实数x, y满足x 2 y 2 4 x 6 y 12 0, 求下列式子的最值： y (1) ; (2) x 2 y 2 ; (3) x y; (4) x y. x
与圆有关最值问题课件
最小周长问题在材料科学、机械工程等领 域有应用，例如材料强度分析、机械零件 优化等。
最大面积问题
详细描述
最大面积问题通常涉及到圆的半径和面积 的关系，通过利用圆的面积公式，可以推
导出最大面积的条件和计算方法。
A 总结词
最大面积问题主要研究在给定条件 下，圆的面积的最大可能值。
B
C
D
应用场景
最大面积问题在资源开发、环境保护等领 域有应用，例如土地资源利用、生态保护 等。
02
与圆有关的最值问题
最大弦长问题
总结词
最大弦长问题主要研究在给定条件下，圆内弦长的最大可 能值。
公式
最大弦长 = 2 × √(R^2 - d^2)，其中 R 是圆的半径，d 是圆心到弦的垂直距离。
详细描述
最大弦长问题通常涉及到圆心角和半径的关系，通过利用 圆心角与弧长、弦长的关系，可以推导出弦长与半径的关 系式，进而求出最大弦长。
应用场景
最大弦长问题在几何、工程、建筑等领域有广泛应用，例 如桥梁设计、建筑结构分析等。
最小周长问题
总结词
详细描述
最小周长问题主要研究在给定条件下，圆 的周长的最小可能值。
最小周长问题通常涉及到圆的直径和半径 的关系，通过利用圆的周长公式，可以推 导出最小周长的条件和计算方法。
公式
应用场景
最小周长 = π × d，其中 d 是圆的直径。
详细描述
几何方法包括利用图形变换、对称性 等来求解最值问题。例如，在求圆上 一点到圆内某点的距离最值问题时， 可以通过作对称点并利用图形变换来 找到该点的位置和距离。
04
与圆有关最值问题的应用
在几何题中的应用
总结词
利用圆的性质求最值
《最值问题》配套练习题
《最值问题》配套练习题
一、解答题
1、将135个人分成若干小组，要求任意两个组的人数都不同，则最多可以
分成多少组？
2、将数字1，2，3，4，5，6，7，8，9填入□□□□×□□□×□□中，每一个□只限填一个数且每个数只能使用一次，请写出乘积最大的式子．
3、有13个不同的自然数，它们的和是100．问其中偶数最多有多少个？最少有多少个？
4、农场计划挖一个面积为432m2的长方形养鱼池，鱼池周围两侧分别有3m 和4m的堤堰如图所示，要想占地总面积最小，水池的长和宽应各为多少米？
5、在一个带有余数的除法算式中，商比除数大2，且其中的最大数与最小数之差是1023，那么此算式中的4个数的和最大可能是多少？
6、一个三角形的三条边长是三个两位的连续偶数，它们的末位数字和能被
7整除，这个三角形的最大周长等于多少？
7、已知a，b，c，d都是非0的自然数，a×b＋c×d＝60，那么a＋b＋c ＋d最小是多少？
1。
“隐圆”最值问题习题.doc
B M CDA “隐圆”最值问题重难点：分析题目条件发现题目中的隐藏圆，并利用一般的几何最值求解方法来解决问题【例1】在平面直角坐标系中，直线y = - x + 6分别与x 轴、y 轴交于点A 、B 两点，点C 在y 轴的左边，且∠ACB = 90°，则点C 的横坐标x C 的取值范围是__________．分析：在构造圆的前提下 考虑90°如何使用。
直角对直径所以以AB 为直径画圆。
使用垂径定理即可得到3-20c x ≤<3【练】（2013-2014·六中周练·16）如图，已知Rt △ABC 中，∠ACB =90°，AC = 3，BC = 4，点D 是AB 的中点，E 、F 分别是直线AC 、BC上的动点，∠EDF = 90°，则EF 长度的最小值是__________．分析：过D 点作DE 垂直AB 交AC 于点M 可证△FBD ∽△ECD 即可求出最小值【例2】如图，在Rt △ABC 中，∠ACB = 90°，D 是AC 的中点， M 是BD 的中点，将线段AD 绕A 点任意旋转（旋转过程中始终保持点M 是BD 的中点），若AC = 4，BC = 3，那么在旋转过程中，线段CM 长度的取值范围是_______________． 分析：将线段AD 绕A 点任意旋转隐藏着以A 为圆心AD 为半径的圆构造出来。
接下来考虑重点M 的用途即可。
中点的用法可尝试下倍长和中位线。
此题使用中位线。
答案是3722c x ≤≤ 【练】已知△ABC 和△ADE 都是等腰直角三角形，∠ACB =∠ADE= 90°，AC = 22，AD = 1，F 是BE 的中点，若将△ADE 绕点A旋转一周，则线段AF 长度的取值范围是424222AC -+≤≤． 分析：同例题【例3】如图，已知边长为2的等边△ABC ，两顶点A 、B 分别在平面直角坐标系的x 轴、y 轴的正半轴上滑动，点C 在第一象限，连接OC ，则OC长的最大值是（ ）A ．2B ．1C ． 1 +3D ．3分析：取AB 中点M 连接OM 、CM 。
隐圆问题大全[精选.]
![隐圆问题大全[精选.]](https://img.taocdn.com/s3/m/ff5191bca5e9856a5712600f.png)
隐圆问题1.已知四边形ABCD中,AB∥CD,BC=6cm,AB=AC=AD=5cm,求BD=＿＿＿思路分析：以A为圆心,AB为半径作圆,作直径BM,连DM,可证DM=BC=6,BM=10,BD=82.如图,在△ABC内有一点D,且DA=DB=DC,若∠DAB=20°,∠ACB=＿＿＿思路分析：以D为圆心,DA为半径作圆,∠ADB=1400,∠ACB=700.3．(2013武汉）如图，E，F是正方形ABCD的边AD上两个动点，满足AE＝DF．连接CF 交BD于G，连接BE交AG于点H．若正方形的边长为2，则线段DH长度的最小值是．思路分析：先证AG⊥BE，则H是⊙O上一点，O、D、H共线，DH最小。
DH=15-4.(2013武汉）．如图，⊙A与⊙B外切于点D，PC，PD，PE分别是圆的切线，C，D，E是切点，若∠CED＝x°，∠ECD＝y°，⊙B的半径为R，则⋂DE的长度是（）A．()9090Rx-πB．()9090Ry-πC．()180180Rx-πD．()180180Ry-π思路分析：C、D、E在⊙P上22yDCEDPE=∠=∠)2180(yDBE-=∠故选B第16题图HGFEDC BAEPABCD第10题图FBDAOO /C 5.如图,半径为4的⊙O 中,CD 为直径,弦AB ⊥CD 且过半径OD 的中点,点E 为⊙O 上一动点,CF ⊥AE 与点F.当点E 从点B 出发顺时针运动到点D 时,点F 所经过的路径长为( ). A π3π B.23π C.332π D.33π答案:C 提示:点F 在⊙O /上运动,∠ACF=300,∠O /=600,6.在平面直角坐标系中,直线y=-x+ 6分别与x 轴、y 轴交与点A 、B 两点，点C 在y 轴左边，且∠ACB=90°，则点C 的横坐标ｘｃ的取值范围是________.答案:3-32≦Xc <0提示:隐圆问题,以AB 为直径作圆P. PC ⊥y 轴Xc 最小.7.如图,铁路MN 和公路PQ 在点O 处交汇,∠QON=30°,公路PQ上A 处距O 点240米,如果火车行驶时,周围200米以内会受到噪音的影响,呢么货车在铁路MN 上沿ON 方向以72千米/时的速度行驶时,A 处受噪音影响的时间为( )A.12秒B.16秒C.20秒D.24秒 答案:B提示:以A 为圆心200为半径画圆,交MN 于CD,火车在CD 上行驶的时间即为所求.8.在坐标系中,点A 的坐标为(3,0),点B 为y 轴正半轴上的一点,点C 时第一象限内一点,且AC=2,设tan ∠BOC=m,则m 的取值范围是_________. 答案:m ≥25 提示:隐圆问题;OC 与⊙A 相切时,m 最小为259.如图,等腰三角形ABC 中,AB=AC,将△ABC 沿DE 折叠,使底角顶点C 落在三角形三边的垂直平分线的交点O 处,若BE=BO,则∠ABC 的度数为( )A.540B.600C.630D.720答案:C提示:以O 为圆心,OB 为半径作圆,连OC,设∠OBC=x=∠OCB=∠EOC,则∠BOE=∠BEO=2x,5x=1800,x=360,∠A=540,∠ABC=630.最新文件 仅供参考 已改成word 文本 。
隐圆及几何最值训练题
隐圆及几何最值训练题一、利用“直径是最长的弦”求最值1.如图，在等腰Rt △ABC 中，∠C=90°，AC=BC=4，D 是AB 的中点，点E 在AB 边上运动（点E 不与点A 重合），过A 、D 、E 三点作⊙O ，⊙O 交AC 于另一点F ，在此运动变化的过程中，线段EF 长度的最小值为（ ） ．2.如图，在△ABC 中，∠ABC=90°，AB=6，BC=8D 为AC 的中点，过点D 作DE ⊥DF ，DE 、DF 分别交射线AB 、AC 于点E 、F ，则EF 的最小值为 .二、利用“定点定长存隐圆”求最值 3．（2012年武汉市中考）在坐标系中，点A 的坐标为(3，为y 限内一点，且AC=2．，则m 的取值范围是4.如图，在Rt △ABC °，AC=4，BC=3，点D 是平面内的一个动点，且AD=2，M 为BD 的中点，在D 点运动过程中，线段CM 长度的取值范围是.5．正方形ABCD 中，E ，F 分别为射线BC ，CD 且满足BE=CF ，设AE ，BF 交于G ，则DG 的最小值为（ ）。
E6.（2013年武汉市中考）如图，E 、F 是正方形ABCD 的边AD 上两个动点，满足AE ＝DF ，连接CF 交BD 于点G ，连接BE 交AG 于点H ，若正方形的边长为2，则线段DH 长度的最小值是7.（2015、△EFG 均是边长为2点D 是边BC 、EF 、FC 相交于点M ．当△EFG 绕点D 旋转时，线段BM 长的最小值是（ ）8.如图，在边长为2的菱形ABCD 中，M A'D CBA∠A ＝60°，M 是AD 边的中点，N 是AB 边上一动点，将△AMN 沿MN 所在的直线翻折得到△A 'MN ，连接A 'C ，则A 'C 长度的最小值是.9.（2013如图，圆A 与圆B 外切于点D ，PC 、PD 、PE 分别是圆的切线，C 、D 、E 是切点，若∠CDE ＝x °,∠ECD ＝y °，⊙B 的半径为R ，则弧DE 的长度是( )A.90)90(Rx -π B.90)90(Ry -π C.180)180(R x -π D.180)180(R y -π 10.系中，O为原点，点A（-2，0），点B （0，2），点E，点F分别为OA，OB 的中点.若正方形OEDF绕点O顺时针旋转，得正方形OE’D’F’，若直线AE’与直线BF’相交于点P. （1）求∠PAO的最大值（2）点P运动的路径长三、利用“对角互补存隐圆”求最值11.如图，定长弦CD在以AB为直径的⊙O上滑动（点C、D与点A、B不重合），M是CD的中点，过点C作CP⊥AB于点P，若CD=3，AB=8，求PM长度的最大值四、利用“定弦定角存隐圆”求最值12.（2014扇形AOD中，∠AOD＝906，点P为弧AD上任意一点（不与点A 和D重合），PQ⊥OD于Q，点I为△OPQ的内心，过O，I和D三点的圆的半径为r. 则当点P在弧AD上运动时，r的值满足（）A．0＜r＜3 B．r=3 C．3＜r＜3 2 D．r=3 2 13.如图, 边长为3的等边△ABC, D、E分别为边BC、AC上的点, 且BD＝CE, AD、BE交于P点, 则CP的最小值为14.如图，点A与点B的坐标分别是（1，0），（5，0），点P是该直角坐标系内的一个动点．（1）使∠APB=30°的点P有个；（2）若点P在y轴上，且∠APB=30°，求满足条件的点P的坐标；（3）当点P在y轴上移动时，∠APB 是否有最大值？若有，求点P的坐标，并说明此时∠APB明理由．五、利用“两边和差”求最值15.如图, ABC, 两顶点A、B分别在直角∠MON的两边上滑动, 点C在∠MON内部, 则OC 的长的最大值为.16.（2013年武汉市四调）如图，∠BAC=60°，半径长为1的圆O与∠BAC 的两边相切，P为圆O上一动点，以P为圆心，PA长为半径的圆P交射线AB、AC于D、E两点，连接DE，则线段DE长度的最大值为( ).A．3 B．6 C D．x17．△ABC 中，∠，BC=2，当点A 在x C点也在y 的最大值18．△ABC 中，0，AC=BC= 5 ，CP 绕C 点顺时针旋转900得到线段CD ，当P 点绕B 点旋转一周时，D 点也随之运动，求BD 的最大值和最小值。
隐形圆解决最值及面积问题 - 含答案
定弦定角最值问题【定弦定角题型的识别】有一个定弦，一个主动点，一个从动点，定弦所对的张角固定不变。
【题目类型】图形中一般求一个从动点到一个定点线段长度最值问题，一般涉及定弦定角最值问题【解题原理】同弧所对的圆周角相等，定弦的同侧两个圆周角相等，则四点共圆，因此动点的轨迹是圆。
（线段同侧的两点对线段的张角相等，则这两点以及线段的两个端点共圆。
）【一般解题步骤】①让主动点动一下，观察从动点的运动轨迹，发现从动点的运动轨迹是一段弧。
②寻找不变的张角（这个时候一般是找出张角的补角，这个补角一般为45°、60°或者一个确定的三角函数的对角等）③找张角所对的定弦，根据三点确定隐形圆。
④确定圆心位置，计算隐形圆半径。
⑤求出隐形圆圆心至所求线段定点的距离。
⑥计算最值：在此基础上，根据点到圆的距离求最值（最大值或最小值）。
典型例题讲解1.如图，△ABC中，AC＝3，BC＝24，∠ACB＝45°，D为△ABC内一动点，⊙O为△ACD的外接圆，直线BD交⊙O于P点，交BC于E点，弧AE＝CP，则AD的最小值为（）A．1 B．2 C．2D．2414解：∵∠CDP＝∠ACB＝45°∴∠BDC＝135°（定弦定角最值）如图，当AD过O′时，AD有最小值∵∠BDC＝135°∴∠BO′C＝90°∴△BO′C为等腰直角三角形∴∠ACO′＝45°＋45°＝90°∴AO′＝5又O′B＝O′C＝4 ∴AD＝5－4＝12.如图，AC＝3，BC＝5，且∠BAC＝90°，D为AC上一动点，以AD为直径作圆，连接BD交圆于E点，连CE，则CE的最小值为（）16A．213+C．5 D．13-B．29解：连接AE∵AD为⊙O的直径∴∠AEB＝∠AED＝90°∴E点在以AB为直径的圆上运动当CE过圆心O′时，CE有最小值为213-3.如图，在△ABC中，AC＝3，BC＝24，∠ACB＝45°，AM∥BC，点P在射线AM上运动，连BP交△APC的外接圆于D，则AD的最小值为（）A．1 B．2C．2D．34-2解：连接CD∴∠PAC＝∠PDC＝∠ACB＝45°∴∠BDC＝135°如图，当AD过圆心O′时，AD有最小值∵∠BDC＝135°∴∠BO′C＝90°∴O′B＝O′C＝4又∵∠ACO′＝90°∴AO′＝5 ∴AD的最小值为5－4＝14.如图，⊙O的半径为2，弦AB的长为32，点P为优弧AB上一动点，AC⊥AP交直线PB 于点C，则△ABC的面积的最大值是（）A．312+D．346+6312+B．336+C．35.如图，⊙O 的半径为1，弦AB ＝1，点P 为优弧AB 上一动点，AC ⊥AP 交直线PB 于点C ，则△ABC 的最大面积是（ ）A ．21 B ．22 C ．23 D ．436.如图，A(1，0)、B(3，0)，以AB 为直径作⊙M ，射线OF 交⊙M 于E 、F 两点，C 为弧AB 的中点，D 为EF 的中点．当射线绕O 点旋转时，CD 的最小值为__________解：连接DM∵D 是弦EF 的中点 ∴DM ⊥EF ∴点D 在以A 为圆心的，OM 为直径的圆上运动当CD 过圆心A 时，CD 有最小值，连接CM∵C 为弧AB 的中点∴CM ⊥AB ∴CD 的最小值为127.如图，AB 是⊙O 的直径，AB ＝2，∠ABC ＝60°，P 是上一动点，D 是AP 的中点，连接CD ，则CD 的最小值为__________解：连接OD ∵D 为弦AP 的中点∴OD ⊥AP ∴点D 在以AO 为直径的圆上运动当CD 过圆心O ′时，CD 有最小值，过点C 作CM ⊥AB 于M∵OB ＝OC ，∠ABC ＝60°∴△OBC 为等边三角形∴OM ＝21，CM ＝23∴O ′C ＝47∴CD 的最小值为2147- 8.如图，在矩形ABCD 中，AB ＝4，AD ＝6，E 是AB 边的中点，F 是线段BC 边上的动点，将△EBF 沿EF 所在直线折叠得到△EB ′F ，连结B ′D ，则B ′D 的最小值是（ ）．A． B.6 C. D.4【思路探究】根据E 为AB 中点，BE ＝B ′E 可知，点A 、B 、B ′在以点E 为圆心，AE 长为半径的圆上，D 、E 为定点，B ′是动点，当E 、B ′、D 三点共线时，B ′D 的长最小，此时B ′D ＝DE －EB ′，问题得解.【解析】∵AE ＝BE ，BE ＝B ′E ，由圆的定义可知，A 、B 、B ′在以点E 为圆心，AB 长为直径的圆上，如图所示. B ′D 的长最小值= DE －EB.故选A．【启示】此题属于动点（B ′）到一定点（E ）的距离为定值（“定点定长”），联想到以E 为圆心，EB ′为半径的定圆，当点D 到圆上的最小距离为点D 到圆心的距离－圆的半径.当然此题也可借助三角形三边关系解决，如，当且仅当点E 、B ′、D 三点共线时，等号成立.9.如图，E 、F 是正方形ABCD 的边AD 上两个动点，满足AE ＝DF ，连接CF 交BD 于点G ，连结BE 交AG 于点H ，若正方形的边长是2，则线段DH 长度的最小值是 .【思路探究】根据正方形的轴对称性易得∠AHB＝90°，故点H 在以AB 为直径的圆上.取AB 中点O ，当D 、H 、O 三点共线时，DH 的值最小，此时DH ＝OD －OH ，问题得解.【解析】由△ABE ≌△DCF ，得∠ABE ＝∠DCF ，根据正方形的轴对称性，可得∠DCF ＝∠DAG ，∠ABE ＝∠DAG ，所以∠AHB ＝90°，故点H 在以AB 为直径的圆弧上.取AB 中点O ，OD交⊙O 于点H ，此时DH 最小，∵OH ＝，OD ，∴DH 的最小值为OD －OH . 22=B D DE B E ''≤-HGB A 112AB =1【启示】此题属于动点是斜边为定值的直角三角形的直角顶点，联想到直径所对圆周角为直角（定弦定角），故点H 在以AB 为直径的圆上，点D 在圆外，DH 的最小值为DO －OH.当然此题也可利用的基本模型解决.如图，在矩形ABCD 中，AB ＝4，AD ＝6，E 是AB 边的中点，F 是线段BC 边上的动点，将△EBF 沿EF 所在直线折叠得到△EB′F ，连结B′D ，则B′D 的最小值是（ ）．A． B .6 C . D .4【思路探究】根据E 为AB 中点，BE ＝B′E 可知，点A 、B 、B′在以点E 为圆心，AE 长为半径的圆上，D 、E 为定点，B′是动点，当E 、B′、D 三点共线时，B′D 的长最小，此时B′D ＝DE －EB′，问题得解.【解析】∵AE ＝BE ，BE ＝B′E ，由圆的定义可知，A 、B 、B′在以点E 为圆心，AB 长为直径的圆上，如图所示. B′D 的长最小值= DE －EB′.故选A ．【启示】此题属于动点（B′）到一定点（E ）的距离为定值（“定点定长”），联想到以E 为圆心，EB′为半径的定圆，当点D 到圆上的最小距离为点D 到圆心的距离－圆的半径.当然此题也可借助三角形三边关系解决，如，当且仅当点E 、B′、D 三点共线时，等号成立.【典例2】如图，E 、F 是正方形ABCD 的边AD 上两个动点，满足AE ＝DF ，连接CF 交BD 于点G ，连结BE 交AG 于点H ，若正方形的边长是2，则线段DH 长度的最小值是.【思路探究】根据正方形的轴对称性易得∠AHB ＝90°，故点H 在以AB 为直径的圆上.取AB 中点O ，当D 、H 、O 三点共线时，DH 的值最小，此时DH ＝OD －OH ，问题得解.【解析】由△ABE ≌△DCF ，得∠ABE ＝∠DCF ，根据正方形的轴对称性，可得∠DCF ＝∠DAG ，∠ABE ＝∠DAG ，所以∠AHB ＝90°，故点H 在以AB 为直径的圆弧上.取AB 中点O ，OD 交⊙O 于点H ，此时DH 最小，∵OH ＝，OD ，∴DH 的最小值为OD －OH .【启示】此题属于动点是斜边为定值的直角三角形的直角顶点，联想到直径所对圆周角为直角（定弦定角），故点H 在以AB 为直径的圆上，点D 在圆外，DH 的最小值为DO －OH .当然此题也可利用的基本模型解决.DH OD OH ≤-22=B D DE B E ''≤-HGA 112AB =1DH OD OH ≤-【针对训练 】1. 如图，在△ABC 中，∠ACB ＝90°，AC ＝2，BC ＝1，点A ，C 分别在x 轴，y 轴上，当点A 在轴正半轴上运动时，点C 随之在轴上运动，在运动过程中，点B 到原点O 的最大距离为（ ）.A． B ． C ． D ．3作AC 的中点D ，连接OD 、BD ，∵OB ≤OD+BD ，∴当O 、D 、B 三点共线时OB 取得最大值，∵BD=2，OD=AD=21AC=1， ∴点B 到原点O 的最大距离为1+2．故选C2.如图，在矩形ABCD 中，AB ＝4，BC ＝6，E 是矩形内部的一个动点，且AE ⊥BE ，则线段CE 的最小值为（ ）.A ．B .C .D .4 3. 如图，在△ABC 中，AB ＝10，AC ＝8，BC ＝6，以边AB 的中点O 为圆心，作半圆与AC 相切，点P 、Q 分别是边BC 和半圆上的运点，连接PQ ，则PQ 长的最大值与最小值的和是（ ）.A .6B .C .9D .优质解答如图，设 O 与AC 相切于点E ，连接OE ，作OP 1⊥BC 垂足为P 1交 O 于Q 1，此时垂线段OP 1最短，P 1Q 1最小值为OP 1-OQ 1，∵AB=10，AC=8，BC=6，∴AB 2=AC 2+BC 2，∴∠C=90°，∵∠OP 1B=90°，∴OP 1∥AC ∵AO=OB ，∴P 1C=P 1B ，∴OP 1=21AC=4，∴P 1Q 1最小值为OP 1-OQ 1=1， x y 5612+32210-2213-22131+322如图，当Q 2在AB 边上时，P 2与B 重合时，P 2Q 2经过圆心，经过圆心的弦最长， P 2Q 2最大值=5+3=8，∴PQ 长的最大值与最小值的和是9．故答案为：9．4.如图，AC ＝3，BC ＝5，且∠BAC ＝90°，D 为AC 上一动点，以AD 为直径作圆，连接BD 交圆于E 点，连CE ，则CE 的最小值为（ ）.A. B . C .5 D .5．如图，已知正方形ABCD 的边长为2，E 是BC 边上的动点，BF ⊥AE 交CD 于点F ，垂足为G ，连结CG ，则CG 的最小值为（ ）．A ．B ．C .D .6．如图，△ABC 、△EFG 是边长为2的等边三角形，点D 是边BC 、EF 的中点，直线AG 、FG 相交于点M ，当△EFG 绕点D 旋转时，线段BM 长的最小值是A ．B ．C .D .7．如图，在边长为2的菱形ABCD 中，∠A ＝60°，M 是AD 边的中点，N 是AB 边上一动点，将△AMN 沿MN 所在的直线翻折得到△A′MN ，连结A′C ，则A′C 长度的最小值是 .8．（2017威海）如图，△ABC 为等边三角形，AB =2，若点P 为△ABC 内一动点，且满足∠PAB =∠ACP ，则线段PB 长度的最小值为 ．解答 解：∵△ABC 是等边三角形，∴∠ABC=∠BAC=60°，AC=AB=2，∵∠PAB=∠ACP ，∴∠PAC+∠ACP=60°，∴∠APC=120°，∴点P 的运动轨迹是弧AC ， 当O 、P 、B 共线时，PB 长度最小，设OB 交AC 于D ，如图所示：213-213+91651-31-21-21+23-31+231-此时PA=PC，OB⊥AC，。
(完整word版)圆中最值问题10种求法
圆中最值的十种求法在圆中求最值是中考的常见题型，也是中考中的热点、难点问题,有的学生对求最值问题感到束手无策，主要原因就是对求最值的方法了解不多,思路不够灵活。
现对在圆中求最值的方法，归纳如下：一、利用对称求最值1．如图：⊙O的半径为2，点A、B、C在⊙O上,OA⊥OB，∠AOC=60°，P是OB上一动点，求PA+PC 的最小值。
[分析]：延长AO交⊙O于D，连接CD交⊙O于P，即此时PA+PC最小,且PA+PC的最小值就等于弦CD的长。
解：延长AO交⊙O于D，连接CD交OB于P连接PA，过O作OE⊥CD，垂足为E在△OCD中，因为∠AOC=60°所以∠D=∠C=30°在Rt△ODE中cos30°=即DE=2×cos30°= 所以CD=2DE=2即PA+PC的最小值为2.二、利用垂线段最短求最值2．如图:在直角坐标系中，点A的坐标为（－3, －2)，⊙A的半径为1，P为x轴上一动点,PQ切⊙A于点Q，则PQ长度的最小值为。
[分析］：连接AQ、PA，可知AQ⊥PQ。
在Rt△PQA中,PQ=,求PQ的最小值转化为求PA的最小值,根据垂线段最短易求PA的最小值为2.解：连接PA、QA因为PQ切⊙A于点Q 所以PQ⊥AQ在Rt△APQ中,PQ2=PA2－AQ2即PQ=又因为A（－3，－2) ，根据垂线段最短。
所以PA的最小值为2所以PQ的最小值=三、利用两点之间线段最短求最值3．如图：圆锥的底面半径为2，母线PB的长为6，D为PB的中点,一只蚂蚁从点A出发,沿着圆锥的侧面爬行到点D，则蚂蚁爬行的最短路程为（)A．B．2 C．3 D．3[分析]：因为圆锥的侧面是曲面蚂蚁从A爬行到点D，不好求爬行的最小值，要把立体图形展开为平面图形,再利用两点之间线段最短来解决问题。
解：圆锥的侧面展开图如图2，连接AB根据题意得：弧AC的长为2πr=2π·2=4π，PA=6因为4π= 所以n=120°即∠APB=60°又因为PA=PB所以△PAB是等边三角形因为D为PB中点所以AD⊥PB PD=DB=3在Rt△PAD中,AD=,故选C。
隐形圆模型的最值问题-含答案
隐形圆模型的最值问题【母题示例】如图，在矩形ABCD中，AB＝4，BC＝2，点E是CD上一动点，沿AE折叠矩形，使得点D落在矩形ABCD内的点D′处，连接CD′，则CD′的最小值为________．【命题形式】常在几何图形中，结合折叠、旋转问题计算最值，一般会出现直角、定点和定长等特征信息．【母题剖析】先判断点D′在以A为圆心，AD为半径的圆上，再根据勾股定理确定CD′的最小值即可．【母题解读】隐形圆模型的最值问题是一种特殊的最值问题，其中以基本图形(三角形、矩形等)为背景，结合图形变换(折叠、旋转)来计算图形中某条线段的最值．常见的模型有：直角模型；定角模型；折叠旋转模型等．解题的关键是先确定动点轨迹所在圆的圆心，再连接定点与圆心，从而实现问题的解决.模型一直角模型【模型解读】直角模型是在问题中出现“直角”“垂直”“90°”等关键词，利用“90°的圆周角所对的弦是直径”从而确定动点所在轨迹，以及动点的圆心，再确定定点和圆的位置关系，最后利用勾股定理等方法求线段的最值．【基本图形】基本图形BM⊥BN，点C是∠MBN内一点，且AC⊥BC，则点C在说明以AB为直径的圆上【核心突破】1.如图，正方形ABCD的边长为6，点E、F分别从点D和点C出发，沿射线DA、射线CD运动，且DE＝CF，直线AF、直线BE交于点H，连接DH，则线段DH长度的最小值为( )A．35－3 B．25－3 C．33－3 D．32．如图，在平面直角坐标系中，点A的坐标为(－3，0)，点B的坐标为(3，0)，点P是平面内一点，且AP⊥BP，点M的坐标为(3，4)，连接MP，则MP的最小值为________．模型二定角模型【模型解读】定角模型是直角模型的一种变形形式，其依据是已知定角，则根据“同弧所对的圆周角相等”得到动点的轨迹为圆弧，再画出对应图形进行计算．【基本图形】基本图形说明点P是正方形ABCD内一点，且∠APB＝60°，则以AB为边在正方形ABCD 内作等边△ABM，点P在△ABM的外接圆在正方形内的部分弧上基本图形说明点P是平面内一点，且∠APB＝45°，则以AB为斜边作等腰Rt△AOB，点P在以O为圆心，OA为半径的圆的优弧上【模型突破】1．如图，矩形ABCD中，AD＝5，AB＝23，点P是矩形ABCD内(含边界)上一点，且∠APB＝60°，连接CP，则CP的最小值为________．2．如图，在平面直角坐标系中，矩形ABCD的顶点A，D均在x轴上，点B在第三象限，且OA＝2，OD＝1，AB＝4，点E是AB的中点，连接OE，动点P是平面内一点，且∠OPE＝45°，连接CP，求CP的最小值．模型三折叠、旋转模型【模型解读】折叠、旋转模型是在几何图形中，通过折叠或旋转变换得到动点，而此时动点的轨迹为以定点为圆心，定长为半径的圆，从而画出动点轨迹，并进行计算．【基本图形】基本图形沿过矩形ABCD的顶点A折叠△ADE，得到△AD′E，则点D′说明在以A为圆心，AD为半径的圆弧上基本图形△AEF绕正方形ABCD的顶点A旋转，则点F的轨迹为以A 说明为圆心，AF为半径的圆【模型突破】1．如图，在Rt△ABC中，∠ACB＝90°，AC＝4，BC＝6，点D是边BC的中点，点E是边AB上任意一点(点E不与点B重合)，沿DE翻折△DBE，使点B落在点F处，连接AF，则线段AF的长取最小值时，BF的长为________．。
中考专题北师大版本九下专题隐形圆的最值问题
3、应用隐圆解决实际问题；最值问题之“隐圆再现”的问题【知识要点】点到圆的最小距离和最大距离总结：（圆外一点到圆上最短距离是与圆心的连线；最长距离是与圆心连线的延长线。
）圆内一点P到圆上的最短距离为PA，最长距离为PB；(P、A、0、B四点在同一条直线上，即P，A，B三点过圆心O) ．二、圆的存在条件（常见的类型，还有定半径长度类）类型1、圆的定义：（定长）在一个平面内，线段 AB 绕它固定的一个端点 A 旋转一周，另一个端点 B 所形成的图形叫做圆；类型2、定直角：直径所对的圆周角为90°；应用几何性质：①三角形的三边关系：两边之和大于第三边，两边之差小于第三边；②两点间线段最短；③连接直线外一点和直线上各点的所有线段中，垂线段最短；④定圆中的所有弦中，直径最长．【例题精讲】知识点一、翻折定点定长--隐圆现。
例1．如图，在Rt△ABC中，∠C=6，BC=8，点F在边AC上，并且CF=2，点E为边BC上的动点，将△CEF沿直线EF翻折，点C落在点P处，则点P到边AB距离的最小值是．2.如图，在矩形ABCD中，AC=6，BC=8，点F是边AC的中点，点E为边BC上的动点，将△CEF 沿直线EF翻折，点C落在点P处，则点P到点D的距离的最小值是．3．如图，在矩形ABCD中，AB＝4，AD＝6，E是AB边的中点，F是线段BC边上的动点，将△EBF沿EF所在直线折叠得到△EB′F，连接B′D，则B′D的最小值是．5．如图，菱形ABCD边长为4，∠A＝60°，M是AD边的中点，N是AB边上一动点，将△AMN沿MN 所在的直线翻折得到△A1MN，连接A1C，则A1C的最小值是．知识点二、动点定直角---隐圆现1.如图，在等腰Rt△ABC中，∠BAC=90°，AB=AC，BC=，点D是AC边上一动点，连接BD，以AD为直径的圆交BD于点E，则线段CE长度的最小值为．2．如图，在Rt△ABC中，BC＝AC＝2，点M是AC边上一动点，连接BM，以CM为直径的⊙O 交BM于N，则线段AN的最小值为．3．如图，Rt△ABC中，∠ACB＝90°，AC＝BC＝4，D为线段AC上一动点，连接BD，过点C作CH⊥BD于H，连接AH，则AH的最小值为．4．如图，在矩形ABCD中，AB＝4，BC＝6，E是矩形内部的一个动点，且AE⊥BE，则线段CE 的最小值为．6．如图，正方形ABCD中，AB＝2，动点E从点A出发向点D运动，同时动点F从点D出发向点C运动，点E、F运动的速度相同，当它们到达各自终点时停止运动，运动过程中线段AF、BE相交于点P，M是线段BC上任意一点，则MD+MP的最小值为．4、（湖北武汉3分）如图，E，F是正方形ABCD的边AD上两个动点，满足AE＝DF．连接CF 交BD于G，连接BE交AG于点H．若正方形的边长为2，则线段DH长度的最小值是．知识点三、动点定长隐圆现1．如图，⊙O的半径为2，AB.CD是互相垂直的两条直径，点P是⊙O上任意一点，过点P作PM⊥AB于点M，PN⊥CD于点N，点Q是MN的中点，当点P从点A运动到点D时，点Q所经过的路径长为（）．2．如图，正方形ABCD的边长为2，将长为2的线段QR的两端放在正方形的相邻的两边上同时滑动．如果点Q从点A出发，沿图中所示方向按A⇒B⇒C⇒D⇒A滑动到A止，同时点R从点B 出发，沿图中所示方向按B⇒C⇒D⇒A⇒B滑动到B止，在这个过程中，线段QR的中点M所经过的路线围成的图形的面积为（）A．2B．4﹣πC．πD．π﹣13．如图，矩形ABCD中，AB＝2，AD＝3，点E、F分别为AD、DC边上的点，且EF＝2，点G 为EF的中点，点P为BC上一动点，则P A+PG的最小值为（）A．3B．4C．2D．5【立马试试】2．如图，在矩形ABCD中，AB=4，AD=2，M是AD边的中点，N是AB边上的一动点，将△AMN 沿MN所在直线翻折得到△A'MN，连接A'C．在MN上存在一动点P．连接A'P、CP，问△A'PC 周长是否存在最小值是，若存在，请计算出这个最小值；若不存在，请说明理由．7．如图，一块∠BAC为30°的直角三角板ABC的斜边AB与量角器的直径恰好重合，点E在量角器的圆弧边缘处从A到B运动，连接CE，交直径AB于点D．(1)当点E在量角器上对应的刻度是90°时，则∠ADE的度数为多少？(2)若AB=8，P为CE的中点，当点E从A到B的运动过程中，点P也随着运动，则点P所走过的路线长为多少？类型四、三条相等线段造成的隐形圆1．如图，已知AB＝AC＝AD，∠CBD＝2∠BDC，∠BAC＝44°，则∠CAD的度数为（）A．68°B．88°C．90°D．112°2．如图，四边形ABCD中，DC∥AB，BC＝1，AB＝AC＝AD＝2．则BD2的值为（）A．14B．15C．18D．12【课堂总结】隐形圆的几种存在情况1.2.3.4.【2019锦江1诊真题再现】（武侯二诊）24．（4分）如图，点O是矩形ABCD的对角线的交点，AB＝15，BC＝8，直线EF 经过点O，分别与边CD，AB相交于点E，F（其中0＜DE＜）．现将四边形ADEF沿直线EF折叠得到四边形A′D′EF，点A，D的对应点分别为A′，D′，过D′作D′G⊥CD于点G，则线段D′G的长的最大值是，此时折痕EF的长为．（2018•锦江区模拟）如图，在矩形ABCD中，AB＝4，BC＝43，对角线AC、BD相交于点O，现将一个直角三角板OEF的直角顶点与O重合，再绕着O点转动三角板，并过点D作DH⊥OF 于点H，连接AH．在转动的过程中，AH的最小值为．【课后练习】3．如图，在△OAB中，OA＝OB，∠AOB＝15°，在△OCD中，OC＝OD，∠COD＝45°，且点C在边OA上，连接CB，将线段OB绕点O逆时针旋转一定角度得到线段OE，使得DE＝CB，则∠BOE的度数为（）A．15°B．15°或45°C．45°D．45°或60°4．直线y＝x+4分别与x轴、y轴相交于点M，N，边长为2的正方形OABC一个顶点O在坐标系的原点，直线AN与MC相交于点P，若正方形绕着点O旋转一周，则点P到点（0，2）长度的最小值是（）A．2﹣2B．3﹣2C．D．1二．填空题（共5小题）5．如图，在△ABC中，∠ACB＝90°，AB＝5，BC＝3，P是AB边上的动点（不与点B重合），将△BCP沿CP所在的直线翻折，得到△B′CP，连接B′A，则B′A长度的最小值是．三．解答题（共2小题）7．（阿氏圆）问题背景如图1，在△ABC中，BC＝4，AB＝2AC．问题初探请写出任意一对满足条件的AB与AC的值：AB＝，AC＝．问题再探如图2，在AC右侧作∠CAD＝∠B，交BC的延长线于点D，求CD的长．问题解决求△ABC的面积的最大值．8．已知A（2，0），B（6，0），CB⊥x轴于点B，连接AC画图操作：（1）在y正半轴上求作点P，使得∠APB＝∠ACB（尺规作图，保留作图痕迹）理解应用：（2）在（1）的条件下，①若tan∠APB＝，求点P的坐标；②当点P的坐标为时，∠APB最大拓展延伸：（3）若在直线y＝x+4上存在点P，使得∠APB最大，求点P的坐标．9．如图，边长为2的正方形ABCD的顶点A，B在一个半径为2的圆上，顶点C，D在该圆内，将正方形ABCD绕点A逆时针旋转，当点D第一次落在圆上时，点C运动的路线长为______．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
B
M
C D A
E
F
D C
B
A
B
D
C
F A
“隐圆”最值问题
重难点：分析题目条件发现题目中的隐藏圆，并利用一般的几何最值求解方法来解决问题
【例1】在平面直角坐标系中，直线y = - x + 6分别与x 轴、y 轴交于点A 、B 两点，点C 在y 轴的左边，且∠ACB = 90°，则点C 的横坐标x C 的取值范围是__________．
分析：在构造圆的前提下 考虑90°如何使用。
直角对直径所以以AB 为直径画圆。
使用垂径定理即可得到3-20c x ≤<3
【练】（2013-2014·六中周练·16）如图，已知Rt △ABC 中，∠ACB = 90°，AC = 3，BC = 4，点D 是AB 的中点，E 、F 分别是直线AC 、BC 上的动点，∠EDF = 90°，则EF 长度的最小值是__________．
分析：过D 点作DE 垂直AB 交AC 于点M 可证△FBD ∽△ECD 即可 求出最小值
【例2】如图，在Rt △ABC 中，∠ACB = 90°，D 是AC 的中点，
M 是BD 的中点，将线段AD 绕A 点任意旋转（旋转过程中始 终保持点M 是BD 的中点），若AC = 4，BC = 3，那么在旋转 过程中，线段CM 长度的取值范围是_______________．
分析：将线段AD 绕A 点任意旋转隐藏着以A 为圆心AD 为半径的圆构造 出来。
接下来考虑重点M 的用途即可。
中点的用法可尝试下倍长和中位线。
此题使用中位线。
答案是
3722
c x ≤≤
【练】已知△ABC 和△ADE 都是等腰直角三角形，∠ACB =∠ADE = 90°，AC 2，AD = 1，F 是BE 的中点，若将△ADE 绕点A
旋转一周，则线段AF 4242
22
AC -+≤≤ 分析：同例题
【例3】如图，已知边长为2的等边△ABC ，两顶点A 、B 分别在平面直角
坐标系的x轴、y轴的正半轴上滑动，点C在第一象限，连接OC，则OC
长的最大值是（）
A．2 B．1 C．3D．3
分析：取AB中点M连接OM、CM。
因为OM=1，3，所以
3
【练1】如图，在矩形ABCD中，AB = 2，BC3，两顶点A、B分别在平面
直角坐标系的x轴、y轴的正半轴上滑动，点C在第一象限，连接OC，则OC
长的最大值为_______3___．
分析：取AB中点M，方法同例题
【练2】如图，E、F是正方形ABCD的边AD上两个动点，
满足AE = DF，连接CF交BD于点G，连接BE交AG于点H，若正方形的边
长为2，则线段DH长度的最小值是51____．
分析：取AB中点M，方法同例题
【例4】如图，∠XOY = 45°，一把直角三角尺ABC的两个顶点A、B分别在
OX、OY上移动，其中AB = 10，那么点O到AB的距离的最大值为__________．
分析：构造△ABO的外接圆。
点O可以在圆上任意动，利用垂径定理即可得到
+
O到AB的最大距离为：552
【练1】已知线段AB = 4，在线段AB上取一点P，在AB的同侧作等边△APC和等边△BPD，则线段CD的最小值为____2______．
分析：可构造一个以CD为斜边的水平的直角三角形，快速得到当AP=BP时最小，CD最小
【练2】如果满足∠ABC = 60°，AC = 12，BC = k的△ABC恰有一个，那么k的取值范围是
A
D
C
B
O
y x
N
M
B
Q
C
P
A
____012k <≤______．
分析：画出△ABC 的外接圆，观察动点B 在弧上面的运动即可
【例5】已知A （2，0），B （4，0）是x 轴上的两点，点C 是y 轴上的动点，当∠ACB 最大时，则点C 的坐标为__________．
分析：画出△ABC 的外接圆M 。
要保证∠ACB 最大，即圆周角最大，只要圆心角最大即可。
所以在等腰△MAB 中只要半径最小即可，半径什么时候最小呢？只要圆与Y 轴相切即可所以得答案为：(0,2)±
【练】当你站在博物馆的展厅中时，你知道站在何处观赏最理想吗？ 如图，设墙壁上的展品最高点P 距底面2.5米，最低点Q 距底面 2米，观察者的眼睛E 距底面1.6米，当视角∠PEQ 最大时，站 在此处观赏最理想，则此时E 到墙壁的距离为（ B ）
A ．1米
B ．0.6米
C ．0.5米
D ．0.4米
分析：只要△PQE 的外接圆与人眼所在的水平线相切即可，通过垂径定理可得答案是B
【提升】
1．如图，Rt △ABC 中，∠C = 90°，∠ABC = 30°，AB = 6， 点D 在AB 边上，点E 是BC 边上一点（不与点B 、C 重合），且DA = DE ，则AD 的取值范围是（ ）
A ．2 < AD < 3
B ．2 ≤ AD < 3
C ．2 ≤ A
D ≤ 3 D ．1 ≤ AD < 2 2．（2012·济南）如图，矩形ABCD 中，AB = 2，AD = 1，当A 、B 两点 分别在x 轴正半轴和y 轴正半轴上移动时，矩形ABCD 的形状不变，则 OD 的最大值为（ ）
A 2+ 1
B 5
C 145
D ．5
2
3．（2013-2014·黄陂区九上期中·10）在△ABC 中，∠ACB = 90°，∠ABC = 30°，将△ABC 绕顶点C 顺时针旋转，旋转角为θ（0° < θ < 180° ），得 到△MNC ，P 、Q 分别是AC 、MN 的中点，AC = 2t ，连接PQ ，则旋转时 PQ 长度的最大值是（ ）
A ．6
B ．3t
C 6
D ．3t
4．已知点A 、B 的坐标分别是（0，1）、（0，3），点C 是x 轴正半轴上一动点，当∠ACB 最大时，点C 的坐标为__________．。