资料分析公式
(完整版)资料分析计算公式

资料分析计算公式
基本概念:
基期:统计中计算指数或变化情况等动态指标时,作为参照标准的时期。
(参照物)现期:相对基期而言,是与基期相比较的后一时期。
同比增长:与上一年同一时期相比的增长情况。
环比增长:与之紧紧相邻的上一个统计周期相比较的增长情况。
贸易顺差与贸易逆差
贸易顺差:进口额< 出口额
贸易顺差= 出口额—进口额
贸易逆差:进口额> 出口额
贸易逆差= 进口额—出口额
年均增长率、年均增长量:
现期量= 基期量()N
⨯,其中n为相差年数;
+
1年均增长率
年均增长量= ()n÷
现期量,其中n为相差年数;
-基期量。
资料分析公式汇总

资料分析公式汇总速算技巧一、估算法精度要求不高的情况下,进行粗略估值的速算方式。
选项相差较大,或者在被比较的数字相差必须比较大,差距的大小将直接决定对“估算”时对精度的要求。
二、直除法在比较或者计算较复杂的分数时,通过“直接相除”的方式得到商的首位(首一位、首两位、首三位),从而得出正确答案的速算方式。
常用形式: 1.比较型:比较分数大小时,若其量级相当,首位最大∕小数为最大∕小数2.计算型:计算分数大小时,选项首位不同,通过计算首位便可得出答案。
难易梯度:1.基础直除法:①可通过直接观察判断首位的情形;②需要通过手动计算判断首位的情形。
2.多位直除法:通过计算分数的“首两位”或“首三位”判断答案情形。
三、插值法1.“比较型”插值法如果A与B的比较,若可以找到一个数C,使得A﹥C,而B﹤C,既可以判定A﹥B;若可以找到一个数C,使得A﹤C,而B﹥C,既可以判定A﹤B;2.“计算型”插值法若A﹤C﹤B,则如果f﹥C,则可以得到f=B;如果f﹤C,则可以得到f=A;若A﹥C﹥B,则如果f﹥C,则可以得到f=A;如果f﹤C,则可以得到f=B。
四、放缩法当计算精度要求不高时,可以将中间结果进行大胆的“放”(扩大)或者“缩”(缩小),从而迅速得到精度足够的结果。
常用形式:1. A﹥B,C﹥D,则有A+C﹥B+D;A-D﹥B-C;2. A﹥B﹥0,C﹥D﹥0,则有A×C﹥B×D;A÷D﹥B÷C五、割补法在计算一组数据的平均值或总和值时,首先选取一个中间值,根据中间值将这组数据“割”(减去)或“补”(追上),进而求取平均值或总和值。
常用形式:1.根据该组数据,粗略估算一个中间值;2.将该组值分别减去中间值得到一组数值;3.将得到的新数值相加得到和值,用和值除以该组数值的项数得到商值,将商值加上中间值,即为该组数值的精确平均值;4.用中间值乘以数据项数再加上最后的和值即为总和值。
资料分析公式汇总
资料分析公式汇总速算技巧一、估算法精度要求不高的情况下,进行粗略估值的速算方式。
选项相差较大,或者在被比较的数字相差必须比较大,差距的大小将直接决定对“估算”时对精度的要求。
二、直除法在比较或者计算较复杂的分数时,通过“直接相除”的方式得到商的首位(首一位、首两位、首三位),从而得出正确答案的速算方式。
常用形式: 1.比较型:比较分数大小时,若其量级相当,首位最大∕小数为最大∕小数2.计算型:计算分数大小时,选项首位不同,通过计算首位便可得出答案。
难易梯度:1.基础直除法:①可通过直接观察判断首位的情形;②需要通过手动计算判断首位的情形。
2.多位直除法:通过计算分数的“首两位”或“首三位”判断答案情形。
三、插值法1.“比较型”插值法如果A与B的比较,若可以找到一个数C,使得A﹥C,而B﹤C,既可以判定A﹥B;若可以找到一个数C,使得A﹤C,而B﹥C,既可以判定A﹤B;2.“计算型”插值法若A﹤C﹤B,则如果f﹥C,则可以得到f=B;如果f﹤C,则可以得到f=A;若A﹥C﹥B,则如果f﹥C,则可以得到f=A;如果f﹤C,则可以得到f=B。
四、放缩法当计算精度要求不高时,可以将中间结果进行大胆的“放”(扩大)或者“缩”(缩小),从而迅速得到精度足够的结果。
常用形式:1. A﹥B,C﹥D,则有A+C﹥B+D;A-D﹥B-C;2. A﹥B﹥0,C﹥D﹥0,则有A×C﹥B×D;A÷D﹥B÷C五、割补法在计算一组数据的平均值或总和值时,首先选取一个中间值,根据中间值将这组数据“割”(减去)或“补”(追上),进而求取平均值或总和值。
常用形式:1.根据该组数据,粗略估算一个中间值;2.将该组值分别减去中间值得到一组数值;3.将得到的新数值相加得到和值,用和值除以该组数值的项数得到商值,将商值加上中间值,即为该组数值的精确平均值;4.用中间值乘以数据项数再加上最后的和值即为总和值。
资料分析公式

现期量:已知基期量和增长率r 求现期量=基期量*(1+r)
基期量:已知现期量和增长量求基期量=现期量-增长量
已知现期量和增长率r 求基期量=现期量/(1+增长率)
增长率:已知增长量和基期量求增长率=增长量/基期量
已知增长量和现期量求增长率=增长量/(现期量-增长量)
已知基期量和现期量求增长率=(现期量-基期量)/基期量
增长量:已知基期量和现期量求增长量=现期量-基期量
已知基期量和增长率r 求增长量=基期量*r
已知现期量和增长率r 求增长量=[现期量/(1+r)]*r
已知现期量增长率比较增长量大小:大大则大。
资料分析常用公式

在学习前复习常用的公式: 1.同比增加量 Aa/1+a 2.隔年求增长率 r1+r2+r1r2 3.比重公式模型 A/B *(1+b)/(1+a) 4.乘除转换A/(1+a)=A*(1-a),a的绝对值<10% 5.比重变化量:A/B* (a-b)/(1+a) 6.比重变化率 (a-b)/(1+b) 问题分类击破 一、资料分析抓年份 去年今年和明年 年份问题是个小问题,但是,千里之堤毁于蚁穴,小细节上更容易出大问题,首先用笔画出年份,务必不要搞错,费了精力和时间,最后由于年份而功亏一篑,实不应该,公考的1分可能决定太多。
二、选项差距看难易 该放弃时就放弃 这是山东2013题目,较之往年,简单很多,一般用选项差距来衡量难易程度。
因为说到怎么算,大家都知道步骤,重要的还是如何很快的选出答案。
选项差距: 1 和2 差距很大,其实1.1和1.2,选项差距也接近10%呢,所以遇到这样的选项是很容易选出的。
比如101题,属于秒杀的题目。
而当遇到161 163 这样的恶心选项是,有时间就算,没时间就选一个走人。
比重问题:求比重、比重变化率、比重变化趋势、 比重变化趋势常考:口诀: 部分>整体,比重上升。
部分<整体,比重下降。
(这里的部分和整体分别指的部分和整体的增长率) 推导过程: 去年:部分A/(1+a) 整体:B/(1+b) 今年:部分A 整体B 去年比重:A(1+b)/B(1+a) 今年比重:A/B ---》到这里就很明显啦解题妙招 1、比较大小: 常规通分 例题:11793/1.302 9848/1.053比较大小 1053----1302 250 9848+250*9=2XXXX>11793 所以右边大于左边 差分法:(应用前提:分子分母都比另一个数小) 3.3 3.8 0.5 --------- ------- -------- (口诀:大就大值大 小就大值小) 1.092 1.163 0.7多 截位法、倍数法不赘述 补充:资料分析中的经典比较大小问题: 1150.9*7.8%/(1+7.8%) 1067.12*15%/(1+15%) 1246.97*10.9%/(1+10.9%) 1067.67*13%/(1+13%) 典型的A*a/(1+a)的形式,首先考虑A*a 2、乘除转换的应用: a=b/(1+X)=b*(1-x) x的绝对值要小于10%才适用 a=b*(1+x)=b/(1-x) 应用乘除转化时,绝对误差和选项误差比较,如果小于选项误差,则可以使用,绝对误差可以以-b*x2来近似估算(x的平方) 举例: 3772÷(1+3.4%)=( )。
资料分析公式汇总

资料分析公式汇总在进行资料分析时,掌握一些关键的公式可以帮助我们更高效、准确地处理数据和得出结论。
下面就为大家汇总一下常见的资料分析公式。
一、增长类公式1、增长量=现期量基期量增长量用于衡量某个指标在两个时期之间的绝对变化量。
2、增长量=基期量 ×增长率这个公式通过基期量和增长率来计算增长量。
3、增长率=(现期量基期量)÷基期量 × 100%增长率反映了指标的相对增长程度。
4、年均增长量=(末期量初期量)÷间隔年份用于计算在一段时间内平均每年的增长量。
5、年均增长率=\(\sqrtn{\frac{末期量}{初期量}} 1\)(n 为间隔年份)计算一段时间内的平均每年的增长率。
二、比重类公式1、比重=部分值÷整体值 × 100%比重表示部分在整体中所占的比例。
2、整体值=部分值÷比重通过已知的部分值和比重来计算整体值。
3、部分值=整体值×比重根据整体值和比重求出部分值。
三、平均数类公式1、平均数=总数÷个数这是平均数的基本计算公式。
2、总数=平均数×个数通过平均数和个数来计算总数。
四、倍数类公式1、倍数= A÷BA 是B 的多少倍,用 A 除以 B 即可。
2、增长倍数=(现期量基期量)÷基期量增长倍数是指现期量相对于基期量的增长幅度。
五、其他常用公式1、隔年增长率=现期增长率+基期增长率+现期增长率×基期增长率用于计算隔年的增长情况。
2、拉动增长率=部分增长量÷整体基期量 × 100%反映某个部分的增长对整体增长的拉动作用。
3、贡献率=部分增长量÷整体增长量 × 100%衡量部分增长量对整体增长量的贡献程度。
在实际运用中,需要根据具体的题目条件选择合适的公式。
同时,要注意数据的单位和计算的准确性。
比如,在计算增长率时,要确保基期量的数值是准确的;在计算比重时,要明确部分和整体的范围。
资料分析报告公式汇总

资料分析公式汇总速算技巧一、估算法精度要求不高的情况下,进行粗略估值的速算方式。
选项相差较大,或者在被比较的数字相差必须比较大,差距的大小将直接决定对“估算”时对精度的要求。
二、直除法在比较或者计算较复杂的分数时,通过“直接相除”的方式得到商的首位(首一位、首两位、首三位),从而得出正确答案的速算方式。
常用形式: 1.比较型:比较分数大小时,若其量级相当,首位最大∕小数为最大∕小数2.计算型:计算分数大小时,选项首位不同,通过计算首位便可得出答案。
难易梯度:1.基础直除法:①可通过直接观察判断首位的情形;②需要通过手动计算判断首位的情形。
2.多位直除法:通过计算分数的“首两位”或“首三位”判断答案情形。
三、插值法1.“比较型”插值法如果A与B的比较,若可以找到一个数C,使得A﹥C,而B﹤C,既可以判定A﹥B;若可以找到一个数C,使得A﹤C,而B﹥C,既可以判定A﹤B;2.“计算型”插值法若A﹤C﹤B,则如果f﹥C,则可以得到f=B;如果f﹤C,则可以得到f=A;若A﹥C﹥B,则如果f﹥C,则可以得到f=A;如果f﹤C,则可以得到f=B。
四、放缩法当计算精度要求不高时,可以将中间结果进行大胆的“放”(扩大)或者“缩”(缩小),从而迅速得到精度足够的结果。
常用形式:1. A﹥B,C﹥D,则有A+C﹥B+D;A-D﹥B-C;2. A﹥B﹥0,C﹥D﹥0,则有A×C﹥B×D;A÷D﹥B÷C五、割补法在计算一组数据的平均值或总和值时,首先选取一个中间值,根据中间值将这组数据“割”(减去)或“补”(追上),进而求取平均值或总和值。
常用形式:1.根据该组数据,粗略估算一个中间值;2.将该组值分别减去中间值得到一组数值;3.将得到的新数值相加得到和值,用和值除以该组数值的项数得到商值,将商值加上中间值,即为该组数值的精确平均值;4.用中间值乘以数据项数再加上最后的和值即为总和值。
资料分析常考公式

资料分析常考公式资料分析是一门重要的课程,它不仅能够为学生提供一些有用的知识,还能够让学生学习一些有用的技能。
在大多数学术课程中,资料分析常常涉及到公式,学生需要记住这些公式,并将其用于实际研究中。
首先,提到资料分析常考公式,最常考的莫过于卡方公式,它用于计算两组资料之间的差异。
卡方公式也被称为卡方检验,它可以用于查看两组不同资料的差异,让研究者可以比较两组资料的差异是否有统计学上的意义。
卡方公式的公式为:$ X^2 = sum_{i=1}^{n} frac{(O_i - E_i)^2}{E_i} $ 其中,$ O_i $是观察到的实际值, $ E_i $预期值。
此外,t检验也是一种常见的资料分析检验,它可以帮助研究者检验两组样本的差异是否具有统计学上的意义。
t检验的公式为:$ t = frac{bar{x}_1 -bar{x}_2}{s_psqrt{frac{1}{n_1}+frac{1}{n_2}}} $其中,$ bar{x}_1 $ $ bar{x}_2 $ 代表两组样本的均值,$ s_p $ 代表两组样本的池化标准差, $ n_1 $ $ n_2 $ 代表两组样本的大小。
此外,要进行有效的资料分析,你还需要记住线性回归的公式: $ Y = a + bX + epsilon $其中,$ Y $变量,$ a $ $ b $系数,$ X $自变量,$ epsilon $误差项。
最后,有一些技术也是常见的资料分析方法,例如因子分析和主成分分析。
因子分析是一种统计学方法,用于发现多变量资料中的隐藏模式,它可以帮助研究者更好地理解数据的结构。
而主成分分析是一种统计学方法,用于将资料维度降低,从而使它更加容易解释。
资料分析非常重要,以上只是常见的几种资料分析的常见公式,学习者必须掌握这些公式才能更好地理解资料分析的原理。
当然,学习者需要不断练习,才能更好地掌握这些公式,以便将其运用到实际研究中。
通过对各种资料分析公式的研究和实践,学生可以更好地理解资料分析的基本原理和技能,从而将其用于实际研究。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
直接读数类
(30)方法:读题做标记,辅助工具(直尺)
综合分析题
(31)四项基本原则:题干短原则,不计算原则(时间与材料时间一致),信息易得原则,简单计算原则
(3)估算法(近似取整估算)
比重比较
(27)某部分现期量为A,整体现期量为B
相当于分数大小比较,同上述做法
(28)基期比重与现期比重比较:某部分现期量为A,增长率a%,整体现期量为B,增长率b%
当部分增长率大于整体增长率,则现期比重大于基期比重。(方法为“看”增长率)
平均数计算
(29)已知N个量的值,求平均数
(20)已知现期量与基期量
(1)截位直除法
(2)插值法
增长贡献率
(21)已知部分增长量与整体增长量
(1)截位直除法
(2)插值法
拉动增长
(22)如果B是A的一部分,B拉动A增长x%
(1)截位直除法
(2)插值法
比重计算
(23)某部分现期量为A,整体现期量为B
(1)截位直除法
(2)插值法
(24)某部分基期量为A,增长率a%,整体基期量为B,增长率b%
一般先计算 ,然后根据a和b的大小判断大小
(25)某部分现期量为A增长率a%,整体现期量B,增长率b%
一般先计算 ,然后根据a和b的大小判断大小
(26)基期比重-现期比重:某部分现期量为A增长率a%,整体现期量B,增长率b%
两期比重值计算:
(1)先根据a与b的大小判断差值计算结果是正数还是负数;
(2)答案小于丨a-b丨
(17)合成增长率:整体分为A、B两个部分,分别增长a%与b%,整体增长率r%
(18)混合增长率:整体为A,增长率为rA,分为两个部分B和C,增长率为rB和rC
则rA介于rB和rC之间
混合增长率大小居中
增长率比较
(19)已知现期量与增长量
比较 代替增长率进行大小比较
相当于分数大小比较,同上述做法
发展速度
资料分析
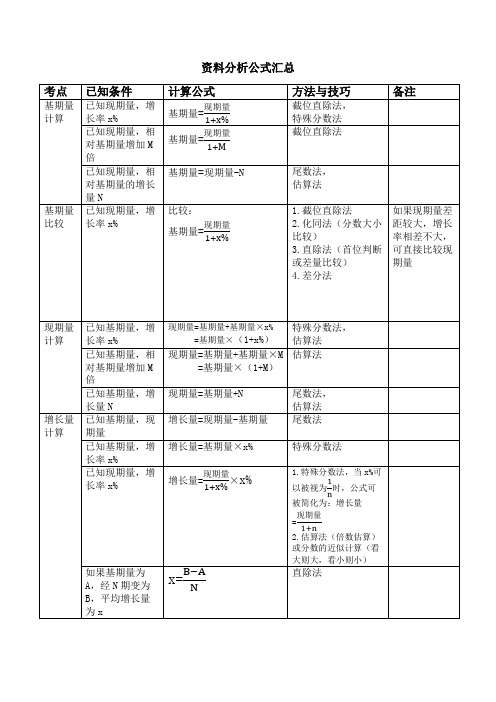
基期量计算
(1)已知现期量,增长率x%
截位直除法,特殊分数法
(2)已知现期量,相对基期量增加M倍
截位直除法
(3)已知现期量,相对基期量的增长量N
尾数法,估算法
基期量比较
(4)已知现期量,增长率x%
比较:
(1)截位直除法(2)如果现期量差距较大,增长率相差不大,可直接比较现期量。
(3)化同法
分数大小比较:
(1)特殊分数法,当x%可以被视为 时,公式可被化简为: ;
(2)估算法(倍数估算)或分数的近似计算(看大则大,看小则小)
(11)如果基期量为A,经N期变为B,平均增长量为x
直除法
增长量比较
(12)已知现期量与增长率x%
(1)特殊分数法,当x%可以被视为 时,公式可被化简为:
(2)公式可变换为: ,其中 为增函数,所以现期量大,增长率大的情况下,增长量一定大。
增长率计算
(13)已知基期量与增长量
(1)截位直除法
(2)插值法
(14)已知现期量与基期量
截位直除法
(15)如果基期量为A,经N期变为B,平均增长率为x%
代入法或公式法
(16)两期混合增长率:如果第二期与第三期增长率分别为 ,那么第三期相对第一期增长率
简单记忆口诀:连续增长,最终增长大于增长率之和;连续下降,最终下降小于增长率之和
(1)直除法(首位判断或差量比较)
(2)化同法,差分法或其它
现期量计算
(5)已知基期量,增长率x%
特殊分数法,估算法
(6)已知基期量,相对基期量增加M倍
估算法
(7)已知基期量,增长量N
尾数法,估算法
增长量计算
(8)已知基期量与现期量
尾数法
(9)已知基期量与增长率x%
特殊分数法
(10)已知现期量与增长率x%
