优胜教育五年级数学讲义三角形的周长和面积
优胜教育五年级数学讲义三角形的面积和周长答案
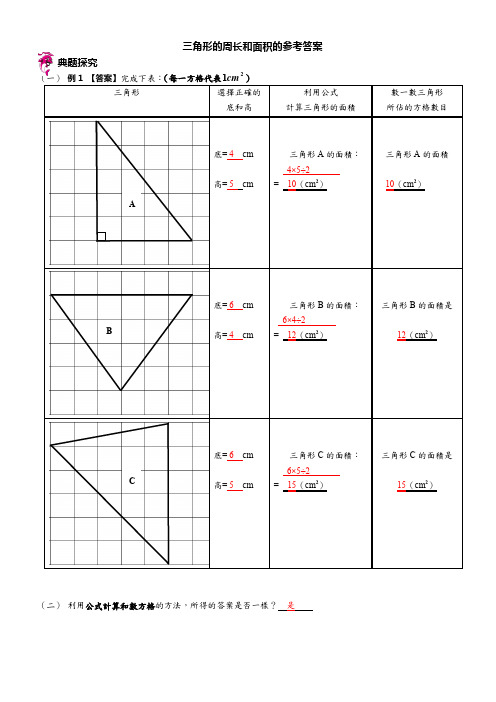
三角形的周长和面积的参考答案典题探究(一) 例1 【答案】完成下表:(每一方格代表21cm )三角形選擇正確的底和高利用公式 計算三角形的面積數一數三角形 所佔的方格數目底= 4 cm高= 5 cm三角形A 的面積: 4×5÷2 = 10(cm 2)三角形A 的面積10(cm 2)底= 6 cm高= 4 cm三角形B 的面積: 6×4÷2 = 12(cm 2)三角形B 的面積是12(cm 2)底= 6 cm高= 5 cm三角形C 的面積: 6×5÷2 = 15(cm 2)三角形C 的面積是15(cm 2)(二) 利用公式計算和數方格的方法,所得的答案是否一樣? 是ABC12cm9cm 13cm18cm 8cm9cm 12cm16cm 8cm8cm 4cm 9cm 7cm8cm10cm (三) 小心選擇三角形的底及其對應高,然後運用公式計算三角形的面積: 1.三角形的底 = 9 或12 cm 三角形的高 = 12或9 cm三角形的面積: 9×12÷2 或 12×9÷2 = 108 ÷2 = 54(cm 2)2.三角形的底 = 12 cm 三角形的高 = 8 cm三角形的面積: 12×8÷2 = 96 ÷2 = 48(cm 2)3.三角形的底 = 16或8 cm 三角形的高 = 4或8 cm三角形的面積: 16×4÷2 或 8×8÷2= 64 ÷2 = 32(cm 2)4.三角形的底 = 10 cm 三角形的高 = 7 cm三角形的面積:10×7÷2 = 70 ÷2 = 35(cm 2)例2:平行四边形 三角形的底 三角形的高 平行四边形面积的一半 底乘高 底乘高除以2 a ×h÷2例3:D 解析:下图中都为三角形,三角形的面积等于底乘高除以2,甲乙丙的底和高都是长方形的长和宽,所以他们的面积相等例4:1.82 cm解析:高不变时,底增加1cm面积增加1.22cm,因此高为1.2cm,原来三角形的面积为3×1.2÷2=1.82 cm例5:92 cm解析:做斜边上的高等于斜边的一半,因此,6×3÷2=92 cm演练方阵A档(巩固专练)一填空题1、502、183、64、底5、42 216、172二、判断题。
三角形的周长和面积计算

三角形的周长和面积计算三角形是几何学中最基本的图形之一,它由三条线段组成,每两条线段之间形成一个角。
计算三角形的周长和面积是我们在解决几何问题中常遇到的需求。
本文将介绍如何计算三角形的周长和面积,以及一些相关的知识和公式。
1. 三角形的周长三角形的周长指的是三角形三条边的长度之和。
假设三角形的三边长度为a、b、c,那么三角形的周长公式为:周长 = a + b + c2. 三角形的面积2.1 海伦公式海伦公式是一种计算三角形面积的常用公式,适用于所有三角形。
假设三角形的三边长度为a、b、c,那么三角形的面积公式为:面积= √(s(s-a)(s-b)(s-c))其中s为三角形周长的一半,即s = (a + b + c) / 2。
2.2 直角三角形的面积直角三角形是指其中一个角为90度的三角形。
直角三角形的面积可以通过两条直角边的长度计算得到,公式如下:面积 = (直角边1 ×直角边2) / 22.3 等边三角形的面积等边三角形是指三条边的长度都相等的三角形。
等边三角形的面积可以通过边长计算得到,公式如下:面积 = (边长 ×边长× √3) / 43. 例题解析例题1:已知三角形的三边长度分别为3cm、4cm、5cm,求其周长和面积。
解析:周长 = 3cm + 4cm + 5cm = 12cms = (3cm + 4cm + 5cm) / 2 = 6cm面积= √(6cm × (6cm - 3cm) × (6cm - 4cm) × (6cm - 5cm)) = √(6cm × 3cm × 2cm × 1cm) = √(36cm^2) = 6cm^2例题2:已知直角三角形的两条直角边分别为6cm和8cm,求其周长和面积。
解析:周长= 6cm + 8cm + √(6cm^2 + 8cm^2) = 6cm + 8cm + 10cm = 24cm 面积 = (6cm × 8cm) / 2 = 24cm^2例题3:已知等边三角形的边长为9cm,求其周长和面积。
三角形的面积和周长

三角形的面积和周长在几何学中,三角形是最基本的形状之一,它由三条边和三个角组成。
计算三角形的面积和周长是我们常见的几何问题之一。
本文将介绍如何求解三角形的面积和周长,并提供相关的计算公式和例题。
一、三角形的面积计算三角形的面积计算是通过底长和高(或两边夹角)进行计算的。
以下是常见的三角形面积计算公式:1. 通过底长和高计算当我们已知三角形的底长和高时,可以用以下公式计算面积:面积 = 底长 ×高 ÷ 2例如,假设三角形的底长为5cm,高为8cm,那么它的面积可以计算为:面积 = 5cm × 8cm ÷ 2 = 40cm²2. 通过两边夹角和边长计算当我们已知两边夹角和两边的长度时,可以用以下公式计算面积:面积 = 1/2 ×边1 ×边2 × sin(夹角)其中,sin表示正弦函数。
例如,假设我们已知三角形两边的长度分别为5cm和8cm,夹角为60度,那么它的面积可以计算为:面积= 1/2 × 5cm × 8cm × sin(60°) ≈ 17.32cm²二、三角形的周长计算三角形的周长计算是通过三边的长度进行计算的。
周长 = 边1 + 边2 + 边3例如,假设三角形的三边长度分别为3cm、4cm和5cm,那么它的周长可以计算为:周长 = 3cm + 4cm + 5cm = 12cm三、案例分析接下来,我们通过几个实例来进一步说明如何计算三角形的面积和周长。
案例一:已知三角形的底长为6cm,高为9cm,求其面积和周长。
解析:根据底长和高的公式计算面积:面积 = 6cm × 9cm ÷ 2 = 27cm²由于题目未给出两边的长度,无法计算周长。
案例二:已知三角形的边1长度为7cm,边2长度为9cm,夹角为45度,求其面积和周长。
解析:根据两边夹角和边长的公式计算面积:面积= 1/2 × 7cm × 9cm × sin(45°) ≈ 22.57cm²根据三边长度计算周长:周长 = 7cm + 9cm + 边3由于题目未给出边3的长度,无法计算周长。
三角形的周长和面积

三角形的周长和面积三角形是几何学中最简单的基本图形之一,它有着丰富的性质和特点。
在本文中,我们将探讨三角形的周长和面积,并了解它们之间的关系。
一、三角形的周长三角形的周长是指三条边的总长度。
对于一个一般的三角形,我们可以通过三边的长度来计算周长。
设三角形的三边分别为a、b、c,则三角形的周长C为:C = a + b + c针对特殊的情况,例如等边三角形和等腰三角形,我们可以利用其特性来简化周长的计算。
对于等边三角形,三条边的长度相等,假设边长为a,则周长C为:C = 3a对于等腰三角形,两边的长度相等,假设边长为a,底边的长度为b,则周长C为:C = 2a + b二、三角形的面积三角形的面积是指三角形所包围的平面区域的大小。
有多种方法可以计算三角形的面积,我们将介绍两种常见的方法。
1. 海伦公式海伦公式是一种通过三边长度来计算三角形面积的方法。
设三角形的三边长度分别为a、b、c,其中s为半周长(即s = (a + b + c) / 2),则三角形的面积S可以通过以下公式计算得出:S = √(s × (s - a) × (s - b) × (s - c))2. 底边高公式对于已知底边长度b和高h的三角形,我们可以使用底边高公式来计算面积。
三角形的面积S可以通过以下公式计算得出:S = 0.5 × b × h三、周长和面积的关系三角形的周长和面积之间存在一定的关系。
设三角形的周长为C,面积为S,则有以下结论成立。
1. 海伦公式的推论根据海伦公式,我们可以得出以下关系:S = √(s × (s - a) × (s - b) × (s - c))C = a + b + c其中s = (a + b + c) / 2可以发现,面积S只与三边的长度有关,而周长C则直接由三边的长度确定。
因此,周长和面积是密切相关的。
2. 等边三角形和等腰三角形的关系对于等边三角形和等腰三角形,我们可以得到以下结论:- 对于等边三角形,三条边的长度相等,因此周长C和面积S的比值为:C:S = 3a : (a^2√3/4) ≈ 4:√3- 对于等腰三角形,底边长度为b,高为h,则周长C和面积S的比值为:C:S = (2a + b) : (0.5bh)结论可以推广到其他类型的三角形,根据特定的边长关系,周长和面积之间的比值也会有相应的变化。
三角形的周长与面积

三角形的周长与面积三角形是最基本的几何图形之一,它由三条边和三个角组成。
在数学中,计算三角形的周长和面积是非常基础且重要的内容。
下面将详细介绍如何计算三角形的周长和面积。
一、三角形的周长三角形的周长是指三条边的长度之和。
假设三角形的三条边分别为a、b、c,那么周长P可以通过以下公式计算:P = a + b + c二、三角形的面积三角形的面积是指三角形所覆盖的平面区域的大小。
常用的计算三角形面积的方法有以下两种:1. 海伦公式海伦公式适用于所有类型的三角形,使用三条边的长度来计算面积。
假设三角形的三条边分别为a、b、c,周长为P,面积为S,海伦公式可以表示为:S = √(p × (p - a) × (p - b) × (p - c))其中,p = P/2,即半周长。
2. 高度乘以底边的一半这种方法适用于已知底边和高度的直角三角形或等腰三角形。
假设底边长度为b,高度为h,则三角形的面积可以表示为:S = 0.5 × b × h三、实例分析下面通过几个实例来演示如何计算三角形的周长和面积。
1. 实例一:已知三角形的三边分别为8、6、10,计算周长和面积。
周长P = 8 + 6 + 10 = 24可使用海伦公式计算面积:p = 24/2 = 12S = √(12 × (12 - 8) × (12 - 6) × (12 - 10)) = √(12 × 4 × 6 × 2) ≈ √(576) ≈ 242. 实例二:已知三角形的底边长度为6,高度为8,计算周长和面积。
周长P = 6 + 8 + 10 = 24使用高度乘以底边的一半计算面积:S = 0.5 × 6 × 8 = 24通过以上实例可以看出,不同的三角形计算周长和面积的方法有所差异,具体选择哪种方法取决于已知的条件。
综上所述,计算三角形的周长和面积是数学中的基本内容。
三角形的周长与面积

三角形的周长与面积三角形是几何学中最简单且最基础的形状之一,而其周长和面积是我们常常需要计算和探讨的数学概念。
本文将详细探讨三角形周长和面积的计算方法,并介绍一些与三角形密切相关的概念和性质。
一、三角形的周长三角形的周长是指三个边的长度之和。
设三角形的三边分别为a、b、c,那么三角形的周长P可表示为:P = a + b + c这是一个基本的计算公式,通过该公式我们可以很方便地计算出三角形的周长。
需要注意的是,为了计算准确,我们需要确保三角形的三边长度已知且符合三角形的边长关系。
二、三角形的面积三角形的面积是三角形内部的区域大小,常用符号S来表示。
有多种方法可以计算三角形的面积,下面将介绍几种常用的方法。
1. 海伦公式海伦公式是计算三角形面积的一种常用方法。
设三角形的三边长度分别为a、b、c,周长为P,利用海伦公式,可以得到三角形的面积S:S = √(P/2 * (P/2 - a) * (P/2 - b) * (P/2 - c))这个公式可以通过三角形的周长求得,需要注意的是,由于海伦公式包含开方运算,所以计算结果可能是一个实数。
2. 底边高公式底边高公式主要适用于高是已知的情况。
设底边长度为b,高为h,那么三角形的面积S可表示为:S = (1/2) * b * h这个公式比较简单易懂,适用于在平面直角坐标系中已知三角形的底边和高的情况。
3. 三角形内接圆半径公式三角形内接圆半径公式计算三角形面积的方法也比较常用。
设三角形的内接圆半径为r,那么三角形的面积S可表示为:S = (P * r) / 2其中P为三角形的周长。
这个公式适用于在三角形内接圆半径已知的情况。
三、三角形的性质除了周长和面积的计算,三角形还有很多有趣的性质值得我们了解。
下面将介绍几个常见的三角形性质。
1. 直角三角形的勾股定理直角三角形的勾股定理是三角学中一个重要的定理。
在一个直角三角形中,边长分别为a、b、c(c为斜边),满足勾股定理的关系:a^2 + b^2 = c^2这个定理提供了计算直角三角形边长的关键方法,也常常用于解决各种实际问题。
三角形的周长公式和面积公式

三角形的周长公式和面积公式三角形是几何学中最基本的图形之一,其具有广泛的应用。
对于一个三角形,可以通过其三边的长度来计算三角形的周长和面积。
本文将详细介绍三角形的周长公式和面积公式。
一、三角形的周长公式:L=a+b+c二、三角形的面积公式:三角形的面积是指三角形所包含的平面面积。
三角形的面积A可以通过下列公式计算:A=0.5*底边长度*高底边长度可以是三角形的任意一条边,而高是从底边所对应的顶点垂直向下的直线到底边的距离。
三、特殊类型的三角形的周长和面积计算:1.等边三角形:等边三角形是指三边相等的三角形。
由于三边长度相等,其周长和面积公式可以简化为:L=3aA = (sqrt(3) * a^2) / 4其中,a为等边三角形的边长。
2.等腰三角形:等腰三角形是指两边相等的三角形。
若等腰三角形的两边长度为a,底边长度为b,则其周长和面积公式为:L=2a+bA=(b*h)/2其中,h为等腰三角形的高。
3.直角三角形:直角三角形是指其中一个角为90度的三角形。
若直角三角形的两直角边的长度分别为a和b,斜边的长度为c,则其周长和面积公式为:L=a+b+cA=(a*b)/2以上是三角形周长和面积的计算公式的基础内容,下面我们将介绍一些应用。
四、三角形的周长和面积的应用:1.建筑设计:三角形的周长和面积计算在建筑设计中有广泛的应用。
例如,在地板铺设和墙面装修时,需要计算三角形的面积来估算所需的材料量。
同时,计算三角形的周长有助于确保建筑结构的稳定性。
2.导航和测量:在导航中,三角形的周长和面积计算常用于测量地理区域的大小和距离。
例如,通过测量三角形的侧边长度和角度,可以计算出离岸距离及位置。
3.地理地形分析:地理学家和地质学家经常使用三角形的周长和面积来分析地理地形特征。
通过测量和计算三角形的面积和周长,可以了解地球上的山脉、湖泊和河流的大小和形状。
4.工程和建筑施工:在工程和建筑施工中,测量和计算三角形的周长和面积是很常见的需求。
数学认识三角形的周长与面积

数学认识三角形的周长与面积三角形是数学中一个非常重要的图形,它由三条边和三个内角组成。
在我们的日常生活和实际应用中,我们经常会遇到三角形,并需要计算它的周长和面积。
本节课我们将学习如何认识三角形的周长与面积,并掌握相应的计算方法和公式。
一、三角形的周长周长是指围绕一个图形的边的总长度。
对于三角形来说,它的周长等于三条边的长度之和。
我们记三角形的三条边为a、b、c,则三角形的周长P可以表示为:P = a + b + c例如,对于一个三边长分别为5cm、4cm和3cm的三角形,它的周长可以计算为:P = 5cm + 4cm + 3cm = 12cm二、三角形的面积面积是指一个图形所占的平面面积大小。
对于三角形来说,它的面积可以通过不同的公式计算,根据给定的条件选择合适的公式进行计算。
1. 根据三角形的底和高求面积当我们已知三角形的底和高时,可以使用以下公式来计算其面积:S = (底 ×高) ÷ 2其中,S表示面积,底表示三角形的底的长度,高表示从底到对边的垂直距离。
2. 根据三角形的两条边和夹角求面积当我们已知三角形的两条边和它们的夹角时,可以使用以下公式来计算其面积:S = (1/2) ×边1 ×边2 ×正弦(夹角)其中,S表示面积,边1和边2表示两条边的长度,夹角表示两条边之间的夹角。
例如,对于一个底长为6cm、高为4cm的三角形,可以使用第一种方法计算面积:S = (6cm × 4cm) ÷ 2 = 12cm²再例如,对于一个边长分别为5cm和7cm,夹角为60°的三角形,可以使用第二种方法计算面积:S = (1/2) × 5cm × 7cm ×正弦(60°) ≈ 10.2cm²三、应用举例三角形的周长与面积在我们的日常生活和实际应用中具有广泛的应用。
以下是两个实际问题的例子:例1:河流景区的标志性山峰形状类似一个三角形,其中两边长度分别为8km和10km,夹角为90°。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形的周长和面积知识梳理教学重、难点作业完成情况典题探究例1 (一)完成下表:(每一方格代表21cm)三角形選擇正確的底和高利用公式計算三角形的面積數一數三角形所佔的方格數目底= cm 高= cm 三角形A的面積:=(cm2)三角形A的面積是(cm2)A12cm 9cm 13cm 18cm8cm 9cm12cm 16cm8cm8cm 4cm底= cm 高= cm三角形B 的面積: = (cm 2) 三角形B 的面積是(cm 2)底= cm高= cm三角形C 的面積: = (cm 2) 三角形C 的面積是(cm 2)(二)、利用公式計算和數方格的方法,所得的答案是否一樣? (三)、小心選擇三角形的底及其對應高,然後運用公式計算三角形的面積: 1. 三角形的底 = cm三角形的高 = cm 三角形的面積: == (cm 2)2. 三角形的底 = cm三角形的高 = cm 三角形的面積: = = (cm 2) 3. 三角形的底 = cm 三角形的高 = cm三角形的面積: == (cm 2)BC9cm7cm8cm10cm4. 三角形的底 = cm三角形的高 = cm三角形的面積:== (cm2)例2:两个完全一样的三角形能拼(),拼成平行四边形的底等于(),拼成平行四边形的高等于(),每个三角形的面积等于(),因为平行四边形的面积等于(),所以三角形的面积等于()。
用字母表示是()。
例3:如图,三个相同的长方形中,阴影部分的面积()A、甲面积大B、乙面积大C、丙面积大D、一样大E、无法比较例4:一个三角的底长3m,如果底延长1m,那么三角形的面积就增加1.2 m2。
原来三角形的面积是多少m2?例5:一个等腰直角三角形的斜边长是6分米,这个等腰直角三角形的面积是多少?演练方阵A档(巩固专练)一、填空。
1、一个三角形的面积是25平方厘米,和它等底等高的平行四边形的面积是( )平方厘米。
2、在一个长9厘米,周长26厘米的长方形内画一个最大的三角形,这个三角形的面积是( )平方厘米。
3、三角形的底扩大3倍,高扩大2倍,面积扩大()倍。
4、一个三角形与梯形的高相等,它们的面积也相等。
那梯形的上底与下底的和等于三角形( )的长度。
5、一个平行四边形的底是6厘米,高是14厘米,它的面积是()平方厘米,与它等底等高的三角形面积是()平方厘米。
6、有一个长方形长15厘米,宽8厘米,另一直角梯形上底长7厘米,下底长6厘米,高8厘米,将它们拼成一个梯形,梯形的面积是( )平方厘米。
二、判断题。
1、平行四边形面积等于长方形面积。
( )2、等底等高的三角形可拼成一个平行四边形。
( )3、长是a,宽是b的长方形,底是a,高是b的平行四边形,底是2a,高是b的三角形,这三个图形的面积必相等。
( )4、只要知道梯形的两底之和的长度和它的高,就可以求出它的面积。
( )5、两个周长相等的等边三角形,面积必相等。
( )6、两个面积相等的三角形能拼成一个平行四边形。
( )7、平行四边形内最大的三角形的面积是平行四边形的一半。
( )8、两个三角形的高相等,面积不一定相等。
()9、任意两个三角形都能拼成平行四边形。
()10、一个平行四边形可以分成两个完全相同的三角形。
()三、选择题。
将正确答案的序号填在括号里。
1、能拼成一个平行四边形的两个三角形是()。
A、任意两个三角形B、形状一样C、面积相等D、形状一样而且面积相等2、一个正方形周长扩大2倍后,新正方形面积是原来正方形面积的()倍。
A、2B、4C、8D、163、将一个长方形拉成一个平行四边形(四条边长度不变),它的面积( )。
A.比原来小B.比原来大C.与原来相等4、两个完全一样的直角三角形,不可能拼成一个()。
A.梯形B.正方形C. 三角形5、把三根同样长的铁丝分别围成长方形,正方形和平行四边形,围成图形的面积,()。
A.正方形大B.长方形大C.平行四边形大6、在面积为42平方米的平行四边形内画一个最大的三角形,这个三角形的面积是()。
A.21B. 30C.14四、计算下面三角形的面积五、一个三角形的底是18厘米,面积是126平方厘米,高是多少厘米?六、一个三角形的面积是0.24 m2,高是6dm,底是多少dm?七、一块三角形地,底长是150m,高是50m,共收油菜籽1762.5千克,平均每平方米产油菜籽多少千克?八、现在有一块长6m,宽2.5m的黄布,要做成底0.2米,高0.15米的小三角形旗,可以做多少面?B档(提升精练)一、填空题1、一个三角形的面积是20平方厘米,它的高是8厘米,底是( )厘米.2、一个三角形的底扩大2倍,高不变,这个三角形的面积扩大()倍3、在推导平行四边形面积计算公式时,可把平行四边形通过割补平移转化为( )形去推导,推导三角形面积计算公式时,可把两个完全一样的三角形拼成一个( )形去推导,推导梯形面积计算公式时,可把两个完全一样的梯形拼成一个( )形进行推导。
4、一个平行四边形的面积为S,则与它等底等高的三角形面积是( )。
5、直角三角形的两条直角边长分别为3厘米和4厘米,这个直角三角形面积是( )平方厘米。
6、1.25公顷=()平方米 5600平方分米=()平方米7、三角形的面积是18平方分米,底边长是6分米,它的底边上的高是( )分米。
8、两个完全一样的三角形一定可以拼成一个( )。
二、判断题1、如果两个三角形面积相等,那么它们一定等底等高。
()2、两个三角形可以拼成一个平行四边形。
( )3、三角形花圃,底4米,高3米,如果在里面种花每平方米种3株月季花,一共可种36株月季花。
()4、直角三角形的三条边是5米,4米和3米,面积是10平方米。
()5、三角形的面积等于平行四边形面积的一半。
()6、两个完全一样的梯形可以拼成一个平行四边形。
()7、一个长方形内画一个最大的三角形,这个三角形的面积是长方形的一半。
()8、两个长方形的周长相等,它们的面积也一定相等。
()9、三角形的高等于这个三角形的面积的2倍除以底。
()10、两个等底等高的三角形,面积一定相等且形状一定相同。
()三、计算题1.两个完全一样的三角形拼成一个平行四边形.平行四边形的底是8厘米,高是6厘米,其中一个三角形的面积是多少平方厘米?2.一块三角形钢板,底长38米,高是5米,如果每平方米的钢板重4080千克,这块钢板重多少千克?3.一块三角形地,底是48米,是高的2倍,在这块地里栽树苗,每棵树苗占地2平方米,这块地一共可以栽树苗多少棵?4、一块三角形的广告板,底26米,高7.2米,如果要油漆这块广告牌,每平方米要用油漆0.85千克。
至少需要准备多少千克油漆?(得数保留整数)5、一块三角形地,底长38米,高是27米,如果每平方米收小麦0.7千克,这块地可以收小麦多少千克?6、人民医院用一块长60米,宽0.8米的白布做成底和高都是0.4米的包扎三角巾,一共可做多少块?7、计算图中阴影部分的面积(单位:厘米)C档(跨越导练)一、填空题1、一个三角形的底和高分别扩大4倍,它的面积扩大()倍。
2、一个等腰三角形,已知一个底角是55度,顶角是()度。
3一个直角三角形,其中一个锐角是另一个锐角的2倍,较小的锐角是()度。
4、一个三角形的底是6厘米,高是3厘米,面积是()平方厘米,与它等底等高的平行四边形面积是()平方厘米。
5、一个平行四边形面积是18平方厘米,与它等底等高的三角形面积是()平方厘米;如果三角形面积是18平方厘米,与它等底等高的平行四边形面积是()平方厘米。
6、在一个面积是36平方米的长方形里剪一个最大的三角形,这个三角形的面积是()平方厘米。
二、计算题1、有一块平行四边形的地,分成三部分种菜。
其中左边黄瓜地(三角形),中间苦瓜地(平行四边形)占地18平方米,右边冬瓜地(梯形)并且三种形状的底在这整块地的同一条底边上都是3米,求黄瓜、冬瓜各占地几平方米?2、一块三角形的地,底是500米,高是360米,这块地的面积是多少?如果用拖拉机每天耕1.8公顷,这块地几天才能耕完?3、一块三角形稻田,底是90米,相当于高的1.5倍,如果每平方米施肥0.2千克,这块田施肥多少千克?4、一个平行四边形池塘的底是400米,高相当于底的1.2倍,这个水塘一共可以收水草1.6吨,那么平均每公顷水面可以收水草多少吨?5、医院做三角形外伤包扎巾,已知包扎巾的两条直角边分别为40厘米和30厘米,斜边是50厘米,如果要做这样的包扎巾900条,至少需用布多少平方米?6、如图,一个三角形的底长5米,如果底延长1米,那么面积就增加1.5平方米。
那么原来三角形的面积是多少平方米?7、一个平行四边形,若高增加6厘米,底不变,面积就增加18平方厘米;若高不变,底减少4厘米,面积就减少24平方厘米。
原来平行四边形的面积是多少平方厘米?成长足迹课后检测学习(课程)顾问签字:负责人签字:教学主管签字:主管签字时间:。
