大型抛物面天线的FEKO仿真计算概要
微波仿真论坛_Feko 在天线罩设计中的应用概要

媒体文章Feko在天线罩设计中的应用安世亚太(ANSYS-CHINA贾云峰天线罩是航空器中广泛采用的天线保护装置,其引入会影响天线的方向图等电磁特性。
由于天线罩仿真计算规模较大,因此通常软件难于解决。
Feko完美结合了矩量法和高频近似方法,在处理这类问题时游刃有余。
本文通过Feko对某型天线罩的分析展示了Feko在处理电大尺寸问题上的卓越能力。
在航空领域作为探测、测量、瞄准、通信的手段,雷达不可或缺,其性能至关重要,雷达天线就是决定雷达性能的关键部件之一。
雷达工作环境恶劣,其天线大多设有天线罩。
从理论上讲,作为雷达天线保护装置的天线罩对电磁波应该是完全透明的,但由于材料、工艺和结构的限制,这种透明是有限的,因此,必须在兼顾结构强度和稳定性要求的同时,考虑天线罩的电性能,使其尽量接近无罩状态的理想值。
采用仿真软件,构造虚拟样机并进行性能分析与优化设计,可以大大降低成本,加快研究进度。
FEKO是针对天线设计、天线布局、RCS分析等而开发的专业电磁场分析软件。
FEKO从严格的积分方程出发,以矩量法(MOM及多层快速多级子(MLFMM算法为基础,不需建立吸收边界条件,没有数值色散误差。
Feko完美结合了高频分析方法(物理光学PO,一致性绕射理论UTD,因此非常适合于分析天线设计、雷达散射截面(RCS、开域辐射、电磁兼容中的各类问题。
Feko还混合了有限元法(FEM:Finite Element Method,能更精确的处理多层复杂电介质、生物体比吸收率等问题。
对于电小结构的天线等电磁场问题,FEKO采用完全的矩量法进行分析,保证了结果的高精度。
对于具有电小与电大尺寸混合的结构,可以将问题分解后选用合适的混合方法(如用矩量法、多层快速多级子分析电小结构部分,而用高频方法分析电大结构部分,从而保证了高精度和高效率的完美结合。
采用以上的技术路线, Feko可以针对不同的具体问题选取不同的方法来进行快速精确的仿真分析,使得应用更加灵活,适用范围更广泛,突破了单一数值计算方法只能局限于某一类电磁问题的限制。
微波仿真论坛_阵列天线的FEKO仿真分析概要

第18卷第1期2009年3月计算机辅助工程Computer A ided EngineeringVol . 18No . 1Mar . 2009・安世亚太软件应用・文章编号:1006-0871(2009 0120073205阵列天线的FEK O 仿真分析刘源, 焦金龙(安世亚太科技(北京有限公司, 北京100026摘要:为在有限的硬件资源下, 对复杂单元的大规模阵列天线进行有效分析,提出采用FEK O 软件分析任意大规模阵列天线的有效方法. 首先应用FEK O 进行相控阵分析, 然后根据阵列天线的单元激励方向图(Active Ele ment Pattern, AEP 进行阵列天线FEK O 仿真分析. 实例表明, 在普通硬件资源条件下, FEK O 仿真分析可以在考虑单元互耦等实际因素的影响下, 分析任意大规模阵列的方向图和端口特性等指标.关键词:阵列天线; 单元激励方向图; 互耦; FEK O 中图分类号:U441. 5; U444. 18; T B115文献标志码:S i m ul a ti on tenna usi n g FEK OI U Yuan, J I A O J inl ong(PERA Tech . (Beijing Co . , L td . , Beijing 100026, ChinaAbstract:To i m p le ment the effective analysis of large 2scale array antenna with comp licated ele ments under the conditi on of li m ited hardware res ources, an effective method is p r oposed t o analyze arbitrary large 2scale array antenna by using FEK O. The phased array is analyzed . By intr oducing the concep t of Active Ele ment Pattern (AEP , an array antenna is si m ulated by FEK O. The app licati on indicates that the radiati on pattern and i m pedance of arbitrary large 2scale array antenna can be si m ulated and analyzed by FEK O under the nor mal conditi on of hard ware res ources, while considering the influence of the mutual coup ling bet w een the elements and s o on .Key words:array antenna; active ele ment pattern; mutual coup ling; FEK O收稿日期:2009202202修回日期:2009203204作者简介:刘源(1978— , 男, 北京人, 博士, 研究方向为电磁仿真分析、阵列综合和阵列信号处理等, (E 2mail yuan . liu@peraglobal . com0引言阵列天线[1]是由不少于2个天线单元规则或随机排列, 并通过适当激励获得预定辐射特性的1类特殊天线. 阵列可由各种类型的天线组成, 数目可以是2个甚至几十万个. 通过选择和优化阵单元的结构形态、排列方式和馈电幅相特性, 阵列天线能够实现单个天线难以提供的优异特性, 如更高的增益、方位分辨率、系统信噪比等指标, 因此在雷达和通信等领域被广泛地应用.在仿真分析阵列天线的过程中, 由于阵列天线孔径很大, 经常会达到数十、上百个波长, 计算过程中会划分大量网格, 产生大量未知量, 给仿真分析带来很大困难.1FEK O 简介FEK O 是针对天线分析、天线布局及RCS 等分析而开发的专业电磁场分析软件. 它从严格的电磁场积分方程出发, 以经典的矩量法(Method of Moment,MOM 为基础, 采用多层快速多极子(Multi2Level FastMulti poleMethod, MLF MM 算法在保持精度的前提下大大提高计算效率, 同时将矩量法与经典的高频分析方法(物理光学(Physical Op tics, P O , 一致性绕射理论(Unif or m Theory of D iffracti on, UT D 完美结合起来, 非常适合于分析开域辐射和雷达散射截面(Radar Cr oss Secti on, RCS 领域的各类电磁场问题.对于电大尺寸类问题, FEK O 具备强大的分析能力, 因此在阵列天线分析中的性能非常好.2应用FEK O 进行相控阵分析考虑如图1所示的阵列形式. 该阵列由30×4个半波振子构成, 各阵元间距均为半波长. 其中, 沿x 方向的4个单元构成子阵, 采用端射阵加权方式, 即整个阵列由30个阵元间距为半波长的端射阵构成. 端射阵的方向图可直接通过FEK O 计算得到, 见图2.图1偶极子阵列模型图2端射阵方向首先考虑均匀加权时的情况. 通过在FEK O 中对各阵元添加端口, 加入激励和负载等, 可直接计算得到阵列方向图(见图3 , 可计算得到方向性系数为19. 6dB.在实际工程中, Chebyshev [2]阵列也是常用的形式之一, 可以在FEK O 中调整各单元的加权幅度及相位实现不同主瓣指向的Chebyshev 阵列. 图4为主瓣指向180°方向, 即构成旁射阵时, 控制旁瓣为-30dB 时的阵列方向图. 图5为主瓣指向210°, 同样旁瓣为-30d B 的阵列方向图.图3均匀加权时阵列方向图4Chebyshev旁射阵方向图5主瓣扫描时的Chebyshev 方向上述结果表明, 通过FEK O 软件能够进行相控阵的分析及设计. 由于采用矩量法进行计算时无须对空气进行网格剖分和设置边界条件等, 所以对上述30×4的阵列进行仿真, 仅需要14MB 的内存, 在20s 内就能完成.47计算机辅助工程2009年3阵列天线单元激励方向图综上所述, 已经看到可以在FEK O 中快速进行相控阵的分析和设计. 上例采用的单元形式为线天线, 在应用矩量法分析时, 未知量很小, 耗费内存也很小. 若考虑单元为面天线或其他复杂天线形式, 仍可能产生大量未知量, 对计算机硬件要求非常高.在FEK O 多种激励模式中, 包含等效源(在CADFEK O 中可直接定义, 也可在ED I TFEK O 中应用AR 卡的激励模式, 可读入计算或测量得到的方向图作为激励源. 下面利用这一特点进行超大阵列及复杂阵单元构成阵列的仿真分析.对于任意类型的N 元阵列, 其方向图F (θ, < =w H・v (θ, <(1 式中:w =[w 1, w 2, …, w N ]T为阵列的加权向量; v (θ, < 为阵列导向矢量; 上标H 和T 分别表示共轭转置和转置. 若各阵元的方向图为g k (θ, < , k =1, 2, …, N , 则有v (θ, < =[g 1(θ, < exp (j 2πf 0τ1 , …,g N (θ, < (f 0N 2式中:f 0为工作频率; τk (…, .根据文献[3]引入单元激励方向图(Active Ele ment Pattern, AEP 的概念. 阵元q 接归一化信号源, 其他单元接阻抗值与信号源相同的无源负载, 这种工作模式称为阵元q 的单元激励模式, 用e q (θ, < 表征阵元q 的AEP, 则阵列的方向图[3]F (θ, < =∑Nq =1w q ・e q (θ, < ・ej2πf 0τq (3AEP 与一般意义上的单元方向图不同, 最重要的差别在于一般使用的单元方向图均为单个天线单元的方向图, 而AEP 则是在考虑其他阵元的影响、考虑互耦的前提下得到的单元方向图. 由于各无源单元的负载阻抗与阵列实际工作时的信号源阻抗相同, 因此AEP 不仅考虑单元互耦的影响, 而且考虑天线单元端口与信号源间的失配影响. 在通过计算或者测量得到AEP 后, 可以采用多种方法进行阵列综合[4, 5], 这样得到的阵列综合已充分考虑互耦影响. 因此, 如果由式(3 得到各个单元的e q (θ, < , 即可以得到真实的阵列方向图.下面利用AEP 的概念计算阵列方向图.4基于AEP 的阵列天线FEK O 仿真分析首先考虑如图6所示13×3的阵列. 为说明采用的分析方法, 这里仍旧采用线天线构成的阵列.单元均为半波振子, 阵元间距均为1/4波长.图6偶极子阵列2模型仍然将该阵列视为由13个单元(3个偶极子构成的端射阵构成, 且按图中所示排列. 并称之为阵元1, 阵元2, ……, 阵元13. 按上述AEP 的定义, 通过对阵元1加激励, 其他各阵元均加负载即可计算得到阵元1的AEP . 1的AEP , 因此在计算AEP , . , 3个, 4个和51的AEP, 并将计算到的方8中. 图中, endfire 是阵元1单独存在时的方向图; t w o more endfire 对应图7中模型1的方向图; with 3endfire 对应图7中模型2的方向图; with 4endfire 对应图7中模型3的方向图.图7阵元1AEP的计算模型图8阵元1AEP 的确定由图8可见, 模型3和模型4的结果已经较好重合, 这表明阵元4对阵元1的影响很小, 可以忽略(相应的阵元5到阵元13与阵元1的耦合也很小, 可以忽略 , 所以可以将模型2中单元1的AEP 作为整个阵列阵元1的AEP . 因此, 可以采用阵元1到阵元7构成的7元阵列(见图9 , 来等效计算得到实际阵列各个阵元的AEP . 其中, 各阵单元记为a 1, a 2, …, a 7, 则图6中阵元1的AEP 对应于a 1的AEP; 阵元2对应于a 2;阵元3对应于a 3; 阵元4到阵元10的AEP 均对应于a 4的AEP; 阵元11对应于a 5; 阵元12对应于a 6; 阵元13对应于a 7.图9偶极子阵列3模型在FEK O 中, 各阵元的AEP 在计算时可被分别自动存为扩展名为ffe 的数据文件, 并可在后续计算中以等效源的方式(CADFEK O 中radiati on point s ource 的激励模式被读入. 按上述方式读入各阵元的410位置上读入的均为图的 , 各阵元读入时选择的空间位置已经包含式(3 中的相位信息.图10等效源构成的13元阵列按图10所示计算得到的方向图即为根据式(3 得到的阵列方向图, 采用均匀加权激励的结果见图11. 在图11中, “fullarray ”是应用FEK O 对整体阵列进行仿真分析的结果; “equivalent ”是采用上述方法, 通过等效源的方式得到的结果. 可以看出两者的结果完全重合. 这种方法充分考虑单元间互耦的影响, 并能够对等效源构成的阵列进行相位和幅度加权, 实现相控阵. 采用这种基于AEP 的方法, 实际上只对少量单元(此例为7个进行网格剖分, 从而计算出整体阵列的方向图. 由这种方法能够得到任意多个(此例为13个同样单元(此例为3元端射阵按照等间距(这里为1/4波长组成阵列的方向图, 并且实际参与计算的单元数并不随着阵列规模的增大而增加. 因此, 对于复杂形式单元构成的大规模阵列, 该方法能够在得到有效计算结果的前提下, 极为显著地减小计算规模及内存需求.图11阵列方向对该方法的具体归纳如下:(1 确定计算AEP所需的最小阵元数; (2 计算由最小阵元数所构成阵列的各阵元的AEP; (3 通过等效源的方式, 计算阵列的方向图.下面考虑图12所示的16×4微带阵列. 阵单元采用FEK O . 4例10, 工作频率为3GHz . , O 中的快速多, 12G B.图12微带阵列模型对于该阵列, 将纵向的4个单元作为子阵. 按照上述分析步骤, 首先确定所需最小阵元数为9个, 并分别计算9个子阵构成阵列的各单元的AEP, 用p 1, p 2, …, p 9表示. 随后, 以等效源的方式读入, 图12中阵元1对应p 1, 阵元2对应p 2, 阵元3对应p 3, 阵元4对应p 4, 阵元5到阵元12对应p 5, 阵元13~16分别对应于p 6, p 7, p 8, p 9. 最后, 对等效源构成的阵列进行计算, 结果见图13和14. 图13和14分别是在xO z 面和xO y 面上对阵列实际建模分析计算的结果(full array 以及采用基于AEP 的等效源方式(equivalent 计算的结果. 从结果可见, 等效源的结果已与实际阵列的仿真结果较好地吻合, 完全能图13xO z 面方向图图14xO y 面方向够满足工程计算的要求, 所需内存仅为6. 5G B (直接计算需要内存12G B , 并能够得到任意多个这样的4单元子阵所构成的阵列. 同时, 在计算过程中并不需要引入子阵的概念. 例如, 仍考虑阵单元为FEK O 5. 4例10的微带天线组成的25×25的阵列, 可以取出5×5的阵列来进行计算, 分别计算各阵元的AEP (共25个 , 随后通过等效源的方式依次读入, 得到整个25×25阵列的方向图. 由于E D I TFEK O 中提供循环操作的文本输入方式, 使得多次读取文件非常易于操作.5总结首先以实例表明FEK O 在阵列天线分析方面的良好性能, 继而引入AEP 的概念, 提出在FEK O 中对大规模阵列进行分析的有效方法. 通过计算由最小阵元数构成的小阵列的AEP, 可有效得到任意大规模规则阵列的方向图, 从而在有限的硬件资源下, 对复杂单元的大规模阵列进行有效分析. 多个算例表明该算法的有效性.参考文献:[1]张祖稷, 金林, 束咸荣. 雷达天线技术[M].电子工业出版社, [2]DOLPH C L. A current distributi on for br oadside op ti m bet w een bea m width and side l obe level[J ].Pr oc I RE,1946, 34(6 :3352348.[3]KELLEY D F, ST UTZ modeling methods that include mutual coup ling effects[J ].I EEE Trans Antennas &Pr opagati on, 1993, 41(12 :[4]张志军, 冯正和. 考虑互耦的圆形天线阵列方向图综合[J ].电波科学学报, 1997, 12(4 :3612368. [5]刘源, 邓维波, 李雷, 等. 一种超方向性阵列天线综合方法[J ].电子学报, 2006, 34(3 :4592463.(编辑廖粤新(上接第59页参考文献:[1]肖晓玲, 卢正鼎, 张翔. VC 与Fortran 语言混合编程[J ].江汉石油学院学报, 2000, 22(2 :71274. [2]周振红, 颜国红, 吴虹娟. Fortran 与V isual C ++混合编程研究[J ].武汉大学学报, 2001, 34(2 :84287. [3]张志华, 王林江, 吕庆风. 混合编程与Fortran 计算程序可视化[J ].计算机应用, 1999, 19(6 :33235. [4]罗金炎, 陈庆强. 船舶面向对象有限元的应用研究[J ].计算机辅助工程, 2004, 13(1 :18222.[5]谭德强, 何险峰, 周家驹. V isual C ++和Fortran 的混合编程———CAS AC 软件W indows 版的研制[J ].计算机与应用化学, 2001, 18(4 :3242328.[6]边炳传, 龙连春, 隋允康, 等. 基于C ++和Fortran 混合编程的优化系统设计[J ].计算机工程与设计, 2006, 27(11 :204622048. [7]夏舒杰, 谭建荣, 陈洪亮. 基于文件操作的VC ++和Fortran 模块交互通信方法[J ].计算机工程, 2003, 29(9 :63265.[8]李伟. 基于Access 数据库的反舰导弹智能导引知识库设计[J ].控制与制导, 2007(3 :59262. [9]田晓青. 对ANSYS 创建面命令A 的改进[J ].计算机辅助工程, 2007, 16(4 :47250.(编辑廖粤新。
使用FEKO进行电磁场模拟和分析

使用FEKO进行电磁场模拟和分析第一章:引言FEKO是一种广泛应用于电磁场模拟与分析的软件。
本文将介绍FEKO的基本原理、应用领域以及其在电磁场模拟和分析中的重要作用。
第二章:FEKO的基本原理FEKO是一种基于有限元和边界元方法的电磁场模拟软件,可以用于分析各种电磁问题。
其基本原理是将电磁问题转化为求解最优适应Electric 或Magnetic Field Integral Equations (EFIE 或MFIE)的问题。
第三章:FEKO的应用领域FEKO的应用领域非常广泛,包括天线设计、射频与微波设计、电磁兼容性分析等。
其中,天线设计是FEKO最常见的应用之一。
使用FEKO进行天线设计可以优化天线的性能,提高接收和发射的效率,确保无线通信系统的稳定性。
第四章:电磁场模拟与分析的流程电磁场模拟与分析的流程通常包括几个步骤。
首先,需要对模拟问题进行建模。
这是一个非常关键的步骤,需要根据实际情况选择合适的模型建立方法,并确定模型的准确性和适用性。
然后,将模型导入FEKO软件中进行模拟计算。
根据模型的不同,可以选择不同的求解器和求解方法。
完成模拟计算后,还需要进行结果的后处理和分析,得到所需的电磁场参数。
第五章:FEKO的优势与不足使用FEKO进行电磁场模拟和分析具有一些明显的优势。
首先,FEKO具有非常强大的求解能力和高效率,可以处理复杂的电磁问题。
其次,FEKO具有友好的用户界面和丰富的建模和后处理功能,使得用户可以更加方便地进行模拟计算和分析。
然而,FEKO也存在一些不足之处,比如需要较高的计算资源和较长的计算时间,对用户的计算机性能有一定的要求。
第六章:FEKO的案例分析为了更好地了解FEKO的应用效果,我们对几个典型的案例进行了模拟和分析。
这些案例包括天线设计、电磁兼容性分析等。
通过对这些案例的模拟和分析,我们可以清楚地了解到FEKO在电磁场模拟和分析中的重要作用以及其实际应用的效果。
天线布局:利用FEKO仿真的解决方案

天线布局:利用FEKO仿真的解决方案Altair/FEKOFEKO助力大量工业领域的OEM厂商及其供应商解决其在产品设计、分析和测试验证过程中遇到的EMC问题。
通过使用FEKO等仿真工具,减少了试制样品的数量和测试的次数,将传统的以测试驱动的开发流程转变为以仿真驱动设计。
FEKO在EMC/EMI领域的重要应用包括了电磁辐射、电磁抗干扰、雷电效应、高强度辐射场(HIRF)、电磁脉冲(EMP)、电磁屏蔽、电磁辐射危害以及天线耦合等。
天线布局在自由空间中进行天线仿真时,有多种技术可选。
在实际应用中,这样的天线被安装在实体结构上,严重影响天线的自由空间辐射特性。
对于安装在大型平台上的天线,测量其辐射特性非常困难,有时甚至无法测量。
因此,进行精确仿真的挑战是,天线与大型电子环境的交互。
多年来,FEKO 在天线布局方面已经赢得良好声誉,成为车辆、飞机、卫星、轮船、蜂窝基站、塔、建筑及其他地点的天线布局的标准EM 仿真工具。
MLFMM 和FEKO 中的渐进求解器(PO、RL-GO 和UTD)以及模型分解共同作用,使FEKO 成为解决大型或超大型电子平台上天线布局和共址干扰问题的理想工具。
战斗机和轮船上的天线布局(表面电流如图显示)FEKO仿真基于平台上多天线间的隔离度问题(图1)是FEKO最擅长处理的问题之一。
该飞机模型是EMC计算电磁学(CEMEMC)专题研讨会上展示的一个测试模型,属于EV55(属于HIRF-SE FP7 EU项目,EVEKTOR,spol.s r.o.和HIRF SE联盟拥有其版权)的变形版本。
用户只需要根据求解问题的类型、电尺寸大小和复杂度等来选择FEKO中的一种求解器进行计算。
FEKO中快速计算天线间互耦的一种方法是通过S参数,用户可以在不重复启动求解器的情况下通过一次计算可视化显示天线负载的变化对天线间耦合的影响,直观显示大量天线端口的耦合并绘制共址干扰矩阵来识别和分析耦合强度的等级。
FEKO算法描述

FEKO算法描述FEKO是一种电磁场模拟软件,被广泛应用于电磁场仿真和分析中。
它是一种全面的电磁场模拟软件,可以用于求解各种电磁场问题,包括天线设计、电磁兼容性、微波器件设计等。
FEKO具有广泛的功能和灵活的特点,能够满足不同领域的电磁场仿真需求。
FEKO的算法描述如下:1. 电磁场方程求解:FEKO利用Maxwell方程组求解电磁场问题。
Maxwell方程组是描述电磁场的基本方程,包括高斯定理、法拉第电磁感应定律、安培环路定律和麦克斯韦方程等。
FEKO根据Maxwell方程组的不同形式,采用合适的数值方法进行求解,包括有限元法(FEM)、时域积分方程法(TDIE)、时域有限差分法(TDFD)等。
2.有限元法(FEM):FEKO使用有限元法求解复杂的电磁场问题。
有限元法是一种将有限个单元组合成整个结构的数值方法,通过数值计算得到结构的电磁场分布。
FEKO利用有限元法对电磁场问题进行离散化处理,将复杂问题简化为有限数量的单元,然后通过迭代计算得到整个结构的电磁场分布。
3.时域积分方程法(TDIE):FEKO使用时域积分方程法求解电磁场的时域行为。
时域积分方程法是一种基于电磁场的表面积分方程建模方法,它可以精确地描述电磁场在时域内的响应。
FEKO将电磁场问题转化为表面积分方程,并通过迭代求解得到电磁场的时域行为。
4.时域有限差分法(TDFD):FEKO使用时域有限差分法求解电磁场问题。
时域有限差分法是一种基于网格的数值方法,通过将时域分隔成离散时间步长,将空间分隔成网格单元,计算电磁场在每个时间步长和网格单元内的变化。
FEKO通过时域有限差分法对电磁场问题进行离散化处理,然后通过迭代计算得到电磁场的时域行为。
5.自适应网格技术:FEKO采用自适应网格技术提高电磁场仿真的准确性和效率。
自适应网格技术能够根据电磁场问题的特点和复杂度自动调整网格的精细度,使得仿真结果更加精确。
FEKO通过自适应网格技术对电磁场问题进行网格划分,根据不同区域的电磁场分布特征自动调整网格的密度,提高模拟效率和准确性。
FEKO课件1抛物面建模
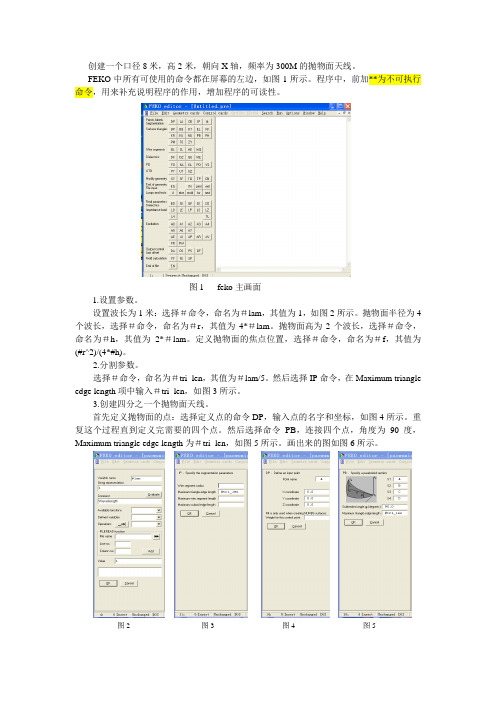
创建一个口径8米,高2米,朝向X轴,频率为300M的抛物面天线。
FEKO中所有可使用的命令都在屏幕的左边,如图1所示。
程序中,前加**为不可执行命令,用来补充说明程序的作用,增加程序的可读性。
图1 feko主画面1.设置参数。
设置波长为1米:选择#命令,命名为#lam,其值为1,如图2所示。
抛物面半径为4个波长,选择#命令,命名为#r,其值为4*#lam。
抛物面高为2个波长,选择#命令,命名为#h,其值为2*#lam。
定义抛物面的焦点位置,选择#命令,命名为#f,其值为(#r^2)/(4*#h)。
2.分割参数。
选择#命令,命名为#tri_len,其值为#lam/5。
然后选择IP命令,在Maximum triangle edge length项中输入#tri_len,如图3所示。
3.创建四分之一个抛物面天线。
首先定义抛物面的点:选择定义点的命令DP,输入点的名字和坐标,如图4所示。
重复这个过程直到定义完需要的四个点。
然后选择命令PB,连接四个点,角度为90度,Maximum triangle edge length为#tri_len,如图5所示。
画出来的图如图6所示。
图2 图3 图4 图5图6 四分之一抛物面结构图4.使用几何结构对称。
选择SY命令,依次选择None,Magnetic和Electrical。
如图7。
5.利用PO近似。
选择命令PO,在Use PO on all surfaces with label项中填0,第一个单选框中选Assume all surfaces to be illuminated项,勾选Use symmetry in ray tracing,第二个单选框中选Program determines maximum triangles/box。
如图8所示。
6.完成几何学结构。
选择EG命令,第一个单选框选择Warnings,errors,progress messages,勾选Switch normal geometry checking off,下拉列表中选Normal FEKO version,在第二个单选框中选择Do notuse a*.edg file(default)。
电磁场分析软件FEKO

电磁兼容分析软件FEKO (FEKO Suite 5.3)来文娟(04085065)电磁场分析软件FEKO(5.3)1. 软件背景介绍FEKO是复杂形状三维结构的电磁场分析软件,是复杂专业电磁场仿真领域中最强大的软件,应用范围非常广泛,由南非的EMSS公司开发。
FEKO基于著名的矩量法(MoM)对Maxwell方程组求解,可以解决任意复杂结构的电磁问题,是世界上第一个把多层快速多极子(MLFMM:Multi-Level Fast Multipole Method)算法推向市场的商业代码,在保持精度的前提下大大提高了计算效率,使得精确仿真电大问题成为可能(典型的如简单介质模型的RCS、天线罩、介质透镜)。
在此之前,求解此类问题只能选择高频近似方法。
FEKO中有两种高频近似技术可用,一个是物理光学(PO),另一个是一致性绕射理论(UTD)。
在MoM和MLFMM 需求的资源不够时,这两种方法提供求解的可能性。
FEKO中通过混合MoM/PO和MoM/UTD 来为电大尺寸问题的精度提供保证,非常适合于分析开域辐射、雷达散射截面(RCS)领域的各类电磁场问题。
FEKO还针对许多特定问题,例如平面多层介质结构、金属表面的涂覆等等,开发了量身定制的代码,在保证精度的同时获得最佳的效率。
2. 主要功能1.电大问题的求解:FEKO通过MLFMM、MoM/PO、MoM/UTD从算法上提供了电大问题求解的途径;2.丰富的求解器选择:FEKO提供多种核心算法,矩量法(MoM)、多层快速多极子方法(MLFMM)、物理光学法(PO)、一致性绕射理论(UTD)、有限元(FEM)、平面多层介质的格林函数,以及它们的混合算法来高效处理各类不同的问题;3.优化功能:FEKO提供了离散点计算方法、单纯形方法、共轭梯度法、准牛顿法等多种优化方法;4.快速宽频响应计算:FEKO通过自适应频率点采样和插值,提供宽频率响应的快速计算能力;5.时域求解:FEKO基于频域分析,同时通过FFT提供时域响应分析能力;6.强大的前后处理功能:CADFEKO提供直接面向求解器的3D图形建模和网格划分功能,支持多种CAD格式的网格文件导入:包括FEMAP Neutral (*.neu),AUTOCAD (*.dxf),特定的ASCII,NASTRAN (*.nas),STL(*.stl),ANSYS (*.cdb),ParaSolid等等;POSTFEKO提供图形化后处理能力。
FEKO_天线仿真应用_微带天线

•
•
删除释放出来的”substrate”模型;
Demo2: 定义介质层
• 进入”Construct” Tab, 点击”Planes/arrays”下拉按钮, 选择”Plane/ground”, 弹出”Plane/ground”对话框:
– Ground medium: planar multiplayer substrate – Layer1:
• Medium: substrate
– 点击”OK”
Demo1:建模-substrate底部面设定为PEC
• 在树型浏览器的” Construct”中, 选中 “substrate”,在”Details”中, 展开”Faces”, 选中右图所示的Faces:”Face6”, 点击鼠标右 键,弹出”Face properties”对话框:
• 计算完成之后, 进入”Solve/Run”, 点 击”PostFEKO”, 弹出”PostFEKO”.
DEMO1: 格林函数MOM+线端口
线端口:Wire Port
Demo2: 创建工程
• 把上述建立的工程” Microstrip_Patch_Antenna_Pin_Feed_Finite_Ground.cfx”另存为” Microstrip_Patch_Antenna_Pin_Feed_Infinite_Ground.cfx”; 进入左侧树型浏览器中的”Construct”, “展开Model->Geometry>antenna”, 选中”substrate”, 按住鼠标左键不放, 拖动鼠标位置 到”Geometry”节点, 释放鼠标左键, 在弹出的浮动窗口中选择”Move out”;
– – – – 选择: Continous (interpolated) range Start frequency: fmin End frequency: fmax 点击 OK
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
馈源方向图可以作为激励引入。
大型抛物面天线的FEKO仿真计算
发表时间:2009-8-8 作者: 陈鑫*余川来源: 安世亚太
关键字: FEKO 仿真抛物面天线方向图
本文利用FEKO 软件仿真计算得到了抛物面天线的方向图。
在仿真过程中将喇叭馈源生成的方向图做为激励加入, FEKO 软件的这一特点不但提高了计算速度、节约了所需要的系统资源,也为进一步对抛物面天线阵的仿真打下了基础。
1 前言
在电子对抗、跟踪遥测等工程应用领域内,由于抛物面天线具有发射功率大、副瓣较低、结构简单易加工、相关技术较成熟等优点,常常被选做发射天线或者阵列单元。
在频率较高频段,特别是C 波段以上的频段,其波长已经在10 厘米以内,对于直径在一米以上的大型抛物面天线或者天线阵列来说,市面上其他电磁场仿真软件在对于电大天线的仿真计算能力很弱,有些根本无法计算,而FEKO 软件恰恰弥补了这一空白。
本文利用FEKO 软件仿真计算得到了直径为110 厘米的抛物面天线方向图(X 波段),在仿真过程中将喇叭馈源生成的方向图数据文件做为激励加入,抛物面表面采用PO 算法,大大提高了计算效率,节省了所需硬件资源,为进一步对抛物面天线阵的仿真打下了基础。
2 馈源仿真计算
对于传统前馈抛物面的仿真,一般都是将喇叭馈源和抛物面整体建模、整体计算的方法。
在计算机硬件资源和时间允许的情况下,其优点是操作简单,直接得出计算结果;但是如果需要计算天线阵列或者更大的抛物面天线,也许对于计算机资源要求就太高,往往无法满足需要。
因此,我们首先用SABOR 软件快速设计喇叭几何尺寸,计算喇叭的大致远场方向图和增益(图1)。
在FEKO 中用MLFMM 计算该尺寸的喇叭方向图,如图2 所示,计算结果与设计一致,满足下一步计算要求。
图1 喇叭设计尺寸和预计增益
图2 FEKO 计算喇叭馈源方向图
3 抛物面仿真计算
得到馈源数据文件后,以激励的方式将文件导入抛物面模型中,馈源位于抛物面焦点处,如图3所示。
抛物面计算过程中在Meshes 处选用PO 算法,这样在X 频段范围内可以提高计算效率,减少硬件资源占用量,例如在该模型中,FEKO 进行运算只需要内存20M 左右。
经过计算得到抛物面天线远场方向图,增益>35dB, 副瓣电平低于主瓣约25dB,达到了设计要求。
抛物面天线远场方向图见图4所示。
图3 抛物面仿真示意图
图4 抛物面仿真方向图
4 结论
本文利用FEKO 软件对X 波段抛物面天线进行仿真计算。
在计算过程中,使用喇叭馈源方向图做为激励源来照射抛物面,大大减小了计算过程中计算机资源占用量,提升了计算效率。
使得在个人PC 机上计算抛物面天线阵列(例如:由抛物面单元组成的5 米×5 米左右的天线阵列)成为可能。
