第3章 静力学平衡问题 (3)
工程力学(静力学和材料力学)范钦珊主编答案全集 (3)

习题 3-6 图
FD
D
A
45D
D BM
FRA
FRC
M
C
FRC
FRA
A
FD'
B
D
习题 3-6a 解图
习题 3-6b 解 1 图
习题 3-6b 解 2 图
解:对于图(a)中的结构,CD 为二力杆,ADB 受力如习题 3-6a 解图所示,根据力偶 系平衡的要求,由
ΣMi = 0,
FRA = FRC =
M 2
解得,
FT=50.99kN,
FN= 10kN
即 连 杆 AB作 用 于 曲 柄 上 的 推 力 大 小 为 5 0.99 k N,方 向 与 FT相 反 ,十 字 头 A 对 导 轨 的压力
大小为10kN,方向与FN方向相反。
3-13 异步电机轴的受力如图所示,其中G=4kN为转子铁心绕组与轴的总重量,Pδ =31.8kN为磁拉力,FP=12kN为胶带拉力。试求轴承A、B处的约束力。
10
由几何关系得 cosα = 4500 = 0.9 , 5000
列平衡方程
sin α = 0.436
∑ MO (F ) = 0 : 2FA × 4500 −F Wcosα × 5000 +F Wsinα ×1250 = 0
解得 FA = 27.25 kN
∑ Fx = 0 : FOx = FW sin α = 27.03kN ∑ Fy = 0 : FOy = FW cosα − 2FA = 1.3kN
FP
FP
FA
FB
习题 3-13 图
解:分析轴承受力为一组平行力系,由平衡方程:
习题 3-13 解图
∑ M B (F ) = 0 : − FP ×1380 − FA ×1020 + (G + Pδ ) × 640 = 0
静力学中的平衡问题与解法

静力学中的平衡问题与解法静力学是力学中的一个分支,研究物体在静止或匀速直线运动时的力、力之间的关系以及物体的平衡条件等内容。
在静力学中,平衡问题是一个重要的研究内容。
本文将讨论静力学中的平衡问题以及常见的解法。
静力学中,平衡是指物体所受的合外力合力矩为零的状态。
平衡可以分为两种类型:平衡在点和平衡在体。
1. 平衡在点平衡在点指的是物体受力的合力通过一个点,也就是力矩为零。
这要求物体所受的合外力矢量的代数和为零,并且力矩的代数和也为零。
平衡在点的解法一般包括以下步骤:步骤一:画出物体受力的示意图,并标注出力的大小、方向。
步骤二:通过几何图形或代数方法求出合外力的代数和,判断合外力的大小和方向。
步骤三:通过几何图形或代数方法求出力矩的代数和,判断力矩的大小和方向。
步骤四:根据力矩为零的条件,确定物体的平衡条件。
如果力矩不为零,则说明物体不处于平衡状态。
平衡在点的解法中,可以利用力矩的性质,如力矩的叠加原理、力矩的向量性质等,来简化计算。
此外,还可以运用平衡条件求解未知的力或力矩。
2. 平衡在体平衡在体指的是物体受力的合外力和合力矩都为零的状态。
这要求物体所受的合外力矢量的代数和为零,并且力矩的代数和也为零。
平衡在体的解法一般包括以下步骤:步骤一:画出物体受力的示意图,并标注出力的大小、方向。
步骤二:通过几何图形或代数方法求出合外力的代数和,判断合外力的大小和方向。
步骤三:通过几何图形或代数方法求出力矩的代数和,判断力矩的大小和方向。
步骤四:根据合外力和力矩都为零的条件,确定物体的平衡条件。
如果合外力或力矩不为零,则说明物体不处于平衡状态。
平衡在体的解法中,通常需要考虑物体所受力的叠加效应。
常见的方法有力的分解、力矩的叠加等。
除了上述两种平衡问题的解法,静力学中还有一些特殊情况的解法,如斜面上物体的平衡、悬挂物体的平衡等。
对于这些特殊情况,可以利用相关的几何关系和平衡条件,采取相应的解法进行求解。
总之,静力学中的平衡问题是一个重要的内容,通过合理的求解方法可以确定物体的平衡条件。
清华大学版理论力学课后习题答案大全_____第3章静力学平衡问题习题解
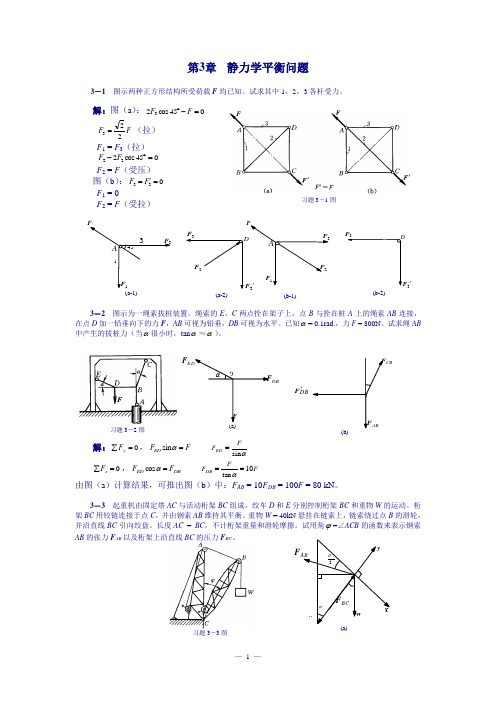
F DBCBDBF '习题3-3图第3章 静力学平衡问题3-1 图示两种正方形结构所受荷载F 均已知。
试求其中1,2,3各杆受力。
解:图(a ):045cos 23=-︒F FF F 223=(拉) F 1 = F 3(拉) 045cos 232=︒-F F F 2 = F (受压) 图(b ):033='=F F F 1 = 0F 2 = F (受拉)3-2 图示为一绳索拔桩装置。
绳索的E 、C 两点拴在架子上,点B 与拴在桩A 上的绳索AB 连接,在点D 加一铅垂向下的力F ,AB 可视为铅垂,DB 可视为水平。
已知α= 0.1rad.,力F = 800N 。
试求绳AB 中产生的拔桩力(当α很小时,tan α≈α)。
解:0=∑y F ,F F ED =αsin αs i nFF ED = 0=∑x F ,DB ED F F =αcos F FF DB 10tan ==α由图(a )计算结果,可推出图(b )中:F AB = 10F DB = 100F = 80 kN 。
3-3 起重机由固定塔AC 与活动桁架BC 组成,绞车D 和E 分别控制桁架BC 和重物W 的运动。
桁架BC 用铰链连接于点C ,并由钢索AB 维持其平衡。
重物W = 40kN 悬挂在链索上,链索绕过点B 的滑轮,并沿直线BC 引向绞盘。
长度AC = BC ,不计桁架重量和滑轮摩擦。
试用角ϕ=∠ACB 的函数来表示钢索AB 的张力F AB 以及桁架上沿直线BC 的压力F BC 。
(b-1)习题3-1图(a-1)(a-2)'3(b-2)习题3-2图F习题3-5图习题3-4图 解:图(a ):0=∑x F ,0sin 2cos=-ϕϕW F AB ,2sin2ϕW F AB =0=∑y F ,02sincos =---ϕϕAB BC F W W F即 2s i n 2c o s 2ϕϕW W W F BC ++=W W W W 2)c o s 1(c o s =-++=ϕϕ3-4 杆AB 及其两端滚子的整体重心在G 点,滚子搁置在倾斜的光滑刚性平面上,如图所示。
工程力学3-力系的平衡条件和平衡方程

例1 例1 求图示刚架的约束反力。
解:以刚架为研究对象,受力如图。
F x0:F A xq b0
P a A
q
b
F y0:F A yP0
P
MA(F)0:
MA
MAPa12q b2 0
FAx
A
FAy
q
解之得:
FAx qb
FAy P
MAPa 1 2qb 2
例2 例2 求图示梁的支座反力。
解:以梁为研究对象,受力如图。
坐标,则∑Fx=0自然满足。于是平面 平行力系的平衡方程为:
O
F2
x
F y 0 ; M O ( F ) 0
平面平行力系的平衡方程也可表示为二矩式:
M A ( F ) 0 ; M B ( F ) 0
其中AB连线不能与各力的作用线平行。
[例5] 已知:塔式起重机 P=700kN, W=200kN (最大起重量), 尺寸如图。求:①保证满载和空载时不致翻倒,平衡块
解: 1.分析受力
建立Oxy坐标系。 A处约束力分量为FAx和FAy ;钢 索的拉力为FTB。
解: 2.建立平衡方程
Fx=0
MAF= 0
- F Q 2 l- F W xF T Blsi= n0
FTB= FPlxs+ iF nQ2 l= 2FlWxFQ
FAx F TBco = s0
Fy=0
F A = x 2 F W x l F Q l co= s3 3 F lW 0xF 2 Q
[例1] 已知压路机碾子重P=20kN, r=60cm, 欲拉过h=8cm的障碍物。 求:在中心作用的水平力F的大小和碾子对障碍物的压力。
解: ①选碾子为研究对象 ②取分离体画受力图
理论力学第3章 力系的平衡

基础部分——静力学第3 章力系的平衡主要内容:§3-7 重心即:力系平衡的充分必要条件是,力系的主矢和对任一点3-2-1 平衡方程的一般形式∑=iF F R ∑=)(i O O F M M 已知∑=iF F R ∑=)(i O O F M M 投影式:平衡方程i即:力系中所有力在各坐标轴上投影的代数和分别等于零;所有力对各坐标轴之矩的代数和分别等于零。
说明:¾一般¾6个3个投影式,3个力矩式;¾一般形式基本形式3-2-2 平面一般力系的平衡方程xy zOF1F2Fn平面内,¾一般形式¾3个2个投影式,1个力矩式;¾ABAzzCC附加条件:不垂直附加条件:不共线Bx二矩式的证明必要性充分性合力平衡AA 点。
B 点。
过ABBx故必有合力为零,力系平衡证毕平面问题3个3个 解题思路BAMFo45l l[例3-1] 悬臂梁,2解:M A 校核:0)(=∑F MB满足!解题思路?AyF AxF[例3-2] 伸臂梁F AxF AyF BF q 解:0=∑x F 0)(=∑F AM3(F −+0=∑yF3(F −+(F −+0)(=∑F AM=∑yF0=∑x F F AxF AyF BF q 思考:如何用其他形式的平衡方程来求解?0=∑x F 3(F −+0)(=∑F AMF AxF F BF q 0)(=∑F BM(F −+二矩式思考练习][练习FFlll F ACB DlllACB DM=F l[思考][思考]lll F ACB DlllACB DF见书P54例3-1—约束lllACB DF—约束CBADEFM—约束—约束—整体平衡局部平衡CB ADEFM研究对象的选取原则¾仅取整体或某个局部,无法求解;¾一般先分析整体,后考虑局部;¾尽量做到一个方程解一个未知力。
qCBAm2m2m2m2MBCM[例3-3] 多跨梁,求:如何选取研究对象?F CqF CFAxF AyM ABAqF'BxF'ByM A F Ax F AyF Bx F By解:先将分布力用合力来代替。
静力学力的平衡与受力分析

静力学力的平衡与受力分析在物理学中,力是物体之间相互作用的结果,是描述物体受到的外界作用的量。
静力学力的平衡与受力分析是力学中的重要概念和方法。
本文将通过对静力学平衡和受力分析的讨论,阐述力的平衡条件以及如何进行受力分析。
静力学平衡的概念使我们能够了解物体在静止状态下所受的力的关系。
在一个封闭的系统中,如果物体保持静止,则该物体的受力和力的矩之和为零。
这可以用以下公式表示:ΣF = 0其中,ΣF表示所有作用在物体上的力的矢量和。
这个方程称为力的平衡条件,它是静力学平衡的基础。
平衡条件的主要应用在于解决各种物体和结构的受力问题。
通过对平衡条件的分析,我们可以确定物体上受力的大小、方向和作用点的位置。
在进行受力分析时,我们首先需要明确物体所处的受力系统。
受力系统包括物体所受的所有外力和内力。
外力是由外界环境对物体施加的力,如重力、摩擦力等。
内力是物体内部不同部分之间相互作用的力,如张力、弹力等。
确定了受力系统后,我们可以使用受力分析方法来计算物体所受力的大小和方向。
下面介绍几种常见的受力分析方法:1. 自由体图法:将物体从整体中分离出来形成自由体,只考虑物体受到的力,不考虑周围物体的作用。
通过绘制自由体图,我们可以清楚地看到物体所受的各个力的大小和方向,从而计算出受力平衡的条件。
2. 悬挂点法:对于悬挂在一定点上的物体,我们可以通过设定悬挂点作为坐标原点,建立力的平衡方程来求解物体所受的力。
通过受力分析,我们可以确定物体所受力的大小、方向和作用点的位置。
3. 斜面分解法:对于放置在斜面上的物体,我们可以将受力分解为平行和垂直于斜面的分力,通过受力分析得到物体所受力的大小和方向。
受力分析在工程学和物理学中有着广泛的应用。
它可以帮助我们解决各种实际问题,如桥梁的结构稳定性分析、机械装置的设计优化等。
除了上述介绍的受力分析方法,还有其他一些分析方法,如向量分解法、平衡方程法等。
不同的问题需要选择合适的受力分析方法,以便得到准确的结果。
3章力系的平衡方程及应用

A
FAx
3m
P
1m
2m
由: 解得:
3 3FAy 3P 4 P 0 1
l
P1
FT 17.33kN FAx 15.01kN FAy 5.33kN
• 结果均为正,表明实际受力方向与假设方向相同。 • 为使平衡方程尽可能包含较少的未知量,避免联立求 解,通常将矩心取在两个未知力的交点。
M A (Fi ) 0 M B (Fi ) 0 M C (Fi ) 0
限制条件:A、B、C矩心不能在同一直线上(共线)。
y
C B A O
FR
因为平衡方程
满足,但不能排除图 示不平衡的情形。
x
3.1 空间任意力系的平衡条件和平衡方程
• 以上三种形式的平衡方程均为平衡的 必要与充分条件。
F X 0
x
F Y 0
y
•两个独立平衡方程,可以求解两个未知数。
3.1 空间任意力系的平衡条件和平衡方程 2. 空间平行力系的平衡方程
z
F1 F2
O x
y
F
iz
0
M x ( Fi ) 0
M y ( Fi ) 0
可以求解三个未知数。
F3
Fn F4
平面平行力系的平衡方程
3.1 空间任意力系的平衡条件和平衡方程
六个方程相互独立。联立,可求解六个未知量。 由平衡条件导出的方程称为平衡方程的基本形式。 • • 空间任意力系平衡方程:基本形式、四矩 应当注意:每一种形式最多只能列6个独立 式、五矩式和六矩式。
平衡方程,解6个未知数,任何多于6个的方程都
是这些方程的线性组合。
y
(Fi ) 0
工程力学03章静力学平衡问题

FP
l
l
FP
l
l
M
q
M
q
2l l
2l l
A
FAx A MA
解:1.选择研究对象。
FAy
2 受力分析,画出受力图如图所示。
8
2l l
FP
l
l
M
FAx
A MA
FAy
3. 建立平衡方程求解未知力 应用平衡方程
Fx = 0, FAx ql 0
q Fy = 0, FAy FP 0
MA= 0,
B
C
M1
A 60o
M2
60o D
20
解: 取杆AB为研究对象画受力图。
杆AB只受力偶的作用而平衡且C处为光滑面约束,则A 处约束反力的方位可定。
B
B FA = FC = F,
M1
A 60o
C
C AC = a
FC
Mi = 0
M2 M1
60o D A
FA
a F - M1 = 0
M1 = a F (1)
的各坐标轴上投影的代数和及所有力对
各轴之矩的代数和均等于零
Fx 0 Fy 0 Fz 0
M M
x y
(F ) (F )
0 0
M
z
(F
)
0
26
§3-3 简单的刚体系统平衡问题
一、刚体系统静定与静不定的概念
1、静定问题:一个静力平衡问题,如果系统中未知量 的数目正好等于独立的平衡方程数,单用平衡方程就 能解出全部未知量。
y
4. 联立求解,得
FAB 54.5KN FBC 74.5KN
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
FD
D
M
E
FE
(2)取DE为研究对象
所以A处约束力沿AC方位
§3-3 简单的刚体系统平衡问题
例题
B
A
D
M
E
C (4)再次以整体为研究对象,简化受力图 ∑ MC=0 FBy ×4l -M= 0 M
4������
FBy =
M
4������
FAy =FBy =
§3-3 简单的刚体系统平衡问题
例题
【例3-13】 三铰拱由T形杆ACD和三角块BDE构成,尺寸及所受 载荷如图所示,已知F1=100N,F2=120N,M=250N•m, q=20N/m, α=30˚ ,求铰链支座A和B处的约束力。
例题
再取三角块BDE为研究对象,受 力如图所示。列平衡方程
FDx D FDy F2 E
M
D
0
M
FBx FBy B
FBy 4 M F2 2 FBx 4 0
代入数据得
FBx 36.37 N
将所得结果代入前页式得
FAx 66.37 N
作业 (P85-88): 3-18 3-19 3-26 (b) (d) 3-30 3-31
§3-3 简单的刚体系统平衡问题
刚体系统静定与静不定的概念
§3-3 简单的刚体系统平衡问题 物体系统的平衡问题
物系平衡问题的特点与解法
物体系统: 由若干个物体通过约束所组成的系统。
FBy FAy A FʹBx B C FCx B FAx FBx
外力:外界物体作用于系统上的力叫外力。
内力:系统内部各物体之间的相互作用力叫内力。
要分清外力和内力:
考虑以整体作为研究对象的平衡时,不考虑内力。 建立平衡方程必须考虑。
约束力的确定,作用力与反作用力:
以局部或单个刚体作为研究对象时,这些内力就变成外力。
受力分析时,必须严格按照约束的性质来确定约束力。
尤其要注意作用力与反作用力。
§3-3 简单的刚体系统平衡问题 物系平衡的特点:
F1 α
q
A 2m D F2
C 2m
E
M
B 2m 2m
2m
2m
(整体是静不定,但可求出部分未知量)
§3-3 简单的刚体系统平衡问题
例题
解:先取整体为研究对象,
受力如图所示。
列平衡方程
C
F1 α q
D
F2
E
M
FAx A FAy FBy
F
x
0 FBx 4q FAx F1 cos 0
FNB=2.89 kN
§3-3 简单的刚体系统平衡问题
FAx
例题
F α
B
MA A
FAy
q C a a a
M
FNB
a
a
a
再研究整个组合梁,受力如图 。
F F
M
x
0
0
(F ) 0
FAx F cos FNB sin 0
FAy FNB cos q 2a F sin 0
静定问题:若所研究的问题的未知量的数目等于或少于独立平衡方程的数 目时,则所有未知量都能由平衡方程求出,这类问题称为静定问题。
§3-3 简单的刚体系统平衡问题 静定与静不定问题的概念
刚体系统静定与静不定的概念
静不定问题:若未知量的数目多于独立平衡方程的数目,则未知量不能全 部由平衡方程求出,这类问题称为静不定问题(或称超静定问题),总未
FʹBy
FCy
§3-3 简单的刚体系统平衡问题
整体平衡与局部平衡:
物系平衡问题的特点与解法
系统整体是平衡的,那么组成系统的每一个局部以及刚 体必然是平衡的。 研究对象选取: 一般先以整体作为研究对象,可求解出部分未知力,再 以局部作为研究对象,求解其余未知力。
§3-3 简单的刚体系统平衡问题
物系平衡问题的特点与解法
q
M
F α B
A
a a
C
a a a
α
a
(整体是静不定,要先研究局部)
§3-3 简单的刚体系统平衡问题
例题
q
FCx FCy
M
F α B FNB
C a a a
a
解:先研究CB杆,受力如图。 ∑ MC=0
FNB cos 4a qa
a M F sin 3a 0 2
代入数值得
y
A
M A q 2a 2a M FNB cos 6a F sin 5a 0
FAx 4.91kN
代入数值得
FAy 7.5kN
M A 26kN m
§3-3 简单的刚体系统平衡问题
【例3-12】图示结构,已知:DE∥AB ,∠ACB=90°,AC=3l,
FBx
B
Fy 0 FAy FBy F1 sin F2 0
M
A
0
FBy 6 F1 cos 4 F1 sin 2 M F2 4 4q 2 0
解得
FBy 86.13 N
FAy 120.47 N
§3-3 简单的刚体系统平衡问题
① 物系静止。
物系平衡问题的特点与解法
② 物系中每个单体也是平衡的。每个单体可列3个平衡方程,
整个系统可列3n个方程(设物系中有n个物体)
解物系问题的一般方法:
先整体后局部;
先局部后整体; 先整体后局部再整体。
§3-3 简单的刚体系统平衡问题
求解刚体系统平衡问题的一般步骤和注意点如下:
(1)根据题意选取研究对象。这是很关键的一步,选得 恰当,解题就能简捷顺利。一般可先取系统中待求未知力少 的物体研究,逐向未知力多的物体过渡。 (2)进行受力分析。画受力图时,只画研究对象本身所 受的外力。必须弄清每一个力的性质和来历。 (3)按照待求力的个数列出足够的平衡方程,根据受力
例题
BC=4l;在杆DE上作用一顺转的矩为M的力偶,D端铰于杆AC上,E 端搁在光滑的BC杆上,杆重不计。试求铰链A、B处的约束力。
A
D M E
B
C
§3-3 简单的刚体系统平衡问题
例题
B
A
D
M
E
FʹD
A C 解:(1)取整体为研究对象 D
C
(3)取AC为研究对象 ∑ MC=0 FAx ×3l = 0 FAx = 0
知量数与总独立平衡方程数两者之差称为静不定次数。
§3-3 简单的刚体系统平衡问题
刚体系统静定与静不定的概念
FAx FAy
FP
B
FAx
A
FAy
FP FBy
B FBx
FNB
静定(未知数三个) 静定结构
静不定(未知数四个) 静不定结构/ 超静定结构
说明:静不定问题在强度力学(材力,结力,弹力)中用位移条 件来求解。
§3-3 简单的刚体系统平衡问题
刚体系统静定与静不定的概念
【例3-10】请观察下面的 受力图,比较两者有何不同之处? FP FNB
A
FAx FAy
B
FAx
FAy
A
FP
FBy
B
FBx
FTA
FTB
FTA
FTC C FG
FTB
A
C
FG
B
A
B
§3-3 简单的刚体系统平衡问题 静定与静不定问题的概念
刚体系统静定与静不定的概念
图的具体特点,选取平衡方程的适当形式,使其简单易解。
另外,还要灵活选取矩心和投影轴。常选多个未知力的交 点作矩心;与多个未知力垂直的直线作投影轴。
§3-3 简单的刚体系统平衡问题
例题
【例3-11】 组合梁ACB如图所示,已知q=2kN/m,F=4kN,
M=4kN· m,a=2m,α=30˚ 。试求A、B处的约束力。
