第3 章 静力学平衡问题-课件·PPT
合集下载
第三章 静力学平衡问题

Fy 0 M O ( F ) 0 Fx 0
平面一般力系有三个独立的平衡方程,可求解三个未知数。
M A ( F ) 0 限制条件 M ( F ) 0 2.二力矩形式 B Fx 0
M A (F ) 0 3.三力矩形式 M B ( F ) 0 限制条件 M C ( F ) 0
45°
_ 2
FC
2M 2 2M FA FC b) 45 l sin l
a)
例3-3
塔式起重机机架重W1=700kN,作用线通过塔架的
中心。最大起重量W2=200kN,最大悬臂长为12m,轨道AB的 间距为4m。平衡重W3到机身中心线距离为6m。试问:保证起 重机在满载和空载时都不致翻到,平衡重W3应为多少? 解:取起重机为研究对象,起重机受平行 力系作用。 (一)满载 临界情况下,FA=0
第三章
静力学平衡问题
第一节 平面力系的平衡条件和平衡方程
第二节 物体系统的平衡问题 第三节 考虑摩擦的平衡问题 第四节 空间一般力系的平衡问题
本章重点:
平面力系平衡方程及其应用。
求解物体系统的平衡问题。
第一节 平面力系的平衡条件和平衡方程
一、平面一般力系的平衡条件
FR=0,MO=0。
二、 平面一般力系平衡方程的三种形式 1.一般形式
M D (F ) 0
F 'Cy 1.5 F 'Cx 2 FT 1.5 0
F 'Cx FCx 0.375 kN
(3)再考虑ACE,写出其第三个平衡方程,
Fx 0
解得
FCx FEx FT 0 FEx FCx FT 1.375 kN
平面一般力系有三个独立的平衡方程,可求解三个未知数。
M A ( F ) 0 限制条件 M ( F ) 0 2.二力矩形式 B Fx 0
M A (F ) 0 3.三力矩形式 M B ( F ) 0 限制条件 M C ( F ) 0
45°
_ 2
FC
2M 2 2M FA FC b) 45 l sin l
a)
例3-3
塔式起重机机架重W1=700kN,作用线通过塔架的
中心。最大起重量W2=200kN,最大悬臂长为12m,轨道AB的 间距为4m。平衡重W3到机身中心线距离为6m。试问:保证起 重机在满载和空载时都不致翻到,平衡重W3应为多少? 解:取起重机为研究对象,起重机受平行 力系作用。 (一)满载 临界情况下,FA=0
第三章
静力学平衡问题
第一节 平面力系的平衡条件和平衡方程
第二节 物体系统的平衡问题 第三节 考虑摩擦的平衡问题 第四节 空间一般力系的平衡问题
本章重点:
平面力系平衡方程及其应用。
求解物体系统的平衡问题。
第一节 平面力系的平衡条件和平衡方程
一、平面一般力系的平衡条件
FR=0,MO=0。
二、 平面一般力系平衡方程的三种形式 1.一般形式
M D (F ) 0
F 'Cy 1.5 F 'Cx 2 FT 1.5 0
F 'Cx FCx 0.375 kN
(3)再考虑ACE,写出其第三个平衡方程,
Fx 0
解得
FCx FEx FT 0 FEx FCx FT 1.375 kN
第3章 静力学平衡问题 (2)
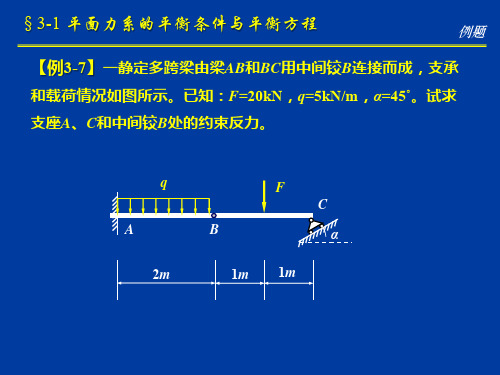
例题
(2)再研究轮
FOx FOy FʹB
M
O
(F ) 0
FB cos R M 0
F
F
解得:
x
0
0
FOx FB sin 0
FB cos FOy 0
y
M FP R
FOx FP tg
FOy FP
【负号表示力的方向与图中所设方向相反】
由图示几何关系,在Rt△BFE和 Rt△EDA中
BD=BE+DE=1.2 2+
1.8 2
≈2.97(m)
∑ MA(F) =0 M-FA×BD=0
解得 FA=M/BD=269.36(N) FC=FA=269.36N
B
解法二:以整体作为研究对象, 画出受力图。
C
M FCy
FAx
FCx
列平衡方程
∑ Fx=0 ∑ Fy=0
§3-1 平面力系的平衡条件与平衡方程
例题
M A (F ) 0 : MB (F ) 0 MC (F ) 0
解得:
2 3M FA 3a 3P 3
FC
3 aM 0 2
3 a FA aP M 0 2 2 3 a FB a P M 0 2 2
FAx=FCx=190.48kN
【3-5】为了测定飞机螺旋桨所受的空气阻力偶,可将飞机水平放
置,其一轮搁置在地秤上。当螺旋桨未转动时,测得地秤所受的压
力为4.6 kN;当螺旋桨转动时,测得地秤所受的压力为6.4 kN。已 知两轮间的距离l=2.5 m。试求螺旋桨所受的空气阻力偶的力偶矩 M 的数值。
B
α
FNC
∑ MB(F) =0
4-第三章 静力学平衡问题

a
a
再回到原系统,可建立3个平衡 方程解得:
5 2M FOX 0 , FAY 2 F qa , 2 a M FOY F qa a
FOX
O A
F
B
a
a
M
q
FCY qa
C D
FOY FAY FBY
FBX
B
x
D M
a a FCY
[例3-3]图示一结构由AB、BC 与CE 三个构件构成。E 处有一滑轮,细绳 通过该轮悬挂一重为 12 kN 的重物。A为固定铰支座,B 为滑动铰支座, C、D 与E 为圆柱铰。AD = BD = l1= 2m,CD = DE = l2= 1.5m。不计杆件 与滑轮的重量,求支座处的反力。
• 上述第一种情况称为静滑动摩擦力(静摩擦力)
• 第二种情况称为极限摩擦力 • 第三种情况称为动滑动摩擦力(动摩擦力) • 可见极限摩擦力与维持平衡的静摩擦力的关系为: 1、(静)滑动摩擦力的计算、干摩擦与粘性摩擦
Fmax
Fmax F f 0
由大量实验,库仑给出一近似公式:
Fmax f s FN
如果是平面问题(设为xy平面),则平 衡方程简化为 3 个:
X 0 , Y 0 , mO F 0
上式称为平衡方程一矩式,而二矩式和三矩式分别为:
X 0 或 Y 0 mA F 0 mB F 0 m A F 0 mB F 0 m F 0 C
如图 a 所示建立参考基 分析: 系统主动力只有重力 G 约束反力有4个显然无法直接求解
FT
y
C
q FAy A D B
人体静力学与平衡解析课件
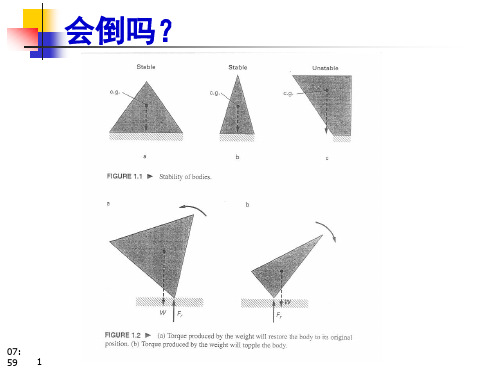
在人着地的瞬间,其速度是4.5m/s,设地面 在5ms内使人体停止,此时所受的力约是其 体重的100倍。
如果人落在体操垫上,则其减速时间会长一 些,
另外,如果他按照人体的正常反应,先将脚 尖着地然后曲膝,使减速的时间更长,则可 07: 2 减少着地力。
59 9
人体在加速和减速力作用下的行为,是和 飞机、汽车、太空飞行器有关的人员感兴趣 的领域。人体经受得起的加速度的量值,决 定于人体的方位和加速度的持续时间。
07: 2 59 3
二、摩擦力 Friction
f N
接触表面 钢与钢 橡胶轮胎在干水泥地上 橡胶轮胎在湿水泥地上 钢在冰上 润滑的骨关节
u (摩擦系数) 0.15 1.0 0.7 0.03 0.003
07: 2 59 4
2.1 Standing at an Incline
f G cos
Ft G sin
三、动力学 Dynamics
习题
1.12 1.14 1.15 1.16 1.17 1.18
07: 3 59 7
r
F
力矩 T rF
大小:T rF sin
矢量差积
是r与F所夹 的锐角
07: 59 3
重心
刚体的重心: 刚 体 的 重 量 可 以 认 为 集中 在 该 点 上 。
密 度 均 匀 且 几 何 形 状 对称 的 物 体 的 重 心 位于它们的几何中心。
形状不规则的物体的重心?
07: 59 4
会倒吗?
07: 59 1
一、静力学 Static Forces
研究作用在处于平衡和静止的物体上的
力。
质点平衡的条件:
T r F 其受到的各力之和为零
刚体平衡的条件:
如果人落在体操垫上,则其减速时间会长一 些,
另外,如果他按照人体的正常反应,先将脚 尖着地然后曲膝,使减速的时间更长,则可 07: 2 减少着地力。
59 9
人体在加速和减速力作用下的行为,是和 飞机、汽车、太空飞行器有关的人员感兴趣 的领域。人体经受得起的加速度的量值,决 定于人体的方位和加速度的持续时间。
07: 2 59 3
二、摩擦力 Friction
f N
接触表面 钢与钢 橡胶轮胎在干水泥地上 橡胶轮胎在湿水泥地上 钢在冰上 润滑的骨关节
u (摩擦系数) 0.15 1.0 0.7 0.03 0.003
07: 2 59 4
2.1 Standing at an Incline
f G cos
Ft G sin
三、动力学 Dynamics
习题
1.12 1.14 1.15 1.16 1.17 1.18
07: 3 59 7
r
F
力矩 T rF
大小:T rF sin
矢量差积
是r与F所夹 的锐角
07: 59 3
重心
刚体的重心: 刚 体 的 重 量 可 以 认 为 集中 在 该 点 上 。
密 度 均 匀 且 几 何 形 状 对称 的 物 体 的 重 心 位于它们的几何中心。
形状不规则的物体的重心?
07: 59 4
会倒吗?
07: 59 1
一、静力学 Static Forces
研究作用在处于平衡和静止的物体上的
力。
质点平衡的条件:
T r F 其受到的各力之和为零
刚体平衡的条件:
理论力学第三章(静力学平衡1)

1.空间任意力系的平衡方程
Fxi 0, Fyi 0, Fzi 0
M xi 0, M yi 0, M zi 0
空间平行力系的平衡方程
Fzi 0, Mxi 0, M yi 0
2020年9月29日星期二
平行力系
4
F1 O F2
《理论力学》
汇交力系的平衡
Fxi 0, Fyi 0, Fzi 0
13《理论力学》yFra bibliotek2qa
A
YA
XA
2a
C
B
M Pa P
4a
YB
x
Fx 0
Fy
0
M A(F)
0
2020年9月29日星期二
1,研究对象 2,选取坐标 3,受力分析 4,列解方程求解
14
《理论力学》
Fx Fy M
0 0
A (F )
0
XA 0 YA YB 2aq P 0
4aYB Pa 2aP 2a2q 0
2020年9月29日星期二
30
物系平衡的特点:物体系统的平衡
《理论力学》
1 物系静止且静定
要分清内力与外力,内力
2 物系中每部分也是平衡的。 不画在受力图上。
3 选择所需的研究对象,分析研究对象的受力,列出相应的平衡
方程; 如果要求的未知量没有全部求出,再一次选择所需的研
究对象,分析研究对象的受力,列出相应的平衡方程……
R
两个简化的结果是等效 的,则结果只能是
A
Fx 0 。Rcos 0
由 90 ,知 R 0
B
α
原力系平衡.
o
x
2020年9月29日星期二
9
《理论力学》
《工程力学第三章》PPT课件

F A y - F Q - F W + F T B sin= 0
FA= y - l- l xFW+F2Q
h
15
平面力系的平衡条件与平衡方程
平面一般力系的平衡条件与平衡方程-例题 1
FTB=FWlxs+ iF nQ2l=2FlWxFQ
解: 3.讨论 由结果可以看出,当x=l,即电动机移动到吊车大梁 右端B点处时,钢索所受拉力最大。钢索拉力最大值为
因此,力系平衡的必要与充分条件是力系的主矢和对任意一 点的主矩同时等于零。这一条件简称为平衡条件
满足平衡条件的力系称为平衡力系。 本章主要介绍构件在平面力系作用下的平衡问题。
h
8
平面力系的平衡条件与平衡方程
平面一般力系的平衡条件与平衡方程
对于平面力系,根据第2章中所得到的主矢和主矩 的表达式,力系的平衡条件可以写成
吊 车 大 梁 AB 上 既 有 未 知 的 A 处 约 束力和钢索的拉力,又作用有已知的 电动机和重物的重力以及大梁的重力。 所以选择吊车大梁AB作为研究对象。 将吊车大梁从吊车中隔离出来。
h
12
平面力系的平衡条件与平衡方程
平面一般力系的平衡条件与平衡方程-例题 1
解: 1.分析受力
建立Oxy坐标系。 A处约束力分量为FAx和FAy ;钢 索的拉力为FTB。
平面一般力系的平衡条件与平衡方程-例题 1
解: 2.建立平衡方程
Fx=0
MAF= 0
- F Q2 l- F W xF T Blsi= n0
FTB=FWlxs+ inFQ2l=2FlWxFQ
FAxFTBco= s0
Fy=0
F A= x 2F W x lF Q l co= s3 3 0 F lW xF 2 Q
FA= y - l- l xFW+F2Q
h
15
平面力系的平衡条件与平衡方程
平面一般力系的平衡条件与平衡方程-例题 1
FTB=FWlxs+ iF nQ2l=2FlWxFQ
解: 3.讨论 由结果可以看出,当x=l,即电动机移动到吊车大梁 右端B点处时,钢索所受拉力最大。钢索拉力最大值为
因此,力系平衡的必要与充分条件是力系的主矢和对任意一 点的主矩同时等于零。这一条件简称为平衡条件
满足平衡条件的力系称为平衡力系。 本章主要介绍构件在平面力系作用下的平衡问题。
h
8
平面力系的平衡条件与平衡方程
平面一般力系的平衡条件与平衡方程
对于平面力系,根据第2章中所得到的主矢和主矩 的表达式,力系的平衡条件可以写成
吊 车 大 梁 AB 上 既 有 未 知 的 A 处 约 束力和钢索的拉力,又作用有已知的 电动机和重物的重力以及大梁的重力。 所以选择吊车大梁AB作为研究对象。 将吊车大梁从吊车中隔离出来。
h
12
平面力系的平衡条件与平衡方程
平面一般力系的平衡条件与平衡方程-例题 1
解: 1.分析受力
建立Oxy坐标系。 A处约束力分量为FAx和FAy ;钢 索的拉力为FTB。
平面一般力系的平衡条件与平衡方程-例题 1
解: 2.建立平衡方程
Fx=0
MAF= 0
- F Q2 l- F W xF T Blsi= n0
FTB=FWlxs+ inFQ2l=2FlWxFQ
FAxFTBco= s0
Fy=0
F A= x 2F W x lF Q l co= s3 3 0 F lW xF 2 Q
论力学第三章课件
Fq
FAx
MA
FAy
解:取ABD为对象,受力图如图示。 其中Fq=1/2×q×3l=30kN
∑X=0: FAx+Fq–Fsin600=0
∑Y=0: FAy–P–Fcos600=0
MA–M–Fql+Fcos600l+Fsin6003l=0
解得:FAx=316.4kN; FAy=300kN MA=–1188kN.m (与图示转向相反)
静力学/第三章:平面任意力系
■ 平衡方程的其它形式
1 二矩式: X = 0
B
A
x
C
A
A、B 连线不垂直 于x 轴
A、B、C 三点不 在同一条直线上
附加条件:
附加条件:
B
2 三矩式:
静力学/第三章:平面任意力系
■二矩式的证明:
必要性
即
力系平衡
二矩式成立
由力系平衡→
F1
F2
F3
Fn
二、 平面任意力系向一点简化,主矢和主矩
1、 简化 思路:用力的平移定理将各力移至同一点,然后再合成。
将每个力向简化中心O平移
任选一个 简化中心O
其中:
O
因此:
平面任意力系
平面汇交力系
+ 平面力偶系
O
F1’
M1
F2’
M2
F3’
M3
Fn’
Mn
静力学/第三章:平面任意力系
向O点简化
F1
静力学/第三章:平面任意力系
几点讨论: 根据题意选择研究对象 分析研究对象的受力情况,正确地画出其受力图 研究对象与其他物体相互连接处的约束,按约束的性质表示约束反力 正确地运用二力杆的性质和三力平衡定理来确定约束反力的方位
FAx
MA
FAy
解:取ABD为对象,受力图如图示。 其中Fq=1/2×q×3l=30kN
∑X=0: FAx+Fq–Fsin600=0
∑Y=0: FAy–P–Fcos600=0
MA–M–Fql+Fcos600l+Fsin6003l=0
解得:FAx=316.4kN; FAy=300kN MA=–1188kN.m (与图示转向相反)
静力学/第三章:平面任意力系
■ 平衡方程的其它形式
1 二矩式: X = 0
B
A
x
C
A
A、B 连线不垂直 于x 轴
A、B、C 三点不 在同一条直线上
附加条件:
附加条件:
B
2 三矩式:
静力学/第三章:平面任意力系
■二矩式的证明:
必要性
即
力系平衡
二矩式成立
由力系平衡→
F1
F2
F3
Fn
二、 平面任意力系向一点简化,主矢和主矩
1、 简化 思路:用力的平移定理将各力移至同一点,然后再合成。
将每个力向简化中心O平移
任选一个 简化中心O
其中:
O
因此:
平面任意力系
平面汇交力系
+ 平面力偶系
O
F1’
M1
F2’
M2
F3’
M3
Fn’
Mn
静力学/第三章:平面任意力系
向O点简化
F1
静力学/第三章:平面任意力系
几点讨论: 根据题意选择研究对象 分析研究对象的受力情况,正确地画出其受力图 研究对象与其他物体相互连接处的约束,按约束的性质表示约束反力 正确地运用二力杆的性质和三力平衡定理来确定约束反力的方位
第3章 静力学平衡问题
α
FQ Cx FN
习题 3-11b 解图
取节点C为研究对象,见习题3-11b解图,
∑ Fy = 0 : F'BC cosα = FN
∴ FN
=
FP cosα 2 sin α
=
FP 2 tan α
=
3 × 15 2×2
= 11.25kN
3-12 蒸汽机的活塞面积为0.1m2,连杆AB长2m,曲柄BC长0.4m。在图示位置时, 活塞两侧的压力分别为p0=6.0×105Pa, p1=1.0×105Pa, ∠ABC=90D 。试求连杆AB作用于曲柄 上 的 推 力 和 十 字 头 A对 导 轨 的压力(各部件之间均为光滑接触)。
图(b):ΣMi = 0
∴ 由对称性知
FRB
=
M d
(←)
FRA
=
M d
(→)
FBy = FAy = 0
FBx
=
M d
M
FB
3-10 固定在工作台上的虎钳如图所示,虎钳丝杠将一铅垂力 F=800N 施加于压头上, 且沿着丝杠轴线方向。压头钳紧一段水管。试求压头对管子的压力。
习题 3-10 图
FNB
FNC FN
10
由几何关系得 cosα = 4500 = 0.9 , 5000
列平衡方程
sin α = 0.436
∑ MO (F ) = 0 : 2FA × 4500 −F Wcosα × 5000 +F Wsinα ×1250 = 0
解得 FA = 27.25 kN
∑ Fx = 0 : FOx = FW sin α = 27.03kN ∑ Fy = 0 : FOy = FW cosα − 2FA = 1.3kN
FQ Cx FN
习题 3-11b 解图
取节点C为研究对象,见习题3-11b解图,
∑ Fy = 0 : F'BC cosα = FN
∴ FN
=
FP cosα 2 sin α
=
FP 2 tan α
=
3 × 15 2×2
= 11.25kN
3-12 蒸汽机的活塞面积为0.1m2,连杆AB长2m,曲柄BC长0.4m。在图示位置时, 活塞两侧的压力分别为p0=6.0×105Pa, p1=1.0×105Pa, ∠ABC=90D 。试求连杆AB作用于曲柄 上 的 推 力 和 十 字 头 A对 导 轨 的压力(各部件之间均为光滑接触)。
图(b):ΣMi = 0
∴ 由对称性知
FRB
=
M d
(←)
FRA
=
M d
(→)
FBy = FAy = 0
FBx
=
M d
M
FB
3-10 固定在工作台上的虎钳如图所示,虎钳丝杠将一铅垂力 F=800N 施加于压头上, 且沿着丝杠轴线方向。压头钳紧一段水管。试求压头对管子的压力。
习题 3-10 图
FNB
FNC FN
10
由几何关系得 cosα = 4500 = 0.9 , 5000
列平衡方程
sin α = 0.436
∑ MO (F ) = 0 : 2FA × 4500 −F Wcosα × 5000 +F Wsinα ×1250 = 0
解得 FA = 27.25 kN
∑ Fx = 0 : FOx = FW sin α = 27.03kN ∑ Fy = 0 : FOy = FW cosα − 2FA = 1.3kN
第3章 静力学平衡问题 理论力学
FP
FP
F2
F1
F3
(a)
F2 F1
F4 F3
(b) 图3-8
如图 3-8(a)所示的三脚凳, FP 为人和凳的总重,F1、F2、F3 为地对凳的约束力,以 上 4 个力组成空间平行力系,而空间平行力系有三个独立的平衡方程,因此 3 个未知的约束
力都可以通过独立的平衡方程加以求解,所以这是一个静定问题。
3.1.4 平衡方程的几种特殊形式
式(3-2)的 6 个平衡方程都是相互独立的,可以求解 6 个未知量。这 6 个平衡方程是 针对空间一般力系给出的,对于不同的特殊情形,例如力偶系、平行力系等,并不一定都有 6 个独立的平衡方程,其中的某些方程是自然满足的,因此独立的平衡方程数是有所不同。 下面介绍几种特殊的情况。
看作集中力 F ,如图 3-5(a)。柱子轴线到墙面的距离为 l 。求梁固定端的约束力。
q
l (a)
F
y
q
F
MA
x
FAx
A
B
FAy
(b)
图3-5
解:(1)取梁为研究对象。
(2)受力分析如图 3-5(b)所示。
梁 AB 用直线代替, A 端视为固定端约束。建立图 3-5(b)所示的直角坐标系。
(3)列平衡方程有
第 3 章ΣM z (F ) 0 自然满足。于是,平衡方程为
ΣFz 0
ΣM x (F ) 0
ΣM
y
(
F
)
0
(3-5)
可以求解三个未知量。
对于平面平行力系,若各力位于 Oxy 平面内且与 y 轴平行,则式(3-2)的 6 个平衡方
程中的 ΣFx 0 , ΣFz 0 , ΣM x (F ) 0 , ΣM y (F ) 0 自然满足,注意平面上 ΣM z (F )
《静力平衡》课件
03
静力平衡模型的求解过程需要 考虑模型的稳定性和收敛性, 以确保计算结果的准确性和可 靠性。
PART 03
静力平衡的应用
工程结构静力平衡分析
桥梁设计
在桥梁设计中,静力平衡分析用 于确定桥墩和桥跨的承载能力, 以确保桥梁在各种载荷下的稳定 性。
建筑结构
在建筑设计过程中,静力平衡分 析用于评估建筑物的整体稳定性 ,确保建筑物在各种载荷下不会 发生过大变形或破坏。
静力平衡在各领域的应用前景
航空航天领域
静力平衡理论在航空航天领域的应用将更加广泛,如飞行 器的设计和优化、卫星姿态控制等。
01
建筑领域
静力平衡理论在建筑领域的应用将更加 深入,如高层建筑的结构设计、地震作 用下的建筑稳定性等。
02
03
生物医学领域
静力平衡理论在生物医学领域的应用 将更加广泛,如人体组织的力学特性 研究、医疗器械的设计和优化等。
该模型适用于弹性体、塑性体、流体等复杂介质的分析。
非线性静力平衡模型的建立需要考虑更多的物理效应,如应变硬化、应变 率效应等,求解方法包括有限元法、有限差分法等数值计算方法。
静力平衡模型的建立与求解
01
静力平衡模型的建立需要考虑 物体的几何形状、材料属性、 边界条件等因素。
02
求解静力平衡模型的方法包括 解析法和数值法,解析法适用 于简单问题,数值法适用于复 杂问题。
PART 02
静力平衡的数学模型
线性静力平衡模型
01
线性静力平衡模型是假设物体受力与变形之间的关系
是线性的,即满足胡克定律。
02
该模型适用于小变形、材料性质稳定的情况,如弹簧
、细杆等。
03
线性静力平衡模型可以通过拉格朗日方程或哈密顿原
