工程力学03章 静力学平衡问题
合集下载
工程力学(静力学与材料力学)-3-静力学平衡问题

z
O
y
∑ Fx = 0, ∑ Fy = 0, ∑ MO= 0
其中矩心O 其中矩心O为力系作用面内的任 意点. 意点. 通常将上述平衡方程中的第1 两式称为力的平衡方程; 通常将上述平衡方程中的第1,2两式称为力的平衡方程; 式称为力矩平衡方程. 第3式称为力矩平衡方程. 上述平衡方程表明,平面力系平衡的必要与充分条件是: 上述平衡方程表明,平面力系平衡的必要与充分条件是: 力系中所有的力在直角坐标系Oxy的各坐标轴上的投影的代 力系中所有的力在直角坐标系 Oxy的各坐标轴上的投影的代 数和以及所有的力对任意点之矩的代数和同时等于零. 数和以及所有的力对任意点之矩的代数和同时等于零.
平面力系的平衡条件与平衡方程
平面一般力系的平衡条件与平衡方程-例题 1 平面一般力系的平衡条件与平衡方程-
解: 1.分析受力 建立Oxy坐标系 建立Oxy坐标系. 坐标系. A处约束力分量为FAx和FAy ;钢 处约束力分量为F 索的拉力为F 索的拉力为FTB. 因为要求电动机处于任意位 置时的约束力, 所以假设力F 置时的约束力 , 所以假设力 FW 作 用在坐标为x 于是, 用在坐标为 x 处 . 于是 , 可以画出 吊车大梁AB的受力图 的受力图. 吊车大梁AB的受力图. 在吊车大梁AB 的受力图中 在吊车大梁 AB的受力图中 , 的受力图中, Fax , FAy 和 FTB 均为未知约束力与 已知的主动力F 已知的主动力FW和FQ组成平面力 因此,应用平面力系的3 系.因此,应用平面力系的3个平 衡方程可以求出全部3 衡方程可以求出全部3个未知约束 力.
平面力系的平衡条件与平衡方程
平面一般力系的平衡条件与平衡方程
例题1 例题1
悬臂式吊车结构中AB为吊车大梁 悬臂式吊车结构中AB为吊车大梁, 为吊车大梁, BC 为钢索 , A , 处为固定铰链支座 , BC为钢索 为钢索, 处为固定铰链支座, B 处为铰链约束 . 已知起重电动电动 处为铰链约束. 与重物的总重力为F 机 E 与重物的总重力为 FP( 因为两滑轮 之间的距离很小, 之间的距离很小 , FP 可视为集中力作 用在大梁上) 梁的重力为F 用在大梁上),梁的重力为FQ.已知角 30 度θ=30. 求:1. 电动机处于任意位置时, 电动机处于任意位置时, 钢索BC 所受的力和支座 处的约束力; 所受的力和支座A 钢索 BC所受的力和支座A处的约束力 ; 2. 分析电动机处于 什么位置时,钢索受力的最大, 什么位置时 , 钢索受力的最大 , 并确 定其数值. 定其数值.
工程力学(静力学和材料力学)范钦珊主编答案全集 (3)

习题 3-6 图
FD
D
A
45D
D BM
FRA
FRC
M
C
FRC
FRA
A
FD'
B
D
习题 3-6a 解图
习题 3-6b 解 1 图
习题 3-6b 解 2 图
解:对于图(a)中的结构,CD 为二力杆,ADB 受力如习题 3-6a 解图所示,根据力偶 系平衡的要求,由
ΣMi = 0,
FRA = FRC =
M 2
解得,
FT=50.99kN,
FN= 10kN
即 连 杆 AB作 用 于 曲 柄 上 的 推 力 大 小 为 5 0.99 k N,方 向 与 FT相 反 ,十 字 头 A 对 导 轨 的压力
大小为10kN,方向与FN方向相反。
3-13 异步电机轴的受力如图所示,其中G=4kN为转子铁心绕组与轴的总重量,Pδ =31.8kN为磁拉力,FP=12kN为胶带拉力。试求轴承A、B处的约束力。
10
由几何关系得 cosα = 4500 = 0.9 , 5000
列平衡方程
sin α = 0.436
∑ MO (F ) = 0 : 2FA × 4500 −F Wcosα × 5000 +F Wsinα ×1250 = 0
解得 FA = 27.25 kN
∑ Fx = 0 : FOx = FW sin α = 27.03kN ∑ Fy = 0 : FOy = FW cosα − 2FA = 1.3kN
FP
FP
FA
FB
习题 3-13 图
解:分析轴承受力为一组平行力系,由平衡方程:
习题 3-13 解图
∑ M B (F ) = 0 : − FP ×1380 − FA ×1020 + (G + Pδ ) × 640 = 0
第3章 静力学平衡问题 (2)
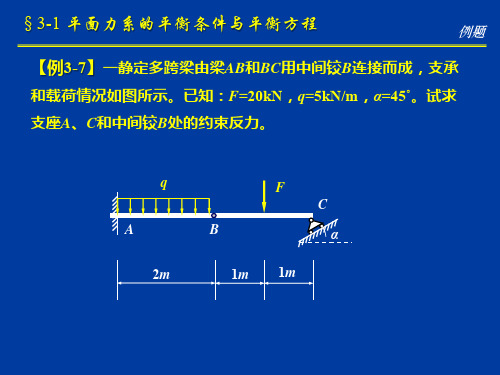
例题
(2)再研究轮
FOx FOy FʹB
M
O
(F ) 0
FB cos R M 0
F
F
解得:
x
0
0
FOx FB sin 0
FB cos FOy 0
y
M FP R
FOx FP tg
FOy FP
【负号表示力的方向与图中所设方向相反】
由图示几何关系,在Rt△BFE和 Rt△EDA中
BD=BE+DE=1.2 2+
1.8 2
≈2.97(m)
∑ MA(F) =0 M-FA×BD=0
解得 FA=M/BD=269.36(N) FC=FA=269.36N
B
解法二:以整体作为研究对象, 画出受力图。
C
M FCy
FAx
FCx
列平衡方程
∑ Fx=0 ∑ Fy=0
§3-1 平面力系的平衡条件与平衡方程
例题
M A (F ) 0 : MB (F ) 0 MC (F ) 0
解得:
2 3M FA 3a 3P 3
FC
3 aM 0 2
3 a FA aP M 0 2 2 3 a FB a P M 0 2 2
FAx=FCx=190.48kN
【3-5】为了测定飞机螺旋桨所受的空气阻力偶,可将飞机水平放
置,其一轮搁置在地秤上。当螺旋桨未转动时,测得地秤所受的压
力为4.6 kN;当螺旋桨转动时,测得地秤所受的压力为6.4 kN。已 知两轮间的距离l=2.5 m。试求螺旋桨所受的空气阻力偶的力偶矩 M 的数值。
B
α
FNC
∑ MB(F) =0
4-第三章 静力学平衡问题

a
a
再回到原系统,可建立3个平衡 方程解得:
5 2M FOX 0 , FAY 2 F qa , 2 a M FOY F qa a
FOX
O A
F
B
a
a
M
q
FCY qa
C D
FOY FAY FBY
FBX
B
x
D M
a a FCY
[例3-3]图示一结构由AB、BC 与CE 三个构件构成。E 处有一滑轮,细绳 通过该轮悬挂一重为 12 kN 的重物。A为固定铰支座,B 为滑动铰支座, C、D 与E 为圆柱铰。AD = BD = l1= 2m,CD = DE = l2= 1.5m。不计杆件 与滑轮的重量,求支座处的反力。
• 上述第一种情况称为静滑动摩擦力(静摩擦力)
• 第二种情况称为极限摩擦力 • 第三种情况称为动滑动摩擦力(动摩擦力) • 可见极限摩擦力与维持平衡的静摩擦力的关系为: 1、(静)滑动摩擦力的计算、干摩擦与粘性摩擦
Fmax
Fmax F f 0
由大量实验,库仑给出一近似公式:
Fmax f s FN
如果是平面问题(设为xy平面),则平 衡方程简化为 3 个:
X 0 , Y 0 , mO F 0
上式称为平衡方程一矩式,而二矩式和三矩式分别为:
X 0 或 Y 0 mA F 0 mB F 0 m A F 0 mB F 0 m F 0 C
如图 a 所示建立参考基 分析: 系统主动力只有重力 G 约束反力有4个显然无法直接求解
FT
y
C
q FAy A D B
第三章静力学平衡问题

第三章 静力学平衡问题
2016/10/10
1
力系的主矢和主矩
FR’
O
F FR 对O点的主矩: M o M o ( F )
力系的主矢:
Mo
力系主矢的特点: 对于给定的力系,主矢唯一; 主矢仅与各力的大小和方向有关,主矢与简 化中心O 的位置无关。
力系主矩的特点: 力系主矩MO与简化中心O 的位置有关。 对于主矩必须指明简化中心。
sds
1 5
由几何关系:
, sin
E y A x
P
45 o
解出:
FA 5P 22.3 (kN) ,
FC 2 2 P 28.28 (kN)
FA
C
B
FC
说明:FA的负号表示它的实际方向与图示的假设 方向相反。 解题要求 24
例
如图2-15(a)所示,重量为 G=5kN的球悬挂在绳上,且和 光滑的墙壁接触,绳和墙的夹 角为30°。试求绳和墙对球的 约束反力。
sds y A A FA FAy FAx x
45 o
E P P FC F C C C B B
X 0 Y 0
FA cos FC cos 45 0 FA sin FC sin 45 P 0
23
X 0 Y 0
cos
2 5
FA cos FC cos 45 0 FA sin FC sin 45 P 0
43
2、平面力偶系的平衡条件 定理:
受平面力偶系作用的刚体平衡的充分必要条件是 各力偶的力偶矩的代数和为零。 即: 受平面力偶系作用的刚体,平衡 Mi 0 平面力偶系的平衡方程 此方程可解一个未知量
2016/10/10
1
力系的主矢和主矩
FR’
O
F FR 对O点的主矩: M o M o ( F )
力系的主矢:
Mo
力系主矢的特点: 对于给定的力系,主矢唯一; 主矢仅与各力的大小和方向有关,主矢与简 化中心O 的位置无关。
力系主矩的特点: 力系主矩MO与简化中心O 的位置有关。 对于主矩必须指明简化中心。
sds
1 5
由几何关系:
, sin
E y A x
P
45 o
解出:
FA 5P 22.3 (kN) ,
FC 2 2 P 28.28 (kN)
FA
C
B
FC
说明:FA的负号表示它的实际方向与图示的假设 方向相反。 解题要求 24
例
如图2-15(a)所示,重量为 G=5kN的球悬挂在绳上,且和 光滑的墙壁接触,绳和墙的夹 角为30°。试求绳和墙对球的 约束反力。
sds y A A FA FAy FAx x
45 o
E P P FC F C C C B B
X 0 Y 0
FA cos FC cos 45 0 FA sin FC sin 45 P 0
23
X 0 Y 0
cos
2 5
FA cos FC cos 45 0 FA sin FC sin 45 P 0
43
2、平面力偶系的平衡条件 定理:
受平面力偶系作用的刚体平衡的充分必要条件是 各力偶的力偶矩的代数和为零。 即: 受平面力偶系作用的刚体,平衡 Mi 0 平面力偶系的平衡方程 此方程可解一个未知量
第3章工程构件静力学平衡问题优秀课件

杆和轮的自重不计,接触处均光滑,已知图示位置的夹角
为 和 ,活塞气体总压力为P。求压板受到滚轮
的压力有多大?
3.1 汇交力系的平衡条件和方程 -例题
解:作用在活塞上的压力通过销钉A推动杆AB,AD, 使滚轮B,D压紧压板,故可首以销钉A为研究对象,再取 取B或D为研究对象。
3.1 汇交力系的平衡条件和方程 -例题
Xi 0 , F B C F Ac B3 o 0 s T 1 c4 o 5 s 0 (1)
Yi 0 , F As B 3 i n 0 T 1 s4 i n 5 T 2 0 (2)
T1 T2 G
(3)
由式(1)(2)(3)解得:
3.1 汇交力系的平衡条件和方程 -例题
FABG (1sis3 ni4 n 05 )5.1k 2N
解得:
FNAFNB62N5
3.2 力偶系的平衡条件和平衡方程 -例题
例题 3-4 已知: 结构受力如图所示, 图中M, r均为已知,且 l = 2r. 求: 画出AB和BDC杆的受
力图;并求A, C处的约束力. 解:
1. 取AB杆为研究对象;
AB杆为二力杆,受 力如图。
2. 取BDC杆,
B 处受力的方位可
例3-3 如图所示的减速箱的输入轴 Ⅰ上受到一主动力偶的作用,力偶 矩的大小为 M112N5m,输出轴 Ⅱ上受到一阻力偶作用,力偶 矩的大小为 M250N 0m;轴Ⅰ和 轴Ⅱ互相平行,减速箱的重 量不计,并于A,B处用螺栓和 支承面固联。求A,B处所受 铅直约束力。(设螺栓无 预紧力)
3.2 力偶系的平衡条件和平衡方程 -例题
F B C F Ac B3 o 0 s G c4 o 5 s 5 .4 k9 N
由于FAB和FBC均为正值,说明受力途中假定的各力 的指向正确,即AB杆受拉,BC杆受压。
为 和 ,活塞气体总压力为P。求压板受到滚轮
的压力有多大?
3.1 汇交力系的平衡条件和方程 -例题
解:作用在活塞上的压力通过销钉A推动杆AB,AD, 使滚轮B,D压紧压板,故可首以销钉A为研究对象,再取 取B或D为研究对象。
3.1 汇交力系的平衡条件和方程 -例题
Xi 0 , F B C F Ac B3 o 0 s T 1 c4 o 5 s 0 (1)
Yi 0 , F As B 3 i n 0 T 1 s4 i n 5 T 2 0 (2)
T1 T2 G
(3)
由式(1)(2)(3)解得:
3.1 汇交力系的平衡条件和方程 -例题
FABG (1sis3 ni4 n 05 )5.1k 2N
解得:
FNAFNB62N5
3.2 力偶系的平衡条件和平衡方程 -例题
例题 3-4 已知: 结构受力如图所示, 图中M, r均为已知,且 l = 2r. 求: 画出AB和BDC杆的受
力图;并求A, C处的约束力. 解:
1. 取AB杆为研究对象;
AB杆为二力杆,受 力如图。
2. 取BDC杆,
B 处受力的方位可
例3-3 如图所示的减速箱的输入轴 Ⅰ上受到一主动力偶的作用,力偶 矩的大小为 M112N5m,输出轴 Ⅱ上受到一阻力偶作用,力偶 矩的大小为 M250N 0m;轴Ⅰ和 轴Ⅱ互相平行,减速箱的重 量不计,并于A,B处用螺栓和 支承面固联。求A,B处所受 铅直约束力。(设螺栓无 预紧力)
3.2 力偶系的平衡条件和平衡方程 -例题
F B C F Ac B3 o 0 s G c4 o 5 s 5 .4 k9 N
由于FAB和FBC均为正值,说明受力途中假定的各力 的指向正确,即AB杆受拉,BC杆受压。
工程力学第三章静力平衡问题

6
平面一般力系平衡方程还可表达为下列二种形式:
M
Fx A(F )
0
0
M B (F ) 0
M M
A B
(F (F
) )
0 0
MC (F ) 0
二力矩式
三力矩式
(AB不垂直于x轴) (A、B、C三点不共线)
注意:平衡方程中,投影轴和矩心可任意选取,可 写出无数个平衡方程。但只要满足了其中一组,其 余方程均应自动满足,故独立平衡方程只有三个。
矩心取在二未知力交点A 解处:,1力)矩画方整程体中受只力有图一。个未 知量F注C,意可B直C为接二求力解杆。。 2)取坐标,列平衡方程。
Fx=FAx-FCcos30=0
Fy=FAy+FCsin30-F-Fq=0
MA(F)=FCL/2-1.5F-FqL/2=0
FC
y
C
Fq=2q=1 kN
FAy
x
FAx 30
26
讨论:判断下述分析的正误。
FACy FAy
FACx
2a
M
3a
P
F
aA
MA
FAyFAx
FAx
B
B FABy
FABx
C
CP
A
FAx FAy
P
A
FFABAyy
A
FFAABxxFFAACyy
FACxx
FAx =F ; FAy =P ;
MA = M ?
MA = M+Fa-2Pa
固定铰的约束力作用于销钉上。 多杆用同一销钉连接,讨论某杆时, 须考虑各杆与销钉间作用的不同。
5
平面力系的平衡条件
平面一般力系处于平衡,充分和必要条件为力系
平面一般力系平衡方程还可表达为下列二种形式:
M
Fx A(F )
0
0
M B (F ) 0
M M
A B
(F (F
) )
0 0
MC (F ) 0
二力矩式
三力矩式
(AB不垂直于x轴) (A、B、C三点不共线)
注意:平衡方程中,投影轴和矩心可任意选取,可 写出无数个平衡方程。但只要满足了其中一组,其 余方程均应自动满足,故独立平衡方程只有三个。
矩心取在二未知力交点A 解处:,1力)矩画方整程体中受只力有图一。个未 知量F注C,意可B直C为接二求力解杆。。 2)取坐标,列平衡方程。
Fx=FAx-FCcos30=0
Fy=FAy+FCsin30-F-Fq=0
MA(F)=FCL/2-1.5F-FqL/2=0
FC
y
C
Fq=2q=1 kN
FAy
x
FAx 30
26
讨论:判断下述分析的正误。
FACy FAy
FACx
2a
M
3a
P
F
aA
MA
FAyFAx
FAx
B
B FABy
FABx
C
CP
A
FAx FAy
P
A
FFABAyy
A
FFAABxxFFAACyy
FACxx
FAx =F ; FAy =P ;
MA = M ?
MA = M+Fa-2Pa
固定铰的约束力作用于销钉上。 多杆用同一销钉连接,讨论某杆时, 须考虑各杆与销钉间作用的不同。
5
平面力系的平衡条件
平面一般力系处于平衡,充分和必要条件为力系
第3章 静力学平衡问题 理论力学

FP
FP
F2
F1
F3
(a)
F2 F1
F4 F3
(b) 图3-8
如图 3-8(a)所示的三脚凳, FP 为人和凳的总重,F1、F2、F3 为地对凳的约束力,以 上 4 个力组成空间平行力系,而空间平行力系有三个独立的平衡方程,因此 3 个未知的约束
力都可以通过独立的平衡方程加以求解,所以这是一个静定问题。
3.1.4 平衡方程的几种特殊形式
式(3-2)的 6 个平衡方程都是相互独立的,可以求解 6 个未知量。这 6 个平衡方程是 针对空间一般力系给出的,对于不同的特殊情形,例如力偶系、平行力系等,并不一定都有 6 个独立的平衡方程,其中的某些方程是自然满足的,因此独立的平衡方程数是有所不同。 下面介绍几种特殊的情况。
看作集中力 F ,如图 3-5(a)。柱子轴线到墙面的距离为 l 。求梁固定端的约束力。
q
l (a)
F
y
q
F
MA
x
FAx
A
B
FAy
(b)
图3-5
解:(1)取梁为研究对象。
(2)受力分析如图 3-5(b)所示。
梁 AB 用直线代替, A 端视为固定端约束。建立图 3-5(b)所示的直角坐标系。
(3)列平衡方程有
第 3 章ΣM z (F ) 0 自然满足。于是,平衡方程为
ΣFz 0
ΣM x (F ) 0
ΣM
y
(
F
)
0
(3-5)
可以求解三个未知量。
对于平面平行力系,若各力位于 Oxy 平面内且与 y 轴平行,则式(3-2)的 6 个平衡方
程中的 ΣFx 0 , ΣFz 0 , ΣM x (F ) 0 , ΣM y (F ) 0 自然满足,注意平面上 ΣM z (F )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. 刚体系统:由几个刚体通过一定的约束方式联 系在一起的系统。
q
A
M
C
B
a
a
a
a
29
返回
2.求解刚体系统平衡问题的一般方法和步骤 方法一:整体
弄清 题意, 标出 已知 量 选整体 为研究 对象画 受力图 ,列平 衡方程 局部 选局部为 研究对象 画受力图 ,列平衡 方程求解 。 检 查 结 果, 验 算
i =1 i =1
三.空间力系的平衡条件
根据空间力系的简化结果,得到空间力系平衡的 必要充分条件是:力系的主矢和对任一点的主矩 为零,即,
FR ' = 0
MO = 0
空间力系平衡方程
力系中所有力在直角坐标系Oxyz 的各坐标轴上投影的代数和及所有力对 各轴之矩的代数和均等于零
Fx 0 Fy 0 Fz 0
Fx 0
Fy 0
独立平衡方程只有三个
Mo (F ) 0
上述平衡方程表明,平面力系平衡的必要与充分条件是: 力系中所有的力在直角坐标系Oxy的各坐标轴上的投影的代 数和以及所有的力对任意点之矩的代数和同时等于零。 3
求解力系平衡问题的方法和步骤。 (1)选取研究对象; (2)分析研究对象受力,画受力图; (3)根据力系的类型列写平衡方程;选取适当的 坐标轴和矩心,以使方程中未知量个数最少;尽可 能每个方程中只有一个未知量。 (4)求解未知量,分析和讨论计算结果。
z
F
直该平面的轴之矩。 力对轴之矩等于该力在与轴垂直的 平面上的投影对轴与平面的交点之矩, 它是力使刚体绕此轴转动的效应的度量。 用记号
Fz
O
B
M z (F )
M z (F ) = M o (Fxy ) = ± xyh = ± ΔOAB F 2
h
A
Fxy
24
二.空间力系的简化
应用力向一点平移定理,将作用在刚体上 的空间力系中各力分别向任意简化中心O 平移, 得到一空间汇交力系和一空间力偶系。其中
6
例题 3-2 例1
求图示刚架的约束反力 。
A
P a
q b
解:以刚架为研究对象,受力如图。
Fx 0: FAx qb 0
Fy 0 : FAy P 0
M A (F ) 0 :
P
MA A
1 2 M A Pa qb 0 2 解得:
FAx qb
FAx
q
2L 2L
B
L
M
B
L
FB
M
A
A
FA
解: 由
Mi=0
FA l M 0
M FA FB l
18
例题 3-8 工件上作用有三个力偶如图所示。已知:
M1= M2= 10N· m, M3 =20N· m,固定螺栓A和B的距
离l=200mm。求两光滑螺栓所受的水平力。 FA A A
M1 M2 M1
qa M FC 4 2a
n
F3 (a)
F5
MO (b) x
M o M o ( Fi )
i 1
n
x
平面一般力系平衡的必要与充分条件是力系的主矢和对任意一 点的主矩同时等于零。这一条件简称为平衡条件。 n Fix 0 n
FR Fi 0
i 1
n i 1
因为
FR FRx FRy
y
A
30°
30°
B
FAB
30°
B
30° F
x
C
P FBC
FT2
T1
解:1.
取滑轮B 连同销钉作为研究对象。 画出受力图
16
2.
3. 列出平衡方程:
Fx 0 : FBC cos300 FAB FT 2 sin 300 0
Fy 0 : FBC sin 300 FT 1 FT 2 cos 300 0
C
M1
A 60o 60o
M2
D
20
解:
取杆AB为研究对象画受力图。
杆AB只受力偶的作用而平衡且C处为光滑面约束,则A
处约束反力的方位可定。
B B
FA = FC = F,
AC = a
C
C
FC
Mi = 0
M1
A 60
o
M2
60o D
M1
A
FA
a F - M1 = 0
M1 = a F
21
(1)
取杆CD为研究对象。因C点约束方位已定 , 则D点
MB (F ) 0 : FAy a m P sin b 0
C
b
M A (F ) 0 : FB a P sin (a b) m 0
解得: FAx P cos
m Pb sin FAy a m P sin (a b) FB a
P FAx
A
m
B C
FAy
FB
12
三、平面汇交力系与平面力偶系的平衡方程 1.平面汇交力系的平衡方程
y y
F4 F5
O
F2 F1
x
FRy
FR
O
F3
FRx
x
FR Fi 0
因为
FR FRx F
2
2 Ry
F F
2 x y
2
0
Fx 0
Fy 0
M A FC 4a 2qa 2a M 0
33
0
2-4 物体系统平衡问题
q
A B
M
C
a
a
a
a
q
M
C
2. BC 梁为研究
F 0 F 0 M 0
x
FBx
FBx 0
B
FBy
FC
y
FBy qa Fc 0
a qa M Fc 2a 0 2
FAx ql FAy FP
二、平面一般力系平衡方程的其它形式
y F1
A
F2
F4
y
B
F R =0
M (a)
F3
F5 x (b) x
F 0 M (F ) 0 M (F ) 0
x A B
二力矩式 (AB不垂直于x轴)
10
y F1
F2
F4
y
C B A
F R=0
B约束反力方位亦可确定,画受力图。 B
C
F′C
C
M2
M1
A 60o
60
o
M2
D A 60o 60o D
FD
FD = FC = F M2 = 0.5 a F
Mi = 0
(2)
- 0.5a F + M2 = 0
22
联立(1)(2)两式得:M1/M2=2
§3-2 简单的空间力系平衡问题
各力的作用线在空间任意分布的力系称为空间 任意力系。 一.力对轴之矩 在平面内,力对点之矩是指力对垂
第 3 章
静力学平衡问题
§3-1 平面力系的平衡条件与平衡方程 §3-2 简单的空间力系平衡问题 §3-3 简单的刚体系统平衡问题
§3-4 考虑摩擦时的平衡问题
1
§3-1 平面力系平衡条件与平衡方程 一、平面一般力系的平衡条件与平衡方程
y F1
O O
F2
F4
y F R
FR Fi
i 1
A
y q
Fy 0 FAy q 2a FNB 0
Mo (F ) 0
解得
Me FAy
C 2a 4a a D
B x FNB
FAx
q 2a a Me FNB 4a 0
FAx 0,
(b)
Me 1 FN B qa , 2 4a Me 3 FAy qa . 2 4a
M (a)
F3
F5 x (b) x
M M M
(F ) 0 B (F ) 0 (F ) 0 C
A
三力矩式 (A、B、C三点不共线)
11
例题 3-4
求图示梁的支座反力。
A
P m a B
解:以梁为研究对象,受力如图。
Fx 0 : FAx P cos 0
F1 ' = F1,F2 ' = F2, … Fn ' = Fn … ,
M1 = M O ( F1 ),M 2 = M O ( F2 ), …, M n = M O ( Fn ) …
FR ' = ∑ i ' = ∑ i F F
i =1
n
n
n
主矢
主 矩
25
i =1
n
M o = ∑ i = ∑ o ( Fi ) M M
y
4. 联立求解,得
FAB 54.5 KN
FAB B
30°
FBC
FT2
反力FAB 为负值,说明该力实际指向与图上假 定指向相反。即杆AB 实际上受拉力。
17
例题 3-7 折杆AB的支承方式如图所示,设有一力矩数
值为M的力偶作用在折杆AB上,求支承处的约束力大小。
注意:
力偶 M 在任一轴上的投影为零; 力偶对任一点之矩即为M。 选取适当的坐标轴和矩心,注意正负号。
30
方法二:局部
选局部 为研究 对象画 受力图 ,列平 衡方程
局部 检 查 结 果, 验 算
弄清 题意, 标出 已知 量
再选局部 为研究对 象画受力 图,列平 衡方程求 解。
q
A
M
C
B
a
a
a
a
29
返回
2.求解刚体系统平衡问题的一般方法和步骤 方法一:整体
弄清 题意, 标出 已知 量 选整体 为研究 对象画 受力图 ,列平 衡方程 局部 选局部为 研究对象 画受力图 ,列平衡 方程求解 。 检 查 结 果, 验 算
i =1 i =1
三.空间力系的平衡条件
根据空间力系的简化结果,得到空间力系平衡的 必要充分条件是:力系的主矢和对任一点的主矩 为零,即,
FR ' = 0
MO = 0
空间力系平衡方程
力系中所有力在直角坐标系Oxyz 的各坐标轴上投影的代数和及所有力对 各轴之矩的代数和均等于零
Fx 0 Fy 0 Fz 0
Fx 0
Fy 0
独立平衡方程只有三个
Mo (F ) 0
上述平衡方程表明,平面力系平衡的必要与充分条件是: 力系中所有的力在直角坐标系Oxy的各坐标轴上的投影的代 数和以及所有的力对任意点之矩的代数和同时等于零。 3
求解力系平衡问题的方法和步骤。 (1)选取研究对象; (2)分析研究对象受力,画受力图; (3)根据力系的类型列写平衡方程;选取适当的 坐标轴和矩心,以使方程中未知量个数最少;尽可 能每个方程中只有一个未知量。 (4)求解未知量,分析和讨论计算结果。
z
F
直该平面的轴之矩。 力对轴之矩等于该力在与轴垂直的 平面上的投影对轴与平面的交点之矩, 它是力使刚体绕此轴转动的效应的度量。 用记号
Fz
O
B
M z (F )
M z (F ) = M o (Fxy ) = ± xyh = ± ΔOAB F 2
h
A
Fxy
24
二.空间力系的简化
应用力向一点平移定理,将作用在刚体上 的空间力系中各力分别向任意简化中心O 平移, 得到一空间汇交力系和一空间力偶系。其中
6
例题 3-2 例1
求图示刚架的约束反力 。
A
P a
q b
解:以刚架为研究对象,受力如图。
Fx 0: FAx qb 0
Fy 0 : FAy P 0
M A (F ) 0 :
P
MA A
1 2 M A Pa qb 0 2 解得:
FAx qb
FAx
q
2L 2L
B
L
M
B
L
FB
M
A
A
FA
解: 由
Mi=0
FA l M 0
M FA FB l
18
例题 3-8 工件上作用有三个力偶如图所示。已知:
M1= M2= 10N· m, M3 =20N· m,固定螺栓A和B的距
离l=200mm。求两光滑螺栓所受的水平力。 FA A A
M1 M2 M1
qa M FC 4 2a
n
F3 (a)
F5
MO (b) x
M o M o ( Fi )
i 1
n
x
平面一般力系平衡的必要与充分条件是力系的主矢和对任意一 点的主矩同时等于零。这一条件简称为平衡条件。 n Fix 0 n
FR Fi 0
i 1
n i 1
因为
FR FRx FRy
y
A
30°
30°
B
FAB
30°
B
30° F
x
C
P FBC
FT2
T1
解:1.
取滑轮B 连同销钉作为研究对象。 画出受力图
16
2.
3. 列出平衡方程:
Fx 0 : FBC cos300 FAB FT 2 sin 300 0
Fy 0 : FBC sin 300 FT 1 FT 2 cos 300 0
C
M1
A 60o 60o
M2
D
20
解:
取杆AB为研究对象画受力图。
杆AB只受力偶的作用而平衡且C处为光滑面约束,则A
处约束反力的方位可定。
B B
FA = FC = F,
AC = a
C
C
FC
Mi = 0
M1
A 60
o
M2
60o D
M1
A
FA
a F - M1 = 0
M1 = a F
21
(1)
取杆CD为研究对象。因C点约束方位已定 , 则D点
MB (F ) 0 : FAy a m P sin b 0
C
b
M A (F ) 0 : FB a P sin (a b) m 0
解得: FAx P cos
m Pb sin FAy a m P sin (a b) FB a
P FAx
A
m
B C
FAy
FB
12
三、平面汇交力系与平面力偶系的平衡方程 1.平面汇交力系的平衡方程
y y
F4 F5
O
F2 F1
x
FRy
FR
O
F3
FRx
x
FR Fi 0
因为
FR FRx F
2
2 Ry
F F
2 x y
2
0
Fx 0
Fy 0
M A FC 4a 2qa 2a M 0
33
0
2-4 物体系统平衡问题
q
A B
M
C
a
a
a
a
q
M
C
2. BC 梁为研究
F 0 F 0 M 0
x
FBx
FBx 0
B
FBy
FC
y
FBy qa Fc 0
a qa M Fc 2a 0 2
FAx ql FAy FP
二、平面一般力系平衡方程的其它形式
y F1
A
F2
F4
y
B
F R =0
M (a)
F3
F5 x (b) x
F 0 M (F ) 0 M (F ) 0
x A B
二力矩式 (AB不垂直于x轴)
10
y F1
F2
F4
y
C B A
F R=0
B约束反力方位亦可确定,画受力图。 B
C
F′C
C
M2
M1
A 60o
60
o
M2
D A 60o 60o D
FD
FD = FC = F M2 = 0.5 a F
Mi = 0
(2)
- 0.5a F + M2 = 0
22
联立(1)(2)两式得:M1/M2=2
§3-2 简单的空间力系平衡问题
各力的作用线在空间任意分布的力系称为空间 任意力系。 一.力对轴之矩 在平面内,力对点之矩是指力对垂
第 3 章
静力学平衡问题
§3-1 平面力系的平衡条件与平衡方程 §3-2 简单的空间力系平衡问题 §3-3 简单的刚体系统平衡问题
§3-4 考虑摩擦时的平衡问题
1
§3-1 平面力系平衡条件与平衡方程 一、平面一般力系的平衡条件与平衡方程
y F1
O O
F2
F4
y F R
FR Fi
i 1
A
y q
Fy 0 FAy q 2a FNB 0
Mo (F ) 0
解得
Me FAy
C 2a 4a a D
B x FNB
FAx
q 2a a Me FNB 4a 0
FAx 0,
(b)
Me 1 FN B qa , 2 4a Me 3 FAy qa . 2 4a
M (a)
F3
F5 x (b) x
M M M
(F ) 0 B (F ) 0 (F ) 0 C
A
三力矩式 (A、B、C三点不共线)
11
例题 3-4
求图示梁的支座反力。
A
P m a B
解:以梁为研究对象,受力如图。
Fx 0 : FAx P cos 0
F1 ' = F1,F2 ' = F2, … Fn ' = Fn … ,
M1 = M O ( F1 ),M 2 = M O ( F2 ), …, M n = M O ( Fn ) …
FR ' = ∑ i ' = ∑ i F F
i =1
n
n
n
主矢
主 矩
25
i =1
n
M o = ∑ i = ∑ o ( Fi ) M M
y
4. 联立求解,得
FAB 54.5 KN
FAB B
30°
FBC
FT2
反力FAB 为负值,说明该力实际指向与图上假 定指向相反。即杆AB 实际上受拉力。
17
例题 3-7 折杆AB的支承方式如图所示,设有一力矩数
值为M的力偶作用在折杆AB上,求支承处的约束力大小。
注意:
力偶 M 在任一轴上的投影为零; 力偶对任一点之矩即为M。 选取适当的坐标轴和矩心,注意正负号。
30
方法二:局部
选局部 为研究 对象画 受力图 ,列平 衡方程
局部 检 查 结 果, 验 算
弄清 题意, 标出 已知 量
再选局部 为研究对 象画受力 图,列平 衡方程求 解。
