三元系统相图分析及析晶规律
第二十讲三元相图总结精选全文完整版

可编辑修改精选全文完整版第二十讲三元相图总结第五节三元相图总结一、主要内容:三元系的两相平衡三元系的三相平衡三元系的四相平衡三元相图的相区接触法则三元合金相图应用举例二、要点:三元系的两相平衡特点,共轭曲面,共轭曲线,三元系三相平衡特点(共晶型,包晶型),等温截面的相区接触法则,三元系的四相平衡特点,三元共晶反应型,包晶反应型,三元包晶反应型,利用单变量线的走向判断四相平衡类型,相区接触法则三、方法说明:掌握三元合金相图的特点,使学生能够看懂并应用三元相图,重点是掌握相区接触法则,利用单变量线判断四相平衡的类型,利用杠杆定律,重心法则估算出各组成相的相对含量授课内容:一、三元系的两相平衡三元相图的两相区以一对共轭曲面为边界,所以无论是等温截面还是变温截面都截取一对曲线为边界。
在等温截面上平衡相的成分由两相区的连线确定,可用杠杆定律计算相的相对含量。
在变温截面上,只能判断两相的温度变化范围,不反应平衡相的成分。
二、三元系的三相平衡三元系的三相平衡区的立体模型是一个三棱柱体,三条棱边为三个相成分的单变量线。
三相区的等温截面图的三个顶点就是三个相的成分点。
各连接一个单相区,三角形的三个边各邻接一个两相区。
可以用重心法则计算三个相的含量。
如何判断三相平衡是二元共晶反应还是二元包晶反应?在垂直截面图中,曲边三角形的顶点在上方的是二元共晶反应;顶点在下方的是二元包晶反应。
三、三元系的四相平衡三元系的四相平衡,为恒温反应。
如果四相平衡中由一个相是液体三个相是固体,会有如下三种类型:1)三元共晶反应:2)包共晶反应:3)三元包晶反应:四个三相区与四相平衡平面的邻接关系有三种类型:1)在四相平面之上邻接三个三相区,是三元共晶反应。
2)在四相平面之上邻接两个三相区,是包共晶反应。
3)在四相平面之上邻接一个三相区,是三元包晶反应。
液相面的投影图应用的十分广泛。
以单变量线的走向判断四相反应类型:当三条液相单变量线相交于一点时,在交点所对应的温度必然发生四相平衡转变。
三元相图(2)

共线法则与杠杆定律 两条推论
(1)给定合金在一定温度下处于两相平衡时,若其中 一个相的成分给定,另一个相的成分点必然位于已知成分 点连线的延长线上。
图中a,b,c分别是组元A,B,C的熔点。在共晶合金中,一个组元的熔点会 由于其他组元的加人而降低,因此在三元相图中形成了三个向下汇聚的液相面。 其中,
ae1Ee3a是组元 A的初始结晶面; be1Ee2b是组元 B的初始结晶面; ce2Ee3c是组元C的初始结晶面。 3个二元共晶系中的共晶转变点el,e2,e3在三元系中都伸展成为共晶转变线, 这就是3个液相面两两相交所形成的3条熔化沟线e1E,e2E和e3E。当液相成分 沿这3条曲线变化时,分别发生共晶转变:
(2)若两个平衡相的成分点已知,合金的成分点必然 位于两个已知成分点的连线上。
重心法则 在一定温度下,三元合金三相平衡时,合金的成分点为三个平衡相
的成分点组成的三角形的质量重心。(由相率可知,此时系统有一个 自由度,温度一定时,三个平衡相的成分是确定的。)
平衡相含量的计算:所计算 相的成分点、合金成分点和二者 连线的延长线与对边的交点组成 一个杠杆。合金成分点为支点。 计算方法同杠杆定律。
2 三元相图的空间模型
包含成分和温度变量的三元合金相图是一个三维的立体图形。图8.2是一种最 简单的三元相图的空间模型。A,B,C 3种组元组成的浓度三角形和温度轴构成 了三柱体的框架,a,b,c三点分别表明A,B,C 3个组元的熔点。由于这3个 组元在液态和固态都彼此完全互溶,所以3个侧面都是简单的二元匀晶相图。在 三棱柱体内,以3个二元素的液相线作为边缘构成的向上凸的空间曲面是三元系 的液相面。以3个二元系的固相线作为边缘构成的向下凹的空间曲面是三元系的 固相面,它表示不同成分的合金凝固终了的温度。液相面以上的区域是液相区, 固相面以下的区域是固相区,中间区域如图中O成分三元系在与液相面和固相面 交点1和2所代表的温度区间内为液、固两相平衡区。三元相图能够实用的方法 是使之平面化。
第五章 三元相图
杠杆定律表达式 α%=EO/DE×100%, β=OD/DE×100% 注意:当一个合金O在液相的凝固 过程中,析出α相成分不变时,液 相成分一定沿α相成分点与O点 连线延长线变化
。
5 直线法则与杠杆定律 两条推论 (1)给定合金在一定温度下处于两相平衡时,若其中一 个相的成分给定,另一个相的成分点必然位于已知成分点连 线的延长线上。 (2)若两个平衡相的成分点已知,合金的成分点必然位 于两个已知成分点的连线上。
三相平衡重心法则(重量三角形重 心) x,y,z分别为α,β,γ成分点, 则 α%=oa/ax×100%,β=ob/by×100%, γ%=oc/cz×100%
三元系相图组成的表示法 f* = 3-Φ + 1= 4 –Φ, Φmin = 1 , f*max= 3
三维坐标→ 等边三角立柱
等边三角形——组成三角形 三个立柱侧面——二元相图面 组成三角形的边——二元组成 组成三角形的顶点——纯组元
相图基本知识
1 三元相图的主要特点 (1)是立体图形,主要由曲面构成; (2)可发生四相平衡转变; (3)一、二、三相区为一空间
三元相图的基本特点为: (1)完整的三元相图是三维的立体模型。 (2)三元系中可以发生四相平衡转变。由相律可以 确定二元系中的最大平衡相数为3,而三元系中的最大 平衡相数为4。三元相图中的四相平衡区是恒温水平面。 (3)除单相区及两相平衡区外,三元相图中三相平 衡区也占有一定空间。根据相律得知,三元系三相平 衡时存在一个自由度,所以三相平衡转变是变温过程, 反映在相图上,三相平衡区必将占有一定空间,不再 是二元相图中的水平线。
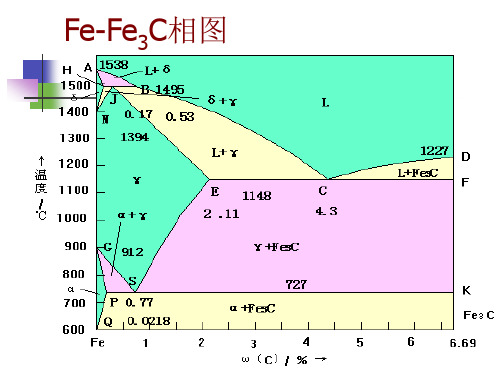
Fe-Fe3C相图
三元相图
一、三元相图的成分表示法 二、杠杆定律及重心法则 三、匀晶三元相图 四、简单三元共晶相图 五、固态有限溶解的三元共晶相图 六、有包共晶反应的三元相图 七、 三元包晶相图 八、形成稳定化合物的三元相图 九、三元相图分析法总结 十、三元相图实例
第七章 三元相图
二元系中两相平衡时,2个平衡相的成分由公切线的切点确定,两个自由能~成 分曲线只有一条公切线
温度一定,其共轭曲线一定,等同于等温截面 S1、S2为两平衡相成分,由共轭连线建立对应关系,即一个 成分只能随着另一个成分的变化而变化 共轭连线不可能相交
思考:
在两相区内,合金的平 均成分点,应落在什么 位置?(直线法则)
(平面三角形A1B1C1)
等温截面图
— 固态互不溶解三元共晶相图
两相区:其中一相为纯组元, 故共轭线从纯组元一方指向液 相(在两相区可利用直线法则、 杠杆定律求出两平衡相的相对 重量) 三相区:为直线共扼三角形 (可利用重心法则求三平衡相 的相对重量) 含有液相的3个三相区在降温 时均发生共晶型转变
因此,a、o、b 三点共线(直线法则成立)
2.杠杆定律
oa 固相质量分数:w固 ab
B
a
o
b
C
液相质量分数:w 液
ob 1 w固 ab
A 推论:
材料在一定温度下处于两相平衡状态时,若其中一相的成分给 定,另一相的成分点必在两已知成分点为连线的延长线上; 若两个平衡相的成分点已知,材料的成分点必然位于此两个成 分点的连线上
第七章 三元相图
Ternary Phase Diagrams
三元相图
实际应用的金属材料,多半是由两种以上的组元构成的
多元合金,陶瓷材料也往往含有不止两种化合物 多组元的加人,引起组元之间溶解度的改变,而且会因 新组成相的出现致使组织转变过程和相图变得更加复杂 二元相图为平面图,三元相图为立体图(多增加一个成 分变量所引起)
等边三角形中特殊线
B B
wC wC
e
wB
p o
物理化学_三元相图详解

A
C
A m B n mA nB
L、C A A
判别方 过渡点没有对应的副三角形,相平衡的组成 法 在一条直线上 是否结 晶终点 否(只是结晶过程经过点)
无对应副三角形,组 成在一条直线上 否
(6)分析冷却析晶过程或加热过程
• 熔体冷却,首先在初晶区析晶,液相组成按背向 线规则变化,此时F=2。 • 液相到达界线上析晶,如果是共熔线,析出两种 晶体,F=1,组成沿着界线温度下降方向变化。 如果在界线上转熔,需要注意固相组成,转熔是 否提前结束进入单相区。 • 熔体析晶结束点,必定在熔体组成所属副三角形 对应的无变量点上。 • 熔体析晶过程中任何时刻,原始熔体组成点、固 相、液相组成点在一条直线上。利用杠杆规则可 计算各相含量。
(7)特殊情况的判别
• 组成点如果正好在界线上,如果是共熔线,则冷 却时同时析出两种晶相,固相组成可以使用切线 规则求出。 • 如果界线是转熔线,则析出单一固相,液相组成 点直接进入单相区,并按照背相线规则变化。 • 如果组成点是三元低共熔点,则同时析出三种晶 体。如果是单转熔点,不发生转熔而是沿某一界 线析晶。如果是双转熔点,不转熔也不沿着界线 析晶,直接析出单一固相,组成的进入单相区按 背向线规则变化。
(1)判断化合物的性质
• 了解相图有哪些化合物,组成的和初晶区的位置, 根据化合物的组成点是否在其初晶区内,判断化 合物的性质。 化合物根据组成可以分为二元化合物和三元 化合物; 化合物在自己的初晶区内为一致熔融化合物, 不在自己的初晶区内为不一致熔融化合物。
(2)把相图划分成若干个副三角形
• 根据划分副三角形的原则和方法,把复杂的三元 相图划分成若干个分三元系统,使复杂相图简化。 根据无变量点划分,除多晶转变点和过渡点 外,每一个无变量点都有自己对应的副三角形。 把无变量点周围的三个初晶区对应的晶相组 成点连结成三角形,就是该无变量点对应的副三 角形。
三元系统相图

※3、无变量点性质的判断
方法一:根据无变量点与对应副△的位置 关系来判断。 —— 重心规则 方法二:根据无变量点周围三条界线的箭
头指向来判断。
4、结晶过程
配料点1:
配料点2:
配料点3:
几点讨论:
(1)P点是单转熔点,不一定是析晶结束点; 三元低共熔点
一定是析晶结束点;
P点:L+B → S+C,有三种析晶结果 1)L先消失,B有剩余,P为析晶结束点,组成点在 ▲BSC内; 2)B先消失,L剩余,转熔结束,组成点在▲PSC内; 3)L与B同时消失,P点结晶结束,产物为S、C两相, 组成点在SC连线上。 (2)转熔线上的穿相区现象,发生在界线转熔过程中,组成
ห้องสมุดไป่ตู้
(一)具有一个低共熔点的简单三元系统相图 (1)立体相图
(2)平面投影图
投影图上温度表示法:
1)等温线法; 2)特殊点温度直接标注或列表
表示;
3)箭头表示温度下降方向。
(3)结晶过程
小结: 1)初晶区规则: 判断最初析出晶相
最初析出晶相
2)杠杆规则:
原始组成点所在相区对应的晶相
相平衡的液相、固相、总组成点始终在一条杠杆上
3)三元低共熔点一定是析晶结束点
(4)加热过程
小结:
1)一种晶相析出时,液相在相区变化,固相组 成在投影图上的△顶点;
2)二种晶相析出时,液相在界线上变化,固相
组成在投影图上的△边上; 3)三种晶相析出时,液相在无变量点上变化, 固相组成进入△内与原始组成重合。
(5)各相量计算 —— 杠杆规则
第五节
三元系统相图
一、三元系统相图概述
三元凝聚系统相律: F=C-P+1=4-P
三元相图(2)

是三元系中的杠杆定律。
由直线法则及杠杆定律可作出下列推论:当给定材料在一定温度下处于两相平衡 状态时,若其中一相的成分给定,另一相的成分点必在两已知成分点连线的延长线 上;若两个平衡相的成分点已知,材料的成分点必然位于此两个成分点的连线上。
三元相图与二元相图比较。组元数增加了一个,即成分变量为两个,故表示成分的坐标轴 应为两个,需要用一个平面来表示,再加上一个垂直该成分平面的温度坐标轴,这样三元相 图就演变成一个在三维空间的立体图形。这里,分隔每一个相区的是一系列空间曲面,而不 是平面曲线。
要实测一个完整的三元相图,工作量很繁重,加之应用立体图形并不方便。因此,在研究 和分析材料时,往往只需要参考那些有实用价值的截面图和投影图,即三元相图的各种等温 截面、变温截面及各相区在浓度三角形上的投影图等。立体的三元相图也就是由许多这样的 截面和投影图组合而成的。
2.截面图 rs和At垂直截面如下图所示。rs截面的成分轴与浓度三角形的AC边平行,图中re
和es是液相线,相当于截面与空间模型中液相面Ae1Ee3A和Ce2Ee3C的截线;曲线 r1d′是截面与过渡面fe1Emf的截痕,de,ei和isl分别是截面与过渡面le3Eml, ke3Epk和je2Epj的交线;水平线r2s2是四相平衡共晶平面的投影。 利用这个垂直截面可以分析成分点在rs线上的所有合金的平衡凝固过程,并可确定 其相变临界温度。以合金O为例。当其冷到1点开始凝固出初晶A,从2点开始进入L +A+C三相平衡区,发生L→A+C共晶转变,形成两相共晶(A+C),3点在共晶 平面mnp上,冷至此点发生四相平衡共晶转变L→A+B+C,形成三相共晶(A+B +C)。继续冷却时,合金不再发生其他变化。其室温组织是初晶A十两相共晶(A +C)十三相共晶(A+B+C)。
第六章 三元相图

表示三元系成分的点位于两个坐标轴所限定的一个三角 形内,该三角形称为成分三角形或浓度三角形。
常用的成分三角形是等边三角形,有时也采用等腰三角 形或直角三角形。
6-1 三元相图基础
(一)等边成分三角形
三角形的三个顶点A、B、C
分别表示三个纯组元,三角形的
三个边AB、BC、CA分别表示三
无论选用哪种方法,得到的图形都是三元立体相图的 一个截面,故称为截面图。
6-1 三元相图基础
(二)水平截面图 三元相图中的温度轴和成分三角形垂直,所以固定温度
的截面图必定平行于浓度三角形,这样的截面图称为水平截 面图(亦称为等温截面图)。
水平截面图表示三元系在某一温度下的状态。利用水平 截面图可以确定给定成分的合金在该温度下具体由哪些相所 构成。
由于第三组元的加入,三个
二元共晶点在三元系中均演化成
为三相共晶转变线 e1E、e2E 和 e3E。当液相成分沿着这三条曲 线变化时,则分别发生三相共晶
转变: e1 E e2E e3E
L AB L BC L AC
a c
e3
l
k
f j
e1
b
e2
m
p
g
A
Eh C
n
B
固态互不溶解的三元共晶相图
6-2 固态互不溶解的三元共晶相图
6-1 三元相图基础
B
A
B
A
C
C
在T 温度的水平截面
水平截面图及其上的共轭线
三元匀晶相图的水平截面图
l1l2为水平截面与液相面的交线,s1s2为水平截面与固相面的
交线,这两条曲线称为共轭曲线。过合金成分点o 连接固相 和
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三元系统相图
8、形成三元连续固溶体的三元系统相图 9、形成一个二元连续固溶体的三元系统相图 10、具有液相分层的三元系统相图
2015物理与电子工程学院青年教师课堂教学比赛
三元系统相图的基本类型
具有一个低共熔点的 三元系统相图
1. 立体图 具有一个低共熔点的三元凝
聚系统立体图,是以浓度三角 形为底,以温度为高的三棱柱 体。当A、B、C三个组分在液 态完全互溶,固态完全不互溶, 不形成固溶体,不生成化合物 时,即形成这种相图。
三条棱、三个侧面、花瓣状 的三个曲面、三条曲线、三条 界线的交点分别表示的意义及 相律公式的应用
2015物理与电子工程学院青年教师课堂教学比赛
2015物理与电子工程学院青年教师课堂教学比赛
4、杠杆规则的应用
(1)当液相组成点刚刚到达D点:
L% CM 100% CD
C% DM 100% CD
(2)当液相组成点刚刚到达E点:
C
L% FM 100% FE
S( AC)
%
ME FE
100%
F Mt1
A CF A% CF ME 100%
量点等,将其温度直接标入图中或列表注明。
2015物理与电子工程学院青年教师课堂教学比赛
4、结晶路程
C F
Mt1
e3
t2
DE t2
t2
A
e1
M.
. .
.
..
e2
t1 B
..
. .
2015物理与电子工程学院青年教师课堂教学比赛
熔体的结晶路程:
液相点:
M
LC D
f 2
LCA E(LE C A
三元系统相图分析及析晶规律
翟海法 2015. 04. 11
2015物理与电子工程学院青年教师课堂教学比赛
三元系统
f 0
f c p 1 4 p
p 1
pmax 4 fmax 3
2015物理与电子工程学院青年教师课堂教学比赛
孟哈日巴拉
三元凝聚系统相图的基本类型
1、具有一个低共熔点的简单三元系统 2、生成一个一致熔融二元化合物的三元系统相图 3、具有一个一致熔融三元化合物的三元系统相图 4、生成一个不一致熔融二元化合物的三元系统相图 5、具有一个不一致熔融三元化合物的三元系统相图 6、具有一个低温稳定、高温分解的二元化合物的
产物; (5) 在E1E2界线上m点是温度最高点。(连线规则)
2015物理与电子工程学院青年教师课堂教学比赛
本系统CS 连线将原来的三角形划分为两个分 三角形,每个分三角形都是一个具有低共熔点的 三元系统。
2、三角形化分的原则:
➢ 副三角形根据三元无变量点来划分,使每个三元无变量 点都对应一个副三角形。 ➢ 副三角形的个数与对应的三元无变量点个数相等。
该三元系统的相图共有 四个初晶区,五条界线, 两个三元无变量点
C
e3
e2
EP
(1)化合物组成点不在
其初晶区范围内。
A
S
B
(2)界线 pP 是一条转熔线,A
e1
冷却时发生固相回吸。
p
S
B
(3)连接CS,将△ABC可划分为两e个11 副三角形,即△ACS和 △BCS,对应的无变量点分别A1为E 和 P,E在对p应1 的副三S1 角形的
f 1
f 0 L消失
B)
固相点:
C CC CA F CAB M
2015物理与电子工程学院青年教师课堂教学比赛
熔体 冷却析晶的规律: (1)原始熔体M在哪个初晶区内,冷却时,该初晶区所对 应的固相首先从液相析出,该组分析晶过程中,液相组成点 的变化路线遵守背向性规则。 (2)冷却过程中系统的组成点始终不动,而且系统的组成 点、液相组成点和固相(或混合物)的组成点始终在一条直 线上。 (3)无论熔体M在三角形的何种位置,析晶产物都是A、 B、C 三种晶相,且都在三元低共熔点上析晶结束,因此三 元低共熔点一定是析晶的结束点。
A
e1
S
e1'
L+A
L+S
e2
B
e2' L+B
2015物理与电子工程学院青年教师课堂教学比赛
相图的特点:
化合物组成点位于其初晶区范围内,并且是它的初晶区 内的温度最高点。
要求:
(1) 确定温度的变化方向; (2) 各界线的性质; (3) 会划分各分三元系统; (4) 分析不同组成点的析晶路程, 析 晶终点和析晶终
内部,是低共熔点,P在对应的副三角形的外部,是转熔点。
2015物理与电子工程学院青年教师课堂教学比B赛1
判断三元相图的几条重要规则
(4)界线: 界线代表了系统的三相平衡状态; f = 1 (5)交点E/: 处于四 相平衡状态 ;f = 0
2015物理与电子工程学院青年教师课堂教学比赛
立体图与平面投影图的关系
平面点→空间点 (1) 立体图的空间曲面(液相面)
e1 E1 e2 E2 e3 E3 E E
投影为平面上的初晶区 A、 B、 C
3、冷却析晶规律:
无论原始组成点在哪个副三角形内,该副三角形所对应的
三元无变量点是其析晶结束点,最终析晶的产物是该副三角 形三个顶点所表示的物质。
2015物理与电子工程学院青年教师课堂教学比赛
副三角形划分法
2015物理与电子工程学院青年教师课堂教学比赛
具有一个不一致熔二元化合物的三元系统相图
C
相图上的特点:
平面界线→空间界线
e1E E1E e2E E2E
e3E E3E
2015物理与电子工程学院青年教师课堂教学比赛
3. 投ቤተ መጻሕፍቲ ባይዱ图上温度表示法
投影图中的温度常用以下方法来表示: (1)用等温线表示 (2)在界线上(包括在三角形的边上)用箭头表示
温度下降的方向 (3)对一些特殊的点 如各组分及化合物的、无变
C AF
AC FE
e3
t2
e2
(3)析晶结束时:
DE t2
t2
t1
A
e1
B
2015物理与电子工程学院青年教师课堂教学比赛
具有一个一致熔二元化合物的三元系统相图
1、相图分析:
该三元系统的相图共有 四个初晶区, 五条界线, 有两个三元低共熔点
C
C
e4
E1
m E2 e3
A
S
B
具有一个一致熔二元化合 物的三元系统相图
2. 平面投影图
C
t1
e3
t2 A
t2
E
t2
e1
e2
t1 B
.
.
.
2015物理与电子工程学院青年教师课堂教学比赛
说明:
(1)三棱边:A、B、C 的三个一元系统; (2)三侧面:构成三个简单二元系统状态图,并具有相 应的二元 低共熔点;
(3)液相面: 液相面代表了一种二相平衡状态 f = 2,三 个液相面以上的空间为 熔体的单相区 f = 3;
