环境流体力学(第三章)
合集下载
环境工程原理第三章1-2节

qm qm1 qm2
uA u1 A1 u2 A2
三、流动系统的能量衡算方程 (一)总能量衡算
2
流体携带能量
2’ 1 1’
系统与外界交换能量
衡算范围:截面1-1’与 2-2’间的管道和设备。 取0-0’为基准水平面。 衡算基准:1kg流体。
稳态流动下,系统内部无能量积累,则能量衡算方程为 输出系统的物质的总能量-输入系统的物质的总能量
二、流动系统的能量衡算方程
一、流体流动的状态 在流动流体系统中,物理量是空间坐标和时间 的函数。
稳态流动:流体流动系统中,各截面上的压力、
流速、流量等物理量仅随位置变化,
而不随时间变化。 非稳态流动:流体在各截面上的有关物理量既随
位置变化,又随时间变化。
qV2、u2、p2
qV1、u1、p1 qV2、u2、p2
输出系统的质量流量:
qm2 2um2 A2
4、写出质量衡算方程: dm 1um1 A1 2um2 A2 dt
(3.1.1)
对于稳态过程
dm 0 dt
1um1 A1 2um2 A2
um1 A1 um2 A2
(3.1.2)
对不可压缩流体,ρ为常数
(3.1.3)
不可压缩流体管内流动的连续性方程 不可压缩流体作稳态流动时平均速度um仅随管截面 积而变化。
对于圆形管道
π 2 π 2 um1 d1 um2 d 2 4 4
um 2 d1 d um1 2
2
(3.1.4)
表明:当体积流量一定时,管内流体的流速与管道 直径的平方成反比;流体在均匀直管内作稳态流动 时,平均速度恒定不变。
思考:如果管道有分支,则稳定流动时的连续性方程 又如何?
环境水利学第3章 随流扩散与紊动扩散 (5)

❖ 各向同性紊流只是一种理想化的最简单的紊流
u1 2u22u32
精品资料
第三节 紊流统计(tǒngjì)量和紊流尺度
❖ 凡不满足均匀性要求的紊流(当然也不满足各向同性),称为剪切紊 流。
❖ 当紊流中存在切应力时,就有流速梯度,导致各处的紊流统计量不 相同,从而破坏了紊流的均匀性和各向同性。这种紊流是最常见的, 它比各向同性紊流复杂得多。
R i(a,) ui(a)ui(a) ui2(a) ui2(a)
对均匀( jūnyún)
紊流有:
(3-3-1)
u u u i2 (a ) i2 (a) i2
均匀紊流的欧拉空间相关系数为:
Ri()ui(a)u uii2(a)
(3-3-2)
当ξ等于零时,Ri(ξ)应等于1;ξ愈大,Ri(ξ)愈小; 当ξ超过一定的值,Ri(ξ)渐趋于零(两点分别位于不同的涡体)。
❖ 各态历经(lì jīnɡ):一个随机过程在重复多次试验出现的所有样 本,亦将在一次试验的相当长时间或相当大的范围内出现,并 且出现的概率相同。
精品资料
第三节 紊流统计量和紊流尺度
一、紊流的分类(fēn lèi)
❖ 紊流按其流动特点可分为可分两大类:均匀各向同性(ɡè xiànɡ tónɡ xìnɡ)紊流和剪切紊流。
第三节 紊流统计量和紊流尺度
3、欧拉紊流尺度(chǐdù) (比尺)
➢从紊流统计(tǒngjì)理论看,其空间点的脉动量可以视为各种不 同尺度(或不同脉动频率)的涡体经过该点所造成的涨落,较大尺 度涡体包含着较小尺度涡体。
➢大尺度涡体频率低,小尺度涡体频率高。 ➢由相关系数的概念,引入涡体的平均尺度(积分尺度)。
的乘积的统计平均值。
R i(t,)
环境工程原理 第三章 第三节 流体流动的内摩擦力 第四节 边界层理论

湍流层 过度层
临界距离
厚度突然增加
层流底层
从平板前缘到xc之间,流体流动为层流,该区称为层流边界层。 在xc点后,边界层内的流动由层流变为湍流。该区称为湍流边界层。 层流区与湍流区之间有一个过渡区(过渡区和湍流边界层界限不易确定)。
湍流边界层内近壁处一薄层,无论边界层内的流型为层流或湍流,其流型 均为层流,称为层流底层;远离壁面的流体为湍流,称为湍流层(中心); 层流底层和湍流层之间为过度(缓冲)层。
单位为m2/s。运动粘度也是流体的物理性质。
(三) 流体类别(课本p62-64,看书2分钟)
理想流体,μ = 0 流体 实际流体,μ≠ 0 非牛顿流体 牛顿流体 假塑性流体 胀塑性流体 粘塑性流体
牛顿流体:气体和大多数低相对分子质量的液体。 非牛顿流体:泥浆、聚合物等高粘度的液体。
(四)流态对剪应力的影响 层流流动:基本特征是分层流动,表现为各层之 间的相互影响和作用较小,剪应力主要是由分子运 动引起的。——服从牛顿粘性定律
大量实验结果表明,流体在直管内流动,
(1)Re≤2000,流动为层流,此区称为层流区; (2)Re≥4000,一般出现湍流,此区称为湍流区; (3)2000< Re <4000 ,流动是层流还是湍流,取决于 外界干扰条件,该区称为不稳定过渡区。 雷诺数的物理意义: Re反映了流体流动中惯性力与粘性力的对比关系,标 志流体流动的湍动程度。其值愈大,流体的湍动愈剧 烈,内摩擦力也愈大。
普兰德边界层理论要点: (1)实际流体沿固体壁面流动,紧贴壁面处存在非常 薄的一层区域——边界层; (2)边界层内流体的流速很小,但速度梯度很大; (3)边界层内粘性力可达到很高的数值,它所起作用 与惯性力同等重要,流动阻力发生在边界层内; (4)边界层外的外部流动区域,法向速度梯度小,粘性 力可忽略,近似看成理想流体的流动。 (5)流动分为两个区域
环境水力学ch3-2h
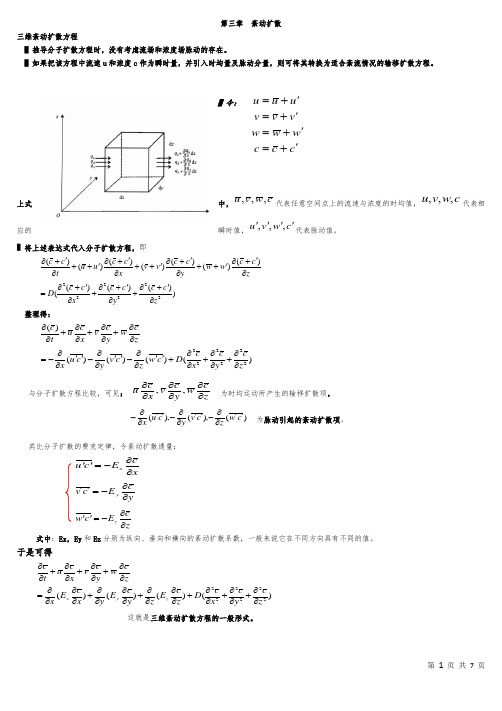
c c c w w w v v v u u u '+='+='+='+=zcw y c v x c u ∂∂∂∂∂∂,,)(),(),(c w zc v y c u x ''∂∂-''∂∂-''∂∂-第三章 紊动扩散三维紊动扩散方程▌推导分子扩散方程时,没有考虑流场和浓度场脉动的存在。
▌如果把该方程中流速u 和浓度c 作为瞬时量,并引入时均量及脉动分量,则可将其转换为适合紊流情况的输移扩散方程。
▌令:中,c w v u ,,,代表任意空间点上的流速与浓度的时均值,c w v u ,,,代表相上式瞬时值,c w v u '''',,,代表脉动值。
应的▌将上述表达式代入分子扩散方程,即))()()(()()()()()()()(222222z c c y c c x c c D z c c w w y c c v v x c c u u t c c ∂'+∂+∂'+∂+∂'+∂=∂'+∂'++∂'+∂'++∂'+∂'++∂'+∂整理得:)()()()()(222222z c y c x c D c w z c v y c u x zc w y c v x c u t c ∂∂+∂∂+∂∂+''∂∂-''∂∂-''∂∂-=∂∂+∂∂+∂∂+∂∂与分子扩散方程比较,可见:为时均运动所产生的输移扩散项,为脉动引起的紊动扩散项。
类比分子扩散的费克定律,令紊动扩散通量:x c E c u x∂∂-=''y c E c v y∂∂-=''z cE c w z∂∂-=''式中:Ex ,Ey 和Ez 分别为纵向、垂向和横向的紊动扩散系数,一般来说它在不同方向具有不同的值。
环境工程原理 第三章 第三节 流体流动的内摩擦力 第四节 边界层理论

3、牛顿粘性定律
实验证明,流体的内摩ห้องสมุดไป่ตู้力F与两层流体的速度差 du 成正比,与两层间的垂直距离 dy 成反比,与两层间 的接触面积A成正比,即
du F A dy
式中:F——内摩擦力,N;
(3.2.2)
du ——法向速度梯度,即在与流体流动方向相垂直的y方向流体 dy 速度的变化率,1/s;
μ——比例系数,称为流体粘度或动力粘度,Pa· s。
动性越小。流体的粘性是流体产生流动阻力的根源。
2、流体流动的内摩擦力 两块面积很大且相距很近 平行板,板间充满静止液 体。下板固定,对上板施 加恒定外力 F,上板以速 度 u 沿 x方向运动。 若u较小,则两板间液体会分成无数平行的薄层运动, 粘附在上板底面的一薄层流体以速度u随上板运动,其 下各层液体的速度依次降低,紧贴在下板表面的一层 液体速度为零,两平板之间的流速呈线性变化。 对相邻两层流体来说,上层速度大,下层速度小,前 者对后者起带动作用,而后者对前者起拖曳作用,流 体层之间的这种相互作用即是内摩擦力,流体的粘性 正是这种内摩擦力的表现。
一、流体的流动类型
1、两种流型--层流和湍流
(1) 雷诺实验 将水箱A注满水,利用 溢水管H保持水箱中的
水位恒定,然后微微打
开玻璃管末端的调节阀
C,水流以很小速度沿
玻璃管流出。再打开颜 色水瓶D上的小阀K,使
颜色水沿细管E流入玻璃
管B中。
第三节 流体流动的内摩擦力
水流速从小到大,有色液体 变化如图所示。实验表明,流体 在管道中流动存在两种截然不同 的流型。 层流 ( 或滞流 ) :图 (a) 水流很小 时管中颜色水质点仅沿着与管轴 平行的方向作直线运动,质点无 径向脉动,质点之间互不混合。
本-环境流体力学-No3

xi (a, b, c, t t ) xi (a, b, c, t ) xi u i (a, b, c, t ) lim t 0 t t
4、质点加速度描述
u i (a, b, c, t t ) u i (a, b, c, t ) ui ai (a, b, c, t ) lim t 0 t t
四、欧拉方法的场描述
1、物理量描述 f=f(x,y,z,t) 2、质点速度描述 ui=ui(x,y,z,t) 3、质点加速度描述 ai=ai(x,y,z,t)
五、拉格朗日描述与欧拉描述
拉格朗日描述着眼于流体质点, 将物理量视为随体(初始)坐标与时间 的函数,而欧拉描述着眼于空间点, 将物理量视为空间坐标与时间的函数。
25 1 (5t )
2 2
10t
10 t3
加速度为
u v 30 ax 10 ,a y 4 t t t
练习题
练习题
第二节 流体基本概念
一、流体的恒定流和非恒定流 用欧拉法描述流动时,如流场中各点的流 动要素与时间无关,成为恒定流,否则为非恒 定流。 恒定流-定常流 非恒定流-非定常流
欧拉法流体质点的加速度组成
欧拉加速度由两部分组成;一是由于某一空间点
上的流体质点的速度随时间的变化而产生的,称为当
地加速度,即
ui t
;二是由于流体质点的速度随空间
ui ui x
点的变化而产生的,称为迁移加速度,即
;当
地加速度和迁移加速度之和称为总加速度。
思考题
如何考虑不可压缩流体流过一个中间有收缩形的
f ( x x, y y, z z, t t ) f ( x, y, z, t ) f f x j Df g ( x, y, z, t ) lim t 0 t t x j t Dt
流体力学水利学第三章水动力学复习资料课件PPT

t = t0 = 给定时刻, (x,y,z)= 变数
(x,y,z)= 给定 点,t = 变数
同一时刻,不同空间 点上液体质点的流速 分布,即流场。
不同液体质点通过给 定空间点的流速变化
2.液体质点运动描述 1)质点运动速度
u=ux+uy+uz
z
ux= ux( x,y,z,t )
uy= uy( x,y,z,t ) uz
F pdA p dpdA gdAdz
2、 微分流段质量与加速度的乘积 Ma dAds du
dt
F Ma 即pdA p dpdA gdAdz dAds du dt
对于恒定元流,u us
du dt
du ds ds dt
u du ds
d u2
ds
2
pdA p dpdA gdAdz dAds du
3、流动稳定性演示
恒定流—运动要素不随时间变化
v=v(x,y,z,), p=p(x,y,z)
3、流动稳定性演示
非恒定流—运动要素随时间变化
v=v(x,y,z,t), p=p(x,y,z,t)
三、均匀流与非均匀流
1、均匀流(Uniform flow)
(1)定义:流线为相互平行直线的水流 或流线上的速度矢量都相同。
二、恒定流与非恒定流
1、恒定流(Steady flow)
所有运动要素≠f(t)-----不随时间变化 u=u(x,y,z), p=p(x,y,z)
ux/t= uy/t= uz/t=p/t=0
2、非恒定流(Unsteady flow)
任一运动要素=f(t)-----随时间变化 u=u(x,y,z,t)或 p=p(x,y,z,t)
因此,该方法在工程上很少采用, 但这个 方法在波浪运动中、PIV水流量测等问题研究中 多用这个方法。
环境水力学(M3)

氧量相对增加,水中溶解氧增多。水质逐渐 恢复。
求极值
由 可得
dD dx xxc 0
xc
k2
u k1
ln[
k2 k1
(1
D0 C0
k2 k1 )] k1
S-P模型广泛应用于河流水质的模拟预测中。上述结 果可用于是u常数,且u很大,横向混合。
S-P模型的各种修正
• 非稳态模型 • Thamas修正 • Dobbins-Camp修正 • O’connor修正
103o 15 30 45 60 x
由于:
C10
m QuCu Qu Qe1
0.5 3106 15 0.5
Qe1=0.5m3/s Qe2=0.25m3/s 滩地
96770 MPN/100 ml
1
2
Qu=15m3/s
x
Cu=0
C20
Qu
m 2 Qe1 Qe2
0.25 3106 15 0.5 0.25
• 对于一维稳态河流的BOD—DO模型:通用性较强的是 多宾斯—坎普(Dobbins-Camp)模型,它全面地考虑 了河水中溶解的CBOD(或因地表径流引起CBOD的变 化)的迁移和反应,同时还考虑了与此相应的耗氧作用, 大气向河水的复氧作用、藻类的呼吸和光合作用等所引 起的溶解氧变化。
xl c2 (x) c20 exp[k1 V2 ], (x l)
c10
式中:c10
m 1 Q1
0
c20
c10
exp( k1
l V1
)
SD k1
(1
exp( k1
l V1
))
c20 浓度分布图
Q2 Q1
V2
Q2 A2
x
求极值
由 可得
dD dx xxc 0
xc
k2
u k1
ln[
k2 k1
(1
D0 C0
k2 k1 )] k1
S-P模型广泛应用于河流水质的模拟预测中。上述结 果可用于是u常数,且u很大,横向混合。
S-P模型的各种修正
• 非稳态模型 • Thamas修正 • Dobbins-Camp修正 • O’connor修正
103o 15 30 45 60 x
由于:
C10
m QuCu Qu Qe1
0.5 3106 15 0.5
Qe1=0.5m3/s Qe2=0.25m3/s 滩地
96770 MPN/100 ml
1
2
Qu=15m3/s
x
Cu=0
C20
Qu
m 2 Qe1 Qe2
0.25 3106 15 0.5 0.25
• 对于一维稳态河流的BOD—DO模型:通用性较强的是 多宾斯—坎普(Dobbins-Camp)模型,它全面地考虑 了河水中溶解的CBOD(或因地表径流引起CBOD的变 化)的迁移和反应,同时还考虑了与此相应的耗氧作用, 大气向河水的复氧作用、藻类的呼吸和光合作用等所引 起的溶解氧变化。
xl c2 (x) c20 exp[k1 V2 ], (x l)
c10
式中:c10
m 1 Q1
0
c20
c10
exp( k1
l V1
)
SD k1
(1
exp( k1
l V1
))
c20 浓度分布图
Q2 Q1
V2
Q2 A2
x
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一般的结论如下: 1.当速度足够慢时,色纹沿着管子延伸成一条美丽的直线。 2.如果水槽中的水没有完全静置达到足够小的速度,色纹会
在管子中改变方向,但是不会出现弯曲现象。
3.随着速度逐步增大,在管子的某个点处,通常在距离喇叭 口或者入口相当远的地方,色带会立马和周围的水混合在一 起,并和大量有色水体一起充满剩余的管子。任何速度增量 都引起了破点更接近喇叭口,但是还没有尝试这样做过。通 过使用电火花的亮光来观察管子,大量的染料分解成大量有 或多或少差异的卷流中,呈现出涡流。
(3)一个正态分布的随机变量的数学期望和方差. X为服从正态分布 N ( , ) 的随机变量,其概率密度为
1 f (X ) exp 2 X的数学期望为 ( x u ) 2 2 2
f ( x)dx 1
( x u ) 2 2 2
1 E( X ) x exp 2
Acheson (1990)得到):
这个实验在三个管子中做。它们大约4英尺6英寸长(1.37m), 进水口呈喇叭形,可使水可以无干扰的进入。水从一个较大的玻 璃槽引进管子,管子在玻璃槽中淹没,做相关安排,以使得高度 着色的水带着清水一条一条的进入管子。
雷诺兹展示的层流(顶图),紊流(中间),以及使用电火花照亮的紊流示意图。
时间平均值和统计值是相等的.
平稳过程是指随机过程的统计特性不随时间推移而改
变的过程,时均恒定紊流中时间平均值和总体平均值是相 等的.
§3-2 数学期望、方差、相关与相关系数、矩
一、数学期望
数学期望是描述位置特征的量(几何分布中心、平均数)
pk , (1)设离散型随机变量X 的 概率为 P X xk k=1,2……,
若以紊流中任意点瞬时流速u作为离散型随机变量系列,令时
间平均流速为 u ,脉动流速为u ,流速的标准差为:
'
ni 2 '2 (ui u) (ui u ) ui N i 1
2
N
标准差为脉动流速的均方根,其量纲仍为流速,反映了脉动 流速的强弱程度,故称脉动强度。
设紊流中任意不同点处的脉动流速为 u1 ' 与 u2 '
2
2
M ( x ut ) exp( )dx 4 Dt 4 Dt
2
2
( x u ) 2 c( x, t )dx
c( x, t )dx
' 2 M2 ' u 2 Dt M0
值越大,正态分布曲线越平坦。
不同 值的曲线族代表不同时刻t的浓度分布曲线族。
2
来
表达.其含义是变量与均值之差平方的数学期望.之所以采用
差值的平方而不是差值来代替,是因为差值会出现负的问题. (1)离散型随机变量
D( x) E X E ( X ) xk E ( x) pk
2 2 k 1
对于连续型随机变量,则方差的表达式为
D( X ) E X E ( X ) [ x E ( X )]2 f ( x)dx
D( X )
三、相关与相关系数
任意两个随机变量X和Y之间有无相互关系用无量纲的相关系数来衡 量,R定义为
EX E ( X )Y E (Y ) R D( X ) D(Y )
随机变量X和Y的协方差
Cov( X , Y ) EX E ( X )Y E (Y )
因为是针对不同空间位置的流速而引出的相关系数,故称作距离
相关系数,以 RL 表示.
RL
1 ' 2 ' 1 '2 2 '2
十九世纪末,Reynolds(雷诺兹)演示了一系列关于有 色溶液在管道中迁移的实验。这些实验是关于紊流的开创性 的观察,他的分析使得Re(雷诺数)而得名。很有意思地发 现,紊流研究的首要贡献是在污染物迁移中的(有色溶液的 线条形式);因此,我们可以假定紊流对输移有很重要的影 响。在他的论文中,Reynolds(1883)这样写到(从
雷诺兹总结到,这些流动特性由无量纲数Re= UL/ν决定, 式中U代表管道流速,L是管径,ν是运动粘度,Re值相 对高时发生紊流。紊流的主要结果是它增大了动量和质 量传递。
拉格朗日观点,如果我们跟踪一个流体质点,它可能开始被冲 进一个大涡流,然后随着涡流分解它会从一个涡流移动到另一
个涡流中去。最终,流体质点会留在一个足够小的涡流中,该
若级数
x
k 1
k
pk 绝对收敛,则称级数 xk pk 为随机变量
k 1
X的数学期ຫໍສະໝຸດ ,记为 E ( X ) ,即E ( X ) xk pk
k 1
,它是一个加权概率平均值,权重为pk
•
(2)连续型随机变量X,若其概率密度为f(x),
若积分
xf ( x)dx 绝对收敛,则称该积分为X的
数学期望,记为 E ( X )
E ( X ) xf ( x)dx
数学期望又称均值,它体现了一个随机变量最有可能(最有希 望)出现的值 。
二、方差 (描述随机变量X相对于E(X)离散程度的量)
随机变量的数值总是忽大忽小,很不规则.如果要度量一个随机
变量与均值的偏离程度,常用量D(X)= E X E ( X )
M ( x ut ) M '1 xc( x, t )dx x exp( ) 4 Dt 4Dt
浓度分布曲线的重心距
坐标原点的水平距离
M '1 x ut M '0
二阶浓度中心矩(关于x)
M 2 ( x x) c( x, t )dx ( x x)
§3-1 紊流的时间平均与统计平均
统计平均法(总体平均法)—在同样条件下重复多次试验,每 次试验要在同一地点、同一时间取样统计.样本的总和称为 总体,如测量某一点流速,样本总和为N,其中测得流速为 ui
的次数为 ni ,该点流速总体平均值为
e
n u
i 1 i
n
i
N
随机过程属于平稳过程而又具有遍历性或各态历经性,其
其相关系数为
E[ X E ( X )][Y E (Y )] R(u1 , u2 ) D( X ) D(Y )
(u1i u1 )(u2i u2 )
i 1 2 n1i (u1i u1 ) N i 1 N1 N2
N
ni N
2
n2i (u2i u2 ) N i 1
' M 其为X的k阶原点矩。(可以写成 k );
) k f ( x)dx, k 1,2, 存在,则称其 若 E[( x E ( X )) )] ( x E ( X)
k
为X的k阶中心矩(可以写成 M k );
四、矩
设X和Y是随机变量,若 E ( X Y )
k l
子扩散则需要几天的时间.紊动扩散是指紊流的脉动或者由
紊流的旋涡运动引起的物质传递.实践证明,由紊动而引起的
物质扩散在数量上比分子扩散大的多,一般在紊流情况下可
忽略分子扩散的作用.
由于紊流的不确定性和随机性,许多学者采用随机事
件的统计方法来研究紊流问题. 水力学中已对紊流的一些特性作了阐述,这里仅介绍 一些与紊流有关的统计特性,以此奠基研究紊动扩散的基 础,然后再讨论紊动扩散的问题.
涡流的粘度将动能转化为热能。这小涡流也是大涡流的一部分; 因此,在任何时候流体中都会存在各种尺寸大小的涡流。
u u(t )
在某点处的紊流脉动流速的测量示意图
在流速测量中,测量的一小部分,速度具有高度的相关性似
乎是确定的。如果大涡流产生长期的速度波动,小涡流产生短
期的速度波动,所有这些同时出现在流体中。上图给出了在某 点处就速度因素测试的紊流速度测量例子。如果我们考虑速度 我们对比下时间轴上的更远处的速度,会发现这些速度变得完 全不相关,似乎是随机的。当速度开始完全不相关和随机时的 时间尺度叫做积分时间尺度tI。在拉格朗日参考系中,需要一定 的时间使水改变它的初始速度。给出积分尺度uI和lI,这个时间
若X与Y是互相独立而无关联的变量,则 Cov( X , Y ) 0 ,R=0 若X与Y是不是相互独立而存在一定关系,则 Cov( X , Y ) 0 , R≠0 若R→1,则两变量关系密切。
四、矩
k E ( X ) x 设X和Y是随机变量,若 f ( x)dx, k 1,2, 存在,则称 k
dx
积分得
E( X ) u
正态分布的随机变量的均值为分布曲线的对称轴所在处的 横坐标值.
设若曲线以纵坐标为对称轴,则该随机变量之均值为零.而方
差为
D( X ) ( x u)2 f ( x)dx
2 D ( X ) 代入f(x)并积分得
将D(X)开方得均方差或标准差,正态分布标准差为:
他所描述的第一种情况中具有缓慢流速的是层流:流体沿着几 乎完美的线条流进平行层面,水的粘度降低了水体干扰。分子扩 散是染色条纹可以在层流中横向延伸的唯一途径;因此,在分子 扩散将染料均匀分散到管子横截面之前需要更长的管道。
另一种情况中具有较快速度的是紊流:流体突然变得不稳定并
发展成为一个涡频谱,并且这些干扰由于不稳定性而增大。随着 涡流的增大,多多少少随着流体被动地流着的染料在横截面迅速 混合,并与紊流一起充满整个管子。使用电火花观察表明,染料 符合涡流形状,但是,过了一段时间后涡流增大并破碎足够多的 次数后染料将不再具有能构出涡流的浓度梯度:这时,染料充分 混合且这种混合或多或少是随机的(即使混合仍然受到离散涡流 的控制)。
