高中数学课时作业：指数与指数函数

合集下载

新教材高中数学第四章指数函数与对数函数指数函数的概念课时作业新人教A版必修第一册

4．2.1 指数函数的概念必备知识基础练1．(多选)下列函数是指数函数的有( ) A ．y ＝x 4B ．y ＝(12)xC ．y ＝22xD ．y ＝－3x2．已知某种细胞分裂时,由1个分裂成2个,2个分裂成4个……依此类推,那么1个这样的细胞分裂3次后,得到的细胞个数为( )A ．4个B ．8个C ．16个D ．32个3．如果指数函数f (x )＝a x(a >0,且a ≠1)的图象经过点(2,4),那么a 的值是( ) A ． 2 B ．2 C ．3 D ．44．若函数f (x )是指数函数,且f (2)＝2,则f (x )＝( ) A ．(2)x B ．2xC ．(12)xD ．(22)x5．已知f (x )＝3x －b(b 为常数)的图象经过点(2,1),则f (4)的值为( )A ．3B ．6C ．9D ．86．已知函数f (x )＝⎩⎪⎨⎪⎧2x，x <0，3x ，x >0，则f (f (－1))＝( )A ．2B ． 3C ．0D ．127．已知函数y ＝a ·2x和y ＝2x ＋b都是指数函数,则a ＋b ＝________．8．已知函数f (x )是指数函数,且f (－32)＝525,则f (3)＝________．关键能力综合练1．若函数y ＝(m 2－m －1)·m x是指数函数,则m 等于( ) A ．－1或2 B ．－1 C ．2 D ．122．函数f (x )＝⎩⎪⎨⎪⎧2x ，x >0，x ＋3，x ≤0，则f (f (－2))的值为( )A ．14B ．12C ．2D ．43．若函数f (x )＝(12a －1)·a x是指数函数,则f (12)的值为( )A ．－2B ．2C ．－2 2D ．2 24．若函数y ＝(2a －1)x(x 是自变量)是指数函数,则a 的取值范围是( ) A ．a >0且a ≠1 B ．a ≥0且a ≠1 C ．a >12且a ≠1 D ．a ≥125．某产品计划每年成本降低p %,若三年后成本为a 元,则现在成本为( ) A ．a (1＋p %)元 B ．a (1－p %)元 C ．a （1－p %）3元 D ．a1＋p %元 6．(多选)设指数函数f (x )＝a x(a >0,且a ≠1),则下列等式中正确的是( ) A ．f (x ＋y )＝f (x )f (y ) B ．f (x －y )＝f （x ）f （y ）C ．f (xy)＝f (x )－f (y ) D ．f (nx )＝[f (x )]n(n ∈Q )7．某厂2018年的产值为a 万元,预计产值每年以7%的速度增加,则该厂到2022年的产值为________万元．8．若函数y ＝(k ＋2)a x＋2－b (a >0,且a ≠1)是指数函数,则k ＝________,b ＝________． 9．已知指数函数f (x )＝a x(a >0,且a ≠1), (1)求f (0)的值；(2)如果f (2)＝9,求实数a 的值．10．已知函数f (x )＝(a 2＋a －5)a x是指数函数． (1)求f (x )的表达式；(2)判断F (x )＝f (x )－f (－x )的奇偶性,并加以证明．核心素养升级练1．某乡镇现在人均一年占有粮食360千克,如果该乡镇人口平均每年增长1.2%,粮食总产量平均每年增长4%,那么x 年后若人均一年占有y 千克粮食,则y 关于x 的解析式为( )A ．y ＝360(1.041.012)x －1B ．y ＝360×1.04xC ．y ＝360×1.04x1.012D ．y ＝360(1.041.012)x2．已知函数f (x )＝⎩⎪⎨⎪⎧3x（x ＞0）2x －3（x ≤0）,若f (a )－f (2)＝0,则实数a 的值等于________．3．截止到2018年底,我国某市人口约为130万．若今后能将人口年平均递增率控制在3‰,经过x 年后,此市人口数为y (万).(1)求y 与x 的函数关系y ＝f (x ),并写出定义域；(2)若按此增长率,2029年年底的人口数是多少？(3)哪一年年底的人口数将达到135万？4．2.1 指数函数的概念必备知识基础练1．答案：BC解析：对于A,函数y ＝x 4不是指数函数, 对于B,函数y ＝(12)x是指数函数；对于C,函数y ＝22x＝4x是指数函数；对于D,函数y ＝－3x不是指数函数． 2．答案：B解析：由题意知1个细胞分裂3次的个数为23＝8. 3．答案：B解析：由题意可知f (2)＝a 2＝4,解得a ＝2或a ＝－2(舍). 4．答案：A解析：由题意,设f (x )＝a x(a >0且a ≠1), 因为f (2)＝2,所以a 2＝2,解得a ＝ 2. 所以f (x )＝(2)x. 5．答案：C 解析：f (2)＝32－b＝1＝30,即b ＝2,f (4)＝34－2＝9.6．答案：B解析：f (－1)＝2－1＝12,f (f (－1))＝f (12)＝312＝ 3.7．答案：1解析：因为函数y ＝a ·2x是指数函数,所以a ＝1, 由y ＝2x ＋b是指数函数,所以b ＝0,所以a ＋b ＝1. 8．答案：125解析：设f (x )＝a x(a >0且a ≠1),则f (－32)＝a －32＝525＝5－32,得a ＝5,故f (x )＝5x,因此,f (3)＝53＝125.关键能力综合练1．答案：C解析：由题意可得⎩⎪⎨⎪⎧m 2－m －1＝1m >0m ≠1,解得m ＝2.2．答案：C解析：由题意f (－2)＝－2＋3＝1,∴f (f (－2))＝f (1)＝2. 3．答案：B解析：因为函数f (x )＝(12a －1)·a x 是指数函数,所以12a －1＝1,即a ＝4,所以f (x )＝4x,那么f (12)＝412＝2.4．答案：C解析：由于函数y ＝(2a －1)x(x 是自变量)是指数函数,则2a －1>0且2a －1≠1,解得a >12且a ≠1.5．答案：C解析：设现在成本为x 元,因为某产品计划每年成本降低p %,且三年后成本为a 元, 所以(1－p %)3x ＝a , 所以x ＝a（1－p %）3.6．答案：ABD解析：因指数函数f (x )＝a x(a >0,且a ≠1),则有：对于A,f (x ＋y )＝ax ＋y＝a x ·a y＝f (x )f (y ),A 中的等式正确；对于B,f (x －y )＝a x －y＝a x·a －y＝a x a y ＝f （x ）f （y ）,B 中的等式正确；对于C,f (x y )＝a x y ,f (x )－f (y )＝a x －a y ,显然,a xy≠a x －a y,C 中的等式错误；对于D,n ∈Q ,f (nx )＝a nx ＝(a x )n ＝[f (x )]n,D 中的等式正确． 7．答案：a (1＋7%)4解析：2018年产值为a ,增长率为7%. 2019年产值为a ＋a ×7%＝a (1＋7%)(万元).2020年产值为a (1＋7%)＋a (1＋7%)×7%＝a (1＋7%)2(万元). ……2022年的产值为a (1＋7%)4万元． 8．答案：－1 2解析：根据指数函数的定义,得⎩⎪⎨⎪⎧k ＋2＝1，2－b ＝0，解得⎩⎪⎨⎪⎧k ＝－1，b ＝2.9．解析：(1)f (0)＝a 0＝1. (2)f (2)＝a 2＝9,∴a ＝3.10．解析：(1)由a 2＋a －5＝1,可得a ＝2或a ＝－3(舍去), ∴f (x )＝2x.(2)F (x )＝2x －2－x,定义域为R , ∴F (－x )＝2－x－2x＝－F (x ), ∴F (x )是奇函数．核心素养升级练1．答案：D解析：不妨设现在乡镇人口总数为a ,则现在乡镇粮食总量为360a ,故经过x 年后,乡镇人口总数为a (1＋0.012)x ,乡镇粮食总量为360a (1＋0.04)x, 故经过x 年后,人均占有粮食y ＝360a （1＋0.04）xa （1＋0.012）x ＝360(1.041.012)x. 2．答案：2解析：由已知,得f (2)＝9；又当x ＞0时,f (x )＝3x, 所以当a >0时,f (a )＝3a, 所以3a－9＝0,所以a ＝2. 当x <0时,f (x )＝2x －3, 所以当a <0时,f (a )＝2a －3, 所以2a －3－9＝0,所以a ＝6, 又因为a <0,所以a ≠6. 综上可知a ＝2.3．解析：(1)2018年年底的人口数为130万；经过1年,2019年年底的人口数为130＋130×3‰＝130(1＋3‰)(万)；经过2年,2020年年底的人口数为130(1＋3‰)＋130(1＋3‰)×3‰＝130(1＋3‰)2(万)；经过3年,2021年年底的人口数为130(1＋3‰)2＋130(1＋3‰)2×3‰＝130(1＋3‰)3(万).……所以经过的年数与(1＋3‰)的指数相同,所以经过x年后的人口数为130(1＋3‰)x(万).即y＝f(x)＝130(1＋3‰)x(x∈N*).(2)2029年年底,经过了11年,过2029年底的人口数为130(1＋3‰)11≈134(万).(3)由(2)可知,2029年年底的人口数为130(1＋3‰)11≈134<135.2030年年底的人口数为130(1＋3‰)12≈134.8(万),2031年年底的人口数为130(1＋3‰)13≈135.2(万).所以2031年年底的人口数将达到135万．。

指数与指数函数

∴ a 2＋ a －2＝47.
47 .
⁠
方法总结
指数幂运算的一般原则
1.有括号的先算括号里的,无括号的先进行指数运算.
2.先乘除后加减,负指数幂化成正指数幂的倒数.
3.底数是负数的,先确定符号;底数是小数的,先化成分数.底数是带分数
的,先化成假分数.
4.若是根式,则化为分数指数幂,尽可能用幂的形式表示,运用指数幂的运
为选项C.
考点三
指数函数的性质及应用
◉角度(一) 比较指数式的大小或解不等式
例3
(1)(2024·吉林白山模拟)已知 a ＝0.310.1， b ＝0.310.2， c ＝
0.320.1，则(
D )
A. a ＞ b ＞ c
B. b ＞ a ＞ c
C. c ＞ b ＞ a
D. c ＞ a ＞ b
由 y ＝0.31 x 单调递减可知0.310.1＞0.310.2，即 a ＞ b ；
即b＜a＜c.
C )
6.
2 −4
1

不等式 3
＞的解集为
27
−∞，1 ∪ 3，＋∞
2 −4
1

由3
＞＝3－3，所以 x 2－4 x ＞－3，即
27
＜1或 x ＞3.
.
− 1 − 3 ＞0，解得 x
7. 函数 y ＝
1
1
－
＋1在区间[－3，2]上的值域是
4
2
因为 x ∈[－3，2]，所以若令 t ＝
关键能力
重点探究
课时作业
巩固提升
必备知识自主梳理
[知识梳理]
知识点一幂的运算
1. 指数与指数运算

数学高一必修1课时作业指数函数的图像和性质

【答案】 B 4．在同一平面直角坐标系中，函数f (x )＝ax 与g (x )＝a x 的图像可能是( )【解析】需要对a 讨论：①当a >1时，f (x )＝ax 过原点且斜率大于1，g (x )＝a x 是递增的；②当0<a <1时，f (x )＝ax 过原点且斜率小于1，g (x )＝a x 是减函数，显然B 正确．【答案】 B5．已知f (x )＝a －x (a >0且a ≠1)，且f (－2)>f (－3)，则a 的取值范围是( )A ．(0，＋∞)B ．(1，＋∞)C ．(－∞，1)D ．(0,1)【解析】 f (x )＝a －x ＝⎝ ⎛⎭⎪⎫1a x ， ∵f (－2)>f (－3)， ∴⎝ ⎛⎭⎪⎫1a －2>⎝ ⎛⎭⎪⎫1a －3，即a 2>a 3. ∴a <1，即0<a <1. 【答案】 D二、填空题(每小题5分，共15分) 6．已知指数函数f (x )的图像过点⎝ ⎛⎭⎪⎫4，116，则f (－3)＝________.【解析】设f (x )＝a x(a >0，且a ≠1)，则a 4＝116，所以a ＝12.所以f (x )＝⎝ ⎛⎭⎪⎫12x .所以f (－3)＝⎝ ⎛⎭⎪⎫12－3＝8. 【答案】 87．(1)若0.2m >1>0.2n ，则________>0>________(填m 或n )；(2)若⎝ ⎛⎭⎪⎫14x <23x ＋1，则x 的取值范围是________．【解析】 (1)由0.2m >1＝0.20>0.2n ，得n >0>m . (2)⎝ ⎛⎭⎪⎫14x＝2－2x <23x ＋1， ∴3x ＋1>－2x ，x >－15. 【答案】 (1)n m (2)x >－158．已知a ＝5－12，函数f (x )＝a x ，若实数m ，n 满足f (m )>f (n )，则m ，n 的大小关系为________．【解析】 a ＝5－12∈(0,1)，故a m >a n ⇒m <n . 【答案】 m <n三、解答题(每小题10分，共20分)9．已知函数f (x )＝a x ＋b (a >0，且a ≠1)．若f (x )的图像如图所示，(1)求a ，b 的值； (2)解不等式f (x ) ≥2.【解析】 (1)由图像得，点(1,0)，(0，－1)在函数f (x )的图像上，所以⎩⎨⎧a 1＋b ＝0，a 0＋b ＝－1，解得⎩⎨⎧a ＝2，b ＝－2，∴f (x )＝2x －2.(2)f (x )＝2x －2≥2， ∴2x ≥4，∴x ≥2. 10．函数f (x )＝2＋xx －1的定义域为集合A ，关于x 的不等式⎝ ⎛⎭⎪⎫122x >2－a －x (a ∈R )的解集为B ，求使A ∩B ＝B 的实数a 的取值范围．【解析】由2＋xx －1≥0，解得x ≤－2或x >1，于是A ＝(－∞，－2]∪(1，＋∞)， ⎝ ⎛⎭⎪⎫122x >2－a －x ⇔⎝ ⎛⎭⎪⎫122x >⎝ ⎛⎭⎪⎫12a ＋x⇔2x <a ＋x ⇔x <a ，所以B ＝(－∞，a )．因为A ∩B ＝B ，所以B ⊆A ，所以a ≤－2，即a 的取值范围是(－∞，－2]． |能力提升|(20分钟，40分) 11．定义运算a b ＝{ a (a ≤b )，b (a >b )，则f (x )＝2x 2－x的图像是( )【解析】当x ≥0时，2x ≥1≥2－x >0；当x <0时，0<2x <1<2－x . 故f (x )＝2x2－x ＝⎩⎨⎧2－x ，x ≥0，2x ，x <0.【答案】 C12．若直线y ＝2a 与函数y ＝|a x －1|(a >0，且a ≠1)的图像有两个公共点，则a 的取值范围是________．【解析】当0<a <1时，如图(1)所示，要使得y ＝2a 与y ＝|a x －1|有两个交点，需0<2a <1，故0<a <12.当a >1时，如图(2)所示，由于y ＝2a >2，所以y ＝2a 与y ＝|a x －1|不存在两个交点，故a 的取值范围为0<a <12.【答案】 ⎝ ⎛⎭⎪⎫0，1213．若函数f (x )＝a x －1(a >0，a ≠1)的定义域和值域都是[0,2]，求实数a 的值．【解析】当a >1时，f (x )在[0,2]上递增， ∴⎩⎨⎧f (0)＝0，f (2)＝2，即⎩⎨⎧a 0－1＝0，a 2－1＝2.∴a ＝±3.又a >1，∴a ＝3；当0<a <1时，f (x )在[0,2]上递减， ∴⎩⎨⎧f (0)＝2，f (2)＝0，即⎩⎨⎧a 0－1＝2，a 2－1＝0.解得a ∈∅.综上所述，实数a 的值为 3.14．已知定义在R 上的函数f (x )＝2x＋a2x ，a 为常数，若f (x )为偶函数，(1)求a 的值；(2)判断函数f (x )在(0，＋∞)内的单调性，并用单调性定义给予证明；(3)求函数f (x )的值域．【解析】 (1)由f (x )为偶函数，得。

山东2021新高考数学一轮复习第二章函数导数及其应用课时作业8指数与指数函数含解析.doc

课时作业8 指数与指数函数一、选择题 1．设a >0，将a 2a ·3a 2表示成分数指数幂，其结果是( C )解析：( C )A ．－2a 3bB ．－8a bC ．－6a bD ．－6ab解析：＝－6ab －1＝－6a b，故选C.3．已知函数f (x )＝a x －1＋4的图象恒过定点P ，则点P 的坐标是( A ) A ．(1,5) B ．(1,4) C ．(0,4)D ．(4,0)解析：令x －1＝0⇒x ＝1，又f (1)＝5，故图象恒过定点P (1,5)． 4．函数f (x )＝a x 与g (x )＝－x ＋a 在同一坐标系中的图象可能是( A )解析：因为函数g (x )单调递减，所以排除选项C ，D ，又因为函数f (x )＝a x 单调递增时，a >1，所以当x ＝0时，g (0)＝a >1＝f (0)，所以排除选项B ，故选A.5．(2019·全国卷Ⅱ)若a >b ，则( C ) A ．ln(a －b )>0 B ．3a <3b C ．a 3－b 3>0D ．|a |>|b |解析：解法1：由函数y ＝ln x 的图象知，当0<a －b <1时，ln(a －b )<0，故A 不正确；因为函数y ＝3x 在R 上单调递增，所以当a >b 时，3a >3b ，故B 不正确；因为函数y ＝x 3在R 上单调递增，所以当a >b 时，a 3>b 3，即a 3－b 3>0，故C 正确；当b <a <0时，|a |<|b |，故D 不正确．故选C.解法2：当a ＝0.3，b ＝－0.4时，ln(a －b )<0,3a >3b ， |a |<|b |，故排除A ，B ，D.故选C.6．函数y ＝a x 在[0,1]上的最大值与最小值的和为54，则函数y ＝3·a 2x －1在[0,1]上的最大值为( C )A ．16B ．15C ．12D.34解析：∵函数y ＝a x 在定义域上是单调函数，且y ＝a x 在[0,1]上的最大值与最小值的和为54，∴1＋a ＝54，解得a ＝14，∴函数y ＝3·a 2x －1＝3·⎝⎛⎭⎫142x －1＝12·⎝⎛⎭⎫116x .∵函数y ＝12·⎝⎛⎭⎫116x 在定义域上为减函数，∴当x ＝0时，函数y ＝3·a 2x －1在[0,1]上取得最大值，且最大值是12，故选C.7．(多选题)已知01，则下列各式中成立的是( AD ) A ．a b >b a B ．c b >c a C ．log a c >log b cD ．b log c a >a log c b解析：由于01，根据指数函数与幂函数的图象与性质有a b >a a >b a ，故选项A 正确；根据指数函数的图象与性质有c b <c a ，故选项B 错误；根据对数函数的图象与性质有log a c <log b c ，故选项C 错误；因为a b >b a ，c >1，则log c a b >log c b a ，即b log c a >a log c b ，故选项D 正确，故选AD.8．已知函数y ＝f (x )的图象关于直线x ＝1对称，当x <1时，f (x )＝⎪⎪⎪⎪⎝⎛⎭⎫12x －1，那么当x >1时，函数f (x )的单调递增区间是( C )A ．(－∞，0)B ．(1,2)C ．(2，＋∞)D ．(2,5)解析：如图所示，画出函数y ＝f (x )的图象，可知当x >1时，函数f (x )的单调递增区间为(2，＋∞)，故选C.二、填空题9．已知实数a ≠1，函数f (x )＝⎩⎪⎨⎪⎧4x ，x ≥0，2a －x ，x <0，若f (1－a )＝f (a －1)，则a 的值为12.解析：当a <1时，41－a ＝21，所以a ＝12；当a >1时，22a －1＝4a －1，无解．所以a 的值为12.10．已知函数f (x )＝2x－12x ，函数g (x )＝⎩⎪⎨⎪⎧f (x )，x ≥0，f (－x )，x <0，则函数g (x )的最小值是0.解析：当x ≥0时，g (x )＝f (x )＝2x －12x 为单调增函数，所以g (x )≥g (0)＝0；当x <0时，g (x )＝f (－x )＝2－x －12－x 为单调减函数，所以g (x )>g (0)＝0，所以函数g (x )的最小值是0.11．对于给定的函数f (x )＝a x －a －x (x ∈R ，a >0，且a ≠1)，下面五个结论中正确的是①③④.(填序号)①函数f (x )的图象关于原点对称； ②函数f (x )在R 上不具有单调性； ③函数f (|x |)的图象关于y 轴对称； ④当0<a <1时，函数f (|x |)的最大值是0； ⑤当a >1时，函数f (|x |)的最大值是0.解析：∵f (－x )＝－f (x )，x ∈R ，∴f (x )为奇函数， ∴f (x )的图象关于原点对称，①正确；当a >1时，f (x )在R 上为增函数，当0<a <1时， f (x )在R 上为减函数，②错误；y ＝f (|x |)是偶函数，其图象关于y 轴对称；③正确；当0<a <1时，y ＝f (|x |)在(－∞，0)上为增函数，在[0，＋∞)上为减函数，∴当x ＝0时，y ＝f (|x |)取得最大值，为0，④正确；当a >1时，y ＝f (|x |)在(－∞，0)上为减函数，在[0，＋∞)上为增函数，∴当x ＝0时，y ＝f (|x |)取得最小值，为0，⑤错误．综上，正确结论是①③④.三、解答题12．已知函数f (x )＝⎝⎛⎭⎫1a x －1＋12x 3(a >0，且a ≠1)．(1)讨论f (x )的奇偶性；(2)求a 的取值范围，使f (x )>0在定义域上恒成立．解：(1)由于a x －1≠0，则a x ≠1，得x ≠0， ∴函数f (x )的定义域为{x |x ≠0}．对于定义域内任意x ，有f (－x )＝⎝⎛⎭⎫1a －x －1＋12(－x )3＝⎝⎛⎭⎫a x1－a x ＋12(－x )3＝⎝⎛⎭⎫－1－1a x －1＋12(－x )3＝⎝⎛⎭⎫1a x －1＋12x 3＝f (x )，∴函数f (x )是偶函数．(2)由(1)知f (x )为偶函数，∴只需讨论x >0时的情况，当x >0时，要使f (x )>0，则⎝⎛⎭⎫1a x －1＋12x 3>0，即1a x －1＋12>0，即a x ＋12(a x －1)>0，则a x >1. 又∵x >0，∴a >1.∴当a ∈(1，＋∞)时，f (x )>0.13．已知函数f (x )＝a ·4x －a ·2x ＋1＋1－b (a >0)在区间[1,2]上有最大值9和最小值1. (1)求a ，b 的值；(2)若不等式f (x )－k ·4x ≥0在x ∈[－1,1]时有解，求实数k 的取值范围．解：(1)令n ＝2x ∈[2,4]，则y ＝an 2－2an ＋1－b (a >0)，n ∈[2,4]有最大值9和最小值1，易知函数y ＝an 2－2an ＋1－b 的图象的对称轴为直线n ＝1，∴当n ＝2时，y min ＝4a －4a ＋1－b ＝1，当n ＝4时，y max ＝16a －8a ＋1－b ＝9，∴a ＝1，b ＝0.(2)由(1)知，4x －2·2x ＋1－k ·4x ≥0在x ∈[－1,1]时有解．设2x ＝t ，∵x ∈[－1,1]，∴t ∈⎣⎡⎦⎤12，2. ∴t 2－2t ＋1－kt 2≥0在t ∈⎣⎡⎦⎤12，2时有解， ∴k ≤t 2－2t ＋1t 2＝1－2t ＋1t 2，t ∈⎣⎡⎦⎤12，2. 再令1t＝m ，则m ∈⎣⎡⎦⎤12，2， ∴k ≤m 2－2m ＋1＝(m －1)2≤1，即k ≤1，故实数k 的取值范围是(－∞，1]．14．(多选题)若函数f (x )＝2x －2－x ，则下列说法正确的是( AC ) A ．f (x )是奇函数 B ．f (x )在R 上是减函数 C ．f (x )无极值D ．f (－1)＝32解析：f (－x )＝2－x －2x ＝－f (x )，则f (x )是奇函数，A 正确；f ′(x )＝2x ln2＋2－x ln2>0，则f (x )在R 上是增函数，且f (x )无极值，故B 错误，C 正确；f (－1)＝2－1－2＝－32，故D 错误，故选AC.15．已知g (x )为偶函数，h (x )为奇函数，且满足g (x )－h (x )＝2x .若存在x ∈[－1,1]，使得不等式m ·g (x )＋h (x )≤0有解，则实数m 的最大值为( B )A ．－1 B.35 C ．1D ．－35解析：解法1：因为g (x )－h (x )＝2x ①，所以g (－x )－h (－x )＝2－x ，又g (x )为偶函数，h (x )为奇函数，所以g (x )＋h (x )＝2－x ②，联立①②，得g (x )＝2x ＋2－x 2，h (x )＝2－x －2x2.由m ·g (x )＋h (x )≤0得m ≤2x －2－x 2x ＋2－x ＝4x －14x＋1＝1－24x ＋1，因为y ＝1－24x ＋1为增函数，所以当x ∈[－1,1]时，(1－24x ＋1)max ＝1－24＋1＝35，故选B.解法2：由解法1知g (x )＝2x ＋2－x 2，h (x )＝2－x －2x2.观察选项，若m ＝1，则g (x )＋h (x )≤0，所以2x ＋2－x 2＋2－x －2x 2≤0，即2－x ≤0，这与2－x>0矛盾，所以m ≠1；若m ＝35，则35g (x )＋h (x )≤0，所以35·2x ＋2－x 2＋2－x －2x 2≤0，即22－x ≤2x ，当x ＝1时，不等式22－x ≤2x 成立，所以m ＝35满足题意，故选B.16．已知定义域为R 的函数f (x )＝－2x ＋b2x ＋1＋a 是奇函数．(1)求a ，b 的值；(2)若对任意的t ∈R ，不等式f (t 2－2t )＋f (2t 2－k )<0恒成立，求k 的取值范围．解：(1)因为f (x )是R 上的奇函数，所以f (0)＝0，即－1＋b2＋a ＝0，解得b ＝1.从而有f (x )＝－2x ＋12x ＋1＋a.又由f (1)＝－f (－1)知－2＋14＋a ＝－－12＋11＋a ，解得a ＝2.(2)由(1)知f (x )＝－2x ＋12x ＋1＋2＝－12＋12x ＋1，由上式易知f (x )在R 上为减函数，又因为f (x )是奇函数，从而不等式f (t 2－2t )＋f (2t 2－k )<0等价于f (t 2－2t )<－f (2t 2－k )＝f (－2t 2＋k )．因为f (x )是R 上的减函数，由上式推得t 2－2t >－2t 2＋k . 即对一切t ∈R 有3t 2－2t －k >0，从而Δ＝4＋12k <0，解得k <－13.故k 的取值范围为⎝⎛⎭⎫－∞，－13.。

指数与指数函数图像及性质(学生版)

指数与指数函数图像及性质【知识要点】 1．根式（1）如果a x n =，那么x 叫做a 的n 次方根.其中1>n ，且*∈N n 。

（2）如果a x n=，当n 为奇数时，n a x =；当n 为偶数时，n a x ±=()0>a .其中n a 叫做根式,n 叫做根指数,a 叫做被开方数. 其中1>n ，且*∈N n 。

(3)()()*∈>==N n n a a nnn ,1,00。

,||,a n a n ⎧=⎨⎩为奇数为偶数其中1>n ，且*∈N n 。

2.分数指数幂(1)正分数指数幂的定义: n m n m a a =()1,,,0>∈>*n N n m a (2)负分数指数幂的定义: nm nm aa1=-()1,,,0>∈>*n Nn m a(3) 要注意四点：①分数指数幂是根式的另一种表示形式； ②根式与分数指数幂可以进行互化； ③0的正分数指数幂等于0； ④0的负分数指数幂无意义。

(4)有理数指数幂的运算性质:①sr sra a a +=⋅()Q s r a ∈>,,0；② ()rs sra a =()Q s r a ∈>,,0；③()r r rb a ab =()Q r b a ∈>>,,0,0.3.无理数指数幂(1)无理数指数幂的值可以用有理数指数幂的值去逼近; (2)有理数指数幂的运算性质同样适用于无理数指数幂。

4．指数函数的概念：一般地，函数()0,1xy a a a =>≠且叫做指数函数，其中x 是自变量，函数的定义域是R 。

5．指数函数的图像与性质第一课时【典例精讲】题型一根式、指数幂的化简与求值1.n a 叫做a 的n 次幂，a 叫做幂的底数，n 叫做幂的指数，规定：1a a =；2. (1,)n a n n N +=>∈,||,a n a n ⎧=⎨⎩为奇数为偶数；3. 1(0,,,)n mnmn a a m n N ma-+=>∈且为既约分数，=a a αβαβ（）. 【例1】计算下列各式的值．（1（2（3；（4)a b >.【变式1】求下列各式的值：（1*1,n n N >∈且）；（2【例2】计算)21313410.027256317--⎛⎫--+-+⎪⎝⎭【变式2】化简34的结果为（）A ．5B ．C ．﹣D ．﹣5【变式3】1332-⎛⎫ ⎪⎝⎭×76⎛⎫- ⎪⎝⎭0＋148＝________.题型二根式、指数幂的条件求值 1. 0a >时，0;b a > 2. 0a ≠时， 01a =； 3. 若,r s a a =则r s =；4. 1111222222()(0,0)a a b b a b a b ±+=±>>； 5. 11112222()()(0,0)a b a b a b a b +-=->>. 【例3】已知11223a a-+=，求下列各式的值.（1）11a a -+；（2）22a a -+；（3）22111a a a a --++++【变式1】已知,a b 是方程2640x x -+=的两根，且0,a b >>的值.【变式2】已知12,9,x y xy +==且x y <，求11221122x y x y-+的值.【变式3】已知11223a a -+=，求33221122a aa a----的值.【变式4】（1）已知122+=xa，求xx xx a a a a --++33；（2）已知a x=+-13，求6322--+-x ax a .【例4】计算下列各式的值：（1）246347625---+-；（2）()2x 3442<--+-x x x ；（3）12121751531311++-+++++++n n ；（4）()54 2222233=++--xxxx x 其中.【变式5】化简或计算出下列各式：（1）121316324(1243)27162(8)--+-+-；（2）化简65312121132ab b a b a ---⎪⎪⎭⎫ ⎝⎛；（3【课堂练习】1. 若()0442-+-a a 有意义,则a 的取值范围是()A.2≥aB.42<≤a 或4>aC. 2≠aD. 4≠a 2. 下列表述中正确的是() A.()()()273336263=-=-=- B.32213421313a a a a a a =⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⋅=⋅ C.无理数指数幂na (n 是无理数)不是一个确定的实数 D.()()()⎩⎨⎧≤-≥=00a a a a a nn3. 已知0>a ,则的值2313123131⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛+--a a a a 为 ()A.3232-+aa B.4 C. 3232--aa D. 4-4. 计算：()=-+-0430625.0833416π ______.【思维拓展】1.化简⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+-----2141811613212121212121的结果是 ( )A.13212121--⎪⎪⎭⎫ ⎝⎛-B.132121--⎪⎪⎭⎫ ⎝⎛- C.32121-- D.⎪⎪⎭⎫ ⎝⎛--3212121第二课时题型三指数函数的概念【例1】已知函数()2()33x f x a a a =-+是指数函数，求实数a 的值。

高中数学必修一课时作业28

课时作业28 指数函数的概念时间：45分钟一、选择题1．若函数f (x )＝(m 2－m －1)a x (a >0，且a ≠1)是指数函数，则实数m ＝( D )A ．2B ．1C ．3D ．2或－1解析：由指数函数的定义，得m 2－m －1＝1，解得m ＝2或－1，故选D.2．若函数f (x )是指数函数，且f (2)＝2，则f (x )＝( A ) A ．(2)xB ．2xC.⎝ ⎛⎭⎪⎫12x D.⎝ ⎛⎭⎪⎪⎫22x解析：由题意，设f (x )＝a x (a >0且a ≠1)，则由f (2)＝a 2＝2，得a ＝2，所以f (x )＝(2)x .3．已知函数f (x )＝⎩⎪⎨⎪⎧a×2x，x≥0，2－x ，x<0(a ∈R )，若f [f (－1)]＝1，则a ＝( A )A.14 B.12 C ．1D ．2解析：∵f (－1)＝2，∴f [f (－1)]＝f (2)＝a ·22＝4a ＝1，∴a ＝14.故选A.4．设函数f (x )＝a －|x |(a >0，且a ≠1)，若f (2)＝4，则( A ) A ．f (－2)>f (－1) B ．f (－1)>f (－2) C ．f (1)>f (2)D ．f (－2)>f (2)解析：f (2)＝a －2＝4，a ＝12，f (x )＝⎝ ⎛⎭⎪⎫12－|x | ＝2|x |，得f (－2)>f (－1)．故选A.5．知f (x )＝2x ＋2－x ，若f (a )＝4，则f (2a )＝( D ) A ．10 B ．12 C ．13D ．14解析：∵f (x )＝2x ＋2－x ，f (a )＝4，∴f (a )＝2a ＋2－a ＝4，∴f (2a )＝22a ＋122a ＝⎝⎛⎭⎪⎫2a ＋12a 2－2＝16－2＝14.6．已知f (x )＝a x ＋b ，a >0，且a ≠1的图象如图所示，则f (3)等于( C )A ．22－2B ．39－3C ．33－3D ．33－3或－33－3解析：由题中图象知，f (0)＝1＋b ＝－2，所以b ＝－3.又f (2)＝a 2－3＝0，所以a ＝3(负值舍去)，故f (x )＝(3)x －3，f (3)＝33－3.7．已知定义在R 上的奇函数f (x )和偶函数g (x )满足f (x )＋g (x )＝a x －a －x＋2(a >0，且a ≠1)．若g (2)＝a ，则f (2)＝( B )A ．2B ．154C.174D ．a 2解析：由已知得f (2)＋g (2)＝a 2－a －2＋2 ①. f (－2)＋g (－2)＝a －2－a 2＋2，由f (x )与g (x )的奇偶性可得－f (2)＋g (2)＝a －2－a 2＋2 ②.由①②解得g (2)＝2，f (2)＝a 2－a －2. 又g (2)＝a ，所以a ＝2，则f (2)＝22－2－2＝154. 8．某乡镇现在人均一年占有粮食360千克，如果该乡镇人口平均每年增长1.2%，粮食总产量平均每年增长4%，那么x 年后，若人均一年占有y 千克粮食，则y 关于x 的解析式为( D )A ．y ＝360⎝⎛⎭⎪⎫1.041.012x －1 B ．y ＝360×1.04xC ．y ＝360×1.04x1.012D ．y ＝360⎝⎛⎭⎪⎫1.041.012x 解析：设该乡镇现在人口数为M ，则该乡镇现在一年的粮食总产量为360M 千克，1年后，该乡镇粮食总产量为360M (1＋4%)千克，人口数为M (1＋1.2%)，则人均占有粮食产量为错误!千克， 2年后，人均占有粮食产量为错误!千克， ……经过x 年后，人均占有粮食产量为错误!千克，即所求解析式为y ＝360⎝⎛⎭⎪⎫1.041.012x . 二、填空题 9．给出下列函数：①y ＝4x ；②y ＝x 4；③y ＝－4x ；④y ＝(－4)x ；⑤y ＝πx ；⑥y ＝4x 2；⑦y ＝x x；⑧y ＝(2a －1)x(a >12且a ≠1)．其中为指数函数的有①⑤⑧(填序号)．解析：本题主要考查指数函数的概念．②中不是指数函数，因为底数不能是自变量；③中是－1与4x 的乘积，不是指数函数；④中底数－4<0，故不是指数函数；⑥中指数不是自变量x ，而是x 2；⑦中底数x 不是常数．由指数函数的概念可知，①⑤⑧中是指数函数．10．已知函数f (x )＝13x ＋1＋a 为奇函数，则a 的值为－12.解析：因为f (x )为奇函数，所以f (－x )＋f (x )＝0，则13－x ＋1＋a ＋13x ＋1＋a ＝0，所以2a ＝－13x ＋1－13－x ＋1＝－3x ＋13x ＋1＝－1，所以a ＝－12. 三、解答题11．设f (x )＝3x，g (x )＝⎝ ⎛⎭⎪⎫13x .计算f (1)与g (－1)，f (π)与g (－π)，f (m )与g (－m )的值，从中你能得到什么结论？解：f (1)＝31＝3，g (－1)＝⎝ ⎛⎭⎪⎫13－1＝3，f (π)＝3π，g (－π)＝⎝ ⎛⎭⎪⎫13－π＝3π，f (m )＝3m，g (－m )＝⎝ ⎛⎭⎪⎫13－m ＝3m .结论：从以上计算的结果看，当两个函数的自变量取值互为相反数时，其函数值相等，即当指数函数的底数互为倒数时，它们的图象关于y 轴对称．12．某车间产生的废气经过过滤后排放，过滤过程中废气的污染物数量P (mg/L)与时间t (h)之间的关系为P ＝P 02－kt (其中P 0表示初始废气中污染物数量)．经过5个小时后，经测试，消除了20%的污染物．问：(1)15小时后还剩百分之几的污染物？ (2)污染物减少36%需要花多长时间？解：(1)由题意得，P ＝P 02－5k ＝(1－20%)P 0，则2－5k ＝0.8，故当t ＝15时，P ＝P 0·2－15k ＝P 0·(2－5k )3＝(80%)3P 0＝51.2%P 0. 故15个小时后还剩51.2%的污染物． (2)由题意，P 02－kt ＝(1－36%)P 0，即(2－5k ) t5 ＝0.64，所以0.8t5＝0.64，所以t5＝2，即t ＝10，故污染物减少36%需要花10 h.13．(多选题)设指数函数f (x )＝a x (a >0，且a ≠1)，则下列等式中正确的是( ABD )A ．f (x ＋y )＝f (x )f (y )B ．f (x －y )＝错误!C ．f ⎝ ⎛⎭⎪⎫x y ＝f (x )－f (y )D ．f (nx )＝[f (x )]n (n ∈Q )解析：f (x ＋y )＝a x ＋y ＝a x a y ＝f (x )f (y )，故A 中的等式正确；f (x －y )＝a x－y ＝a x a －y ＝axay＝错误!，故B 中的等式正确；f 错误!＝a 错误!＝(a x )错误!，f (x )－f (y )＝a x－a y≠(a x)1y，故C 中的等式错误；f (nx )＝a nx ＝(a x )n ＝[f (x )]n ，故D中的等式正确．14．如图所示，面积为8的平行四边形OABC 的对角线AC ⊥CO ，AC 与BO 交于点E .若指数函数y ＝a x (a >0，且a ≠1)的图象经过点E ，B ，则a 等于( A )A.2 B ．3 C ．2D ．3解析：设点C (0，m )(m >0)，则由已知可得A ⎝ ⎛⎭⎪⎫8m ，m ，E ⎝ ⎛⎭⎪⎫4m ，m ，B ⎝ ⎛⎭⎪⎫8m ，2m .②③联立，得m 2－2m ＝0，所以m ＝0(舍)或m ＝2，所以a ＝2.15．已知函数f (x )＝22x 2＋22x ，则f (x )＋f (1－x )＝1；f ⎝ ⎛⎭⎪⎫1101＋f ⎝ ⎛⎭⎪⎫2101＋f⎝ ⎛⎭⎪⎫3101＋…＋f ⎝ ⎛⎭⎪⎫98101＋f ⎝ ⎛⎭⎪⎫99101＋f ⎝ ⎛⎭⎪⎫100101＝50. 解析：因为f (1－x )＝22－2x 2＋22－2x ＝222×22x＋22＝222x ＋2，所以f (x )＋f (1－x )＝1.则原式＝⎣⎢⎡⎦⎥⎤f ⎝ ⎛⎭⎪⎫1101＋f ⎝⎛⎭⎪⎫100101＋⎣⎢⎡⎦⎥⎤f ⎝ ⎛⎭⎪⎫2101＋f ⎝ ⎛⎭⎪⎫99101＋… ＋⎣⎢⎡⎦⎥⎤f ⎝ ⎛⎭⎪⎫50101＋f ⎝ ⎛⎭⎪⎫51101＝50. 16．某化工厂生产一种溶液，按市场要求，杂质含量不能超过0.1%，若初始溶液含杂质2%，每过滤一次可使杂质含量减少13.(1)写出杂质含量y 与过滤次数n 的函数关系式；(2)过滤7次后的杂质含量是多少？过滤8次后的杂质含量是多少？至少应过滤几次才能使产品达到市场要求？解：(1)过滤1次后的杂质含量为2100×⎝⎛⎭⎪⎫1－13＝2100×23；过滤2次后的杂质含量为⎝⎛⎭⎪⎫2100×23×⎝ ⎛⎭⎪⎫1－13＝2100×⎝ ⎛⎭⎪⎫232；过滤3次后的杂质含量为⎣⎢⎡⎦⎥⎤2100×⎝ ⎛⎭⎪⎫232×⎝⎛⎭⎪⎫1－13＝2100×⎝ ⎛⎭⎪⎫233； ……过滤n 次后的杂质含量为2100×⎝ ⎛⎭⎪⎫23n (n ∈N *)．故y 与n 的函数关系式为y ＝2100×⎝ ⎛⎭⎪⎫23n (n ∈N *)．(2)由(1)知，当n ＝7时，y ＝2100×⎝ ⎛⎭⎪⎫237＝6454 675.当n ＝8时，y ＝2100×⎝ ⎛⎭⎪⎫238＝128164 025，因为6454 675>11 000，128164 025<11 000，所以至少应过滤8次才能使产品达到市场要求．。

2020年高考复习数学课时作业17：指数与指数函数 1

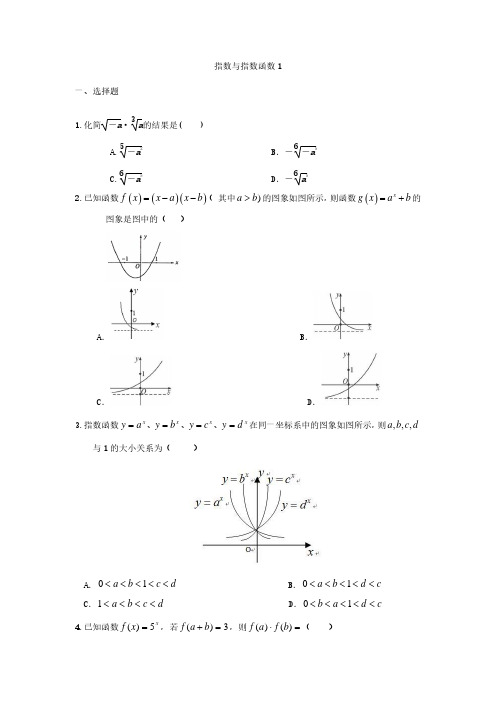
2 【解析】由 x − 8 −2 x 得 x 2或x −4
7.【答案】6
x 【解析】由函数 y = a + b （ a 0 且 a 1 ）过点 (2, 0), (0, −3) 代入表达式得：
a = 2, b = −4 ，所以 a − b = 6
8.【答案】 ( −, −3 【解析】
x 2 − 2 x +1
2 在 (1,3) 上是减函数，且 t = x − 2 x + 1 在 (1,3) 上是增函数，
a +b
= 3 f (a) f (b) = 5a 5b = 5a +b = 3
x 所以函数 y = a 在 ( −, + ) 上是减函数，所以 0 a 1 .由 a 1 得 x 0 ，选 D.
B. {x | x 1}
C.
x
x 0
D. {x | x 0}
二、填空题
x 2－8
6.满足 4 ຫໍສະໝຸດ −2 x 的 x 的取值集合是2
．
7.已知函数 y = a + b （ a 0 且 a 1 ）的图象如下图所示，则 a − b 的值是________．
8.定义
a c
b d
= ad − bc ，如
3.【答案】D 【解析】由 y = c 、 y = d 为增函数可知 c 1, d 1 ，由 y = a 、 y = b 为减函数可知
x x x x
0 a 1, 0 b 1 结合指数函数的渐进性可知 0 b a 1 d c
4.【答案】A 【解析】 f (a + b) = 3 5 5.【答案】D 【解析】因为 f ( x ) = a 二、填空题 6.【答案】 x | x −4或x 2

高中数学人教版A版必修一课时作业及解析：第二章2-1指数函数

∴原式＝－－24x1－≤2x<3 －3<x<1 .
12．解
1
1
1
原式＝
a3
2
a 8b
1
2
a3
2b3
1
1
×a3
4b3 2a3 a 3
a3
13．解 ∵x－ xy－2y＝0，x>0，y>0， ∴( x)2－ xy－2( y)2＝0， ∴( x＋ y)( x－2 y)＝0，由 x>0，y>0 得 x＋ y>0， ∴ x－2 y＝0，∴x＝4y， ∴y2＋x－2 xxyy＝8yy＋－42yy＝65.
6
1
－32>0， 33
<0，C
选项错．故选
D.]
6．B [①中，当 a<0 时，
a2
3 2
a2
1 2
3
＝(－a)3＝－a3，
∴①不正确；
②中，若 a＝－2，n＝3，
则3 －23＝－2≠|－2|，∴②不正确；
x－2≥0， ③中，有3x－7≠0，
即 x≥2 且 x≠73，
故定义域为[2，73)∪(73，＋∞)，∴③不正确； ④中，∵100a＝5,10b＝2， ∴102a＝5,10b＝2,102a×10b＝10，即 102a＋b＝10.
1 2
3
xy
1 2
·(xy)－1
12
＝ x3 ·y 3
1
x6
y
1 6
x
1 2
y
1 2
＝x1 3·x1 31，＝－1，x<0
x>0
.
(2)原式＝ 1 ＋ 1 ＋ 2＋1－22 22
＝2 2－3.

2019年高考数学一轮复习课时作业第8讲指数与指数函数文

课时作业(八)第8讲指数与指数函数时间/ 30分钟分值/ 80分基础热身1.若3x=a,5x=b,则45x等于 ()A. a2bB. ab2C. a2+bD. a2+b22.函数f(x)=的大致图像是()A B C D图K8-13.[2017·南平模拟]已知a=,b=,c=,则a,b,c的大小关系是()A. c<a<bB. a<b<cC. b<a<cD. c<b<a4.计算= .5.不等式>的解集为.能力提升6.下列函数中,满足“f(x-y)=f(x)÷f(y)”的单调递减函数是()A. f(x)=x3B. f(x)=4xC. f(x)=D. f(x)=7.[2017·福州模拟]已知实数a≠1,函数f(x)=若f(1-a)=f(a-1),则a的值为()A. B.C. D.8.[2017·安阳模拟]已知函数f(x)=a x(a>0且a≠1),如果以P(x1,f(x1)),Q(x2,f(x2))为端点的线段的中点在y轴上,那么f(x1)·f(x2)等于()A. 1B. aC. 2D. a29.已知函数y=在区间(-∞,3)上单调递增,则a的取值范围为()A. (-∞,3]B. (-∞,6]C. [3,+∞)D. [6,+∞)10.当x∈(-∞,-1]时,不等式(m2-m)·4x-2x<0恒成立,则实数m的取值范围是()A. (-1,2)B. (1,2)C. (1,+∞)D. (2,+∞)11.若f(x)=,g(x)=,则下列等式不正确的是 ()A. f(2x)=2[g(x)]2+1B. [f(x)]2-[g(x)]2=1C. [f(x)]2+[g(x)]2=f(2x)D. f(x+y)=f(x)f(y)-g(x)g(y)12.已知函数f(x)=a2x-4+n(a>0且a≠1)的图像恒过定点P(m,2),则m+n= .13.[2017·安徽江淮十校联考]已知max{a,b}表示a,b两数中的较大值.若f(x)=max{e|x|,e|x-2|},则f(x)的最小值为.14.设f(x)=则f= .难点突破15.(5分)已知函数f(x)=2x-2-x,若不等式f(x2-ax+a)+f(3)>0对任意实数x恒成立,则实数a 的取值范围是()A. -2<a<4B. -2<a<6C. -6<a<2D. -6<a<416.(5分)若函数f(x)=(a>0且a≠1)的值域是[2,+∞),则实数a的取值范围是.课时作业(八)1. A[解析] 45x=9x×5x=(3x)2×5x=a2b,故选A.2. D[解析] 因为f(x)==结合图像可知选项D正确.3. D[解析] 由指数函数y=的性质及-<-,可得a=>b=>1.由指数函数y=的性质及-<0,可得c=<1,所以c<b<a.故选D.4.[解析] 原式===.5. {x|-1<x<4}[解析] 不等式>化为>,因为y=是减函数,所以x2-2x<x+4,即x2-3x-4<0,解得-1<x<4.6.D[解析] 验证可知,指数函数f(x)=4x,f(x)=满足f(x-y)=f(x)÷f(y),因为f(x)=4x 是增函数,f(x)=是减函数,所以选D.7. B[解析] 当a<1时,41-a=21,所以a=;当a>1时,4a-1=22a-1,无解.故选B.8. A[解析] 因为以P(x1,f(x1)),Q(x2,f(x2))为端点的线段的中点在y轴上,所以x1+x2=0.又因为f(x)=a x,所以f(x1)·f(x2)=·==a0=1.9. D[解析] 函数y=是由函数y=2t和t=-x2+ax+1复合而成的.因为函数t=-x2+ax+1在区间上单调递增,在区间上单调递减,且函数y=2t在R上单调递增,所以函数y=在区间上单调递增,在区间上单调递减.又因为函数y=在区间(-∞,3)上单调递增,所以3≤,即a≥6.故选D.10. A[解析] 原不等式变形为m2-m<,因为函数y=在(-∞,-1]上是减函数,所以≥=2,当x∈(-∞,-1]时,m2-m<恒成立等价于m2-m<2,解得-1<m<2.故选A.11. D[解析] f(2x)=,2[g(x)]2+1=2×+1=,即f(2x)=2[g(x)]2+1,A中等式正确;[f(x)]2-[g(x)]2=1,B中等式正确;[f(x)]2+[g(x)]2==f(2x),C中等式正确;f(x)f(y)-g(x)g(y)=×-×==,f(x+y)= ,显然不相等,所以D中等式不正确.故选D.12. 3[解析] 当2x-4=0,即x=2时,y=1+n,即函数图像恒过点(2,1+n),又函数图像恒过定点P(m,2),所以m=2,1+n=2,即m=2,n=1,所以m+n=3.13. e[解析] f(x)=当x≥1时,f(x)=e x≥e(当x=1时,取等号);当x<1时,f(x)=e|x-2|=e2-x>e.因此f(x)的最小值为f(1)=e.14. 2+2016[解析] f=f+2=f+4=…=f+2016=+2016=2+2016.15. B[解析] 因为y=2x,y=2-x在R上分别为增函数、减函数,所以f(x)=2x-2-x为增函数.因为f(-x)=2-x-2x=-f(x),所以f(x)为R上的奇函数.因为f(x2-ax+a)+f(3)>0,所以f(x2-ax+a)>-f(3)=f(-3),得x2-ax+a>-3,所以x2-ax+a+3>0恒成立,所以(-a)2-4×1×(a+3)<0,所以a2-4a-12<0,解得-2<a<6.16. (1,][解析] 当x≤2时,f(x)≥=2,此时函数的值域为[2,+∞);当x>2且a>1时,f(x)>log a2,此时函数值域为(log a2,+∞),由(log a2,+∞)⊆[2,+∞),得log a2≥2,解得1<a≤;当x>2且0<a<1时,f(x)<log a2,不合题意.所以实数a的取值范围是(1,].。

高一数学上册课时练习题一次函数与二次函数模型、指数函数(答案含解析)

课时作业(二十六)一次函数与二次函数模型、指数函数与对数函数模型1．一天，亮亮发烧了，早晨他烧得很厉害，吃过药后感觉好多了，中午时亮亮的体温基本正常，但是下午他的体温又开始上升，直到半夜亮亮才感觉身上不那么发烫．下列各图中能基本上反映出亮亮这一天(0时～24时)体温的变化情况的是()答案：C解析：观察图象A，体温逐渐降低，不合题意；图象B不能反映“下午体温又开始上升”；图象D不能体现“下午体温又开始上升”与“直到半夜才感觉身上不那么发烫”．故选C.2．某城市出租汽车的收费标准是：起步价为6元，行程不超过2千米者均按此价收费；行程超过2千米，超过部分按3元/千米收费(不足1千米按1千米计价)；另外，遇到堵车或等候时，汽车虽没有行驶，但仍按6分钟折算1千米计算(不足1千米按1千米计价)．陈先生坐了一趟这种出租车，车费24元，车上仪表显示等候时间为11分30秒，那么陈先生此趟行程的取值范围是( )A ．[5,6)B ．(5,6]C ．[6,7)D ．(6,7]答案：B 解析：设陈先生此趟行程为x 千米(x ∈Z )，则6＋(x －2)×3＋2×3＝24，得x ＝6.故实际行程应属于区间(5,6]．3．生产一定数量的商品的全部费用称为生产成本，某企业一个月生产某种商品x 万件时的生产成本为C (x )＝12x 2＋2x ＋20(万元).1万件售价是20万元，为了获取更大利润，该企业一个月应生产该商品数量为( )A ．18万件B ．20万件C ．16万件D ．8万件答案：A 解析：利润L (x )＝20x －C (x )＝－12(x －18)2＋142，当x＝18时，L (x )有最大值．4．若镭经过100年后剩留原来质量的95.76%，设质量为1的镭经过x 年后剩留量为y ，则x ，y 的函数关系是( )A ．y ＝(0.957 6) x 100B ．y ＝(0.957 6)100xC ．y ＝⎝ ⎛⎭⎪⎫0.957 6100x D ．y ＝1－(0.042 4) x 100答案：A 解析：设镭一年放射掉其质量的t %，则有95.76%＝1·(1－t %)100，t %＝1－⎝ ⎛⎭⎪⎫95.761001100 ， ∴y ＝(1－t %)x ＝(0.957 6) x 100 .5．把长为12 cm 的细铁丝截成两段，各自围成一个正三角形，那么这两个正三角形面积之和的最小值是( ) A.332 cm 2B ．4 cm 2C ．3 2 cm 2D ．2 3 cm 2答案：D 解析：设其中一段长为x cm ，则另一段长为(12－x )cm.∴S ＝34⎝ ⎛⎭⎪⎫x 32＋34⎝ ⎛⎭⎪⎫4－x 32＝318(x －6)2＋23≥2 3. 6．某工厂生产某产品x 吨所需费用为P 元，而卖出x 吨的价格为每吨Q 元，已知P ＝1 000＋5x ＋110x 2，Q ＝a ＋x b ，若生产出的产品能全部卖出，且当产量为150吨时利润最大，此时每吨的价格为40元，则有( )A ．a ＝45，b ＝－30B ．a ＝30，b ＝－45C ．a ＝－30，b ＝45D ．a ＝－45，b ＝－30答案：A 解析：设生产x 吨产品全部卖出，获利润为y 元，则y ＝xQ －P ＝x ⎝⎛⎭⎪⎫a ＋x b －⎝ ⎛⎭⎪⎫1 000＋5x ＋110x 2 ＝⎝ ⎛⎭⎪⎫1b －110x 2＋(a －5)x －1 000(x ＞0)．由题意，当x ＝150时，y 取最大值，此时Q ＝40，∴⎩⎪⎨⎪⎧ －a －52⎝ ⎛⎭⎪⎫1b －110＝150，a ＋150b ＝40，解得⎩⎨⎧ a ＝45，b ＝－30.7．衣柜里的樟脑丸，随着时间会挥发而体积缩小，刚放进的新丸体积为a ，经过t 天后体积V 与天数t 的关系式为V ＝a ·e －kt .已知新丸经过50天后，体积变为49a .若一个新丸体积变为827a ，则需经过的天数为( )A ．125B ．100C ．75D ．50答案：C 解析：由已知，得49a ＝a ·e －50k ，∴e －k ＝⎝ ⎛⎭⎪⎫49150 . 设经过t 1天后，一个新丸体积变为827a ，则827a ＝a ·e －kt 1，∴827＝(e －k )t 1＝⎝ ⎛⎭⎪⎫49t 150 ，∴t 150＝32，t 1＝75. 二、填空题8．如图所示，某池塘中浮萍蔓延的面积y (m 2)与时间t (月)的关系为y ＝a t ，有以下几种说法：①这个指数函数的底数为2；②第5个月时，浮萍面积就会超过30 m 2；③浮萍从4 m 2蔓延到12 m 2需要经过1.5个月；④浮萍每月增加的面积都相等．其中所有正确命题的序号是________．答案：①② 解析：由图象，t ＝2时，y ＝4，∴a 2＝4，故a ＝2，①正确；当t ＝5时，y ＝25＝32＞30，②正确；当y ＝4时，由4＝2 t 1，知t 1＝2，当y ＝12时，由12＝2 t 2，知t 2＝log 212＝2＋log 23，t 2－t 1＝log 23≠1.5，故③错误；浮萍每月增长的面积不相等，实际上增长速度越来越快，④错误．9．已知大气压P (百帕)与海拔高度h (米)的关系式为P ＝1000·⎝ ⎛⎭⎪⎫7100h 3 000 ，则海拔6 000米处的大气压为________百帕．答案：4.9 解析：将h ＝6 000，代入P ＝1 000·⎝ ⎛⎭⎪⎫7100h 3 000 ，得P ＝1 000×⎝ ⎛⎭⎪⎫71002＝4.9(百帕)． 10．一个人喝了少量酒后，血液中的酒精含量迅速上升到0.3 mg/mL ，在停止喝酒后，血液中的酒精含量以每小时25%的速度减少，为了保障交通安全，某地根据《道路交通安全法》规定：驾驶员血液中的酒精含量不得超过0.09 mg/mL ，那么，一个喝了少量酒后的驾驶员，至少经过________小时才能开车．(精确到1小时)答案：5 解析：设至少经过x 小时才能开车，由题意，得0.3(1－25%)x ≤0.09，∴0.75x ≤0.3，x ≥log 0.750.3≈5.三、解答题11．如图，△OAB 是边长为2的正三角形，记△OAB 位于直线x ＝t (t >0)左侧的图形的面积为f (t )，试求函数f (t )的解析式．解：OB 所在的直线方程为y ＝3x .当x ∈(0,1]时，由x ＝t ，求得y ＝3t ，所以f (t )＝32t 2；当t ∈(1,2]时，f (t )＝3－32(2－t )2；当t ∈(2，＋∞)时，f (t )＝ 3.∴f (t )＝⎩⎪⎨⎪⎧ 32t 2，t ∈(0，1]，3－32(2－t )2，t ∈(1，2]，3，t ∈(2，＋∞).12．大西洋鲑鱼每年都要逆流而上，游回产地产卵．记鲑鱼的游速为v (m/s)，鲑鱼的耗氧量的单位数为Q ，研究中发现v 与log 3Q 100成正比，且当Q ＝900时，v ＝1.(1)求出v 关于Q 的函数解析式；(2)计算一条鲑鱼的游速是1.5 m/s 时耗氧量的单位数；(3)一条鲑鱼要想把游速提高1 m/s ，其耗氧量的单位数应怎样变化？解：(1)设v ＝k ·log 3Q 100，∵当Q ＝900时，v ＝1，∴1＝k ·log 3900100，∴k ＝12，∴v 关于Q 的函数解析式为v ＝12log 3Q 100.(2)令v ＝1.5，则1.5＝12log 3Q 100，∴Q ＝2 700，故一条鲑鱼的游速是1.5 m/s 时耗氧量为2 700个单位．(3)设鲑鱼耗氧量为Q 1，Q 2时，游速分别为v 1，v 2，由题意v 2－v 1＝1，即12log 3Q 2100－12log 3Q 1100＝1.∴12log 3Q 2Q 1＝1，∴Q 2Q 1＝9，即Q 2＝9Q 1. 故鲑鱼要想把游速提高1 m/s ，其耗氧量单位数应变为原来的9倍．13．某渔场鱼群的最大养殖量为8吨，为保证鱼群的生长空间，实际的养殖量x 要小于8，留出适当的空闲量，空闲量与最大养殖量的比值叫空闲率．已知鱼群的年增加量y (吨)和实际养殖量x (吨)与空闲率的乘积成正比，设比例系数k >0.(1)写出y 与x 的函数关系式，并指出定义域；(2)求鱼群年增长量的最大值；(3)当鱼群年增长量达到最大值时，求k 的取值范围．解：(1)已知实际养殖量为x 吨，年增长量为y 吨，则空闲量为(8－x )吨，空闲率为8－x 8，由此可以建立目标函数y ＝k ·x ·8－x 8＝－k 8x 2＋kx (k >0)．所以y 关于x 的函数关系式为y ＝－k 8x 2＋kx ，定义域为(0,8)．(2)y ＝－k 8x 2＋kx ＝－k 8(x －4)2＋2k ，又x ∈(0,8)．所以当x ＝4时，y 有最大值2k .即当实际养殖量为4吨时，鱼群的年增长量达到最大值，为2k 吨．(3)由题意得0<2k ＋4<8，解得－2<k <2，又k >0，于是0<k <2.所以k 的取值范围是(0,2)．尖子生题库14．已知甲、乙两个工厂在今年的1月份的利润都是6万元，且乙厂在2月份的利润是8万元．若甲、乙两个工厂的利润(万元)与月份x 之间的函数关系式分别符合下列函数模型：f (x )＝a 1x 2－4x ＋6(a 1∈R )，g (x )＝a 23x ＋b (a 2，b ∈R )．(1)求函数f (x )与g (x )的解析式；(2)求甲、乙两个工厂今年5月份的利润；(3)在同一直角坐标系下画出函数f (x )与g (x )的草图，并根据草图比较今年1至10月份甲、乙两个工厂的利润的大小情况．解：(1)依题意，由f (1)＝6，解得a 1＝4，∴ f (x )＝4x 2－4x ＋6.又⎩⎪⎨⎪⎧ g (1)＝6，g (2)＝8，即⎩⎪⎨⎪⎧ 3a 2＋b ＝6，9a 2＋b ＝8，解得⎩⎨⎧ a 2＝13，b ＝5，∴g (x )＝13×3x ＋5＝3x －1＋5.(2)由(1)知甲厂在今年5月份的利润为f (5)＝4×52－4×5＋6＝＝86(万元)，乙厂在今年5月份的利润为g (5)＝35－1＋5＝86(万元)，故有f (5)＝g (5)，即甲、乙两个工厂今年5月份的利润相等．(3)作函数图象如下．从图中可以看出，今年1至10月份甲、乙两个工厂的利润大小情况：当x＝1或x＝5时，有f(x)＝g(x)；当1<x<5时，有f(x)>g(x)；当5<x≤10时，有f(x)<g(x)．。

课时作业8：2.5 指数与指数函数

2.5 指数与指数函数一、选择题(每小题5分，共30分)1．若点(a,9)在函数y ＝3x的图象上，则tan a π6的值为( ) A ．0 B.33 C ．1 D.32．设a ＝22.5，b ＝2.50，c ＝⎝⎛⎭⎫12 2.5，则a ，b ，c 的大小关系是( ) A ．a ＞c ＞bB ．c ＞a ＞bC ．a ＞b ＞cD ．b ＞a ＞c 3．函数y ＝⎝⎛⎭⎫12 2x －x2的值域为( )A.⎣⎡⎭⎫12，＋∞B.⎝⎛⎦⎤－∞，12C.⎝⎛⎦⎤0，12D ．(0,2] 4．若函数y ＝a x ＋b 的图象如图2－5－1，则函数y ＝1x ＋a ＋b ＋1的图象为（）图2－5－15．(2014·济南模拟)若函数f (x )＝⎝⎛⎭⎫a ＋1e x －1cos x 是奇函数，则常数a 的值等于( )A ．－1B ．1C ．－12 D.126．(2013·课标全国卷Ⅱ)若存在正数x 使2x (x －a )＜1成立，则a 的取值范围是( ) A ．(－∞，＋∞)B ．(－2，＋∞)C ．(0，＋∞)D ．(－1，＋∞)二、填空题(每小题5分，共15分)7．已知函数f (x )＝⎩⎪⎨⎪⎧f x ＋2，x ＜2⎝⎛⎭⎫12x ，x ＞2则f (－3)的值为________．8．若函数f (x )＝a x (a >0，a ≠1)在[－1,2]上的最大值为4，最小值为m ，且函数g (x )＝(1－4m )x 在[0，＋∞)上是增函数，则a ＝________.9．已知0≤x ≤2，则y ＝4x－12－3·2x ＋5的最大值为________．三、解答题(本大题共3小题，共35分)10．(10分)(1)计算：；(2)化简：(式中字母都是正数)．11．(12分)已知函数f (x )＝2a ·4x －2x －1.(1)当a ＝1时，求函数f (x )在x ∈[－3,0]的值域；(2)若关于x 的方程f (x )＝0有解，求a 的取值范围．12．(13分)设函数f (x )＝ka x －a －x (a ＞0且a ≠1)是定义域为R 的奇函数；(1)若f (1)＞0，试求不等式f (x 2＋2x )＋f (x －4)＞0的解集；(2)若f (1)＝32，且g (x )＝a 2x ＋a －2x －4f (x )，求g (x )在[1，＋∞)上的最小值．答案一、选择题(每小题5分，共30分)1．【答案】 D2．【答案】 C3．【答案】 A4．【答案】 C5．【答案】 D6．【答案】 D二、填空题(每小题5分，共15分)7．【答案】 188．【答案】 149．【答案】 52三、解答题(本大题共3小题，共35分)10．【答案】 (1)原式＝＝⎝ ⎛⎭⎪⎫49－73＋25×152×4210÷12＝⎝⎛⎭⎫－179＋2×2＝29.＝a 13×a ×a 23＝a 2.11．【答案】 (1)当a ＝1时，f (x )＝2·4x －2x －1＝2(2x )2－2x －1，令t ＝2x，x ∈[－3,0]，则t ∈⎣⎡⎦⎤18，1. 故y ＝2t 2－t －1＝2⎝⎛⎭⎫t －142－98，t ∈⎣⎡⎦⎤18，1，故值域为⎣⎡⎦⎤－98，0 (2)关于x 的方程2a (2x )2－2x －1＝0有解，等价于方程2ax 2－x －1＝0在(0，＋∞)上有解．解法一：记g (x )＝2ax 2－x －1，当a ＝0时，解为x ＝－1＜0，不成立．当a ＜0时，开口向下，对称轴x ＝14a ＜0，过点(0，－1)，不成立．当a ＞0时，开口向上，对称轴x ＝14a ＞0，过点(0，－1)，必有一个根为正，所以，a＞0.解法二：方程2ax 2－x －1＝0可化为a ＝x ＋12x 2＝12⎝⎛⎭⎫1x ＋122－18，∴a 的范围即为函数g (x )＝12⎝⎛⎭⎫1x ＋122－18在(0，＋∞)上的值域所以，a ＞0.12．【答案】 ∵f (x )是定义域为R 的奇函数，∴f (0)＝0，∴k －1＝0，∴k ＝1.(1)∵f (1)＞0，∴a －1a ＞0，又a ＞0且a ≠1，∴a ＞1，f (x )＝a x －a －x ，而当a ＞1时，y ＝a x 和y ＝－a －x 在R 上均为增函数， ∴f (x )在R 上为增函数，原不等式化为：f (x 2＋2x )＞f (4－x )，∴x 2＋2x ＞4－x ，即x 2＋3x －4＞0，∴x ＞1或x ＜－4，∴不等式的解集为{x |x ＞1或x ＜－4}．(2)∵f (1)＝32，∴a －1a ＝32，即2a 2－3a －2＝0，∴a ＝2或a ＝－12(舍去)， ∴g (x )＝22x ＋2－2x －4(2x －2－x )＝(2x －2－x )2－4(2x －2－x )＋2.令t ＝2x －2－x (x ≥1)，则t ＝h (x )在[ 1，＋∞)上为增函数(由(1)可知)，即h (x )≥h (1)＝32.∴g (t )＝t 2－4t ＋2＝(t －2)2－2，∴当t ＝2时，g (x )min ＝－2，此时x ＝log 2(1＋2)，当x ＝log 2(1＋2)时，g (x )有最小值－2.。

高考数学总复习课时作业8 指数与指数函数理北师大版

课时作业(八) 指数与指数函数A 级1．下列函数中值域为正实数集的是( ) A ．y ＝－5xB ．y ＝⎝ ⎛⎭⎪⎫131－xC ．y ＝⎝ ⎛⎭⎪⎫12x －1 D ．y ＝1－2x2．当x >0时，函数f (x )＝(a 2－1)x的值总大于1，则实数a 的取值范围是( ) A ．1<|a |<2 B ．|a |<1 C ．|a |> 2D ．|a |< 23．已知f (x )＝2x＋2－x，若f (a )＝3，则f (2a )等于( ) A ．5 B ．7 C ．9 D ．114．函数f (x )＝a|x ＋1|(a >0，a ≠1)的值域为[1，＋∞)，则f (－4)与f (1)的关系是( )A ．f (－4)>f (1)B ．f (－4)＝f (1)C ．f (－4)<f (1)D ．不能确定5．函数y ＝⎝ ⎛⎭⎪⎫122x －x 2的值域为( )A.⎣⎢⎡⎭⎪⎫12，＋∞B.⎝ ⎛⎦⎥⎤－∞，12C.⎝ ⎛⎦⎥⎤0，12 D ．(0,2]6．当x ∈[－2,0]时，函数y ＝3x ＋1－2的值域是________．7．已知正数a 满足a 2－2a －3＝0，函数f (x )＝a x，若实数m 、n 满足f (m )>f (n )，则m 、n 的大小关系为________．8．函数f (x )＝ax 2＋2x －3＋m (a >1)恒过点(1,10)，则m ＝________.9．函数y ＝|2x－1|在区间(k －1，k ＋1)内不单调，则k 的取值范围是________． 10．化简下列各式(其中各字母均为正数)．11．已知函数f (x )＝⎝ ⎛⎭⎪⎫23|x |－a .(1)求f (x )的单调区间；(2)若f (x )的最大值等于94，求a 的值．B 级1．(2011·湖北卷)已知定义在R 上的奇函数f (x )和偶函数g (x )满足f (x )＋g (x )＝a x－a －x＋2(a >0，且a ≠1)．若g (2)＝a ，则f (2)＝( )A ．2B.154C.174D ．a 22．若函数y ＝2|1－x |＋m 的图像与x 轴有公共点，则m 的取值范围是________．3．已知函数f (x )＝3x，f (a ＋2)＝18，g (x )＝λ·3ax－4x的定义域为[0,1]． (1)求a 的值；(2)若函数g (x )在区间[0,1]上是单调递减函数，求实数λ的取值范围．详解答案课时作业(八)A 级1．B ∵1－x ∈R ，y ＝⎝ ⎛⎭⎪⎫13x的值域是正实数集，∴y ＝⎝ ⎛⎭⎪⎫131－x的值域是正实数集．2．C ∵x >0时，f (x )＝(a 2－1)x的值总大于1， ∴a 2－1>1，∴a 2>2，∴|a |> 2. 3．B 由f (a )＝3得2a ＋2－a＝3，两边平方得22a＋2－2a＋2＝9，即22a＋2－2a＝7，故f (2a )＝7，选B.4．A 由题意知a >1，∴f (－4)＝a 3，f (1)＝a 2，由单调性知a 3>a 2， ∴f (－4)>f (1)，故选A.5．A ∵2x －x 2＝－(x －1)2＋1≤1，又y ＝⎝ ⎛⎭⎪⎫12t在R 上为减函数，∴y ＝⎝ ⎛⎭⎪⎫122x －x 2≥⎝ ⎛⎭⎪⎫121＝12，即值域为⎣⎢⎡⎭⎪⎫12，＋∞.6．解析： ∵x ∈[－2,0]时y ＝3x ＋1－2为增函数，∴3－2＋1－2≤y ≤30＋1－2，即－53≤y ≤1.答案： ⎣⎢⎡⎦⎥⎤－53，1 7．解析： ∵a 2－2a －3＝0，∴a ＝3或a ＝－1(舍)．函数f (x )＝a x在R 上递增，由f (m )>f (n )得m >n . 答案： m >n8．解析： f (x )＝ax 2＋2x －3＋m ，在x 2＋2x －3＝0时，过定点(1,1＋m )或(－3,1＋m )，∴1＋m ＝10，解得m ＝9.答案： 99．解析：由于函数y ＝|2x－1|在(－∞，0)内单调递减，在(0，＋∞)内单调递增，而函数在区间(k －1，k ＋1)内不单调，所以有k －1<0<k ＋1，解得－1<k <1.答案： (－1,1)10．解析： (1)原式＝(2)原式＝＋10.12＋－3＋3748＝53＋100＋916－3＋3748＝100.11．解析： (1)令t ＝|x |－a ，则f (x )＝⎝ ⎛⎭⎪⎫23t，不论a 取何值，t 在(－∞，0]上单调递减，在[0，＋∞)上单调递增，又y ＝⎝ ⎛⎭⎪⎫23t是单调递减的，因此f (x )的单调递增区间是(－∞，0]，单调递减区间是[0，＋∞)；(2)由于f (x )的最大值是94，且94＝⎝ ⎛⎭⎪⎫23－2，所以g (x )＝|x |－a 应该有最小值－2，从而a ＝2.B 级1．B ∵f (x )是奇函数，g (x )是偶函数， ∴由f (x )＋g (x )＝a x －a －x＋2① 得－f (x )＋g (x )＝a －x－a x＋2，②①＋②，得g (x )＝2，①－②得f (x )＝a x－a －x，又g (2)＝a ，∴a ＝2，∴f (x )＝2x －2－x， ∴f (2)＝22－2－2＝154.2．解析：由y ＝2|1－x |与y ＝－m 的图像知m ≤－1.答案： (－∞，－1]．3．解析：方法一：(1)由已知得3a ＋2＝18⇒3a＝2⇒a ＝log 32.(2)此时g (x )＝λ·2x－4x，设0≤x 1<x 2≤1，因为g(x)在区间[0,1]上是单调递减函数，所以g(x1)－g(x2)＝(2x1－2x2)(λ－2x2－2x1)>0恒成立，即λ<2x2＋2x1恒成立．由于2x2＋2x1>20＋20＝2，所以，实数λ的取值范围是λ≤2.方法二：(1)由已知得3a＋2＝18⇒3a＝2⇒a＝log32.(2)此时g(x)＝λ·2x－4x，因为g(x)在区间[0,1]上是单调减函数，所以有g′(x)＝λln 2·2x－ln 4·4x＝2x ln 2·(－2·2x＋λ)≤0成立，所以只需要λ≤2·2x恒成立．所以实数λ的取值范围是λ≤2.。

新教材高中数学指数函数的图象和性质第2课时指数函数的图象和性质的综合应用课时作业新人教A版必修第一册

第2课时指数函数的图象和性质的综合应用必备知识基础练1．函数f (x )＝(a －1)x是R 上的单调减函数,则a 的取值范围是( ) A ．a >2 B ．1<a <2 C ．0<a <1 D ．a >12．已知指数函数f (x )＝(2a 2－5a ＋3)a x在(0,＋∞)上单调递增,则实数a 的值为( ) A ．12 B ．1 C ．32D ．2 3．下列不等式中成立的是( ) A ．1.12.1<1.11.9B ．0.82.1<0.81.9C ．0.82.1>1.11.9D ．1.12.1<0.82.14．[2022·广东汕尾高一期末]若a ＝(12)13,b ＝(14)13,c ＝(12)14,则( )A ．c >a >bB ．c >b >aC ．b >c >aD ．a >b >c5．[2022·江苏宿迁高一期末]函数f (x )＝x 22x＋2－x的图象大致是( )6．(多选)已知函数f (x )＝e x－e －x,则下列说法正确的是( ) A ．函数f (x )是奇函数 B ．函数f (x )是偶函数 C ．函数f (x )在R 上是减函数 D ．函数f (x )在R 上是增函数7．函数f (x )＝2|x |的递增区间是________． 8．已知a ＝5＋12,函数f (x )＝a x,若实数m 、n 满足f (m )>f (n ),则m 、n 的大小关系为________．关键能力综合练1．已知函数y ＝(a －2)x,且当x <0时,y >1,则实数a 的取值范围是( ) A ．a >3 B ．2<a <3 C ．a >4 D ．3<a <42．若(13)2a ＋1>(13)4－a,则实数a 的取值范围是( )A ．(－∞,1)B ．(1,＋∞)C ．(3,＋∞)D ．(－∞,3)3．已知实数x ,y 满足(12)x <(12)y,则下列关系式中恒成立的是( )A.x 2>y 2B ．πx >πyC ．1x <1yD ．x >y4．已知函数f (x )＝⎩⎪⎨⎪⎧（2－a ）x ＋1，x ≥1a x ，x <1是R 上的单调递增函数,则实数a 的取值范围是( )A ．a >1B ．1<a <32C ．1<a <2D ．1<a ≤325．设14<(14)b <(14)a<1,那么( )A ．a a<a b<b aB ．a a<b a<a bC ．a b<a a<b aD ．a b<b a<a a6．[2022·重庆九龙坡高一期末](多选)已知函数f (x )＝2x－12x ＋1,则下列结论正确的是( )A ．函数f (x )的定义域为R B.函数f (x )的值域为(－1,1)C ．函数f (x )的图象关于y 轴对称D ．函数f (x )在R 上为增函数7．若f (x )＝a 2x －1＋12是奇函数．则实数a 的值是________.8．函数f (x )＝(12)x2－2x －3的单调减区间是________．9．[2022·湖南邵阳高一期末]已知函数f (x )＝a 3－x,(a 为常数,a >0且a ≠1),若f (2)＝3.(1)求a 的值； (2)解不等式f (x )>9.10．[2022·广东广州高一期末]已知f (x )＝a ·2x ＋a －22x＋1是定义在R 上的奇函数．(1)求实数a 和f (1)的值；(2)根据单调性的定义证明：f (x )在定义域上为增函数．核心素养升级练1．(多选)设函数f (x )＝2x,对于任意的x 1,x 2(x 1≠x 2),下列命题中正确的是( ) A ．f (x 1＋x 2)＝f (x 1)·f (x 2) B ．f (x 1·x 2)＝f (x 1)＋f (x 2) C ．f （x 1）－f （x 2）x 1－x 2<0D ．f (x 1＋x 22)<f （x 1）＋f （x 2）22．写出一个同时具有下列性质①②③的函数f (x )＝________． ①定义域为R ； ②值域为(－∞,1)；③对任意x 1,x 2∈(0,＋∞)且x 1≠x 2,均有f （x 1）－f （x 2）x 1－x 2>0.3．[2022·湖北十堰高一期末]已知函数f (x )＝2a ＋2x ＋11＋2x .(1)当a ＝6时,求方程f (x )＝2x的解；(2)若对任意x ∈(0,＋∞),不等式f (x )≥a 恒成立,求a 的取值范围．第2课时指数函数的图象和性质的综合应用必备知识基础练1．答案：B解析：函数f (x )＝(a －1)x是R 上的单调减函数, 所以0<a －1<1,解得1<a <2. 2．答案：D解析：由题得2a 2－5a ＋3＝1,∴2a 2－5a ＋2＝0,∴a ＝2或a ＝12.当a ＝2时,f (x )＝2x在(0,＋∞)上单调递增,符合题意；当a ＝12时,f (x )＝(12)x在(0,＋∞)上单调递减,不符合题意．所以a ＝2. 3．答案：B解析：A.因为y ＝1.1x 在R 上是增函数,所以1.12.1>1.11.9,故错误； B ．因为y ＝0.8x 在R 上是减函数,所以0.82.1<0.81.9,故正确； C ．因为0.82.1<1,1.11.9>1,所以0.82.1<1.11.9,故错误； D ．因为1.12.1>1,0.82.1<1,所以1.12.1>0.82.1,故错误． 4．答案：A解析：b ＝(14)13＝(12)23,因为y ＝(12)x 在R 上为减函数,且14<13<23,所以(12)14>(12)13>(12)23,所以c >a >b .5．答案：C 解析：x ∈R ,f (－x )＝x 22－x＋2x＝f (x ),所以f (x )为偶函数,图象关于y 轴对称,排除选项AB ；当x >0时,f (x )＝x 22－x ＋2x >0,故D 错误．6．答案：AD解析：f (－x )＝e －x－e x ＝－f (x ),函数f (x )＝e x －e －x的定义域为R , 函数f (x )是奇函数,A 正确,B 错误；y ＝e x 为R 上的增函数,y ＝e －x 为R 上的减函数,则函数f (x )＝e x－e －x为R 上的增函数,C 错误,D 正确． 7．答案：(0,＋∞)解析：因为f (x )＝2|x |＝⎩⎪⎨⎪⎧2x，x >0（12）x ，x ≤0,故函数f (x )的单调递增区间为(0,＋∞).8．答案：m >n 解析：∵a ＝5＋12>1,所以,函数f (x )＝a x为R 上的增函数, ∵f (m )>f (n ),∴m >n .关键能力综合练1．答案：B解析：∵当x <0时,y >1,∴0<a －2<1,解得2<a <3. 2．答案：A解析：因为函数y ＝(13)x在R 上为减函数,∴(13)2a ＋1>(13)4－a,等价于2a ＋1<4－a ,解得a <1, 所以实数a 的取值范围是(－∞,1). 3．答案：B解析：由(12)x <(12)y 以及指数函数y ＝(12)x为减函数,可得x >y ,对于A,当x ＝1>y ＝－1时,x 2>y 2不成立,故A 不正确；对于B,根据指数函数y ＝πx为R 上的增函数可知,πx>πy恒成立,故B 正确；对于C,当x >0,y <0时,1x <1y不成立,故C 不正确；对于D,当x 或y 为负数时,x 或y 无意义,所以D 不正确． 4．答案：D解析：根据题意可列不等式如下,⎩⎪⎨⎪⎧2－a >0a >1（2－a ）＋1≥a 解得 1<a ≤32,选项D 正确． 5．答案：C解析：∵14<(14)b <(14)a<1,∴0<a a b, 因为y ＝x a在(0,1)单调递增,所以a a0,所以函数f (x )的定义域为R ,因此本选项结论正确；B ：f (x )＝2x－12x ＋1＝1－22x ＋1,由2x >0⇒2x＋1>1⇒0<12x ＋1<1⇒－2<－22x ＋1<0⇒－1<1－22x＋1<1,所以函数f (x )的值域为(－1,1),因此本选项结论正确； C ：因为f (－x )＝2－x －12－x ＋1＝1－2x1＋2x ＝－f (x ),所以函数f (x )是奇函数,其图象关于原点对称,不关于y 轴对称,因此本选项说法不正确；D ：因为函数y ＝2x ＋1是增函数,因为y ＝2x＋1>1,所以函数y ＝22x ＋1是减函数,因此函数f (x )＝1－22x ＋1是增函数,所以本选项结论正确．7．答案：1解析：由题意f (－x )＋f (x )＝0即a2－x－1＋12＋a 2x －1＋12＝0,－a ＋1＝0,a ＝1. 8．答案：(1,＋∞)解析：由题知函数f (x )的定义域为R ,∵y ＝(12)x 单调递减,故只需求出y ＝x 2－2x －3的单调递增区间即可,∵y ＝x 2－2x －3开口向上,对称轴为x ＝1,故在(1,＋∞)单调递增,∴f (x )＝(12)x 2－2x －3的单调递减区间是(1,＋∞).9．解析：(1)∵函数f (x )＝a 3－x,f (2)＝3,∴f (2)＝a3－2＝a ＝3,∴a ＝3.(2)由(1)知f (x )＝33－x,由f (x )>9,得33－x>32,∴3－x >2,即x <1,∴f (x )>9的解集为(－∞,1).10．解析：(1)因为f (x )是定义在R 上的奇函数,所以f (0)＝0,a ＝1, f (x )＝2x－12x ＋1＝1－22x ＋1, f (1)＝13.(2)设任意x 1<x 2,则f (x 1)－f (x 2)＝－22x 1＋1＋22x 2＋1＝2（2x 1－2x 2）（2x 1＋1）（2x 2＋1）, ∵x 1<x 2,∴2x 1<2x 2,2x 1－2x 2<0, 所以f (x 1)－f (x 2)<0,f (x 1)<f (x 2), 故f (x )在定义域上为增函数．核心素养升级练1．答案：AD 解析：2x 1·2x 2＝2x 1＋x 2,所以A 项成立；2x 1＋2x 2≠2x 1x 2,所以B 项不成立；函数f (x )＝2x在R 上是单调递增函数,若x 1>x 2,则f (x 1)>f (x 2),则f （x 1）－f （x 2）x 1－x 2>0,若x 1<x 2,则f (x 1)<f (x 2),则f （x 1）－f （x 2）x 1－x 2>0,故C 项不正确；函数f (x )＝2x任意两点之间的连线在其图象的上方,所以f (x )＝2x的图象满足f (x 1＋x 22)<f （x 1）＋f （x 2）2,故D 项正确．2．答案：f (x )＝1－12x (答案不唯一)解析：f (x )＝1－12x ,定义域为R ；12x >0,f (x )＝1－12x <1,值域为(－∞,1)；是增函数,满足对任意x 1,x 2∈(0,＋∞)且x 1≠x 2,均有f （x 1）－f （x 2）x 1－x 2>0.3．解析：(1)当a ＝6时,由f (x )＝2x,可得12＋2x ＋11＋2x ＝2x,则(2x )2－2x －12＝0,所以2x ＝4或2x＝－3(舍去),解得x ＝2. 故方程f (x )＝2x的解为2.(2)由题意知2a ＋2x ＋11＋2x ≥a 在(0,＋∞)上恒成立,即2×2x ≥a (2x－1)在(0,＋∞)上恒成立．又因为x ∈(0,＋∞),所以2x－1>0,则a ≤2×2x2x －1＝2＋22x －1.因为22x －1>0,所以2＋22x －1>2,所以a ≤2,即a 的取值范围是(－∞,2].。

高中数学(人教B版)必修一课时作业3.1指数与指数函数.1 Word版含解析

第三章
级基础巩固
一、选择题
．设>，将写成分数指数幂，其结果是()
．．
．．
[解析]＝＝＝
的值为()
．．
．．
[解析]＝[×()]＝(＋)＝＝.
．计算(－－)·(－－)÷(－－)，得()
．－．
．－．
[解析](－－)·(－－)÷(－－)
＝＝·＝－.
．将化简成不含根号的式子是()
．－．－－
．－．－
[解析]∵－＝－()＝－，
级能力拔高
．已知＋－＝，求值：
()＋－；
()＋－；
()－－.
[解析]()由＋－＝，得(＋－)＝，
∴＋－＝.
()∵＋－>，
又(＋－)＝＋－＋＝＋＝，
∴＋－＝.
()由(－－)＝＋－－＝，
∴－－＝±.
．Hale Waihona Puke 下列各式的值：()＋－＋－－π＋；
()( )－－－×[－＋()－]－－×.
[解析]
()原式＝＋－＋－－＋
()设＋－＝，求＋－及－－的值．
[解析]()－(－)－＋()－
＝－－＋
＝－－＋＝－.
()∵＋－＝，∴＋＝，
∴＋－＝＋＝－＝－＝.
(－－)＝＝＋－＝－＝，
∴－－＝±.
级素养提升
一、选择题
．若<，则化简的结果是()
．．
．－．－
[解析]∵<，∴－<.
∴＝，故选．
．若<，>，则等于()
．－．
．－．
[解析]∵<，∴＝－，
∴＝－，故选．
二、填空题
．××的值为
[解析]原式＝×·()·(×)
＝×××－××

高中数学课时作业13指数函数及其性质新人教A版必修120170907139

课时作业13指数函数及其性质|基础巩固|(25分钟，60分)一、选择题(每小题5分，共25分)1．下列结论正确的是()A．对于x∈R，恒有3x>2xB．y＝( 2)－x是增函数C．对a>1，x∈R，一定有a x>a－xD．y＝2|x|是偶函数1 2【解析】A．当x<0时，2x>3x；B.y＝(2 )x＝(2 )x在R上单调递减；C.当x＝0时，就有a x＝1，a－x＝1；D.符合偶函数的定义．【答案】 D12．函数y＝(3 ) 的值域是()x－1A．(－∞，0)B．(0,1]C．[1，＋∞)D．(－∞，1]1 1 1【解析】由x－1≥0且y＝(3 )x是减函数，知0<y＝(3 ) x－1≤(3 )0＝1. 【答案】 B3．设x>0，且10，b x>1，得b>1，同理a>1，又由a x>b x>1得b x＝(b)x>1，a所以>1，所以a>b>1，故选C.b 【答案】 C4．在同一平面直角坐标系中，函数f(x)＝ax与g(x)＝a x的图像可能是()【解析】需要对a讨论：①当a>1时，f(x)＝ax过原点且斜率大于1，g(x)＝a x是递增的；②当0<a<1时，f(x)＝ax过原点且斜率小于1，g(x)＝a x是减函数，显然B正确．【答案】 B5．函数y＝a x在区间[0,1]上的最大值和最小值的和为3，则函数y＝3ax－1在区间[0,1] 上的最大值是()A．6 B．113 C ．5 D. 2【解析】由于函数 y ＝a x 在[0,1]上为单调函数，所以有 a 0＋a 1＝3，即 a ＝2. 所以函数 y ＝3ax －1，即 y ＝6x －1在[0,1]上单调递增，其最大值为 y ＝6×1－1＝5.故选 C.【答案】 C二、填空题(每小题 5分，共 15分)136．若指数函数 y ＝f (x )的图象经过点(－2，16)，则 f (－2 )＝________. 【解析】设 f (x )＝a x (a >0且 a ≠1)．1因为 f (x )过点(－2，16)，1 所以＝a－2，16 所以 a ＝4.所以 f (x )＝4x ，331 2所以 f (－2 )＝4＝ .81 【答案】 87．若关于 x 的方程 2x －a ＋1＝0有负根，则 a 的取值范围是________．【解析】因为 2x ＝a －1有负根，所以 x <0，所以 0<2x <1. 所以 0<a －1<1.所以 1<a <2. 【答案】 (1,2)21 x -x-418．函数 y ＝(2)的值域是________． 1 1 1【解析】令 t ＝x 2－x －4＝(x －2 )2－ .21则 t ∈[－，＋∞)，21因此 y ＝(2 )t ∈＝(0， 2]．【答案】 (0， 2]三、解答题(每小题 10分，共 20分)19．设 f (x )＝3x ，g (x )＝(3 )x .(1)在同一坐标系中作出 f (x )，g (x )的图象； (2)计算 f (1)与 g (－1)，f (π)与 g (－π)，f (m )与 g (－m )的值，从中你能得到什么结论？【解析】 (1)函数 f (x )与 g (x )的图象如图所示：21(2)f(1)＝31＝3，g(－1)＝(3 )－1＝3；1f(π)＝3π，g(－π)＝(3 )－π＝3π；1f(m)＝3m，g(－m)＝(3 )－m＝3m. 从以上计算的结果看，两个函数当自变量取值互为相反数时，其函数值相等，即当指数函数的底数互为倒数时，它们的图象关于y轴对称．10．求下列函数的定义域和值域：(1)y＝2 112(3 )2x－2 .x－1；(2)y＝11 1 1【解析】(1)要使y＝21x－1有意义，需x≠0，则2x≠1；故2x－1>－1且2x－1≠0，故函数y＝2x－1的定义域为{x|x≠0}，函数的值域为(－1,0)∪(0，＋∞)．12(3 )2x－2 的定义域为实数集R，由于2x2≥0，则2x2－2≥－2. (2)函数y＝1 12 2(3 ) ( 2x－2 的值域为(0,9]．2x－2 ≤9，所以函数y＝3 )故0<|能力提升|(20分钟，40分)11．函数f(x)＝a x－3＋1(a>0，且a≠1)的图象恒过定点P，则定点P的坐标为()A．(3,3) B．(3,2)C．(3,6) D．(3,7)【解析】由于指数函数y＝a x(a>0，且a≠1)的图象恒过定点(0,1)，故令x－3＝0，解得x＝3，当x＝3时，f(3)＝2，即无论a为何值时，x＝3，y＝2都成立，因此，函数f(x)＝a x－3＋1的图象恒过定点(3,2)，故选B.【答案】 B12．函数g(x)＝2 016x＋m图象不过第二象限，则m的取值范围是________．【解析】函数g(x)＝2 016x＋m为增函数，若g(x)＝2 016x＋m图象不过第二象限，则满足g(0)≤0，则g(0)＝1＋m≤0，则m≤－1.【答案】(－∞，－1]13．若函数f(x)＝a x－1(a>0，a≠1)的定义域和值域都是[0,2]，求实数a的值．【解析】当a>1时，f(x)在[0,2]上递增，∴Error!即Error!∴a＝± 3.3又a>1，∴a＝3；当0<a<1时，f(x)在[0,2]上递减，∴Error!即Error!解得a∈∅. 综上所述，实数a的值为 3.14．已知函数f(x)＝k·a－x(k，a为常数，a>0且a≠1)的图象过点A(0,1)，B(3,8)．(1)求函数f(x)的解析式；f x－1(2)若函数g(x)＝，试判断函数g(x)的奇偶性并给出证明．f x＋1【解析】(1)由已知得Error!1解得k＝1，a＝.21故f(x)＝(2 )－x＝2x.2x－1(2)由(1)知g(x)＝，函数g(x)为奇函数．2x＋1证明：函数g(x)的定义域为R，2－x－1 1－2x2x－1又g(－x)＝＝＝－2－x＋1 1＋2x2x＋1故函数g(x)是奇函数．4。

高三人教B文科数学一轮复习课时作业指数与指数函数A

课时作业(八)A [第8讲指数与指数函数] [时间：35分钟分值：80分]基础热身1．化简[(－2)6]12－(－1)0的结果为( ) A ．－9 B ．7 C ．－10 D ．92．下列函数中，值域为{y |y >0}的是( )A ．y ＝－5xB ．y ＝⎝⎛⎭⎫131－xC ．y ＝⎝⎛⎭⎫12x －1 D ．y ＝1－2x 3．下列等式成立的是( ) A.⎝⎛⎭⎫n m 7＝m 17n 7 B.12(－2)4＝3－2 C 4x 3＋y 3＝(x ＋y )34D.39＝33 4．若a ＝50.2，b ＝0.50.2，c ＝0.52，则( )A ．a >b >cB ．b >a >cC ．c >a >bD ．b >c >a能力提升5．已知f (x )＝2x ＋2－x ，若f (a )＝3，则f (2a )等于( )A ．5B ．7C ．9D ．116．定义一种运算：a b ＝⎩⎪⎨⎪⎧a (a ≥b )，b (a <b )，已知函数f (x )＝2x (3－x )，那么函数y ＝f (x ＋1)的大致图象是( )图K8－17．函数y ＝xa x |x |(0<a <1)的图象的大致形状是( )图K8－2 8．设a ＝⎝⎛⎭⎫3525，b ＝⎝⎛⎭⎫2535，c ＝⎝⎛⎭⎫2525，则a ，b ，c 的大小关系是( ) A ．a ＞c ＞b B ．a ＞b ＞c C ．c ＞a ＞b D ．b ＞c ＞a9.⎝⎛⎭⎫32－13×⎝⎛⎭⎫－760＋814×42－⎝⎛⎭⎫－2323＝________.10．已知集合P ＝{(x ，y )|y ＝m }，Q ＝{(x ，y )|y ＝a x ＋1，a >0，a ≠1}，如果P ∩Q 有且只有一个元素，那么实数m 的取值范围是________．11．函数y ＝a x ＋2012＋2011(a >0且a ≠1)的图象恒过定点________．12．(13分)函数y ＝lg(3－4x ＋x 2)的定义域为M ，当x ∈M 时，求f (x )＝2x ＋2－3×4x 的最值．难点突破13．(12分)(1)已知f (x )＝23x －1＋m 是奇函数，求常数m 的值； (2)画出函数y ＝|3x －1|的图象，并利用图象回答：k 为何值时，方程|3x －1|＝k 无解？有一解？有两解？课时作业(八)A 【基础热身】 1．B [解析] [](－2)612－(－1)0＝8－1＝7. 2．B [解析] ∵y ＝⎝⎛⎭⎫13x 的值域是正实数，而1－x ∈R ，∴y ＝⎝⎛⎭⎫131－x 的值域是正实数． 3．D [解析] ⎝⎛⎭⎫n m 7＝n 7·m －7，12(－2)4＝32，4x 3＋y 3＝(x 3＋y 3)14≠(x ＋y )34. 4．A [解析] a ＝50.2>50＝1,0.52<0.50.2<0.50＝1.【能力提升】5．B [解析] 由f (a )＝3得2a ＋2－a ＝3，∴(2a ＋2－a )2＝9，即22a ＋2－2a ＋2＝9.所以22a＋2－2a ＝7，故f (2a )＝22a ＋2－2a ＝7.6．B [解析] f (x )＝2x (3－x )＝⎩⎪⎨⎪⎧2x (x ≥1)，3－x (x <1)，所以f (x ＋1)＝⎩⎪⎨⎪⎧2x ＋1(x ≥0)，2－x (x <0)，该函数的图象是选项B ，故选B. 7．D [解析] x >0时，y ＝a x ；x <0时，y ＝－a x .即把函数y ＝a x (0<a <1，x ≠0)的图象在x >0时不变，在x <0时，沿x 轴对称．8．A [解析] 由函数y ＝⎝⎛⎭⎫25x 为减函数知，⎝⎛⎭⎫2535<⎝⎛⎭⎫2525，所以，b <c ；由函数y ＝x 25为增函数知，⎝⎛⎭⎫3525>⎝⎛⎭⎫2525，所以，c <a .故a ＞c ＞b ，选A.9．2 [解析] 原式＝⎝⎛⎭⎫2313×1＋234×214－⎝⎛⎭⎫2313＝2. 10．(1，＋∞) [解析] 如果P ∩Q 有且只有一个元素，即函数y ＝m 与y ＝a x ＋1(a >0，且a ≠1)的图象只有一个公共点．∵y ＝a x ＋1>1，且单调，∴m >1.∴m 的取值范围是(1，＋∞)．11．(－2012,2012) [解析] ∵y ＝a x (a >0且a ≠1)恒过定点(0,1)，∴y ＝a x ＋2012＋2011恒过定点(－2012,2012)．12．[解答] 由3－4x ＋x 2＞0，得x ＞3或x ＜1，∴M ＝{x |x ＞3或x ＜1}，f (x )＝－3×(2x )2＋2x ＋2＝－3⎝⎛⎭⎫2x －162＋2512. ∵x ＞3或x ＜1，∴2x ＞8或0＜2x ＜2，∴当2x ＝16，即x ＝log 216时，f (x )最大，最大值为2512，f (x )没有最小值．【难点突破】13．[解答] (1)常数m ＝1.(2)y ＝|3x －1|的图象如下．当k <0时，直线y ＝k 与函数y ＝|3x －1|的图象无交点，即方程无解；当k ＝0或k ≥1时，直线y ＝k 与函数y ＝|3x －1|的图象有唯一的交点，所以方程有一解；当0<k <1时，直线y ＝k 与函数y ＝|3x －1|的图象有两个不同交点，所以方程有两解．。

高中数学课时作业16 指数函数的概念、图象及性质课件 a必修1a高一必修1数学课件

第三页，共二十四页。
3．对任意实数 a<1，函数 y＝(1－a)x＋4 的图象必过定点
(C )
A．(0,4) B．(0,1) C．(0,5) D．(1,5)
解析：令 x＝0 得 y＝5，即函数图象必过定点(0,5)，故选 C.
2021/12/12
第四页，共二十四页。
4．当 x∈[－2,2)时，y＝3－x－1 的值域是( A )
所以所求值域是(0,1]．故选 A.
2021/12/12
第十九页，共二十四页。
14．设函数 f(x)＝24x－x－aa，xx<－1，2a，x≥1，若 a＝1，则 f(x)
的最小值为－1 .
解析：若 a＝1，则 f(x)＝24x－x－11，xx<－1，2，x≥1，作出函数 f(x)的图象如图所示．由图可得 f(x)的最小值为－1.
A.－89，8
B.－89，8
C.19，9
D.19，9
解析：∵－2≤x<2，∴－2<－x≤2，∴3－2<3－x≤32， ∴－89<3－x－1≤8，即 y∈－89，8.
2021/12/12
第五页，共二十四页。
5．设12<12b<12a<1，那么( B )
A．0<b<a<1 B．0<a<b<1
C．a>b>1
解析：∵f(－1)＝2，∴f[f(－1)]＝f(2)＝a·22＝4a＝1，∴a＝ 14.故选 A.
2021/12/12
第七页，共二十四页。
二、填空题
7．若已知函数 f(x)＝1x13，x，x<x0≥，0.
为 {x|－3≤x≤1}．
则不等式|f(x)|≥13的解集