电子科技大学模式识别作业
电子科技大学研究生模式识别试题 2014.04 (附答案)(优.选)
1 / 5word.电子科技大学研究生试卷(考试时间: 至 ,共 2 小时)课程名称 模式识别 教师 学时 40 学分 2 教学方式 课堂教学 考核日期 年 月 日 成绩 考核方式: (学生填写)1、(5分)简述有监督学习和无监督学习的异同。
答:(1)有监督学习必须要有训练集和测试样本,而非监督学习没有训练集; (2)有监督学习的目的就是识别事物,识别结果表现在给待识别数据加上了标号,因此训练样本集必须由带标号的样本组成,而非监督学习方法只有要分析的数据集本身,预先没有什么标号。
(3)非监督学习方法在寻找数据集中的规律性,这种规律性并不一定要达到分数据集的目的,也就是说不一定要“分类”。
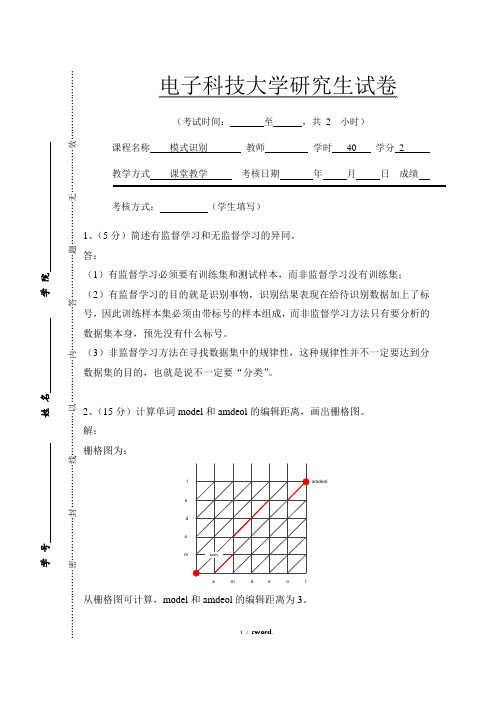
2、(15分)计算单词model 和amdeol 的编辑距离,画出栅格图。
解: 栅格图为:a m d e o lmo d e lamdeol从栅格图可计算,model 和amdeol 的编辑距离为3。
学 号 姓 名 学 院……………………密……………封……………线……………以……………内……………答……………题……………无……………效……………………2 / 5word.3、(15分)已知A 类样本为:123[0,1];[2,2];[2,3]a a a ===,B 类样本为:123[3,1];[4,3];[1,5]b b b ===,计算最小二乘分类面的方程(取值为-1和+1),并写出LMS 算法的流程。
解:(1)计算最小二乘分类面为[]0.4,0.26,1.45Tω=--。
(2)LMS 算法流程:步骤1. 初始化训练样本、权向量;步骤2. 选择一个训练样本,利用下列公式更新权向量:()[][1][1]2()k k T k iiy μ--=--w w x xw 训练样本数目步骤3. 重复所有样本。
4、(15分)在目标识别中,有1ω和2ω两种目标类型,它们的先验概率分别为0.8和0.2,在一次试验中,获得样本的类概率密度分别为()10.2p x ω=,()20.4p x ω=,并且已知110λ=,126λ=,211λ=,220λ=。
模式识别大作业

Iris 数据聚类分析-----c 均值和模糊c 均值一.问题描述Iris 数据集包含150个数据,共有3类,每一类有50个数据,其每个数据有四个维度,每个维度代表鸢尾花特征(萼片,花瓣的长度)中的一个,其三类数据名称分别setosa,versicolor,virginica ,这些就是 Iris 数据集的基本特征。
现在使用c 均值和模糊c 均值的方法解决其聚类分析,并且计算比较两种方法得到的分类结果的正确率。
二.算法介绍1.c-均值算法C 均值算法属于聚类技术中一种基本的划分方法,具有简单、快速的优点。
其基本思想是选取c 个数据对象作为初始聚类中心,通过迭代把数据对象划分到不同的簇中,使簇内部对象之间的相似度很大,而簇之间对象的相似度很小。
其主要思想:(1) 计算数据对象两两之间的距离;(2) 找出距离最近的两个数据对象,形成一个数据对象集合A1 ,并将它们从总的数据集合U 中删除;(3) 计算A1 中每一个数据对象与数据对象集合U 中每一个样本的距离,找出在U 中与A1 中最近的数据对象,将它并入集合A1 并从U 中删除, 直到A1 中的数据对象个数到达一定阈值;(4) 再从U 中找到样本两两间距离最近的两个数据对象构成A2 ,重复上面的过程,直到形成k 个对象集合;(5) 最后对k 个对象集合分别进行算术平均,形成k 个初始聚类中心。
算法步骤:1.初始化:随机选择k 个样本点,并将其视为各聚类的初始中心12,,,k m m m ;2.按照最小距离法则逐个将样本x 划分到以聚类中心12,,,k m m m 为代表的k 个类1,k C C 中;3.计算聚类准则函数J,重新计算k 个类的聚类中心12,,,k m m m ; 4.重复step2和3知道聚类中心12,,,k m m m 无改变或目标函数J 不减小。
2.模糊c-均值模糊C 均值算法就是,在C 均值算法中,把硬分类变为模糊分类。
设()j i μx 是第i 个样本i x 属于第j 类j G 的隶属度,利用隶属度定义的准则函数为211[()]C N b f j i i jj i J μ===-∑∑x x m其中,b>1是一个可以控制聚类结果的模糊程度的常数。
模式识别大作业

模式识别大作业1.最近邻/k近邻法一.基本概念:最近邻法:对于未知样本x,比较x与N个已知类别的样本之间的欧式距离,并决策x与距离它最近的样本同类。
K近邻法:取未知样本x的k个近邻,看这k个近邻中多数属于哪一类,就把x归为哪一类。
K取奇数,为了是避免k1=k2的情况。
二.问题分析:要判别x属于哪一类,关键要求得与x最近的k个样本(当k=1时,即是最近邻法),然后判别这k个样本的多数属于哪一类。
可采用欧式距离公式求得两个样本间的距离s=sqrt((x1-x2)^2+(y1-y2)^2)三.算法分析:该算法中任取每类样本的一半作为训练样本,其余作为测试样本。
例如iris中取每类样本的25组作为训练样本,剩余25组作为测试样本,依次求得与一测试样本x距离最近的k 个样本,并判断k个样本多数属于哪一类,则x就属于哪类。
测试10次,取10次分类正确率的平均值来检验算法的性能。
四.MATLAB代码:最近邻算实现对Iris分类clc;totalsum=0;for ii=1:10data=load('iris.txt');data1=data(1:50,1:4);%任取Iris-setosa数据的25组rbow1=randperm(50);trainsample1=data1(rbow1(:,1:25),1:4);rbow1(:,26:50)=sort(rbow1(:,26:50));%剩余的25组按行下标大小顺序排列testsample1=data1(rbow1(:,26:50),1:4);data2=data(51:100,1:4);%任取Iris-versicolor数据的25组rbow2=randperm(50);trainsample2=data2(rbow2(:,1:25),1:4);rbow2(:,26:50)=sort(rbow2(:,26:50));testsample2=data2(rbow2(:,26:50),1:4);data3=data(101:150,1:4);%任取Iris-virginica数据的25组rbow3=randperm(50);trainsample3=data3(rbow3(:,1:25),1:4);rbow3(:,26:50)=sort(rbow3(:,26:50));testsample3=data3(rbow3(:,26:50),1:4);trainsample=cat(1,trainsample1,trainsample2,trainsample3);%包含75组数据的样本集testsample=cat(1,testsample1,testsample2,testsample3);newchar=zeros(1,75);sum=0;[i,j]=size(trainsample);%i=60,j=4[u,v]=size(testsample);%u=90,v=4for x=1:ufor y=1:iresult=sqrt((testsample(x,1)-trainsample(y,1))^2+(testsample(x,2) -trainsample(y,2))^2+(testsample(x,3)-trainsample(y,3))^2+(testsa mple(x,4)-trainsample(y,4))^2); %欧式距离newchar(1,y)=result;end;[new,Ind]=sort(newchar);class1=0;class2=0;class3=0;if Ind(1,1)<=25class1=class1+1;elseif Ind(1,1)>25&&Ind(1,1)<=50class2=class2+1;elseclass3=class3+1;endif class1>class2&&class1>class3m=1;ty='Iris-setosa';elseif class2>class1&&class2>class3m=2;ty='Iris-versicolor';elseif class3>class1&&class3>class2m=3;ty='Iris-virginica';elsem=0;ty='none';endif x<=25&&m>0disp(sprintf('第%d组数据分类后为%s类',rbow1(:,x+25),ty));elseif x<=25&&m==0disp(sprintf('第%d组数据分类后为%s类',rbow1(:,x+25),'none'));endif x>25&&x<=50&&m>0disp(sprintf('第%d组数据分类后为%s类',50+rbow2(:,x),ty));elseif x>25&&x<=50&&m==0disp(sprintf('第%d组数据分类后为%s类',50+rbow2(:,x),'none'));endif x>50&&x<=75&&m>0disp(sprintf('第%d组数据分类后为%s类',100+rbow3(:,x-25),ty));elseif x>50&&x<=75&&m==0disp(sprintf('第%d组数据分类后为%s类',100+rbow3(:,x-25),'none'));endif (x<=25&&m==1)||(x>25&&x<=50&&m==2)||(x>50&&x<=75&&m==3)sum=sum+1;endenddisp(sprintf('第%d次分类识别率为%4.2f',ii,sum/75));totalsum=totalsum+(sum/75);enddisp(sprintf('10次分类平均识别率为%4.2f',totalsum/10));测试结果:第3组数据分类后为Iris-setosa类第5组数据分类后为Iris-setosa类第6组数据分类后为Iris-setosa类第7组数据分类后为Iris-setosa类第10组数据分类后为Iris-setosa类第11组数据分类后为Iris-setosa类第12组数据分类后为Iris-setosa类第14组数据分类后为Iris-setosa类第16组数据分类后为Iris-setosa类第18组数据分类后为Iris-setosa类第19组数据分类后为Iris-setosa类第20组数据分类后为Iris-setosa类第23组数据分类后为Iris-setosa类第24组数据分类后为Iris-setosa类第26组数据分类后为Iris-setosa类第28组数据分类后为Iris-setosa类第30组数据分类后为Iris-setosa类第31组数据分类后为Iris-setosa类第34组数据分类后为Iris-setosa类第37组数据分类后为Iris-setosa类第39组数据分类后为Iris-setosa类第41组数据分类后为Iris-setosa类第44组数据分类后为Iris-setosa类第45组数据分类后为Iris-setosa类第49组数据分类后为Iris-setosa类第53组数据分类后为Iris-versicolor类第54组数据分类后为Iris-versicolor类第55组数据分类后为Iris-versicolor类第57组数据分类后为Iris-versicolor类第58组数据分类后为Iris-versicolor类第59组数据分类后为Iris-versicolor类第60组数据分类后为Iris-versicolor类第61组数据分类后为Iris-versicolor类第62组数据分类后为Iris-versicolor类第68组数据分类后为Iris-versicolor类第70组数据分类后为Iris-versicolor类第71组数据分类后为Iris-virginica类第74组数据分类后为Iris-versicolor类第75组数据分类后为Iris-versicolor类第77组数据分类后为Iris-versicolor类第79组数据分类后为Iris-versicolor类第80组数据分类后为Iris-versicolor类第84组数据分类后为Iris-virginica类第85组数据分类后为Iris-versicolor类第92组数据分类后为Iris-versicolor类第95组数据分类后为Iris-versicolor类第97组数据分类后为Iris-versicolor类第98组数据分类后为Iris-versicolor类第99组数据分类后为Iris-versicolor类第102组数据分类后为Iris-virginica类第103组数据分类后为Iris-virginica类第105组数据分类后为Iris-virginica类第106组数据分类后为Iris-virginica类第107组数据分类后为Iris-versicolor类第108组数据分类后为Iris-virginica类第114组数据分类后为Iris-virginica类第118组数据分类后为Iris-virginica类第119组数据分类后为Iris-virginica类第124组数据分类后为Iris-virginica类第125组数据分类后为Iris-virginica类第126组数据分类后为Iris-virginica类第127组数据分类后为Iris-virginica类第128组数据分类后为Iris-virginica类第129组数据分类后为Iris-virginica类第130组数据分类后为Iris-virginica类第133组数据分类后为Iris-virginica类第135组数据分类后为Iris-virginica类第137组数据分类后为Iris-virginica类第142组数据分类后为Iris-virginica类第144组数据分类后为Iris-virginica类第148组数据分类后为Iris-virginica类第149组数据分类后为Iris-virginica类第150组数据分类后为Iris-virginica类k近邻法对wine分类:clc;otalsum=0;for ii=1:10 %循环测试10次data=load('wine.txt');%导入wine数据data1=data(1:59,1:13);%任取第一类数据的30组rbow1=randperm(59);trainsample1=data1(sort(rbow1(:,1:30)),1:13);rbow1(:,31:59)=sort(rbow1(:,31:59)); %剩余的29组按行下标大小顺序排列testsample1=data1(rbow1(:,31:59),1:13);data2=data(60:130,1:13);%任取第二类数据的35组rbow2=randperm(71);trainsample2=data2(sort(rbow2(:,1:35)),1:13);rbow2(:,36:71)=sort(rbow2(:,36:71));testsample2=data2(rbow2(:,36:71),1:13);data3=data(131:178,1:13);%任取第三类数据的24组rbow3=randperm(48);trainsample3=data3(sort(rbow3(:,1:24)),1:13);rbow3(:,25:48)=sort(rbow3(:,25:48));testsample3=data3(rbow3(:,25:48),1:13);train_sample=cat(1,trainsample1,trainsample2,trainsample3);%包含89组数据的样本集test_sample=cat(1,testsample1,testsample2,testsample3);k=19;%19近邻法newchar=zeros(1,89);sum=0;[i,j]=size(train_sample);%i=89,j=13[u,v]=size(test_sample);%u=89,v=13for x=1:ufor y=1:iresult=sqrt((test_sample(x,1)-train_sample(y,1))^2+(test_sample(x ,2)-train_sample(y,2))^2+(test_sample(x,3)-train_sample(y,3))^2+( test_sample(x,4)-train_sample(y,4))^2+(test_sample(x,5)-train_sam ple(y,5))^2+(test_sample(x,6)-train_sample(y,6))^2+(test_sample(x ,7)-train_sample(y,7))^2+(test_sample(x,8)-train_sample(y,8))^2+( test_sample(x,9)-train_sample(y,9))^2+(test_sample(x,10)-train_sa mple(y,10))^2+(test_sample(x,11)-train_sample(y,11))^2+(test_samp le(x,12)-train_sample(y,12))^2+(test_sample(x,13)-train_sample(y, 13))^2); %欧式距离newchar(1,y)=result;end;[new,Ind]=sort(newchar);class1=0;class 2=0;class 3=0;for n=1:kif Ind(1,n)<=30class 1= class 1+1;elseif Ind(1,n)>30&&Ind(1,n)<=65class 2= class 2+1;elseclass 3= class3+1;endendif class 1>= class 2&& class1>= class3m=1;elseif class2>= class1&& class2>= class3m=2;elseif class3>= class1&& class3>= class2m=3;endif x<=29disp(sprintf('第%d组数据分类后为第%d类',rbow1(:,30+x),m));elseif x>29&&x<=65disp(sprintf('第%d组数据分类后为第%d类',59+rbow2(:,x+6),m));elseif x>65&&x<=89disp(sprintf('第%d组数据分类后为第%d类',130+rbow3(:,x-41),m));endif (x<=29&&m==1)||(x>29&&x<=65&&m==2)||(x>65&&x<=89&&m==3) sum=sum+1;endenddisp(sprintf('第%d次分类识别率为%4.2f',ii,sum/89));totalsum=totalsum+(sum/89);enddisp(sprintf('10次分类平均识别率为%4.2f',totalsum/10));第2组数据分类后为第1类第4组数据分类后为第1类第5组数据分类后为第3类第6组数据分类后为第1类第8组数据分类后为第1类第10组数据分类后为第1类第11组数据分类后为第1类第14组数据分类后为第1类第16组数据分类后为第1类第19组数据分类后为第1类第20组数据分类后为第3类第21组数据分类后为第3类第22组数据分类后为第3类第26组数据分类后为第3类第27组数据分类后为第1类第28组数据分类后为第1类第30组数据分类后为第1类第33组数据分类后为第1类第36组数据分类后为第1类第37组数据分类后为第1类第43组数据分类后为第1类第44组数据分类后为第3类第45组数据分类后为第1类第46组数据分类后为第1类第49组数据分类后为第1类第54组数据分类后为第1类第56组数据分类后为第1类第57组数据分类后为第1类第60组数据分类后为第2类第61组数据分类后为第3类第63组数据分类后为第3类第65组数据分类后为第2类第66组数据分类后为第3类第67组数据分类后为第2类第71组数据分类后为第1类第72组数据分类后为第2类第74组数据分类后为第1类第76组数据分类后为第2类第77组数据分类后为第2类第79组数据分类后为第3类第81组数据分类后为第2类第82组数据分类后为第3类第83组数据分类后为第3类第84组数据分类后为第2类第86组数据分类后为第2类第87组数据分类后为第2类第88组数据分类后为第2类第93组数据分类后为第2类第96组数据分类后为第1类第98组数据分类后为第2类第99组数据分类后为第3类第102组数据分类后为第2类第104组数据分类后为第2类第105组数据分类后为第3类第106组数据分类后为第2类第110组数据分类后为第3类第113组数据分类后为第3类第114组数据分类后为第2类第115组数据分类后为第2类第116组数据分类后为第2类第118组数据分类后为第2类第122组数据分类后为第2类第123组数据分类后为第2类第124组数据分类后为第2类第133组数据分类后为第3类第134组数据分类后为第3类第135组数据分类后为第2类第136组数据分类后为第3类第140组数据分类后为第3类第142组数据分类后为第3类第144组数据分类后为第2类第145组数据分类后为第1类第146组数据分类后为第3类第148组数据分类后为第3类第149组数据分类后为第2类第152组数据分类后为第2类第157组数据分类后为第2类第159组数据分类后为第3类第161组数据分类后为第2类第162组数据分类后为第3类第163组数据分类后为第3类第164组数据分类后为第3类第165组数据分类后为第3类第167组数据分类后为第3类第168组数据分类后为第3类第173组数据分类后为第3类第174组数据分类后为第3类2.Fisher线性判别法Fisher 线性判别是统计模式识别的基本方法之一。
最新电子科技大学研究生模式识别试题-.04-(附答案)
精品文档电子科技大学研究生试卷(考试时间: 至 ,共 2 小时)课程名称 模式识别 教师 学时 40 学分 2 教学方式 课堂教学 考核日期 年 月 日 成绩 考核方式: (学生填写)1、(5分)简述有监督学习和无监督学习的异同。
答:(1)有监督学习必须要有训练集和测试样本,而非监督学习没有训练集; (2)有监督学习的目的就是识别事物,识别结果表现在给待识别数据加上了标号,因此训练样本集必须由带标号的样本组成,而非监督学习方法只有要分析的数据集本身,预先没有什么标号。
(3)非监督学习方法在寻找数据集中的规律性,这种规律性并不一定要达到分数据集的目的,也就是说不一定要“分类”。
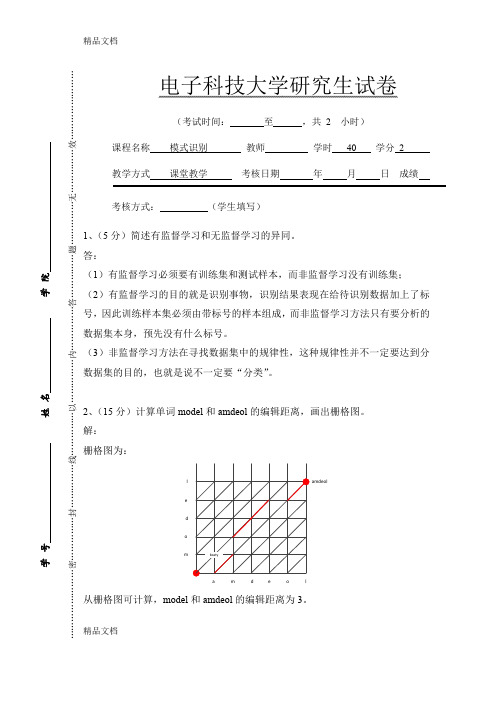
2、(15分)计算单词model 和amdeol 的编辑距离,画出栅格图。
解: 栅格图为:a m d e o lmo d e lamdeolbcaty从栅格图可计算,model 和amdeol 的编辑距离为3。
学 号 姓 名 学 院……………………密……………封……………线……………以……………内……………答……………题……………无……………效……………………精品文档3、(15分)已知A 类样本为:123[0,1];[2,2];[2,3]a a a ===,B 类样本为:123[3,1];[4,3];[1,5]b b b ===,计算最小二乘分类面的方程(取值为-1和+1),并写出LMS 算法的流程。
解:(1)计算最小二乘分类面为[]0.4,0.26,1.45Tω=--。
(2)LMS 算法流程:步骤1. 初始化训练样本、权向量;步骤2. 选择一个训练样本,利用下列公式更新权向量:()[][1][1]2()k k T k iiy μ--=--w w x xw 训练样本数目步骤3. 重复所有样本。
4、(15分)在目标识别中,有1ω和2ω两种目标类型,它们的先验概率分别为0.8和0.2,在一次试验中,获得样本的类概率密度分别为()10.2p x ω=,()20.4p x ω=,并且已知110λ=,126λ=,211λ=,220λ=。
模式识别大作业

模式识别专业:电子信息工程班级:电信****班学号:********** 姓名:艾依河里的鱼一、贝叶斯决策(一)贝叶斯决策理论 1.最小错误率贝叶斯决策器在模式识别领域,贝叶斯决策通常利用一些决策规则来判定样本的类别。
最常见的决策规则有最大后验概率决策和最小风险决策等。
设共有K 个类别,各类别用符号k c ()K k ,,2,1 =代表。
假设k c 类出现的先验概率()k P c以及类条件概率密度()|k P c x 是已知的,那么应该把x 划分到哪一类才合适呢?若采用最大后验概率决策规则,首先计算x 属于k c 类的后验概率()()()()()()()()1||||k k k k k Kk k k P c P c P c P c P c P P c P c ===∑x x x x x然后将x 判决为属于kc ~类,其中()1arg max |kk Kk P c ≤≤=x若采用最小风险决策,则首先计算将x 判决为k c 类所带来的风险(),k R c x ,再将x 判决为属于kc ~类,其中()min ,kkk R c =x可以证明在采用0-1损失函数的前提下,两种决策规则是等价的。
贝叶斯决策器在先验概率()k P c 以及类条件概率密度()|k P c x 已知的前提下,利用上述贝叶斯决策规则确定分类面。
贝叶斯决策器得到的分类面是最优的,它是最优分类器。
但贝叶斯决策器在确定分类面前需要预知()k P c 与()|k P c x ,这在实际运用中往往不可能,因为()|k P c x 一般是未知的。
因此贝叶斯决策器只是一个理论上的分类器,常用作衡量其它分类器性能的标尺。
最小风险贝叶斯决策可按下列步骤进行: (1)在已知)(i P ω,)(i X P ω,i=1,…,c 及给出待识别的X 的情况下,根据贝叶斯公式计算出后验概率:∑==cj iii i i P X P P X P X P 1)()()()()(ωωωωω j=1,…,x(2)利用计算出的后验概率及决策表,按下面的公式计算出采取i a ,i=1,…,a 的条件风险∑==cj j j i i X P a X a R 1)(),()(ωωλ,i=1,2,…,a(3)对(2)中得到的a 个条件风险值)(X a R i ,i=1,…,a 进行比较,找出使其条件风险最小的决策k a ,即()()1,min k i i aR a x R a x ==则k a 就是最小风险贝叶斯决策。
电子科技大学模式识别作业ANN-BP分类器设计

ANN-BP分类器设计(控制工程XXXXXXXXXX)1、问题表述对“data3.m”数据,用其中一半的数据采用ANN-BP算法设计分类器,另一半数据用于测试分类器性能。
二、方法描述神经网络(Neural Networks, NN)是由大量的、简单的处理单元(称为神经元)广泛地互相连接而形成的复杂网络系统,它反映了人脑功能的许多基本特征,是一个高度复杂的非线性动力学系统。
神经网络具有大规模并行、分布式存储和处理、自组织、自适应和自学习能力,特别适合处理需要同时考虑许多因素和条件的、不精确和模糊的信息处理问题。
BP 神经网络的标准学习过程:神经网络在外界输入样本的刺激下,不断改变网络的连接权值,以使网络的输出不断地接近期望的输出。
信号正向传播;若输出层的实际输出与期望的输出(教师信号)不符时,转入反向传播阶段;误差反传,误差以某种形式在各层表示——修正各层单元的权值;依次循环,直到网络输出的误差减少到可接受的程度或者进行到预先设定的学习次数为止。
BP神经网络的标准学习步骤:第一步,网络初始化给各连接权值分别赋一个区间(-1,1)内的随机数,设定误差函数e,给定计算精度值和最大学习次数M。
第二步,随机选取第k个输入样本及对应期望输出。
第三步,计算隐含层各神经元的输入和输出。
第四步,利用网络期望输出和实际输出,计算误差函数对输出层的各神经元的偏导数。
第五步,利用隐含层到输出层的连接权值、输出层的偏导数和隐含层的输出计算误差函数对隐含层各神经元的偏导数。
第六步,利用输出层各神经元的偏导数和隐含层各神经元的输出来修正连接权值。
第七步,利用隐含层各神经元的偏导数和输入层各神经元的输入修正连接权。
第八步,计算全局误差。
第九步,判断网络误差是否满足要求。
当误差达到预设精度或学习次数大于设定的最大次数,则结束算法。
否则,选取下一个学习样本及对应的期望输出,返回到第三步,进入下一轮学习。
BP神经网络的特点:非线性映射能力:能学习和存贮大量输入-输出模式映射关系,而无需事先了解描述这种映射关系的数学方程。
模式识别大作业

模式识别大作业引言:转眼之间,研一就结束了。
这学期的模式识别课也接近了尾声。
我本科是机械专业,编程和算法的理解能力比较薄弱。
所以虽然这学期老师上课上的很精彩,但是这学期的模式识别课上的感觉还是有点吃力。
不过这学期也加强了编程的练习。
这次的作业花了很久的时间,因为平时自己的方向是主要是图像降噪,自己在看这一块图像降噪论文的时候感觉和模式识别的方向结合的比较少。
我看了这方面的模式识别和图像降噪结合的论文,发现也比较少。
在思考的过程中,我想到了聚类的方法。
包括K均值和C均值等等。
因为之前学过K均值,于是就选择了K均值的聚类方法。
然后用到了均值滤波和自适应滤波进行处理。
正文:k-means聚类算法的工作过程说明如下:首先从n个数据对象任意选择 k 个对象作为初始聚类中心;而对于所剩下其它对象,则根据它们与这些聚类中心的相似度(距离),分别将它们分配给与其最相似的(聚类中心所代表的)聚类;然后再计算每个所获新聚类的聚类中心(该聚类中所有对象的均值);不断重复这一过程直到标准测度函数开始收敛为止。
一般都采用均方差作为标准测度函数。
k-means 算法接受输入量k ;然后将n个数据对象划分为k个聚类以便使得所获得的聚类满足:同一聚类中的对象相似度较高;而不同聚类中的对象相似度较小。
聚类相似度是利用各聚类中对象的均值所获得一个“中心对象”(引力中心)来进行计算的。
k个聚类具有以下特点:各聚类本身尽可能的紧凑,而各聚类之间尽可能的分开。
均值滤波是常用的非线性滤波方法 ,也是图像处理技术中最常用的预处理技术。
它在平滑脉冲噪声方面非常有效,同时它可以保护图像尖锐的边缘。
均值滤波是典型的线性滤波算法,它是指在图像上对目标像素给一个模板,该模板包括了其周围的临近像素(以目标象素为中心的周围8个象素,构成一个滤波模板,即去掉目标象素本身)。
再用模板中的全体像素的平均值来代替原来像素值。
即对待处理的当前像素点(x,y),选择一个模板,该模板由其近邻的若干像素组成,求模板中所有像素的均值,再把该均值赋予当前像素点(x,y),作为处理后图像在该点上的灰度个g(x,y),即个g(x,y)=1/m ∑f(x,y)m为该模板中包含当前像素在内的像素总个数。
模式识别作业1230

作业一1.试举一生活中能够用运算机实现模式识别的实例,并说明在这一问题中,模式识别系统各组成部份别离可能对应什么内容批改记录:1.11测31,应收43,实收39,4人须补作业;12测11,应收66,实收64,2人须补作业,5人考虑重做;12测31,应收31,实收31,1人考虑重做;缘故:没有回答下列问题(只列了理论框图)或选题不太适当,没有给成绩,需订正2.部份同窗态度不够认真;3.分数问题;4.英文简写及具体步骤描述不够5.书写层次性问题6.表述准确性:如遥感影像、航摄像片,非“照片”7.选题:(1)车牌识别,声音(语音、演唱曲目)识别,指纹识别(包括指纹解锁),人脸识别(照相、考勤、解锁),海鱼,文字识别,手写体字符识别(签名),电话触摸操作,虹膜识别,颜料表面改性,遥感影像分类,药材识别,蔬菜病害,血液检测,心电图(2) 讨论:电脑录制一首歌曲自动感应门声控灯 ATM 机取钱自动销售机作业二1. 设有10个二维模式样本,如图所示。
假设21=θ,试用最大最小距离算法对他们进行聚类分析。
解:① 取T 11]0,0[==X Z 。
② 选离1Z 最远的样本作为第二聚类中心2Z 。
()()201012221=-+-=D ,831=D ,5841=D ,4551=D5261=D ,7471=D ,4581=D ,5891=D ,651,10=D ∵ 最大者为D 71,∴T 72]7,5[==X Z742121=-=Z Z θT ③ 计算各样本与{}21,Z Z 间距离,选出其中的最小距离。
7412=D ,5222=D ,3432=D ,…,132,10=D }13,20,17,0,2,5,4,8,2,0{),min(21=i i D D ④ ∵742120)},max{min(9221=>==T D D D i i ,T 93]3,7[==∴X Z ⑤ 继续判定是不是有新的聚类中心显现:⎪⎩⎪⎨⎧===58740131211D D D ,⎪⎪⎩⎪⎪⎨⎧===40522232221D D D ,…⎪⎪⎩⎪⎪⎨⎧===113653,102,101,10D D D}1,0,1,0,2,5,4,8,2,0{),,min(321=i i i D D D 74218)},,max{min(31321=<==T D D D D i i i 寻觅聚类中心的步骤终止。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
采用 PCA 对男女生样本数据中的身高,体重,喜欢数学,喜欢文学,喜欢运动, 喜欢模式识别共 6 个特征进行特征提取(自己设定选取的特征个数),并基于所 得到的特征采用 SVM 设计男女生分类器,并计算模型预测性能(包含 SE,SP,ACC 和 AUC )。 试对比分析两种特征选择/提取方法的特点。
二、实验内容
采用遗传算法对男女生样本数据中的身高,体重,喜欢数学,喜欢文学, 喜欢运动, 喜欢模式识别共 6 个特征进行特征选择,并基于所得到的最佳特征采 用 SVM 设计男女生分类器,并计算模型预测性能(包含 SE,SP,ACC 和 AUC )。 提示:可以用 6 位的 0/1 进行编码,适应度函数可以考虑类似
当 J 当 J 当 J
1 2 3
Jd ( ) tr ( S Jd ( ) tr ( S Jd ( )
w -1 w
S b )时; S b )时; S 时
w
tr ( S b )
2,训练过程
训练过程分为一下几个步骤 (1)设定种群规模,随机产生第一代共计 6 个父本作为初始种群,计算各个群体 的适应度,进行排序后做出取舍。 (2)设置遗传 200 次停止,将得到的第二代进行交叉变异,交叉为后三位交叉率 为 0.90%。变异设定为每繁殖 10 次进行一次变异,突变位数为 1.突变方式为翻
根据 PCA 算法得到的实验结果如下所示
SE SP ACC AUC 0.9563 0.7786 0.9526 0.9722
Hale Waihona Puke 所得到的 ROC 图像如下所示:
通过以上数据可以预测本计算模型分类基本准确。有较好的分 类结果。和前次报告的对比可以看到。相比决策树和 BP 算法。采用 PCA 进行特征提取的方法得到的 AUC(线下面积)更大一些。也说明 对男女生分类这一问题上。本次作业的两种算法更合适一些。
三、实验步骤及结果 A:遗传算法
1,计算可分性判据
从直观上考虑,可以用两类中任意两两样本间的距离的平均来代表两类之间的 距离。也就是可以用男生的样本平均和女生样本的平均来代表男女生之间的距 离。 为了讨论不同类内类间的判据对分类结果的影响。这里进行了三个常见类内 类间判据。依次为一下三种情况下的分类。
模式识别实验报告(第三次)
姓名:关浩亮 学号: 201622240018 学院:电科院 时间 2016 年 11 月 6 日
一,实验目的
通过 MATLAB 仿真加深对遗传算法的认识以及对 PCA 决策等分类方式的理 解;在设计的过程中,加深和巩固对模式识别各种分类方法的认识和理解。使其 能更好的应用于社会各个领域。为以后的工作和学习打下坚实的基础。
J_max
J1 J2 J3
0.8073 0.8512 0.8426
111000 111000 111000
注:选择特征从左到右分别为“身高” “体重” “喜欢数学” “喜欢文学” “喜欢运动” “喜 欢模式识别”根据数字组合确定所选则的特征。如果为“101010”则表示“选择身高特征” “不选择体重特征”“选择喜欢数学特征”“不选择喜欢文学特征”“选择喜欢运动特征” “不选择喜欢模式识别特征”以此类推。 根据三种类内间距离判据,基本可以确定选择“身高”“体重”“喜欢数学”三个特征为 最佳选择。
转。计算各个群体的适应度,并排序取舍。 (4)200 次完成后, 计算最终子代中适应度最大的个体。 并找到样本中选择的特征。 B:PCA 算法 在前面的基础上,采用 SVM 分类器中的 linear 核函数进行分类,并计算出 SE, SP,ACC,AUC 的值,做出预测性能图像。
四,实验结论
汇总以上的实验数据,得到如下表 1 的实验结果 表 1 实验结果汇总 类内类间距离最大值 选择特征 所用类内类间距离判据
