2018年秋九年级数学上册专题训练(四)与圆的切线有关的问题归类试题(新版)苏科版
精品 九年级数学上册 圆 切线的性质与判定同步讲义+同步练习题

切线的性质与判定知识点:三角形内切圆画法:三角形的外接圆与三角形的内切圆三角形的外接圆:经过三角形三个顶点的圆叫三角形的外接圆三角形外接圆的圆心叫三角形的外心三角形的外心到三角形三个顶点的距离相等三角形的外心是三角形三边中垂线的交点三角形的内切圆:与三角形三边都相切的圆叫三角形的内切圆三角形内切圆的圆心叫三角形的内心三角形的内心到三角形三边的距离相等三角形的内心是三角形三角平分线的交点切线长定理:从圆外一点可以引圆的____条切线,它们的________相等.这一点和______平分_______.直角三角形内切圆半径与三边关系公式:任意三角形面积、周长与内切圆半径关系公式:例1.如图,已知C为⊙O上一点,DA交⊙O于B,∠DCB=∠CAB.求证:DC为⊙O的切线.CA B DO例2.如图,已知在Rt△ABC中,∠C=900,点C在AC上,CD为⊙O直径,⊙O切AB于E,若BC=5,AC=12,求⊙O的半径.BEA COD例3.如图,已知⊙O内切于△ABC,∠BOC=1050,∠ACB=900,AB=20cm.求BC、AC的长.例4.如图,∠PAQ 是直角,半径为5的⊙O 与AP 相切于点T,与AQ 相交于两点B 、C. (1)BT 是否平分∠OBA?证明你的结论; (2)若已知AT=4,试求AB 的长.例5.如图,P 为⊙O 外一点,PO 交⊙O 于C,过⊙O 上一点A 作弦AB ⊥PO 于E,若∠EAC=∠CAP , 求证:PA 是⊙O 的切线.课堂同步:1.在Rt △ABC 中,∠A=900,点O 在BC 上,以O 为圆心的⊙O 分别与AB 、AC 相切于E 、F ,若AB=a ,AC=b ,则⊙O 的半径为( )A.abB.ab b a + C.b a ab + D.2ba + 2.正方形ABCD 中,AE 切以BC 为直径的半圆于E ,交CD 于F ,则CF:FD=( ) A.1:2 B.1:3 C.1:4 D.2:53.如图,过⊙O 外一点P 作⊙O 的两条切线PA 、PB,切点分别为A 、B,连结AB,在AB 、PB 、PA 上分别取一点D 、E 、F,使AD=BE,BD=AF,连结DE 、DF 、EF,则∠EDF=( ) A.900-∠P B.900-21∠P C.1800-∠P D.450-21∠P 4.如图,直线AB 与⊙O 相切于点B ,BC 是⊙O 的直径,AC 交⊙O 于点D ,连结BD ,则图中直角三角形有______个.第4题图 第5题图 第6题图 第7题图 5.如图,已知PA 、PB 是⊙O 的切线,A 、B 是切点,∠APB=780,点C 是⊙O 上异于A 、B 的任一点, 则∠ACB=6.如图,以O 为圆心的两个同心圆中,大圆的弦AB 与小圆相切于点C,若大圆半径为10cm,小圆半径为6cm,则弦AB 的长为_______cm .7.如图,⊙O 内切于Rt △ABC,∠C=900,D 、E 、F 是切点,若∠BOC=1050,AB=4cm,则∠OBC=________, ∠BAC=_____,BC=______,AC=______,内切圆半径r=_____。
2018-2019学年九年级数学上册专题复习一:与圆有关的线段含答案

专题复习一与圆有关的线段弦、半径、直径是圆中的主要线段,主要应用垂径定理解决与线段有关的计算,弦心距和半径是主要的辅助线,方程思想是计算的主要思想方法.1.如图所示,⊙O的直径CD垂直于弦AB于点E,且CE=2,DE=8,则AB的长为(D).A.2B.4C.6D.8(第1题)(第2题)(第3题)(第4题)2.如图所示,⊙O的半径为6,△ABC是⊙O的内接三角形,连结OB,OC,若∠BAC与∠BOC互补,则线段BC的长为(C).A.33B.3C.63D.63.如图所示,半径为3的⊙O内有一点A,OA=3,点P在⊙O上,当∠OPA最大时,PA的长为(B).A.3B.6C.3D.234.如图所示,在等边三角形ABC中,AB,AC都是⊙O的弦,OM⊥AB,ON⊥AC,垂足分别为点M,N.如果MN=1,那么△ABC的面积为(B).3A.3B.3C.4D.35.如图所示,⊙O的半径OD⊥AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为(D).A.215B.8C.210D.213(第5题)(第6题) (第7题)(第8题)6.“圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”此问题的实质就是解决下面的问题:“如图所示,CD为⊙O的直径,AB ⊥CD于点E,CE=1,AB=10,求CD的长.”根据题意可得CD的长为26 .7.如图所示,已知P为⊙O内一点,且OP=2cm,如果⊙O的半径是3cm,那么过点P的最短的弦长为25cm.8.如图所示,⊙O的半径为5,弦BC=8,点A在⊙O上,AO⊥BC,垂足为点D,E为BC延长线上一点,AE=10,则CE的长为 2 .9.如图所示,AB是半圆O的直径,BC是弦,点P从点A开始,沿AB向点B以1cm/s的速度移动,若AB为10cm,点O 到BC 的距离为4cm .(1)求弦BC 的长.(2)经过几秒,△BPC 是等腰三角形?(第9题)图1图2(第9题答图)【答案】(1)如答图1所示,作OD⊥BC 于点D ,∴BD=21BC.∵OB=21AB=5(cm),OD=4(cm),∴BD=3(cm).∴BC=2BD=6(cm). (2)设经过t(s)后,△BPC 是等腰三角形.①当PC 为底边时,BP=BC ,10-t=6,解得t=4(s).②当BC 为底边时,PC=PB ,点P 与点O 重合,此时t=5(s ).③当PB 为底边时,PC=BC.如答图2所示,连结AC ,作CE⊥AB 于点E ,则BE=210t -,AE=210t +. ∵AB 是直径,∴△ABC 是直角三角形.∴AC=22BC AB -=8. ∵AC 2-AE 2=BC 2-BE 2,∴64-(210t +)2=36-(210t -)2,解得t=2.8(s). 综上可知,经过4s 或5s 或2.8s 后,△BPC 是等腰三角形.10.如图所示,△ABC 是⊙O 的内接等边三角形,弦EF 经过BC 的中点D ,且EF∥BA,若⊙O 的半径为433,则DE 的长为(C ).A. 3-1B. 215+C. 5-1D. 213+ (第10题)(第11题)(第12题) (第13题)(第14题)11.如图所示,有半径为26和43的两个同心圆,矩形ABCD 的边AB ,CD 分别为两圆的弦,当矩形的面积为最大时,它的周长等于(D ). A.22+62 B.20+82 C.18+102 D.16+12212.如图所示,AB 是⊙O 的直径,AB=2,OC 是⊙O 的半径,OC⊥AB,点D 在AC 上,AD=2CD ,P 是半径OC 上一个动点,那么AP+PD 的最小值等于3 .13.如图所示,⊙O 的直径AB=10,P 是OA 上一点,弦MN 过点P ,且AP=2,MP=22,那么弦心距OQ 为7 .14.如图所示,半径为1的半圆O 上有两个动点A ,B ,若AB=1,则四边形ABDC 的面积的最大值是433 . 15.小明学习了垂径定理后,做了以下探究,请根据题目要求帮小明完成探究.(1)更换定理的题设和结论可以得到许多真命题.如图1所示,在⊙O 中,C 是劣弧AB 的中点,直线CD⊥AB 于点E ,则AE=BE.请证明此结论.(2)从圆上任意一点出发的两条弦所组成的折线,称为该圆的一条折弦.如图2所示,PA ,PB 组成⊙O 的一条折弦,C 是劣弧AB 的中点,直线CD⊥PA 于点E ,则AE=PE+PB.可以通过延长DB ,AP 相交于点F ,再连结AD 证明结论成立.请写出证明过程.(3)如图3所示,PA ,PB 组成⊙O 的一条折弦,若C 是的中点,直线CD⊥PA 于点E ,则AE ,PE 与PB 之间存在怎样的数量关系?写出结论,不必证明. (第15题)(第15题答图)【答案】(1)如答图所示,连结AD ,BD.∵C 是劣弧AB 的中点,∴∠CDA=∠CDB.∴△ADB 为等腰三角形.∵CD⊥AB,∴AE=BE.(2)∵四边形ADBP 是圆内接四边形,∴∠PBD+∠PAD=180°.∵∠PBD+∠PBF=180°,∴∠PBF=∠PAD.∵C 是劣弧AB 的中点,∴∠CDA=∠CDF.∵CD⊥PA,∴△AFD 为等腰三角形.∴∠F=∠A,AE=EF.∴∠PBF=∠F.∴PB=PF.∴AE=PE+PB.(3)AE=PE-PB.16.【陕西】如图所示,△ABC 是⊙O 的内接三角形,∠C=30°,⊙O 的半径为5,若点P 是⊙O 上的一点,在△ABP 中,PB=AB ,则PA 的长为(D ). A.5 B. 235 C.52 D.53 (第16题) (第17题)17.【十堰】如图所示,△ABC 内接于⊙O,∠ACB=90°,∠ACB 的平分线交⊙O 于点D.若AC=6,BD=52,则BC 的长为 8 .18.要在半径为1、圆心角为60°的扇形AOB 铁皮上截取一块尽可能大的正方形.小明设计如下两种截取方案. 方案一(如图1所示):点C 在OA 上,点D ,E 在OB 上,点F 在上. 方案二(如图2所示):点C 在OA 上,点D 在OB 上,点E ,F 在上.请计算这两种方案中正方形铁皮的面积,帮小明选择合理的方案(参考数据:2≈1.41, 3≈1.73).(第18题) 图1图2(第18题答图) 【答案】方案一:如答图1所示,连结OF ,设正方形CDEF 的边长为x.∵圆心角为60°,∴OD=33x.在Rt △OFE中,OF 2=OE 2+EF 2,即12=x 2+(x+33x )2,解得x 2=373621-.∴S 四边形CDEF =x 2=373621-≈0.29.方案二:如答图2所示,过点O 作OG⊥EF,交CD 于点H ,交EF 于点G ,连结OE.设EG=x ,则EF =2x.∵四边形CDEF 是正方形,∴OH⊥CD.∴EG=DH=x.∵∠DOC=60°,H 为CD 中点,∴OH=3DH=3x.∴OG=OH+HG=3x+2x.在Rt△OEG 中,OE 2=GE 2+OG 2,即12=x 2+(3x+2x)2,解得x 2=432-.∴S 四边形CDEF =4x 2=2-3≈0.27.∴方案一截取的正方形的面积较大,应选方案一.。
【同步练习】人教版2018年 九年级数学上册 切线的性质与判断 同步练习卷(含答案)
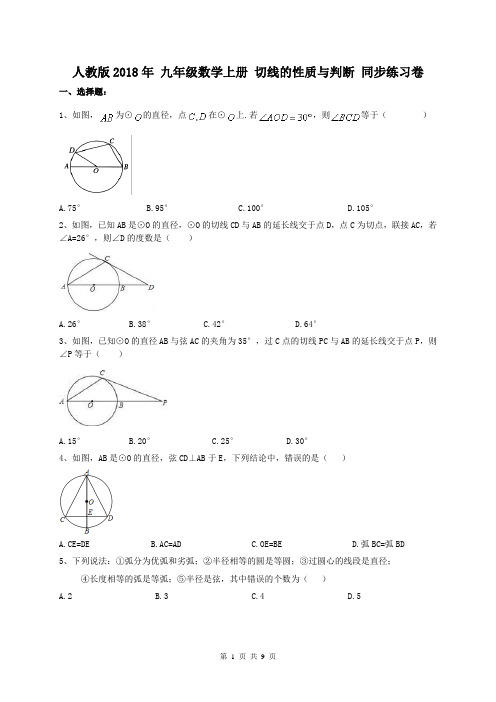
人教版2018年九年级数学上册切线的性质与判断同步练习卷一、选择题:1、如图,为⊙的直径,点在⊙上.若,则等于()A.75°B.95°C.100°D.105°2、如图,已知AB是⊙O的直径,⊙O的切线CD与AB的延长线交于点D,点C为切点,联接AC,若∠A=26°,则∠D的度数是()A.26°B.38°C.42°D.64°3、如图,已知⊙O的直径AB与弦AC的夹角为35°,过C点的切线PC与AB的延长线交于点P,则∠P等于()A.15°B.20°C.25°D.30°4、如图,AB是⊙O的直径,弦CD⊥AB于E,下列结论中,错误的是()A.CE=DEB.AC=ADC.OE=BED.弧BC=弧BD5、下列说法:①弧分为优弧和劣弧;②半径相等的圆是等圆;③过圆心的线段是直径;④长度相等的弧是等弧;⑤半径是弦,其中错误的个数为()A.2B.3C.4D.56、如图,在⊙O中,AD,CD是弦,连接OC并延长,交过点A的切线于点B,若∠ADC=25°,则∠ABO的度数为()A.50°B.40°C.30°D.20°7、如图,AB是⊙O的直径,C、D是⊙O上一点,∠CDB=20°,过点C作⊙O的切线交AB的延长线于点E,则∠E等于()A.40°B.50°C.60°D.70°8、如图,过⊙O上一点C作⊙O切线,交直径AB的延长线于点D,若∠D=40°,则∠A度数为()A.20°B.25°C.30°D.40°9、有下列四个命题:①经过三个点一定可以作圆;②等弧所对的圆周角相等;③三角形的外心到三角形各顶点的距离都相等;④直径是弦.其中正确的有()A.4个B.3个C.2个D.1个10、如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与图中4×7方格中的格点的连线中,能够与该圆弧相切的格点个数有()A.1个B.2个C.3个D.4个11、如图,在△ABC中,∠ACB=90°,∠A=40°,以C为圆心,CB为半径的圆交AB于点D,连接CD,则∠ACD=()A.10°B.15°C.20°D.25°12、如图,在⊙O中,∠AOB=120°,P为弧AB上的一点,则∠APB的度数是()A.100°B.110°C.120°D.130°13、如图,P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=15,则△PCD的周长为()A.15B.30C.18D.2514、如图,AB是圆O的直径,BD、CD分别是过圆O上点B、C的切线,且∠BDC=100°,连接AC,则∠A的度数为()A.15°B.30°C.40°D.45°15、如图,⊙O截△ABC的三条边所得的弦长相等,则下列说法正确的是()A.点O是△ABC的内心B.点O是△ABC的外心C.△ABC是正三角形D.△ABC是等腰三角形16、如图,P为⊙O外一点,PA,PB分别切⊙O于A,B,CD切⊙O于点E,分别交PA,PB于点C,D,若PA=5,则△PCD的周长为()A.5B.7C.8D.1017、如图,在边长为6的菱形ABCD中,∠DAB=60°,以点D为圆心,菱形的高DF为半径画弧,交AD于点E,交CD于点G,则图中阴影部分的面积是()A. B. C. D.18、如图,⊙O的直径AB与弦CD的延长线交于点E,若DE=OB, ∠AOC=84°,则∠E等于()A.42 °B.28°C.21°D.20°19、如图,AB是⊙O的切线,B为切点,AC经过点O,与⊙O分别相交于点D,C.若∠ACB=30°,AB=,则阴影部分的面积是()A. B. C.﹣ D.﹣20、如图,∠ABC=80°,O为射线BC上一点,以点O为圆心,OB长为半径作⊙O,要使射线BA与⊙O相切,应将射线BA绕点B按顺时针方向旋转()A.40°或80°B.50°或100°C.50°或110°D.60°或120°二、填空题:21、如图,在△ABC中,∠ACB=90°,∠A=40°,以C为圆心,CB为半径的圆交AB于点D,连接CD,则∠ACD=___________22、如图,AB是⊙O的直径,点D在AB的延长线上,过点D作⊙O的切线,切点为C,若∠A=25°,则∠D= 度.23、如图,PA,PB分别切⊙O于A,B,并与⊙O的切线,分别相交于C,D,已知△PCD的周长等于10cm,则PA=__________cm.24、如图同心圆,大⊙O的弦AB切小⊙O于P,且AB=6,则圆环的面积为____________.25、如图所示是一圆柱形输水管的横截面,阴影部分为有水部分,如果水面AB宽为8cm,水的最大深度为2cm,则该输水管的直径为___________.26、如图,P是⊙O的直径BA延长线上一点,PD交⊙O于点C,且PC=OD,如果∠P=24°,则∠DOB=________.27、如图,Rt△ABC中,∠C=90°,若AC=4,BC=3,则△ABC的内切圆半径r= .28、如图,CD是⊙O的直径,∠EOD=84°,AE交⊙O于点B,且AB=OC,则∠A的度数是 .29、如图,点O是△ABC的内切圆的圆心,若∠BAC=80°,则∠BOC= (填度数).30、如图,已知P是⊙O外一点,Q是⊙O上的动点,线段PQ的中点为M,连接OP,OM,若⊙O的半径为2,OP=4,则线段OM的最小值是三、解答题:31、如图①,在△ABC中,点D在边BC上,∠ABC:∠ACB:∠ADB=1:2:3,⊙O是△ABD的外接圆.(Ⅰ)求证:AC是⊙O的切线;(Ⅱ)当BD是⊙O的直径时(如图②),求∠CAD的度数.32、如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.(1)求∠ABC的度数;(2)求证:AE是⊙O的切线;(3)当BC=4时,求劣弧AC的长.33、如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于点D,切线DE交AC于点E. (1)求证:∠A=∠ADE;(2)若AD=16,DE=10,求BC的长.34、如图,⊙O的直径AB为10cm,弦BC为5cm,D、E分别是∠ACB的平分线与⊙O,AB的交点,P 为AB延长线上一点,且PC=PE.(1)求AC、AD的长;(2)试判断直线PC与⊙O的位置关系,并说明理由.参考答案1、D2、B3、B4、C5、C6、B7、B8、B;9、B10、C11、A12、C13、B14、C15、A16、D17、A18、B19、C20、C21、答案为:10°;22、答案为:40°;23、答案为:5;24、答案为:9π;25、答案为:10cm;26、答案为:72°;27、答案为:1.28、答案为:28°.29、答案为:130°.30、答案为:131、(1)证明:如解图,连接OA、OD,设∠ABD=x,∵∠ABC:∠ACB:∠ADB=1:2:3,∴∠ADB=3x,∠ACB=2x,∴∠DAC=∠ADB-∠ACB=x,∠AOD=2∠ABC=2x,∴∠OAD=90°-x,∴∠OAC=90°-x+x=90°,∴OA⊥AC,∴AC是⊙O的切线;(Ⅱ)解:∵BD是⊙O的直径,∴∠BAD=90°,∴∠ABC+∠ADB=90°,∵∠ABC:∠ACB:∠ADB=1:2:3,∴4∠ABC=90°,∴∠ABC=22.5°,∴∠ADB=67.5°, ∠ACB=45°,∴∠CAD=∠ADB-∠ACB=22.5°.32、解:(1)∵∠ABC与∠D都是弧AC所对的圆周角,∴∠B=∠D=60°.(2)∵AB是⊙O的直径,∴∠ACB=90°.又∠B=60°∴∠BAC=30°.∴∠BAE=∠BAC+∠EAC=30°+60°=90°,即BA⊥AE.∴AE是⊙O的切线.(3)如图,连接OC,∵∠ABC=60°,∴∠AOC=120°.∴劣弧AC的长为π.33、(1)证明:连接OD,∵DE是切线,∴∠ODE=90°,∴∠ADE+∠BDO=90°,∵∠ACB=90°,∴∠A+∠B=90°,∵OD=OB,∴∠B=∠BDO,∴∠ADE=∠A.(2)连接CD.∵∠ADE=∠A,∴AE=DE,∵BC是⊙O的直径,∠ACB=90°,∴EC是⊙O的切线,∴ED=EC,∴AE=EC,∵DE=10,∴AC=2DE=20,在Rt△ADC中,DC=12,设BD=x,在Rt△BDC中,BC2=x2+122,在Rt△ABC中,BC2=(x+16)2﹣202,∴x2+122=(x+16)2﹣202,解得x=9,∴BC=15.34、解:(1)如图,连接BD,∵AB是直径,∴∠ACB=∠ADB=90°,在Rt△ABC中,AC=(cm),②∵CD平分∠ACB,∴∠ACD=∠BCD,∴AD=BD,∴Rt△ABD是直角等腰三角形,∴AD=5cm;(2)直线PC与⊙O相切理由:连接OC,∵OC=OA,∴∠CAO=∠OCA,∵PC=PE,∴∠PCE=∠PEC,∵∠PEC=∠CAE+∠ACE,∵CD平分∠ACB,∴∠ACE=∠ECB,∴∠PCB=∠CAO=∠ACO,∵∠ACB=90°,∴∠OCP=∠OCB+∠PCB=∠ACO+∠OCB=∠ACB=90°,即OC⊥PC,∴直线PC与⊙O相切.。
北京市海淀区普通中学2018届初三中考数学复习 与圆有关的位置关系-切线的判定与性质 专题复习练

北京市海淀区普通中学2018届初三中考数学复习与圆有关的位置关系-切线的判定与性质专题复习练习题1.如图,AB是⊙O的直径,下列条件中不能判定直线AT是⊙O的切线的是( )A.AB=4,AT=3,BT=5 B.∠B=45°,AB=ATC.∠B=55°,∠TAC=55° D.∠ATC=∠B2. 如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C,如果∠C =40°,则∠ABO的度数是( )A.50° B.40° C.25° D.20°3. 如图,直线l是⊙O的切线,A为切点,B为直线l上一点,连结OB交⊙O 于点C.若AB=12,OA=5,则BC的长为( )A.5 B.6 C.7 D.84. 如图,AB是⊙O的直径,C是⊙O上的点,过点C作⊙O的切线交AB的延长线于点E,若∠A=30°,则sin∠E的值为( )A.12B.22C.32D.335. 如图,⊙O 过正方形ABCD 的顶点A 、B ,且与CD 相切,若正方形ABCD 的边长为2,则⊙O 的半径为( )A .1 B.52 C.43 D.546. 如图所示,A 、B 是⊙O 上的两点,AC 是过A 点的一条直线,如果∠AOB =120°,那么当∠CAB 的度数等于______时,AC 才能成为⊙O 的切线.7. 如图,AB 是⊙O 的直径,C 、D 是⊙O 上的两点,∠DCB=30°,过点D 作⊙O 的切线交AB 的延长线于点E ,若AB =4,则DE 的长为_______.8. 如图,在⊙O 中,AB 为直径,BC 为弦,CD 为切线,连结OC.若∠BCD =50°,则∠AOC 的度数为_______9. 如图,直线AB 与半径为2的⊙O 相切于点C ,D 是⊙O 上一点,且∠EDC =30°,弦EF∥AB,则EF 的长度为______.10. 如图,在直角坐标系中,⊙A 的圆心A 的坐标为(-1,0),半径为1,点P 为直线y =-34x +3上的动点,过点P 作⊙A 的切线,切点为Q ,则切线长PQ 的最小值是_______.11. 如图,△ABC 中,AB =AC ,O 是BC 的中点,⊙O 与AB 相切于点D ,求证:AC 是⊙O 的切线.12. 如图,AB 是⊙O 的直径,点C 在⊙O 上(异于A 、B 两点),AD⊥CD.(1)若BC=3,AB=5,求AC的长;(2)若AC是∠DAB的平分线,求证:直线CD与⊙O相切.13. 如图,AN是⊙M的直径,NB∥x轴,AB交⊙M于点C.(1)若点A(0,6),N(0,2),∠ABN=30°,求点B的坐标;(2)若D为线段NB的中点,求证:直线CD是⊙M的切线.答案:1---5 DCDAD6. 60°7. 2 38. 80°.9. 2 310. 2 211. 证明:过点O作OE⊥AC于点E,连结OD,OA,∵AB与⊙O相切于点D,∴AB⊥OD.∵△ABC为等腰三角形,O是底边BC的中点,∴AO是∠BAC的平分线,∴OE=OD,即OE是⊙O的半径,∴AC是⊙O的切线.12. 解:(1)∵AB是⊙O的直径,∴∠ACB=90°.∵BC=3,AB=5,∴AC=AB2-BC2=52-32=4.(2)证明:∵AC是∠DAB的平分线,∴∠DAC=∠BAC.∵OA=OC,∴∠OCA=∠OAC,∴∠DAC=∠OCA,∴AD∥OC.∵AD⊥CD,∴OC⊥CD,∴直线CD与⊙O相切.13. 解:(1)∵A的坐标为(0,6),N(0,2),∴AN=4.∵∠ABN=30°,∠ANB=90°,∴AB=2AN=8,∴NB=AB2-AN2=43,∴B(43,2).(2)证明:连结MC,NC,∵AN是⊙M的直径,∴∠ACN=∠NCB=90°.在Rt△NCB中,D为NB的中点,∴CD=12NB=ND,∴∠CND=∠NCD. ∵MC=MN,∴∠MCN=∠MNC.∵∠MNC+∠CND=90°,∴∠MCN+∠NCD=90°,即MC⊥CD.∴直线CD是⊙M的切线.。
圆的切线证明 中考数学专项训练(含答案解析)

圆的切线证明(1)求证:CD 为O 切线;(2)若1CD =,5AC =,求PB (1)求证:CD 是O 的切线;(2)若16ABCD S =正方形,求CE3.如图,在Rt ABC △中,90C ∠=︒,AD 平分BAC ∠交BC 于点D ,O 为AB 上一点,经过点A ,D 的O 分别交AB ,AC 于点E ,F 连接OF 交AD 于点G .(1)求证:BC 是O 的切线;(2)若60OFA ∠=︒,半径为4,在圆O 上取点P ,使15PDE ∠=︒,求点P 到直线DE 的距离.4.如图,AB 是O 的直径,CD 是O 的弦,AB CD ⊥,垂足是点H ,过点C 作直线分别与AB ,AD 的延长线交于点E ,F ,且2ECD BAD ∠=∠.(1)求证:CF 是O 的切线;(2)如果20AB =,12CD =,求AE 的长.5.如图,O 是ABC 的外接圆,O 点在BC 边上,BAC ∠的平分线交O 于点D ,连接BD 、CD ,过点D 作BC 的平行线,与AB 的延长线相交于点P .(1)求证:PD 是O 的切线;(2)若3AB =,4AC =,求线段BD 的长.6.如图,已知以Rt ABC △的直角边AB 为直径作O ,与斜边AC 交于点D ,E 为BC 边上的中点,连接DE .(1)求证:DE 是O 的切线;(2)若AD ,AB 的长是方程210240x x -+=的两个根,求直角边BC 的长.(1)求证:DE 是O 的切线;(2)若30C ∠=︒,23CD =,求图中阴影部分的面积.(1)求证:DE 是O 的切线;(2)若2AB =,30C ∠=︒,求9.如图,AB 为O 的直径,C ,D 为O 上的两点,BAC DAC ∠=∠,过点C 作直线EF AD ⊥,交AD 的延长线于点E ,连接BC .(1)求证:EF 是O 的切线;(2)若30CAO ∠=︒,2BC =,求CE 的长.10.如图,AB 是O 的直径,点C 是O 上一点(与点A ,B 不重合),过点C 作直线PQ ,使得ACQ ABC ∠=∠.(1)求证:直线PQ 是O 的切线.(2)过点A 作AD PQ ⊥于点D ,交O 于点E ,若O 的半径为2,30DAC ∠=︒,求图中阴影部分的面积.11.如图,等腰ABC 的顶点A ,C 在O 上, BC 边经过圆心0且与O 交于D 点,30B ∠=︒.(1)求证:AB 是O 的切线;(2)若6AB =,求阴影部分的面积12.如图,AB 是ABC 外接圆O 的直径,PA 是O 的切线,BD OP ∥,点D 在O 上.(1)求证:PD 是O 的切线.(2)若ABC 的边6cm AC =,8cm BC =,I 是ABC 的内心,求IO 的长度.13.如图,AB 是O 的直径,AC 是弦,点D 是O 上一点,OD AB ⊥,连接CD 交AB 于点E ,F 是AB 延长线上的一点,且CF EF =.(1)求证:CF 是O 的切线;(2)若8CF =,4BF =,求弧BD 的长度.14.如图所示,在Rt ABC △中,点O 在斜边AB 上,以O 为圆心,OB 为半径作圆O ,分别与BC 、AB 相交于点D 、E ,连接AD ,已知CAD B ∠=∠.(1)求证:AD 是O 的切线;(2)若23AD CD ==时,求阴影部分的面积.(1)求证:PA是O(2)若tan CAD∠=(3)延长CD,AB交于点(1)求证:DE BG=;(2)求证:BF是O的切线;(3)若23DEEG=时,AE(1)当60A ∠=︒,2AD =时,求(2)求证:DF 是O 的切线.(1)求证:DF 是O (2)若 BE DE =,tan(1)求证:直线AB 为O 的切线;(2)若4tan 3A =,O 的半径为2,求AB (1)求证:BF 是O 的切线;(2)若6EF =,cos ABC ∠①求BF 的长;②求O 的半径.参考答案:∵CD AE ⊥,∴90ADC ∠=︒,∵OC OA =,∴OCA OAC ∠=∠,∵的平分线AC 交O 于∵AB 为O 直径,∴90ACB ∠=︒,∴90ADC ACB ∠=∠=︒,∵DAC OAC ∠=∠,∴,【点睛】此题重点考查正方形的性质、等腰三角形的性质、切线的判定、平行线分线段成比例定理、锐角三角函数与解直角三角形等知识,正确地作出所需要的辅助线是解题的关键.3.(1)见解析(2)232-或423-【分析】(1)连接OD ,可得(2)①过点P 作PN DE ⊥交交于H ,可求60EOD ∠=︒,即可求解;②连接OD ,OP 60EOD ∠=︒,30POE ∠=︒,可证求解.【详解】(1)解:如图,连接∴OA OD =,∴ODA OAD ∠=∠,AD 是BAC ∠的平分线,, ∠=︒PDE15=,PE PE ∴∠=︒POE30,OA OF∠=︒60OFA=,∴∠=︒,OAF60∠的平分线, AD是BAC同理可求60EOD ∠=︒,30POE ∠=︒,1302DOL EOD ∴∠=∠=︒,30DOP EOD POE ∠=∠-∠=︒,DOP DOL ∴∠=∠,AB 是O 的直径,90ACB ∴∠=︒,AO OB =,AB CD ⊥ ,AB ∴平分弦CD ,AB 平分 CD,CH HD ∴=, CBDB =,90CHA CHE ∠=︒=∠,BAD BAC DCB ∴∠=∠=∠,∵AB 是O 的直径,∴90ADB ∠=︒,∴BDC 为直角三角形,∵E 为BC 边上的中点,∴ED EB =,∴12∠=∠,∵OB OD =,3=4∠∠∵AB AC =,∴A ABC CB =∠∠,设OB OD r ==,∴ABC ODB ∠=∠,∵AB AC =,23CD =,C ∠=∴23BD CD ==,30B C ∠=∠=∴1803030120BOD ∠=︒-︒-︒=︒OF BD ⊥==OB OD AB AC,∴∠=∠,B CB ODB∠=∠∴∠=∠.ODB C∴∥.OD AC,=OA OC∴∠=∠,OAC OCAQ,∠=∠DAC BAC∴∠=∠,DAC OCA∥,∴AD OC,EF AD⊥∴⊥,而OC为半径,EF OC的切线;∴是OEF的直径,(2)解:AB为O(1)根据题意连接OC ,可知90ACB ∠=︒,可知AOC 是等腰三角形,OAC OCA ∠=∠,继而可证90OCD ∠=︒;(2)连接OE ,过点E 作EF AB ⊥,根据题意可知60EAO ∠=︒即可得知AEO △为等边三角形,再求出扇形AOE 面积减去AEO △的面积即为阴影面积.【详解】(1)解:连接OC ,,∵OA OC =,AB 是O 的直径,∴90ACB ∠=︒,∴90CAB CBA ∠+∠=︒,∴AOC 是等腰三角形,∴OAC OCA ∠=∠,∵ACQ ABC ∠=∠,∴90ACQ OCA ∠+∠=︒,∴OC PQ ⊥,∴直线PQ 是O 的切线;(2)解:连接OE ,过点E 作EF AB ⊥,,∵AD PQ ⊥,ACQ ABC ∠=∠,∴30DAC CAB ∠=∠=︒,∴60EAO ∠=︒,∵AB 为O 的直径,∴90ADB ∠=︒,∵BD OP ∥,∴OP AD ⊥,OP 是AD 的垂直平分线,∴PD PA =,则IU IV IQ ==,∵AB 为O 的直径,∴90ACB ∠=︒,∵6cm AC =,8cm BC =,∴226810AB =+=,5OB OA ==(2)3π.【分析】本题考查了切线的判定,求弧长;(1)如图,连接OC ,OD .证明90OCF ∠=︒即可;(2)设O 的半径为r ,在Rt COF △中,勾股定理可得6r =,再根据弧长公式可解决问题.【详解】(1)证明:连接OCCF EF= CEF ECF∴∠=∠OD AB⊥ 90DOE ∴∠=︒,90ODE OED ∴∠+∠=︒,OD OC = ,ODE OCD ∴∠=∠,CEF OED ∠=∠ ,OED ECF ∴∠=∠,90OCD ECF ∴∠+∠=︒,即90OCF ∠=︒,OC CF ∴⊥,CF ∴是O 的切线.(2)设O 的半径为r ,∵4BF =,∴4OF r =+,在Rt OCF 中,90,∠=︒ACB∴∠+∠CAD ADC=,OB OD∴∠=∠,B ODB则sin 30OH OD =⋅ODB S S S ∴=-阴影扇形∴CAD BAD ∠=∠,∴5CD BD ==,∵AB 为直径,点∴90ADB ∠=︒,∵2DOB DAB ∠=∠=∠又∵DFO CFA ∠=∠,∴DOF CAF ∽,又∵OB BF OA ==,∴23DF FO FC FA ==,∴90EHB BGF ∠=∠=︒,∵点C 为劣弧BD 中点,∴ CDBC =,∴DAC BAC DBC ∠=∠=∠∵AD 是O 的直径,∴90AED ∠=︒,∵60A ∠=︒,2AD =∴30ADE ∠=︒,则12AE =∴2222DE AD AE =-=∵AD 是直径,∴90AED ∠=︒,∴1809090DEB ∠=︒-︒=︒∵四边形ABCD 为菱形,∴DBE DBF ∠=∠,AD ∥∵BE BF =,DB DB =,∴()SAS DBE DBF ≌,∴90DFB DEB ∠=∠=︒,∵AD BC ∥,∴90ADF DFB ∠=∠=︒,∴AD DF ⊥,∵AD 为直径,∴DF 是O 的切线.【点睛】本题主要考查了直径所对的圆周角为直角,含30度角的直角三角形的性质,勾股定理,切线的判定,解题的关键是作出辅助线,熟练掌握切线的判定方法.18.(1)见解析(2)52AB 是O 的直径,90ADB ∴∠=︒,90BDC ∴∠=︒,90BDF CDF ∠∠∴+=︒,OB OD = ,OBD ODB ∴∠=∠,CDF ABD ∠∠= ,ODB CDF ∠∠∴=,90ODB BDF ∴∠+∠=︒,90ODF ∴∠=︒,DF OD ∴⊥,OD 是O 的半径,DF ∴是O 的切线;(2)如图,连接AE ,∵ BEDE =,BAE CAE ∴∠=∠,AB 是O 的直径,90AEB ∴∠=︒,90AEC ∴∠=︒,AEB AEC ∴∠=∠,∵OC OD =,∴OCD ODC ∠=∠.设OCD ODC α∠=∠=,∴22A BCD α∠=∠=.∵90ACB ∠=︒,。
初三切线练习题

初三切线练习题切线问题在数学中是一个常见的概念,它与圆的关系密切。
初三学生需要通过练习题来巩固和提高对切线的理解和运用。
下面是一些初三切线练习题,让我们一起来挑战一下吧!1. 已知圆O的半径为r,点A是圆上的一个固定点,点B是圆上与点A相对的另一个点。
若直线AB与圆O相交于点C,且BC的长度为x,试判断直线BC与圆O的位置关系。
解析:根据圆的性质可知,圆的半径是所有以圆心为端点的线段中最长的。
由于BC是圆上一条弧所对应的弦,所以BC的长度不能大于直径(2r)。
当x小于2r时,直线BC与圆O的位置关系是相交;当x 等于2r时,直线BC与圆O的位置关系是相切;当x大于2r时,直线BC与圆O的位置关系是相离。
2. 在直角三角形ABC中,∠B=90°,AB=3cm,BC=4cm。
通过点B作直线DE与AC相交于点E,若BE为直线DE上的一条切线,求BE的长度。
解析:由直角三角形ABC可知,根据勾股定理,AC的长度为5cm。
由于BE是与直线DE的交点B相对应的一条切线,所以BE垂直于DE。
根据切线和半径的关系可知,在与切线垂直的半径上,切线的平方等于切点到圆心的距离与半径的乘积。
因此,BE的长度可以通过计算BD与DE的乘积再开平方得到。
根据相似三角形的比例关系,可以得出BD为4/5,DE为3/5。
所以,BE的长度为3/5 * 4/5 = 12/25 cm。
3. 已知圆O的半径为r,点A是圆上的一个固定点,点P是圆外一点,直线AP与圆O相交于点B。
若直线BP为切线,且BP的长度为x,求证:x^2 = AP*BP。
解析:根据切线和半径的关系可知,切线的平方等于切点到圆心的距离与半径的乘积。
在这道题中,BP为切线,所以BP的平方等于切点B到圆心O的距离与半径r的乘积。
而点B是直线AP与圆O的交点,所以AP就是切点B到圆心O的距离。
因此,x^2 = AP*BP。
通过以上的切线练习题,我们可以巩固和提高对切线的理解和运用。
中考数学复习----《切线》知识点总与专项练习题(含答案解析)
中考数学复习----《切线》知识点总与专项练习题(含答案解析)知识点总结1.点与圆的位置关系:OP=,则有:点与圆的位置关系有3种.设⊙O的半径为r,点P到圆心的距离dd>①点P在圆外⇔rd=②点P在圆上⇔rd<①点P在圆内⇔r2.三角形的外接圆与外心:经过三角形的三个顶点的圆,叫做三角形的外接圆。
圆心是三角形三条边垂直平分线的交点,叫做三角形的外心。
3.直线与圆的位置关系:设⊙O的半径为r,圆心O到直线l的距离为d,直线和圆的三种位置关系:d>。
①相离:一条直线和圆没有公共点。
直线l和⊙O相离⇔r②相切:一条直线和圆只有一个公共点,叫做这条直线和圆相切,这条直线叫圆的切d=。
线,唯一的公共点叫切点。
直线l和⊙O相切⇔r③相交:一条直线和圆有两个公共点,此时叫做这条直线和圆相交,这条直线叫圆的d<。
割线。
直线l和⊙O相交⇔r4.切线的性质:①圆的切线垂直于经过切点的半径。
②经过圆心且垂直于切线的直线必经过切点。
③经过切点且垂直于切线的直线必经过圆心。
运用切线的性质进行计算或证明时,常常作的辅助线是连接圆心和切点,通过构造直角三角形或相似三角形解决问题。
5.切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线。
在判定一条直线为圆的切线时,当已知条件中未明确指出直线和圆是否有公共点时,常过圆心作该直线的垂线段,证明该线段的长等于半径,可简单的说成“无交点,作垂线段,证半径”;当已知条件中明确指出直线与圆有公共点时,常连接过该公共点的半径,证明该半径垂直于这条直线,可简单地说成“有交点,作半径,证垂直”。
练习题1、(2022•常州)如图,△ABC是⊙O的内接三角形.若∠ABC=45°,AC=,则⊙O的半径是.【分析】连接AO并延长交⊙O于点D,连接CD,根据直径所对的圆周角是直角可得∠ACD =90°,再利用同弧所对的圆周角相等可得∠ADC=45°,然后在Rt△ACD中,利用锐角三角函数的定义求出AD的长,从而求出⊙O的半径,即可解答.【解答】解:连接AO并延长交⊙O于点D,连接CD,∵AD是⊙O的直径,∴∠ACD=90°,∵∠ABC=45°,∴∠ADC=∠ABC=45°,∴AD===2,∴⊙O的半径是1,故答案为:1.2、(2022•黑龙江)如图,在⊙O中,AB是⊙O的弦,⊙O的半径为3cm.C为⊙O上一点,∠ACB=60°,则AB的长为cm.【分析】连接AO并延长交⊙O于点D,根据直径所对的圆周角是直角可得∠ABD=90°,再利用同弧所对的圆周角相等可求出∠ADB=60°,然后在Rt△ABD中,利用锐角三角函数的定义进行计算即可解答.【解答】解:连接AO并延长交⊙O于点D,∵AD是⊙O的直径,∴∠ABD=90°,∵∠ACB=60°,∴∠ADB=∠ACB=60°,在Rt△ABD中,AD=6cm,∴AB=AD•sin60°=6×=3(cm),故答案为:3.3、(2022•玉林)如图,在5×7网格中,各小正方形边长均为1,点O,A,B,C,D,E均在格点上,点O是△ABC的外心,在不添加其他字母的情况下,则除△ABC外把你认为外心也是O的三角形都写出来.【分析】由网格利用勾股定理分别求解OA,OB,OC,OD,OE,根据三角形的外心到三角形顶点的距离相等可求解.【解答】解:由图可知:OA=,OB=,OC=,OD=,OE=,∴OA=OB=OC=OD≠OE,∴△ABD,△ACD,△BCD的外心都是点O,故答案为:△ABD,△ACD,△BCD.4、(2022•凉山州)如图,在边长为1的正方形网格中,⊙O是△ABC的外接圆,点A,B,O 在格点上,则cos∠ACB的值是.【分析】先连接AD,BD,然后根据题意,可以求得cos∠ADB的值,再根据圆周角定理可以得到∠ACB=∠ADB,从而可以得到cos∠ACB的值.【解答】解:连接AD,BD,AD和BD相交于点D,∵AD是⊙O的直径,∴∠ABD=90°,∵AB=6,BD=4,∴AD===2,∴cos∠ADB===,∵∠ACB=∠ADB,∴cos∠ACB的值是,故答案为:.5、(2022•资阳)如图,△ABC内接于⊙O,AB是直径,过点A作⊙O的切线AD.若∠B=35°,则∠DAC的度数是度.【分析】根据直径所对的圆周角是直角,可得∠BAC=55°,再根据切线的性质可得∠BAD=90°,即可求解.【解答】解:∵AB为直径,∴∠C=90°,∵∠B=35°,∴∠BAC=55°,∵AD与⊙O相切,∴AB⊥AD,即∠BAD=90°,∴∠CAD=90°﹣∠BAC=35°.故答案为:35.6、(2022•衢州)如图,AB切⊙O于点B,AO的延长线交⊙O于点C,连结BC.若∠A=40°,则∠C的度数为.【分析】连接OB,先根据切线的性质求出∠AOB,再根据OB=OC,∠AOB=∠C+∠OBC 即可解决问题.【解答】解:如图,连接OB.∵AB是⊙O切线,∴OB⊥AB,∴∠ABO=90°,∵∠A=40°,∴∠AOB=90°﹣∠A=50°,∵OC=OB,∴∠C=∠OBC,∵∠AOB=∠C+∠OBC,∴∠C=25°.故答案为:25°.7、(2022•盐城)如图,AB、AC是⊙O的弦,过点A的切线交CB的延长线于点D,若∠BAD =35°,则∠C=°.【分析】连接AO并延长交⊙O于点E,连接BE,根据切线的性质可得∠OAD=90°,从而求出∠BAE=55°,然后利用直径所对的圆周角是直角可得∠ABE=90°,从而利用直角三角形的两个锐角互余可求出∠E的度数,最后根据同弧所对的圆周角相等,即可解答.【解答】解:连接OA并延长交⊙O于点E,连接BE,∵AD与⊙O相切于点A,∴∠OAD=90°,∵∠BAD=35°,∴∠BAE=∠OAD﹣∠BAD=55°,∵AE是⊙O的直径,∴∠ABE=90°,∴∠E=90°﹣∠BAE=35°,∴∠C=∠E=35°,故答案为:35.8、(2022•上海)定义:有一个圆分别和一个三角形的三条边各有两个交点,截得的三条弦相等,我们把这个圆叫作“等弦圆”,现在有一个斜边长为2的等腰直角三角形,当等弦圆最大时,这个圆的半径为.【分析】根据题意画出相应的图形,利用圆周角定理、直角三角形的边角关系以及三角形的面积公式进行计算即可.【解答】解:如图,∵圆与三角形的三条边都有两个交点,截得的三条弦相等,∴圆心O 就是三角形的内心,∴当⊙O 过点C 时,且在等腰直角三角形ABC 的三边上截得的弦相等,即CG =CF =DE ,此时⊙O 最大,过点O 分别作弦CG 、CF 、DE 的垂线,垂足分别为P 、N 、M ,连接OC 、OA 、OB , ∵CG =CF =DE ,∴OP =OM =ON ,∵∠C =90°,AB =2,AC =BC ,∴AC =BC =×2=,由S △AOC +S △BOC +S △AOB =S △ABC ,∴AC •OP +BC •ON +AB •OM =S △ABC =AC •BC ,设OM =x ,则OP =ON =x ,∴x +x +2x =×, 解得x =﹣1, 即OP =ON =﹣1,在Rt △CON 中,OC =ON =2﹣,故答案为:2﹣.9、(2022•泰州)如图,PA 与⊙O 相切于点A ,PO 与⊙O 相交于点B ,点C 在AmB ⌒上,且与点A、B不重合.若∠P=26°,则∠C的度数为°.【分析】连接AO并延长交⊙O于点D,连接DB,由切线的性质得出∠OAP=90°,由∠P =26°,求出∠AOP=64°,由圆周角定理即可求出∠C=∠D=32°.【解答】解:如图,连接AO并延长交⊙O于点D,连接DB,∵PA与⊙O相切于点A,∴∠OAP=90°,∵∠P=26°,∴∠AOP=90°﹣∠P=90°﹣26°=64°,∴∠D=∠AOP=×64°=32°,∵点C在上,且与点A、B不重合,∴∠C=∠D=32°,故答案为:32.10、(2022•宁波)如图,在△ABC中,AC=2,BC=4,点O在BC上,以OB为半径的圆与AC相切于点A.D是BC边上的动点,当△ACD为直角三角形时,AD的长为.【分析】根据切线的性质定理,勾股定理,直角三角形的等面积法解答即可.【解答】解:连接OA,过点A作AD⊥BC于点D,∵圆与AC相切于点A.∴OA⊥AC,由题意可知:D点位置分为两种情况,①当∠CAD为90°时,此时D点与O点重合,设圆的半径=r,∴OA=r,OC=4﹣r,∵AC=2,在Rt△AOC中,根据勾股定理可得:r2+4=(4﹣r)2,解得:r=,即AD=AO=;②当∠ADC=90°时,AD=,∵AO=,AC=2,OC=4﹣r=,∴AD=,综上所述,AD的长为或,故答案为:或.11、(2022•金华)如图,木工用角尺的短边紧靠⊙O于点A,长边与⊙O相切于点B,角尺的直角顶点为C.已知AC=6cm,CB=8cm,则⊙O的半径为cm.【分析】连接OA,OB,过点A作AD⊥OB于点D,利用矩形的判定与性质得到BD=AC =6cm,AD=BC=8cm,设⊙O的半径为rcm,在Rt△OAD中,利用勾股定理列出方程即可求解.【解答】解:连接OA,OB,过点A作AD⊥OB于点D,如图,∵长边与⊙O相切于点B,∴OB⊥BC,∵AC⊥BC,AD⊥OB,∴四边形ACBD为矩形,∴BD=AC=6cm,AD=BC=8cm.设⊙O的半径为rcm,则OA=OB=rcm,∴OD=OB﹣BD=(r﹣6)cm,在Rt△OAD中,∵AD2+OD2=OA2,∴82+(r﹣6)2=r2,解得:r=.故答案为:.12、(2022•湖北)如图,点P 是⊙O 上一点,AB 是一条弦,点C 是APB ⌒上一点,与点D 关于AB 对称,AD 交⊙O 于点E ,CE 与AB 交于点F ,且BD ∥CE .给出下面四个结论: ①CD 平分∠BCE ;②BE =BD ;③AE 2=AF •AB ;④BD 为⊙O 的切线.其中所有正确结论的序号是 .【分析】根据题意可得AB 是CD 的垂直平分线,从而可得AD =AC ,BD =BC ,再利用等腰三角形和平行线的性质可得CD 平分∠BCE ,即可判断①;根据圆内接四边形对角互补和平角定义可得∠DEB =∠ACB ,再利用SSS 证明△ADB ≌△ACB ,然后利用全等三角形的性质可得∠ADB =∠ACB ,从而可得∠DEB =∠ADB ,即可判断②;根据等弧所对的圆周角相等可得∠AEF ≠∠ABE ,从而可得△AEF 与△ABE 不相似,即可判断③;连接OB ,交EC 于点H ,利用①②的结论可得BE =BC ,从而可得=,然后利用垂径定理可得∠OHE =90°,最后利用平行线的性质可求出∠OBD =90°,即可解答.【解答】解:∵点C 与点D 关于AB 对称,∴AB 是CD 的垂直平分线,∴AD =AC ,BD =BC ,∴∠BCD =∠BDC ,∵BD ∥CE ,∴∠BDC =∠DCE ,∴CD平分∠BCE;故①正确;∵四边形ACBE是⊙O的内接四边形,∴∠ACB+∠AEB=180°,∵∠AEB+∠DEB=180°,∴∠DEB=∠ACB,∵AD=AC,BD=BC,AB=AB,∴△ADB≌△ACB(SSS),∴∠ADB=∠ACB,∴∠DEB=∠ADB,∴BD=BE,故②正确;∵AC≠AE,∴≠,∴∠AEF≠∠ABE,∴△AEF与△ABE不相似,故③不正确;连接OB,交EC于点H,∵BD=BE,BD=BC,∴BE=BC,∴=,∴OB⊥CE,∵BD∥CE,∴∠OHE=∠OBD=90°,∵OB是⊙O的半径,∴BD为⊙O的切线,故④正确;所以给出上面四个结论,其中所有正确结论的序号是:①②④,故答案为:①②④.。
2018-2019学年度人教版数学九年级上册《24.2.3切线的判定和性质》同步练习含答案
20.如图,在平面直角坐标系 xOy 中,半径为 2 的⊙P 的圆心 P 的坐标为(﹣3,0),将⊙P 沿 x 轴正方向以 0.5 个单位/秒的速度平移,使⊙P 与 y 轴相切,则平移的时间为 秒.
21.已知,如图,AB 是⊙O 的直径,点 P 在 BA 的延长线上,弦 CD 交 AB 于 E,连接 OD、PC、BC,∠AOD=2∠ABC,∠P=∠D,过 E 作弦 GF⊥BC 交圆于 G、F 两点,连接 CF、BG.则下列结论: ①CD⊥AB;②PC 是⊙O 的切线;③OD∥GF;④弦 CF 的弦心距等于 BG.则其中正确的是 (只需填序号)
A.4
B.8
C.4 或 6
D.4 或 8
二.填空题(共 6 小题)
16.在平面直角坐标系中,点 P 的坐标为(﹣4,0),半径为 1 的动圆⊙P 沿 x 轴正方向运动, 若运动后⊙P 与 y 轴相切,则点 P 的运动距离为 .
17.如图,直线 PA 是⊙O 的切线,AB 是过切点 A 的直径,连接 PO 交⊙O 于点 C,连接 BC, 若∠ABC=25°,则∠P 的度数为 .
B.2
C.
D.2
5.如图,∠NAM=30°,O 为边 AN 上一点,以点 O 为圆心,2 为半径作⊙O,交 AN 边于 D、E
两点,则当⊙O 与 AM 相切时,AD 等于( )Fra bibliotekA.4
B.3
C.2
D.1
6.如图,矩形 ABCD 中,G 是 BC 的中点,过 A、D、G 三点的圆 O 与边 AB、CD 分别交于点 E、点 F,给出下列说法:(1)AC 与 BD 的交点是圆 O 的圆心;(2)AF 与 DE 的交点是圆 O 的圆心;(3)BC 与圆 O 相切,其中正确说法的个数是( )
中考数学总复习《圆的切线证明》专题训练(附带答案)
中考数学总复习《圆的切线证明》专题训练(附带答案)学校:___________班级:___________姓名:___________考号:___________⊥于点D,E是AC上一点,以BE为直径的O交1.如图,在ABC中,AB=AC,AD BC∠=︒.BC于点F,连接DE,DO,且90DOB(1)求证:AC是O的切线;(2)若1DF=,DC=3,求BE的长.、2.如图,在O中,BC为非直径弦,点D是BC的中点,CD是ABC的角平分线.∠=∠;(1)求证:ACD ABC(2)求证:AC是O的切线;(3)若1BD=,3BC=时,求弦BD与BD围城的弓形面积.是O的切线;=,且AC BD已知等腰ABC,AB=AC为直径作O交BC于点延长线于点F.是O的切线;CD=2,求O的半径.与O相离,,交O于点A是O上一点,连于点C,且PB(1)求证:PB是O的切线;(2)若25AC=,OP=5,求O的半径.6.如图,点O是ABC的边AC上一点,以点O为圆心,OA为半径作O,与BC相切于点E,连接OB,OE,O交OB于点D,连接AD并延长交CB的延长线于点F,且AOD EOD.∠=∠(1)求证:AB是O的切线;BC=,AC=8,求O的半径.(2)若107.如图,AB 是O 的直径,AC 是O 的弦.(1)尺规作图:过点C 作O 的切线,交AB 的延长线于点D (保留作图痕迹,不写作法);(2)若2BD OB ==,求AC 的长.8.如图,ABCD 的顶点,,A B C 在O 上,AC 为对角线,DC 的延长线交O 于点E ,连接,,OC OE AE .(1)求证:AE BC =;(2)若AD 是O 的切线6,40OC D =∠=︒,求CE 的长.9.如图,Rt ABC △中90C ∠=︒,点E 为AB 上一点,以AE 为直径的O 上一点D 在BC 上,且AD 平分BAC ∠.(1)证明:BC 是O 的切线;(2)若42BD BE ==,,求AB 的长.10.如图,已知O 的弦AB 等于半径,连接OA 、OB ,并延长OB 到点C ,使得BC OB =,连接AC ,过点A 作AE OB ⊥于点E ,延长AE 交O 于点D .(1)求证:AC 是O 的切线;(2)若6BC =,求AD 的长.11.如图,线段AB 经过O 的圆心.O 交O 于A ,C 两点,AD 为O 的弦,连接BD ,30A ABD ∠=∠=︒连接DO 并延长交O 于点E ,连接BE 交O 于点F .(1)求证:BD 是O 的切线;(2)若1BC =,求BF 的长.12.如图,AB 为O 的直径,C 为O 上一点,CD BD ABC CBD ⊥∠=∠.(1)求证:CD 为O 的切线.(2)当1,4BD AB ==时,求CD 的长.13.如图 已知AB 是O 的直径 BC AB ⊥于B E 是OA 上的一点ED BC ∥交O 于D OC AD ∥ 连接AC 交ED 于F .(1)求证:CD 是O 的切线;(2)若8AB = 1AE = 求ED EF 的长.14.如图 AB 是O 的直径 AC BC ,是弦 点D 在AB 的延长线上 且DCB DAC ∠=∠ O 的切线AE 与DC 的延长线交于点E .(1)求证:CD 是O 的切线;(2)若O 的半径为2 30D ∠=︒ 求AE 的长.15.如图 已知AB 是O 的直径 点P 在BA 的延长线上 弦BC 平分PBD ∠且BD PD ⊥于点D .(1)求证:PD 是O 的切线.(2)若8cm 6cm AB BD , 求弧AC 的长.为O的直径在O上连接的延长线交于E.是O的切线;∠tan BDF为O的直径的平分线交O于点E BC的延长线于点(1)求证:DE 为O 切线;(2)若10AB = 6BC = 求DE 的长.18.如图 O 是ABC 的外接圆 点D 在BC 延长线上 且满足CAD B ∠=∠.(1)求证:AD 是O 的切线;(2)若AC 是BAD ∠的平分线 3sin 5B =4BC = 求O 的半径.参考答案:1.【分析】此题重点考查圆周角定理 切线的判定定理 勾股定理 三角形的中位线定理 等腰三角形的“三线合一” 线段的垂直平分线的性质等知识 正确地作出辅助线是解题的关键.是O的切线;+=314是O的直径90︒则22BE=+4(22)⊥AD BC是O的半径是O的切线.)连接EFDC=DF33+=+BD DF∠OE DOBDE=.3是O的直径90︒.中EF=中BE=(3)23312π- 【分析】此题考查了解直角三角形 切线的判定以及扇形的面积.注意掌握辅助线的作法 .(1)点D 是BC 的中点 可以得到BD CD = 即可得到DBC DCB ∠∠= 再根据角平分线的定义得到ACD BCD ∠∠= 进而得到结论;(2)连接OC OD OB 则可得到OD BC ⊥ 然后根据等边对等角可以得到90OCD ACD ∠∠+=︒ 即可得到结论(3)先求出60ODB ∠=︒ 继而利用OBD OBD S S S=-阴影部分扇形求得答案.【详解】(1)解:如图 ∵点D 是BC 的中点∵BD CD =∵DBC DCB ∠∠=又∵CD 是ABC 的角平分线∵ACD BCD ∠∠=∵ACD ABC ∠∠=;(2)证明:如图 连接OC OD OB∵点D 是BC 的中点∵OD BC ⊥∵90ODC BCD ∠∠+=︒∵OD OC =∵ODC OCD ∠∠=又∵ACD BCD ∠∠=∵90OCD ACD ∠∠+=︒即OC AC ⊥∵OC 是O 的半径∵AC 是O 的切线;Rt BDE 中 ODB ∠=60ODB =︒OB OD =∵OBD 是等边三角形BOD ∠=OBD S S==阴影部分.(1)见解析(2)23进而得出BFG 是等边三角形 是O 的切线;)解:如图所示∵OD AC ⊥∵AD CD =∵BD AC =∵BD AC =∵AD BC =∵AD CD BC ==;∵AB 为半圆O 的直径∵90CAB CBA ∠+∠=︒∵30DAC CAB ABD ∠=∠=∠=︒∵60GBF G ∠=∠=︒ 12GB AG =∵BFG 是等边三角形 223AB AG BG BG =-=∵3233BF BG AB ===. 【点睛】本题考查了切线的判定 弧与弦的关系 直径所对的圆周角是直角 勾股定理 等边三角形的性质与判定 垂径定理 熟练掌握以上知识是解题的关键.4.(1)证明(2)233【分析】本题主要考查切线的性质和判定及特殊角的三角函数的应用 掌握切线问题中的辅助线的作法是解题的关键.(1)连接OD 证明ODB C ∠=∠ 推出AC OD ∥ 即可证明结论成立;(2)连接AD 在Rt CED 中 求得利用三角形函数的定义求得30C ∠=︒ 60AOD ∠=︒ 在Rt ADB 中 利用勾股定理列式计算求得圆的半径即可.【详解】(1)证明:连接OD又OB OD=B ODB∴∠=∠ODB∴∠=∠AC OD∥DF AC⊥OD DF∴⊥DF∴是O的切线;(2)连接AD设O半径为Rt CED中3,CE CD=22ED CD∴=-又cosCE CCD ∠=30C∴∠=︒30B∴∠=︒60AOD=∠AB是O的直径.90ADB∴∠=︒12AD AB r ∴== ∵AB AC =∵2CD BD ==又222AD BD AB +=2222(2)r r ∴+=233r ∴=(负值已舍). 5.(1)证明见解析(2)3【分析】本题考查的是勾股定理的应用 等腰三角形的性质 切线的判定 熟练的证明圆的切线是解本题的关键;(1)连接OB 证明PCB PBC ∠=∠ OAB OBA ∠=∠ 再证明90PBC OBA ∠+∠=︒即可;(2)设O 的半径为r 表示()()22222255PC AC AP r =-=-- 222225PB OP OB r =-=- 再利用PB PC =建立方程求解即可.【详解】(1)解:连接OB∵PB PC = OA OB =∵PCB PBC ∠=∠ OAB OBA ∠=∠∵OP l ⊥ OAB PAC ∠=∠∵90BCP CAP BCP OAB ∠+∠=︒=∠+∠∵90PBC OBA ∠+∠=︒∵90OBP ∠=︒∵OB PB ⊥是O 的切线;)设O 的半径为l 2AC =2AC AP =-PB BP 2OP OB =-∵O 的半径为【点睛】.(1)见解析(2)3【分析】本题主要考查切线的判定和性质证AOB EOB ≌ 得出的半径为r 则OE OA =根据AOB EOB ≌得求得4CE = 在Rt OCE 中运用勾股定理列式求出r 的值即可. )证明:在AOB 和EOB 中∵()SAS AOB EOB ≌OAF OEF ∠=∠BC 与O 相切OE BC ⊥90OAB OEB ∠=∠=︒AF是O 的半径是O 的切线;(2)解:在Rt CAB △中 90108CAB BC AC ∠=︒==,,∵22221086AB BC AC =-=-=设圆O 的半径为r 则,OE OA r ==∵8OC r =-∵,AOB EOB ≌∵6BE AB ==∵10,BC =∵1064,CE BC BE =-=-=在Rt OCE 中 222OE CE OC +=∵()22248r r +=-解得3r =.∵O 的半径为3.7.(1)作图见解析(2)4π3【分析】本题考查了作图 复杂作图 切线的性质 等边三角形的判定与性质 弧长的计算 熟练掌握切线的性质 弧长公式是解答本题的关键.(1)根据题意 连接OC 作OC CD ⊥ 交AB 的延长线于点D 由此得到答案. (2)根据题意 得到OBC △是等边三角形 求出120AOC ∠=︒ 再利用弧长公式 得到答案.【详解】(1)解:如图所示 CD 即为所求.(2)如图所示 连接BCBD)证明:在ABCD中AE AD ∴=∵AE BC =.(2)解:连接OA 过点O 作OF CE ⊥于点F 如图所示:AD 是O 的切线OA AD ∴⊥OA BC ∴⊥AB AC ∴=40AEC B D ︒∠=∠=∠=40ACB B ∴∠=∠=︒在ABCD 中 AD BC ∥40DAC ACB ∴∠=∠=︒又180100DAE D AEC ∠=︒-∠-∠=︒60CAE DAE CAD ∴∠=∠-∠=︒2120COE CAE ∴∠=∠=︒OC OE =30OCE ∴∠=︒OF CE ⊥22cos3063CE CF OC ∴==⋅︒=.【点睛】本题主要考查了切线的性质 解直角三角形 圆周角定理 平行四边形的性质垂径定理 等腰三角形的判定 解题的关键是作出辅助线 熟练掌握相关的判定和性质.9.(1)证明详见解析;(2)8.【分析】本题考查了切线的判定 勾股定理等知识 熟练掌握切线的判定定理 勾股定理是解题的关键.(1)连接OD 根据平行线判定推出OD AC ∥ 推出OD BC ⊥ 根据切线的判定推出即可;(2)根据勾股定理求出3OD OA OE === 再根据线段的和差求解即可.【详解】(1)证明:连接OD∵OA OD =∵OAD ODA ∠=∠∵AD 平分BAC ∠∵BAD CAD ∠=∠∵ODA CAD ∠=∠∵OD AC ∥∵180C ODC ∠+∠=︒∵90C ∠=︒∵90ODC ∠=︒∵OD BC ⊥∵OD 为半径∵BC 是O 的切线;(2)解:设OD OE r ==在Rt ODB △中 42BD BE ==,∵2OB r =+由勾股定理 得:()22242r r +=+ 解得:3r =∵3OD OA OE ===∵628AB =+=.10.(1)证明见解析;(2)63.【分析】(1)先证明OAB 是等边三角形 再由性质得出60AOB OAB OBA ∠=∠=∠=︒ 再由BC AB =和角度和差即可求解;(2)先根据等边三角形性质求出132OE OA == 再根据勾股定理求得33AE = 最后由垂径定理即可求解;此题考查了等边三角形的判定与性质 勾股定理和垂径定理 解题的关键是熟练掌握以上知识点的应用.【详解】(1)证明:∵AB OA OB ==∵OAB 是等边三角形∵60AOB OAB OBA ∠=∠=∠=︒∵BC OB =∵BC AB =∵1302BAC BCA OBA ∠=∠=∠=︒ ∵90OAC OAB BAC ∠=∠+∠=︒又∵OA 为O 的半径∵AC 是O 的切线;(2)解:∵6BC =∵6AB OA OB ===∵AD OB ⊥于点E∵30OAE ∠=︒∵132OE OA == ∵2233AE OA OE =-=∵AE OB ⊥∵263AD AE ==.11.(1)见解析∠=)证明:BAD60︒6090︒-︒=OD是O的半径∴直线BD是O的切线;==(2)解:设OD OC△中sin30在Rt BDO解得:1r==+OB OCDE是O的直径∴∠=︒DFE90∠=∠即DFB BDE∠=∠DBF DBE∴△∵BDEBFD△BF BD∴=BD BE337BF ∴= 解得:377BF =. 【点睛】本题考查了切线的判定和性质 相似三角形的性质和判定 圆周角定理 勾股定理等知识点 作出辅助线构造出相似三角形是解题关键.12.(1)见详解(2)3【分析】(1)连接OC 由∠=∠OCB ABC ABC CBD ∠=∠ 得OCB CBD ∠=∠ 则OC BD ∥ 所以18090OCD D ∠=︒-∠=︒ 即可证明CD 为O 的切线;(2)由AB 为的直径 得90ACB ∠=︒ 则ACB D ∠=∠ 而ABC CBD ∠=∠ 所以C ABC BD ∽△△ 则AB CB CB BD = 可求得CB BD AB =⋅ 由勾股定理得22CD CB BD =-.【详解】(1)证明:连接OC 则OC OB =OCB ABC ∴∠=∠ABC CBD ∠=∠OCB CBD ∴∠=∠OC BD ∴∥CD BD ⊥90D ∴∠=︒18090OCD D ∴∠=︒-∠=︒OC 是O 的半径 且CD OC ⊥CD ∴为O 的切线.(2)解:AB 为的直径ABC∠=ABC CBD ∴∽∴AB CBCB BD=1,4BD AB==1 CB BD AB∴=⋅=22CD CB BD∴=-=CD∴的长是【点睛】此题重点考查等腰三角形的性质AD OC∥ADO∴∠OA OD=ADO DAO ∴∠=∠DOC BOC ∴∠=∠OD OB OC OC ==,ODC OBC ∴≌△△∴OBC ODC ∠=∠BC AB ⊥∴90OBC ODC ∠=∠=︒OD 为经过圆心的半径∴CD 是O 的切线;(2)如图所示:作DM BC ⊥交BC 于点M8AB = 1AE =1432OA OB OD AB OE OA AE ∴=====-=, 227DE BM OD OE ==-=令=7CM x CB CD x ==+, 7BE DM ==∴在222Rt DMC CM DM CD +=△,222(7)7x x ∴+=+解得:37x =47BC ∴=DE BC ∥ADE ABC ∴△△∽是O的切线.2)在Rt△是O的切线得出Rt EAD中【详解】(1)证明:连接.是O的直径+∠OCA OCBDCB OCB+∠OCD=︒.90是半径经过O的半径外端∵CD 是O 的切线.(2)解:在Rt OCD △中∵90OCD ∠=︒ 30D ∠=︒ 2OC =∵4OD =.∵6AD AO OD =+=.∵AE 是O 的切线 切点为A∵OA AE ⊥.在Rt EAD 中∵90EAD ∠=︒ 30D ∠=︒ 6AD =∵3tan 306233AE AD =⋅︒=⨯=. 15.(1)见解析(2)4π3【分析】本题考查圆与三角形的综合问题 掌握与圆有关的性质 正确作出辅助线是关键.(1)连接OC 根据条件证明OC BD ∥ 即可证明;(2)根据PCO PDB ∽可得PA 利用余弦值可求出COP ∠ 通过弧长公式求解即可.【详解】(1)证明:连接OC 如图∵OC OB =∵OCB OBC ∠=∠∵弦BC 平分PBD ∠∵DBC OBC ∠=∠∵OCB DBC ∠=∠.∵OC BD ∥∵BD PD ⊥∵OC PD ⊥.为O 的半径是O 的切线;)解:连接OC∵PCO PDB ∽OC PO BD PB= 8cm AB = BD =14cm 2OC AB ==4468PA PA +=+ Rt OCP 中cos COP ∠=60COP =︒AC 的长=(1)证明见解析; 是O 的切线;证明FBD FDA ∽ 得到1tan tan 4BD A BDF AD ∠=∠== 进而得到164DF = 即可求解; 本题考查了切线的判定 相似三角形的判定与性质 等腰三角形的性质 余角性质 根据题意 正确作出辅助线是解题的关键.【详解】(1)证明:连结OD∵CO AB ⊥∵90E C ∠+∠=︒∵FE FD = OD OC =∵E FDE ∠=∠ ∠=∠C ODC∵90FDE ODC ∠+∠=︒∵90ODF ∠=︒∵OD DF ⊥∵FD 是O 的切线;(2)解:连结AD ,OD BD 如图∵AB 为O 的直径∵90ADB ∠=︒∵90∠+∠=︒A ABD∵OB OD =∵OBD ODB ∠=∠∵90A ODB ∠+∠=︒∵FBD FDA ∽DF BD AF AD= 在Rt △ABD 中 tan ∠164DF = 3DF =的平分线交O 于点E∵ED OE ⊥∵DE 为O 切线.(2)过点O 作OM BC ⊥于点M 10AB = 6BC =则132MC MB BC ===,152OB OE AB === 四边形OEDM 时矩形∵DE OM =根据勾股定理 得224DE OM OB BM ==-=.18.(1)见解析(2)103【分析】(1)连接OA OC 与AB 相交于点E 如图 由OA OC = 可得OAC OCA ∠=∠ 根据圆周角定理可得12B AOC ∠=∠ 由已知CAD B ∠=∠ 可得2AOC CAD ∠=∠ 根据三角形内角和定理可得180OCA CAO AOC ∠+∠+∠=︒ 等量代换可得90CAO CAD ∠+∠=︒ 即可得出答案;(2)根据角平分线的定义可得BAC DAC ∠=∠ 由已知可得BAC B =∠∠ 根据垂径定理可得 OC AB ⊥ BE AE = 在Rt BEC △中 根据正弦定理可得3sin 45CE CE B BC === 即可算出CE 的长度 根据勾股定理可算出22BE BC CE =-的长度 设O 的半径为r 则125OE OC CE r =-=- 在Rt AOE △中 222OA OE AE =+ 代入计算即可得出答案. 【详解】(1)证明:连接OA OC 与AB 相交于点E 如图OA OC =OAC ∴∠AC AC =∴12B ∠=CAD ∠=AOC ∴∠=OCA ∠+2CAO ∴∠+CAO ∴∠+OAD ∴∠OA 是O 的半径AD ∴是O 的切线;(2)解:AC 是∠BAC DAC ∴∠=∠CAD B ∠=∠BAC B ∴∠=∠OC AB ∴⊥ BE =在Rt BEC △中4BC =sin CE B BC ∴=125CE ∴=BE BC ∴=设O 的半径为r ,则125OE OC CE r =-=-在Rt AOE △中222OA OE AE =+ 222121655r r ⎛⎫⎛⎫=-+ ⎪ ⎪⎝⎭⎝⎭ 解得:103r =. 【点睛】本题主要考查了切线的性质与判定,垂径定理,勾股定理及解直角三角形, 熟练掌握切线的性质与判定,垂径定理及解直角三角形的方法进行求解是解决本题的关键.。
切线的判定与性质专题练习题含答案
人教版九年级数学上册第二十四章圆24.2点和圆、直线和圆的位置关系切线的判定与性质专题练习题1.下列说法中,正确的是( )A.与圆有公共点的直线是圆的切线B.经过半径外端的直线是圆的切线C.经过切点的直线是圆的切线D.圆心到直线的距离等于半径的直线是圆的切线2.如图,在⊙O中,弦AB=OA,P是半径OB的延长线上一点,且PB=OB,则PA与⊙O的位置关系是_________.3.如图,△ABC的一边AB是⊙O的直径,请你添加一个条件,使BC是⊙O的切线,你所添加的条件为________________.4.如图,在Rt△ABC中,∠C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.求证:AC是⊙O的切线.5. 如图,AB是⊙O的直径,AC切⊙O于A,BC交⊙O于点D,若∠C=70°,则∠AOD的度数为( ) A.70° B.35° C.20° D.40°6.如图,线段AB是⊙O的直径,点C,D为⊙O上的点,过点C作⊙O的切线交AB的延长线于点E,若∠E=50°,则∠CDB等于( )A.20° B.25° C.30° D.40°7.如图,等腰直角三角形ABC中,AB=AC=8,O为BC的中点,以O为圆心作半圆,使它与AB,AC都相切,切点分别为D,E,则⊙O的半径为( )A.8 B.6 C.5 D.48.如图,AB是⊙O的直径,O是圆心,BC与⊙O切于点B,CO交⊙O于点D,且BC=8,CD=4,那么⊙O的半径是______.9.如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.求证:∠BDC=∠A.10.如图,CD是⊙O的直径,弦AB⊥CD于点G,直线EF与⊙O相切于点D,则下列结论中不一定正确的是( )A.AG=BG B.AB∥EF C.AD∥BC D.∠ABC=∠ADC11. 如图,若以平行四边形一边AB为直径的圆恰好与对边CD相切于点D,则∠C=_______度.12. 如图,AB为⊙O的直径,直线l与⊙O相切于点C,AD⊥l,垂足为D,AD交⊙O于点E,连接OC,BE.若AE=6,OA=5,则线段DC的长为______.13.如图,已知△ABC内接于⊙O,BC是⊙O的直径,MN与⊙O相切,切点为A,若∠MAB=30°,则∠B=________度.14.如图,在Rt△ABC中,∠ABC=90°,∠BAC的平分线交BC于D,以D为圆心,DB长为半径作⊙D,求证:AC与⊙D相切.15.如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,且∠D=2∠CAD.(1)求∠D的度数;(2)若CD=2,求BD的长.16.已知△ABC内接于⊙O,过点A作直线EF.(1)如图①,若AB为⊙O的直径,要使EF成为⊙O的切线,还需要添加的一个条件是(至少说出两种):__________________________或者_______________________;(2)如图②,如果AB是不过圆心O的弦,且∠CAE=∠B,那么EF是⊙O的切线吗?试证明你的判断.17.如图,已知直线PA交⊙O于A,B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.(1)求证:CD为⊙O的切线;(2)若DC+DA=6,⊙O的直径为10,求AB的长.答案:1. D2. 相切3. ∠ABC=90°4. 解:连接OD,∵BD为∠ABC平分线,∴∠OBD=∠CBD,∵OB=OD,∴∠OBD=∠ODB,∴∠CBD=∠ODB,∴OD∥BC,∵∠C=90°,∴∠ODA=90°,则AC为⊙O的切线5. D6. A7. D8. 69. 解:连接OD,∵CD是⊙O的切线,∴∠ODC=90°,∴∠ODB+∠BDC=90°,∵AB是⊙O的直径,∴∠ADB=90°,即∠ODB+∠ADO=90°,∴∠BDC=∠ADO,∵OA=OD,∴∠ADO=∠A,∴∠BDC=∠A10. C11. 4512. 413. 6014. 解:过D作DH⊥AC于H,由角平分线的性质可证DB=DH,∴AC与⊙D相切15. 解:(1)∵∠COD=2∠CAD,∠D=2∠CAD,∴∠D=∠COD.∵PD与⊙O相切于点C,∴OC⊥PD,即∠OCD=90°,∴∠D=45°(2)由(1)可知△OCD是等腰直角三角形,∴OC=CD=2,由勾股定理,得OD=22+22=22,∴BD=OD-OB=22-216. (1) ∠BAE=90°∠EAC=∠ABC(2) (2)EF是⊙O的切线.证明:作直径AM,连接CM,则∠ACM=90°,∠M=∠B,∴∠M+∠CAM=∠B+∠CAM=90°,∵∠CAE=∠B,∴∠CAM+∠CAE=90°,∴AE⊥AM,∵AM为直径,∴EF 是⊙O的切线17. 解:(1)连接OC,证∠DAC=∠CAO=∠ACO,∴PA∥CO,又∵CD⊥PA,∴CO⊥CD,∴CD为⊙O 的切线(2)过O作OF⊥AB,垂足为F,∴四边形OCDF为矩形.∵DC+DA=6,设AD=x,则OF=CD=6-x,AF=5-x,在Rt△AOF中,有AF2+OF2=OA2,即(5-x)2+(6-x)2=25,解得x1=2,x2=9,由AD <DF知0<x<5,故x=2,从而AD=2,AF=5-2=3,由垂径定理得AB=2AF=6。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题训练(四) 与圆的切线有关的问题归类
►类型之一利用切线的性质求角的度数
1.2017·镇江如图4-ZT-1,AB是⊙O的直径,AC与⊙O相切,CO交⊙O于点D.若∠CAD =30°,则∠BOD=________°.
图4-ZT-1
2.如图4-ZT-2,在⊙O中,OA⊥OB,D是OB延长线上一点,C是⊙O上一点,AC交OB于点M,且CD切⊙O于点C.猜想∠DMC与∠DCM的关系,并说明理由.
图4-ZT-2
►类型之二利用切线的性质求线段的长度
3.如图4-ZT-3,AB是⊙O的切线,A为切点,AC是⊙O的弦,过点O作OH⊥AC于点H.若OH=2,AB=12,OB=13.
求:(1)⊙O的半径;
(2)AC的长.
图4-ZT-3
►类型之三证明直线是圆的切线
4.如图4-ZT-4所示,已知⊙O的半径为1,DE是⊙O的直径,过点D作⊙O的切线AD,C是AD的中点,AE交⊙O于点B,四边形BCOE是平行四边形.
(1)求AD的长.
(2)BC是⊙O的切线吗?若是,请给出证明;若不是,请说明理由.
图4-ZT-4
►类型之四切线的性质与判定的综合应用
5.2017·凉山如图4-ZT-5,已知AB为⊙O的直径,AD,BD是⊙O的弦,BC是⊙O的切线,切点为B,OC∥AD,BA,CD的延长线相交于点E.
(1)求证:CD是⊙O的切线;
(2)若AE=1,ED=3,求⊙O的半径.
图4-ZT-5
详解详析
1.[答案] 120
[解析] 由AC 与⊙O 相切可得∠CAO=90°,而∠CAD=30°,故∠OAD=60°;由OA =OD ,可得∠ODA=∠OAD=60°;所以∠BOD=∠OAD+∠ODA=60°+60°=120°.
2.解:∠DMC=∠DCM.
理由:连接OC.
∵CD 切⊙O 于点C ,
∴CD ⊥OC ,
∴∠DCM +OCM =90°.
又∵OA⊥OB,
∴∠OMA +∠A=90°.
∵∠OMA =∠DMC,
∴∠DMC +∠A=90°.
∵OA =OC ,
∴∠A =∠OCM,
∴∠DMC =∠DCM.
3.解:(1)连接OA.
∵AB 是⊙O 的切线,A 为切点,
∴OA ⊥AB.
在Rt △AOB 中,
OA =OB 2-AB 2=132-122=5,
∴⊙O 的半径为5.
(2)∵OH⊥AC,
∴在Rt △AOH 中,
AH =OA 2-OH 2=52-22=21.
又∵OH⊥AC,∴AC =2AH =2 21.
4.解:(1)如图,连接BD ,
则∠DBE=90°.
∵四边形BCOE 是平行四边形,
∴BC ∥OE ,BC =OE =1.
在Rt △ABD 中,C 是AD 的中点,
∴BC =1
2AD ,∴AD =2BC =2.
(2)BC 是⊙O 的切线.
证明:如图,连接OB.
由(1)得BC∥OD,
且BC =OD ,
∴四边形BCDO 是平行四边形.
又∵AD 是⊙O 的切线,
∴OD ⊥AD ,∴∠ADO =90°,
∴四边形BCDO 是矩形,
∴∠OBC =90°,
∴OB ⊥BC.
又∵OB 是⊙O 的半径,∴BC 是⊙O 的切线.
5.[解析] (1)证切线有两种方法:(1)连半径,证垂直;(2)作垂线,证半径.首选连接OD ,易证得△COD≌△COB(SAS ),然后由全等三角形的对应角相等,求得∠CDO=90°,即可证得直线CD 是⊙O 的切线;
(2)设⊙O 的半径为R ,则OE =R +1,在Rt △ODE 中,利用勾股定理列出方程,求解即可.
解:(1)证明:如图,连接DO.
∵AD ∥OC ,∴∠DAO =∠COB,∠ADO =∠COD.
又∵OA=OD ,
∴∠DAO =∠ADO,
∴∠COB =∠COD.
在△COD 和△COB 中,
⎩⎪⎨⎪⎧OD =OB ,∠COD =∠COB,OC =OC ,
∴△COD ≌△COB(SAS ),
∴∠CDO =∠CBO.
∵BC 是⊙O 的切线,
∴∠CBO =90°,
∴∠CDO =90°.
又∵点D 在⊙O 上,
∴CD 是⊙O 的切线.
(2)设⊙O 的半径为R ,则OD =R ,OE =R +1.
∵∠CDO =90°,∴∠EDO =90°,
∴ED 2+OD 2=OE 2,
即32+R 2=(R +1)2,解得R =4,
∴⊙O 的半径为4.。
