八年级数学上册第七章平行线的证明一单元综合测试(无答案)(新版)北师大版
北师大版八年级数学上册第七单元《平行线的证明》单元练习题(含答案)

北师大版八年级数学上册第七单元《平行线的证明》单元练习题(含答案)一、单选题1.如图,AB∥CD,AD与BC 相交于点E,若∠A=40°,∠C=35°,则∠BED=()A.70°B.75°C.80°D.85°2.下列四个命题中:①两条直线被第三条直线所截,同位角相等;②平面内的一条直线和两条平行线中的一条相交,则它与另一条也相交;③相等的两个角是对顶角;④垂直于同一条直线的两条直线相互垂直. 真命题有()A.0个 B.1个 C.2个 D.3个3.如图,把一张长方形纸片ABCD沿EF折叠后,点C、D分别落在C'、D'的位置上,ED'的延长线与BC的交点为G,若∠EFG=50°,那么∠1=()A.50°B.60°C.70°D.80°4.如图所示,如果∠D=∠EFC,那么()A.AD∥BC B.EF∥BC C.AB∥DC D.AD∥EF5.在△ABC中,已知∠A=∠B=12∠C,则三角形是( )A.等腰三角形B.等边三角形C.直角三角形D.等腰直角三角形6.下列语句中,是命题的是( )①若∠1=60°,∠2=60°,则∠1=∠2;②同位角相等吗?③画线段AB=CD;④如果a>b,b>c,那么a>c;⑤直角都相等.A.①④⑤B.①②④C.①②⑤D.②③④⑤7.如图,下列判断中错误的是()A.由∠A+∠ADC=180°得到AB∥CDB.由AB∥CD得到∠ABC+∠C=180°C.由∠1=∠2得到AD∥BCD.由AD∥BC得到∠3=∠48.如图,AB∥CD,∠B=20°,∠D=60°,则∠BED的度数为( )A.40°B.80°C.90°D.l00°9.下列结论中。
第七章 平行线的证明 单元测试 2022-2023学年北师大版数学八年级上册
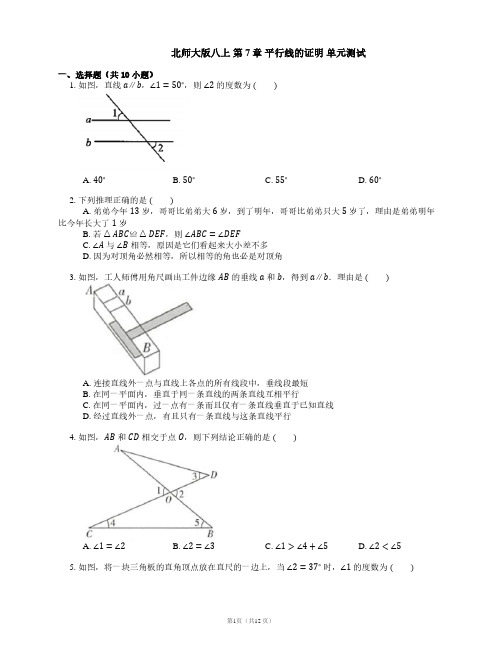
北师大版八上第7章平行线的证明单元测试一、选择题(共10小题)1. 如图,直线a∥b,∠1=50∘,则∠2的度数为( )A. 40∘B. 50∘C. 55∘D. 60∘2. 下列推理正确的是( )A. 弟弟今年13岁,哥哥比弟弟大6岁,到了明年,哥哥比弟弟只大5岁了,理由是弟弟明年比今年长大了1岁B. 若△ABC≌△DEF,则∠ABC=∠DEFC. ∠A与∠B相等,原因是它们看起来大小差不多D. 因为对顶角必然相等,所以相等的角也必是对顶角3. 如图,工人师傅用角尺画出工件边缘AB的垂线a和b,得到a∥b.理由是( )A. 连接直线外一点与直线上各点的所有线段中,垂线段最短B. 在同一平面内,垂直于同一条直线的两条直线互相平行C. 在同一平面内,过一点有一条而且仅有一条直线垂直于已知直线D. 经过直线外一点,有且只有一条直线与这条直线平行4. 如图,AB和CD相交于点O,则下列结论正确的是( )A. ∠1=∠2B. ∠2=∠3C. ∠1>∠4+∠5D. ∠2<∠55. 如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=37∘时,∠1的度数为( )A. 37∘B. 43∘C. 53∘D. 54∘6. 下列命题中,是真命题的是( )A. √9的算术平方根是3B. 数据−2,1,0,2,2,3的方差是83C. y=kx+b(k,b为常数)是一次函数D. 如果一个角的两边与另一个角的两边分别平行,那么这两个角相等7. 如图,在△ABC中,点D在AC上,延长BC至E,连接DE,则下列结论不成立的是( )A. ∠DCE>∠ADBB. ∠ADB>∠DBCC. ∠ADB>∠ACBD. ∠ADB>∠DEC8. 如图是汽车灯的剖面图,从位于O点的灯发出光照射到凹面镜上反射出的光线BA,CD都是水平线,若∠ABO=α,∠DCO=60∘,则∠BOC的度数为( )A. 180∘−αB. 120∘−αC. 60∘+αD. 60∘−α9. 如图,a∥b,M,N分别在a,b上,P为两平行线间一点,那么∠1+∠2+∠3=( )A. 180∘B. 360∘C. 270∘D. 540∘10. 如图,△ABC中,将∠A沿DE翻折,点A落在Aʹ处,∠CEAʹ,∠BDAʹ,∠A三者之间的关系是( )A. ∠CEAʹ=∠BDAʹ+∠AB. ∠CEAʹ−3∠A=∠BDAʹC. ∠CEAʹ=2(∠BDAʹ+∠A)D. ∠CEAʹ−∠BDAʹ=2∠A二、填空题(共6小题)11. 命题“没有公共点的两条直线是平行的”的条件是,结论是,这个命题是命题.12. 如图,若AB∥CD,∠A=110∘,则∠1=∘.13. 如图,AB∥CD,EF分别与AB,CD交于点B,F.若∠E=30∘,∠EFC=130∘,则∠A=.14. 如图,将分别含有30∘,45∘角的一副三角板重叠,使直角顶点重合,若两直角重叠形成的角为65∘,则图中角α的度数为.15. 如图,点E是AD延长线上一点,如果添加一个条件,使BC∥AD,则可添加的条件为.(任意添加一个符合题意的条件即可)16. 一个大门栏杆的平面示意图如图所示,BA垂直地面AE于点A,CD平行于地面AE,若∠BCD=150∘,则∠ABC=∘.三、解答题(共5小题)17. 补全证明过程:(括号内填写理由)如图,一条直线分别与直线BE,直线CE,直线BF,直线CF相交于A,G,H,D,如果∠1=∠2,∠A=∠D,求证:∠B=∠C.证明:∵∠1=∠2,(已知)∠1=∠3,()∴∠2=∠3()∴CE∥BF,()∴∠C=∠4,()又∵∠A=∠D,()∴AB∥,()∴∠B=∠4,()∴∠B=∠C.(等量代换)18. 如图,把一张长方形纸片ABCD沿EF折叠后,点D,C分别落在Dʹ,Cʹ的位置上,EDʹ与BC的交点为G,若∠EFG=55∘,求∠1,∠2的度数.19. 如图①,在三角形ABC中,∠BAE=1∠BAC,∠C>∠B,且FD⊥BC于点D.2(1)试推出∠EFD,∠B,∠C之间的关系;(2)如图②,当点F在AE的延长线上时,其他条件不变,(1)中推导的结论还成立吗?请直接写出结论.20. 如图,AD是△ABC的角平分线,点E在BC的延长线上,求证:∠B+∠1=2∠2.21. 如图①,在平面直角坐标系中,A(0,1),B(4,1),C为x轴正半轴上一点,且AC平分∠OAB.(1)求证:∠OAC=∠OCA;(2)如图②,若分别作∠AOC的三等分线及∠OCA的邻补角的三等分线交于点P,即∠POC=1 3∠AOC,∠PCE=13∠ACE,求∠P的大小;(3)如图③,若∠POC=1n ∠AOC,∠PCE=1n∠ACE,猜想∠OPC的大小.(用含n的式子表示)答案1. B2. B【解析】由全等三角形的性质可知,B 正确.3. B 【解析】由题意得 a ⊥AB ,b ⊥AB ,∴a ∥b (在同一平面内,垂直于同一条直线的两条直线平行).4. A【解析】∵∠1 和 ∠2 是对顶角,∴∠1=∠2,故A 正确;∵∠2=∠A +∠3,∴∠2>∠3,故B 错误;∵∠1=∠4+∠5,故③错误;∵∠2=∠4+∠5,∴∠2>∠5,故D 错误.故选A .5. C【解析】如图,∵AB ∥CD ,∠2=37∘,∴∠2=∠3=37∘,∵∠1+∠3=90∘,∴∠1=53∘.6. B【解析】A .√9=3,3 的算术平方根是 √3,原命题是假命题,不符合题意;B .数据 −2,1,0,2,2,3 的平均数是 1,方差=16×[(−2−1)2+(1−1)2+(0−1)2+(2−1)2×2+(3−1)2]=83,原命题是真命题,符合题意;C .y =kx +b (k ,b 为常数,且 k ≠0)是一次函数,原命题是假命题,不符合题意;D .如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补,原命题是假命题,不符合题意.故选B .7. A【解析】A 选项无法判断;∵∠ADB 是 △BCD 的一个外角,∴∠ADB >∠DBC ,∠ADB >∠ACB ,故选项B ,C 均成立;∵∠ACB 是 △CDE 的一个外角,∴∠ACB >∠DEC ,∴∠ADB >∠DEC ,故选项D 成立.8. C【解析】连接 BC ,∵AB∥CD,∴∠ABO+∠CBO+∠BCO+∠OCD=180∘,又∠CBO+∠BCO+∠BOC=180∘,∴∠BOC=∠ABO+∠DCO=α+60∘.9. B 【解析】过点P作PA∥a,∵a∥b,PA∥a,∴a∥b∥PA,∴∠1+∠MPA=180∘,∠3+∠APN=180∘,∴∠1+∠MPA+∠3+∠APN=180∘+180∘=360∘,∴∠1+∠2+∠3=360∘.10. D【解析】如图,由折叠得∠A=∠Aʹ,∵∠CEAʹ=∠A+∠1,∠1=∠Aʹ+∠BDAʹ,∴∠CEAʹ=∠A+∠Aʹ+∠BDAʹ=2∠A+∠BDAʹ,∴∠CEAʹ−∠BDAʹ=2∠A.故选D.11. 两条直线没有公共点,这两条直线互相平行,假12. 70【解析】如图,∵AB∥CD,∴∠2=∠A=110∘.又∵∠1+∠2=180∘,∴∠1=180∘−∠2=180∘−110∘=70∘.13. 20∘【解析】∵AB∥CD,∴∠ABF+∠EFC=180∘,∵∠EFC=130∘,∴∠ABF=50∘,∵∠A+∠E=∠ABF=50∘,∠E=30∘,∴∠A=20∘.14. 140∘【解析】如图,∵∠ACB=90∘,∠DCB=65∘,∴∠ACD=∠ACB−∠BCD=90∘−65∘=25∘,∵∠A=60∘,∴∠DFB=∠AFC=180∘−∠ACD−∠A=180∘−25∘−60∘=95∘,∵∠D=45∘,∴∠α=∠D+∠DFB=45∘+95∘=140∘.15. ∠A+∠ABC=180∘或∠C+∠ADC=180∘或∠CBD=∠ADB或∠C=∠CDE(答案不唯一)【解析】若∠A+∠ABC=180∘,则BC∥AD;若∠C+∠ADC=180∘,则BC∥AD;若∠CBD=∠ADB,则BC∥AD;若∠C=∠CDE,则BC∥AD,故答案为∠A+∠ABC=180∘或∠C+∠ADC=180∘或∠CBD=∠ADB或∠C=∠CDE(答案不唯一).16. 120【解析】如图,过点B作BG∥CD.∵CD∥AE,CD∥BG,∴∠C+∠CBG=180∘,BG∥AE,∴∠BAE+∠ABG=180∘,又易知∠BAE=90∘,∴∠ABG=90∘,∵∠C=150∘,∴∠CBG=30∘,∴∠ABC=∠ABG+∠CBG=90∘+30∘=120∘.17. 对顶角相等;等量代换;同位角相等,两直线平行;两直线平行,同位角相等;已知;CD;内错角相等,两直线平行;两直线平行,内错角相等18. ∵AD∥BC,∠EFG=55∘,∴∠2=∠GED,∠DEF=∠EFG=55∘,由折叠知∠GEF=∠DEF=55∘,∴∠GED=110∘,∴∠1=180∘−∠GED=70∘,∠2=110∘.19. (1)∠EFD=90∘−∠FED=90∘−(∠B+∠BAE)=90∘−∠B−12∠BAC=90∘−∠B−12(180∘−∠B−∠C)=90∘−∠B−90∘+12∠B+12∠C=12(∠C−∠B).(2)(1)中推导的结论仍成立,∠EFD=12(∠C−∠B).20. ∵AD是△ABC的角平分线,∴∠BAC=2∠BAD,∵∠1=∠B+∠BAC,∠2=∠B+∠BAD,∴∠B+∠1=∠B+∠B+∠BAC=2∠B+2∠BAD=2∠2.21. (1)∵A,B的纵坐标相等,所以AB∥OC,∴∠BAC=∠OCA,又AC平分∠OAB,∴∠OAC=∠BAC,∴∠OAC=∠OCA.(2)由(1)得∠OAC=∠OCA,∴OA=OC,∴∠OAC=∠OCA=45∘,∴∠ACE=135∘,∵∠POC=13∠AOC,∠PCE=13∠ACE,∴∠P=∠PCE−∠POC=13∠ACE−13∠AOC=13×(∠ACE−∠AOC)=13×(135∘−90∘)=15∘.(3)∠OPC=45∘n .证明:∠OPC=∠PCE−∠POC(∠ACE−∠AOC)=1n(135∘−90∘)=1n=45∘.n第11页(共12 页)第12页(共12 页)。
北师大版八年级数学上册第7章《平行线的证明》单元测试(含答案)

第7章《平行线的证明》单元测试一、选择题(本题共10小题,每小题3分,共30分)1.下列语句中,是命题的为().A.延长线段AB到C B.垂线段最短C.过点O作直线a∥b D.锐角都相等吗2.下列命题中是真命题的为().A.两锐角之和为钝角B.两锐角之和为锐角C.钝角大于它的补角D.锐角大于它的余角3.“两条直线相交,有且只有一个交点”的题设是().A.两条直线B.交点C.两条直线相交D.只有一个交点4.如果∠A和∠B的两边分别平行,那么∠A和∠B的关系是().A.相等B.互余或互补C.互补D.相等或互补5.若三角形的一个外角等于与它不相邻的一个内角的4倍,等于与它相邻的内角的2倍,则三角形各角的度数为().A.45°,45°,90°B.30°,60°,90°C.25°,25°,130°D.36°,72°,72°6.如图所示,AB⊥EF,CD⊥EF,∠1=∠F=30°,则与∠FCD相等的角有().A.1个B.2个C.3个D.4个7.下列四个命题中,真命题有().(1)两条直线被第三条直线所截,内错角相等.(2)如果∠1和∠2是对顶角,那么∠1=∠2.(3)一个角的余角一定小于这个角的补角.(4)如果∠1和∠3互余,∠2与∠3的余角互补,那么∠1和∠2互补.A.1个B.2个C.3个D.4个8.如图所示,∠B=∠C,则∠ADC与∠AEB的大小关系是().A.∠ADC>∠AEB B.∠ADC=∠AEBC.∠ADC<∠AEB D.大小关系不能确定9.如图所示,AD平分∠CAE,∠B=30°,∠CAD=65°,则∠ACD=().A.50°B.65°C.80°D.95°10.如图所示,已知AB∥CD,AD和BC相交于点O,若∠A=42°,∠C=58°,则∠AOB 的度数为().A.45°B.60°C.80°D.90°二、填空题(本大题共10小题,每小题4分,共40分)11.如图所示,∠1=∠2,∠3=80°,那么∠4=__________.12.如图所示,∠ABC=36°40′,DE∥BC,DF⊥AB于点F,则∠D=__________.13.如图所示,AB∥CD,∠1=115°,∠3=140°,则∠2=__________.14.如果一个三角形三个内角的比是1∶2∶3,那么这个三角形是__________三角形.15.一个三角形的三个外角的度数比为2∶3∶4,则与此对应的三个内角的比为__________.16.如图所示,在△ABC中,BF平分∠ABC,CF平分∠ACB,∠A=65°,则∠BFC=__________.17.“同角的余角相等”的题设是__________,结论是__________.18.如图所示,AB∥EF∥CD,且∠B=∠1,∠D=∠2,则∠BED的度数为__________.19.如果一个等腰三角形底边上的高等于底边的一半,那么这个等腰三角形的顶角等于__________.20.过△ABC的顶点C作AB的垂线,如果该垂线将∠ACB分为40°和20°的两个角,那么∠A,∠B中较大的角的度数是__________.三、解答题(本大题共5小题,共30分)21.(5分)如图所示,已知∠1=∠2,AE∥BC,求证:△ABC是等腰三角形.22.(5分)如图所示,已知直线BF∥DE,∠1=∠2,求证:GF∥BC.23.(6分)如图所示,已知直线AB∥CD,FH平分∠EFD,FG⊥FH,∠AEF=62°,求∠GFC的度数.24.(6分)如图所示,已知直线AB∥CD,∠AEP=∠CFQ,求证:∠EPM=∠FQM.25.(8分)在△ABC中,BE平分∠ABC,AD为BC边上的高,且∠ABC=60°,∠BEC =75°,求∠DAC的度数.参考答案1答案:B2答案:C3答案:C4答案:D5答案:B6答案:B7答案:C8答案:B9答案:C10答案:C11答案:80°∴∠4=∠3=80°.12答案:53°20′13答案:75°14答案:直角15答案:5∶3∶116答案:122.5°17答案:两个角是同一个角的余角这两个角相等18答案:90°19答案:90°20答案:70°21证明:∵AE∥BC,(已知)∴∠2=∠C,(两直线平行,内错角相等)∠1=∠B.(两直线平行,同位角相等)∵∠1=∠2,(已知)∴∠B=∠C.(等量代换)∴AB=AC,△ABC是等腰三角形.(等角对等边)22证明:∵BF∥DE,(已知)∴∠2=∠FBC.(两直线平行,同位角相等)∵∠2=∠1,(已知)∴∠FBC=∠1.(等量代换)∴GF∥BC.(内错角相等,两直线平行)23解:∵AB∥CD,∴∠AEF=∠EFD=62°,∠CFE=180°-∠AEF=118°.又FH平分∠EFD,∴∠EFH=31°.又GF⊥FH,∴∠EFG=90°-31°=59°.∴∠GFC=∠CFE-∠EFG=59°24证明:∵AB∥CD,(已知)∴∠AEF=∠CFM.(两直线平行,同位角相等)又∵∠PEA=∠QFC,(已知)∴∠AEF+∠PEA=∠CFM+∠QFC,(等式性质)即∠PEF=∠QFM.∴PE∥QF.(同位角相等,两直线平行)∴∠EPM=∠FQM.(两直线平行,同位角相等)25解:∵BE平分∠ABC,且∠ABC=60°,∴∠ABE=∠EBC=30°.∴∠C=180°-∠EBC-∠BEC=180°-30°-75°=75°. 又∵∠C+∠DAC=90°,∴∠DAC=90°-∠C=90°-75°=15°.。
第七章平行线的证明单元测试卷20222023学年北师大版八年级数学上册1

第七章 平行线的证明 单元测试卷一、选择题(本大题共10小题,共30分。
在每小题列出的选项中,选出符合题目的一项)1.如图,直线a,b被直线c,d所截.下列条件能判定a/¿b的是( )A. ∠1=∠3B. ∠2+∠4=180∘C. ∠4=∠5D. ∠1=∠22.如图所示,过点P画直线a的平行线b的作法的依据是( )A. 两直线平行,同位角相等B. 同位角相等,两直线平行C. 两直线平行,内错角相等D. 内错角相等,两直线平行3.如图,在下列给出的条件中,不能判定AB/¿DF的是( )A. ∠A+∠2=180°B. ∠A=∠3C. ∠1=∠4D. ∠1=∠34.如图,点E在BC的延长线上,下列条件中能判断AB/¿CD的是( )A. ∠DBC=∠DACB. ∠ABC=∠DCEC. ∠ADC=∠DCED. ∠ADC+∠BCD=180°5.将一把直尺和一块含30°和60°角的三角板ABC按如图所示的位置放置,如果∠CDE=40°,那么∠BAF的大小为( )A. 10°B. 15°C. 20°D. 25°6.如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=37∘时,∠1的度数为( )A. 37∘B. 43∘C. 53∘D. 54∘7.如下图,BF是∠ABD的平分线,CE是∠ACD的平分线,BF与CE交于点G,若∠BDC=130∘,∠BGC=100∘,则∠A的度数为( )A. 60∘B. 70∘C. 80∘D. 90∘8.等腰三角形的一个内角是100°,它的另外两个角的度数是( )A. 50°和50°B. 40°和40°C. 35°和35°D. 60°和20°9.如图要判断一块纸带的两边a,b相互平行,甲、乙、丙三人的折叠与测量方案如下:下列判断正确的是( )A. 甲、乙能得到a ¿/¿ b,丙不能B. 甲、丙能得到a ¿/¿ b,乙不能C. 乙、丙能得到a ¿/¿ b,甲不能D. 甲、乙、丙均能得到a ¿/¿ b10.如图:①②③中,∠A=42°,∠1=∠2,∠3=∠4,则∠O1+∠O2+∠O3=¿度.( )A. 84B. 111C. 225D. 201二、填空题(本大题共8小题,共24分)11.如图,a,b,c三根木条相交,∠1=50°,固定木条b,c,转动木条a,当木条a转到与b所成的∠2为__________时,a ¿/¿ c,理由是_____________________________________.12.将一副三角板(∠A=30∘)按如图所示方式摆放,使得AB/¿EF,则∠1 .13.如图,在△ABD和△ACE中,有下列四个论断:①AB=AC;②AD=AE;③∠B=∠C;④BD=CE.请以其中三个论断作为条件,余下的一个论断作为结论,写出一个正确的命题 .¿用序号⊗⊗⊗⇒⊗的形式写出¿14.如图,点E在AD的延长线上.若添加一个条件,使BC/¿AD,则可添加的条件为 .¿任意添加一个符合题意的条件即可¿15.如图,在△ABC中,∠A=60∘,BM,CM分别是∠ABC,∠ACB的平分线,BN,CN是外角的平分线,则∠M−∠N=¿ .16.如图,AB/¿CD,∠BED=110°,BF平分∠ABE,DF平分∠CDE,则∠BFD=¿______.17.如图所示,AB/¿CD,EC⊥CD.若∠BEC=30°,则∠ABE的度数为______.18.如图,已知直线EF⊥MN,垂足为F,且∠1=140°,则当∠2=¿ (1) 时,AB/¿CD.三、解答题(本大题共8小题,共66分。
北师大版八年级数学上册第七章 平行线的证明 单元测试卷

北师大版八年级数学上册第七章平行线的证明单元测试卷一、选择题(每小题3分,共30分)1、下列语句中,属于定理的是(D)A.在直线AB上取一点EB.如果两个角相等,那么这两个角是对顶角C.同位角相等D.同角的补角相等2、下列结论你能肯定的是(B)A.若5个数的积为负数,则这5个数中只有一个负数B.三个连续整数的积一定能被6整除C.小明的数学成绩一向很好,因此后天的数学竞赛中他一定能获得一等奖D.对顶角相等,两直线垂直3、如图,下列能判定AB∥CD的条件有(C)①∠1=∠2;②∠3=∠4;③∠B=∠5;④∠B+∠BCD=180°.A.1个 B.2个 C.3个 D.4个4、如图,直线AD∥BC.若∠1=42°,∠BAC=78°,则∠2的度数为(C)A.42° B.50° C.60° D.68°5、已知:如图,在△ABC中,∠A=60°,∠C=70°,点D,E分别在AB和AC上,且DE∥BC,则∠ADE的度数是(B)A.40° B.50° C.60° D.70°6、如图,将木条a,b与c钉在一起,∠1=70°,∠2=50°.要使木条a与b平行,木条a旋转的度数至少是(B)A.10° B.20° C.50° D.70°7、如图,直线l l∥l2,直角三角板的直角顶点C在直线l1上,一锐角顶点B在直线l2上,若∠1=35°,则∠2的度数是(B)A.65° B.55° C.45° D.35°8、如图,直线AB∥CD,则下列结论正确的是(D)A.∠1=∠2 B.∠3=∠4C.∠1+∠3=180° D.∠3+∠4=180°9、如图,AB∥CD,EF∥GH,∠1=60°,则∠2补角的度数为(D)A.60° B.100° C.110° D.120°10、如图,在△ABC中,DE是AC的垂直平分线,且分别交BC,AC于点D和E,∠B=60°,∠C=25°,则∠BAD为(B)A.50° B.70° C.75° D.80°二、填空题(每小题3分,共18分)11、如图,点E是AD延长线上一点.若添加一个条件,使BC∥AD,则可添加的条件为∠A+∠ABC=180°或∠C+∠ADC=180°或∠CBD=∠ADB或∠C=∠CDE.(任意添加一个符合题意的条件即可)12、已知代数式-x2+40x-399,小明发现:当x=1时,代数式的值小于0,当x=2,x=3时,代数式的值均小于0,于是得出结论“对于任意的正整数x,代数式-x2+40x-399的值均小于0”.小红认为小明的说法是错误的,请你帮她举个反例:当x=20时,-x2+40x-399>0(答案不唯一).13、将一张长方形纸片按如图所示折叠,若∠1=40°,则∠2的度数是70°.14、如图,把△ABC的纸片沿DE折叠,当点A落在四边形BCED的内部时,则∠A与∠1、∠2之间有一种数量关系始终保持不变,请试着找出这个规律为2∠A=∠1+∠2.15、如图,在△ABC中,∠B=∠C,∠BAD=40°,∠ADE=∠AED,则∠CDE的度数为20°.16、如图,将一张三角形纸片ABC 的一角折叠,使点A 落在△ABC 外的A′处,折痕为DE.如果∠A=α,∠CEA ′=β,∠BDA ′=γ,那么α,β,γ三个角的关系是γ=2α+β.三、解答题(共72分)17、一个两位数,它的十位数字为a ,个位数字为b ,如果把它的十位数字和个位数字对调,得到一个新的两位数,那么这两个数的和能被11整除.我们可以验证一下,如23,对调后得到32,而23+32=55,55能被11整除.上述说法正确吗?解:这个说法是正确的.理由如下: 由题意,得原来的两位数可表示为(10a +b), 对调后的两位数可表示为(10b +a).所以(10a +b)+(10b +a)=11a +11b =11(a +b). 因为11(a +b)能被11整除, 所以这个说法是正确的.18、如图,∠ABC =∠ACB,BD 平分∠ABC,CE 平分∠ACB,∠DBF =∠F.试说明:EC∥DF.解:∵BD 平分∠ABC, ∴∠DBF =12∠ABC.∵CE 平分∠ACB, ∴∠ECB =12∠ACB.∵∠ABC =∠ACB,∴∠DBF =∠ECB. ∵∠DBF =∠F,∴∠ECB =∠F. ∴EC ∥DF.19、如图,∠AFD =∠1,AC ∥DE. (1)求证:DF∥BC;(2)若∠1=68°,DF 平分∠ADE,求∠B 的度数.解:(1)证明:∵AC∥DE, ∴∠C =∠1. ∵∠AFD =∠1, ∴∠C =∠AFD. ∴DF ∥BC.(2)∵DF∥BC,∴∠EDF =∠1=68°, ∵DF 平分∠ADE,∴∠ADF =∠EDF=68°, ∵DF ∥BC ,∴∠B =∠ADF=68°.19、如图,已知∠ABC=80°,∠BCD =30°,∠CDE =130°,试确定AB 与DE 的位置关系,并说明理由.解:AB∥DE.理由:过点C 作FG∥AB, ∴∠GCB =∠ABC=80°. ∵∠BCD =30°,∴∠DCG =∠GCB-∠BCD=80°-30°=50°. 又∵∠CDE=130°, ∴∠DCG +∠CDE=180°. ∴DE ∥FG.∴AB ∥DE.20、如图,在△ABC 中,AD 平分∠BAC,P 为线段AD 上的一个动点,EP ⊥AD 交直线BC 于点E.(1)若∠B=35°,∠ACB =85°,求∠E 的度数;(2)当点P 在线段AD 上运动时,求证:∠E=12(∠ACB-∠B).解:(1)∵∠B=35°, ∠ACB =85°, ∴∠BAC =60°. ∵AD 平分∠BAC, ∴∠DAB =∠DAC=30°. ∴∠ADC =∠B+∠DAB=65°. 又∵EP⊥AD,∴∠DPE =90°. ∴∠ADC +∠E=90°. ∴∠E =90°-65°=25°.(2)证明:∵∠B+∠BAC+∠ACB=180°,∴∠BAC =180°-(∠B+∠ACB). ∵AD 平分∠BAC,∴∠BAD =12∠BAC=90°-12(∠B+∠ACB).∴∠ADC =∠B+∠BAD=90°-12(∠ACB-∠B).∵EP ⊥AD ,∴∠DPE =90°. ∴∠ADC +∠E=90°. ∴∠E =90°-∠ADC, 即∠E=12(∠ACB-∠B).21、观察下列等式:第1个等式:a 1=11×3=12×(1-13);第2个等式:a 2=13×5=12×(13-15);第3个等式:a 3=15×7=12×(15-17);…请按以上规律解答下列问题: (1)列出第5个等式: a 5=19×11=12×(19-111);(2)a 1+a 2+a 3+…+a n =12(1-12n +1)(用含n 的代数式表示),并证明.证明:由题意,得a n =12(12n -1-12n +1)所以a 1+a 2+a 3+…a n=12×[(1-13)+(13-15)+…+(12n-1-12n+1)]=12(1-12n+1).22、如图,EF∥AB,∠DCB=70°,∠CBF=20°,∠EFB=130°.(1)直线CD与AB平行吗?为什么?(2)若∠CEF=68°,求∠ACB的度数.解:(1)平行.理由如下:∵EF∥AB,∠EFB=130°,∴∠ABF=180°-130°=50°.∵∠CBF=20°,∴∠CBA=∠ABF+∠CBF=70°.∵∠DCB=70°,∴∠CBA=∠DCB.∴CD∥AB.(2)∵EF∥AB,∠CEF=68°,∴∠A=68°.∵CD∥AB,∴∠ACD+∠A=180°.∴∠ACD=180°-∠A=180°-68°=112°.∵∠DCB=70°,∴∠ACB=∠ACD-∠DCB=112°-70°=42°.∴∠ACB的度数为42°.23、如图,已知∠A=90°+x°,∠B=90°-x°,∠CED=90°,4∠C-∠D=30°,射线EF∥AC.(1)判断射线EF 与BD 的位置关系,并说明理由; (2)求∠C,∠D 的度数.解:(1)EF∥BD.理由:∵∠A +∠B=90°+x °+90°-x °=180°, ∴AC ∥BD. ∵EF ∥AC , ∴EF ∥BD. (2)∵AC∥EF∥BD, ∴∠CEF =∠C,∠DEF =∠D. ∵∠CED =∠CEF+∠DEF=90°, ∴∠C +∠D=90°.联立⎩⎪⎨⎪⎧∠C+∠D=90°,4∠C -∠D=30°,解得⎩⎪⎨⎪⎧∠C=24°,∠D =66°.∴∠C 的度数是24°,∠D 的度数是66°.24、(1)如图1,BD 平分∠ABC,CD 平分∠ACB.猜想∠A 与∠D 有什么数量关系?并证明你的结论;(2)如图2,BD 平分∠CBP,CD 平分∠BCQ,(1)中的猜想还正确吗?如果不正确,请你写出正确的结论,并证明你的结论.解:(1)猜想:∠D=90°+12∠A.证明:∵∠DBC=12∠ABC,∠DCB =12∠ACB,∴∠DBC +∠DCB=12(∠ABC+∠ACB)=12(180°-∠A)=90°-12∠A.∴∠D =180°-(∠DBC+∠DCB)=180°-(90°-12∠A)=90°+12∠A.(2)不正确.结论:∠D=90°-12∠A.证明:∵∠DBC=12∠PBC,∠DCB =12∠QCB,∴∠DBC +∠DCB=12(∠PBC+∠QCB)=12(∠A+∠ACB +∠A+∠ABC)=12(180°+∠A)=90°+12∠A.∴∠D =180°-(∠DBC+∠DCB)=180°-(90°+12∠A)=90°-12∠A.25、在△ABC 中,射线AG 平分∠BAC 交BC 于点G ,点D 在BC 边上运动(不与点G 重合),过点D 作DE∥AC 交AB 于点E.(1)如图1,点D 在线段CG 上运动时,DF 平分∠EDB.①若∠BAC=100°,∠C =30°,则∠AFD=115°;若∠B=40°,则∠AFD=110°; ②试探究∠AFD 与∠B 之间的数量关系?请说明理由;(2)如图2,点D 在线段BG 上运动时,∠BDE 的角平分线所在直线与射线AG 交于点F ,试探究∠AFD 与∠B 之间的数量关系,并说明理由.解:(1)②∠AFD=90°+12∠B.理由如下: ∵DE ∥AC ,∴∠EDB =∠C.∵AG 平分∠BAC,DF 平分∠EDB,∴∠BAG =12∠BAC,∠FDG =12∠EDB=12∠C . ∵∠DGF =∠B+∠BAG,∴∠AFD =∠DGF+∠FDG=∠B+∠BAG+∠FDG=∠B+12(∠BAC+∠C) =∠B+12(180°-∠B) =90°+12∠B. (2)∠AFD=90°-12∠B.理由如下: ∵∠EDB =∠C,∠BAG =12∠BAC,∠BDH =12∠EDB=12∠C, 又∵∠AHF=∠B+∠BDH,∴∠AFD =180°-∠BAG-∠AHF=180°-12∠BAC-∠B-∠BDH =180°-12∠BAC-∠B-12∠C =180°-∠B-12(∠BAC+∠C) =180°-∠B-12(180°-∠B)=180°-∠B-90°+12∠B =90°-12∠B.。
北师大版八年级上册数学第七章平行线的证明综合素质评价试题(含答案)

八年级上册数学第七章综合素质评价一、选择题:本大题共12小题,每小题3分,共36分.在每小题列出的四个选项中,只有一个选项是符合题目要求的.1.下列选项中,是命题的是()A.画两条相等的线段B.等于同一个角的两个角相等吗C.延长线段AO到点C,使OC=OAD.两直线平行,内错角相等2.【2022•广东佛山南海区模拟】如图,a∥b,∠1=120°,则∠2等于() A.30°B.90°C.60°D.50°(第2题) (第3题)3.如图,下列条件中,能判定AD∥BC的有()①∠1=∠4;②∠2=∠3;③∠1+∠2=∠3+∠4;④∠A+∠C=180°;⑤∠A+∠ABC=180°;⑥∠A+∠ADC=180°.A.1个B.2个C.3个D.4个4.下列命题中,是假命题的是()A.能够完全重合的两个图形全等B.两边和一角对应相等的两个三角形全等C.等腰三角形的两底角相等D.三个角都相等的三角形是等边三角形5.某学员在驾校练习驾驶汽车,两次拐弯后,行驶的方向与原来的方向相反,则两次拐弯的角度可能是()A.第一次向左拐30°,第二次向右拐30°B.第一次向左拐45°,第二次向左拐45°C.第一次向左拐60°,第二次向右拐120°D.第一次向左拐53°,第二次向左拐127°6.已知在同一平面内有三条不同的直线a,b,c,下列说法错误的是() A.如果a∥b,a⊥c,那么b⊥cB.如果b∥a,c∥a,那么b∥cC.如果b⊥a,c⊥a,那么b⊥cD.如果b⊥a,c⊥a,那么b∥c7.下列说法正确的是()A.命题一定是定理,但定理不一定是命题B.公理和定理都是真命题C.定理和命题一样,有真有假D.“取线段AB的中点C”是一个真命题8.如图,F是△ABC的角平分线CD和BE的交点,CG⊥AB于点G.若∠ACG=36°,则∠DFE的度数是()A.117°B.108°C.144°D.148°(第8题) (第9题)9.如图,在△ABC中,∠A=30°,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D,则∠D等于()A.10°B.15°C.20°D.30°10.如图,在△CEF中,∠E=80°,∠F=50°,AB∥CF,AD∥CE,连接BC,CD,则∠A的度数是()A.45°B.50°C.55°D.80°(第10题) (第11题)11.如图,在△ABC中,AD是BC边上的高,AE平分∠BAC,∠B=45°,∠C =73°,则∠DAE的度数是()A.14°B.24°C.19°D.9°12.如图,AD∥BC,∠D=∠ABC,点E是DC上一点,连接AE并延长,交BC的延长线于点H.点F是AB上一点,且∠FBE=∠FEB,∠FEH的平分线EG交BH于点G,若∠DEH=100°,则∠BEG的度数为()A.30°B.40°C.50°D.60°(第12题) (第14题)二、填空题:本大题共6小题,每小题4分,共24分.13.将命题“等角的余角相等”写成“如果…,那么…”的形式为__________________________________________________________________.14.三角板是我们学习数学的好工具,将一副直角三角板按如图所示的方式摆放,点C在FD的延长线上,点B在DE上,AB∥CF,∠EFD=∠A=90°,∠E =30°,∠ABC=45°,则∠CBD=__________°.15.要说明命题“若a<b,c<d,则a-c<b-d”是假命题,可以举反例:a=4,b=5,c=________,d=________.16.如图,在△ABC中,点D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC =66°,则∠DAC的度数是________.(第16题) (第17题) (第18题)17.如图,在△ABC中,BD平分∠ABC交AC于点D,EF∥BC交BD于点G,若∠BEG=130°,则∠DGF=________°.18.如图,将一张三角形纸片ABC沿DE折叠,使点A落在四边形BCDE外部的点A′处,且点A′与点C在直线AB的异侧,已知∠C=90°,∠A=30°.若△A′DE 的一边与BC平行,则∠ADE的度数是____________.三、解答题(一):本大题共2小题,每小题8分,共16分.19.如图,∠BAC=∠EDF=90°,∠E=45°,∠C=30°,AB与DF交于点M,BC∥EF,求∠BMD的度数.20.如图,已知AB∥CD,E是直线AB上的一点,CE平分∠ACD,CF⊥CE,∠1=32°.(1)求∠ACE的度数;(2)若∠2=58°,求证:CF∥AG.四、解答题(二):本大题共2小题,每小题10分,共20分.21.如图,把△ABC沿EF折叠,使点A落在点D处.(1)若DE∥AC,试判断∠1与∠2的数量关系,并说明理由;(2)若∠B+∠C=130°,求∠1+∠2的度数.22.如图,在四边形ABCD中,CE⊥AD于点E.若(),(),则().(1)从①CB=CD,②∠D+∠ABC=180°,③AC平分∠DAB中选择两个作为条件,剩下的一个作为结论,构成一个真命题,并说明理由,条件:________,________,结论:________.(2)在(1)的条件下,若AD=8,DE=2,CE=3,求△ABC的面积.五、解答题(三):本大题共2小题,每小题12分,共24分.23.已知直线a∥b,直线c和直线a,b分别相交于A,B两点,直线d和直线a,b分别相交于C,D两点.(1)如图①,当点P在线段AB上(点P不与点A,B重合)运动时,猜测∠1,∠2,∠3之间的数量关系,并说明理由;(2)如图②,当点P在线段AB的延长线上运动时,∠1,∠2,∠3之间的数量关系为________;(3)如图③,当点P在线段BA的延长线上运动时,∠1,∠2,∠3之间的数量关系为________.24.钱塘江汛期即将来临,防汛指挥部在一危险地带两岸各安置了一盏探照灯,便于夜间查看江水及两岸河堤的情况.如图,灯A射出的光束自AM顺时针旋转至AN便立即回转,灯B射出的光束自BP顺时针旋转至BQ便立即回转,两灯不停交叉照射.若灯A射出的光束转动的速度是a°/秒,灯B射出的光束转动的速度是b°/秒,且a,b满足|a-3b|+(a+b-4)2=0.假设钱塘江两岸河堤是平行的,即PQ∥MN,且∠BAN=45°.(1)求a,b的值;(2)若灯B射出的光束先转动30秒,灯A射出的光束才开始转动,在灯B射出的光束到达BQ之前,灯A射出的光束转动几秒,两灯射出的光束互相平行?(3)两灯射出的光束同时转动,在灯A射出的光束到达AN之前,若与灯B射出的光束交于点C,过点C作CD⊥AC交PQ于点D,则两灯射出的光束在转动过程中,∠BAC与∠BCD的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请求出其取值范围.答案一、1.D2.C3.B4.B5.D6.C7.B8.A点拨:因为CG⊥AB,∠ACG=36°,所以∠A=90°-∠ACG=54°.所以∠ABC +∠ACB =180°-∠A =126°.因为CD 和BE 是△ABC 的角平分线,所以∠BCD =12∠ACB ,∠CBE =12∠ABC ,所以∠BCD +∠CBE =12(∠ACB +∠ABC )=63°.所以∠BFC =180°-(∠BCD +∠CBE )=117°.又因为∠DFE =∠BFC ,所以∠DFE =117°.9.B 点拨:因为BD ,CD 分别为∠ABC ,∠ACE 的平分线, 所以∠DBC =∠ABD ,∠DCE =∠ACD .因为∠ACE =∠A +∠ABC ,所以∠DCE +∠ACD =∠DBC +∠ABD +∠A .所以2∠DCE =2∠DBC +∠A .因为∠DCE =∠DBC +∠D ,所以2∠DBC +2∠D =2∠DBC +∠A .所以∠D =12∠A =12×30°=15°. 10.B 点拨:如图,连接AC 并延长,交EF 于点M .因为AB ∥CF ,所以∠3=∠1.因为AD ∥CE ,所以∠2=∠4. 所以∠BAD =∠3+∠4=∠1+∠2=∠FCE .因为∠FCE =180°-∠E -∠F =180°-80°-50°=50°.所以∠BAD =50°.故选B .11.A点拨:因为∠B=45°,∠C=73°,所以∠BAC=180°-∠B-∠C=62°.因为AE平分∠BAC,所以∠CAE=12∠BAC=31°.因为AD是BC边上的高,所以∠ADC=90°,所以∠CAD=180°-∠ADC-∠C=17°,所以∠DAE=∠CAE-∠CAD=31°-17°=14°.12.B点拨:设∠FBE=∠FEB=α,则∠AFE=∠FBE+∠FEB=2α.因为EG平分∠FEH,所以∠GEH=∠GEF.设∠GEH=∠GEF=β,则∠AEF=180°-∠GEF-∠GEH=180°-2β.因为AD∥BC,所以∠ABC+∠BAD=180°.又因为∠D=∠ABC,所以∠D+∠BAD=180°,所以AB∥CD,所以∠CEH=∠F AE.因为∠DEH=100°,所以∠CEH=180°-∠DEH=80°.所以∠F AE=80°.因为∠F AE+∠AFE+∠AEF=180°,所以80°+2α+180°-2β=180°,所以β-α=40°,所以∠BEG=∠GEF-∠FEB=β-α=40°.二、13.如果两个角相等,那么它们的余角相等14.1515.2;3(答案不唯一)16.28°17.25点拨:因为EF∥BC,所以∠EGB=∠CBG.因为BD平分∠ABC,所以∠EBG=∠CBG,所以∠EBG=∠EGB.因为∠BEG=130°,所以∠EGB=180°-130°2=25°,所以∠DGF=∠EGB=25°.18.45°或30°点拨:当A′D∥BC时,∠A′DA=∠C=90°.由折叠的性质得∠ADE=∠A′DE,所以∠ADE=12∠A′DA=45°;当A′E∥BC时,∠A′EF=∠ABC.因为∠C=90°,∠A=30°,所以∠A′EF=∠ABC=180°-∠C-∠A=60°. 所以∠A′EA=180°-∠A′EF=120°.由折叠的性质得∠A′ED=∠AED,所以∠AED=12(360°-∠A′EA)=120°.所以∠ADE=180°-∠A-∠AED=30°.综上所述,∠ADE的度数为45°或30°.三、19.解:因为∠BAC=90°,∠C=30°,所以∠B=180°-∠BAC-∠C=60°.因为∠EDF=90°,∠E=45°,所以∠F=180°-∠EDF-∠E=45°.因为BC∥EF,所以∠MDB=∠F=45°,所以∠BMD=180°-∠B-∠MDB=75°. 20.(1)解:因为AB∥CD,所以∠DCE=∠1=32°.因为CE平分∠ACD,所以∠ACE=∠DCE=32°.(2)证明:因为CF⊥CE,所以∠FCE=90°.又因为∠ACE=32°,所以∠FCH=∠FCE-∠ACE=58°.因为∠2=58°,所以∠FCH=∠2,所以CF∥AG.四、21.解:(1)∠1=∠2,理由如下:因为∠D是由∠A翻折得到的,所以∠D=∠A.因为DE∥AC,所以∠1=∠A,∠2=∠D,所以∠1=∠2.(2)因为∠A+∠B+∠C=180°,∠A+∠AEF+∠AFE=180°,所以∠AEF+∠AFE=∠B+∠C=130°.因为△DEF是由△AEF翻折得到的,所以∠AEF=∠DEF,∠AFE=∠DFE,所以∠AED=2∠AEF,∠AFD=2∠AFE,所以∠AED+∠AFD=2(∠AEF+∠AFE)=260°.因为∠1+∠AED+∠2+∠AFD=360°,所以∠1+∠2=100°.22.解:(1)②;③;①理由:如图,在AD上取一点T,使得AT=AB,连接TC.因为AC平分∠DAB,所以∠TAC=∠CAB.在△TAC 和△BAC 中,⎩⎨⎧AT =AB ,∠CAT =∠CAB ,AC =AC ,所以△TAC ≌△BAC ,所以CB =CT ,∠ABC =∠ATC .因为∠ABC +∠D =180°,∠ATC +∠CTD =180°,所以∠D =∠CTD ,易得CT =CD ,所以CB =CD .(答案不唯一)(2)由(1)可知,CT =CD ,因为CE ⊥DT ,所以DE =TE .因为△TAC ≌△BAC ,所以AB =AT =AD -2DE =8-4=4,所以S △ABC =S △ACT =12AT •CE =12×4×3=6.五、23.解:(1)∠3=∠1+∠2,理由如下:过点P 作PE ∥a 交CD 于点E ,如图.因为PE ∥a ,a ∥b ,所以PE ∥a ∥b ,所以∠1=∠CPE,∠2=∠DPE.因为∠3=∠CPE+∠DPE,所以∠3=∠1+∠2.(2)∠1=∠2+∠3(3)∠3=∠2-∠124.解:(1)因为|a-3b|+(a+b-4)2=0,|a-3b|≥0,(a+b-4)2≥0,所以a=3b,a+b=4,所以a=3,b=1.(2)设灯A射出的光束转动t秒,两灯射出的光束互相平行,①当0<t<60时,3t=(30+t)×1,解得t=15;②当60<t<120时,3t-3×60+(30+t)×1=180,解得t=82.5;③当120<t<150时,3t-180×2=(30+t)×1,解得t=195(不合题意,舍去).综上所述,灯A射出的光束转动15秒或82.5秒,两灯射出的光束互相平行.(3)不发生变化.设灯A射出的光束转动时间为x秒,因为∠CAN=180°-3°•x,所以∠BAC=45°-(180°-3°•x)=3°•x-135°.又因为PQ∥MN,所以易得∠BCA=∠CBD+∠CAN=1°•x+180°-3°•x=180°-2°•x.因为∠ACD=90°,所以∠BCD=90°-∠BCA=90°-(180°-2°•x)=2°•x-90°,2所以∠BCD=3∠BAC.。
八年级数学上册 第七章《平行线的证明》单元测试(扫描版)(新版)北师大版

平行线的证明第七章 平行线的证明一、选择题:1. A2. B3. A4. C5. D6.A7. B 8. C 9. D 10 . B 11.A 12.B二、填空题:13. 如果正比例函数 y =kx 中,k >0,那么正比例函数的图象经过一、三象限. 14. 2115.140° 16.100°三、解答题:17. 两直线平行,同位角相等;MFQ ;FQ ;同位角相等,两直线平行.18.解:∵AC∥BD, ∴∠ABE=∠1=64°.∴∠BAC=180°﹣∠1=180°﹣64°=116°.∵AE 平分∠BAC, ∴∠BAE=∠BAC=58°.∴∠2=∠BAE+∠ABE=58°+64°=122°.19. 证明:∵BF 、DE 分别是∠ABC ,∠ADC 的角平分线,∴∠CDE=∠ADC ,∠2=∠ABC ,∵∠ABC =∠ADC ,∴∠CDE =∠2,∵∠1=∠2,∴∠1=∠CDE ,∴DC ∥AB .20. (1)证明:∵BO、CO 分别是∠ABC 和∠ACB 的平分线∴∠ABO =∠CBO, ∠ACO =∠BCO∵EF ∥BC ∴∠EOB =∠CBO, ∠FOC =∠BCO∴∠ABO=∠EOB, ∠ACO=∠FOC ∴OE=BE,OF=CF∵EF=OE+OF ∴EF=BE+CF(2)解:∵∠ABC=52°,∠ACB=60°,BO 、CO 分别是∠ABC 和∠ACB 的平分线, ∴∠OBC+∠OCB=(∠ABC+∠ACB)=(52°+60°)=56°,∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣56°=124°.21.解:∵∠A=30°,∠B=62°,∴∠ACB=180°﹣(∠A+∠B)=180°﹣(30°+62°)=180°﹣92°=88°,∵CE 平分∠ACB,∴∠ECB=∠ACB=44°,∵CD⊥AB 于D ,∴∠CDB=90°,∴∠BCD=90°﹣∠B=90°﹣62°=28°,∴∠ECD=∠ECB﹣∠BCD=44°﹣28°=16°,∵DF⊥CE 于F ,∴∠CFD=90°,∴∠CDF=90°﹣∠ECD=90°﹣16°=74°.22.证明:(1)∵AE ⊥CE , ∴∠AEC =90°, ∴∠2+∠3=90°且∠1+∠4=90°.又∵EC 平分∠DEF , ∴∠3=∠4, ∴∠1=∠2, ∴EA 平分∠BEF .(2)∵AE⊥CE,∴∠AEC=90°,∴∠1+∠4=90°.∵∠1=∠A,∠4=∠C,∴∠B+∠D=180°-2∠1+180°-2∠4=360°-2(∠1+∠4)=180°,∴AB∥CD.23.解:(1)∠F=(∠B+∠D);理由如下:∵∠DHF是△DEH的外角,∠EHC是△FCH的外角,∠DHF=∠EHC,∴∠D+∠1=∠3+∠F①同理,∠2+∠F=∠B+∠4 ②又∵∠DEA,∠BCA的平分线EF、CF相交于F,∴∠1=∠2,∠3=∠4;∴①﹣②得:∠B+∠D=2∠F,即∠F=(∠B+∠D).(2)∵∠B:∠D:∠F=2:4:x,∴设∠B=2α,则∠D=4α,∴∠F=(∠B+∠D)=3α,又∠B:∠D:∠F=2:4:x,∴x=3.。
新北师大版八年级数学上册单元测试卷附答案第七章 平行线的证明

第七章平行线的证明
一、选择题(共15小题;共45分)
1. 如图,已知:,那么下列结论正确的是
A. B. C. D.
2. 下列命题中:
①相等的角是对顶角;
②如果三角形中有一个角是钝角,那么另外两个角为锐角;
③若两直线平行,则内错角相等;
④若,则.其中是真命题的有几个
A. B. C. D.
3. 下列语言是命题的是
A. 画两条相等的线段
B. 等于同一个角的两个角相等吗
C. 延长线段到,使
D. 两直线平行,内错角相等
4. 命题“垂直于同一条直线的两条直线平行”的题设是
A. 垂直
B. 两条直线
C. 同一条直线
D. 两条直线垂直于同一条直线
5. 如图,下列推理中错误的是
A. ,
B. ,
C. ,
D. ,
6. 如图,直线,射线与直线相交于点,过点作于点,已知
,则的度数为
A. B. C. D.
7. 如图,,,,则的大小为
A. B. C. D.
8. 把一块直尺与一块三角板如图放置,若,则的度数为
A. B. C. D.
9. 下列命题中,是假命题的是
A. 平方根等于本身的数是
B. 如果,都是无理数,那么也一定是无理数
C. 坐标平面内的点与有序实数对一一对应
D. 与可以合并同类项
10. 如图,,直线分别交直线,于点,,过点作于点
.若,则的度数为
A. B. C. D.
11. 将一直角三角板与两边平行的纸条如图所示放置,下列结论:(1);(2);
(3);(4),其中正确的个数是
A. B. C. D.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
证明
一、填空题
1.命题“任意两个直角都相等”的条件是________, 结论是___________,
它是________(真或假)命题.
2.在△ABC 中,∠C =2(∠A +∠B ),则∠C =________.
二、选择题
1.下列语言是命题的是( )
A.画两条相等的线段
B.等于同一个角的两个角相等吗?
C.延长线段AO 到C ,使OC =OA
D.两直线平行,内错角相等.
2.下列语句错误的是( )
A.同角的补角相等
B.同位角相等
C.同垂直于一条直线的两直线平行
D.两条直线相交只有一个交点
三、解答题
1.如图AD 、BE 、CF 为△ABC 的三条角平分线,求∠1+∠2+∠3的度数
2.已知,如图AB ∥CD ,BC ∥DE ,求∠B +∠D 的度数
3.已知,如图AB ∥CD ,若∠ABE =130°,∠CDE =152°, 求∠BED 的度数
4.如图6-80,△ABC 中,∠B =55°,∠C =63°,DE ∥AB ,则∠DEC 等于( )
5.已知,如图6-81,AE ∥BD ,∠1=3∠2,∠2=26°,求21
∠C.
四、证明题
图1 图2
1.已知,如图6-82,AD ⊥BC ,EF ⊥BC ,∠4=∠C.
求证:∠1=∠2.
2.已知,如图6-83,△ABC 中,∠C >∠B ,AD ⊥BC 于D ,AE 平分∠BA C.
求证:∠DAE =21
(∠C -∠B ).
3.举例说明“两个锐角的和是锐角”是假命题.。
