人口总量发展模型
数学建模论文-基于双线性系统、差分方程的人口增长模型模板

基于双线性系统、差分方程的人口增长模型摘要社会经济的许多领域的规划都必须考虑人口这一重要因素。
而人口普查只能为我们提供某几个时间点的横截面数值,但在现实生活中,人们常常需要其他时间点的人口总数及其构成。
于是一个迫切的任务就是如何用少数的几个时点的信息比较准确的得到较详尽的其他时点的人口数据。
人口系统发展是一个动力学过程,为强惯性系统,人口死亡率和出生率构成人口增长的双线性系统。
针对中短期预测,基于统计理论,将5年的死亡出生率,死亡率求期望,建立了人口增长的定常差分方程模型,预测至2015的人口发展趋势,通过MATLAB求解得到2015年的总人口为14.17亿,乡村城镇化趋势明显;并且人口在2025左右出现峰值,约为15.1亿。
针对长期预测,根据动力学发展过程理论,当时间尺度接近惯性系统的时间常数(社会人口的平均寿命)时,人口状态将发生明显改变。
由此建立了人口增长的时变差分模型。
并通过MATLAB求解,预测2050年的人口总数为14.33亿,人口系统达稳定状态。
然后,利用Leslie矩阵分析模型的稳定性。
当时间t(年)充分大时人口增长也趋于稳定。
针对长期模型的检验,对不同的总和生育率做出了人口总数的变化曲线。
得出当总和生育率的更替水平临界值略大于2.0。
关键词:差分方程,强惯性系统,Leslie矩阵,总和生育率一.问题重述与分析1.1问题重述中国乃泱泱人口大国,人口规模是城市规划和土地利用总体规划中一项重要的控制性指标,人口规模是否合理,不仅影响到未来地区经济和社会发展,而且会影响到地区生态环境可持续发展。
因此准确地预测未来人口的发展趋势,制定合理的人口规划和人口布局方案具有重大的理论意义和现实意义。
根据国家人口报告,对短期、中期和长期人口预测作如下定义:十年内为短期,十到十五年为中期,五十年及其以上为长期。
人口发展过程是一个很缓慢的过程。
它的“时间常数”接近平均期望寿命约七、八十年的时间。
人口状态随时间变化的过程称为人口发展过程。
GDP与经济发展及人口变化关系模型

GDP与经济发展及人口变化关系模型摘要本文讨论了国内生产总值与经济发展及人口变化的关系问题.针对问题一:国内生产总值是衡量经济发展的重要指标,而固定资产投资和进出口贸易的快速发展推动了我国经济的增长,因此有必要站在宏观的角度对我国国内生产总值与固定资产投资及进出口总额的关系进行分析.通过查找数据建立三者之间的基本回归模型,利用matlab进行求解,结果见文中表1.考虑到固定资产投资与进出口总额之间可能存在交互作用,将模型进行改进求解结果见文中表2.对两个模型进行结果的检验和预测,通过分析对比两者的数据得出改进的模型拟合度更高,更符合实际.针对问题二:当经济中总产出、收入和就业连续6个月到一年有明显下降,经济出现普遍收缩时,标志着经济衰退,因此分别建立国内生产总值与财政收入及失业率之间的回归模型.通过模型预测2012年财政收入为103.7925千亿元,同比增长0.0506%,失业率为4.1026% ,同比增长0.0634%.由于0.0506%与0.0634%都是相当小的数字,财政收入和失业率的增幅均是非常微小的,因此在一定程度上不能说明经济有衰退的迹象,只能说明经济涨幅不大.针对问题三:国内生产总值增长率、通货膨胀率和失业率是判断宏观经济运行状况的三个主要指标.通货膨胀率一般是用国内生产总值缩减指数来衡量的,通过奥肯定律可以得出国内生产总值与失业率的关系,进而得出国内生产总值是通过影响通货膨胀率及失业率对经济形势起决定性影响.针对问题四:建立关于人口数量与国内生产总值的自回归分布滞后模型,对其求解结果见文中表7,可以看出人口数量不仅与国内生产总值有关系,而且与其自身前一年的人口数量也存在着紧密的联系.问题一各项经济指标均会随时间的变化而变化,将问题一进行推广建立关于国内生产总值与固定资产投资及进出口总额的混合有限多项式分布滞后模型.此外统计回归模型是用途最广泛的一类随机模型.该模型不仅适用于对各个经济指标间关系的讨论,也可用于产品销售量的预测、教学评估、人口预测.关键词奥肯定律;统计回归模型;经济衰退;自回归分布滞后模型一、问题重述一个国家的国内生产总值往往反映该国的经济发展状况,中国亦无例外.改革开放以来,中国经济持续保持高速发展,特别是近20年更是基本保持10%以上的增长速度.据统计局数据,1979-2010年中国经济的平均增速是9.9%;1991-2010年平均增速是10.5%;2001-2010年平均增速也是10.5%.经过30多年的高速增长,中国经济已变得体量巨大、基数巨大.在2012年之前,我国国内生产总值逐步呈上升趋势,而在2012年的国内生产总值有所放缓,这与我国的经济政策发生变化相关联.请查找资料,利用数学建模给出如下四个问题的探讨:(1)通过一个或两个方面探讨2012年以前中国国内生产总值与其经济变化的关系.(2)中国2012年国内生产总值放缓能否证明经济形势有衰退的迹象.(3)如何评价中国国内生产总值对经济形势的影响.(4)中国人口变化与国内生产总值有无关系.二、问题分析国内生产总值是衡量经济发展的重要指标,它与我国经济及人口的变化均有着一定的联系,根据考虑问题的侧重点不同,以下从四个方面作详细讨论.针对问题一:固定资产投资和进出口贸易的发展,对我国经济的增长起到了推动的作用.但它们对经济增长的拉动作用是否显著,国内生产总值与固定资产投资和进出口总额三者之间存在什么样的关系,是需要进一步统计和检验的.通过查找1992-2011年20年的国内生产总值、进出口贸易额和固定资产投资额(全文数据均来自《中国统计年鉴》)的处理,建立统计回归模型,进而可以分析得出国内生产总值与固定资产投资额和进出口贸易额之间的关系.针对问题二:当经济中总产出、收入和就业连续6个月到一年的明显下降,经济出现普遍收缩时,标志着经济衰退.因此对1992-2011年20年的国内生产总值与财政收入及其与就业率的数据进行分析,分别建立关于国内生产总值与财政收入和国内生产总值与就业率的回归模型,通过预测2012年国内生产总值、财政收入和就业率来判断当国内生产总值放缓时经济是否有衰退的迹象.针对问题三:国内生产总值增长率、通货膨胀率和失业率是判断宏观经济运行状况的三个主要指标.通货膨胀率一般是用国内生产总值缩减指数来衡量的,由此国内生产总值缩减指数可以直接由国内生产总值计算得出.因此可以通过奥肯定律找出失业率与其增长率的函数关系,以此来判断出中国国内生产总值对经济形势的影响.针对问题四:人口总量与国内生产总值是随时间变化而发生改变的.当年的人口总量与最近三年的人口总量和国内生产总值都有关系,因此建立关于从1992年到2011年20年人口总量与国内生产总值的自回归分布滞后模型分析得人口变化与国内生产总值的关系.三、基本假设1.数据以年为基准,不考虑一年内的波动和变化;2.数据均为按当年价格计算的名义值;3.所有数据均真实可靠.四、符号表示与名词解释固定资产投资:是以货币形式表现的在一定时期内全社会建造和购置固定资产的工作量以及与此有关的费用的总称.财政收入:指国家财政参与社会产品分配所取得的收入,是实现国家职能的财力保证.进出口总额:指实际进出我国国境的货物总金额.五、模型建立与求解国内生产总值的增长对经济发展起着越来越重要的作用,因此必须正确认识国内生产总值增长与经济发展之间的关系.在我国,人口问题也不容忽视,它制约着中国经济和社会的发展.下面通过对各问题的分析,建立相应的模型,并求解.文中所有数据见附表一.5.1 国内生产总值与进出口贸易总额和固定资产投资的回归模型基本回归模型 设第t 年的国内生产总值为t G ,固定资产投资为t I ,进出口总额为t E ,t =1,…,n ( n =20).因变量t G 与自变量t I 和t E 的散点图见图1和图2.图1 t G 对t I 的散点图 图2 t G 对t E 的散点图由图1可以看出,随着固定资产投资额的增加,国内生产总值向上弯曲增长的趋势渐缓,图中曲线是用二次函数模型2012=+++t t t G I I βββε (1)拟合的(其中ε是随机误差).而图2中,当进出口总额增大时,国内生产总值向上弯曲增长的趋势加强,图中曲线仍是用二次函数模型2012=+++t t t G E E βββε (2)拟合的.综合上面的分析,结合(1)和(2)建立如下的回归模型2201234=+++++t t t t t G I E I E βββββε (3) 根据附表一的数据,对(3)利用matlab 统计工具箱求解(见附录程序一),得到回归系数的参数估计及其置信区间(置信水平=0.05α)、检验统计量2R ,F 和p 的结果见表1=0.9941R 表明t G 的99.41%可由(3)确定,F 值远远超过其检验的临界值,p远小于α,因而模型(3)从整体上看是可用的.将回归系数的估计值代入(3),得到基本回归模型22=27.7677+0.9937+0.7844-0.00004-0.001t t t t t G I E I E (4)模型改进 从表面上看基本模型(4)的拟合度已经很高2=0.9941R ,但模型(4)中回归变量t I 和t E 对因变量t G 的影响是相互独立的.实际中由于t I 和t E 均与t G 存在很大的依赖关系,因此t I 与t E 之间应存在着交互作用会对t G 产生影响.不妨简单地用t I 与t E 的乘积代表它们的交互作用,于是将(3)增加一项,得到22012345=++++++t t t t t t t G I E I E I E ββββββε (5)对(5)求解(见附录程序二) 得到回归系数的参数估计及其置信区间(置信水平=0.05α)、检验统计量2R ,F 和p 的结果见表2表2与表1的结果相比,=0.9961R 有所提高,说明(5)比(3)有所改进.并且,所有参数的置信区间,特别是t I 与t E 交互项系数5β的置信区间不包含零点,这就说明t I 与t E 之间存在着交互作用并对t G 产生影响.F 值也远远超过其检验的临界值,p 也远小于α,所以(5)比(3)更符合实际.将回归系数的估计值代入(5),得到改进的回归模型22=17.6708+0.9993+1.2295-0.0138-0.0204+0.0316t t t t t t t G I E I E I E (6)结果分析及预测 从机理上看,对于经济规律作用下的时间序列数据,加入交互项的模型(6)更为合理.将模型(4)和模型(6)的计算值t G 与实际数据t G 的比较以及两个模型的残差t e (=-t t t e G G )表示在表3、图3和图4上.可以看出模型(6)更合适些.表3:模型(4)和模型(6)的计算值G 与残差et G (模型t G (模型48.2305 43.0398 60.2638 58.2552 65.5259 64.6390图3 模型(4),(6)的t G 与t G 图4 模型(4),(6)的t e(注:图3和图4中蓝色表示实际数据,绿色表示模型(4)计算出的数据,红色表示模型(6)计算出的数据)5.2 国内生产总值放缓与经济衰退关系模型分析国内生产总值与财政收入的关系模型 设第t 年财政收入为t F ,画出因变量t F 与自变量t G 的散点图(t =1,…,n ( n =20)),并直接利用matlab 统计工具箱(CFTOOL 命令)拟合曲线见图5.图5 t F 与t G 的散点图 拟合函数的表达式为2012=+++t t t F G G βββε (7)其中(7)各参数的值及其置信区间见表4=0.9986R 表明t F 的99.86%可由(7)确定.RMES 为回归系统的拟合标准差,其越小说明曲线拟合的越好.表4显示 1.72RMES =,因此模型(7)是可用的.将回归系数的估计值代入(7)得到2=-3.381+0.1638+0.0001346t t t F G G (8)查看中国科学院预测科学研究中心关于《2012年我国GDP 预测及宏观经济形势分析》知道预计2012年国内生产总值的增长率为8.5%.因此预计2012年国内生产总值为471.564(千亿元),将其代入(8)得到2012年财政收入为103.7925(千亿元).与2011年财政收入103.740(千亿元)相比,同比增长了0.0506%,因此2012年我国财政收入仍是增长的,只是增长幅度非常小而已.国民生产总值与失业率的关系模型 设第t 年失业率为t U (t =1,…,20),画出因变量t U 与自变量t G 的散点图,并直接利用matlab 统计工具箱(CFTOOL 命令)拟合曲线见图6.图6 t U 与t G 的散点图拟合函数的表达式为222471582------036=+++t t t G G G t U eeeβββββββββε⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(9)其中(9)中各参数的值及其置信区间见表5=0.9412R 表明t F 的94.12%可由(7)确定.0.2103RMES =,因此模型(7)是可用的.将回归系数的估计值代入(7)得到222-41.48-19.41-38.83---8.21421.29 3.965=5.425+4.24-3.141t t t G G G t U eee⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(10)将预计的2012年国内生产总值471.564(千亿元)代入(8)得出2012年失业率为4.1026%,与2011年失业率4.1%相比,同比增长了0.0634%.因此2012年我国公失业率仍是增长的,只是增幅很小而已. 而经济衰退是指当经济中总产出、收入和就业连续6个月到一年的明显下降,经济中很多部门出现普遍收缩,则这种经济下降称为衰退. 0.0634%的增长是很微小的,因此可视为失业率基本没有变化.通过以上讨论分析可得当GDP 增幅减小为8.5%时,财政收入同比增长了0.0506%,失业率同比增长了0.0634%.由于0.0506%与0.0634%都是相当小的数字,因此不能说明经济有衰退的迹象,只能说明经济涨幅不大. 5.3 国内生产总值对经济形势影响关系模型设第t 年经济状况指数为t λ,国内生产总值增长率为t g ,失业变化率为t U ∆.通过奥肯定律:=-0.5(-2.25)t t U g ∆ 可以得出失业率t U 与t g 的关系为=-0.5(-2.25)t t U g dt ⎰ (11)又t λ受t g 及t U 的影响,设i a (i =1,2)分别表示t g 、t U 对t λ的权重,则12=+t t t a g a U λ (12) 由(11)和(12)可得t g 对经济形势影响的关系模型为12=+-0.5(-2.25)t t t a g a g dt λ⎰ (13)通过(13)可得国内生产总值通过对失业率的影响对经济形势起决定性影响. 5.4 中国人口变化与国内生产总值关系模型自回归分布滞后模型 设第t 年人口总数为t P ,(t =1,…,n ( n =33)).数据(见附表二)借鉴计量经济学中的自回归分布滞后模型,首先建立初始模型012132112233t t t t t t t t P G G G P P P ααααβββε-----=+++++++ (14)即当年的人口总量与最近三年的人口总量和国内生产总值都有关系,t ε为随机干扰项.查找近三十年我国人口总量(数据见附表一),利用matlab 进行求解得回归系数的参数估计及其置信区间(置信水平=0.05α)、检验统计量2R ,F 和p 的结果见表6=0.99995R 表明t P 的99.995%可由(14)确定,F 值远远超过其检验的临界值,p 远小于α,因而模型(3)从整体上看是可用的.检查参数的置信区间发现1α,2α,3α和3β的置信区间均包含零点,表明回归变量t G ,1t G -,2t G -和3t P -对t P 的影响不太显著.模型改进 由于每年P 和G 的值都分别与其前几年的值有关,且P 与G 两者之间也存在着一定的关系,因此通过对1t G -,2t G -和3t P -逐项剔除后重新拟合并检查其2R ,F 和p 的值及各参数的置信区间,得到最终改进的模型0121t t t P G P βββ-=-+ (15) 求解(15)结果见表7=0.99979R 表明t P 的99.979%可由(15)确定有所提高,表7与表6的结果相比,所有参数的置信区间均不包含零点,F 值也远远超过其检验的临界值,p 也远小于α,所以(16)更符合实际.将回归系数的估计值代入(15)得到1=3351.5-0.0015122+0.98296t t t P G P - (16)从(16)可以看出人口数量不仅与国内生产总值有关系,而且与其自身前一年的人口数量也存在着紧密的联系.结果分析及预测 将用模型(16)的计算值t P 与实际数据t P 的比较以及两个模型的残差t e (=-t t t e P P )表示在表8、图7上.图7 模型(16)'.'t P ,''t P o ,'*'t e表8和图7显示用模型(16)预计的人口数量与实际人口数量非常吻合,因此模型(16)更贴合实际.六、模型评价和推广模型的评价本文在正确查找数据基础上建立了多个统计回归模型.在对原始数据进行拟合时,采用多种方法,对模型不断进行改进,使其愈来愈完善且具有很高的拟合精度.在此基础,对模型作进一步分析讨论得到一系列可靠而实用的信息.但由于时间紧迫以及数据量的不足,部分模型较为粗糙,需要进一步改进. 模型检验通过已有数据进行拟合与比较来检验模型,经检验证实建立的模型对原始数据有很高的拟合度,基本符合模型建立的初衷. 模型的推广推广一:由于各项经济指标都会随时间的变化而变化,针对问题一可以采用混合有限多项式分布滞后模型进行拟合,模型如下:01213212132112233t t t t t t t t t t G I I I E E E G G G ααααβββγγγε-------=++++++++++ 其中i α,i β和i γ为参数,0,1,2,3i =.推广二:统计回归模型是用途最广泛的一类随机模型.该模型不仅适用于对各个经济指标间关系的讨论,也可用于产品销售量的预测、教学评估、人口预测等问题.参考文献[1]姜启源,谢金星,叶俊.数学模型[M].北京:高教出版社,2011.1.[2]国家统计局编.中国统计年鉴(2011)[M].北京:中国统计出版社,2012.2. [3]中国国家统计局网站 /2012-8-15.[4]陈锡康,祝坤福 王会娟.2012年我国GDP 预测及宏观经济形势分析[M]. 北京:高教出版社,2012.1. [5]萨谬尔森,诺德豪斯.经济学[M].北京:高教出版社,2000.6. 附录表一11。
宋健人口发展模型

g
为出生当年的净迁移人数
00
gX 为X 岁的净迁移人数
H X 为X 岁妇女的生育模式函数
1
HX
n 2
n
2
e n 1
2 1
1
,
1
0,
1
函数
n
n
x2
1e
xdx
2
0
标准化生育模式
根据出生人数三要素: 育龄妇女人数W X 、生育水平TFR、生育模式H X 有出生人数为
Bt
2 TFR W X
1
将其标准化处理:
分布尚不完全服从卡方分布,并将其调整为
H2 X
1r
n 2
n
r1
n 2
1e
r r1
2 ,r
r1
2
0
,r r1
式中: 为可调参数
总和生育率 15-19 20-24 25-29 30-34 35-39 40-44 45-49
1000 800 600 400 200 0
中国年龄别出生率 1964 1981 1990 2000
第二,确定生育模式
由以上数据, 有
1, n Xmax 1 2 25 15 2 12
n
n 1 ! 5!
22
1 HX 120
0,
15 5 e 15 ,
15
15
16,17,18, , 49
生育模式函数值
当 16时,HX 0.0031; 当 17,时,HX 0.0361; 当 18时,HX 0.1008;
g 00
P 1
t
1
P 0
t
S0
g0
P 2t 1
P 1t
S1
人口模型

即可求得
b 2.695 1012。于是,世界人口的极限值
9 3.34 10 为初值,则2000年的 若以1965年的人口数
r 0.029 107.6 12 b 2.695 10
(亿)
世界人口将达到
0.029 3.34 109 y |t 2000 59.6 0.029(2000 1965) 0.009 0.02e
人口模型
模型1 马尔萨斯(Malthus)模型
英国的经济系家马尔萨斯首先提出了人口增长 模型。他的基本假设是:任一单位时刻人口的 增长量与当时的人口总数成正比。于是,设t ) 时刻的人口总数为 y(t,则单位时间内人口的 增长量即为 y (t t ) y (t ) t 根据基本假设,有
y (t t ) y (t ) ry (t ) (r为比例系数) t
dy 其中,dt
9
表示人口的理论增长率,而 则表示 人口的实际增长率。如果我们以1965年的人口数 3.34 10 为初值,并把某些生态学家估计的r的自然 值0.029及人口的实际增长率0.02代入上式,有
0.02=0.029-b(3.34 109 )
dy dt r by y
dy dt y
dy 2 ry by dt y |t t y0 0
(3)
这是一个可分离变量的一阶微分方程。解之, ry 可得 y (4)
by0 (r by0 )e r (t t0 )
0
这就是人口y随时间t的变化规律。下面,我们 就对(4)作进一步的讨论,并根据它对人口的 发展情况作一些预测。 3.模型的进一步讨论及其在人口预测中的应用 首先,由于
这个结果与2000年的世界实际人口是非常接近的。
人口增长问题数学模型

人口增长问题数学模型人口增长问题是一个复杂的社会现象,它涉及到众多因素,如生育率、死亡率、移民、出生性别比等。
为了更好地理解和预测人口增长趋势,人们常常建立数学模型来描述人口变化的规律。
下面是一个简单的人口增长问题数学模型的示例。
假设人口数量为P(t),时间t为以年为单位。
则人口增长可以用以下微分方程表示:dP(t)/dt = rP(t)其中,r是人口自然增长率,是一个常数。
这个微分方程描述了人口数量随着时间的变化情况,即人口数量呈指数增长。
然而,实际情况要复杂得多。
以下是一个更复杂的人口增长模型,考虑到生育率、死亡率和移民等因素:dP(t)/dt = (b - d)P(t) + I其中,b是每单位时间的出生率,d是每单位时间的死亡率,I是每单位时间的移民人数。
这个模型可以更好地描述人口增长的趋势,特别是当存在外部干扰(如战争、自然灾害等)时。
除了以上两个模型,还有其他更复杂的模型,如Logistic增长模型、Malthusian模型等。
这些模型考虑的因素更加全面,可以更准确地描述人口增长的趋势。
例如,Logistic增长模型考虑了环境承载能力对人口增长的限制,而Malthusian 模型则考虑了人口增长与资源供给之间的关系。
建立数学模型有助于我们更好地理解和预测人口增长趋势。
这些模型可以帮助我们评估不同政策对人口增长的影响,如计划生育政策、移民政策等。
此外,这些模型还可以帮助我们预测未来人口数量和结构的变化情况,从而为社会发展规划提供科学依据。
然而,需要注意的是,数学模型只是对现实世界的近似描述,它可能无法完全准确地预测未来情况。
因此,在使用数学模型进行人口增长预测时,需要结合实际情况和专家意见进行综合分析。
总之,数学模型是研究人口增长问题的重要工具之一。
通过建立数学模型,我们可以更好地理解和预测人口增长的规律和趋势。
这些模型可以帮助我们评估不同政策对人口增长的影响,为社会发展规划提供科学依据。
人口预测方法(总结)
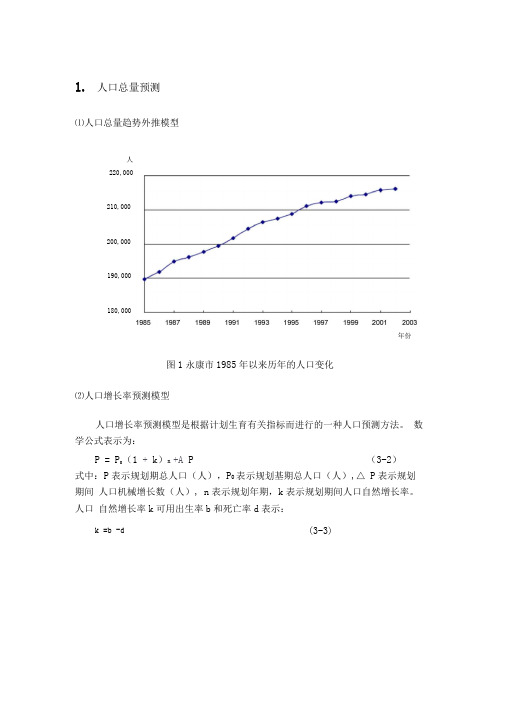
1. 人口总量预测⑴人口总量趋势外推模型图1永康市1985年以来历年的人口变化⑵人口增长率预测模型人口增长率预测模型是根据计划生育有关指标而进行的一种人口预测方法。
数学公式表示为:P = P 0(1 + k )n +A P (3-2)式中:P 表示规划期总人口(人),P 0表示规划基期总人口(人),△ P 表示规划期间 人口机械增长数(人), n 表示规划年期,k 表示规划期间人口自然增长率。
人口 自然增长率k 可用出生率b 和死亡率d 表示:(3-3)人 220,000k =b -d210,000200,000190,000180,000年份年份永康市1989年以来历年的人口出生率、死亡率和自然增长率%图3永康市1989年以来历年的户籍人口迁移数量(3)人口离散预测模型人口离散预测模型也即人口差分方程预测模型,又称“宋健模型”,是我国自行提出的比较成功的人口发展预测模型,能较好的运用人口普查资料对未来人口进行预测。
该模型是根据分年龄的人口结构递推公式进行预测,模型的数学表达如下:r2X o(t)=[1-4oo(t)] ^(t)送h i(t) k i(t) X(t) (3_6)XF(t +1)=[1-B(t)] "Xe + fe i =0,12..,m—1式中:X o(t)为t年代O岁出生婴儿数,X i(t)为t年代之年龄组人口数,卩oo(t)为t 年出生婴儿当年死亡率,P(t)为妇女总和生育率,即社会人中平均意义下一个妇女在整个育龄时期的生育总数(「2, r1即为生育年龄的上下限),h i(t)为生育模式,反映某一地区某一个育龄妇女生育状态分布,k i(t)为t年代之年龄组女性性别比,M(t)为t年代之年龄组人口死亡率,f i(t)为t年代之年龄组净迁移数。
在模型的具体应用中,课题组工作的重点是如何确定公式3-6中的各种参数。
①第五次人口普查资料中的数据是2000年11月1日的数据,而规划所需的数据是年末的数据,课题组将普查的户籍人口分龄人口数按比例修正到2000年底的统计人口总数作为X i(t);②从普查资料来看45岁以下的性别比比较稳定,为了简化模型,t年代之年龄组女性性别比k i(t)用常量k表示,即采用普查资料中的45岁以下的男女性别比=104.85(女性=100)推算,故k= 0.488326;③根据普查资料,妇女总和生育率取2000年的数据P(t)= 0.8795;④模型中出生婴儿当年死亡率Moo(t)假定与2000年出生婴儿当年死亡率的80%,即采用4OO=3.88%O。
人口增长模型14

人口增长模型简介人口增长模型是指根据人口变化规律和影响因素建立的数学模型,通过模拟和预测不同条件下的人口数量变化。
人口增长是一个复杂的系统,受到多方面因素的影响,包括出生率、死亡率、移民率等。
建立一个合理的人口增长模型对于政府制定人口政策、规划城市发展具有重要意义。
历史人口增长模型的研究可以追溯至18世纪。
英国数学家马尔萨斯在其著作《人口论》中首次提出了人口增长问题。
马尔萨斯认为人口会呈指数增长,而生产食物的增长是线性的,因此会导致人口增长超过食物供给能力,最终出现人口过剩。
这种观点引发了很多后续研究者对人口增长规律的探讨。
人口增长模型的类型基于不同的假设和数学方法,人口增长模型可以分为多种类型,其中比较常见的包括:马尔萨斯模型马尔萨斯模型是最早的人口增长模型之一。
它假设人口呈指数增长,而食物生产是线性增长。
这导致了人口的快速增长会超出食物供给能力,最终导致人口崩溃。
Logistic模型Logistic模型在马尔萨斯模型的基础上加入了环境资源有限的观点,即当资源接近极限时,人口增长率会减缓,最终趋于稳定。
这种模型更贴近实际情况,能更好地解释人口的增长规律。
Lotka-Volterra模型Lotka-Volterra模型是一种描述群体动态的模型,常用于描述捕食者-猎物关系。
将其应用在人口增长模型中,可以考虑到更多的因素对人口数量的影响,如资源竞争、捕食等。
应用人口增长模型在人口学、经济学、城市规划等领域有着广泛的应用。
通过建立合理的模型,可以预测人口数量、优化资源配置、制定人口政策等。
特别是在城市规划领域,人口增长模型可以帮助规划者更好地调整城市结构,提高城市的可持续发展性。
结语人口增长模型是对人口变化规律的抽象和数学化,它有助于我们更好地理解人口增长的规律性,为未来的决策提供科学依据。
通过不断优化和改进人口增长模型,我们可以更好地应对人口问题带来的挑战,实现人口与资源的平衡发展。
以上是对人口增长模型的简要介绍,希望能为您带来一些启发。
人口增长模型

一、 人口增长模型: 1. 问题下表列出了中国1982—1998年的人口统计数据,取1982年为起始年(t=0),…人口自然增长率14%,以36亿作为我国的人口容纳量,是建立一个较好的数学模型并给出相从图中我们可以看到人口数在1982—1998年是呈增长趋势的,而且我们很容易发现上述图像和我们学过指数函数的图像有很大的相似性,所以我们很自然想到建立指数模型,但是指数模型有个不妥之处就是没有考虑社会因素的,即资源的有限性,也就是人口不可能无限制的增长,所以有必要改进模型,这里我们假设人口增长率随人口增加而呈线性递减,从而建立起比较优越阻滞增长模型 模型一:指数增长模型(马尔萨斯模型)1.假设:人口增长率r 是常数.2.建立模型:记时刻t=0时人口数为0X ,时刻t 的人口为X (t ),由于量大,X (t )可以视为连续、可微函数,t 到t+t ∆时间段人口的增量为:)()()(t rX tt X t t X =∆-∆+于是X (t )满足微分方程:)1()0(0⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧==X X rX dt dx3.模型求解:解得微分方程(1)得: X (t )=0X )(0t t r e- (2)表明:t ∞−→−时,t X )0.(>∞−→−r . 4.模型的参数估计要用模型2对人口进行预报,必须对其中的参数r 进行估计,这可以用表1通过Matlab 拟合: 程序:x=[1982 1983 1984 1985 1986 1987 1988 1989 1990 1991 1992 1993 1994 1995 1996 19971998]';X=[ones(17,1),x]Y=[101654 103008 104357 105851 107507 109300 111026 112704 114333 115823 117171 118517 119850 121121 122389 123626 124810]';[b,bint,r,rint,stats]=regress(Y,X); %回归分析b,bint,stats%输出这些值rcoplot(r,rint);%画出残差及其置信区间z=b(1)+b(2)*x;plot(x,Y,'k+',x,z,'r'),%预测及作图运行结果:b =1.0e+006 *-2.84470.0015bint =1.0e+006 *-2.9381 -2.75130.0014 0.0015stats =1.0e+005 *0.0000 0.0455 0 1.9800图1各数据点及回归方程的图形 即回归模型为:y=-2844700+1500x从上图可用看出拟和得效果比较好。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人口总量发展模型1. 马尔萨斯人口模型设时刻t 时人口为)(t x ,单位时间内人口增长率为r ,则t ∆时间内增长的人口为: t r t x t t x ∆=-∆+.)()( 当0→∆t ,得到微分方程:0)0(,x x r dtdx== 则: tr e x t x .0.)(=待求参数r x ,0。
为便于求解,两边取对数有:t r a y .+=,其中0ln ,ln x a x y ==,该模型化为线性求解。
2. 阻滞型人口模型设时刻t 时人口为)(t x ,环境允许的最大人口数量为m x ,人口净增长率随人口数量的增加而线性减少,即 )1.()(mx x r t r -= 由此建立阻滞型人口微分方程:0)0(,).1(x x x x xr dt dx m=-= 则: tr m mex x x t x .0.11)(-⎪⎪⎭⎫ ⎝⎛-+=待求参数r x x m ,,0。
此即为Logistic 函数. 当2m x x =时,x 增长最快,即dtdx 最大。
2~,1~/图形见图图见图t x x dt dx 。
三、实际数据处理年1790 1800 1810 1820 1830 1840 1850 1860实际3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 人口指数4.18845.5105 7.2498 9.538 12.549 16.5097 1.7209 28.5769 模型阻滞7.6981 9.5096 11.7361 14.4667 17.807 21.8782 26.8229 32.7987 模型年1870 1880 1890 1900 1910 1920 1930 1940实际38.6 50.2 62.9 76.0 92.0 106.5 123.2 131.7 人口指数37.597 49.464 65.077 85.618模型阻滞39.979 48.5470 58.6861 70.5673 84.331 100.065 117.779 137.387 模型年1950 1960 1970 1980 1990 2000实际150.7 179.3 204.0 226.5 251.4 281.4人口指数模型阻滞158.683 181.3439 204.938 228.951 252.834 276.048模型(1) 由指数增长模型得到模型为t e y .2743.01936.3= (1790~1900年数据)均方误差根为0215.3=RMSE 结果图见图1. (效果好)t e y .2022.09384.4= (1790~1900年数据)均方误差根为8245.39=RMSE 结果图见图2.(效果不好)图1 指数模型(1790~1900),’*’为原数据,实线为拟合值图2 美国人口指数模型(1790~2000),’*’为原数据,实线为拟合值指数模型求解Matlab程序population_america1.m:%美国人口模型,指数增长模型x=[3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,38.6,50.2,62.9,76.0,...92.0,106.5,123.2,131.7,150.7,179.3,204.0,226.5,251.4,281.4]';n=12;xx=x(1:n);%1790年到1900年数据t=[ones(n,1),(1:n)'];y=log(xx(1:n));[b,bint,r,rint,stats]=regress(y,t);RR=stats(1);%复相关系数F=stats(2);%F统计量值prob=stats(3); % 概率x0=exp(b(1)); %参数x0;r=b(2); %参数rpy=x0*exp(r*t(:,2)); %预测数据err=xx-py;rmse=sqrt(sum(err.^2)/n); %均方误差根plot(1:n,xx,'*',1:n,py); %作对比图(二) 阻滞型模型拟合1790年到2000年数据,得到结果为:2155.0,572.446,2267.60===r x x mety .2155.07191.701572.446-+=均方误差根为5614.4=RMSE ,并预测2010年美国人口为298.1138百万. 结果图见图3. (效果好)图3 美国人口阻滞型模型(1790~2000),’*’为原数据,实线为拟合值Matlab 程序population_america2.m%美国人口模型,阻滞型增长模型 %非线性回归x=[3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,38.6,50.2,62.9,76.0,...92.0,106.5,123.2,131.7,150.7,179.3,204.0,226.5,251.4,281.4]';n=22;y=x(1:n);%1790年到1900年数据 t=(1:n)';beta0=[5.3,0.22,400,]; %[x0,r,xm] [beta,R,J]=nlinfit(t,y,'logisfun',beta0); %R 为残差,beta 为待求参数py=beta(3)./(1+(beta(3)/beta(1)-1)*exp(-beta(2)*t));%预测各年人口p23=beta(3)./(1+(beta(3)/beta(1)-1)*exp(-beta(2)*23));%预测2010年年人口rmse=sqrt(sum(R.^2)/n); %均方误差根plot(1:n,y,'*',1:n,py); %作对比图%拟合函数%function yhat=logisfun(beta,x)%yhat=beta(3)/(1+(beta(3)/beta(1)-1)*exp(-beta(2)*x));世界人口数据拟合1991年到2004年数据,得到结果为:045.0,7756.8,1649.50===r x x mety .045.06991.017756.8-+=(单位:十亿)均方误差根为117.0=RMSE .表2 世界人口数据(单位:十亿)Matlab 程序population_world.m %世界人口模型,阻滞型增长模型 %非线性回归x=[5.384,5.420,5.0506,5.607,5.702,5.771,5.840,5.926,5.982,...6.067,6.137,6.215,6.314,6.396]';%世界1991~2004年人口数据,单位十亿n=length(x);y=x(1:n);%1991年到2004年数据 t=(1:n)';beta0=[5.3,0.22,80,]; %[x0,r,xm][beta,R,J]=nlinfit(t,y,'logisfun',beta0);%R为残差,beta为待求参数py=beta(3)./(1+(beta(3)/beta(1)-1)*exp(-beta(2)*t));%预测各年人口p23=beta(3)./(1+(beta(3)/beta(1)-1)*exp(-beta(2)*23));%预测2010年年人口rmse=sqrt(sum(R.^2)/n); %均方误差根plot(1:n,y,'*',1:n,py); %作对比图%拟合函数%function yhat=logisfun(beta,x)%yhat=beta(3)/(1+(beta(3)/beta(1)-1)*exp(-beta(2)*x))图4 世界人口阻滞型模型(1991~2004),’*’为原数据,实线为拟合值中国人口数据处理拟合1949年到2001年数据,得到结果为:0342.0,2939.18,1306.50===r x x mety .0342.05656.212939.18-+=(单位:亿)均方误差根为1346.0=RMSE .表3 中国人口数据(单位:亿)图5 中国人口阻滞型模型(1949~2001),’*’为原数据,实线为拟合值Matlab程序population_china.m%中国人口模型,阻滞型增长模型%非线性回归x=[5.4167,5.5196,5.6300,5.7482,5.8796,6.0266,6.1465,6.2828,6.4653,...6.5994,6.7207,6.6207,6.5859,6.7295,6.9172,7.0499,7.2538,7.4542,...7.6368,7.8534,8.0671,8.2992,8.5229,8.7177,8.9211,9.0859,9.2420,...9.3717,9.4974,9.6259,9.7542,9.8705,10.0072,10.1654,10.3008,...10.4357,10.5851,10.7507,10.9300,11.1026,11.2704,11.4333,11.5823,...11.7171,11.8517,11.9850,12.1121,12.2389,12.3626,12.4761,12.5786,...12.6743,12.7627]';%中国1949~2001年人口数据,单位亿n=length(x);y=x(1:n);%1991年到2004年数据t=(1:n)';beta0=[5.3,0.12,20,]; %[x0,r,xm][beta,R,J]=nlinfit(t,y,'logisfun',beta0);%R为残差,beta为待求参数py=beta(3)./(1+(beta(3)/beta(1)-1)*exp(-beta(2)*t));%预测各年人口rmse=sqrt(sum(R.^2)/n); %均方误差根plot(1:n,y,'*',1:n,py); %作对比图。
