复习题-ch1
信号与系统:习题Ch1(2013)
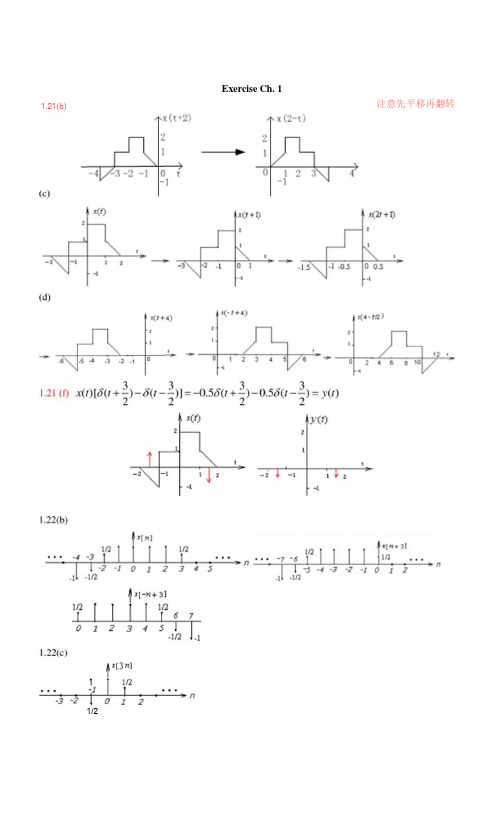
Exercise Ch. 11.21(b)注意先平移再翻转1/21.11 Determine the fundamental period of the signal = 1 +e """式Solution: The period of eNi=7. jl^iSThe period of e isN :=5.So N = N I N2=35 1.25. (a). Periodic. T=-T/2.Solution: T=2^/4=^/2.(b) . Periodic. T=2.Solution: T=2^/^=2.(c) x(r) = [ 1 + cos(4l-2勿/3)]/2. Periodic, pcri(Kl= 2^/4 = /rZ2(d) . Peritxlic. T=0.5.Solution: x(/) = E v {cos(4^r)w(/)J=-{ COS (4E )M (I ) + COS (4TT (T ))W (T ) }*=-cos(4^r) {:/(/) + w(-z)}—= -cos(4^r)2So. T=2^/4^=0.51.26 Determine whether or no each of (he following discrete-time signals is periodic. If (he signals is periodic, determineits fundamental period.(a) . Periodic. N=7(d) (e) x[n]u[n-3]-x[n}is2“Solution: N=———* m =7, m=3.6Z7(b). Not periodic.Solution: N= --------- * m = 16〃m , it s not rational number.1/8(c)Periodic. period=8 + J = cos| —(?: + ^V)2] = cos(—+—nN + —N2)8 8 4 8若乌N +服2=2Jbr・k为整数,对所有n成立.HP2nN^N2 = \6k对所有n成立,则有 4 8 2N + N?均为16的整故倍.故x[n|为周期的,基波周期为8(d)= cosG〃)cosg〃)As 饲/2芥=1/4,躲/2芥=1/8, the fundamental period is T= 8.(e). Periodic. N=16Solution as follow:A n] = 2cos(—n) + sm(—〃) 一2cos(— " + —)4 8 2 6in (his equation,sin(—n), it's period is N=2^ #m/(^/8)=16, m=l.it's period is N=2 龙*m/( n /2)=4. m=l.So, the fundamental period of.v| n] is N=(8,16,4)=16.1.49. (f) Solution:(1 +,)5= (VI)%,=4y[2e|1 + ,| = + = Z^ = tan l(I) = -补充:Please represent the Figure R1.2I in P. 60 with the step function w(lo).Solution:x(r) = -(2+0[w(/ + 2)-M(r+l)]+[w(r+l)-u(/)]+2[M(n-w(r-l)]+(2-0[w(/-l)-w(/-2)]= -(2+t)u(t+2)+(3++1)+w(/) T • u(t-1)+(2 2)1.19 For each of the following inpul-output relationships, determine whether the corresponding system is linear, timeinvariant or both.(c ) The system is linear and time-invariant.1.22(0 同"一 一 2]=上[0]况〃一 2] = y[n]vl») ・・・三i I~1 -i .|l -i/2 1.31 In this problem wc illustrate one of the most important consequences of the properties of linearity and time invariance.Specifically, once we know the response of a linear system or a linear time-invariant (LTI) system to a single input or the responses to several inputs, wc can directly compute the responses (o many other input signals. Much of the remainder of this book deals with a thorough exploitation of 【his fact in order to develop results and techniques for analyzing and synthesizing LTI systems.(a) Consider an LTI system whose response to the signal xi(r) in Figure Pl.31 (a) is the signal yi(z) illustrated inFigure Pl.31(b). Determine and sketch carefully the response of the system to the input X2(l) depicted in Figure1.31(c).(b) Determine and sketch the response of the system considered in part (a)(o the input xj(/) shown in Figure PI.3I(d)..弓(。
(题)数据结构复习题_ch1

}
Key:
8、设n为正整数,分析下列各程序段中加下划线的语句的执行次数。
(1)for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
c[i][j]=0.0;
for(int k = 1;k <= n;k++)
算法效率的度量分为(②)和(③)。(②)主要通过在算法的某些部位插装时间函数来测定算法完成某一规定功能所需的时间。而(③)不实际运行算法,它是分析算法中语句的执行次数来度量算法的时间复杂性。
程序所需的存储空间包含两个部分(④)和(⑤)。(④)空间的大小与输入输出数据的个数多少,数值大小无关;(⑤)空间主要包括其大小与问题规模有关的成分变量所占空间,引用变量所占空间,以及递归栈所用的空间,还有在算法运行过程中动态分配和回收的空间。
s += a[i];
return s;
}
Key:2n+3
6、试计算以下递归求和程序中所有语句的总执行次数。
float rsum(float a[ ], int n)
{
if(n <= 0)return a[0];
else return rsum(a, n-1)+ a[n-1];
}
Key:
7、试用大O表示法给出下面程序的时间复杂性。
()数据结构是指相互之间存在一种或多种关系的数据元素的全体。
()从逻辑关系上讲,数据结构主要分为两大类:线性结构和非线性结构。
机械工程材料老师给的复习题华南理工大学广州学院答案精选

机械工程材料老师给的复习题华南理工大学广州学院答案篇一:机械工程材料习题集答案-华南理工大学习题集参考答案Ch1 金属的晶体构造三、1. bcc、fcc、hcp,bcc、fcc、hcp。
2. 致密度,配位数3. 2/a2 、1.4/a2、2.31/a2 ;1/a、1.4/a、0.58/a。
{111}、lt;110。
4. 多、晶体缺陷。
5. fcc、hcp。
6. 4、2a、12、0.74。
47. 空位、间隙原子;位错;晶界和亚晶界。
8. [121]、(121)9. 畸变,升高,下降。
10.晶体中已滑移的部分,未滑移部分。
11.⊥、∥12.位错线和。
1;无数。
四、Ch2纯金属的结晶三、 1. 低于理论结晶温度才结晶,理论结晶温度-实际结晶温度。
2. 形核与长大。
3. 大、细、高、好。
4. 液、固相自由能差,液相过冷。
5. 平面、密排面。
6. 外表细等轴晶、柱状晶、中心粗等轴晶。
7. 偏析、疏松、气孔、夹杂物。
8. (1)细,(2)细,(3)细。
四、五、Ch3 金属的塑性变形与再结晶三、1. 滑移、孪生,滑移2. 原子密度最大。
3. {110},6,lt;111,2,12;{111},4,lt;110,3,12。
Fcc,滑移方向较多。
4. ?k??scos?cos?或??ks?cos?cos?,小,软位向。
5. 晶界、晶体位向差,较高。
6. 提高,升高,下降。
再结晶退火。
7. 织构。
8. 回复、再结晶、晶粒长大。
9. 去应力退火,200-3000C。
10. 去应力退火。
11. 再结晶退火,降低硬度、恢复塑性。
12. 再结晶温度。
低于再结晶温度,高于再结晶温度。
13. 偏析、杂质、夹杂物,热加工纤维组织(流线)。
14. 优于。
四、Ch4 合金的相构造与二元合金相图三、 1. 固溶体;金属化合物2. 溶剂,溶质,溶剂。
3. 溶质,溶剂;置换固溶体、间隙固溶体。
4. 升高,提高,下降。
5. 正常价化合物;电子化合物;间隙化合物。
2009-2011广东省高中学业水平考试分章节题目 必修1Ch1 从实验学化学

高中学业水平考试题目分章节知识点排必修1 Ch1 从实验学化学§1 化学实验基础考纲目标:化学实验基础1.了解化学实验是科学探究过程中的一种重要方法。
2.了解化学实验室常用仪器的主要用途和使用方法。
3.掌握化学实验的基本操作,能识别化学品安全使用标识,了解实验室一般事故的预防和处理方法。
4.了解常见气体的实验室制法(包括所用试剂、仪器,反应原理和收集方法)。
5.能对常见的物质进行检验、分离和提纯,能根据要求配制溶液。
6.了解控制实验条件的方法;能简单分析或处理实验数据,得出合理结论。
7.了解科学探究的基本过程,学习运用以实验和推理为基础的科学探究方法。
认识化学是一门以实验为基础的科学。
一、加热的仪器61.(09广东)下列能够用酒精灯加热的仪器是A.量筒B.烧杯C.容量瓶D.蒸发皿28.(10广东)能使用酒精灯直接加热的器皿是二、仪器读数8.(09广东)观察右图,量筒中液体的体积读数是A.1.3mLB.1.4mLC.1.5mLD.1.6mL三、试剂保存26.(09广东)铝制器皿能够盛放的物质是A.KOH溶液B.浓硫酸C.NaOH溶液D.稀硫酸36.(10广东)下列试剂保存或盛放方法正确的是A.浓硝酸盛放在铜质器皿中B.稀硝酸盛放在铁质器皿中C.NaOH溶液保存在带橡胶塞的试剂瓶中D.NaOH溶液保存在带玻璃塞的试剂瓶中四、物质的分离和提纯或除杂34.(09广东)下列各组混合物中能够使用分液漏斗分离的是A.乙醇和乙酸B.苯和水C.乙酸和乙酸乙酯D.汽油和柴油59.下(11广东)列实验操作过程中不需要使用圆底烧瓶的是A.过滤B.蒸馏C.溶解D.分液30.(10广东)向碘水中加入适量CCl4并振荡,静置后观察到的现象是A.形成均匀的无色溶液B.形成均匀的紫红色溶液C.液体分层,下层呈紫红色D.液体分层,上下层均呈无色56.(10广东)实验室里由粗盐制备精盐的实验中,必需的操作步骤有A.溶解B.过滤C.分液D.蒸发浓缩43.(10广东)通常用活性炭去除冰箱中的异味,主要利用了活性炭的A.吸附性B.还原性C.稳定性D.氧化性25.(11广东)向盛有KI溶液的试管中加入一定量CCl4后,滴加少量氯水,振荡,CCl4层变成紫色,继续滴加氯水,振荡,CCl4层颜色会逐渐变浅直至无色。
《普通化学》《Ch1原子结构与分子结构》复习题及答案

《普通化学》《Ch1原子结构与分子结构》复习题及答案一、是非题(对的在括号内填“√”号,错的填“×”号)1. ψ是核外电子运动的轨迹。
2. 微观粒子的特性主要是波、粒二象性。
3. 2p有三个轨道,可以容纳3个电子。
4. 1s轨道上只可容纳1个电子。
5. n =1时,l可取0和1。
6. 主量子数n=3时,有3s,3p,3d,3f等四种原子轨道。
7. 一组n,l,m组合确定一个波函数。
8. 一组n,l,m,m s组合可表述核外电子一种运动状态。
9. 轨道角度分布图是角度分布函数对,θφ作图得到的图像。
10. d区元素外层电子构型是n s1~2。
11. 电负性越大的元素的原子越容易获得电子。
12. 同周期元素从左至右原子半径减小。
13. 共价键的重叠类型主要有σ键π键两种。
14. NH3和BF3都是4原子分子,故二者空间构型相同。
15. 色散力是主要的分子间力。
16. μ= 0的分子中的化学键一定是非极性键。
17. 非极性分子内的化学键一定是非极性键。
18. 键能越大,键越牢固,分子也越稳定。
19. sp2杂化轨道是由某个原子的1s轨道和2p轨道混合形成的。
20. 当原子中电子从高能级跃迁到低能级时,两能级间的能量相差越大,则辐射出的电磁波的波长越长。
21. 波函数ψ是描述微观粒子运动的数学函数式。
22. 电子具有波粒二象性,就是说它一会是粒子,一会是波动。
23. 电子云图中黑点越密之处表示那里的电子越多。
24. 氢原子中原子轨道的能量由主量子数n来决定。
25. 色散力只存在于非极性分子之间,取向力只存在于极性分子之间。
26. 分子中的化学键为极性键,则分子为极性分子。
27. van der Waals 力属于一种较弱的化学键。
28. He2的分子轨道表示式为 (σ1s)2(σ1s*)2。
29. 中心原子中的几个原子轨道杂化时,必形成数目相同的杂化轨道。
30. 在CCl4、CHCl2和CH2Cl2分子中,碳原子都采用sp2杂化,因此这些分子都呈四面体形。
ch1参考答案

第一章作业参考答案1.1、令A[1…60]=11,12,…,70,用算法BINARYSEARCH搜索下列x值时执行了多少次比较运算?(a)33 (b) 7 (c) 70 (d) 77解:当x=33,第一次比较中,数组的中间元素A[30]=40; 33<40,剩余的子序列为A[1…29]=11,12,…39;第二次比较中,A[15]=25;33>25,剩余的子序列为A[16…29]=26,27,…39;第三次比较中,A[22]=32; 33>32,剩余的子序列为A[23…29]= 33,…39;第四次比较中,A[26]=36;33<36;剩余的子序列为A[23…25]= 33,34,35;第五次比较中,A[24]=34;33<34;剩余的子序列为A[23]= 33;第六次比较中,A[23]=33;33=33;搜索成功共进行6次比较当x=7,第一次比较中,数组的中间元素A[30]=40; 7<40,剩余的子序列为A[1…29]=11,12,…39;第二次比较中,A[15]=25;7<25,剩余的子序列为A[1…14]=11,12,…24;第三次比较中,A[7]=17;7<17,剩余的子序列为A[1…6]=11,12,…16;第四次比较中,A[3]=13;7<13,剩余的子序列为A[1…2]=11,12;第五次比较中,A[1]=11;7<11,此时high=0;low=1;high<low;停止比较。
共进行6次比较当x=70,第一次比较中,数组的中间元素A[30]=40; 70>40,剩余的子序列为A[31…60]=41,42,…70;第二次比较中,A[45]=55;70>55,剩余的子序列为A[46…60]=56,57,…70;第三次比较中,A[53]=63;70>63,剩余的子序列为A[54…60]=64,65,…70;第四次比较中,A[57]=67;70>67,剩余的子序列为A[58…60]=68,69,70;第五次比较中,A[59]=69;70>69,剩余的子序列为A[60]=70;第六次比较中,A[60]=70;比较结束;共进行6次比较;当x=77,第一次比较中,数组的中间元素A[30]=40; 77>40,剩余的子序列为A[31…60]=41,42,…70;第二次比较中,A[45]=55;77>55,剩余的子序列为A[46…60]=56,57,…70;第三次比较中,A[53]=63;77>63,剩余的子序列为A[54…60]=64,65,…70;第四次比较中,A[57]=67;77>67,剩余的子序列为A[58…60]=68,69,70;第五次比较中,A[59]=69;77>69,剩余的子序列为A[60]=70;第六次比较中,A[60]=70;77>70,high=60;low=61;停止比较,共进行6次比较1.10:BOTTOMUPSORT对于数组A[1...16]的运作过程如下:共执行47次该算法执行的比较次数为:8+2+3+2+3+7+7+15=471.15 用Θ符号表示㏒2n+n+㏒㏒n。
河海高数ch1习题答案

第一章 函数、极限与连续Ex1 函数一、1.× 2. √ 3.√二、1.(-∞,+∞),a a f =)( 2.f (x )与h (x )3.(1)[-1,1](2)[1, 10](3)[-2,-1]4.,2)1(+-=+x xx f x x f f =)]([ 5.65)(2+-=x x x f 6.2)(2-=x x f 7.x x x f -=-1log )(21,其定义域为(0,1)8.偶函数 9.⎩⎨⎧=≠=0001sgn 2x x x⎪⎩⎪⎨⎧∈-∈--∈-=]2,1(1]1,1[)1,2[1)(x x xx x F 三、⎪⎪⎩⎪⎪⎨⎧≥≤≤-+-≤<-≤≤=4643108311210)(22x x x x x x x x x S 四、⎩⎨⎧>-≤≤=50525.050015.0x x x xy 五、 ⎩⎨⎧+<≤<≤--=ππππππ)12(20222)(n x n n x n n x x f 六、⎪⎩⎪⎨⎧-<---=>-=-110111x x x x x x f )(七、八、将x 换成x1,可解方程组得⎪⎭⎫⎝⎛--=bcx x ac b a x f 221)(,是奇函数。
Ex2 数列极限的概念一、1、,N ∃ 当n >N 时, 记为 )(lim ∞→→=∞→n A u A u n n n 或 2、只要ε21>n , 取⎥⎦⎤⎢⎣⎡=ε21N , 13.只要ε999.0log >n ,取[]ε999.0log =N , 即有极限 = 0 二、1. C 2. C 3. B三、1.证:要 n n n n 1)13((31341314222<+=-++ <ε, 取⎥⎦⎤⎢⎣⎡=ε1N , 则当n > N 时,就有 ε<-++34131422n n .2. 证:要επ<<-++n n n 20)1(2cos1 , 取⎥⎦⎤⎢⎣⎡=ε2N ,3、证:{}n x Θ有界,M x N n M n ≤∈∀>∃∴|,,0都有对;又0lim =∞→n n y ,My N n N n εε<>∃>∀∴都有当对,,,0因此,对上述N ,当n >N 时,就有ε<n n y x ,0lim =∴∞→n n n y x .Ex3 函数极限的概念一、1.证:.sin ,,01,1,1sin ,022εεεεε<>>=><<>∀xxX x X x x x x 就有时则当故取则有要使得对 0sin lim =∴+∞→xxx 2.证:.1,,01,1,1111,022εεεεε<-+>>=><<++=-+>∀x x X x X x xx x x x 就有时则当故取则有要使得对0)1(lim 3=-+∴→x x x3. 证:.1153,20,03,32,231153,0εδεδεεε<-+<-<>=<-<-=-+>∀x x x x x 就有时则当故取则有要使得对 11)53(lim 2=+∴→x x .9,30,01,7min ,79,13,3,339,0:.4222εδεδεεε<-<-<<>⎭⎬⎫⎩⎨⎧=<-<-∴→<+-=->∀x x x x x x x x 就有时 则当故取因此可以限制 要使得 对证Θ9lim 23=∴→x x ,1lim 0=+→xx x Θ二、证: ,1lim 0-=-→x xxx x x 0lim→∴不存在。
CH1习题及答案

1. 2. 3. 4. 5.6.有四批零件,第一批有2000个零件,其中5%是次品。
第二批有500个零件,其中40%是次品。
第三批和第四批各有1000个零件,次品约占10%。
我们随机地选择一个批次,并随机地取出一个零件。
(1) 问所选零件为次品的概率是多少?(2) 发现次品后,它来自第二批的概率是多少?解:(1)用i B 表示第i 批的所有零件组成的事件,用D 表示所有次品零件组成的事件。
()()()()123414P B P B P B P B ====()()()()12341002000.050.420005001001000.10.110001000P D B P D B P D B P D B ========()11110.050.40.10.10.16254444P D =⨯+⨯+⨯+⨯=(2)发现次品后,它来自第二批的概率为,()()()()2220.250.40.6150.1625P B P D B P B D P D ⨯===7. 8.9. 设随机试验X 的分布律为X 1 2 3P0.2 0.5 0.3求X 的概率密度和分布函数,并给出图形。
解:()()()()0.210.520.33f xx x x δδδ=-+-+-()()()()0.210.520.33F x u x u x u x =-+-+-10.11. 设随机变量X 的概率密度函数为()xf x ae -=,求:(1)系数a ;(2)其分布函数。
解:(1)由()1f x dx ∞-∞=⎰()()2xxx f x dx ae dx ae dx e dx a ∞∞∞---∞-∞-∞==+=⎰⎰⎰⎰所以12a =(2)()1()2xxtF x f t dt e dt --∞-∞==⎰⎰所以X 的分布函数为()1,0211,02xx e x F x e x -⎧<⎪⎪=⎨⎪-≥⎪⎩12.13.14. 若随机变量X 与Y 的联合分布律为Y X-1 0 1 0 0.070.18 0.15 10.080.320.20求:(1)X 与Y 的联合分布函数与密度函数;(2)X 与Y 的边缘分布律;(3)Z XY =的分布律;(4)X 与Y 的相关系数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
复变函数复习题 CH1 复数与复变函数1. (cos θ+i sin θ)3=( ) A.cos(3θ)+i sin(3θ)B.cos3sin3θθi + C.cos(3θ)+3i sin(3θ)D.cos3sin33θθi +2. 下列集合为无界单连通区域的是( ) A.Re(z-5i )2≥ B.| z-5i |3≤ C.| z-5i |>0D.Im(z-5i )<-13. Re(e2x+iy)=()A.e 2x B.e y C.e 2x cosyD.e 2xsiny4. Re(cosi)=()A .2e e 1-+ B .2e e 1-- C .2ee1+-- D .2ee1--5. 复数e 3-2i 所对应的点( )。
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限6. 设z=(-i)i ,则|z|=__________.7. Z=4i 3i3ee 2ππ则argZ=________.8. 23.设z=e 2+i ,则argz=. 9. 5.复数e3+i所对应的点在()A.第一象限B.第二象限C.第三象限D.第四象限10. 复数z=--355(cos sin)ππi 的三角表示式为( )A.-+34545(cossin)ππi B.34545(cos sin)ππ-i C. 34545(cos sin)ππ+i D.--34545(cossin)ππi11. 在w=Z 3的映射下,Z 平面上的区域-6π<argZ<6π映射成W 平面上的区域________.12. 下列集合为有界单连通区域的是() A.0<|z-3|<2B.Rez>3C.|z+a|<1D.π≤<πargz 2113. 设z=x+iy ,则|e 2i+2z |=( )A.e 2+2x B.e |2i+2z|C.e 2+2z D.e 2x 14. 下列集合为无界多连通区域的是( ) A.0<|z-3i|<1B.Imz>πC.|z+ie|>4D.π<<π2z arg 2315. 设z=cos(π+5i),则Rez 等于( )。
A. 2e e55+-- B.2e e55+- C.2e e55-- D. 016. 复数i -3的指数表达式是___________(辐角在主值范围内)。
17. 设z=x+iy,则(1+i )z 2的实部为( )A.x 2-y 2+2xyB.x 2-y 2-2xyC.x 2+y 2+2xyD.x 2+y 2-2xy18. 设复数)2)(1(--=i i i z ,(1)求z 的实部和虚部;(2)求z 的模;(3)指出z 是第几象限的点.19. 设iy x z +=.将方程1Re ||=+z z 表示为关于x ,y 的二元方程,并说明它是何种曲线. 20. 求解方程z 4+16=0。
21. 设z =1-i ,则Im(21z)=( )A .-1B .-21C .21D .122. 复数z =ii -+23的幅角主值是( )A .0B .4πC .2πD .43π23. 复数-1-i 的指数形式为__________.24. 设z =x +iy 满足x -1+i (y +2)=(1+i )(1-i ),则z =__________. 25. 区域0<arg z<4π在映射w =z 3下的像为__________.26. 将曲线的参数方程z =3e it +e -it (t 为实参数)化为直角坐标方程.27. 设z=i +-11,则z 为()A .21i +- B .21i--C .21i- D .21i+28. 复数1-3i 的三角表达式是_________________.29. 用θcos 与θsin 表示θ5cos.30. 设z 为非零复数,a ,b 为实数,若ib a zz+=_,则a 2+b 2的值( )A .等于0B .等于1C .小于1D .大于131. 设2,3z w i z =+=,则( )A .3arg π=w B .6arg π=w C .6arg π-=w D .3arg π-=w32. 设i z 101103+-=,则=_z ____________.33. 设z 为非零复数,a ,b 为实数,若ib a zz+=_,则a 2+b 2的值( )A .等于0B .等于1C .小于1D .大于134. 设2,3z w i z =+=,则( )A .3arg π=w B .6arg π=w C .6arg π-=w D .3arg π-=w35. 设iz 101103+-=,则=_z____________.36. 设复数)2)(1(--=i i iz ,(1)求z 的实部和虚部;(2)求z 的模;(3)指出z 在第几象限.37. 设iy x z +=.将方程1Re ||=+z z 表示为关于x ,y 的二元方程,并说明它是何种曲线.38. z=2-2i ,|z 2|=( = |z|2)A.2B.8C.4D.839. 复数方程z=cost+isint 的曲线是()A.直线B.圆周C.椭圆D.双曲线 40. 若z 1=e1+i π,z 2=3+i ,求解z 1·z 241. 计算复数z=327-的值.42. 包含了单位圆盘|z|<1的区域是( )A.Re z<-1B.Re z<0C.Re z<1D.Im z<0 43. arg (-1+3i )=.44. 求z =(-1+i )6的共轭复数z 及共轭复数的模|z |.45. 设t 为实参数,求曲线z=re it+3(0≤t <2π的直角坐标方程. 46. arg(2-2i)=( )A.43π-B.4π-C.4π D.43π47. 复数方程z=3t+it 表示的曲线是( )A.直线B.圆周C.椭圆 D.双曲线 48. 若ii z -+=31,则z =___________.49. 解方程z 4=-1.50. 设z=1+2i ,则Im z 3=( )A.-2B.1C.8D.1451. z=(1+cost)+i(2+sint),0≤t<2π所表示的曲线为( ) 52. arg(3-i)=___________. 53. 求方程z 3+8=0的所有复根.54. 复数i 31z +-=的幅角主值为( )A.32π B.6πC. 6π-D. 32π-55. 下列点集不是区域的是( )A.{z|Rez>0};B.{z|Rez<0};C.{z||z|≤|i|};D.{z||z|>1} 56. 下列方程不表示...圆周的是( ) A.z=3e it -1(0≤t<2π)B.z=re it (r>0,0≤t<2π)C.z=sint+icost(0≤t<2π) D.z-z =i57. 方程z 3+1=0的所有复数根为___________. 58. 复数21i z -=的指数形式为___________.59. 平面点集E={(x,y )|x 2+y 2-2y ≤0}(其中z=x+iy )用复数模的不等式可表示成___________. 60. 设复数.)19991998)(20001999()20001999)(19991998(z i i i i z ,求-+-+=61. 设z=3+4i,,则Re z 2=( )A .-7B .9C .16D .2562. 下列复数中,使等式z1=-z 成立的是( )A .z=e2πiB .z=eπiC .z=i2eπ-D .z=i43eπ63. 设0<t ≤2π,则下列方程中表示圆周的是( ) A .z=(1+i)tB .z=e it +2iC .z=t+t iD .z=2cost+i3sint64. 下列区域为有界单连通区域的是( ) A .0<|z-i|<1 B .0<Imz<πC .|z-3|+|z+3|<12 D .0<argz<43π65. arg(1+i)=.66. 设z=x+iy,则曲线|z-1|=1的直角坐标方程为. 67. 已知方程(1+2i)z=4+3i ,则z 为( )。
A. 2+iB. -2+iC. 2-iD. -2-i68. 2.方程Re(z+2)=1所代表的曲线是( )。
A. 直线 B. 椭圆C. 双曲线D. 抛物线69. 3.复数z=-(cos 3π+isin 3π)的三角形式是( )。
A. (cos32π+isin32π)B. (cos 3π+isin3π)C. (cos32π+isin32π-)D. (cos3π-+isin3π-)70. 复变函数f(z)=Imz 在复平面上可导的点集为______. 71. 设复数z 满足arg(z+2)=3π,arg(z -2)=65π,试求z.72. 复数方程z=2+θi e (θ为实参数,0≤θ<2π)所表示的曲线为() A .直线B .圆周C .椭圆D .抛物线 73. 已知4arg 2π=z ,则argz=()A .8πB .4πC .2π D .π74. 求出复数z=4)31(i +-的模和辐角.75. 设z=x+iy ,满足Re(z 2+3)=4,求x 与y 的关系式. 76. z=6+i,则 |z|=__________,argz=__________. 77. z=e -3+i 则argz=__________.78. 复数-1+3i 的三角形式是__________.79. 一曲线的复数方程是|z-i|=1,则此曲线的直角坐标方程为__________. 80. 试证:设1z 1-z +是纯虚数,则必有|z|=1.81. 求z 4+3-i=0的根.82. Z=x+iy,已知x=-1,argZ=32-π,则y ,|Z|分别等于________.83. 曲线的复数方程为Z=t-ti,t ≠0. t ∈R ,它的直角坐标方程是________.84. 复数Z 满足|Z|=2及|Z-2|=2,求Z. 85. 解方程Z 4+i=0.86. 复数z=1625825-i的辐角为()A.arctan12B.-arctan 12C.π-arctan 12D.π+arctan1287. 方程Rez 2=1所表示的平面曲线为()A.圆 B.直线C.椭圆D.双曲线88. 复数z=4+48i 的模|z|=. 89. 设z=(1+i)100,则Imz=.90. 若),(,),(21d c z b a z ==,则=⋅21z z ( ).(A) ),(a bd ac + (B) ),(b bd ac - (C) ),(ad bc bd ac +-(D) ),(ad bc bd ac -+ 91. 若0>R ,则:{),(z R N =∞( )}.(A) R z <(B) R z <<0(C) +∞<<z R (D) R z >92. 若y x z i +=,则=y ( ).(A)2z z + (B) 2z z - (C)i2z z + (D)i2z z -93. 若)i 1)(i 4()i 1)(i 4(+--+=A ,则=A ( ). (A) 3 (B) 0 (C) 1 (D) 294. 若y x z i +=,v u z w i 2+==,则=v . 95. 复平面上满足4Re =z 的点集为 . 96. 设00i y x z +=,),2,1(i =+=n y x z n n n ,则{}n z 以0z 为极限的充分必要条件是=+∞→n n x lim 且=+∞→n n y lim .97. 求复数i 1--的实部、虚部、模与主辐角. 98. 写出复数i -的三角式.99. 写出复数ii 1i1i -+-的代数式.100. 求根式327-的值.101. 证明:若i ii b a y x y x +=+-,则122=+b a .102. 证明:)Re(2212221221z z z z z z ++=+.103.设iz -=11,求Re Im z z 和。
