三角形 梯形的中位线精典例题
三角形、梯形的中位线
第3章《中心对称图形(一)》易错题集(08):3.6 三角形、梯形的中位线选择题1.(2010•威海)如图,在△ABC中,D,E分别是边AC,AB的中点,连接BD.若BD 平分∠ABC,则下列结论错误的是()A.BC=2BE B.∠A=∠EDA C.BC=2AD D.BD⊥AC2.(2009•锦州)如图所示,在△ABC中,AB=AC,M,N分别是AB,AC的中点,D,E 为BC上的点,连接DN、EM,若AB=5cm,BC=8cm,DE=4cm,则图中阴影部分的面积为()A.1cm2 B.1.5cm2C.2cm2 D.3cm23.(2009•绍兴)如图,D,E分别为△ABC的AC,BC边的中点,将此三角形沿DE折叠,使点C落在AB边上的点P处.若∠CDE=48°,则∠APD等于()A.42°B.48°C.52°D.58°4.(2009•衢州)在△ABC中,AB=12,AC=10,BC=9,AD是BC边上的高.将△ABC按如图所示的方式折叠,使点A与点D重合,折痕为EF,则△DEF的周长为()A.9.5 B.10.5 C.11 D.15.55.(2009•赤峰)将一张三角形纸片沿中位线剪开,拼成一个新的图形,这个新的图形可能是()A.三角形B.平行四边形C.矩形 D.正方形6.(2008•铜仁地区)如图,M是△ABC的边BC的中点,AN平分∠BAC,且BN⊥AN,垂足为N,且AB=6,BC=10,MN=1.5,则△ABC的周长是()A.28 B.32 C.18 D.257.(2008•随州)如图,点D、E、F分别是△ABC三边的中点,则下列判断错误的是()A.四边形AEDF一定是平行四边形B.若∠A=90°,则四边形AEDF是矩形C.若AD平分∠A,则四边形AEDF是正方形D.若AD⊥BC,则四边形AEDF是菱形8.(2008•嘉兴)如图,△ABC中,已知AB=8,BC=6,CA=4,DE是中位线,则DE=()A.4 B.3 C.2 D.19.(2008•大庆)如图,将非等腰△ABC的纸片沿DE折叠后,使点A落在BC边上的点F 处.若点D为AB边的中点,则下列结论:①△BDF是等腰三角形;②∠DFE=∠CFE;③DE是△ABC的中位线,成立的有()A.①②B.①③C.②③D.①②③10.(2007•随州)如图,沿Rt△ABC的中位线DE剪切一刀后,用得到的△ADE和四边形DBCE拼图,下列图形中不一定能拼出的是()A.平行四边形B.矩形 C.菱形 D.等腰梯形11.(2007•娄底)如图,将一张等腰直角三角形纸片沿中位线DE剪开后,可以拼成的四边形是()A.矩形或等腰梯形B.矩形或平行四边形C.平行四边形或等腰梯形D.矩形或等腰梯形或平行四边形12.(2007•贵港)如图,在△ABC中,AB=AC=5,BC=6,D、E分别是AB、AC的中点,F、G为BC上的两点,FG=3,线段DG,EF的交点为O,当线段FG在线段BC上移动时,三角形FGO的面积与四边ADOE的面积之和恒为定值,则这个定值是()A.15 B.12 C.9 D.613.(2006•韶关)如图,已知△ABC的周长为1,连接△ABC三边的中点构成第二个三角形,再连接第二个三角形三边的中点构成第三个三角形,…,依此类推,则第10个三角形的周长为()A.B.C.D.14.(2006•杭州)如图,△ABC、△ADE及△EFG都是等边三角形,D和G分别为AC和AE的中点.若AB=4时,则图形ABCDEFG外围的周长是()A.12 B.15 C.18 D.2115.(2006•滨州)如图,DE是△ABC的中位线,M是DE的中点,CM的延长线交AB于点N,则S△DMN:S四边形ANME等于()A.1:5 B.1:4 C.2:5 D.2:716.(2006•青海)如图DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于点G,则AG:GD等于()A.2:1 B.3:1 C.3:2 D.4:317.(2003•内蒙古)已知第一个三角形的周长为1,它的三条中位线组成第二个三角形,第二个三角形的三条中位线又组成第三个三角形,以此类推,则第2003个三角形的周长为()A.B.C.D.18.(2008•河南)如图所示,有一张一个角为60°的直角三角形纸片,沿其一条中位线剪开后,不能拼成的四边形是()A.邻边不等的矩形B.等腰梯形C.有一个角是锐角的菱形 D.正方形19.(2013•德庆县二模)已知△ABC的三边长分别为3cm,4cm,5cm,D,E,F分别为△ABC 各边的中点,则△DEF的周长为()A.3cm B.6cm C.12cm D.24cm20.(2009•漳州自主招生)△ABC的三边长分别为a、b、c,三条中位线组成第一个中点三角形,第一个中点三角形的三条中位线又组成第二个中点三角形,以此类推,求第2009中点三角形的周长为()A.B.C.D.21.如果连接等边三角形各边中点所成的三角形的周长为6,那么该等边三角形的边长为()A.2 B.3 C.4 D.922.(2008秋•邗江区月考)如图,在钝角△ABC中,点D、E分别是边AC、BC的中点,且DA=DE.有下列结论:①∠1=∠2;②∠1=∠3;③∠B=∠C;④∠B=∠3.其中一定正确的结论有()个.A.0 B.1 C.2 D.323.(2009秋•开县月考)如图,在△ABC中,D、E、F分别为BC、AC、AB的中点,AH⊥BC于点H,FD=8cm,则HE的值为()A.20cm B.16cm C.12cm D.8cm24.如图,D,E,F分别为△ABC三边的中点,且AB=AC≠BC,那么△DEF为()A.等边三角形B.等腰直角三角形C.等腰三角形D.不等边三角形25.(2010•鼓楼区校级模拟)如图,在△ABC中,DE为中位线,则S△ADE:S梯形BCED等于()A.B.C.D.26.(2013•绍兴模拟)如图,△ABC纸片中,AB=BC>AC,点D是AB边的中点,点E 在边AC上,将纸片沿DE折叠,使点A落在BC边上的点F处.则下列结论成立的个数有()①△BDF是等腰直角三角形;②∠DFE=∠CFE;③DE是△ABC的中位线;④BF+CE=DF+DE.A.1个B.2个C.3个D.4个27.(2006•内江)在如图所示的梯形ABCD中,AD∥BC,AD=5,BC=11,①中A1B1是连接两腰中点的线段,易知A1B1=8,②中A1B1,A2B2是连接两腰三等分点且平行于底边的线段,可求出A1B1+A2B2的值…,照此规律下去,③中A1B1,A2B2,…A10B10是连接两腰十一等分点且平行于底边的线段,则A1B1+A2B2+…+A10B10的值为()A.50 B.80 C.96 D.10028.(2001•昆明)平面上A、B两点到直线l的距离分别是和,则线段AB的中点C到直线l的距离是()A.3 B.C.3或D.以上答案都不对29.(2009春•丽水期末)等腰梯形的高是4,对角线与下底的夹角是45°,则该梯形的中位线是()A.4 B.6 C.8 D.1030.(2005•金华)如图1,在△ABC中,D、E分别是AB、AC的中点,将△ADE沿线段DE向下折叠,得到图2.下列关于图2的四个结论中,不一定成立的是()A.点A落在BC边的中点 B.∠B+∠1+∠C=180°C.△DBA是等腰三角形D.DE∥BC第3章《中心对称图形(一)》易错题集(08):3.6 三角形、梯形的中位线参考答案与试题解析选择题1.(2010•威海)如图,在△ABC中,D,E分别是边AC,AB的中点,连接BD.若BD 平分∠ABC,则下列结论错误的是()A.BC=2BE B.∠A=∠EDA C.BC=2AD D.BD⊥AC【分析】根据D,E分别是边AC,AB的中点,得出DE是△ABC的中位线,所以DE∥BC 且BC=2DE;又BD平分∠ABC,所以∠CDB=∠DBE=∠BDE,所以BE=DE=AE,所以AB=2DE,所以AB=BC,即可得出B、D选项正确.【解答】解:∵D,E分别是边AC,AB的中点,∴DE∥BC且BC=2DE,∵BD平分∠ABC,∴∠CBD=∠DBE=∠BDE,∴BE=DE=AE,∴AB=2DE,BC=2DE=2BE,故A正确;∴AB=BC,∴∠A=∠C=∠EDA,故B正确;C、∵AE=DE,与AD不一定相等,故本选项不一定成立;D、∵AB=BC,点D是AC的中点,∴BD⊥AC,故本选项正确.故选C.2.(2009•锦州)如图所示,在△ABC中,AB=AC,M,N分别是AB,AC的中点,D,E 为BC上的点,连接DN、EM,若AB=5cm,BC=8cm,DE=4cm,则图中阴影部分的面积为()A.1cm2 B.1.5cm2C.2cm2 D.3cm2【专题】压轴题;整体思想.【分析】根据题意,易得MN=DE,从而证得△MNO≌△EDO,再进一步求△ODE的高,进一步求出阴影部分的面积.【解答】解:连接MN,作AF⊥BC于F.∵AB=AC,∴BF=CF=BC=×8=4,在Rt△ABF中,AF==,∵M、N分别是AB,AC的中点,∴MN是中位线,即平分三角形的高且MN=8÷2=4,∴NM=BC=DE,∴△MNO≌△EDO,O也是ME,ND的中点,∴阴影三角形的高是AF÷2=1.5÷2=0.75,∴S阴影=4×0.75÷2=1.5.故选B.3.(2009•绍兴)如图,D,E分别为△ABC的AC,BC边的中点,将此三角形沿DE折叠,使点C落在AB边上的点P处.若∠CDE=48°,则∠APD等于()A.42°B.48°C.52°D.58°【专题】操作型.【分析】由翻折可得∠PDE=∠CDE,由中位线定理得DE∥AB,所以∠CDE=∠DAP,进一步可得∠APD=∠CDE.【解答】解:∵△PED是△CED翻折变换来的,∴△PED≌△CED,∴∠CDE=∠EDP=48°,∵DE是△ABC的中位线,∴DE∥AB,∴∠APD=∠CDE=48°,故选B.4.(2009•衢州)在△ABC中,AB=12,AC=10,BC=9,AD是BC边上的高.将△ABC按如图所示的方式折叠,使点A与点D重合,折痕为EF,则△DEF的周长为()A.9.5 B.10.5 C.11 D.15.5【专题】压轴题.【分析】根据折叠图形的对称性,易得△EDF≌△EAF,运用中位线定理可知△AEF的周长等于△ABC周长的一半,进而△DEF的周长可求解.【解答】解:∵△EDF是△EAF折叠以后形成的图形,∴△EDF≌△EAF,∴∠AEF=∠DEF,∵AD是BC边上的高,∴EF∥CB,又∵∠AEF=∠B,∴∠BDE=∠DEF,∴∠B=∠BDE,∴BE=DE,同理,DF=CF,∴EF为△ABC的中位线,∴△DEF的周长为△EAF的周长,即AE+EF+AF=(AB+BC+AC)=(12+10+9)=15.5.故选:D.5.(2009•赤峰)将一张三角形纸片沿中位线剪开,拼成一个新的图形,这个新的图形可能是()A.三角形B.平行四边形C.矩形 D.正方形【专题】压轴题;操作型.【分析】可动手画图解答,在拼图时注意将相等的线段拼凑,得出所有可能出现的图形,然后再进行判定.【解答】解:因为此三角形没说明是特殊三角形,所以沿中位线剪开,拼成一个新的图形,只能可能是平行四边形.故选B.6.(2008•铜仁地区)如图,M是△ABC的边BC的中点,AN平分∠BAC,且BN⊥AN,垂足为N,且AB=6,BC=10,MN=1.5,则△ABC的周长是()A.28 B.32 C.18 D.25【专题】压轴题.【分析】延长线段BN交AC于E,从而构造出全等三角形,(△ABN≌△AEN),进而证明MN是中位线,从而求出CE的长.【解答】解:延长线段BN交AC于E.∵AN平分∠BAC,∴∠BAN=∠EAN,AN=AN,∠ANB=∠ANE=90°,∴△ABN≌△AEN,∴AE=AB=6,BN=NE,又∵M是△ABC的边BC的中点,∴CE=2MN=2×1.5=3,∴△ABC的周长是AB+BC+AC=6+10+6+3=25,故选D.7.(2008•随州)如图,点D、E、F分别是△ABC三边的中点,则下列判断错误的是()A.四边形AEDF一定是平行四边形B.若∠A=90°,则四边形AEDF是矩形C.若AD平分∠A,则四边形AEDF是正方形D.若AD⊥BC,则四边形AEDF是菱形【分析】一组对边平行且相等的四边形是平行四边形;有一个角是直角的平行四边形是矩形;对角线互相垂直的平行四边形是菱形.【解答】解:A、∵点D、E、F分别是△ABC三边的中点,∴DE、DF为△ABC得中位线,∴ED∥AC,且ED=AC=AF;同理DF∥AB,且DF=AB=AE,∴四边形AEDF一定是平行四边形,正确.B、若∠A=90°,则四边形AEDF是矩形,正确;C、若AD平分∠A,延长AD到M,使DM=AD,连接CM,由于BD=CD,DM=AD,∠ADB=∠CDB,(SAS)∴△ABD≌△MCD∴CM=AB,又∵∠DAB=∠CAD,∠DAB=∠CMD,∴∠CMD=∠CAD,∴CA=CM=AB,因AD平分∠A∴AD⊥BC,则△ABD≌△ACD;AB=AC,AE=AF,结合(1)四边形AEDF是菱形,因为∠A不一定是直角∴不能判定四边形AEDF是正方形;D、若AD⊥BC,则△ABD≌△ACD;AB=AC,AE=AF,结合(1)四边形AEDF是菱形,正确.故选C.8.(2008•嘉兴)如图,△ABC中,已知AB=8,BC=6,CA=4,DE是中位线,则DE=()A.4 B.3 C.2 D.1【分析】由D,E分别是边AB,AC的中点,首先判定DE是三角形的中位线,然后根据三角形的中位线定理求得DE的值即可.【解答】解:∵DE是△ABC的中位线,∴DE=BC,∵BC=6,∴DE=BC=3.故选B.9.(2008•大庆)如图,将非等腰△ABC的纸片沿DE折叠后,使点A落在BC边上的点F 处.若点D为AB边的中点,则下列结论:①△BDF是等腰三角形;②∠DFE=∠CFE;③DE是△ABC的中位线,成立的有()A.①②B.①③C.②③D.①②③【专题】压轴题.【分析】根据图形可知△DFE是△ADE对折而成,所以两三角形全等,可得AD=DF,而D 是AB中点,故有BD=DF,那么①可证;再利用∠ADF是△BDF的外角,可证∠DFB=∠EDF,那么DE∥BC,即DE是△ABC的中位线,②得证;利用DE∥BC,以及△DFE和△ADE 的对折,可得∠EFC=∠ECF,即△EFC也是等腰三角形,而∠B≠∠C,即∠DFB,∠DFE,∠EFC,不会同时为60°,那么∠DFE≠∠CFE,故②不成立.【解答】解:由于△DFE是△ADE对折而成,故△DFE≌△ADE,∴AD=FD,又∵点D为AB边的中点,∴AD=BD,∴BD=DF,即△BDF是等腰三角形,故(1)正确;由于△DFE是△ADE对折而成,故△DFE≌△ADE,∴∠ADE=∠FDE,∵∠ADF=2∠FDE=∠B+∠DFB=2∠DFB,∴∠FDE=∠DFB,∴DE∥BC,点E也是AC的中点,故(3)正确;同理可得△EFC也为等腰三角形,∠C=∠EFC,由于△ABC是非等腰的,∴∠C≠∠B,也即∠EFC≠∠DFB,∴∠EFC与∠DFB,∠DFE不都等于60°,∴②∠DFE=∠CFE就不成立.故选B.10.(2007•随州)如图,沿Rt△ABC的中位线DE剪切一刀后,用得到的△ADE和四边形DBCE拼图,下列图形中不一定能拼出的是()A.平行四边形B.矩形 C.菱形 D.等腰梯形【专题】压轴题;操作型.【分析】可动手拼图,先画出图形再根据已知条件解答.【解答】解:如图:①为矩形;②为平行四边形,若∠B=60°时为菱形;③等腰梯形.故选C.11.(2007•娄底)如图,将一张等腰直角三角形纸片沿中位线DE剪开后,可以拼成的四边形是()A.矩形或等腰梯形B.矩形或平行四边形C.平行四边形或等腰梯形D.矩形或等腰梯形或平行四边形【分析】能够根据图形的变换:平移,轴对称,旋转三种变换进行拼图.【解答】解:如图示,若把△ADE绕点E旋转180°可得矩形;若把△ADE绕点D旋转180°,即可得到平行四边形;若把△ADE向下平移AD个单位长度,再沿BD翻折,即可得到等腰梯形,故选D.12.(2007•贵港)如图,在△ABC中,AB=AC=5,BC=6,D、E分别是AB、AC的中点,F、G为BC上的两点,FG=3,线段DG,EF的交点为O,当线段FG在线段BC上移动时,三角形FGO的面积与四边ADOE的面积之和恒为定值,则这个定值是()A.15 B.12 C.9 D.6【专题】压轴题;动点型.【分析】连接DE,过A作AH⊥BC于H.由于DE是AB、AC的中点,利用三角形中位线定理可得DE∥BC,并且可知△ADE的高等于AH,再结合等腰三角形三线合一性质,以及勾股定理可求AH,那么△ADE的面积就可求.而所求S△FOG+S四边形ADOE=S△ADE+S△DOE+S△FOG,又因为△DOE和△FOG的底相等,高之和等于AH的一半,故它们的面积和可求,从而可以得到S△FOG+S四边形ADOE的面积.【解答】解:如图:连接DE,过A向BC作垂线,H为垂足,∵△ABC中,D、E分别是AB、AC的中点,∴DE,AH分别是△ABC的中位线和高,BH=CH=BC=×6=3,∵AB=AC=5,BC=6,由勾股定理得AH===4,∴S△ADE=BC•=×3×=3,设△DOE的高为a,△FOG的高为b,则a+b==2,∴S△DOE+S△FOG=DE•a+FG•b=×3(a+b)=×3×2=3,∴三角形FGO的面积与四边ADOE的面积之和恒为定值,则这个定值是S△ADE+S△DOE+S△FOG=3+3=6.故选D.13.(2006•韶关)如图,已知△ABC的周长为1,连接△ABC三边的中点构成第二个三角形,再连接第二个三角形三边的中点构成第三个三角形,…,依此类推,则第10个三角形的周长为()A.B.C.D.【专题】压轴题;规律型.【分析】根据三角形的中位线定理建立周长之间的关系,按规律求解.【解答】解:根据三角形中位线定理可得第二个三角形的各边长都等于最大三角形各边的一半,那么第二个三角形的周长=△ABC的周长×=1×=,第三个三角形的周长为=△ABC 的周长××=()2,第10个三角形的周长=()9,故选C.14.(2006•杭州)如图,△ABC、△ADE及△EFG都是等边三角形,D和G分别为AC和AE的中点.若AB=4时,则图形ABCDEFG外围的周长是()A.12 B.15 C.18 D.21【分析】利用平移性质可得图形ABCDEFG外围的周长等于等边三角形△ABC的周长加上AE,GF长,利用三角形中位线长定理可得其余未知线段的长.【解答】解:∵△ABC、△ADE及△EFG都是等边三角形,D和G分别为AC和AE的中点,AB=AC=BC=4∴DE=CD=AC=×4=2,EF=GF=AG=DE=×2=1∴图形ABCDEFG外围的周长是AB+CD+BC+DE+EF+GF+AG=4+2+4+2+1+1+1=15故选B.15.(2006•滨州)如图,DE是△ABC的中位线,M是DE的中点,CM的延长线交AB于点N,则S△DMN:S四边形ANME等于()A.1:5 B.1:4 C.2:5 D.2:7【专题】几何综合题;压轴题.【分析】本题的关键是求出S△DMN,先连接AM,由于DE是△ABC的中位线,那么DE∥BC,且DE=BC,M是DE中点,于是可知,DM=BC,在△BCN中,利用平行线分线段成比例定理的推论,可得DN=BD,即,DN=AD,于是S△DMN=S△ADM,而S△ADM=S△ADE=S△ABC(可设S△ABC=1),那么S四边形ANME也可求,两者面积比也就可求.【解答】解:∵DE是△ABC的中位线,∴DE∥BC,DE=BC,若设△ABC的面积是1,根据DE∥BC,得△ADE∽△ABC,∴S△ADE=,连接AM,根据题意,得S△ADM=S△ADE=S△ABC=,∵DE∥BC,DM=BC,∴DN=BN,∴DN=BD=AD.∴S△DNM=S△ADM=,∴S四边形ANME==,∴S△DMN:S四边形ANME=:=1:5.故选A.16.(2006•青海)如图DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于点G,则AG:GD等于()A.2:1 B.3:1 C.3:2 D.4:3【专题】压轴题.【分析】过E作EM∥AB与GC交于点M,构造全等三角形把DG转移到和AG有关的中位线处,可得所求线段的比.【解答】解:过E作EM∥AB与GC交于点M,∴△EMF≌△DGF,∴EM=GD,∵DE是中位线,∴CE=AC,又∵EM∥AG,∴△CME∽△CGA,∴EM:AG=CE:AC=1:2,又∵EM=GD,∴AG:GD=2:1.故选A.17.(2003•内蒙古)已知第一个三角形的周长为1,它的三条中位线组成第二个三角形,第二个三角形的三条中位线又组成第三个三角形,以此类推,则第2003个三角形的周长为()A.B.C.D.【专题】压轴题;规律型.【分析】根据三角形的中位线定理,第一个三角形的周长为1,推导出第二个三角形的周长,第三个三角形的周长为,然后由前几个三角形的周长,寻找周长之间的规律.【解答】解:由于三角形的中位线平行于第三边并且等于它的一半,三条中位线组成的三角形的周长是原三角形的周长的一半,以此类推,第2003个三角形的周长为(×××…×)[2002个]=.故选C.18.(2008•河南)如图所示,有一张一个角为60°的直角三角形纸片,沿其一条中位线剪开后,不能拼成的四边形是()A.邻边不等的矩形B.等腰梯形C.有一个角是锐角的菱形 D.正方形【分析】可画出图形,令相等的线段重合,拼出可能出现的图形,然后再根据已知三角形的性质,对拼成的图形进行具体的判定.【解答】解:如图:此三角形可拼成如图三种形状,(1)为矩形,∵有一个角为60°,则另一个角为30°,∴此矩形为邻边不等的矩形;(2)为菱形,有两个角为60°;(3)为等腰梯形.故选:D.19.(2013•德庆县二模)已知△ABC的三边长分别为3cm,4cm,5cm,D,E,F分别为△ABC 各边的中点,则△DEF的周长为()A.3cm B.6cm C.12cm D.24cm【分析】利用三角形中位线定理可知,中点三角形的周长等于原三角形周长的一半,即可求.【解答】解:∵△ABC的三边长分别为3cm,4cm,5cm,∵D,E,F分别为△ABC各边的中点,∴△DEF的各边长分别为△ABC的三边长的一半,∴△DEF的周长为(3+4+5)=6cm.故选B.20.(2009•漳州自主招生)△ABC的三边长分别为a、b、c,三条中位线组成第一个中点三角形,第一个中点三角形的三条中位线又组成第二个中点三角形,以此类推,求第2009中点三角形的周长为()A.B.C.D.【专题】压轴题;规律型.【分析】由三角形的中位线定理可知,第一个中点三角形的周长是原三角形周长的,即第一个中点三角形的周长是×(a+b+c),第二个中点三角形的周长是(a+b+c),第三个中点三角形的周长是(a+b+c),第四个中点三角形的周长是(a+b+c),依照此规律,可以得出第2009个中点三角形的周长.【解答】解:根据中位线定理,第一个中点三角形的周长是原三角形的;第二个中点三角形的周长是第一个中点三角形的;第三个中点三角形的周长是第二个中点三角形的,…于是,第2009中点三角形的周长为(××××…×)(a+b+c)=.故选B.21.如果连接等边三角形各边中点所成的三角形的周长为6,那么该等边三角形的边长为()A.2 B.3 C.4 D.9【分析】根据等边三角形的中位线所围成的三角形仍是等边三角形可求得中位线的长为2,则等边三角形的边长为4.【解答】解:∵等边三角形的中位线所围成的三角形的周长为6,∴中位线的长为2,∴等边三角形的边长为4.故选C.22.(2008秋•邗江区月考)如图,在钝角△ABC中,点D、E分别是边AC、BC的中点,且DA=DE.有下列结论:①∠1=∠2;②∠1=∠3;③∠B=∠C;④∠B=∠3.其中一定正确的结论有()个.A.0 B.1 C.2 D.3【分析】由D、E是AC、AB中点,可知DE是△ABC的中位线,那么DE∥AB,即∠1=∠3,又AD=DE,又可得∠2=∠3,那么可知①②是正确的,有D是AC中点,AD=DE,可证CD=DE,再利用DE∥AB,可得出∠B=∠C.在Rt△AEC中,∠2不一定等于∠C,所以④不正确.【解答】解:由题意可证明△ADE、△DEC、△ABC都是等腰三角形,△AEC是直角三角形,则结论正确的是①②③.故选D.23.(2009秋•开县月考)如图,在△ABC中,D、E、F分别为BC、AC、AB的中点,AH⊥BC于点H,FD=8cm,则HE的值为()A.20cm B.16cm C.12cm D.8cm【分析】先根据三角形中位线定理求出AC的长,再利用直角三角形斜边上的中线等于斜边的一半解答.【解答】解:∵D、F是BC、AB的中点,∴AC=2FD=2×8=16cm,∵E是AC的中点,AH⊥BC于点H,∴EH=AC=8cm.故选D.24.如图,D,E,F分别为△ABC三边的中点,且AB=AC≠BC,那么△DEF为()A.等边三角形B.等腰直角三角形C.等腰三角形D.不等边三角形【分析】由三角形中位线定理可得,△DEF的边长为原三角形边长的一半,由于AB=AC≠BC,故原三角形是等腰三角形,所以DF=EF≠DE,故△DEF为等腰三角形.【解答】解:∵D,E,F分别为△ABC三边的中点,∴DE、DF、EF为三角形ABC的三条中位线,∴DE∥BC且等于BC的一半,DF∥AC且等于AC的一半,EF∥AB且等于AB的一半,∵AB=AC≠BC,∴DF=EF≠DE,∴△DEF为等腰三角形.故选C.25.(2010•鼓楼区校级模拟)如图,在△ABC中,DE为中位线,则S△ADE:S梯形BCED等于()A.B.C.D.【分析】三角形的高和梯形的高相等,那么面积之比等于的三角形的底边和梯形上下底边之和的比.【解答】解:∵在△ABC中,DE为中位线,∴BC=2DE,设高为h.∴S△ADE=DE•h=DE•h;S梯形BCED=(DE+BC)•h=DE•h,∴S△ADE:S梯形BCED=,故选B.26.(2013•绍兴模拟)如图,△ABC纸片中,AB=BC>AC,点D是AB边的中点,点E 在边AC上,将纸片沿DE折叠,使点A落在BC边上的点F处.则下列结论成立的个数有()①△BDF是等腰直角三角形;②∠DFE=∠CFE;③DE是△ABC的中位线;④BF+CE=DF+DE.A.1个B.2个C.3个D.4个【专题】压轴题;操作型.【分析】根据题意可知△DFE是△DAE对折的图形,所以全等,故AD=DF,而AD=BD,所以BD=DF,但是∠B不一定等于45°,所以△BDF不一定是等腰直角三角形,①不成立;结合①中的结论,BD=DF,而∠ADE=∠FDE,∠ADF=∠DBF+∠DFB,可证∠BFD=∠EDF,故DE∥BC,即DE是△ABC的中位线,③成立;若③成立,利用△ADE≌△FDE,DE∥BC,∠AEF=∠EFC+∠ECF,可证∠DFE=∠CFE,②成立;根据折叠以及中位线定理得右边=AB,要和左边相等,则需CE=CF,则△CEF应是等边三角形,显然不一定,故④不成立.【解答】解:①根据折叠知AD=DF,所以BD=DF,即一定是等腰三角形.因为∠B不一定等于45°,所以①错误;②连接AF,交DE于G,根据折叠知DE垂直平分AF,又点D是AB边的中点,在△ABF 中,根据三角形的中位线定理,得DG∥BF.进一步得E是AC的中点.由折叠知AE=EF,则EF=EC,得∠C=∠CFE.又∠DFE=∠A=∠C,所以∠DFE=∠CFE,正确;③在②中已证明正确;④根据折叠以及中位线定理得右边=AB,要和左边相等,则需CE=CF,则△CEF应是等边三角形,显然不一定,错误.故选B.27.(2006•内江)在如图所示的梯形ABCD中,AD∥BC,AD=5,BC=11,①中A1B1是连接两腰中点的线段,易知A1B1=8,②中A1B1,A2B2是连接两腰三等分点且平行于底边的线段,可求出A1B1+A2B2的值…,照此规律下去,③中A1B1,A2B2,…A10B10是连接两腰十一等分点且平行于底边的线段,则A1B1+A2B2+…+A10B10的值为()A.50 B.80 C.96 D.100【专题】压轴题;规律型.【分析】首先利用梯形的中位线定理求得图①中的结论;再根据图①的结论,进一步发现:在中位线两边离中位线距离相等的线段和为中位线的2倍;根据上述结论,推而广之.【解答】解:①中A1B1是连接两腰中点的线段,易知A1B1=8;②中A1B1,A2B2是连接两腰三等分点且平行于底边的线段,根据梯形的中位线定理,得A1B1+A2B2=2×8=16,可知,在中位线两边离中位线距离相等的线段和为16;③中A1B1,A2B2,…A10B10是连接两腰十一等分点且平行于底边的线段,则A1B1+A2B2+…+A10B10的值为(A1B1+A10B10)+(A2B2+A9B9)+(A3B3+A8B8)+(A4B4+A7B7)+(A5B5+A6B6)=16+16+16+16+16=80.故选B.28.(2001•昆明)平面上A、B两点到直线l的距离分别是和,则线段AB的中点C到直线l的距离是()A.3 B.C.3或D.以上答案都不对【专题】压轴题;分类讨论.【分析】此题应该分A,B在直线l的同侧和异侧两种情况进行分析.【解答】解:本题要分两种情况讨论(1)如图(一)A,B在直线l的同侧时∵C是AB的中点∴CD是梯形AEFB的中位线∴CD=(AE+BF)=(3﹣+3+)=3.(2)如图(二)A,B在直线l的两侧时连接AF,EB,延长CD交AF与G,反向延长CD交BE于H∵AE⊥EF,BF⊥EF,CD⊥EF,C为AB的中点∴AE∥CD∥BF,AC=BC,ED=DF∴GH是梯形AEBF的中位线∴GH=(AE+BF)=(3﹣+3+)=3在△ABF中,∵AC=BC,HG∥BF∴CG是△ABF的中位线∴CG=BF=(3﹣)同理,DH=BF=(3+)CD=GH﹣CG﹣DH=3﹣(3﹣)﹣(3+)=∴线段AB的中点C到直线l的距离是3或.故选C.29.(2009春•丽水期末)等腰梯形的高是4,对角线与下底的夹角是45°,则该梯形的中位线是()A.4 B.6 C.8 D.10【分析】由等腰梯形的高是4,对角线与下底的夹角是45°,可以得到上底+下底,中位线=×(上底+下底),则可得到结果.【解答】解:如图所示:BG为高,EF为中位线,AB平行CD,AB是上底BG⊥CD,AH⊥CD∵BG⊥CD∠BCG=45°,则CG=4又∵AH⊥CD∠ADH=45°,所以DH=4.又DH+CG=CH+DG+HG+HG=CD+HG其中HG=AB所以AB+CD=CD+HG=DH+CG=8所以中位线===4.故选(A).30.(2005•金华)如图1,在△ABC中,D、E分别是AB、AC的中点,将△ADE沿线段DE向下折叠,得到图2.下列关于图2的四个结论中,不一定成立的是()A.点A落在BC边的中点 B.∠B+∠1+∠C=180°C.△DBA是等腰三角形D.DE∥BC【专题】操作型.【分析】根据折叠的性质明确对应关系,易得∠A=∠1,DE是△ABC的中位线,所以易得B、D答案正确,D是AB中点,所以DB=DA,故C正确.【解答】解:根据题意可知DE是三角形ABC的中位线,所以DE∥BC;∠B+∠1+∠C=180°;∵BD=AD,∴△DBA是等腰三角形.故只有A错,BA≠CA.故选A.参与本试卷答题和审题的老师有:星期八;zxw;算术;lanchong;CJX;心若在;王岑;郝老师;bjy;438011;127078;lf2-9;张超。
三角形、梯形中位线典型题120906

三角形、梯形中位线一、选择1.三角形的三边长分别为12cm 、16cm 、20cm,则它的中位线构成的三角形的周长与面积分别为____ 和___.2.在Rt △ABC 中,∠C=90°,D 、E 、F 分别为AB 、BC 、AC 边上的中点,AC=4 cm ,BC=6 cm,那么四边形CEDF 为__________,它的边长分别为_________________.3.三角形一条中位线分三角形所成的新三角形与原三角形周长之和为60 cm ,则原三角形的周长为_______.4. 已知梯形的上底长为3cm ,下底长为7cm ,则此梯形中位线长为__________cm .5.等腰三角形的两条中位线长分别是3和4,则它的周长是____________.6. 已知D 、E 、F 分别是△ABC 三边的中点,当△ABC 满足条件______时,四边形AFDE 是菱形.7.已知等腰梯形的周长为80cm ,中位线长与腰长相等,则它的中位线长等于_____cm .8.如图,已知等腰梯形ABCD 的中位线EF 的长为5,腰AD 的长为4,则这个等腰梯形的周长为 . 9.如图,ABC ∆沿DE 折叠后,点A 落在BC 边上的A '处,若点D 为AB 边的中点, 50=∠B ,则A BD '∠的度数为 . 10、等腰梯形上、下底长分别为,且两条对角线互相垂直,则这个梯形的面积为 . 二、选择题:1、如果顺次连结四边形各边中点组成的四边形是菱形,那么原来的四边形的对角线( ) A.互相平分 B.互相垂直 C.相等 D.相等且互相平分2、顺次连结下列各四边形中点所得的四边形是矩形的是( ).A .等腰梯形B .矩形C .平行四边形D .菱形或对角线互相垂直的四边形3、已知三角形的3条中位线分别为3cm 、4cm 、6cm ,则这个三角形的周长是( ). A .3cm B .26cm C .24cm D .65cm4.已知DE 是△ABC 的中位线,则△ADE 和△ABC 的面积之比是( ) (A) 1:1 (B) 1:2 (C) 1:3 (D ) 1:45.若梯形中位线的长是高的2倍,面积是18cm 2,则这个梯形的高等于( ) (A )62cm(B )6cm(C )32cm(D )A D EF D6.如图,梯形ABCD 中,AD //BC ,BD 为对角线,中位线EF 交 BD 于O 点,若FO -EO =3,则BC -AD 等于( ) A .4 B .6 C .8 D .107.如图,△ABC 中,D 、E 分别为AC 、BC 边上的点,AB ∥DE ,CF 为AB 边上的中线,若AD =5,CD =3,DE =4,则BF 的长为( ) A.332 B. 316 C. 310 D. 388.小明作出了边长为的第1个正△A 1B 1C 1,算出了正△A 1B 1C 1的面积。
初二数学三角形梯形的中位线试题

初二数学三角形梯形的中位线试题1.如果三角形的两边分别为3和5,那么连接这个三角形三边中点所得的三角形的周长可能是( ) A.4B.4.5C.5D.5.5【答案】D【解析】根据三角形的三边关系,可求第三边大于2小于8,原三角形的周长大于10小于16,连接中点的三角形周长是原三角形周长的一半,那么新三角形的周长应大于5而小于8,看哪个符合就可以了.设三角形的三边分别是a、b、c,令a=3,b=5,∴2<c<8,∴10<三角形的周长<16,∴5<中点三角形周长<8.故选D.【考点】本题重点考查了三角形的中位线定理,三角形的三边关系点评:解答本题的关键是熟练掌握三角形的中位线定理:三角形的中位线平行于第三边,且等于第三边的一半;三角形的任两边之和大于第三边.2.如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若BC=6,则DF的长是(A)2 (B)3 (C) (D)4【答案】B【解析】由已知可得DE为△ABC的中位线,从而可得到DE∥AB,根据两直线平行内错角相等可得到∠BFD=∠ABF,再根据角平分线的性质推出∠FBD=∠BFD,根据等角对等边可得到DF=DB,已知BC的长,从而不难求得DF的长.∵D、E分别是BC、AC的中点,∴DE∥AB,∴∠BFD=∠ABF,∵BF为角平分线,∴∠ABF=∠FBD,∴∠FBD=∠BFD,∴DF=DB,∵DB=DC,∴DF=BC=3,故选B.【考点】本题重点考查了三角形的中位线定理,角平分线的性质点评:解答本题的关键是熟练掌握三角形的中位线定理:三角形的中位线平行于第三边,且等于第三边的一半.3.如图,在ABCD中,EF∥AB,点F为BD的中点,EF=4,则CD的长为( )A.B.8C.10D.16【答案】B【解析】先根据三角形的中位线定理求得AB的长,再根据平行四边形的性质即可求得结果。
由题意得EF是△ABD的中位线,∴AB=2EF=8,∵ABCD,∴AB=CD=8,故选B.【考点】本题考查了三角形的中位线定理,平行四边形的性质点评:解答本题的关键是熟练掌握三角形的中位线定理:三角形的中位线平行于第三边,且等于第三边的一半;平行四边形的对边相等.4.在等腰△ABC的底边BC上任取一点D,作DE∥AC、DF∥AB,分别交AB、AC于点E、F,若等腰△ABC的腰长为m,底边长为n,则四边形AEDF的周长为( )A、2mB、2nC、m+nD、2m-n【答案】A【解析】根据等腰三角形和平行四边形的性质,可推出DF=CF、BE=DE,从而将四边形AEDF的周长转化到等腰△ABC的腰上求解.∵AB=AC,∴∠B=∠C,∵DF∥AB,∴∠B=∠FDC,∴∠FDC=∠C,∴DF=FC,同理DE=BE,∵DF∥AB,DE∥AC,∴四边形AEDF是平行四边形,∴▱AEDF的周长=AE+DE+DF+AF=AE+BE+AF+CF=AB+AC=2AC=2m,故选A.【考点】本题考查了三角形的中位线定理,等腰三角形的性质点评:解答本题的关键是熟练掌握三角形的中位线定理:三角形的中位线平行于第三边,且等于第三边的一半.5.如图,DE是ABC的中位线,F是DE的中点,CF的延长线交AB于点G,则AG:GD等于A.2:1B.3:1C.3:2D.4: 3【答案】A【解析】取CG的中点M,连接EM,构造全等三角形把DG转移到和AG有关的中位线处,即可得所求线段的比.取CG的中点M,连接EM,∵F是DE的中点,∴DF=EF,∴∠GFD=∠MFE,∴△EMF≌△DGF,∴EM=GD,∵E是AC的中点,M是CG的中点,∴EM=,∵EM=GD,∴AG:GD=2:1.故选A.【考点】本题考查三角形中位线定理和全等三角形的性质点评:解答本题的关键是由中点构造全等三角形与中位线,从而将求解同一直线上的两条线段的比值问题转化为不共线的两条线段的比值问题.6.如图,已知四边形ABCD中,R、P分别是BC、CD上的点,E、F分别是AP、RP的中点,当点P在CD上从C向D移动而点R不动时,那么下列结论成立的是( )A.线段EF的长逐渐增大B.线段EF的长逐渐减小C.线段EF的长不变D.线段EF的长与点P的位置有关【答案】C【解析】连接AR,因为R不动,所以AR不变,根据三角形中位线定理即可判断.如图,连接AR,∵E、F分别是AP、RP的中点,∴,∵点R不动,AR不变,∴线段EF的长不变,故选C.【考点】本题考查了三角形的中位线定理点评:解答本题的关键是熟练掌握三角形的中位线定理:三角形的中位线平行于第三边,且等于第三边的一半.7.如图,点D、E分别是△ABC的边AB、AC的中点,且DE=1,则BC的长为___________.【答案】2【解析】根据三角形的中位线定理即可得到结果。
三角形梯形的中位线(精典例题+跟踪训练+参考答案)

三角形、梯形的中位线(精典例题+跟踪训练+参考答案)三角形、梯形的中位线精典例题+跟踪训练+参考答案知识考点:掌握三角形、梯形的中位线定理,并会用它们进行有关的论证和计算。
精典例题:【例1】如图,梯形ABCD中,AD∥BC,M是腰AB的中点,且AD+BC=DC。
求证:MD⊥MC。
分析:遇到腰上中点的问题构造梯形中位线可证明,也可以因为腰上有中点,延长DM 与CB的延长线交于E点进行证明。
ADACDQPMNEDMCGFBCB例1图 AB例2图问题图【例2】如图,△ABC的三边长分别为AB=14,BC=16,AC=26,P为∠A的平分线AD上一点,且BP⊥AD,M为BC的中点,求PM的长。
分析:∠A的平分线与BP边上的垂线互相重合,通过作辅助线延长BP交AC于点Q,由△ABP≌△AQP知AB=AQ=14,又知M是BC的中点,所以PM是△BQC的中位线,于是本题得以解决。
答案:PM=6 探索与创新:【问题一】 E、F为凸四边形ABCD的一组对边AD、BC的中点,若EF=四边形?请说明理由。
分析与结论:如图,利用三角形和梯形的中位线定理,连结AC,取AC的中点G,连EG、FG,则EG∥FG∥1(AB?CD),问:ABCD为什么21CD,211AB,∴EG+FG=(AB?CD),即EG+FG=EF,则G点在EF上,EF∥CD,EF∥AB,故AB∥CD。
22(1)若AD∥BC,则凸四边形ABCD为平行四边形;(2)若AD不平行于BC,则凸四边形ABCD为梯形。
评注:利用中位线构造出11CD、AB,其关键是连AC,并取其中点G。
22跟踪训练:一、填空题:1、三角形各边长为5、9、12,则连结各边中点所构成的三角形的周长是。
2、一个等腰梯形的周长为100cm,如果它的中位线与腰长相等,它的高为20cm,那么这个梯形的面积是。
3、若梯形中位线被它的两条对角线分成三等分,则梯形的两底之比为。
4、直角梯形的中位线长为a,一腰长为b,且此腰与底所成的角为600,则这个梯形的面积为。
3.6 三角形、梯形的中位线(2)(1)

类比定义
A
M B N M
A
D
N C
C
B
定义:连接梯形两腰中点的线段叫做梯形的 中位线。
梯形的中位线与底边之间既有位置上的 平行关系,也有数量上的特殊关系。 梯形面积公式
S梯形
中位线x高
1 (a b)h 2
练一练
1.梯形的上底长为4cm,下底长为6cm, 则中位线长为_____ 5 cm。 2.梯形的一底长为6cm,中位线长 为10cm,另一底长为_____cm 。 14 3.梯形的高为10cm,中位线长为 2. 150 15cm,则梯形的面积为_____cm 4.梯形的上下底长之比为2:3,中位线 6 长为5cm,则下底长为____cm.
5.等腰梯形的腰长是6cm, 中位线长是5cm,则梯形的周长为 22 。 6.若梯形的面积为32,高为8,则梯形的 中位线长为 4 。 7.梯形上底与中位线之比是2:5,则 8:5 梯形下底与中位之比是 。 9.如图,DE是三角形ABC的中位线,FG为 6 梯形中位线,DE=4,则FG=__________
A D F B E G C
例题
已知:梯子各横木间互相平行,且 A1A2=A2A3=A3A4=A4A5, B1B2=B2B3=B3B4=B4B5。
A5 A4
32 36 40
B5 B4 B3 B2 B1
A3
(1)若横木A1B1=48cm, A2 A2B2=44cm,求:横木A3B3、A4B4、 A1 A5B5的长。 (2)若A1B1+A5B5=a,求A2B2+A3B3+A4B4
44 48
例 2 : 如 图 , 在 梯 形 ABCD 中 , AD∥BC , AB=AD+BC , P 为 CD 的 中点.则AP、BP有怎样的位置关系? 为什么?
3.6.1三角形、梯形的中位线 练习

三角形中位线三角形中位线定义:三角形两边中点的连线叫做中位线中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半如右图,如果点D 、E 分别是AB 和AC 的中点,则DE ∥BC ,且DE=BC 21补充:新的三角形周长=21原三角形周长 新的三角形面积=41原三角形面积即C △ADE =21C △ABC S △ADE =41S △ABC练一练:1.如图1所示,D ,E 分别为AB ,AC 的中点,BC=8cm ,则DE=______cm .图1 图2 图32.如图2所示,A ,B 两点被池塘隔开,在AB 外选一点C ,连结AC 和BC ,•并分别找出其中点M ,N ,若测得MN=15m ,则A ,B 两点的距离为_______.3.如图3所示,□ABCD 中,对角线AC ,BD 交于点O ,E 是CD 中点,•连结OE ,•若OE=3cm ,则AD 的长为( )A .3cmB .6cmC .9cmD .12cm4.在△ABC 中D ,E ,F 分别是AB ,BC ,AC 的中点,若△ABC 的周长为20cm ,则△DEF •的周长为( )A .5cmB .10cmC .12cmD .15cm5.(体验探究题)如图4所示,已知第一个三角形的周长为1,它的三条中位线组成第二个三角形,•第二个三角形的中位线又组成第三个三角形,•以此类推,•第2009个三角形的周长是多少?图4 图5 6.如图5在△ABC 中,D ,E 分别是AB ,AC 的中点,且AB=10,AC=•14,•BC=16,则DE 等于( )A .5B .7C .8D .127.(2008,广东)在△ABC 中,M ,N 分别是AB ,AC 的中点,且∠A+∠B=120°, 则∠ANM=_______.8.三角形一条中位线所截成的新三角形与原三角形周长之和等于60cm 则原三角形周长为_______. 9.如图所示,EF 是△ABC 的中位线,BD 平分∠ABC 交EF 于D ,若DE=2, • 则EB=_______.10.如图所示,在四边形ABCD 中,已知E ,F ,G ,H 分别是AB ,BC ,CD ,DA 的中点,试判断四边形EFGH 的形状,并说明理由.11.如图所示,已知E 为□ABCD 中DC 边延长线上一点,且CE=DC ,连结AE ,分别交BC ,BD于点F ,G ,连结AC 交BD 于O ,连结OF . 求证:(1)△ABF ≌△ECF ;(2)AB=2OF .平行四边形的性质与判定复习 1、下面给出了在四边形ABCD 中, ∠A 、 ∠B 、∠C 、∠D 的度数之比,其中能判定四边形ABCDDF ECB A是平行四边形的是( )A 、1:2:3:4B 、2:2:3:3C 、2:3:2:3D 、2:3:3:22、四边形ABCD 中,AC ,BD 相交于点O ,在下列给出的条件中,不能判定四边形ABCD 为平行四边形的是( )A 、AB//CD ,AD//BCB 、∠A=∠C ,∠B=∠DC 、AB=CD ,AD=BC D 、 AB=AD ,CB=CD3、已知:AD 为△ABC 的角平分线,DE ∥AB ,在AB 上截取BF =AE 。
22.6三角形梯形的中位线
2.梯形的中位线
A
D
M
N
B
C
问题1:梯形中位线与梯形
上下两条底边有何位置关系?
问题2:梯形中位线与梯形 上下两条底边有何数量关系?
2.梯形的中位线
已知:如图在梯形ABCD中,AD ∥BC,AM=MB,DN =NC,求证:MN ∥ BC,MN=(12 BC+AD)
A
D
M
N
B
CE
2.梯形的中位线
A
D
M
N
B
C
梯形中位线定理 梯形的中位
线平行于两底,并且等于两底
和的一半
3.基础练习 1.若梯形上底长4cm,下底长6cm,
则中位线长 5 cm
2.若梯形上底长4cm,中位线长 6cm,则下底长 8 cm
例7:
木工师傅制作了一把梯子,如图其中四边形AKLB是 梯形.已知AC=CE=EG=GK,BD=DF=FH=HL,AB=0.6m, CD=0.7m,求EF、GH、KL的长.
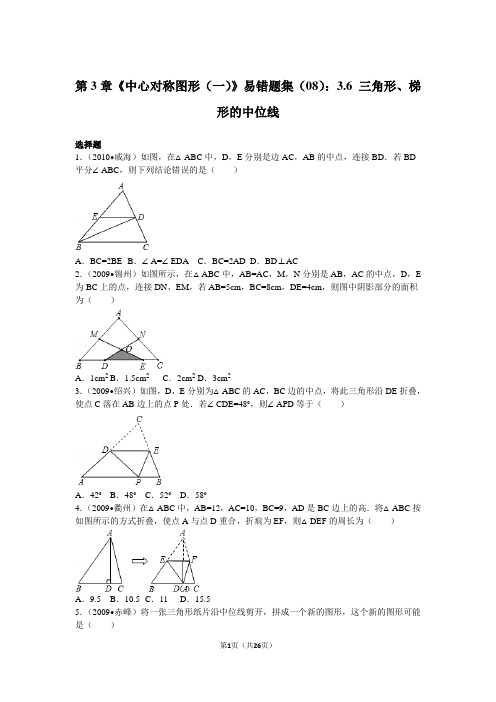
1.三角形的中位线
A
联结三角形两边的中点
的线段叫做三角形的中
D
E 位线
DE//BC
DE=
1 2
BC
B
C
三角形中位线定理 三角形的
中位线平行于第三边,并且等
于第三边的一半
2.梯形的中位线
A
D
M
N
B
C
联结梯形两腰的中点的线段 叫做梯形的中位线
2.梯形的中位线
判断:联结梯形一组对边中点的 线段是梯形的中位线吗?
KL=2EF-AB=2 0.8-0.6=1(m)
例8:
已知:梯形ABCD中,AD//BC,E为AB中点, AD+BC=DC.求证:DE ⊥ EC,DE平分<ADC,
三角形、梯形的中位线习题1

三角形、梯形的中位线习题-1一、三角形的中位线1、定义定义三角形ABC的中位线为连接三角形的任意两个顶点A、B、C的那条线段上的中点,例如AC被BC平分的线段AC的中点D便是三角形ABC的中位线。
2、性质(1)三角形ABC中,中位线的三个中点D、E、F共线,且所在直线MN平分三角形ABC的面积。
(2)对于任何三角形,中位线的长度都不小于1/2的底边长,且平行于底边。
(3)对于等腰三角形来说,中位线也是高线和角平分线。
3、求解大多数情况下,给出的是三角形的三边长,接下来我们分别介绍如何求解三角形ABC的中位线。
(1)已知三角形三边长已知三角形的三个边长分别为a、b、c,我们可以通过以下公式求解中位线的长度。
$DE=\\dfrac{\\sqrt{((a+b+c)(a+b-c)(a-b+c)(-a+b+c)}}{2a}$$EF=\\dfrac{\\sqrt{((a+b+c)(a+b-c)(a-b+c)(a+b-c))}}{2b}$$FD=\\dfrac{\\sqrt{((a+b+c)(a-b+c)(-a+b+c)(a+b-c))}}{2c}$其中,DE为连接BC的中位线,EF为连接AC的中位线,FD为连接AB的中位线。
(2)已知三角形三角高和底边长当已知三角形ABC的高h和底边长a时,可以使用以下公式求解中位线。
$DE=EF=FD=\\dfrac{1}{2}\\sqrt{a^2-\\dfrac{h^2}{4}}$其中,h为三角形的高,a为底边长。
(3)已知三角形两个角和夹边若已知三角形ABC的两个角和夹边b,则可求出连接夹边的中位线BD,以及在BD上的中点E。
首先求出第三个角,然后根据正切函数求出高,再根据已知角和高求得BD,最后利用平移和相似性质求解出中点E的坐标。
二、梯形的中位线1、定义定义梯形ABCD的中位线为连接梯形的底边AB和CD中点E和F的那条线段上的中点G,例如连接CD中点D和底边中点A的线段DG的中点G便是梯形ABCD的中位线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形梯形的中位线精典例题
10.三角形、梯形的中位线
知识考点:
掌握三角形、梯形的中位线定理,并会用它们进行有关的论证和计算。
精典例题:
【例1】如图,梯形ABCD中,AD∥BC,M是腰AB的中点,且AD+BC=DC。
求证:MD⊥MC。
分析:遇到腰上中点的问题构造梯形中位线可证明,也可以因为腰上有中点,延长DM与CB的延长线交于E点进行证明。
ADACDMNQPEGFBCBDMC例1图 AB
例2图问题图
【例2】如图,△ABC的三边长分别为AB=14,BC=16,AC=26,P为∠A的平分线AD上一点,且BP⊥AD,M为BC 的中点,求PM的长。
分析:∠A的平分线与BP边上的垂线互相重合,通过作辅助线延长BP交AC于点Q,△ABP≌△AQP知AB=AQ=14,又知M是BC的中点,所以PM是△BQC的中位线,于是本题得以解决。
答案:PM=6 探索与创新:
【问题一】 E、F为凸四边形ABCD的一组对边AD、BC 的中点,若EF=
1(AB?CD),2问:ABCD为什么四边形?请说明理。
分析与结论:如图,利用三角形和梯形的中位线定理,连结AC,取AC的中点G,连EG、FG,则EG∥
111CD,FG∥AB,∴EG+FG=(AB?CD),即EG+FG=EF,则222G点在EF上,EF∥CD,EF∥AB,故AB∥CD。
若AD∥BC,则凸四边形ABCD为平行四边形;若AD不平行于BC,则凸四边形ABCD为梯形。
评注:利用中位线构造出
11CD、AB,其关键是连AC,并取其中点G。
22跟踪训练:
一、填空题:
1、三角形各边长为5、9、12,则连结各边中点所构成的三角形的周长是。
2、一个等腰梯形的周长为100cm,如果它的中位线与腰长相等,它的高为20cm,那么这个
梯形的面积是。
3、若梯形中位线被它的两条对角线分成三等分,则梯形的两底之比为。
4、直角梯形的中位线长为a,一腰长为b,且此腰与底所成的角为600,则这个梯形的面积为。
5、如图,梯形ABCD中,AD∥BC,EF是梯形的中位线,G是BC上任意一点,如果
S?GEF?22cm2,那么梯形ABCD的面积是。
ADANDFAGEQPBDCEFEFMCBGCB
第5题图
第6题图
第7题图
6、如图,在梯形ABCD中,AD∥BC,∠B=300,∠C=600,E、F、M、N分别为AB、
CD、BC、DA的中点,已知BC=7,MN=3,则EF=。
7、如图,D、E、F分别为△ABC三边上的中点,G为AE 的中点,BE与DF、DG分别交于P、Q两点,则PQ∶BE=。
AD8、如图,直角梯形ABCD的中位线EF=a,垂直于底的腰AB=b,则图中阴影部分的面积是。
9、在梯形ABCD中,AD∥BC,BD是对角线,EF为中位线,若S?ABD∶
EFS?BDC=1∶2,则S梯形AEFD∶S?EBCF=。
BC填空第8题图二、选择题:
1、等腰梯形的两条对角线互相垂直,中位线长为8cm,则它的高为
A、4 cm
B、42cm
C、8cm
D、82cm 2、已知等腰梯形ABCD中,BC∥AD,它的中位线长为28cm,周长为104cm,AD比AB少6cm,则AD∶AB∶BC=
A、8∶12∶5
B、2∶3∶5
C、8∶12∶20
D、9∶12∶19
3、如图,已知△ABC的周长为1,连结△ABC三边的中点构成第二个三角形,再连结第二个三角形三边的中点构成第三个三角形,依此类推,第2004个三角形的周长为A、 1111B、C、2003D、2004 2003200422AAHDGAMNOCDETBCBFBC
选择第3题图
选择第4题图
解答第1题图
4、如图,E、F、G、H分别是BD、BC、AC、AD的中点,又AB=DC,下列结论:①EFGH为矩形;②FH平分EG于T;
③EG⊥FH;④HF平分∠EHG。
其中正确的是A、①和②
B、②和③
C、①②④
D、②③④三、解答题:
1、如图,在矩形ABCD中,BC=8cm,AC与BD交于O,M、N分别为OA、OD的中点。
求证:四边形BCNM是等腰梯形;求这个等腰梯形的中位线长。
2、如图,在四边形ABCD中,AB>CD,E、F分别是对角线BD、AC的中点,求证:EF>
1(AB?CD) 2ADEFDCEBCFBA解答第2题图
解答第3题图
3、如图,在等腰梯形ABCD中,AB∥DC,∠ABC=600,AC平分∠DAB,E、F是对角线AC、BD的中点,且EF=a,求梯形ABCD的面积。
跟踪训练参考答案
一、填空题:
1、13;
2、500cm2;
3、1∶2;
4、
13
ab;5、82;6、4;7、1∶4;8、ab;
22
9、5∶7
二、选择题:CDCD 三、解答题:
1、证MN∥BC且MN≠BC;6cm。
2、取BC的中点构造三角形的中位线。
3、解:设上底为x,下底为y,高为h,题意知EF=
1(y?x),即y?x?2a,2h?3(y?x)?3a,y?x?23h?23?3a?6a,所以: 2梯形ABCD的面积为:
1?6a?3a?33a2 2。
