等边三角形经典习题
等边三角形的判定和性质习题及答案

等边三角形的判定和性质(参考用时:30分钟)1.下列三角形,①有两个角等于60°的三角形;②有一个角等于60°的等腰三角形;③一腰上的中线也是这条腰上的高的等腰三角形.其中能判定是等边三角形的个数是( A )(A)3个(B)2个(C)1个(D)0个2.如图,在 Rt△ABC 中,CM平分∠ACB交AB于点M,过点M作MN∥BC 交AC于点N,且MN平分∠AMC.若AN=1,则BC的长为( B )(A)4 (B)6 (C)4(D)8第2题图3.如图,在等边三角形ABC中,点D是边BC的中点,则∠BAD= 30°.第3题图4.如图,已知∠AOB=30°,点P在边OA上,点M,N在边OB上,且PM=PN=10,MN=12,则OP= 16 .第4题图5.如图,等腰直角三角形BDC的顶点D在等边三角形ABC的内部,∠BDC=90°,连接AD,过点D作一条直线将△ABD分割成两个等腰三角形,则分割出的这两个等腰三角形的顶角分别是120,150 度.第5题图6. 如图,等边△ABC中,点D为BC延长线上一点,点E为CA延长线上一点,且AE=DC,求证:AD=BE.证明:在等边△ABC中,∠BAC=∠ACB=60°,AB=AC,所以∠BAE=∠ACD=120°.因为AE=CD,所以△ABE≌△CAD.所以AD=BE.7. 已知:如图,点D在等边三角形ABC的边AB上,点F在边AC上,连接DF并延长交BC的延长线于点E,FE=FD.求证:AD=CE.证明: 过点D作DM∥BE交AC于点M,则有∠MDF=∠E.在△MDF与△CEF中,因为∠MFD=∠CFE,FD=FE,∠MDF=∠E,所以△MDF≌△CEF,所以DM=CE.因为△ABC为等边三角形,所以∠A=∠B=60°.因为DM∥BE,所以∠ADM=∠B=60°,∠ADM=∠A=60°,所以△ADM为等边三角形,所以DM=AD,所以AD=CE.8. 如图所示,已知a∥b,c∥b,试用反证法证明:a∥c.证明:假设a与c不平行,即a与c相交,不妨设交点为P,由于a∥b,c ∥b,于是可得经过P点有两条直线a,c与直线b平行,这与“经过直线外一点有且只有一条直线与这条直线平行”相矛盾,故假设不成立.所以a∥c.9. 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=3,AD是△ABC的角平分线,DE⊥AB于点E,连接CE,求CE的长.解:因为AD是△ABC的角平分线,所以∠EAD=∠CAD.因为∠ACB=90°,DE⊥AB,所以∠ACD=∠AED.在△ACD与△AED中,∠ACD=∠AED=90°,∠EAD=∠CAD,AD=AD,所以△ACD≌△AED,所以AE=AC.因为∠B=30°,所以∠BAC=60°,所以△ACE是等边三角形,所以CE=AC=3.10. (核心素养—逻辑推理)(2018荆门)如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,E为AB边的中点,以BE为边作等边△BDE,连接AD,CD.(1)求证:△ADE≌△CDB;(2)若BC=,在AC边上找一点H,使得BH+EH最小,并求出这个最小值.(1)证明:在Rt△ABC中,∠BCA=90°,∠BAC=30°,所以BC=AB,E为AB边的中点,所以BE=AB,所以BC=EA,∠ABC=60°.因为△DEB是等边三角形,所以DB=DE,∠DEB=∠DBE=60°.所以∠DEA=∠DBC=120°,所以△ADE≌△CDB.(2)解:作点B关于AC的对称点B′,连接EB′交AC于点H,则点H即为所求.连接CE,则△CBE是等边三角形.所以CE=CB=CB′.所以∠BEB′=90°.所以BH+EH的最小值为EB′==3.。
等边三角形性质与判定练习题

第1课时等边三角形的性质和判定(课堂训练)一.选择题(共8小题)1.如图,一个等边三角形纸片,剪去一个角后得到一个四边形,则图中∠α+∠β的度数是()A. 180° B. 220°C.240° D. 300°2.下列说法正确的是()A.等腰三角形的两条高相等 C.有一个角是60°的锐角三角形是等边三角形B.等腰三角形一定是锐角三角形 D.三角形三条角平分线的交点到三边的距离相等3.在△ABC中,①若AB=BC=CA,则△ABC为等边三角形;②若∠A=∠B=∠C,则△ABC为等边三角形;③有两个角都是60°的三角形是等边三角形;④一个角为60°的等腰三角形是等边三角形.上述结论中正确的有()A. 1个 B. 2个C. 3个 D. 4个4.如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于()A.25°B. 30° C.45° D. 60°5.如图,已知D、E、F分别是等边△ABC的边AB、BC、A C上的点,且DE⊥BC、EF⊥AC、FD⊥AB,则下列结论不成立的是()A.△DEF是等边三角形 B.△ADF≌△BED≌△CFEC.DE=AB D.S△ABC=3S△DEF6.如图,在△ABC中,D、E在BC上,且BD=DE=AD=AE=EC,则∠BAC的度数是()A. 30° B. 45° C. 120°D. 15°7.如图,在△ABC中,AB=AC,∠A=120°,BC=6cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为()A. 4cm B. 3cm C. 2cm D. 1cm第 1 题第4题第5题第7题 8.已知∠AOB=30°,点P在∠AOB内部,P1与P关于OB对称,P2与P关于OA对称,则P1,O,P2三点所构成的三角形是()A.直角三角形 B.钝角三角形 C.等腰三角形D.等边三角形二.填空题(共10小题)9.已知等腰△ABC中,AB=AC,∠B=60°,则∠A= _________ 度.10.△ABC中,∠A=∠B=60°,且AB=10cm,则BC= _________ cm.11.在△ABC中,∠A=∠B=∠C,则△ABC是_________ 三角形.12.如图,将两个完全相同的含有30°角的三角板拼接在一起,则拼接后的△ABD的形状是_________13.如图,M、N是△ABC的边BC上的两点,且BM=MN=NC=AM=AN.则∠BAN= _________ .14.如图,用圆规以直角顶点O为圆心,以适当半径画一条弧交两直角边于A、B两点,若再以A为圆心,以OA为半径画弧,与弧AB交于点C,则∠AOC等于多少?ED C A15.已知:如图,△ABC 是等边三角形,BD 是中线,延长BC 到E ,使CE=CD ,不添辅助线,请你写出三个正确结论(1)______________;(2)______________;(3)______________.16.如图,将边长为6cm 的等边三角形△ABC 沿BC 方向向右平移后得△DEF ,DE 、AC 相交于点G ,若线段CF=4cm ,则△GEC 的周长是 _________ cm .17.如图,在等边△ABC 中,D 、E 分别是AB 、AC 上的点,且AD=CE ,则∠BCD+∠CBE= _________ 度.课后作业1.2.等边三角形是轴对称图形,它有_________条对称轴。
等边三角形性质与判定练习题

第 1课时等边三角形的性质和判定(课堂训练)一.选择题(共 8 小题)1.如图,一个等边三角形纸片,剪去一个角后得到一个四边形,则图中∠α+∠ β的度数是()A . 180°B. 220°C. 240° D . 300°2.下列说法正确的是()A .等腰三角形的两条高相等C.有一个角是 60 °的锐角三角形是等边三角形B .等腰三角形一定是锐角三角形 D .三角形三条角平分线的交点到三边的距离相等3.在△ABC 中,① 若 AB=BC=CA ,则△ ABC 为等边三角形;②若∠ A= ∠ B=∠ C,则△ABC为等边三角形;③有两个角都是 60°的三角形是等边三角形;④一个角为 60°的等腰三角形是等边三角形.上述结论中正确的有()A.1个B.2个C.3个D.4个4.如图, CD 是 Rt△ABC 斜边 AB 上的高,将△ BCD 沿 CD 折叠, B 点恰好落在AB 的中点 E 处,则∠ A 等于()A.25°B. 30°C.45°D. 60°5.如图,已知D、 E、 F 分别是等边△ABC的边AB、BC、A C上的点,且 DE⊥ BC 、 EF⊥ AC 、FD ⊥AB ,则下列结论不成立的是()A .△ DEF是等边三角形B.△ ADF ≌△ BED ≌△ CFEC.DE=ABD .S△ABC=3S △ DEF6.如图,在△ ABC 中,D、E 在 BC 上,且 BD=DE=AD=AE=EC,则∠ BAC的度数是()A. 30°B. 45°C. 120°D. 15°7.如图,在△ ABC 中, AB=AC ,∠ A=120 °, BC=6cm ,AB 的垂直平分线交BC 于点 M ,交 AB 于点 E , AC 的垂直平分线交BC 于点 N ,交 AC 于点 F,则 MN 的长为()A . 4cmB. 3cmC. 2cmD. 1cm第 1 题第 4 题第 5 题第 7 题8.已知∠ AOB=30 °,点 P 在∠ AOB 内部, P1与 P 关于 OB 对称, P2与 P 关于 OA 对称,则 P1, O, P2三点所构成的三角形是()A .直角三角形B .钝角三角形C.等腰三角形D.等边三角形二.填空题(共10 小题)9.已知等腰△ ABC 中, AB=AC ,∠ B=60 °,则∠A= _____ ____ 度.10.△ ABC 中,∠ A= ∠B=6 0°,且 AB=10cm ,则BC= _________ cm.11.在△ ABC 中,∠ A= ∠ B= ∠ C,则△ABC是_________ 三角形.12.如图,将两个完全相同的含有 30°角的三角板拼接在一起,则拼接后的△ ABD 的形状是_________13.如图, M 、 N 是△ ABC 的边 BC 上的两点,且BM=MN=NC=AM=AN.则∠ BAN=_________...14.如图,用圆规以直角顶点O 为圆心,以适当半径画一条弧交两直角边于A、 B 两点,若再以 A 为圆心,以OA 为半径画弧,与弧AB 交于点 C,则∠ AOC 等于多少?15.已知:如图,△ ABC是等边三角形, BD是中线,延长 BC到 E,使 CE=CD,不添辅助线,请你写出三个正确结论(1)_______ _______;(2)______________ ;(3)______________.ADBCE16.如图,将边长为6cm 的等边三角形△ABC沿BC方向向右平移后得△DEF,DE、AC相交于点 G,若线段CF=4cm ,则△ GEC 的周长是_________cm.17.如图,在等边△ABC 中,D、E 分别是 AB 、AC 上的点,且 AD=CE ,则∠ BCD+ ∠CBE=_________度...课后作业1.2.等边三角形是轴对称图形,它有_________条对称轴。
等边三角形的性质复习题精选附答案

等边三角形的性质习题精选一.选择题(共14小题)1.(2005•郴州)附加题:下图是由九个等边三角形组成的一个六边形,当最小的等边三角形边长为2cm时,这个六边形的周长为()cm.2345A30 B 40 . 50 D 602.(2009•江干区模拟)如图,△ABC中,AB=AC,△DEF为等边三角形,则α、β、γ之间的关系为()A B C D3.如图,等边△ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点,若AE=2,当EF+CF 取得最小值时,则∠ECF的度数为()A15° B 22.5° C 30° D 45°4.如图,△ABC是等边三角形,P是BC上任意一点,PD⊥AB,PE⊥AC,连接DE.记△ADE的周长为L1,四边形BDEC的周长为L2,则L1与L2的大小关系是()A Ll=L2 B L1>L2.L2>L1 D 无法确定5.如图,△ABC为边长是5的等边三角形,点E在AC边上,点F在AB边上,ED⊥BC,且ED=AE,DF=AF,则CE 的长是()A B C 20+10 D 20﹣106.如图中左边图形,连接等边三角形的各边中点将得到一个小等边三角形,右边的图形就是这样得到的,请问右边图形中的阴影部分面积大还是空白部分面积大()7910A阴影部分面积大B 空白部分面积大C 一样大D 不确定7.如图,等边三角形ABC内有一点P,过点P向三边作垂线,垂足分别为S、Q、R,且PQ=6,PR=8,PS=10,则△ABC的面积等于()A190 B 192 C 194 D 1968.在边长为2cm的等边三角形内,随意取一些点,如果要保证所取的点中一定存在距离小于1cm的两点,那么取的点至少应有()A4个 B 5个 C 6个 D 7个9.如图,已知等边△ABC外有一点P,P落在∠ABC内,设点P到BC、CA、AB三边的距离分别为h1、h2、h3,且满足h2+h3﹣h1=6,那么等边△ABC的面积为()A12 B 9 C 8 D 410.如图所示,△ABC为正三角形,P是BC上的一点,PM⊥AB,PN⊥AC,设四边形AMPN,△ABC的周长分别为m、n,则有()A B C D11.如图,AC=BC,AC⊥BC于C,AB=AD=BD,CD=CE=DE.若AB=,则BE=()121314A 1B 2C 3D 412.如图,D,E,F为等边三角形ABC三边中点,AE、BF、CD交于O,DE,EF,FD为三条中位线,则图中能数出不同的直角三角形的个数是()A36 B 32 C 30 D 2813.如图,由四个全等的正三角形砌成一个大的正三角形,如果小正三角形的面积为25,则大正三角形的周长是()A120° B 135° C 150° D 165°二.填空题(共9小题)15.(2007•沈阳)如图,△ABC是边长为3的等边三角形,△BDC是等腰三角形,且∠BDC=120°.以D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN,则△AMN的周长为_________ .1617192016.(2012•南开区一模)如图,将边长为3+的等边△ABC折叠,折痕为DE,点B与点F重合,EF和DF分别交AC于点M、N,DF⊥AB,垂足为D,AD=1,则重叠部分的面积为_________ .17.如右图,以等边△OAB的高OC为边向逆时针方向作等边△OCD,CD交OB于点E,再以OE为边向逆时针方向作等边△OEF,EF交OD于点G,再以OG为边向逆时针方向作等边△OGH,…,按此方法操作,最终得到△OMN,此时ON在OA上.若AB=1,则ON= _________ .18.已知正△ABC的面积是1,P是△ABC内一点,并且△PAB、△PBC、△PCA的面积相等,那么满足条件的点P共有_________ 个;△PAB的面积是_________ .19.如图,从等边三角形内一点向三边作垂线,已知这三条垂线段的长分别为1、3、5,则这个等边三角形的边长为_________ .20.如图所示,直线AB、CD相交于点O.若OM=ON=MN,那么∠APQ+∠CQP=_________ .21.在正△ABC中(如图),D为AC上一点,E为AB上一点,BD,CE相交于P,若四边形ADPE与△BPC的面积相等,那么∠BPE=_________ .2222.如图,平行于BC的线段MN把等边△ABC分成一个三角形和一个四边形,已知△AMN和四边形MBCN的周长相等,则BC与MN的长度之比是_________ .23.正三角形ABC的边长BC=2,以该等边三角形的高AD为正方形的边长,则正方形的面积为_________ .三.解答题(共7小题)24.阅读材料:如图,△ABC中,AB=AC,P为底边BC上任意一点,点P到两腰的距离分别为r1,r2,腰上的高为h,连接AP,则S△ABP+S△ACP=S△ABC,即:,∴r1+r2=h(定值).(1)类比与推理如果把“等腰三角形”改成“等边三角形”,那么P的位置可以由“在底边上任一点”放宽为“在三角形内任一点”,即:已知等边△ABC内任意一点P到各边的距离分别为r1,r2,r3,等边△ABC的高为h,试证明r1+r2+r3=h (定值).(2)理解与应用△ABC中,∠C=90°,AB=10,AC=8,BC=6,△ABC内部是否存在一点O,点O到各边的距离相等?_________ (填“存在”或“不存在”),若存在,请直接写出这个距离r的值,r= _________ .若不存在,请说明理由.25.小明在找等边三角形ABC一边的三等分点时,他是这样做的,先做∠ABC、∠ACB的角平分线并且相交于点O,然后做线段BO、CO的垂直平分线,分别交BC于E、F,他说:“E、F就是BC边的三等分点.”你同意他的说法吗?请说明你的理由.26.在等边△ABC中,D是AC的中点,E是BC延长线上一点,且CE=CD,(1)请说明DB=DE的理由.(2)若等边△ABC的边长为4cm,求△BDE的面积.27.如图,设O为△ABC内一点,且∠AOB=∠BOC=∠COA=120°,P为任意一点(不是O).求证:PA+PB+PC>OA+OB+OC.28.如图,等边△ABC,D、E分别在BC、AC上,且CD=AE,AD、BE相交于点P,试求∠BPD的度数.29.阅读下列材料,解答相应问题:已知△ABC是等边三角形,AD是高,设AD=h.点P(不与点A、B、C重合)到AB的距离PE=h1,到AC的距离PF=h2,到BC的距离PH=h3.如图1,当点P与点D重合时,我们容易发现:h1=h,h2=h,因此得到:h1+h2=h.小明同学大胆猜想提出问题:如图2,若点P在BC边上,但不与点D重合,结论h1+h2=h还成立吗?通过证明,他得到了肯定的答案.证明如下:证明:如图3,连接AP.∴S△ABC=S△ABP+S△APC.设等边三角形的边长AB=BC=CA=a.∵AD⊥BC,PE⊥AB,PF⊥AC,∴BC•AD=AB•PE+AC•PF∴a•h=a•h1+a•h2.∴h1+h2=h.(1)进一步猜想:当点P在BC的延长线上,上述结论还成立吗?若成立,请你证明;若不成立,请猜想h1,h2与h之间的数量关系,并证明.(借助答题卡上的图4)(2)我们容易知道,当点P在CB的延长线及直线AB,AC上时,情况与前述类似,这里不再说明.继续猜想,你会进一步提出怎样的问题呢?请在答题卡上借助图5画出示意图,写出你提出的问题,并直接写出结论,不必证明.30.如图△ABC是边长为2的等边三角形,D是AB边的中点,P是BC边上的动点,Q是AC边上的动点,当P、Q的位置在何处时,才能使△DPQ的周长最小?并求出这个最值.等边三角形的性质习题精选参考答案与试题解析一.选择题(共14小题)1.(2005•郴州)附加题:下图是由九个等边三角形组成的一个六边形,当最小的等边三角形边长为2cm时,这个六边形的周长为()cm.A.30 B.40 C.50 D.60考点:等边三角形的性质.专题:压轴题;规律型.分析:因为每个三角形都是等边的,从其中一个三角形入手,比右下角的以AB为边的三角形,设它的边长为x,则等边三角形的边长依次为x,x+x+2,x+2,x+2×2,x+2×2,x+3×2.所以六边形周长是2x+2(x+2)+2(x+2×2)+(x+3×2)=7 x+18,而最大的三角形的边长AF等于AB的2倍,所以可以求出x,则可求得周长.解答:解:设AB=x,∴等边三角形的边长依次为x,x+x+2,x+2,x+2×2,x+2×2,x+3×2,∴六边形周长是2x+2(x+2)+2(x+2×2)+(x+3×2)=7 x+18,∵AF=2AB,即x+6=2x,∴x=6cm,∴周长为7 x+18=60cm.故选D点评:结合等边三角形的性质,解一元一次方程,关键是要找出其中的等量关系.2.(2009•江干区模拟)如图,△ABC中,AB=AC,△DEF为等边三角形,则α、β、γ之间的关系为()A.B.C.D.考点:等边三角形的性质;对顶角、邻补角;三角形内角和定理;等腰三角形的性质.专题:证明题.分析:根据等腰三角形的性质推出∠B=∠C,根据三角形的内角和定理求出∠2﹣∠1=∠α﹣∠γ,根据等边三角形的性质和邻补角定义求出∠2﹣∠1=∠β﹣∠α,代入上式即可求出答案.解答:解:∵AB=AC,∴∠B=∠C,∴∠2+∠γ=∠1+∠α,∴∠2﹣∠1=∠α﹣∠γ,∵等边△DEF,∴∠5=∠3=60°,∴∠2+∠α=∠1+∠β=120°,∴∠2﹣∠1=∠β﹣∠α,∴∠α﹣∠γ=∠β﹣∠α,∴2∠α=∠β+∠γ,∴α=,故选B.点评:本题主要考查对三角形的内角和定理,等边三角形的性质,等腰三角形的性质,邻补角的定义等知识点的3.如图,等边△ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点,若AE=2,当EF+CF 取得最小值时,则∠ECF的度数为()A.15°B.22.5°C.30°D.45°考点:轴对称-最短路线问题;等边三角形的性质.分析:过E作EM∥BC,交AD于N,连接CM交AD于F,连接EF,推出M为AB中点,求出E和M关于AD对称,根据等边三角形性质求出∠ACM,即可求出答案.解答:解:过E作EM∥BC,交AD于N,∵AC=4,AE=2,∴EC=2=AE,∴AM=BM=2,∴AM=AE,∵AD是BC边上的中线,△ABC是等边三角形,∴AD⊥BC,∵EM∥BC,∴AD⊥EM,∵AM=AE,∴E和M关于AD对称,连接CM交AD于F,连接EF,则此时EF+CF的值最小,∵△ABC是等边三角形,∴∠ACB=60°,AC=BC,∵AM=BM,∴∠ECF=∠ACB=30°,故选C.点评:本题考查了轴对称﹣最短路线问题,等边三角形的性质,等腰三角形的性质,平行线分线段成比例定理等知识点的应用.4.如图,△ABC是等边三角形,P是BC上任意一点,PD⊥AB,PE⊥AC,连接DE.记△ADE的周长为L1,四边形BDEC 的周长为L2,则L1与L2的大小关系是()A.L=L2B.L1>L2C.L2>L1D.无法确定l考点:等边三角形的性质;三角形三边关系.专题:计算题.分析:等边三角形各内角为60°,故∠B=∠C=60°,即可求得BP=2BD,CP=2CE,∴BD+CE=BC,即可求得L=L2.1解答:解:∵等边三角形各内角为60°,∴∠B=∠C=60°,∵∠BPD=∠CPE=30°,∴在Rt△BDP和Rt△CEP中,∴BP=2BD,CP=2CE,∴BD+CE=BC,∴AD+AE=AB+AC﹣BC=BC,∴BD+CE+BC=BC,L1=BC+DE,L2=BC+DE,点评:本题考查了直角三角形中特殊角的正弦函数值,考查了等边三角形各边相等的性质,本题中求证L1=BC+DE,L2=BC+DE是解题的关键.5.如图,△ABC为边长是5的等边三角形,点E在AC边上,点F在AB边上,ED⊥BC,且ED=AE,DF=AF,则CE的长是()A.B.C.20+10 D.20﹣10考点:等边三角形的性质.专题:计算题.分析:根据ED⊥BC可得∠CED=30°,即可求得EC与ED的关系,设DE=x,则AE=x,根据DE即可计算CE,根据AE+CE=5即可计算x的值,根据CE=AC﹣AE即可求CE的值.解答:解:∵ED⊥BC,∠C=60°,∴∠CED=30°,设DE=x,则AE=x,且CE=x,又∵AE+CE=5,∴x+x=5,解得x=10﹣15,∴CE=5﹣(10﹣15)=20﹣10.故选D.点评:本题考查了特殊角的正弦值,等边三角形各内角为60°的性质,本题中根据AE、CE求x的值是解题的关键.6.如图中左边图形,连接等边三角形的各边中点将得到一个小等边三角形,右边的图形就是这样得到的,请问右边图形中的阴影部分面积大还是空白部分面积大()A.阴影部分面积大B.空白部分面积大C.一样大D.不确定考点:等边三角形的性质.分析:根据等边三角形的性质及三角形的中位线定理解答即可.解答:解:如图,∵D、E、F分别为三角形三边的中点,△ABC为等边三角形,∴AD=BD=BF=CF=AE=EC=DE=EF=DF,∴△ADE≌△DBF≌△EFC≌△FED,∴阴影部分面积与空白部分面积一样大.故选C.点评:此题比较简单,解答此题的关键是熟知三角形的中位线定理及等边三角形的性质.7.如图,等边三角形ABC内有一点P,过点P向三边作垂线,垂足分别为S、Q、R,且PQ=6,PR=8,PS=10,则△ABC 的面积等于()A.190 B.192 C.194 D.196考点:等边三角形的性质.专题:计算题.解答:解:连接AP、BP、CP,过点A作AD⊥BC于D,等边三角形面积S=BC•(PQ+PR+PS)=BC•AD故PQ+PR+PS=AD,∴AD=6+8+10=24,∵∠ABC=60°∴AB=24×=16,∴△ABC的面积S=BC•AD=×24×16=192,故选 B.点评:本题考查了等边三角形面积的计算,考查了等边三角形高线与边的关系,本题中求证PQ+PR+PS=AD是解题的关键.8.在边长为2cm的等边三角形内,随意取一些点,如果要保证所取的点中一定存在距离小于1cm的两点,那么取的点至少应有()A.4个B.5个C.6个D.7个考点:等边三角形的性质.专题:计算题;开放型.分析:把三角形每条边分成n份,相应点之间连线,则可把三角形分成分成n2个边长为的小三角形,则比三角形的个数多1可以保证至少有两个点落在同一小三角形内,即可解题.解答:解:把三角形每条边分成n份,相应点之间连线,可以把三角形分成n2个边长为的小三角形,n2+1个点可以保证至少有两个点落在同一个小三角形内,所以那两个点的距离是不超过的,∴取得点至少为n2+1,当根据题意n=2,∴n2+1=5.故选B.点评:本题考查了等边三角形各边长相等的性质,学生探究发现规律的能力,本题中构建n2个三角形是解题的关键.9.如图,已知等边△ABC外有一点P,P落在∠ABC内,设点P到BC、CA、AB三边的距离分别为h1、h2、h3,且满足h2+h3﹣h1=6,那么等边△ABC的面积为()A.12 B.9C.8D.4考点:等边三角形的性质.专题:计算题.分析:根据等边三角形的面积即可计算(h+h2﹣h1)是等边三角形ABC的高,根据等边三角形的高即可求得BC的值,3即可求得△ABC的面积,即可解题.解答:解:设等边△ABC的边长为a,连接PA、PB、PC,则S△PAB+S△PAC﹣S△PBC=S△ABC,从而ah3+ah2﹣ah1=a2,即a(h3+h2﹣h1)=a2,∵(h3+h2﹣h1)=6,∴a=4,点评:本题考查了等边三角形面积的计算,等边三角形高线长与边长的关系,本题中根据等边三角形的高计算等边三角形的面积是解题的关键.10.如图所示,△ABC为正三角形,P是BC上的一点,PM⊥AB,PN⊥AC,设四边形AMPN,△ABC的周长分别为m、n,则有()A.B.C.D.考点:等边三角形的性质.专题:计算题.分析:设BM=x,CN=y,用x、y分别表示m、n的值,化简m、n的表达式,可得四边形AMPN,△ABC的周长的比值,可以解题.解答:解:设BM=x,CN=y则BP=2x,PC=2y,PM=x,PN=yAM+AN=2BC﹣(BM+CN)=3(x+y),故==≈0.7887.故选D.点评:本题考查了等边三角形各内角为60°的性质,等边三角形周长的计算,本题中用x、y表示m、n的值是解题的关键.11.如图,AC=BC,AC⊥BC于C,AB=AD=BD,CD=CE=DE.若AB=,则BE=()A.1B.2C.3D.4考点:等边三角形的性质.专题:计算题.分析:根据等边三角形边长相等的性质,可以证明△ACD≌△BED,故AC=BE,已知AB,根据勾股定理即可求AC 的长,即可解题.解答:解:∵∠ADC+∠CDB=60°,∠CDB+∠BDE=60°,∴∠ADC=∠BDE,在△ACD和△BED中,,∴△ACD≌△BED,∴AC=BE,∵AC=BC,AB=,∴AC=BC=1,∴BE=1.故选A.点评:本题考查了勾股定理在直角三角形中的运用,全等三角形的证明和全等三角形对应边相等的性质,本题中求证△ACD≌△BED是解题的关键.12.如图,D,E,F为等边三角形ABC三边中点,AE、BF、CD交于O,DE,EF,FD为三条中位线,则图中能数出不同的直角三角形的个数是()A.36 B.32 C.30 D.28考点:等边三角形的性质.专题:证明题.分析:根据等边三角形的“三线合一”的性质来找直角三角形.解答:解:①∵DE,EF,FD为等边△ABC三条中位线,∴AB=AC=BC,∴EFAB,EDAC,∴四边形CEDF是菱形,∴EF⊥CD,∴在菱形CEDF中有6个不同的直角三角形:Rt△CEG、Rt△CFG、Rt△DGE、Rt△DFG、Rt△EOG、Rt△FOG;同理,在菱形ADEF、菱形BEFD中各有6个不同的直角三角形;②∵D为等边三角形ABC三边中点,∴CD⊥AB,∴△ADC、△BDC、AOD、△BOD是直角三角形;同理,以BF、AE为直角边的三角形各有4个;综上所述,图中能数出的直角三角形由6×3+4×3=30(个);故选C.点评:本题考查了等边三角形的性质.解题时,充分利用了三角形中位线定理、等边三角形的“三线合一”的性质.13.如图,由四个全等的正三角形砌成一个大的正三角形,如果小正三角形的面积为25,则大正三角形的周长是()A.100 B.60 C.100 D.60考点:等边三角形的性质.专题:计算题.分析:根据三角形面积公式和中位线定理求解.解答:解:设小三角形的边长为a.∴小三角形的面积为a2sin60°=25,解得a=10∵正三角形的三条中位线构成一个小的正三角形∴大三角形的边长为小三角形边长的2倍,为2a∴大的正三角形的周长为2a×3=6a=6×10=60.故选D.点评:考查了学生对三角形面积公式和中位线定理的掌握和理解.14.在凸四边形ABCD中,DA=DB=DC=BC,则这个四边形中最大角的度数是()A.120°B.135°C.150°D.165°考点:等腰三角形的性质;三角形内角和定理;等边三角形的性质.专题:计算题.分析:设∠CDA=x,∠ABC=y,根据DA=DB=DC=BC,求得x=2y,由四边形的内角和是360°得∠BAC=360°﹣∠DBA﹣∠DCA﹣∠BD C,解得即可得出答案.解答:解;设∠CDA=x,∠ABC=y,∵DA=DB=DC=BC,∴∠BDC=∠DBC=∠DCB=60°,∠DBA=∠DAB,∠DAC=∠DCA,∵∠DBA+∠BAD+∠BDA=180°,∴60°﹣x+2(60°+y)=180°,即x=2y,∠BAC=360°﹣∠DBA﹣∠DCA﹣∠BDC,=360°﹣(60°+y)﹣﹣60°,=150°.点评:此题主要考查学生对等腰三角形的性质和等边三角形性质的理解和掌握,此题的关键是有已知条件得到∠CAD 和∠ABC之间的关系,进一步求出结果.二.填空题(共9小题)15.(2007•沈阳)如图,△ABC是边长为3的等边三角形,△BDC是等腰三角形,且∠BDC=120°.以D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN,则△AMN的周长为 6 .考点:等边三角形的性质.专题:压轴题.分析:要求△AMN的周长,根据题目已知条件无法求出三条边的长,只能把三条边长用其它已知边长来表示,所以需要作辅助线,延长AB至F,使BF=CN,连接DF,通过证明△BDF≌△C ND,及△DMN≌△DMF,从而得出MN=MF,△AMN的周长等于AB+AC的长.解答:解:∵△BDC是等腰三角形,且∠BDC=120°∴∠BCD=∠DBC=30°∵△ABC是边长为3的等边三角形∴∠ABC=∠BAC=∠BCA=60°∴∠DBA=∠DCA=90°延长AB至F,使BF=CN,连接DF,在Rt△BDF和Rt△CND中,BF=CN,DB=DC∴△BDF≌△CND∴∠BDF=∠CDN,DF=DN∵∠MDN=60°∴∠BDM+∠CDN=60°∴∠BDM+∠BDF=60°,∠FDM=60°=∠MDN,DM为公共边∴△DMN≌△DMF,∴MN=MF∴△AMN的周长是:AM+AN+MN=AM+MB+BF+AN=AB+AC=6.点评:此题主要利用等边三角形和等腰三角形的性质来证明三角形全等,构造另一个三角形是解题的关键.16.(2012•南开区一模)如图,将边长为3+的等边△ABC折叠,折痕为DE,点B与点F重合,EF和DF分别交AC 于点M、N,DF⊥AB,垂足为D,AD=1,则重叠部分的面积为.考点:翻折变换(折叠问题);等边三角形的性质.专题:压轴题.分析:观察图形可知重叠部分的面积即是△DEF的面积减去△MNF的面积.由折叠的性质,可求得∠BDE=∠EDF=45°,由四边形的内角和为360°,求得∠BEF为150°,得到∠CEM为30°,则可证得∠EMC 为90°;作△BDE的高,根据45°与60°的三角函数,借助于方程即可求得其高的值,则各三角形的面积可解.解答:解:过点E作EG⊥AB于G,∴∠EGB=90°,∵△ABC是等边三角形,∴∠A=∠B=∠C=60°,AB=BC=AC=3+,根据题意得:∠BDE=∠FDE,∠F=∠B=60°,∵DF⊥AB,∴∠FDB=90°,∴∠BEF=360°﹣∠B﹣∠F﹣∠BDF=150°,∠BDE=∠FDE=∠FDB=45°∴∠MEC=180°﹣∠BEF=30°,∴∠EMC=180°﹣∠C﹣∠EMC=90°,在Rt△ADN中,AD=1,tan∠A=tan60°==,∴DN=,∴S△ADN=AD•DN=×1×=,在△BDE中,DB=AB﹣AD=3+﹣1=2+,∵∠EDG=45°,∴∠DEG=45°,∴DG=EG,∵tan∠B=tan60°==,设EG=x,则DG=x,BG=x,∴x+x=2+,解得:x=,∴EG=DG=,∴S△BDE=BD•EG=×(2+)×=,∵∠B=∠C=∠F=60°,∴BE==+1,∴EC=BC﹣BE=2,∵∠BED=∠FED=180°﹣∠B﹣∠BDE=75°,∴∠FNM=∠MEC=30°,∴∠FMN=∠EMC=90°,∴EM=EC•cos30°=,∴FM=EF﹣EM=BE﹣EM=1,∴MN=FM•tan60°=,∴S四边形MNDE=S△DEF﹣S△MNF=S△BDE﹣S△MNF=﹣×1×=.点评:此题考查了等边三角形的性质,折叠的性质以及三角函数的性质等知识.此题综合性很强,解题的关键是抓住数形结合思想的应用.17.如右图,以等边△OAB的高OC为边向逆时针方向作等边△OCD,CD交OB于点E,再以OE为边向逆时针方向作等边△OEF,EF交OD于点G,再以OG为边向逆时针方向作等边△OGH,…,按此方法操作,最终得到△OMN,此时ON在OA上.若AB=1,则ON= ()10.考点:等边三角形的性质.专题:压轴题;规律型.分析:利用正三角形的性质和正三角形的边长求得OC的长,然后逆时针旋转30°后可以求得OE的长,直至线段ON与线段OA重合,一共旋转了12次,从而可以求得ON的长.解答:解:∵OC为等边三角形的高,且等边三角形的边长为1,∴NC=,∵△OCD为等边三角形,∴∠OCD=60°,∴OE⊥CD,∴OE==()2,以此类推,当ON与OA重合时,一共旋转了10次,∴ON的长为()10,故答案为()10点评:本题考查了正三角形的性质,解题的关键是正确地得到一共旋转了多少次.18.已知正△ABC的面积是1,P是△ABC内一点,并且△PAB、△PBC、△PCA的面积相等,那么满足条件的点P共有 1 个;△PAB的面积是.考点:等边三角形的性质;三角形的面积.专题:计算题.分析:根据三角形面积的计算和△PAB、△PBC、△PCA的面积相等可得P到AB、BC、AC的距离相等,故P点为等边三角形三个角平分线的交点,故P点只有一个,且△PAB的面积为等边△ABC面积的.解答:解:∵△PAB、△PBC、△PCA的面积相等,AB=BC=AC,∴P到AB、BC、AC的距离相等,故点P为等边三角形三角平分线的交点,等边三角形三角平分线交于一点,故点P只有一个,且△PAB的面积为.故答案为:1,.点评:本题考查了等边三角形各边长相等的性质,三角形面积的计算,本题中求得P点是等边三角形三个角平分线的交点是解题的关键.19.如图,从等边三角形内一点向三边作垂线,已知这三条垂线段的长分别为1、3、5,则这个等边三角形的边长为.考点:等边三角形的性质;三角形的面积.专题:计算题.分析:作AM⊥BC,根据等边三角形的面积计算可以求得AM=PE+PD+PF,再根据等边三角形的高线长可以计算等边三角形的边长,即可解题.解答:解:过A作AM⊥BC,则AM为BC边上的高,连接PA、PB、PC,则△ABC的面积S=BC•AM=(BC•PD+AB•PF+AC•PE),∴BC•AM=BC•PD+AB•PF+AC•PE,∵△ABC是等边三角形,∴AB=BC=AC,∴BC•AM=BC•PD+BC•PF+BC•PE=BC•(PD+PF+PE),∴PD+PE+PF=AM,∴△ABC的高为:1+3+5=9,∴△ABC的边长为:AB===9×=6,故答案为6.点评:本题考查了三角形面积的计算,考查了等边三角形边长和高线长的关系,本题中求AM=PD+PE+PF是解题的关键.20.如图所示,直线AB、CD相交于点O.若OM=ON=MN,那么∠APQ+∠CQP=240°.考点:等边三角形的性质;三角形的外角性质.专题:计算题.分析:根据OM=ON=MN即可判定△OMN为等边三角形,根据等边三角形各内角为60°的性质,可求得∠OPQ+∠OQP的值,进而根据∠APQ+∠CQP=360°﹣(∠OPQ+∠OQP)即可解题.解答:解:∵OM=ON=MN,∴三角形OMN为正三角形,所以∠APQ+∠CQP=(180°﹣∠OPQ)+(180°﹣∠OQP),=360°﹣(∠OPQ+∠OQP),=360°﹣(180°﹣∠POQ),=180°+60°,=240°.故答案为:240°.点评:本题考查了等边三角形各内角为60°的性质,考查了外角的定义,本题中求得∠APQ+∠CQP=360°﹣(∠OPQ+∠OQP)是解题的关键.21.在正△ABC中(如图),D为AC上一点,E为AB上一点,BD,CE相交于P,若四边形ADPE与△BPC的面积相等,那么∠BPE=60°.考点:等边三角形的性质;三角形的面积.专题:计算题.分析:根据可以证明AD=BE,即AE=CD,即可证△ACE≌△BCD,可得∠DBC=∠ACE,根据∠BPE=∠BCE+∠DBC,∠ACE+∠BCE=60°即可求得∠BPE=∠ACB,即可解题.解答:解:∵△ABD的面积=四边形ADPE的面积+△BPE的面积△BCE的面积=三角形BPC的面积+△BPE的面积四边形ADPE与△BPC的面积相等,∴AD=BE,即AE=CD,又∵AC=BC,∠BAC=∠ACB=60°∴△ACE≌△BCD,∴∠DBC=∠ACE又∵∠BPE=∠BCE+∠DBC,∠ACE+∠BCE=60°,∴∠BPE=∠ACB=60°,故答案为60°.点评:本题考查了三角形面积的计算,考查了等边三角形各内角为60°的性质,考查了全等三角形的证明和全等三角形对应角相等的性质,本题中求证△ACE≌△BCD是解题的关键.22.如图,平行于BC的线段MN把等边△ABC分成一个三角形和一个四边形,已知△AMN和四边形MBCN的周长相等,则BC与MN的长度之比是4:3 .考点:等边三角形的性质.专题:计算题.分析:设=n,根据平行于BC的线段MN把等边△ABC分成一个三角形和一个四边形和△AMN和四边形MBCN的周长相等,得出3AM=AM+BC+2BM,然后整理此等式即可得出答案.解答:解:设==n,∵3AM=AM+BC+2BM,△ABC为等边三角形,∴BM=AB﹣AM=BC﹣AM,∴2AM=+2(BC﹣AM),即2AM=+2(﹣AM),∴2AM=+2AM(﹣1),即2=+﹣2,4=.∴BC与MN的长度之比是4:3.故答案为:4:3.点评:此题主要考查等边三件形的性质这一知识点,解答此题的关键是设=n 利用等边三角形的性质和△AMN和四边形MBCN的周长相等,列出3AM=AM+BC+2BM这样一个等式,然后整理即可.此题有一定的拔高难度,属于难题.23.正三角形ABC的边长BC=2,以该等边三角形的高AD为正方形的边长,则正方形的面积为 3 .考点:等边三角形的性质.专题:计算题.分析:根据等边三角形三线合一的性质可得D为BC的中点,即BD=CD,在直角三角形ABD中,已知AB、BD,根据勾股定理即可求得AD的长,即可求正方形的面积,即可解题.解答:解:∵等边三角形三线合一,∴D为BC的中点,即BD=DC=1,∴AD==,∴正方形的面积为×=3.故答案为3.点评:本题考查了勾股定理在直角三角形中的运用,正方形面积的计算,本题中根据勾股定理计算AD的值是解题的关键.三.解答题(共7小题)24.阅读材料:如图,△ABC中,AB=AC,P为底边BC上任意一点,点P到两腰的距离分别为r1,r2,腰上的高为h,连接AP,则S△ABP+S△ACP=S△ABC,即:,∴r1+r2=h(定值).(1)类比与推理如果把“等腰三角形”改成“等边三角形”,那么P的位置可以由“在底边上任一点”放宽为“在三角形内任一点”,即:已知等边△ABC内任意一点P到各边的距离分别为r1,r2,r3,等边△ABC的高为h,试证明r1+r2+r3=h (定值).(2)理解与应用△ABC中,∠C=90°,AB=10,AC=8,BC=6,△ABC内部是否存在一点O,点O到各边的距离相等?存在(填“存在”或“不存在”),若存在,请直接写出这个距离r的值,r= 2 .若不存在,请说明理由.考点:等边三角形的性质;三角形的面积;等腰三角形的性质.分析:(1)连接AP,BP,CP.根据三角形ABC的面积的两种计算方法进行证明;(2)根据角平分线上的点到角两边的距离相等进行求作.解答:证明:(1)连接AP,BP,CP.(2分)则S△ABP+S△BCP+S△ACP=S△ABC,(4分)即,(6分)∵△ABC是等边三角形,∴AB=BC=AC,∴r1+r2+r3=h(定值);(8分)(2)存在.(10分)r=2.(12分)点评:此题主要是考查了等边三角形的性质、角平分线的性质以及三角形的面积公式.注意:直角三角形斜边上的高等于两条直角边的乘积除以斜边.25.小明在找等边三角形ABC一边的三等分点时,他是这样做的,先做∠ABC、∠ACB的角平分线并且相交于点O,然后做线段BO、CO的垂直平分线,分别交BC于E、F,他说:“E、F就是BC边的三等分点.”你同意他的说法吗?请说明你的理由.考点:等边三角形的性质;线段垂直平分线的性质.分析:连接OE,OF构建等腰三角形BOE和CFO,利用等腰三角形的“三线合一”推知的性质BE=OE、OF=CF,然后等边三角形ABC中,根据等边三角形的三个内角都是60°的性质、角平分线的性质证得△OEF是等边三角形(有两个内角60°的三角形是等边三角形);最后由等边三角形OEF的三条边都相等、等量代换证明BE=EF=FC即E,F是BC的三等分点.解答:解:E,F是BC的三等分点.理由:连接OE,OF,∵DE垂直平分OB∴BE=OE(线段垂直平分线上的点到线段两端点距离相等),同理OF=CF,∴∠EBO=∠BOE,∠FCO=∠FOC,∵等边三角形ABC中,∴∠ABC=∠ACB=60°(等边三角形各角相等且为60°)∵BO平分∠ABC,CO平分∠ACB∴∠EBO=∠ABC=30°,∠FCO=∠ACB=30°∴∠BOE=∠EBO=30°,∠FOC=∠FCO=30°∴∠OEF=∠BOE+∠EBO=60°,∠OFE=∠FOC+∠FCO=60°,∴△OEF是等边三角形(有两个内角60°的三角形是等边三角形)∴OE=OF=EF(等边三角形各边相等)∴BE=EF=FC,即E,F是BC的三等分点.点评:本题综合考查了等边三角形的性质、线段垂直平分线的性质.解答该题时,充分利用了等腰三角形的底边上的高线、中线、对角的角平分线三线合一的特性.26.在等边△ABC中,D是AC的中点,E是BC延长线上一点,且CE=CD,(1)请说明DB=DE的理由.(2)若等边△ABC的边长为4cm,求△BDE的面积.考点:等边三角形的性质;三角形的面积;三角形的外角性质.专题:计算题.分析:(1)根据等边三角形三线合一的性质可得BD是∠ABC的角平分线,即可得∠CBD=30°,根据三角形外角性质即可得∠DCE=120°﹣60°,根据CD=CE,可得∠CDE=∠CED=30°,即可得∠CED=∠CBD=30°,即DB=DE.(2)过D作DF⊥BC,则DF=AG,根据等边三角形的性质可以求得BE的长,根据BE、DF的长即可计算△BDE 的面积.解答:解:(1)∵△ABC为等边三角形,D为AC的中点,即BD为AC边上的中线,∴BD是∠ABC的角平分线,∠ABC=60°,∴∠CBD=∠ABC=30°,。
等边三角形性质与判定练习题

第1课时等边三角形的性质和判定(课堂训练)一•选择题(共8小题)1 •如图,一个等边三角形纸片,剪去一个角后得到一个四边形,则图中 / a+ / B的度数是()A •180 ° B .220 ° C •240 ° D .300 °2 .下列说法正确的是()A .等腰三角形的两条高相等C.有一个角是60。
的锐角三角形是等边三角形B .等腰三角形一定是锐角三角形 D •三角形三条角平分线的交点到三边的距离相等3 .在△ABC中,①若AB=BC=CA,则△ABC为等边三角形;②若/ A= / B= / 6则厶ABC为等边三角形;③有两个角都是60。
的三角形是等边三角形;④一个角为60。
的等腰三角形B D EC 是等边三角形•上述结论中正确的有()A •1个B •2个C •3个D •4个4 .如图,CD是Rt△ABC斜边AB上的高,将△ BCD沿CD折叠,B点恰好落在AB的中点E 处,则/ A 等于()A . 25 °B . 30 °C. 45 °D . 60 °5 .如图,已知D、E、F分别是等边△ ABC的边AB、BC、AC上的点,且DE丄BC、EF丄AC、FD丄AB,则下列结论不成立的是()A . △DEF 是等边三角形B . △ADF ◎△ BED ◎△ CFEC. DE=ABD. S △ABC=3S △DEF6 .如图,在厶ABC中,D、E在BC上,且BD=DE=AD=AE=EC ,则/ BAC的度数是()A . 30 °B. 45 °C . 120 ° D . 15 °7 .如图,在△ ABC中,AB=AC , / A=120 °BC=6cm , AB的垂直平分线交BC于点M,交AB于点E , AC的垂直平分线交BC于点N,交AC于点F,则MN的长为()A. 4cmB. 3cmC. 2cmD. 1cm第1题第4题第5题第7题8 .已知/ AOB=30 °点P在/ AOB内部,P1与P关于0B对称,P2与P关于OA对称,则P l, 0 , P2三点所构成的三角形是()A.直角三角形 B . 钝角三角形C. 等腰三角形D.等边三角形二.填空题(共10小题)9 .已知等腰△ABC 中,AB=AC , / B=60 °贝U / A= 度.10 . △ABC 中,/ A= / B=6 0 °且AB=10cm,贝U BC= __________________ cm .11 .在△ABC中,/ A= / B= /。
等边三角形的面积等边三角形环的面积练习题

等边三角形的面积等边三角形环的面积练习题一、等边三角形的面积练题1. 已知等边三角形的边长为10cm,求其面积。
解答:等边三角形的面积可以通过以下公式计算:面积 = (边长的平方× √3) / 4代入已知条件,计算得到:面积= (10 × 10 × √3) / 4 = 25√3 cm²2. 已知等边三角形的面积为12√3 cm²,求其边长。
解答:等边三角形的边长可以通过以下公式计算:边长= √(面积× 4 / √3)代入已知条件,计算得到:边长= √(12√3 × 4/ √3) = √48 cm = 4√3 cm二、等边三角形环的面积练题1. 已知等边三角形环的边长为12cm,内部等边三角形的边长为8cm,求等边三角形环的面积。
解答:等边三角形环的面积可以通过以下公式计算:面积 = (外部等边三角形的面积 - 内部等边三角形的面积)外部等边三角形的面积可以使用之前提到的公式计算:外部等边三角形的面积 = (边长的平方× √3) / 4内部等边三角形的面积也可以使用之前提到的公式计算。
代入已知条件,计算得到:外部等边三角形的面积 = (12 ×12 × √3) / 4 = 36√3 cm²内部等边三角形的面积= (8 × 8 × √3) / 4 = 12√3 cm²面积= (36√3 - 12√3) cm² = 24√3 cm²2. 已知等边三角形环的面积为18√3 cm²,内部等边三角形的边长为6cm,求等边三角形环的边长。
解答:可以使用类似的方法解答这个题目。
首先,计算内部等边三角形的面积:内部等边三角形的面积= (6 × 6 × √3) / 4 = 9√3 cm²然后,计算外部等边三角形的面积:外部等边三角形的面积 = 内部等边三角形的面积 + 等边三角形环的面积代入已知条件,计算得到:外部等边三角形的面积= 9√3 + 18√3 = 27√3 cm²最后,通过计算外部等边三角形的边长,可以求得等边三角形环的边长:边长= √(面积× 4 / √3) = √(27√3 × 4 / √3) = √108 cm = 6√3 cm以上是等边三角形的面积和等边三角形环的面积的练习题解答。
等边三角形练习题

等边三角形练习题1. 已知等边三角形的边长为6cm,求其高。
解:设等边三角形的高为h,根据等边三角形的性质,高将底边平分,形成两个30°-60°-90°的直角三角形。
在这种三角形中,较短的直角边(即高)是斜边(即边长)的一半的根号3倍。
因此,h = √3 * (6/2)。
2. 若等边三角形的周长为18cm,求其面积。
解:设等边三角形的边长为a,则a = 18/3 = 6cm。
等边三角形的面积公式为A = √3/4 * a²,代入a = 6cm,得A = √3/4 * 6²。
3. 等边三角形的顶角为60°,求其底角。
解:等边三角形的三个内角都相等,每个角都是60°。
因此,底角也是60°。
4. 已知等边三角形的高为4cm,求其边长。
解:设等边三角形的边长为a,高为h。
根据30°-60°-90°三角形的性质,斜边(即边长)是高(即较短的直角边)的两倍的根号3倍。
因此,a = 2 * h / √3 = 2 * 4 / √3。
5. 等边三角形的面积为12平方厘米,求其边长。
解:设等边三角形的边长为a,面积为A。
等边三角形的面积公式为A = √3/4 * a²。
代入A = 12,得√3/4 * a² = 12,解得a = √(12 * 4/√3)。
6. 已知等边三角形的边长为8cm,求其内切圆半径。
解:设等边三角形的内切圆半径为r。
等边三角形的内切圆半径r 等于高h的1/3,而高h = √3 * (8/2)。
因此,r = (√3 * 8/2) /3。
7. 等边三角形的边长为10cm,求其外接圆半径。
解:设等边三角形的外接圆半径为R。
等边三角形的外接圆半径R等于边长a的一半的根号3倍。
因此,R = √3 * (10/2)。
8. 已知等边三角形的面积为27平方厘米,求其周长。
解:设等边三角形的边长为a,面积为A。
等边三角形培优专项练习试题与答案
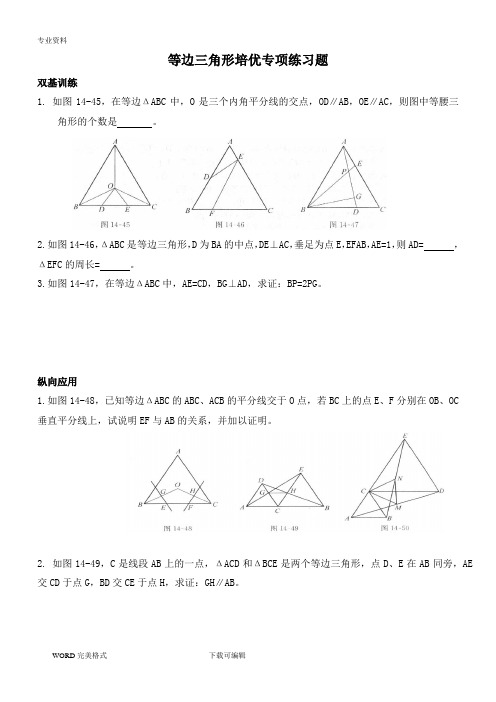
等边三角形培优专项练习题双基训练1. 如图14-45,在等边ΔABC中,O是三个内角平分线的交点,OD∥AB,OE∥AC,则图中等腰三角形的个数是。
2.如图14-46,ΔABC是等边三角形,D为BA的中点,DE⊥AC,垂足为点E,EFAB,AE=1,则AD= ,ΔEFC的周长= 。
3.如图14-47,在等边ΔABC中,AE=CD,BG⊥AD,求证:BP=2PG。
纵向应用1.如图14-48,已知等边ΔABC的ABC、ACB的平分线交于O点,若BC上的点E、F分别在OB、OC垂直平分线上,试说明EF与AB的关系,并加以证明。
2. 如图14-49,C是线段AB上的一点,ΔACD和ΔBCE是两个等边三角形,点D、E在AB同旁,AE 交CD于点G,BD交CE于点H,求证:GH∥AB。
3.如图14-50,已知ABC是等边三角形,E是AC延长线上一点,选择一点D使得ΔCDE是等边三角形,如果M是线段AD的中点,N是线段BE的中点,求证:ΔCMN是等边三角形。
4.如图14-51,C是线段AB上一点,分别以BC、AC为边作等边ΔACD和ΔCBE,M为AE的中点,N为DB的中点,求证:ΔCMN为等边三角形。
5. 如图14-52,在四边形ABCD中,∠A+∠B=1200,AD=BC,以CD为边向形外作等边ΔCDE,连结AE,求证:ΔABE为等边三角形。
6. 如图14-53,已知ΔABC是等边三角形,D为AC上一点,∠1=∠2,BD=CE,求证:ΔADE是等边三角形。
7. 如图14-54,设在四边形ABCD中,∠A+∠B=1200,AD=BC,M、N、P分别是AC、BD、CD的中点。
求证:ΔMNP是等边三角形。
8. 如图14-55,在等腰梯形ABCD中,AB∥CD,AB>CD,AD=BC,对角线AC、BD交于点O,∠AOB=600,且E、F分别是OD、OA的中点,M是BC的中点,求证:ΔEFM是等边三角形。
9. 如图14-56,在ABCD中,ΔABE和ΔBCF都是等边三角形,求证:ΔDEF是等边三角形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
等边三角形练习题
一、选择题
1.正△ABC 的两条角平分线BD 和CE 交于点I ,则∠BIC 等于( )
A .60°
B .90°
C .120°
D .150°
2.下列三角形:①有两个角等于60°;②有一个角等于60°的等腰三角形;•③三个外角(每个顶点处各取一个外角)都相等的三角形;•④一腰上的中线也是这条腰上的高的等腰三角形.其中是等边三角形的有( )
A .①②③
B .①②④
C .①③
D .①②③④
3.如图,D 、E 、F 分别是等边△ABC 各边上的点,且AD=BE=CF ,则△DEF•的形状是( )
A .等边三角形
B .腰和底边不相等的等腰三角形
C .直角三角形
D .不等边三角形 题3 题5
4.Rt △ABC 中,CD 是斜边AB 上的高,∠B=30°,AD=2cm ,则AB 的长度是( ) A .2cm B .4cm C .8cm D .16cm
5.如图,E 是等边△ABC 中AC 边上的点,∠1=∠2,BE=CD ,则对△ADE 的形状最准确的判断是( ) A .等腰三角形 B .等边三角形 C .不等边三角形 D .不能确定形状
二、填空题
1.△ABC 中,AB=AC ,∠A=∠C ,则∠B=_______.
2.在直角三角形ABC 中,︒=∠90C ,如果A B ∠=∠2,那么=∠A ______,=AB ________BC .
3.如图,已知:ABC ∆是等边三角形,cm AB 5=,BC AD ⊥,AB DE ⊥,AD AF =, 则=∠BAD ________,=∠ADF _______,=BD _________cm ,=∠FDC _____. 3题图 10题图 11题图
4.一辆汽车沿︒30角的山坡从山底开到山顶,共走了4000米,那么这座山的高度是____ _米.
5.一等腰三角形的一个底角为︒30,底边上的高为cm 9,则这个等腰三角形的腰长是________cm ,
顶角是_______.
6.ABC ∆为等边三角形,D 为BC 边上的一点,AB DE //,交AC 于点E ,则EDC ∆为______三角形.
7.在ABC ∆中,︒=∠30B ,︒=∠45C ,
若BC AD ⊥,D 为垂足,1=CD ,则=AB ______. 8.已知AD 是等边△ABC 的高,BE 是AC 边的中线,AD 与BE 交于点F ,则∠AFE=______.
9.△ABC 中,∠B=∠C=15°,AB=2cm ,CD ⊥AB 交BA 的延长线于点D ,•则CD•的长度是_______.
10. 如图,ΔABC 是等边三角形,D 为BA 的中点,DE ⊥AC ,垂足为点E ,EF ∥AB ,AE=1,则AD= ,ΔEFC 的周长= 。
11.如图,已知:在ABC ∆中,cm AC AB 4==,︒=∠15ABC ,AC BD ⊥于点D ,则=BD ______.
三、解答题
1.如图,△ABC 中,AB=AC ,∠BAC=120°,AD ⊥AC 交BC•于点D ,•求证:•BC=3AD.
2. 如图,已知:在ABC ∆中,︒=∠=120,BAC AC AB ,D 是BC 上的一点,AB DE ⊥,
AC DF ⊥,垂足分别为E 、F 。
求证:BC DF DE 2
1=
+。
3. 如图,已知:在ABC ∆中,AC AB =,︒=∠120BAC ,P 为BC 边的中点,AC PD ⊥。
E D C A B F
求证:AD CD 3=。
4.如图,已知:在等边三角形ABC 中,D 为AB 中点,BC DE ⊥于E 。
求证:BE BC 4=。
5.如图,已知:在ABC ∆中,︒=∠︒=∠30,90A ABC ,CD 平分ACB ∠。
求证:BD AD 2=。
6. 如图,已知:在直角三角形ABC 中,︒=∠90C ,︒=∠75ABC ,从顶点B 引BD 交CA 于D ,使︒=∠30CDB .
求证:BC AD 2=.
7. 如图,已知:在ABC Rt ∆中,︒=∠90ACB ,︒=∠30A ,AB CD ⊥,BC DE ⊥,D 、E 是垂足,cm AB 24=。
求BE 。
8. 如图,已知,在ABC ∆中,︒=∠60A ,高BD ,EC 相交于点H ,且1=HD ,2=HE 。
求BD ,CE 的长。
9.如图,在ABC ∆中,AC AB =,︒=∠30BAD ,且AD AE =,求EDC ∠的度数。
10.如图,已知:在ABC ∆中,AD 是BAC ∠的平分线,AC DE //交AB 于E ,AB DF //交AC 于F ,又6=AE 。
求:四边形AFDE 的周长。
11.已知D 、E 分别是等边△ABC 中AB 、AC 上的点,且AE=BD ,求BE 与CD•的夹角是多少度?
12. 如图,已知等边ΔABC 的∠ABC 、∠ACB 的平分线交于O 点,若BC 上的点E 、F 分别在OB 、OC 垂直平分线上,试说明EF 与AB 的关系,并加以证明。
13.如图,已知ΔABC 是等边三角形,D 为AC 上一点,∠1=∠2,BD=CE ,求证:ΔADE 是等边三角形。
14.如图,已知点B 、C 、D 在同一条直线上,△ABC 和△CDE•都是等边三角形.BE 交AC 于F ,AD 交CE 于H ,
①求证:BE=AD ; ②求证:CF=CH ;
③判断FH•与BD 的位置关系,并证明. E D C A
B H F。
