专题-经济订货批量模型-(EOQ模型)-教案2014-06
讲课经济订货批量模型

每年的订货次数和每次的订货之间的间隔时间,幷计算
T(Q*),T(Q*+100),T(Q*-100),你能得出什么结论 。
6
解:经济批量
2DC0 2 10000 100 Q* EOQ 500(个) H 8
每年的订货次数N=D/Q*=10000/500=20(次/年)每次订货的时间间隔
定货点R
Q
订货提前期 图3-14 经济订货模型示意图
时间
2
1)经济订货批量模型
因为:库存总费用=货物成本+订货成本+存储成本 D Q 即: T DC C H
式中,
C
0
Q
2
TC为一定时期(年或月)物资库存总费用; C为物资的购买成本或单位生产成本; D为库存物资的一定时期(年或月)的需求; Q为订货批量; 成本 H为单位物资的一定时期存储成本; C0为订货成本。
4
1)经济订货批量模型
(2)订货点 该模型中假设需求与交货提前期是固定的,而且不允 许缺货。 因此,订货点就是提前期内的需求, 即: R=Ld
式中,L为交货提前期,d为物资的需求率(月或日)。
5
例1:
长城公司是生产某机械器具的制造企业,依计划每年需 采购A零件10000个,每次订货成本是100元,每个A零件 每年的保管仓储成本是8元。求A零件的经济订货批量,
1)经济订货批量模型
经济订货批量模型是最基本的订货模型,它是按照库存 总费用最小的原则来决定订货量。 为此需要下列基本假设:
①需求率固定; ②交货提前期固定; ③订货费用与批量无关; ④不允许缺货; ⑤一次性交货; ⑥存储成本是存储量的线性函数; ⑦产品的价格固定。
EOQ经济模型
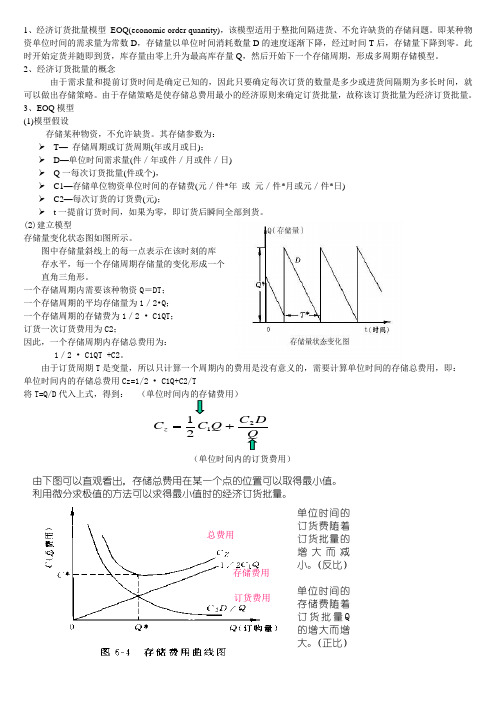
1、经济订货批量模型EOQ(economic order quantity),该模型适用于整批间隔进货、不允许缺货的存储问题。
即某种物资单位时间的需求量为常数D,存储量以单位时间消耗数量D的速度逐渐下降,经过时间T后,存储量下降到零。
此时开始定货并随即到货,库存量由零上升为最高库存量Q,然后开始下一个存储周期,形成多周期存储模型。
2、经济订货批量的概念由于需求量和提前订货时间是确定已知的,因此只要确定每次订货的数量是多少或进货间隔期为多长时间,就可以做出存储策略。
由于存储策略是使存储总费用最小的经济原则来确定订货批量,故称该订货批量为经济订货批量。
3、EOQ模型(1)模型假设存储某种物资,不允许缺货。
其存储参数为:T—存储周期或订货周期(年或月或日);D—单位时间需求量(件/年或件/月或件/日)Q一每次订货批量(件或个),C1—存储单位物资单位时间的存储费(元/件*年或元/件*月或元/件*日)C2—每次订货的订货费(元);t一提前订货时间,如果为零,即订货后瞬间全部到货。
(2)建立模型存储量变化状态图如图所示。
图中存储量斜线上的每一点表示在该时刻的库存水平,每一个存储周期存储量的变化形成一个直角三角形。
一个存储周期内需要该种物资Q=DT;一个存储周期的平均存储量为1/2•Q;一个存储周期的存储费为1/2 • C1QT;订货一次订货费用为C2;因此,一个存储周期内存储总费用为:1/2 • C1QT +C2。
由于订货周期T是变量,所以只计算一个周期内的费用是没有意义的,需要计算单位时间的存储总费用,即:单位时间内的存储总费用Cz=1/2 • C1Q+C2/T将T=Q/D代入上式,得到:(单位时间内的存储费用)(单位时间内的订货费用)总费用存储费用订货费用单位时间的订货费随着订货批量的增大而减小。
(反比)单位时间的存储费随着订货批量Q 的增大而增大。
(正比)由下图可以直观看出,存储总费用在某一个点的位置可以取得最小值。
EOQ经济订货批量解析教学内容

E O Q经济订货批量解析经济订货批量EOQ 的概念,公式,案例分析,公式推导证明,适用情况,缺陷经济订货批量EOQ 的概念,公式,案例分析,公式推导证明,适用情况,缺陷;1.经济订货批量EOQ 的概念经济订货批量是固定订货批量模型的一种,可以用来确定企业一次订货(外购或自制)的数量。
当企业按照经济订货批量来订货时,可实现订货成本和储存成本之和最小化。
2.公式为Q* = SQRT(2*DS/C)Q*-- 经济订货批量D -- 商品年需求量S -- 每次订货成本C --单位商品年保管费用3.案例分析仓储的管理很类似于生活中自来水水塔现象:水塔是个蓄水池,不停的漏水,快漏完的时候,就要迅速加水至满,保持平衡。
对于某医药配送企业仓库管理,可以看作它是集中大量采购,然后慢慢销售;快完的时候,在集中大量采购,如此循环;为了便于建模,我们把上面问题看的再理想化些:水塔的水是均匀漏的,加水时是瞬间加满的;该医药配送企业的某种药品的销售也是均匀的已一个固定的速度出库,采购的动作也是瞬间完成的;要解决的问题描述(水塔现象的对照)1.水塔负责的小区居民,一年有1000吨的用水量,每吨水的价格1元,每吨水的保管费用平均为一年0.1元,每次水泵抽水至水塔需要费用2元;那么我们根据这些数据,想到的结论是什么呢?那就是这个水塔要建立多大,每隔多长时间送一次水?一年的总费用是多少?2 .该医药配送企业某种药品一年销售10000箱,每箱进价100元,每箱货的保管费用平均为一年5元,每次供应商送货的手续费170元;根据这个数据,我们想知道:每次采购多少箱?多长时间采购一次?一年的总费用是多少?年费用的计算该医药配送企业一年的总费用计算公式=商品的总进价+全年的保管费+全年订货手续费=每箱进价*销售总箱数+(每箱年保管费/2*销售总箱数)/订货次数+每次订货手续费*订货次数这里有人概念容易误解,就是全年的保管费的计算;很容易让人感觉 :全年的保管费=每箱年保管费*销售总箱数;下面我举一个最简单的例子否定上面想法:比如仓库月初进了30箱货,每箱每天的保管费用为1元,那么到月底的时候保管总费用是不是(1元/箱.天)*30箱*30天=900元呢?实际上你要考虑到箱子在均匀出库。
专题经济订货批量模型(EOQ模型)-教案2014-06(大全五篇)

专题经济订货批量模型(EOQ模型)-教案2014-06(大全五篇)第一篇:专题经济订货批量模型 (EOQ模型)-教案2014-06 专题经济订货批量模型(EOQ模型)一、关于存储论1.为什么要储存?联系到餐饮业,前讲讲授过了。
储存物品的现象是为了解决供应(生成)与需求(消费)之间的不协调的一种措施,这种不协调性一般表现为供应量与需求量和供应时期与需求时期的不一致性上,出现供不应求或供过于求。
与存储量有关的问题,需要人们做出抉择,在长期实践中人们摸索到一些规律,也积累了一些经验。
专门研究这类有关存储问题的科学,构成运筹学的一个分支,叫做存储论(inventory),也称库存论。
2.存储论的基本概念:(1)需求:从存储中取出一定的数量,使存储量减少,是存储的输入。
需求有间断式的,有连续均匀的;有的需求是确定性的,有的需求是随机性的。
(2)补充(订货或生产):存储的输入。
存储论要解决的问题是:多少时间补充一次,每次补充的数量应该是多少。
(3)费用:存储费;订货费;生产费;缺货费(4)存储策略:决定多少时间补充一次以及每次补充数量的策略称为存储策略。
抽象为数学模型,把复杂问题尽量加以简化。
存储模型大体可以分为两类:确定性模型,即模型中的数据皆为确定的数值;另外一类叫作随机性模型,即模型中含有随机变量,而不是确定的数值。
一个好的存储策略,既可以使总费用最小,又可以避免缺货影响生产(或对顾客失去信用)。
二、存储模型简介1.存储模型(1)确定性存储模型:模型一——不允许缺货,备货时间很短;模型二——不允许缺货,生产需要一定时间;模型三:允许缺货,备货时间很短;模型四——允许缺货(需补足缺货)、生产需一定时间;价格有折扣的存储问题。
(2)随机性存储模型:模型五——需求是随机离散的(定期订货法);模型六——需求是连续的随机变量(定点订货法,(前)永续盘存法);模型七——(s,S)型存储策略(结合五六模型,达到s 订货,是存储量达到S);模型八——需求和备货都是随机离散的。
经济订货量模型

R Ld
4、涉及保险储备的经济订货量模型
例如,某企业订货日至到货期的时间为10天,每日存货需 要量为10千克,那么:
R L d =10*10=100(千克)
即企业在尚存100千克存货时,就应当再次订货,等到 下批订货到达时(再次发出订货单10天后),原有库存刚 好用完。此时,有关存货的每次订货批量、订货次数、订 货间隔时间等并无变化,与瞬时补充相同。订货提前期的 情形如下图所示(假定瞬时补充情况下的经济订货批量为 300千克)
TC(S、B)=CS +CB
CS KU S N
CB B KC
TC(S、B) KU S N B KC
2 KD Kc K c 2 KDK c 2
最佳订货周期公式:
1 t * N
*
1 DK c 2K
3、存货陆续供应和使用的经济订货量模型
在建立基本模型时,是假设存货一次全部入库,故存货增加 时存量变化为一条垂直的直线。事实上,各批存货可能陆 续入库,使存量陆续增加。尤其是产成品入库和在产品转 移,几乎总是陆续供应和陆续耗用的。在这种情况下存货 数量变化如下图
4、涉及保险储备的经济订货量模型
这就是说,订货提前期对经济订货量并无影响,可仍以 原来瞬时补充情况下的300千克为订货批量,只不过在达 到再订货点(库存100千克)时即发出订货点罢了。
4、涉及保险储备的经济订货量模型
(2)保险储备 之前讨论假定存货的供需稳定且确定,即每日需求量不 变,交货时间也固定不变。实际上,每日需求量可能变化, 交货时间也可能变化。按照某一订货量(如经济订货批量) 和再订货点发出订单后,如果需求增大或送货延迟,就会 发生缺货或供货中断。 为防止由此造成的损失,就需要多储备一些存货以备应 急之需,称为保险储备(安全存量)。
经济订货批量模型

经济订货批量(重定向自经济订货批量模型)经济订货批量(Economic Order Quantity,EOQ)又称整批间隔进货模型、EOQ模型目录[隐藏]• 1 经济订货批量概述• 2 经济订货批量基本公式o 2.1 订货费用o 2.2 存贮及其他费用• 3 经济批量的计算• 4 计算经济订货批量最有效的方法[1]• 5 EOQ延伸[1]• 6 间断订货批量[1]•7 对经济批量方法的评价[2]•8 相关条目•9 参考文献[编辑]经济订货批量概述经济订货批量(EOQ),即Economic Order Quantity是固定订货批量模型的一种,可以用来确定企业一次订货(外购或自制)的数量。
当企业按照经济订货批量来订货时,可实现订货成本和储存成本之和最小化。
订货批量概念是根据订货成本来平衡维持存货的成本。
了解这种关系的关键是要记住,平均存货等于订货批量的一半。
因此,订货批量越大,平均存货就越大,相应地,每年的维持成本也越大。
然而,订货批量越大,每一计划期需要的订货次数就越少,相应地,订货总成本也就越低。
把订货批量公式化可以确定精确的数量,据此,对于给定的销售量,订货和维持存货的年度联合总成本是最低的。
使订货成本和维持成本总计最低的点代表了总成本。
上述讨论介绍了基本的批量概念,并确定了最基本的目标。
简单地说,这些目标是要识别能够使存货维持和订货的总成本降低到最低限度的订货批量或订货时间。
购进库存商品的经济订货批量,是指能够使一定时期购、存库存商品的相关总成本最低的每批订货数量.企业购、存库存商品的相关总成本包括购买成本、相关订货费用和相关储存成本之和。
经济订货批量模型是目前大多数企业最常采用的货物定购方式.该模型适用于整批间隔进货、不允许缺货的存储问题,即某种物资单位时间的需求量为常D,存储量以单位时间消耗数量D的速度逐渐下降,经过时间T后,存储量下降到零,此时开始定货并随即到货,库存量由零上升为最高库存量Q,然后开始下—个存储周期,形成多周期存储模型。
EOQ经济订货批量解析

经济订货批量EOQ 的概念,公式,案例分析,公式推导证明,适用情况,缺陷经济订货批量EOQ 的概念,公式,案例分析,公式推导证明,适用情况,缺陷;1.经济订货批量EOQ 的概念经济订货批量是固定订货批量模型的一种,可以用来确定企业一次订货(外购或自制)的数量。
当企业按照经济订货批量来订货时,可实现订货成本和储存成本之和最小化。
2.公式为Q* = SQRT(2*DS/C)Q*-- 经济订货批量D -- 商品年需求量S -- 每次订货成本C --单位商品年保管费用3.案例分析仓储的管理很类似于生活中自来水水塔现象:水塔是个蓄水池,不停的漏水,快漏完的时候,就要迅速加水至满,保持平衡。
对于某医药配送企业仓库管理,可以看作它是集中大量采购,然后慢慢销售;快完的时候,在集中大量采购,如此循环;为了便于建模,我们把上面问题看的再理想化些:水塔的水是均匀漏的,加水时是瞬间加满的;该医药配送企业的某种药品的销售也是均匀的已一个固定的速度出库,采购的动作也是瞬间完成的;要解决的问题描述(水塔现象的对照)1.水塔负责的小区居民,一年有1000吨的用水量,每吨水的价格1元,每吨水的保管费用平均为一年0.1元,每次水泵抽水至水塔需要费用2元;那么我们根据这些数据,想到的结论是什么呢?那就是这个水塔要建立多大,每隔多长时间送一次水?一年的总费用是多少?2 .该医药配送企业某种药品一年销售10000箱,每箱进价100元,每箱货的保管费用平均为一年5元,每次供应商送货的手续费170元;根据这个数据,我们想知道:每次采购多少箱?多长时间采购一次?一年的总费用是多少?年费用的计算该医药配送企业一年的总费用计算公式=商品的总进价+全年的保管费+全年订货手续费=每箱进价*销售总箱数+(每箱年保管费/2*销售总箱数)/订货次数+每次订货手续费*订货次数这里有人概念容易误解,就是全年的保管费的计算;很容易让人感觉:全年的保管费=每箱年保管费*销售总箱数;下面我举一个最简单的例子否定上面想法:比如仓库月初进了30箱货,每箱每天的保管费用为1元,那么到月底的时候保管总费用是不是(1元/箱.天)*30箱*30天=900元呢?实际上你要考虑到箱子在均匀出库。
经济订货批量模型讲义

经济订货批量模型讲义
摘要:
一、经济订货批量模型的基本概念
二、经济订货批量模型的假设条件
三、经济订货批量模型的数学描述
正文:
经济订货批量模型讲义
经济订货批量模型(EOQ 模型)是一种用于确定企业一次订货(外购或自制)的最佳数量的方法。
该模型主要涉及订货成本、库存成本和需求量等因素,旨在实现总成本最小化。
本讲义将介绍经济订货批量模型的基本概念、假设条件和数学描述等内容。
一、经济订货批量模型的基本概念
经济订货批量模型是一种用于确定企业一次订货最佳数量的方法。
该模型通过考虑订货成本、库存成本和需求量等因素,以实现总成本最小化。
在这一部分,我们将详细讲解订货成本、库存成本和需求量等概念。
二、经济订货批量模型的假设条件
为了建立经济订货批量模型,我们需要对一些关键变量进行假设。
这些假设条件包括:需求率为常量、订货提前期已知、订货费与订货批量无关、维持库存费是库存量的线性函数等。
本部分将详细介绍这些假设条件。
三、经济订货批量模型的数学描述
经济订货批量模型的数学描述主要包括年总成本公式和求解最优订货批量
的过程。
年总成本公式为:TC = D × C × (1 - (1/2) × (Q/K)),其中TC 表示年总成本,D 表示年需求量,C 表示每次订货成本,Q 表示订货批量,K 表示订货次数。
要实现总成本最小化,我们需要求解使年总成本最小的订货批量Q。
总之,经济订货批量模型是一种用于确定企业一次订货最佳数量的方法,通过考虑订货成本、库存成本和需求量等因素,以实现总成本最小化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题经济订货批量模型 (EOQ模型)
一、关于存储论
1.为什么要储存?
联系到餐饮业,前讲讲授过了。
储存物品的现象是为了解决供应(生成)与需求(消费)之间的不协调的一种措施,这种不协调性一般表现为供应量与需求量和供应时期与需求时期的不一致性上,出现供不应求或供过于求。
与存储量有关的问题,需要人们做出抉择,在长期实践中人们摸索到一些规律,也积累了一些经验。
专门研究这类有关存储问题的科学,构成运筹学的一个分支,叫做存储论(inventory),也称库存论。
2.存储论的基本概念:
(1)需求:从存储中取出一定的数量,使存储量减少,是存储的输入。
需求有间断式的,有连续均匀的;有的需求是确定性的,有的需求是随机性的。
(2)补充(订货或生产):存储的输入。
存储论要解决的问题是:多少时间补充一次,每次补充的数量应该是多少。
(3)费用:存储费;订货费;生产费;缺货费
(4)存储策略:决定多少时间补充一次以及每次补充数量的策略称为存储策略。
抽象为数学模型,把复杂问题尽量加以简化。
存储模型大体可以分为两类:确定性模型,即模型中的数据皆为确定的数值;另外一类叫作随机性模型,即模型中含有随机变量,而不是确定的数值。
一个好的存储策略,既可以使总费用最小,又可以避免缺货影响生产(或对顾客失去信用)。
二、存储模型简介
1.存储模型
(1)确定性存储模型:模型一——不允许缺货,备货时间很短;模型二——不允许缺货,生产需要一定时间;模型三:允许缺货,备货时间很短;模型四——允许缺货(需补足缺货)、生产需一定时间;价格有折扣的存储问题。
(2)随机性存储模型:模型五——需求是随机离散的(定期订货法);模型六——需求是连续的随机变量(定点订货法,(前)永续盘存法);模型七——(s,S)型存储策略(结合五六模型,达到s订货,是存储量达到S);模型八——需求和备货都是随机离散的。
2.模型一:不允许缺货,备货时间很短(最简单,以它为了讲解)
EOQ模型的出发点和假设如下:
1.EOQ模型涉及两种费用:一是采购费用。
二是存储费用。
采购费用是指每次进行采购所需的定单费、电传或电话费、验收费用等。
这部分费用与批量的大小没有什么关系,应视力固定费用。
存储费用是指因存货而产生的保管费、保险费、人工成本费、场地占用费等。
由于存储费用的高低取决于存货里的多少,因此应视为可变费用。
2.缺货费用为无穷大。
3. 当存储降至零时,可以立即得到补充(即备货时间或拖后时间很短,可以近似地看作零)。
4. 需求是连续的、均匀的,设需求速度R(单位元时间的需求量)为常数,则t时间的需求量为Rt。
5.订货量不变,订购费不变(每次备货量不变,装配费不变)。
6.存储费不变。
3.具体模型求解过程及公式(见餐饮业EOQ模型)
三、餐饮业企业中的经济订货批量模型(EOQ模型)
经济订货批量模型又称为EOQ模型(Economic Ordering Quantity),是大型企业在确定采购数量时常用的数学模型。
由于我国餐饮业大多以中小型企业为主,且市场供求关系不太稳定,因此,我国的饭店或管厅很少使用。
但是,随着市场经济的完善和集中采购的推广、经济采购批量模型对企业采购还是具有较好的指导意义。
进货批量增大,平均库存就增加,相应的存储费用就高;同时,由于进货批量大,年进货次数势必减少,因而采购费用肯定会降低。
若进货批量减少,存储费用也会减少,但进货次数增加,会造成采购费用加大。
EOQ模型的出发点是当进货批量为多大时,总费用最低。
为便了计算,我们假设:
Q为经济定货批量;
F为每次采购的费用;
D为某种原料的年需求量;
C为单位原料的储存费用;
TC为全年采购与储存总费用;
这样,我们可以得到以下关系:
TC=F·D/Q+C·Q/2
其中,D/Q为采购次数,F·D/Q则为年总采购费用,Q/2为平均库存量,CQ/2则为年总储存费用。
若使总成本TC值最小、应使总成本TC’=0,且TC’>0,则:
TC’=-F·D/Q2十C/2
TC”=2P·D/Q3
显然,当TC’=0时,有F.D/Q2=C/2
2•
=(1)
Q/
D
C
F
此时,Q即为最佳经济批量,总成本TC最低
例如,某餐饮集团采购中心对路装竹笋的年需求量为4000箱,每次采购费用为200元,单位存储费用为10元,则最佳订货批量为:
⨯
Q=400(箱)
2⨯
=
10
4000
/
200
事实上,某种原料的单位存储费用很难确定,但全年的存储费用是一定的,因此可按全年总存储费用占全年存货价值的百分比来计算,然后按此比例分到每一存货项目上,这样比较可行。
假设P为单位原料进价,S为存储费用占存货价值的百分比,即:C=PS,则某种原料的年存储费用为PS·Q/2,即:
TC=F·D/Q十PS·Q/2
TC’=-F.D/Q2十PS/2=0
FD/Q2=PS/2
2•
=(2)
Q/
F
D
PS
例如,某采供中心对罐装菠萝的年需求量为1200箱,每次采购费用为100元,每箱菠萝进价为60元,该中心年存储费用占存货总额的10%,求最佳采购批量,即:
D=1200 F=100 P=60 S=10%
根据公式(2)则有:
2⨯
1200
Q=400(箱)
=
⨯
⨯
%
600
10
60
/
也就是说,该采供中心菠萝的最佳进货批量为每次200箱。
注意事项:
其它模型感兴趣的同学,可以参考清华大学出版的《运筹学》(第三版)相关教材学习!!!
如模型二,设生成速度为Ps,需求速度为R,则
/
Q-
/
=
F
2•
)
(R
Ps
Ps
PS
D。
