波利亚解题理论
波利亚的解题理论_2022年学习资料
解题过程：-·第1弄清问题-·条件（已知）：-■1c-10:-2CosA/cosB-b/a=4/3-·③点 为△ABC内切圆上的动点、-口问题（未知）：-·求点P到项点A、B、C的距离的平方和的-最小值和最大值。6
第2拟订计划-回忆原来有没有见过同类问题（没有），但见-过相关的问题：-o-1已知三角形的某些边角关系，判 三角形-的形状、解三角形等（知三求一，已知的三个-边角元素中至少有一个是边，题目基本符-合-·②如果三角形 以确定，那么此题就是求这-个三角形的某个特征曲线上的动点到三个顶-点的距离的平方和的最值问题。-17
如何解题-1.积累认识的资源-2.掌握转化的方法-3。及时调控的能力-4.良好信念系统的支持
波利亚的怎样解题表-解题过程分为以下四个阶段：-1.弄清问题-2.拟订计划-3.实现计划-4.回顾
波利亚的怎样解题表-1弄清问题-1未知数是什么？已知数据是什么？条件是什么？-满足条件是否可能？要确定未知 ，条件是否充分？或-者它是否不充分？或者是多余的？或者是矛盾的？-2画张图，并引入适当的符号.-3把条件的 部分分开，并把它们写下来。
波利亚《怎样解题表》简介-波利亚的数学教育思想概述-波利亚George Polya数学教育思想的核心问题数 学教育的目的是什么？-1波利亚主张数学教学的目的应当是提高学生的一般素-养：首先和主要的目标应当是教会青年 考、-2教什么样的思考？数学是什么？数学有什么特点？对数-学及其意义的认识的教学观起着决定性的作用。
我国数学解题研究的代表人物和代表作-罗增儒-戴再平-单蹲-朱华伟-·中学数学解题的-理论与实践M.-数学习 理论-南宁：广西教育-[M上海：上-出版社，2008-解题研究M.-海教育出版社，-年9：前言-南京：南京 -•数学解题策略-范大学出版社，-1991.3:-·数学解题学引论-2002.6-1996.10.-[M西 .陕西-•北京：科学出-师范大学出版社，-版社，2009.8.-1997.6-4
波利亚的解题理论
23
第三步
实现计划
解析：设原来的进价为 x ，售价为 y ，则由题 意可知现在的进价为 x1 10% ，由等量关系 列出方程
y x(1 10%) y x (1 25%) x(1 10%) x
13
1. 弄清问题
“弄清问题”阶段，重述问题，教会学生形成 正确的审题方法 ① 首先，了解已知是什么?未知是什么?条件 是什么?要确定未知数,条件是否充分? 是否 不充分?
② 其次，形成正确的审题方法。
③ 最后，注意引导学生挖掘已知条件与所求之 间的关系，特别是挖掘题中的隐含条件。
14
例如：计算 C
y ( x 0) 2 (0 2) 2 [ x (1)] 2 (0 3) 2
17
3. 实现计划
“实现计划”阶段，加强基础教学，善用 一题多变加深和提高解题能力 ① 实现你的求解计划,检验每一步骤. ② 你能否清楚地看出这一步骤是正确的?你 能否证明这一步骤是正确的?
波利亚的数学教育理论
1
回顾一下，我们学过的教育理论有哪些？ 弗赖登塔尔数学教育理论 建构主义理论 数学教学理论
2
一、波利亚简介
二、波利亚数学教育理论 三、波利亚《怎样解题》
四《怎样解题》在中学数学中的应用
3
一、波利亚简介
波 利 亚 （ 1887-1985 ） ， 美 籍匈牙利数学家。生于布达佩 斯，卒于美国。青年时期曾在布 达佩斯、维也纳、巴黎等地攻读 数学、物理和哲学，获博士学 位。1914年在瑞士苏黎世工业大 学任教 ， 1938 年任数理学院院 长。1940年移居美国，历任布朗 大学、斯坦福大学教授。1963年 获美国数学会功勋奖。
波利亚解题理论
四部曲
改善学生数学解题中的元认知的教学策略
问题与思考
• 设计一个解决某类问题的解题表． • 根据你的解题经历，选一个典型例子，详细介绍
解题的具体过程． • 实践解题表，求解下题：如果3个有相同半径的
圆过一点，则通过它们的另外3个交点的圆具有 相同的半径． • 对解题表，谈谈你想说的任何看法，写一篇不少 于1000字的小论文． • 基于波利亚的解题理论谈数学解题教学
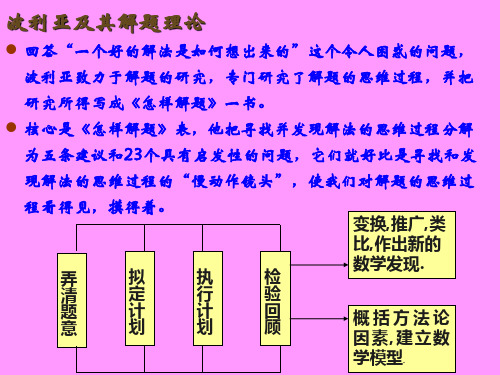
程看得见，摸得着。
弄
拟
执
检
清
定
行
验
题
计
计
回
意ቤተ መጻሕፍቲ ባይዱ
划
划
顾
变换,推广,类 比,作出新的 数学发现.
概括方法论 因素,建立数 学模型.
波利亚的教育思想
数学教学的目的应当是提高学生的一般素养：首 先和主要的目标应当是教会青年思考。
教什么样的思考?数学是什么?数学有什么特点? 对数学及其意义的认识决定性的作用。
波利亚及其解题理论
回答“一个好的解法是如何想出来的”这个令人困惑的问题，
波利亚致力于解题的研究，专门研究了解题的思维过程，并把
研究所得写成《怎样解题》一书。
核心是《怎样解题》表，他把寻找并发现解法的思维过程分解
为五条建议和23个具有启发性的问题，它们就好比是寻找和发
现解法的思维过程的“慢动作镜头”，使我们对解题的思维过
弗赖登塔尔的数学教育理论及波利亚的解题理论
一名好的数学教师具备两方面的知识
一是数学内容的知识。
二是数学教学法的知识。
波利亚给数学教师提出了“十条建议”
1. 要对所讲的课题有兴趣 2. 要懂得所讲的课题; 3. 要懂得学习的途径—发现; 4. 要观察学生的脸色,弄清他们的期望和困难, 置身于他们之中; 5. 不仅要传授知识,而且要教给学生才智,思维的方式和工作习惯; 6. 要让他们学习猜测; 7. 要让他们学习证明; 8. 要找出手边题目中那些对后来题目有用的特征; 9. 不要立即吐露你的全部秘密—让学生在你说出来之前先去猜, 尽量让他们自己找出来; 10. 要建议,不要强迫别人去接受.
你以前曾见过它吗？ 你知道什么与此有关的问题？ 注视未知数！试想出一个有相同或相似的未知数的熟
悉的问题。 这里有一个与你有关而且以前解过的问题，你能应用 它吗？ 你可以概述这个问题吗？ 你若不能解这个问题，试先解一个有关的问题。你能 想出一个更容易的有关问题吗？一个更一般的问题？一 个更特殊的问题？一个类似的问题？你能解问题的一部 分吗？ 你用了全部的条件吗？
最佳动机
循序渐进
主动学习
“学东西的最好方式是发现它”，“亲自发现 能够在你脑海里留下一条小路；今后一旦需要， 你便可以利用它”。因而，教师应该“尽量让 学生在现有条件下亲自发现尽可能多的东西”。 思想应在学生头脑里产生，教师则只起助产士 的作用。
最佳动机
为了使学习富有成效，学生应该对学习倍感兴 趣并且在学习活动中寻求欢乐。最佳的刺激应 该是对所学知识的兴趣。另外，还可以在学生 做题之前，让他们猜测学习的结果。在科学家 的工作中，猜想几乎是证明的先导。
现实 数学化 再创造
现实
(完整版)波利亚的解题理论
波利亚的解题理论（讲稿）同学们好!今天我们大家一起来学习波利亚的解题理论。
首先，让我们了解一下波利亚的生平.乔治·波利亚（George Polya,1887-1985）美籍匈牙利数学家，生于匈牙利,青年时期曾在布达佩斯、维也纳、哥廷根、巴黎等地攻读数学、数学、物理和哲学,1912年获数学博士学位。
他是法国科学院、美国全国科学院和匈牙利科学院的院士，是20世纪举世公认的数学家和数学教育家,也是享有国际盛誉的数学方法论大师,为数学方法论的现代研究,特别是为数学解题教学研究奠定了必要的理论基础。
他的成就主要包括解题理论、数学教学理论和教师教育理论,发表200多篇论文和许多专著，主要著作包括:《怎样解题》（1944)、《数学的发现》（1954）、《数学与猜想》（1961)等。
其中《怎样解题》与《数学的发现》集中论述了怎样解题的问题,而《数学与猜想》则对合情推理进行了生动地、富有创造性地论述。
在数学方面,对实变函数、复变函数和概率论等若干分支领域作出了开创性的贡献,留下了以他的名字命名的术语和定理。
在数学解题研究领域,波利亚是一面旗帜，也是一代宗师。
这里主要介绍他的解题理论。
学习波利亚的解题理论，首先需要了解对“解题”过程的界定。
波利亚认为，解题是智力的特殊成就，题目是数学的心脏，数学教学的本质在于教会学生解题，解题思想“应当诞生在学生心里，教师仅仅像助产士那样行事"（苏格拉底语),由此,数学教师的首要任务是发展学生解决问题的能力.为了帮助学生，为了回答“一个好的解法是如何想出来的”这个令人困惑的问题，他专门研究可解题的思维过程，用朴素而现代化的形式来阐明探索法（既有助于发现的探索方法），并集几十年教学与科研之大成写成《怎样解题》一书,与1948年出版，风靡世界.其中“怎样解题"表仔细分析了求解各种数学问题时的思维过程，成为经典之作。
概括的说来，“怎样解题”表是波利亚的解题理论的核心内容。
波利亚的《怎样解题》[word版]
![波利亚的《怎样解题》[word版]](https://img.taocdn.com/s3/m/b81648d6162ded630b1c59eef8c75fbfc67d945e.png)
波利亚的《怎样解题》[word版]乔治·波利亚是20世纪举世公认的数学家，著名的数学教育家，享有国际盛誉的数学方法论大师．波利亚在数学教育领域最突出的贡献是开辟了数学启发法研究的新领域，为数学方法论研究的现代复兴奠定了必要的理论基础。
波利亚致力于解题的研究，为了回答“一个好的解法是如何想出来的”这个令人困惑的问题，他专门研究了解题的思维过程，并把研究所得写成《怎样解题》一书。
这本书的核心是他分解解题的思维过程得到的一张《怎样解题表》。
波利亚的四步解题法：
1.彻底理解问题
2.形成解决思路
3.执行
4.总结
1、彻底理解问题：为了确保真正理解问题，你最好把问题用自已的话换成各种形式反复重新表达，但另忘了指出问题的主干：要求解的是什么？已知什么？要满足哪些条件？但凡能画图，一定要画出来。
2、形成解题思路：要专注，用过往经验，已撑握的知识，并调整适用性来形成思路。
如果不行，就改变这个问题的各个组件：已知、未知、条件，先构造简单一点的，引入辅助，条件是否用足，甚至改变求解的未知数，看能否找到解题线索？直到找到与之相似而你又解决过的问题。
3、执行：一要有耐心，二需要及时的检查每一步，可
凭直觉或证明（两个都有用，但是两回事），要问自已每一步都检查了吗？能看出来这一步是对的吗？能证明这一步是对的吗？
4、总结：巩固与提升的关键，多想想，再论证，尝试另外的解法，找更明快简捷的方法，还要问，这次的解法还能用在什么地方？总结是最好的启法时刻。
四个常用的解题模式波利亚
四个常用的解题模式波利亚
一、双轨迹模式
1.把问题归结为要确定一个‘点'；
2.把条件分成两部分，使得对每一部分，未知点都在一轨迹上。
这两个轨迹
的‘交点'即所求。
二、笛卡尔模式
1.把问题归结为要确定若干个‘未知量'；
2.设想问题已经解出，列出已知量和未知量之间根据条件必须满足的一切关
系式；
3.把某些关系式转化为方程，得出一个方程组；
4.把方程组通过消元化归为一个方程。
三、递归模式
1.设法将要求的量归结为某个依次排列的序列中的一项；
2.确定这序列中的第一项或前几项；
3.找出递推关系，将序列的一般项与前几项联系起来，从而可递推得到所求
项。
四、叠加模式
1.先处理一、两种特殊情形（称之为导引特款）；
2.利用导引特款的叠加去得出一般问题的解。
波利亚的“怎样解题表”
波利亚的“怎样解题表”第一：你必须弄清问题。
——弄清问题。
未知数是什么？已知数据是什么？条件是什么？满足条件是否可能？要确定未知数，条件是否充分？或者它是否不充分？或者它是多余的？或者是矛盾的？画张图。
引入适当的符号。
把条件的各个部分分开。
你能否把它们写下来？第二：找出已知数与未知数之间的关系。
如果找不出直接的联系，你可能不得不考虑辅助问题。
你应该最终得出一个求解的计划。
——拟订计划。
你以前见过它吗？你是否见过相同的问题而形式稍有不同？你是否知道与此有关的问题？你是否知道一个可能用得上的定理？看着未知数！试想出一个具有相同未知数或相似未知数的熟悉的问题。
这里有一个与你现在的问题有关，且早已解决的问题。
你能不能利用它？你能利用它的结果吗/你能利用它的方法吗？为了能利用它，你是否应该引入某些辅助元素？你能不能重新叙述这个问题？你能不能用不同的方法重新叙述它？回到定义去。
如果你不能解决所提出的问题，可先解决一个与此有关的问题。
你能不能想出一个更容易着手的有关问题？一个更普遍的问题？一个更特殊的问题？一个类比的问题？你能否解决这个问题的一部分？仅仅保持条件的一部分而舍去其余部分，这样对于未知数能确定到什么程度？它会怎样变化？你能不能从已知数据导出某些有用的东西？你能不能想出适于确定未知数的其他数据？如果需要的话，你能不能改变未知数或数据，或者二者都改变，以使新未知数和新数据彼此更接近？你是否利用了所有的已知数据？你是否利用了整个条件？你是否考虑了包含在问题中的所有必要的概念？第三：实行你的计划。
——实现计划。
实现你的求解计划，检验每一步骤。
你能否清楚地看出这一步骤是正确的？你能否证明这一步骤是正确的？第四：验算所得到的解。
——回顾。
你能否检验这个论证？你能否用别的方法导出这个结果？你能不能一下子看出它来？你能不能把这个结果或方法用于其他的问题？这一步骤是正确的？乔治·波利亚的简历美籍匈牙利数学家乔治·波利亚（George Polya,1887～1985）对回答上述问题非常感兴趣，他先后写出了《怎样解题》、《数学的发现》和《数学与猜想》。
波利亚的解题理论
波利亚的解题理论一、波利亚的生平及主要著作对于我们数学学习者而言，大多都有过这样的经历：一道题，自己怎么想也想不出解法，而老师却给出了一个绝妙的解法。
这时候，我们最想知道“老师是怎么想出这个解法的”，如果这个解法不是很难，我们也许会问“自己完全可以想出，但为什么我没有想到呢？”要回答这个问题，实际上牵涉到对揭发数学问题解决规律的深入研究。
综观历史来看，美籍匈牙利数学家乔治。
波利亚（George Polya，1887-1985）不仅对上述问题特别感兴趣，而且在该领域做出了许多奠基性的工作。
波利亚是法国科学院，美国科学院和匈牙利科学院的院士，1887年出生在匈牙利，青年时期曾在布达佩斯、维也纳、哥廷根、巴黎等地攻读数学、物理和哲学，获博士学位。
1914年在苏黎世著名的瑞士联邦理工学院任教。
1940年移居美国，1942年起任美国斯坦福大学教授。
他一生发表200多篇论文和许多专著。
他在数学的广阔领域内有精深的造诣，对实变函数、复变函数、组合论、概率论、数论、几何等若干分支领域都做出了开创性的贡献，一些术语和定理都以他的命名。
由于他在数学教育方面所取得的成就和对世界数学教育所产生的影响，在他93岁高龄时，还被ICME（国际数学教育大会）聘为名誉主席。
《怎样解题》（1944），《数学的发展》（1945）和《数学与猜想》（1961）这三本书就是他智慧的结晶。
这些书被译成很多国家的文字出版，其中《怎样解题》一书被译成17种文字，仅平装本就销售了100万册以上。
著名数学家范。
德。
瓦尔登1952年2月2日在瑞士苏黎世大学的会议致辞中说：“每个大学生，每个学者，特别是每个老师都应该都读读这本引人入胜的书”。
这些书成了世界范围内的数学教育名著，对数学教育产生了深刻的影响。
二、波利亚对数学教育的基本看法波利亚对于数学教育的目的、价值、方法非常关注。
他认为，“中小学生到底为什么要学习数学？要学什么样的数学？通过什么途径学好数学？”具体一点就是，在中小学阶段，是以“学数学”为主呢，还是以学如何“用数学”为主呢？这一点必须弄清楚。
“波利亚解题理论”在几何作图题中的应用
生(思考后回答):三个! 还可以以B 为圆心,分别以AC 的长为半径画弧,再以 C 为圆心,以 AB 为半径画弧,确定另 外两个 D 点(如图４).
师:请再思考:是不是只有三个 D 点呢? 学生 陷 入 沉 思,因 为 对 于 全 等 的 情 况 学 生 比 较 好 理 解, 也容易 想 到,但 是 如 何 过 渡 到 更 一 般 的 情 况,需 要 教 师 的 启发. 师:(拿 出 事 先 准 备 好 的 纸 板 )∠ABC 是 一 个 可 移 动 的 纸板,纸板移动的过程中保证两条 边 始 终 经 过 B、C 两 点,那 么点 A 的运动轨 迹 是 什 么 呢? (通 过 动 态 图 引 发 学 生 的 思 考 ,关 联 已 学 知 识 发 现 问 题 本 质 ) 生:应该是 个 圆,不,应 该 是 一 段 弧. 作 △ABC 的 外 接 圆O,根据“弧所对的圆周角相等”,在优 弧 BAC 上 可 以 找 出 无数个D 点,使 ∠BDC ＝ ∠BAC(如图５). 师:优弧 BAC(除去端点)上 的 点 D,均 满 足 ∠BDC ＝ ∠BAC;反过来,是不是所有的 D 点都在优弧BAC 上? 生:应该是吧? (不太确定自己的 答 案,思 考 后 发 现 还 有 所遗漏) 生:不对,应 该 还 有 一 段 和 弧 BAC 对 称 的 弧. 可 以 画 △BCD２ 的外接圆上,优弧 BD２C(除去 端 点)上 的 所 有 点 也 满足 ∠BDC ＝ ∠BAC (如图６).
师:求作的角有什么特点? (引导 学 生 深 入 理 解 题 意,挖 掘深层次条件.)
生:∠BDC 的两边上的点B 和C 就 是 三 角 形 的 两 个 顶 点 . (学 生 发 现 了 隐 含 条 件 )
师 :你 能 解 决 这 个 问 题 吗 ? 生:以 B、C 两点所在的直线为对称轴,将 ∠A 翻折过来 就可以了得到一个角和 ∠BAC 相等.(第二步:拟 定 计 划. 学生想到了翻折) 师:你说的“翻折”用 尺 规 作 图 如 何 实 现? (提 示 学 生 用 尺规执行方案) 生:首先过点 A 作已知直线BC 的垂线交BC 于点E,在 AE 的延长线上截取ED ＝ AE,连 接 BD,CD,那 么 ∠BDC ＝ ∠BAC(如图２).(第三 步:实 施 计 划. 学 生 进 一 步 将 拟 定的计划实施) 师:你能说说 ∠BDC ＝ ∠BAC 的 理 由 吗? (引 导 学 生 思 考 作 图 正 确 的 原 理 ,进 一 步 确 定 答 案 ) 生:由作图知:直 线 BC 垂 直 平 分 AD,∵AC ＝ DC,AB ＝ DB,又 ∵BC ＝ BC,∴△ABC ≌ △DBC. 师:非常 好! 你 从 对 称 的 角 度 作 一 个 角 等 于 已 知 角,并 用全等证明它的正确性. 如果教师就题论题,可 以 认 为 本 题 “做 完 了 ”,但 却 没 有 很好地锻炼学生的思维,更忽略了波利亚 解 题 理 论 中 的 最 后 一步:回顾.因此在每道题目结束后,一 定 要 学 会 反 思“本 题 是 否 有 更 好 的 解 决 方 法 ”“我 的 方 法 是 否 全 面 ”等 问 题 . 对 于 本 题 ,我 和 学 生 做 了 更 深 层 次 的 探 究 . 师 :大 家 想 一 想 ,还 有 没 有 其 他 解 决 方 法 . 生:(思考后回答)可以作全等三角形! 直接通过作三边 相等,作一个 △BCD 和 △ABC 全等. 师:把 你 的 想 法 用 几 何 作 图 的 语 言 描 述 出 来. (培 养 学 生用规范的几何作图语言描述问题的习惯) 生:以B 为圆心,AB 的长为半径画弧,再以C 为圆心,以 AC 为半径画弧,两弧交于点 D,那么 ∠D ＝ ∠A(如图３).
波利亚及其解题理论
概括方法论因 素,建立数学 模型.
弄清题意
1) 已知是什么? 2) 未知是什么? 3) 题目要求你干什么? 4) 可否画一个图形? 5) 可否数学化?
拟定计划(核心)
6)你能否一眼看出结果? 7)是否见过形式上稍有不同的题目? 8) 你是否知道与此有关的题目,是否知道用得上的定 义,定理公式? 9) 有一个与你现在的题目有关且你已解过的题目,你 能利用它吗? 10) 已知条件A,B,C……可否转化?可否建立一个等式或 不等式? 11) 你能否引入辅助元素? 12) 如果你不能解这个题,可先解一个有关的题,你能 否想出一个较易下手的,较一般的,特殊的,类似的题?
解题必须实践
• 解题是一种实践性的技能，就像游泳、滑 雪或弹钢琴一样，只能通过模仿和实践学 到它……你想学会游泳，你就必须下水，你 想成为解题的能手，你就必须去解题． ——波利亚 • 学习数学要做到熟练化．熟能生巧，进而 出神入化．而要这样，就必须练。 ——华罗庚
问题的种类
• 按数学内容来分，可以分成几何、代数、数 论(算术)、组合数学等． • 按问题的结论来分，可以分为计算题、求解 题、证明题． • 从形式上分，有选择题、填充题、综合题． • 从与已有经验关系分，有固定模式、没有或 较少固定模式．
• 图中D是小镇，E是傍晚休息处．D、E之间 的距离是 400千米．EB是CE的二分之一， AD是AC的三分之一，AC比CB多100千 米．求AB的长．
A D C E B
弄清问题
• 实际上，改变问题的提法已不仅是弄清题 意，可以说是向问题的解决进了一大步． • 波利亚主张‚不断地变换你的问题‛， ‚我们必须一再地变化它，重新叙述它， 变换它，直到最后成功地找到某些有用的 东西为止‛．
波利亚“怎样解题表”的研读与实践
波利亚“怎样解题表”的研读与实践乔治·波利亚（George Polya，1887—1985）是20世纪杰出的数学家、伟大的数学教育家、享有国际盛誉的数学方法论大师。
波利亚十分重视解题在数学教学中的作用，为了回答“一个好的解法是如何想出来的”这个令人困惑的问题，他对解题的思维过程进行了多年的专门研究和实践，其解题思想集中反映在他的《怎样解题》一书中，该书的核心是分解解题的思维过程得到的一张“怎样解题表”。
这张包括“弄清问题”“拟订计划”“实现计划”和“回顾”四部分内容。
弄清问题是为好念头的出现作准备；拟订计划是试图引发它；在引发之后,我们实现它；回顾此过程和求解的结果，是试图更好地利用它。
所有这一切，使得数学解题的研究摆脱了就题论题的狭窄天地，进入到规律探索的较高层次。
从解题论的观点看，这实际上是既提出了“怎样解题”又提出了“怎样学会解题”的问题。
一、波利亚的“怎样解题”表第一步：你必须弄清问题。
（弄清问题）(1)已知是什么？未知是什么？条件是什么？满足条件是否可能？要确定未知数，条件是否充分？或者它是否不充分？或者是多余的？或者是矛盾的？(2)画张图，将已知标上。
(3)引入适当的符号。
(4)把条件的各个部分分开，你能否把它们写下来？第二步：找出已知与未知的联系(如果找不出直接的联系，你可能不得不考虑辅助问题。
你应该最终得出一个求解的计划)。
(制订计划)(1)你以前见过它吗？你是否见过相同的问题而形式稍有不同？(2)你是否知道与此有关的问题？你是否知道一个可能用得上的定理？(3)看着未知数！试想出一个具有相同未知数或相似未知数的熟悉的问题。
(4)这里有一个与你现在的问题有关，且早已解决的问题。
你能不能利用它？你能利用它的结果吗？你能利用它的方法吗？为了能利用它，你是否应该引入某些辅助元素？你能不能重新叙述这个问题？你能不能用不同的方法重新叙述它？(5)回到定义去。
(6)你能否解决问题的一部分？如果你不能解决所提出的问题，可先解决一个与此有关的问题。
波利亚四步解题法
波利亚四步解题法1. 什么是波利亚四步解题法？波利亚四步解题法（Polya’s Four-Step Problem Solving Method）是由匈牙利数学家乔治·波利亚（George Pólya）提出的一种解决问题的方法。
这个方法适用于各种领域的问题，包括数学、科学、工程等。
波利亚四步解题法的核心思想是通过有序、系统的方式来解决问题，以确保每个步骤都得到适当的考虑和分析。
这种方法强调了问题解决过程中的创造性思维和灵活性，而不仅仅是机械地应用公式和算法。
2. 波利亚四步解题法的四个步骤2.1 理解问题（Understand the problem）在解决任何问题之前，首先需要全面理解问题的要求和限制。
这包括明确问题所涉及的概念、条件和目标。
在这一步骤中，可以通过以下几个方面来帮助理解问题：•仔细阅读问题陈述，并将其转化为自己理解的语言。
•将关键信息提取出来，并进行归纳总结。
•确定问题的目标和要求，明确需要解决的具体内容。
理解问题的过程中，可以使用思维导图、流程图等工具来帮助整理和梳理思路。
2.2 制定计划（Devise a plan）在理解问题之后，接下来需要制定解决问题的计划。
这个步骤是一个关键的思考过程，它要求我们考虑使用哪些方法、公式或算法来解决问题。
以下是一些常见的解题策略：•找出类似的问题，并尝试将其应用到当前问题上。
•将大问题分解为小问题，并逐一解决。
•使用图表、模型或示意图来帮助理清思路。
制定计划时，可以尝试不同的方法和角度，寻找最适合自己的解题策略。
2.3 执行计划（Carry out the plan）在制定好计划之后，就可以开始执行计划了。
这一步骤是具体操作和计算的过程。
根据制定的计划，按照一步一步地进行操作，直到得出最终结果。
在执行计划时，需要注意以下几点：•确保每个步骤都正确无误地执行。
•保持记录和注释，以便追溯和复查。
•尝试不同的方法和技巧，以获得更好的结果。
(完整版)波利亚的解题理论
波利亚的解题理论一、波利亚的生平及主要著作对于我们数学学习者而言，大多都有过这样的经历：一道题，自己怎么想也想不出解法，而老师却给出了一个绝妙的解法。
这时候，我们最想知道“老师是怎么想出这个解法的”，如果这个解法不是很难，我们也许会问“自己完全可以想出，但为什么我没有想到呢？”要回答这个问题，实际上牵涉到对揭发数学问题解决规律的深入研究。
综观历史来看，美籍匈牙利数学家乔治。
波利亚（George Polya，1887-1985）不仅对上述问题特别感兴趣，而且在该领域做出了许多奠基性的工作。
波利亚是法国科学院，美国科学院和匈牙利科学院的院士，1887年出生在匈牙利，青年时期曾在布达佩斯、维也纳、哥廷根、巴黎等地攻读数学、物理和哲学，获博士学位。
1914年在苏黎世著名的瑞士联邦理工学院任教。
1940年移居美国，1942年起任美国斯坦福大学教授。
他一生发表200多篇论文和许多专著。
他在数学的广阔领域内有精深的造诣，对实变函数、复变函数、组合论、概率论、数论、几何等若干分支领域都做出了开创性的贡献，一些术语和定理都以他的命名。
由于他在数学教育方面所取得的成就和对世界数学教育所产生的影响，在他93岁高龄时，还被ICME（国际数学教育大会）聘为名誉主席。
《怎样解题》（1944），《数学的发展》（1945）和《数学与猜想》（1961）这三本书就是他智慧的结晶。
这些书被译成很多国家的文字出版，其中《怎样解题》一书被译成17种文字，仅平装本就销售了100万册以上。
著名数学家范。
德。
瓦尔登1952年2月2日在瑞士苏黎世大学的会议致辞中说：“每个大学生，每个学者，特别是每个老师都应该都读读这本引人入胜的书”。
这些书成了世界范围内的数学教育名著，对数学教育产生了深刻的影响。
二、波利亚对数学教育的基本看法波利亚对于数学教育的目的、价值、方法非常关注。
他认为，“中小学生到底为什么要学习数学？要学什么样的数学？通过什么途径学好数学？”具体一点就是，在中小学阶段，是以“学数学”为主呢，还是以学如何“用数学”为主呢？这一点必须弄清楚。
《波利亚解题理论》
• 这就要求教师要做到：
五 对波利亚“怎样解题”表的评 价
• 波利亚“怎样解题”表具有巨大的理论价 值。解题表中不仅蕴含着重要的思想方 法——化归、变换的思想方法，而且是各 种数学思想方法的源泉，在教学中利用解 题表，学生的自学能力有较快的提高，独 立思考校和进行创造性活动的能力也逐步 增强。 。
六 波利亚《怎样解题》启示
——你可以改述这个问题吗?回到定义！ ——你若能解决这个问题，试先解决 一个有关的问题。你能想出一个更 容易着手的有关问题吗？一个更一 般的问题？一个更特殊的问题？一 个类似的问题？你能解决问题的一 部分吗？ ——你用了全部的计划 ——实行你的解决计划，校核每一步骤。
（一）必须了解问题 ——未知数是什么？已知数是什么？ 条件是什么？ ——可能满足什么条件 ——画一个图，引入适当的符号。
拟订计划
（二）找出已知数和未知数之间的 关系。假使你不能找出关系，就得 考虑辅助问题，最后应该想出一个 计划。
——你以前见过它吗？ ——你知道什么有关的问题吗？ ——注视未知数!试想出一个有相同 或相似的未知数的熟悉问题。
讲解 第三步：实现计划: • 证明: 过直线a任作一个平面γ, 和平面α相交于直 线b 直线a∥平面α a∥b 直线a ⊥平面β b⊥平面β
γ β
a b
α
而平面α过直线b，则 平面α⊥平面β. • 检查：直线和平面平行的性质定理， 直线和直线 平行的性质定理，平面和平面垂直的判定定理， 三个定理清晰保证每步成立。
波利亚解题理论
波利亚的怎样解题表陕西师范大学罗增儒罗新兵１乔治·波利亚乔治·波利亚(George Polya，1887～1985)是美籍匈牙利数学家、数学教育家．在解题方面，是数学启发法(指关于发现和发明的方法和规律，亦译为探索法)现代研究的先驱．由于他在数学教育方面取得的成就和对世界数学教育所产生的影响，在他93岁高龄时，还被ＩＣＭＥ（国际数学教育大会）聘为名誉主席．作为一个数学家，波利亚在函数论、变分法、概率、数论、组合数学、计算和应用数学等众多领域，都做出了开创性的贡献，留下了以“波利亚”命名的定理或术语；他与其他数学家合著的《数学分析中的问题和定理》、《不等式》、《数学物理中的等周问题》、《复变量》等书堪称经典；而以200多篇论文构成的四大卷文集，在未来的许多年里，将是研究生攻读的内容．作为一个数学教育家，波利亚的主要贡献集中体现在《怎样解题》(1945年)、《数学与似真推理》(1954年)、《数学的发现》(1962年)三部世界名著上，涉及“解题理论”、“解题教学”、“教师培训”三个领域．波利亚对数学解题理论的建设主要是通过“怎样解题”表来实现的，而在尔后的著作中有所发展，也在“解题讲习班”中对教师现身说法．他的著作把传统的单纯解题发展为通过解题获得新知识和新技能的学习过程，他的目标不是找出可以机械地用于解决一切问题的“万能方法”，而是希望通过对于解题过程的深入分析，特别是由已有的成功实践，总结出一般的方法或模式，使得在以后的解题中可以起到启发的作用．他所总结的模式和方法，包括笛卡儿模式、递归模式、叠加模式、分解与组合方法、一般化与特殊化方法、从后往前推、设立次目标、归纳与类比、考虑相关辅助问题、对问题进行变形等，都在解题中行之有效．尤其有特色的是，他将上述的模式与方法设计在一张解题表中，并通过一系列的问句或建议表达出来，使得更有启发意义．著名数学家互尔登在瑞士苏黎世大学的会议致词中说过：“每个大学生、每个学者、特别是每个教师都应该读这本引人入胜的书”(1952年2月2日)．２怎样解题表波利亚是围绕“怎样解题”、“怎样学会解题”来开展数学启发法研究的，这首先表明其对“问题解决”重要性的突出强调，同时也表明其对“问题解决”研究兴趣集中在启发法上．波利亚在风靡世界的《怎样解题》（被译成14种文字）一书中给出的“怎样解题表”，正是一部“启发法小词典”．２．１“怎样解题”表的呈现弄清问题第一，你必须弄清问题未知是什么?已知是什么?条件是什么?满足条件是否可能?要确定未知，条件是否充分?或者它是否不充分?或者是多余的?或者是矛盾的?画张图，引入适当的符号．把条件的各个部分分开．你能否把它们写下来?拟定计划第二，找出已知数与未知数之间的联系．如果找不出直接的联系，你可能不得不考虑辅助问题．你应该最终得出一个求解的计划你以前见过它吗?你是否见过相同的问题而形式稍有不同?你是否知道与此有关的问题?你是否知道一个可能用得上的定理?看着未知数，试想出一个具有相同未知数或相似未知数的熟悉的问题．这里有一个与你现在的问题有关，且早已解决的问题．你能不能利用它?你能利用它的结果吗?你能利用它的方法吗?为了能利用它，你是否应该引入某些辅助元素?你能不能重新叙述这个问题?你能不能用不同的方法重新叙述它?回到定义去．如果你不能解决所提出的问题，可先解决一个与此有关的问题．你能不能想出一个更容易着手的有关问题?一个更普遍的问题?一个更特殊的问题?一个类比的问题?你能否解决这个问题的一部分?仅仅保持条件的一部分而舍去其余部分．这样对于未知数能确定到什么程度?它会怎样变化?你能不能从已知数据导出某些有用的东西?你能不能想出适合于确定未知数的其他数据?如果需要的话，你能不能改变未知数或数据，或者二者都改变，以使新未知数和新数据彼此更接近?你是否利用了所有的已知数据?你是否利用了整个条件?你是否考虑了包含在问题中的必要的概念?实现计划第三，实行你的计划实现你的求解计划，检验每一步骤．你能否清楚地看出这一步骤是正确的?你能否证明这一步骤是正确的?回顾第四，验算所得到的解．你能否检验这个论证?你能否用别的方法导出这个结果?你能不能一下子看出它来?你能不能把这一结果或方法用于其他的问题?下面是实践波利亚解题表的一个示例，能够展示波利亚解题风格的心路历程，娓娓道来，栩栩如生．２．２“怎样解题”表的实践例1给定正四棱台的高h，上底的一条边长a和下底的一条边长b，求正四棱台的体积F．(学生已学过棱柱、棱锥的体积)讲解第一，弄清问题．问题1．你要求解的是什么?要求解的是几何体的体积，在思维中的位置用一个单点F象征性地表示出来(图1)．问题2．你有些什么?一方面是题目条件中给出的3个已知量a、b、h；另一方面是已学过棱柱、棱锥的体积公式，并积累有求体积公式的初步经验．把已知的三个量添到图示处(图2)，就得到新添的三个点a、b、h；它们与F之间有一条鸿沟，象征问题尚未解决，我们的任务就是将未知量与已知量联系起来．第二，拟定计划．问题3．怎样才能求得F?由于我们已经知道棱柱、棱锥的体积公式，而棱台的几何结构(棱台的定义)告诉我们，棱台是“用一个平行于底面的平面去截棱锥”，从一个大棱锥中截去一个小棱锥所生成的．如果知道了相应两棱锥的体积B和A，我们就能求出棱台的体积Ｆ＝Ｂ－Ａ．① 我们在图示上引进两个新的点A和B，用斜线把它们与F联结起来，以此表示这三个量之间的联系(图3，即①式的几何图示)．这就把求F转化为求A、B．图3问题4．怎样才能求得A与B?依据棱锥的体积公式(V＝13Ｓｈ)，底面积可由已知条件直接求得，关键是如何求出两个棱锥的高．并且，一旦求出小棱锥的高x，大棱锥的高也就求出，为ｘ＋ｈ．我们在图示上引进一个新的点x，用斜线把A与x、ａ连结起来，表示A能由a、ｘ得出，A ＝13ａ2ｘ；类似地，用斜线把B 与b 、ｈ、ｘ连结起来，表示B 可由ｂ、ｈ、ｘ得出，Ｂ＝13ｂ2（ｘ＋ｈ）(图4)，这就把求A 、B 转化为求x ．图4问题5．怎样才能求得x ？为了使未知数x 与已知数a 、ｂ、ｈ联系起来，建立起一个等量关系．我们调动处理立体几何问题的基本经验，进行“平面化”的思考．用一个通过高线以及底面一边上中点(图5中，点Q)的平面去截两个棱锥，在这个截面上有两个相似三角形能把a 、b 、h 、x 联系起来(转化为平面几何问题)，由△ＶＰＯ1∽△ＶＱＯ2得图5x a x h b =+②这就将一个几何问题最终转化为代数方程的求解．解方程②，便可由a 、b 、h 表示x,在图示中便可用斜线将x 与ａ、ｂ、h 连结起来．至此，我们已在F 与已知数a 、b 、h 之间建立起了一个不中断的联络网，解题思路全部沟通．第三，实现计划．作辅助线(过程略)如图5，由相似三角形的性质，得x a x h b =+，解得x=ah b a-． 进而得两锥体的体积为Ａ＝13ａ2x ＝13·3a h b a-，Ｂ＝13ｂ2（ｘ＋ｈ）＝13·3b hb a-，得棱台体积为Ｆ＝Ｂ－Ａ＝13·33()b a hb a--＝13（a2＋ab＋b2）h．③第四，回顾．(1)正面检验每一步，推理是有效的，演算是准确的．再作特殊性检验，令ａ→０，由③可得正四棱锥体的体积公式；令ａ→ｂ，由③可得正四棱柱体的体积公式．这既反映了新知识与原有知识的相容性，又显示出棱台体积公式的一般性；这既沟通了三类几何体极限状态间的知识联系，又可增进三个体积公式的联系记忆．(2)回顾这个解题过程可以看到，解题首先要弄清题意，从中捕捉有用的信息(如图1所示，有棱台，a、b、h、F共5条信息)，同时又要及时提取记忆网络中的有关信息(如回想：棱台的定义、棱锥的体积公式、相似三角形的性质定理、反映几何结构的运算、调动求解立体几何问题的经验积累等不下6条信息)，并相应将两组信息资源作合乎逻辑的有效组合．这当中，起调控作用的关键是如何去构思出一个成功的计划(包括解题策略)．由这一案例，每一个解题者还可以根据自己的知识经验各自进一步领悟关于如何制定计划的普遍建议或模式．(3)在解题方法上，这个案例是分析法的一次成功应用，从结论出发由后往前找成立的充分条件．为了求F，我们只需求A、B(由棱台体积到棱锥体积的转化——由未知到已知，化归)；为了求A、B，我们只需求x(由体积计算到线段计算的转化——由复杂到简单，降维)；为了求x，我们只需建立关于x的方程(由几何到代数的转化——数形结合)；最后，解方程求x，解题的思路就畅通了，在当初各自孤立而空旷的画面上(图1)，形成了一个联接未知与已知间的不中断网络(图5)，书写只不过是循相反次序将网络图作一叙述．这个过程显示了分析与综合的关系，“分析自然先行，综合后继；分析是创造，综合是执行；分析是制定一个计划，综合是执行这个计划”．(4)在思维策略上，这个案例是“三层次解决”的一次成功应用．首先是一般性解决(策略水平上的解决)，把F转化为A，B的求解（Ｆ＝Ａ－Ｂ），就明确了解题的总体方向；其次是功能性解决(方法水平的解决)，发挥组合与分解、相似形、解方程等方法的解题功能；最后是特殊性解决(技能水平的解决)，比如按照棱台的几何结构作图、添辅助线找出相似三角形、求出方程的解、具体演算体积公式等，是对推理步骤和运算细节作实际完成．(5)在心理机制上，这个案例呈现出“激活——扩散”的基本过程．首先在正四棱台(条件)求体积(结论)的启引下，激活了记忆网络中棱台的几何结构和棱锥的体积公式，然后，沿着体积计算的接线向外扩散，依次激活截面知识、相似三角形知识、解方程知识(参见图1～图5)，……直到条件与结论之间的网络沟通．这种“扩散——激活”的观点，正是数学证明思维中心理过程的一种解释．(6)在立体几何学科方法上，这是“组合与分解”的一次成功应用．首先把棱台补充(组合)为棱锥，然后再把棱锥截成(分解)棱台并作出截面，这种做法在求棱锥体积时曾经用过(先组合成一个棱柱、再分解为三个棱锥)，它又一次向我们展示“能割善补”是解决立体几何问题的一个诀窍，而“平面化”的思考则是沟通立体几何与平面几何联系的一座重要桥梁．这些都可以用于求解其他立体几何问题，并且作为一般化的思想(化归、降维)还可以用于其他学科．(7)“你能否用别的方法导出这个结果?”在信念上我们应该永远而坚定地做出肯定的回答，操作上未实现只是能力问题或暂时现象．对于本例，按照化棱台为棱锥的同样想法，可以有下面的解法．如图6，正四棱台ABCD-Ａ1Ｂ1Ｃ1Ｄ1中，连结DA 1，ＤB 1，ＤＣ1，ＤＢ，将其分成三个四棱锥Ｄ-Ａ1Ｂ1Ｃ1Ｄ1，Ｄ-ＡＡ1Ｂ1Ｂ，Ｄ-ＢＢ1Ｃ1Ｃ，其中1111D A B C D V -＝13b 2ｈ， 11D AA B B V -＝11D BB C C V -．（等底等高)图6 图7 为了求11D AA B B V -，我们连结A Ｂ1，将其分为两个三棱锥Ｄ-ＡＢＢ1与Ｄ-ＡＡ1Ｂ1（图7），因11AA B S ∆＝b a1ABB S ∆， 故11D AA B B V -＝b a1D ABB V -， 但1D ABB V -＝1B ABD V -＝13·12ａ2·ｈ＝16a 2ｈ， 故11D AA B B V -＝1D ABB V -＋11D AA B V -＝16a 2ｈ＋b a ·16a 2ｈ＝16(a 2＋ａｂ)ｈ． 从而1111ABC D A B C D V -＝11D AA B B V -＋11D BB C C V -＋1111D A B C D V -＝16 (a 2＋ａｂ)ｈ＋16 (a 2＋ａｂ)ｈ＋13b 2ｈ ＝13（a 2＋ab ＋b 2）h ．(8)“你能不能把这一结果或方法用于其他问题?”能，至少我们可以由正四棱台体积公式一般化为棱台体积公式(方法是一样的)．注意到a2＝Ｓ1，b2＝Ｓ2，ａｂ＝12S S，可一般化猜想棱台的体积公式为Ｖ台＝13(Ｓ1＋12S S＋Ｓ2)ｈ．３波利亚的解题观对于波利亚的怎样解题表及有关著作，人们从不同的角度阐发了对波利亚解题思想的认识(见参考文献)，我们将其归结为5个要点．３．１程序化的解题系统怎样解题表，就“怎样解题”、“教师应教学生做些什么”等问题，把“解题中典型有用的智力活动”，按照正常人解决问题时思维的自然过程分成四个阶段——弄清问题、拟定计划、实现计划、回顾，从而描绘出解题理论的一个总体轮廓，也组成了一个完整的解题教学系统．既体现常识性，又体现由常识上升为理论(普遍性)的自觉努力．这四个阶段首先是一个四步骤的宏观解题程序，其中“实现计划”虽为主体工作，但较为容易完成，是思路打通之后具体实施信息资源的逻辑配置，“我们所需要的只是耐心”；其次，“弄清问题”是认识问题、并对问题进行表征的过程，应成为成功解决问题的一个必要前提；与前两者相比，“回顾”是最容易被忽视的阶段，波利亚将其作为解题的必要环节而固定下来，是一个有远见的做法，在整个解题表中“拟定计划”是关键环节和核心内容．“拟定计划”的过程是在“过去的经验和已有的知识”基础上，探索解题思路的发现过程，波利亚的建议是分两步走：第一，努力在已知与未知之间找出直接的联系(模式识别等)；第二，如果找不出直接的联系，就对原来的问题做出某些必要的变更或修改，引进辅助问题，为此，波利亚又进一步建议：看着未知数，回到定义去，重新表述问题，考虑相关问题，分解或重新组合，特殊化，一般化，类比等，积极诱发念头，努力变化问题．这实际上是阐述和应用解题策略并进行资源的提取与分配．于是，这个系统就集解题程序、解题基础、解题策略、解题方法等于一身，融理论与实践于一体．３．２启发式的过程分析(1)还在当学生的时候，波利亚就有一个问题一再使他感到困惑：“是的，这个解答好像还行，它看起来是正确的，但怎样才能想出这样的解答呢?是的，这个实验好像还行，它看起来是个事实，但别人是怎样发现这样的事实?而且我自己怎样才能想出或发现它们呢?”从解题论的观点看，这实际上是既提出了“怎样解题”又提出了“怎样学会解题”的问题，波利亚说，这“终于导致他写出本书”(指《怎样解题》)．波利亚认为“数学有两个侧面”，“用欧几里得方式提出来的数学看来像是一门系统的演绎科学；但在创造过程中的数学看来却像是一门实验性的归纳科学．这两个侧面都像数学本身一样古老．但从某一点说来，第二个侧面则是新的，因为以前从来就没有‘照本宣科’地把处于发现过程中的数学照原样提供给学生，或教师自己，或公众．”他以数十年的时间悉心研究数学启发法，其“怎样解题”的基本思想就可以概括为“知识＋启发法”．在解题表中，波利亚给出了“启发法小词典”，让读者通过阅读词典来开阔思路、指导实践，自己学会怎样解题．这些看法来源于波利亚对数学教育宗旨的认识，波利亚认为，数学教育应“教会年轻人去思考”，培养学生的“独立性、能动性和创新精神”；他认为一个人在学校所受的教育应该受益终生，他赞成，良好的教育应该“系统地给学生自己发现事物的机会”，“应该帮助学生自己再发现所教的内容”，“学东西的最好途径是亲自去发现它”；他特别重视发展学生的数学思维能力，强调数学教学要加强思维训练，要发展学生运用所学知识的能力，发展技能、技巧、有益的思考方式和科学的思维习惯，他反复指出，数学教育的目的不仅仅是传授知识，还要“发展学生本身的内蕴能力”．教师要“教学生证明问题”，也要“教他们猜想问题”．波利亚提出“合情推理”的概念，号召：“让我们教猜想吧!”(2)在解题表的展开中，波利亚则通过剖析典型例题的思维过程来研究“发现和发明的方法和规律”．波利亚不断地提问、不断地建议，“怎样才能想出这样的解答呢?”“我自己怎样才能想出或发现它们呢?”既驱使人们去分析解题过程，又要求人们去总结发现的规律．波利亚在《数学的发现》序言中提出：“领会方法的最佳时机，可能是读者解出一道题的时候，或是阅读它的解法的时候，也可能是阅读解法形成过程的时候”．波利亚书中的例题，其实就是对典型例题进行解题过程的分析，就是暴露数学解题的思维过程，也就是教人“怎样学会解题”．在例1中，数学操作与思维开展相结合的图解或阐释，使我们既领会到了这样的意图，也见到了这样的行动．波利亚对解题过程淋漓尽致的剖析，实质上已接触到心理层面，但没有用到多少教育学或思维学的相关名词，基本上都是其数学前沿研究中切身体验的自然流露，数学功底和过程体验发挥了重要作用．这正是数学家研究数学教育的优势，处处有数学的“真刀真枪”，绝非“纸上谈兵”．波利亚说“货源充足和组织良好的知识仓库是一个解题者的重要资本”，在“知识”与“组织良好”之间，波利亚更强调后者，他说“良好的组织使得所提供的知识易于用上，这甚至可能比知识的广泛更为重要．”用现在的话来说，波利亚在这里强调了“原有的知识经验”和“优化的认知结构”对问题解决的基础作用．３．３开放型的念头诱发．波利亚解释说：“我们表中的问题和建议并不直接提到念头；但实际上，所有的问题和建议都与它有关(可以说解题表中的每一个问句，都是从认知或元认知的角度向读者启发解题念头．），弄清问题是为好念头的出现做准备；拟订计划是试图引发它；在引发之后，我们实现它；回顾此过程和求解的结果，我们试图更好地利用它．”他强调指出：“老师为学生所能做的最大的好事是通过比较自然的帮助，促使他自己想出一个好念头．”在《怎样解题》一书里，出现“念头”这个词不下四五十次．念头有什么用?波利亚说：“它会给你指出整个或部分解题途径”．“也许有些念头会把你引入歧途”，但这并不可怕，“在明显失败的尝试和一度犹豫不决之后”会“突然闪出一个‘好念头’”，最糟糕的是没有任何念头，还“笨头呆脑地干等着某个念头的降临，而不会做任何事情去加速其来到．”这里说的念头不仅在字面上比“问题表征”更为浅白，而且在内涵上更为丰富，其实质是开展积极活跃的思维活动，产生念头与找出解题途径完全可以理解为同义语．那么产生念头的基础是什么呢?波利亚的回答是：“过去的经验和已有的知识”．(解题力量)“如果我们对该论题知识贫乏，是不容易产生好念头的．如果我们完全没有知识，则根本不可能产生好念头．”波利亚一再提到“好念头”，其实这就是直觉、顿悟或灵感，“想出一个好念头是一种‘灵感运动’”，“想像力有了一个突然的跳跃，产生了一个好念头，这是天才的一次闪烁”，“是我们观点上的重大突变，我们看问题方式的一个骤然变动，在解题步骤方面的一个刚刚露头的有信心的预感”．波利亚关于念头的种种议论，正是开展积极思维活动的激发与激活．３．４探索性的问题转换这里说的“问题转换”，在《怎样解题》一书中亦叫“变化问题”、“题目变更”，它揭示了探索解题思路的数学途径，也体现了解题策略的实际运用．波利亚强调：“解题的成功要靠正确思路的选择，要靠从可以接近它的方向去攻击堡垒，为了找出哪个方面是正确的方面，哪一侧是好接近的一侧，我们从各个方面、各个侧面去试验，我们变更问题．”“变化问题使我们引进了新的内容，从而产生了新的接触，产生了和我们有关的元素接触的新可能性．”“新问题展现了接触我们以前知识的新可能性，它使我们做出有用接触的希望死而复苏．通过变化问题，显露它的某个新方面，新问题使我们的兴趣油然而生”．在“怎样解题”表中，波利亚拟出了启引我们不断转换问题的30多个问句或建议：把问题转化为一个等价的问题，把原问题化归为一个已解决的问题，去考虑一个可能相关的问题，先解决一个更特殊的问题、或更一般的问题、或类似的问题……那些启发新念头的问句，也往往与问题转换有关．“如果我们不用‘题目变更’，几乎是不能有什么进展的”——这就是波利亚的结论．３．５朴素的数学解题元认知观念．元认知是对认知的再认知，包括元认知知识，元认知体验和元认知监控．虽然元认知概念提出较晚，但元认知思想早就存在，在波利亚的解题思想中存在着朴素的元认知观念．波利亚解题表的大量问句或建议，都不是问别人，而是自己给自己提问题、提建议，这是解题者的自我诘问、自我反思．问题中的一部分，其对象针对具体的数学内容，属于认知性的；另一部分则以解题者自身为对象，属于元认知性的．比如，“你以前见过它吗?”“你是否知道一个与此有关的问题?”“这里有一个与你现在的问题有关，且早已解决的问题．你能不能利用它?”等等，都不涉及问题的具体内容，都是针对解题主体、对其解题思维活动的反思，都属于元认知提问，而不完全是认知提问．波利亚解题表中的“回顾”也并不完全是常规解题中的“检验”，主要是有分析地领会所得的解法(参见例1的回顾)，它包含着把“问题及其解法”(认知)作为对象进行自觉反思的元认知意图．至于解题表本身所给出的解题程序(一种程序性知识)，所体现的解题策略(一种策略性知识)及所进行的元认知提问，都属于元认知知识．波利亚对具体范例的分析，基本上是对“问题及其解法”的再认知，已反映出开发元认知的朴素意图．波利亚的另一些问句，如“你能不能重新叙述这个问题?你能不能用不同的方法重新叙述它?”“你能不能改变未知数或数据，或者二者都改变，以使新未知数和新数据彼此更接近?”(接近度)，“你能不能一下子看出它来?”(题感)等，则属于朴素的元认知体验．至于解题表本身，则自始至终体现着元认知调控．综上所述，“解题系统”是波利亚解题思想的整体框架，“分析解题过程”是波利亚解题思想的思维实质，“念头诱发”是波利亚解题思想的外在表现，“问题转换”是波利亚解题思想的具体实现，朴素的元认知观念是波利亚解题思想的心理学基础．而这一切的背后，丰富的数学前沿研究经历和发现体验是波利亚解题思想的物质基础，现代启发法是波利亚解题思想的灵魂，揭示“发现和发明的方法和规律”是波利亚解题思想的目标．４波利亚解题研究的发展４．１反思数学上存在证明的方法与发现的方法，在逻辑实证主义占主导地位的历史时期，关于数学发现方法的研究一度陷于停顿，波利亚的贡献就在于自觉承担起复兴数学启发法的重任，并提出合情推理，为数学启发法的现代研究提供了必要基础．20世纪80年代初期，美国数学教育界兴起的“问题解决”研究是对波利亚现代启发法的直接继承，曾经有“对波利亚的重新发现”、“数学启发法…几乎成了问题解决的同义词”等提法．但是，已有数学实践却未能获得预期的成功，尽管学生已经具备了必要的数学知识，也已经了解了相关的方法原则，或者说已执行了解题表的建议，却仍不能有效地解决问题，这不能不引起数学教育界的反思．(1)波利亚构建的“四阶段”解题系统具有开创性的意义，但局限于“四阶段”对学会。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
日)．
波利亚及其解题理论
回答“一个好的解法是如何想出来的”这个令人困惑的问题，
波利亚致力于解题的研究，专门研究了解题的思维过程，并把
研究所得写成《怎样解题》一书。 核心是《怎样解题》表，他把寻找并发现解法的思维过程分解
为五条建议和23个具有启发性的问题，它们就好比是寻找和发
波利亚及其解题理论
作为一个数学教育家，波利亚的主要贡
献集中体现在《怎样解题》(1945年)、 《数学与似真推理》(1954年)、《数学 的发现》(1962年)三部世界名著上，涉 及“解题理论”、“解题教学”、“教 师培训”三个领域．波利亚对数学解题 理论的建设主要是通过“怎样解题”表 来实现的。著名数学家互尔登在瑞士苏 黎世大学的会议致词中说过：“每个大 学生、每个学者、特别是每个教师都应 该读这本引人入胜的书”(1952年2月2
现解法的思维过程的“慢动作镜头”，使我们对解题的思维过 程看得见，摸得着。 变换,推广, 类比,作出新 的数学发现. 概括方法论 因素,建立数 学模型.
弄 清 题 意
拟 定 计 划
ቤተ መጻሕፍቲ ባይዱ
执 行 计 划
检 验 回 顾
波利亚的教育思想
数学教学的目的应当是提高学生的一般素养：首 先和主要的目标应当是教会青年思考。
教什么样的思考?数学是什么?数学有什么特点?
对数学及其意义的认识决定性的作用。 教有目的的思考,教正规的演绎推理，也教非正 规的似真的合情推理。
四部曲
改善学生数学解题中的元认知的教学策略
问题与思考
• 设计一个解决某类问题的解题表． • 根据你的解题经历，选一个典型例子，详细介绍 解题的具体过程． • 实践解题表，求解下题：如果3个有相同半径的 圆过一点，则通过它们的另外3个交点的圆具有 相同的半径． • 对解题表，谈谈你想说的任何看法，写一篇不少 于1000字的小论文． • 基于波利亚的解题理论谈数学解题教学