5.3任意角的正弦函数,余弦函数,正切函数 ppt课件
合集下载
中职教育-数学(基础模块)上册课件:第5章 三角函数.ppt

(4)奇偶性
正弦曲线关于原点O中心对称,因此正弦函数y=sin x是奇 函数.
(5)单调性
当x由-π/2增大到π/2时,正弦曲线逐渐上升,y=sin x的 值由-1增大到1;当x由π/2增大到3π/2时,正弦曲线逐渐下降, y=sin x的值由1减小到-1.
根据周期性可知,正弦函数在每一个区间
[-π/2+2kπ, π/2+2kπ](k∈Z)上都是增函数,其函数值 由-1增大到1;在每一个区间[π/2+2kπ,3π/2+2kπ](k∈Z)
学习目标:了解角的概念推广,理解弧度制的概念和意义, 理解任意角的正弦函数、余弦函数和正切函数;掌握利用计算 器求三角函数的值,理解同角三角函数的基本关系,了解诱导 公式的推导及简单应用,理解正弦函数的图像和性质;了解余 弦函数的图像和性质,掌握利用计算器求角度;了解“已知一 个角的三角函数值,求在指定范围内的角”的方法。
因此,所有与30°角终边相同的角(包括30°角),都 可以表示成30°与360°的整数倍的和,即都可以写成
30°+k ▪360°(k∈Z)的形式.所以,与30°角终边相
同的角的集合为
{β| β=30°+k ▪360°(k∈Z) }.
一般地,所有与角α终边相同的角(包括角α在内)都可
以写成α+k ▪360°(k∈Z)的形式,它们所组成的集合为 {β| β=α+k ▪360°(k∈Z) }
r
r
x
图5-8
根据相似三角形的知识,对于每一个确定的角α,其正弦、 余弦和正切(当x≠0时)的值都是唯一确定的,而与点P在角α 终边上的位置无关.
因此,正弦、余弦和正切都是以角α为自变量的函数,分 别称为角α的正弦函数、余弦函数和正切函数,它们都是角α的 三角函数.
正弦曲线关于原点O中心对称,因此正弦函数y=sin x是奇 函数.
(5)单调性
当x由-π/2增大到π/2时,正弦曲线逐渐上升,y=sin x的 值由-1增大到1;当x由π/2增大到3π/2时,正弦曲线逐渐下降, y=sin x的值由1减小到-1.
根据周期性可知,正弦函数在每一个区间
[-π/2+2kπ, π/2+2kπ](k∈Z)上都是增函数,其函数值 由-1增大到1;在每一个区间[π/2+2kπ,3π/2+2kπ](k∈Z)
学习目标:了解角的概念推广,理解弧度制的概念和意义, 理解任意角的正弦函数、余弦函数和正切函数;掌握利用计算 器求三角函数的值,理解同角三角函数的基本关系,了解诱导 公式的推导及简单应用,理解正弦函数的图像和性质;了解余 弦函数的图像和性质,掌握利用计算器求角度;了解“已知一 个角的三角函数值,求在指定范围内的角”的方法。
因此,所有与30°角终边相同的角(包括30°角),都 可以表示成30°与360°的整数倍的和,即都可以写成
30°+k ▪360°(k∈Z)的形式.所以,与30°角终边相
同的角的集合为
{β| β=30°+k ▪360°(k∈Z) }.
一般地,所有与角α终边相同的角(包括角α在内)都可
以写成α+k ▪360°(k∈Z)的形式,它们所组成的集合为 {β| β=α+k ▪360°(k∈Z) }
r
r
x
图5-8
根据相似三角形的知识,对于每一个确定的角α,其正弦、 余弦和正切(当x≠0时)的值都是唯一确定的,而与点P在角α 终边上的位置无关.
因此,正弦、余弦和正切都是以角α为自变量的函数,分 别称为角α的正弦函数、余弦函数和正切函数,它们都是角α的 三角函数.
中职数学基础模块上册《任意角的正弦函数、余弦函数和正切函数》ppt课件

数
故故ssiinn2475327 cos 4327
0, c00o,,s 275
0,
ttaann2475327 0. 0.
巩固知识 典型例题
三
角
例3 根据条件 sin 0 且 tan 0 , 确定 是第几象限的角.
函
y
y
++
-+
数
-o - x
+o - x
sinα
tanα
三 角 函 数
应用知识 强化练习 练习5.3.2
三
应用知识 强化练习 练习5.3.3
角 1.计算:
函 数
5sin 90 2cos 0 3 tan180 cos180 ;
2.计算:
cos tan 1 tan2 sin 3 cos
2
43 3
2
计算器
三 角 函 数
归纳小结 自我反思
本次课学习 哪些内容?
你会解决 哪些新问题?
体会到哪些 学习方法?
1.判断下列角的各三角函数符号
(1)525º;(2)-235
º;(3)
19 6;(4)来自3 4.2.根据条件 sin 0 且 tan 0 ,
确定 是第几象限的角.
三 角 函 数
自我探索 使用工具
观察计算器上的按键并阅读相关的使用说明书, 小组完成计算器计算三角函数值.
sin
cos
tan
0
2
3 2
.
x
运用知识 强化练习
练习5.3.1
已知角 的终边经过点 P, 求:角 的正弦、余弦、正切值:
⑴ P(3,−4); ⑵ P(−1,2); ⑶ P( 1 , 3 ).
《三角函数的概念》PPT教学课件(第1课时三角函数的概念)

象限.
(2)先判断已知角分别是第几象限角,再确定各三角函数值的符号,最
后判断乘积的符号.
栏目导航
25
(1)C
[因为点P在第四象限,所以有tan cos
α>0, α<0,
由此可判断角α终边
在第三象限.]
(2)[解] ①∵145°是第二象限角,
∴sin 145°>0,
∵-210°=-360°+150°,
终边关于
x
轴对称,若
sin
α=15,则
交于点P(x,y), 则角β的终边与单位圆相交于点
sin β=________.
Q(x,-y),
由题意知y=sin α=15,所以sin β
=-y=-15.]
栏目导航
4.求值:(1)sin 180°+cos 90°+tan 0°. (2)cos253π+tan-154π. [解] (1)sin 180°+cos 90°+tan 0°=0+0+0=0. (2)cos253π+tan-154π =cos8π+π3+tan-4π+π4 =cosπ3+tanπ4=12+1=32.
栏目导航
24
三角函数值符号的运用
【例 2】 (1)已知点 P(tan α,cos α)在第四象限,则角 α 终边在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
(2)判断下列各式的符号:
①sin 145°cos(-210°);②sin 3·cos 4·tan 5.
[思路点拨] (1)先判断 tan α,cos α 的符号,再判断角 α 终边在第几
5.公式一
sin α cos α tan α
8
栏目导航
1.sin(-315°)的值是( )
任意角的三角函数(第二课时)PPT课件

于第一或第三象限。 因为① ②式都成立,所以角θ的终边只能位于第
三象限。 于是角θ是第三象限角。
2020年10月2日
12
(1). 若sinα=1/3,且α的终边经过点p(—1,y), 则α是第几象限的角?并求secα,tanα的值。
(答案:α为第二象限的角,sec3 2,tan2 2)
4
(2)下列四个命题中,正确的是 A.终边相同的角都相等 B.终边相同的角的三角函数相等 C.第二象限的角比第一象限的角大 D.终边相同的角的同名三角函数值相等
练习P19-4、5、6
2020年10月2日
10
例3 (1)
解: ①因为2500是第三象限的角,
所以cos 2500 <0。
②因为tan(11π/3)=tan(5π/3+2π)
=tan(5π/3),
而5π/3是第四象限角,所以
(2)
tan(11π/3)<0。
解: ①cos(9π/4)=cos(π/4+2π)
值的问题,可以转化为求0°~360° (0~2π)间角的三角函数值的问题。
2020年10月2日
9
应用举例 例 3 (1) 确定下列三角函数值的符号:
① cos2500
② tan(11π/3)
(2)求下列三角函数值: ① cos (9π/4) ② tan (-11π/6)
例4 求证,θ为第三象限角的充分必要条件是: sinθ<0 ① 且 tanθ>0 ②
2020年10月2日
1
温故知新
正弦函数、余弦函数、正切函数的定义? 正弦:sinα =MP =y/r 余弦:cosα =OM =x/r 正切:tanα=AT =y/x
三象限。 于是角θ是第三象限角。
2020年10月2日
12
(1). 若sinα=1/3,且α的终边经过点p(—1,y), 则α是第几象限的角?并求secα,tanα的值。
(答案:α为第二象限的角,sec3 2,tan2 2)
4
(2)下列四个命题中,正确的是 A.终边相同的角都相等 B.终边相同的角的三角函数相等 C.第二象限的角比第一象限的角大 D.终边相同的角的同名三角函数值相等
练习P19-4、5、6
2020年10月2日
10
例3 (1)
解: ①因为2500是第三象限的角,
所以cos 2500 <0。
②因为tan(11π/3)=tan(5π/3+2π)
=tan(5π/3),
而5π/3是第四象限角,所以
(2)
tan(11π/3)<0。
解: ①cos(9π/4)=cos(π/4+2π)
值的问题,可以转化为求0°~360° (0~2π)间角的三角函数值的问题。
2020年10月2日
9
应用举例 例 3 (1) 确定下列三角函数值的符号:
① cos2500
② tan(11π/3)
(2)求下列三角函数值: ① cos (9π/4) ② tan (-11π/6)
例4 求证,θ为第三象限角的充分必要条件是: sinθ<0 ① 且 tanθ>0 ②
2020年10月2日
1
温故知新
正弦函数、余弦函数、正切函数的定义? 正弦:sinα =MP =y/r 余弦:cosα =OM =x/r 正切:tanα=AT =y/x
单位圆与任意角的正弦余弦函数的定义课件
对于任意一个角x,每增加2π的整数倍,其正弦、余弦
函数值均不变.所以,正弦、余弦函数值均是随角的变化 呈周期性变化的.我们把这种随自变量的变化呈周期性变 化的函数叫作周期函数.有
sin(x 2k) sin x,k Z cos(x 2k) cos x,k Z
正弦函数、余弦函数是周期函数,称 2 k(k Z, k 0) 为正弦函数、余弦函数的周期.
0
1 2
2 31
22
1
3 2
2 2
1 2
0
31 0
22
1 2
1 3 -1 3
22
2
3 -1 3
2
2
10
2
1 2
0
1 2
31
2
如图,已知角x,作出2π+x
y
P(x,y) x
O
x
终边相同的角的正弦函数值相等,
即 sin(x 2k) sin x, k Z ;
终边相同的角的余弦函数值相等, 即 cos(x 2k) cos x,k Z .
设op=r,根据三角形相似可知,
sin v y yBiblioteka r x2 y2 cos v x x
r x2 y2
. P(yu,v) P'(x, y)
O M M' x
说明:①三角函数的值与点在终边上的位置无关, 仅与角的大小有关
②上式为计算正、余弦函数值的第二种方式
当α在第一、二等象限时,sinα的符号如何?cosα呢?
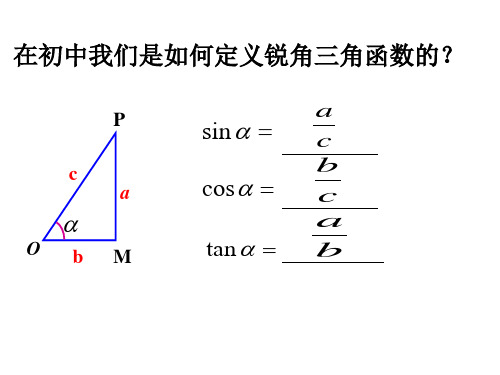
在初中我们是如何定义锐角三角函数的?
P
c a
O bM
a
sin c
b
cos c
a
tan b
新知学习
任意角的三角函数PPT优秀课件

2.确定下列三角函 符数 号值 :的
(1)sin256;
(2)cos(406);
23
(3)tan .
3
3.角 的终边 P (上 m ,5)且 ,有 co 一 sm (点 m 0),
13
求 sin co 值 s.
小结: 1.任意角的三角函数的定义; 2.三角函数的定义域; 3.正弦、余弦、正切函数的值在各象限的符号.
1.2.1任意角的三角函数(1)
问题1:你能回忆一下初中里学过的锐角三角函数(正弦, 余弦,正切)的定义吗?
在RtPO中 M
如何 将POM 放到平面直角 坐标系中?
sin PM
P
OP
co sOM OP
tanPM OM
O
M
锐角三角函数
问题2:将POM 放到平面直角坐, 标系中
87.当一切毫无希望时,我看着切石工人在他的石头上,敲击了上百次,而不见任何裂痕出现。但在第一百零一次时,石头被劈成两半。我体会到,并非那一击,而是前面的敲打使它裂开。――[贾柯·瑞斯] 88.每个意念都是一场祈祷。――[詹姆士·雷德非]
89.虚荣心很难说是一种恶行,然而一切恶行都围绕虚荣心而生,都不过是满足虚荣心的手段。――[柏格森] 90.习惯正一天天地把我们的生命变成某种定型的化石,我们的心灵正在失去自由,成为平静而没有激情的时间之流的奴隶。――[托尔斯泰]
(1)cos 7 ; (2)sin4(6)5; (3)tan11 .
12
3
解: (1) 7 是第二象限角 co, s7所 0.以
12
12
(2) 因为 4652360225,即465是第三象限角,所 sin(465)0.
(3) 因为 1125,即11 是第四象 ,所限 以角
任意三角函数的定义PPT课件

加强数形结合数学思想的培养。
情感目标:培养合作交流、独立思考等良好的个性品质;
这里没以及有打用破成“规使、敢学于生创新掌的科握学…精神…。”、 教学“重使点:学任生意角学的会正弦…、…余弦”等、正通切的常定字义。眼,保 教学障难了点:学用生单位的圆主中的体有地向线位段,表示反三角映函了数值教。法
与学法的结合,尽量体现新教材新 理念。
加强。
第5页/共40页
二. 教法分析
(二)教学方法
建构主义认为,知识是在原有知识的基础上, 在人与环境的相互作用过程中,通过同化和顺应, 使自身的认知结构得以转换和发展。元认知理论指 出,学习过程既是认识过程又是情感过程,是“知、 情、意、行的” 和谐统一。结合本节课的具体内 容,确立讨论法和启发引导法为主要教学方法。
y
T
y
P
P
O MA
A
MO
y T
M
OA
P
T y
这几条与单位圆有关的有向线段 MP,OM,AT叫做角 的正弦线,余弦线, 正切线
MA
O
P
思考:当角 的终边在x轴上或在y 轴上时这些线有何特点?
T
第21页/共40页
技能演练
演--提供范例,规范解题格式; 演--设置平台,促进讨论交流; 演--学法指导,提炼求解步骤.
示例 理解
实质
理解
直观理解侧重数学符号、图形等,培养思维的具体和简 约,体现数形结合的思想;程序理解揭示内在联系,并 为后继学习三角函数的图象和性质奠定基础;示例理解 呼应引入,强化认识;归纳理解关注归纳思维,提升综 合能力;实质理解揭示了任意角的三角函数的内涵。
第20页/共40页
(3)三角函数的一种几何表示 利用单位圆有关的有向线段,作出正弦线,余弦线,正切线
情感目标:培养合作交流、独立思考等良好的个性品质;
这里没以及有打用破成“规使、敢学于生创新掌的科握学…精神…。”、 教学“重使点:学任生意角学的会正弦…、…余弦”等、正通切的常定字义。眼,保 教学障难了点:学用生单位的圆主中的体有地向线位段,表示反三角映函了数值教。法
与学法的结合,尽量体现新教材新 理念。
加强。
第5页/共40页
二. 教法分析
(二)教学方法
建构主义认为,知识是在原有知识的基础上, 在人与环境的相互作用过程中,通过同化和顺应, 使自身的认知结构得以转换和发展。元认知理论指 出,学习过程既是认识过程又是情感过程,是“知、 情、意、行的” 和谐统一。结合本节课的具体内 容,确立讨论法和启发引导法为主要教学方法。
y
T
y
P
P
O MA
A
MO
y T
M
OA
P
T y
这几条与单位圆有关的有向线段 MP,OM,AT叫做角 的正弦线,余弦线, 正切线
MA
O
P
思考:当角 的终边在x轴上或在y 轴上时这些线有何特点?
T
第21页/共40页
技能演练
演--提供范例,规范解题格式; 演--设置平台,促进讨论交流; 演--学法指导,提炼求解步骤.
示例 理解
实质
理解
直观理解侧重数学符号、图形等,培养思维的具体和简 约,体现数形结合的思想;程序理解揭示内在联系,并 为后继学习三角函数的图象和性质奠定基础;示例理解 呼应引入,强化认识;归纳理解关注归纳思维,提升综 合能力;实质理解揭示了任意角的三角函数的内涵。
第20页/共40页
(3)三角函数的一种几何表示 利用单位圆有关的有向线段,作出正弦线,余弦线,正切线
第五章三角函数5.3任意角的正弦函数、余弦函数和正切函数分析

课程名称:《数学》第周次 授课时间:年月日
授课班级
1421班
1431班
学 时
2
课 程 类 型
理论+习题课
课题或
章节题目
第五章 三角函数
5.3任意角的正弦函数、余弦函数和正切函数
教学目标
知识目标
理解任意角的三角函数的定义及定义域,理解三角函数在各象限的正负号,掌握界限角的三角函数值
能力目标
会利用定义求任意角的三角函数值,培养学生的观察能力
解 取角的公共范围得 为第四象限的角.
通过本次课程理解任意角的三角函数的定义及定义域,理解三角函数在各象限的正负号,掌握界限角的三角函数值,会利用定义求任意角的三角函数值,培养学生的观察能力。
P114 练习1、3、4T
情感目标
结合学生生活实际,创设情境,激发兴趣
教学要求
理解任意角的三角函数的定义及定义域,理解三角函数在各象限的正负号,掌握界限角的三角函数值,会利用定义求任意角的三角函数值,培养学生的观察能力。
教学重点
任意角的三角函数的定义及定义域
教学难点
判断三角函数在各象限的正负号,求任意角的三角函数值
教学方法
讨论、启发、设问
教学手段
教具
教案、板书
主要教学内容及步骤
时间分配(分钟)一、织教学二、导入新课三、讲授新课
四、课堂小结
五、布置作业
1'
2'
74'
2'
1'
板书
设计
第五章 三角函数
5.3任意角的正弦函数、余弦函数和正切函数
一、三角函数
二、定义域
三、练习
四、正负号
五、练习
讨 论
思考题
作 业
授课班级
1421班
1431班
学 时
2
课 程 类 型
理论+习题课
课题或
章节题目
第五章 三角函数
5.3任意角的正弦函数、余弦函数和正切函数
教学目标
知识目标
理解任意角的三角函数的定义及定义域,理解三角函数在各象限的正负号,掌握界限角的三角函数值
能力目标
会利用定义求任意角的三角函数值,培养学生的观察能力
解 取角的公共范围得 为第四象限的角.
通过本次课程理解任意角的三角函数的定义及定义域,理解三角函数在各象限的正负号,掌握界限角的三角函数值,会利用定义求任意角的三角函数值,培养学生的观察能力。
P114 练习1、3、4T
情感目标
结合学生生活实际,创设情境,激发兴趣
教学要求
理解任意角的三角函数的定义及定义域,理解三角函数在各象限的正负号,掌握界限角的三角函数值,会利用定义求任意角的三角函数值,培养学生的观察能力。
教学重点
任意角的三角函数的定义及定义域
教学难点
判断三角函数在各象限的正负号,求任意角的三角函数值
教学方法
讨论、启发、设问
教学手段
教具
教案、板书
主要教学内容及步骤
时间分配(分钟)一、织教学二、导入新课三、讲授新课
四、课堂小结
五、布置作业
1'
2'
74'
2'
1'
板书
设计
第五章 三角函数
5.3任意角的正弦函数、余弦函数和正切函数
一、三角函数
二、定义域
三、练习
四、正负号
五、练习
讨 论
思考题
作 业
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y
sinα>0 cosα<0 tanα<0
sinα<0 o
cosα<0 tanα>0
sinα>0 cosα>0 tanα>0
x
sinα<0 cosα>0 tanα<0
PPT课件
10
动脑思考 探索新知
三
任意角三角函数的符号:
y
角++
y
-+
y
-+
函
- o - x - o + x +o - x
sinα
cosα>0
观察计算器上的按键并阅读相关的使用说明书, 小组完成计算器计算三角函数值.
sin
cos
tan
0
3 2
2
2
计算器
PPT课件
15
三 角 函 数
巩固知识 典型例题
例 4 求下列各式的值:
(1) 5cos180 3sin 90 2 tan 0 6sin 270 ;
(2) cos sin tan 3 sin sin cos
y
P(x , y)
ry
o x Bx
sin y
r
cos x
r
tan y
x
PPT课件
4
三 角 函 数
动脑思考 探索新知
sin y cos x tan y
r
r
x
在比值存在的情况下,对角α的每一个确定的值,按照 相应的对应关系,角α的正弦、余弦、正切、都分别 有唯一的比值与之对应,他们都是以角α为自变量的 函数,分别叫做正弦函数、余弦函数、正切函数,统 称为三角函数.
PPT课件
5
三
动脑思考 探索新知
正弦函数、余弦函数和正切函数的定义域如下表所示:
角
三角函数
定义域
函
sin
R
数
cos
tan
R
{ k , k Z}
2
PPT课件
6
三 角 函 数
动脑思考 探索新知
当角α采用弧度制时,角α的取值集合与实数集R之 间具有一一对应的关系,所以三角函数是以实数α 为自变量的函数.
tanα>0
数
y
正弦正 全正
正切正o 余弦正 x
PPT课件
11
三 角 函 数
巩固知识 典型例题
例 2 判定下列角的各三角函数符号. (1)4327º; (2) 27 .
5
判断任意角三角函数值的符号时,首先要判断出角所在的象限, 然后再根据在各象限角三角函数值的符号来进行判断 .
解解 ((12))因因为为 2475327角º角为为第第 象限象角限,角,
tanα
PPT课件
13
三 角 函 数
应用知识 强化练习 练习5.3.2
1.判断下列角的各三角函数符号
(1)525º;(2)-235
º;(3)
19 6
;(4)
3 4
.
2.根据条件 sin 0 且 tan 0 ,
确定 是第几象限的角.
PPT课件
14
三 角 函 数
自我探索 使用工具
,
sin y
, cos x
,
r
r
tan y
.
x
PPT课件
8
运用知识 强化练习
练习5.3.1
已知角 的终边经过点 P, 求:角 的正弦、余弦、正切值:
⑴ P(3,−4); ⑵ P(−1,2); ⑶ P( 1 , 3 ).
22
PPT课件
9
创设情景 兴趣导入
当角α的终边在第一二三四象限时,点P在第一象限,x 0, y 0, 所以, sinα 0,cosα 0,tanα 0;
故故ssiinn2475327 cos 4327
0, c00o,,s 275
0,
ttaann2475327 0. 0.
PPT课件
12
三 角 函 数
巩固知识 典型例题
例3 根据条件 sin 0 且 tan 0 , 确定 是第几象限的角.
y
++
-o - x sinα
y
-+ +o - x
2
43 3
2
计算器
PPT课件
17
三 角 函 数
归纳小结 自我反思
本次课学习 哪些内容?
你会解决 哪些新问题?
体会到哪些 学习方法?
PPT课件
18
三 角 函 数
布置作业 继续探究
阅读
书面
实践
教材章节5.3
再见
PPT课件
20
y
C(x , y)
sin ay
cr
r
ox
y
cos bx cr
tan ay
Bx
bx
PPT课件
3
三 角 函 数
动脑思考 探索新知
设 是任意大小的角,点 P(x, y) 为角 的终边上 不与原点重合的任意一点,点 P 到原点的距离为
r x2 y2 ,角 的正弦、余弦、正切分别定义为
PPT课件
7
三 角 函 数
巩固知识 典型例题 例 1 已知角 的终边经过点 P(2, 3) ,求角 的
正弦、余弦、正切值.
首先要根据关系式 r x2 y2 ,求出点 P 到坐标原点的距离 r ,
然后根据三角函数定义进行计算.
解 因为 x
,y
,
所以 r 22 (3)2
第5章 三角函数
5.3任意角的正弦函数、 余弦函数、正切函数
PPT课件
1
创设情景 兴趣导入
锐角三角函数的定义是什么?
C
在 RtABC 中,
sin
cos
ba
tan
.
A
cB
PPT课件
2
创设情景 兴趣导入
将 Rt⊿ABC 放在直角坐标系中,使得点 A 与坐标原点重合,
AC 边在 x 轴的正半轴上.三角函数的定义可以写作:
36 4
34 4
这类问题需要首先计算出界限角的三角函数值, 然后再进行代数运算.
计算器
PPT课件
16
三 角 函 数
应用知识 强化练习 练习5.3.3
1.计算:
5sin 90 2cos0 3 tan180 cos180 ;
2.计算:
cos tan 1 tan2 sin 3 cos
