理论力学第五章
合集下载
理论力学第五章
r Fi
g rri q
0
由虚功原理
P1 x1 P2 x2 F y3 0
x1
1 2
l1
sin
x2
l1 sin
1 2
l2
sin
y3 l1 cos l2 cos
P1 x1, y1 P2 x2, y2 B x3, y3
1 2
P1l1
cos
P2l1
cos
Fl1
sin
1 2
P2l2
2.理想约束
虚功：作用在质点上的力F在任意虚位移上做的功
理想约束：质点上的所有约束反力的虚功之和为零
n
r Ri
g
rr
0
i 1
引入虚位移可以消去这些约束反力 3.虚功原理
受理想约束的力学体系的平衡充要条件是所有主动力 的虚功之和等于零。
W
n
r Fi
g
rri
n
Fix xi Fiy yi Fiz zi 0
速度 s&2 r&2 r2&2 r2 sin2 &2
动能 T 1 ms&2 1 m r&2 r2&2 r2 sin2 &2
2
2
注意 Qr Fr , Q rF , Q r sin F
1 2
m
d dt
s&2 r&
s&2 r
Fr
1
2
1 2
m m
d
dt
2．稳定约束时
ri t
0 a ,a 0 T1 ,T0 0, T
T2
H T V 常量(E ) 能量积分
说明： L 不显含时间，且稳定约束条件下，系统能量守恒. 具有可加性（广延量）的运动积分称为守恒量.
理论力学(第7版)第五章 点的运动学
a 4、匀速运动： v 常数， 0, s s0 vt
运 动 规 律
[例5-1 ] 已知点的运动方程为x=2sin 4t m，y=2cos 4t m， z=4t m。 求：点运动轨迹的曲率半径 。
解：
vx x 8 cos 4t , ax 32 sin 4t x
r r t
—以矢量表示的 点的运动方程
矢端曲线：动点M在运动过程中，矢 径r的末端绘出的一条连续曲线。 ——动点M的运动轨迹
3
二.点的速度
dr v r dt
方向：沿着矢径r的矢端曲线的切线 方向，且与此点的运动方向一致。
大小：速度矢的模，表明点运动的快慢。
三.加速度
dv d 2r a r 2 dt dt
dv v2 a a a n a a n n n dt
17
5-3 自然法 曲率(1 / ) ：
定义——曲线切线的转角对弧长 一阶导数的绝对值。表示曲线的 弯曲程度。
d lim| | t 0 S dS 1
由于a , an均在密切面内，全加速a必在密切面内。 度
— 与 弧 坐 标 的 正 向 一 致 n — 指 向 曲 线 内 凹 一 侧 b — 与 , n 构 成 右 手 系
b n
[注]：自然坐标系是沿曲 13 线而变动的游动坐标系。
(动画自然坐标轴的几何性质)
曲线在P点的密切面形成
5-3 自然法
二.点的速度
当t 0时，r MM' S
v y y 8 sin 4t , a y 32 cos 4t y
v z z 4, a z 0 z
2 2 2 2 v v x v 2 v z 80 m s , a a x a 2 a z 32m s 2 y y
运 动 规 律
[例5-1 ] 已知点的运动方程为x=2sin 4t m，y=2cos 4t m， z=4t m。 求：点运动轨迹的曲率半径 。
解：
vx x 8 cos 4t , ax 32 sin 4t x
r r t
—以矢量表示的 点的运动方程
矢端曲线：动点M在运动过程中，矢 径r的末端绘出的一条连续曲线。 ——动点M的运动轨迹
3
二.点的速度
dr v r dt
方向：沿着矢径r的矢端曲线的切线 方向，且与此点的运动方向一致。
大小：速度矢的模，表明点运动的快慢。
三.加速度
dv d 2r a r 2 dt dt
dv v2 a a a n a a n n n dt
17
5-3 自然法 曲率(1 / ) ：
定义——曲线切线的转角对弧长 一阶导数的绝对值。表示曲线的 弯曲程度。
d lim| | t 0 S dS 1
由于a , an均在密切面内，全加速a必在密切面内。 度
— 与 弧 坐 标 的 正 向 一 致 n — 指 向 曲 线 内 凹 一 侧 b — 与 , n 构 成 右 手 系
b n
[注]：自然坐标系是沿曲 13 线而变动的游动坐标系。
(动画自然坐标轴的几何性质)
曲线在P点的密切面形成
5-3 自然法
二.点的速度
当t 0时，r MM' S
v y y 8 sin 4t , a y 32 cos 4t y
v z z 4, a z 0 z
2 2 2 2 v v x v 2 v z 80 m s , a a x a 2 a z 32m s 2 y y
理论力学第五章
30o
第一种情况： 第一种情况：
摩擦力阻止其向下运动
∑F
x
=0
Q min cos α + Fm − G sin α = 0
− Q min sin α + N − G cos α = 0
∑F
利用
y
=0
Fm = f s N
Q min sin α − f s cos α =G = 135.31 N cos α + f s sin α
[例4] 例
宽a，高b的矩形柜放置 ， 的矩形柜放置 a 在水平面上，柜重 ，重心C 在水平面上，柜重P，重心 在其几何中心，柜与地面间 在其几何中心， F h P C 的静摩擦因数是 fs，在柜的 b 侧面施加水平向右的力F， 侧面施加水平向右的力 ， 求柜发生运动时所需推力F 求柜发生运动时所需推力 的最小值。 的最小值。
再以整体为对象， 再以整体为对象，有平衡方程 整体为对象
∑X = 0
FAx − FBx = 0
FAx = FBx = 72.17 N
下面判断系统是否处于静平衡 脚端A 极限静摩擦力分别为 脚端 与B 的极限静摩擦力分别为 ：
r y
C
Fm A = f s A FAy = 75 N
r G
Fm B = f s B FBy = 75 N
解:
取矩形柜为研究对象,受力分析如图。 1 .假设不翻倒但即将滑动，考虑临界平衡。
y
列平衡方程
∑F = 0,
x
F − FA − FB = 0
F P
C
∑F
FB
x
y
= 0,
FNA + FNB − P = 0
FB = fs × FNB
第一种情况： 第一种情况：
摩擦力阻止其向下运动
∑F
x
=0
Q min cos α + Fm − G sin α = 0
− Q min sin α + N − G cos α = 0
∑F
利用
y
=0
Fm = f s N
Q min sin α − f s cos α =G = 135.31 N cos α + f s sin α
[例4] 例
宽a，高b的矩形柜放置 ， 的矩形柜放置 a 在水平面上，柜重 ，重心C 在水平面上，柜重P，重心 在其几何中心，柜与地面间 在其几何中心， F h P C 的静摩擦因数是 fs，在柜的 b 侧面施加水平向右的力F， 侧面施加水平向右的力 ， 求柜发生运动时所需推力F 求柜发生运动时所需推力 的最小值。 的最小值。
再以整体为对象， 再以整体为对象，有平衡方程 整体为对象
∑X = 0
FAx − FBx = 0
FAx = FBx = 72.17 N
下面判断系统是否处于静平衡 脚端A 极限静摩擦力分别为 脚端 与B 的极限静摩擦力分别为 ：
r y
C
Fm A = f s A FAy = 75 N
r G
Fm B = f s B FBy = 75 N
解:
取矩形柜为研究对象,受力分析如图。 1 .假设不翻倒但即将滑动，考虑临界平衡。
y
列平衡方程
∑F = 0,
x
F − FA − FB = 0
F P
C
∑F
FB
x
y
= 0,
FNA + FNB − P = 0
FB = fs × FNB
理论力学第五章 摩擦(Y)
0 Fs Fs,max
——平衡
0 f
f Fs Fs ,max ——临界平衡状态 摩擦角 f —— 物体处于临界平衡状态时全反力与
法线之间的夹角。
tan f
Fs ,max FN
f s FN fs FN
摩擦角的正切等于静滑动摩擦系数——几何意义。
当物体平衡时（包括平衡的临界状态）全约束反力 的作用线一定在摩擦角之内
摩擦轮传动——将左边轴的转动传给右边的轴
摩擦的分类：
摩擦
滑动摩擦
滚动摩擦
静滑动摩擦 ——仅有相对运动趋势 动滑动摩擦 ——已有相对运动 静滚动摩擦 动滚动摩擦
干摩擦 ——由于接触表面之间没有液体时产生的摩擦。 湿摩擦 ——由于物体接触面之间有液体。
摩擦
一、滑动摩擦
研究滑动摩擦规律的实验：
MB 0
l sin 30 0 M P cos 30 0 FND l cos 30 0 0 FSD 2
3 P 3l
(1 FSD
FSD f s FND
3 2 3 M M min Pl 8
（1）当M较大时，BD杆逆时针转动。 分别以OA、 BD杆为研究对象， 画受力图。 l 0 FND l cos 30 P 0 对于OA杆： M O 0 2
Y 0
Fs,max f s FN
（库仑摩擦定律）
（2）最大静摩擦力的方向：沿接触处的公切线，与相对 滑动趋势反向；
Fs,max f s FN f s ——静滑动摩擦系数——静摩擦系数
与两接触物体表面情况（粗糙度，干湿度，温度等） 和材料有关，与两物体接触面的面积无关。
理论力学-第五章
PS f'ct(fg)Q ct(3g 0.4 0 15 )200 50(N 0)0
精品文档
31
[练习1] 已知：Q=10N， f '动 =0.1 f 静 =0.2 求：P=1 N; 2N, 3N 时摩擦力F？
解： F m afx 静 N 0 .2 1 0 2 N
P 1 N 时 ,由 X 0 ,F P 1 N （没动，F 等于外力）
精品文档
7
三、摩擦角：
①定义：当摩擦力达到最大值Fmax 时其全反力
与法线的夹角 m 叫做摩擦角。
②计算：
翻
页
tgmFN maxfN Nf
请 看
动
画
精品文档
8
精品文档
9
四、自锁
①定义：当物体依靠接触面间的相互作用的摩擦 力 与正
压力（即全反力），自己把自己卡 紧，不会松开 （无论外力多大），这种现象称为自锁。
N'=N
d
M N
'
M dN 'dN
dd
从图中看出，滚阻力偶M的力偶臂正是d（滚阻系
数），所以，d 具有长度量纲。
由于滚阻系数很小，所以在工程中大多数情况下滚阻力
偶不计，即滚动摩擦忽略不计。
精品文档
23
第四章 《摩擦》习题课
本章小结 一、概念： 1、摩擦力----是一种切向约束反力，方向总是
与物体运动趋势方向相反。
由 X 0 ,R co ) s R 1 c ( o 0
由二力平衡条 :R件 R1
, 2 又tg0.1f , tg10.15043' 211026' (极限状)态 即当211026'时能自锁
精品文档
精品文档
31
[练习1] 已知：Q=10N， f '动 =0.1 f 静 =0.2 求：P=1 N; 2N, 3N 时摩擦力F？
解： F m afx 静 N 0 .2 1 0 2 N
P 1 N 时 ,由 X 0 ,F P 1 N （没动，F 等于外力）
精品文档
7
三、摩擦角：
①定义：当摩擦力达到最大值Fmax 时其全反力
与法线的夹角 m 叫做摩擦角。
②计算：
翻
页
tgmFN maxfN Nf
请 看
动
画
精品文档
8
精品文档
9
四、自锁
①定义：当物体依靠接触面间的相互作用的摩擦 力 与正
压力（即全反力），自己把自己卡 紧，不会松开 （无论外力多大），这种现象称为自锁。
N'=N
d
M N
'
M dN 'dN
dd
从图中看出，滚阻力偶M的力偶臂正是d（滚阻系
数），所以，d 具有长度量纲。
由于滚阻系数很小，所以在工程中大多数情况下滚阻力
偶不计，即滚动摩擦忽略不计。
精品文档
23
第四章 《摩擦》习题课
本章小结 一、概念： 1、摩擦力----是一种切向约束反力，方向总是
与物体运动趋势方向相反。
由 X 0 ,R co ) s R 1 c ( o 0
由二力平衡条 :R件 R1
, 2 又tg0.1f , tg10.15043' 211026' (极限状)态 即当211026'时能自锁
精品文档
理论力学第五章
(1) (2)
FS1 f s FN 1 (3)
解得： F1
F 设物块有下滑趋势时，推力为， 2 画物块受力图：
Fx 0,
Fy 0,
sin f s cos P cos f s sin
F2 cos P sin Fs 2 0 F2 sin P cos FN 2 0
r (b f s c) f s Ra
例5-5 已知：均质木箱重 求： （1）当D处拉力
o P 5kN , f s 0.4 , h 2a 2m , 30 ；
F 1kN 时，木箱是否平衡?
（2）能保持木箱平衡的最大拉力.
解： （1）取木箱，设其处于平衡状态.
Fx 0
求：拉动拖车最小牵引力 F（ F 平行于斜坡）.
解： 取整体
Fx 0
Fy 0
F FAs FBs P sin 0 FAN FBN P cos 0
M A MB 0
（1）
（2）
M B 0
FAN (a b) Fh P cos b P sin H
共有 FD , FC , F , FND 四个未知数
在 f D 0.3 时，解得 F 4.62 N
D 即在 f D 0.3 时， 处不会先滑动.
当 f D 0.15 时，解得 FND 172.4N
FD F C f D FND 25.86N
C 处无滑动
Fmin 47.81N .
第五章
摩 擦
摩擦
滑动摩擦 滚动摩擦 干摩擦 湿摩擦
静滑动摩擦 动滑动摩擦 静滚动摩擦 动滚动摩擦
理论力学第五章
6
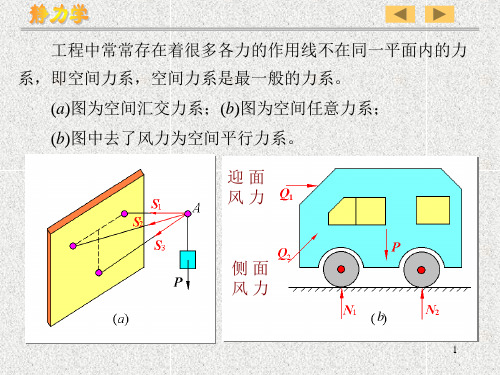
例1
如图所示起重杆A端用球形铰链固定在地面上，B端用绳 CB和DB拉住，连线CD平行于 x 轴。已知：CE=EB=DE，
=30，CDB平面与水平面的夹角 EBF=30 ，重物
P=10 kN，试求起重杆所受的压力和绳的拉力。
7
解： 取节点B 为研究对象，受力分 析如图。由空间汇交力系的平 衡方程有：
通过O点作任一轴Z，则：
mz (F )mz (Fxy )2OA'B'
由几何关系： OABcosg OA'B' 所以： 2OABcosg 2OA'B'
即： mO (F ) cosg mz (F )
[mO (F )]z mz (F )
定理：力对点的矩矢在通过该点的任意轴上的投影等于这力
对于该轴的矩。这就是力对点之矩与对通过该点轴之矩的关系18。
MO (mx (F ))2 (my (F ))2 (mz (F ))2
所以空间任意力系的平衡方程为：
X 0,mx (F )0 Y 0,my (F )0
还有四矩式，五矩式和六矩式， 同时各有一定限制条件。
Z 0,mz (F )0
29
空间汇交力系的平衡方程为：
X 0 Y 0 Z 0
因为各力线都汇交于一点，各轴都通过 该点，故各力矩方程都成为了恒等式。
g
O
q
Fxy
大小： F F
作用点：在物体的哪点就是哪点 方向：
由、、g三个方向角确定
2
2、一次投影法（直接投影法） 由图可知：
X Fcos, Y Fcos , Z Fcosg
3
3、力沿坐标轴分解：
若以 Fx ,Fy ,Fz 表示力沿直角
理论力学 第五章 桁架和摩擦
理想桁架 工程实际中计算桁架受力情况时，常 作如下简化： (1) 构成桁架的杆件都是直杆； (2) 杆件两端都用光滑铰链连接； (3) 所有外力（主动力及支座反力） 都作用在节点上； (4) 杆件自重略去不计。
这种桁架称为理想桁架。
平面桁架各杆内力
1.节点法 2.截面法
汇交力系 平面一般力系
已知平面桁架尺寸、载荷。求：各杆内力。
3 因 0 Fs Fmax ，问题的解有时在一个范围内．
考虑摩擦的平衡问题
(1)判断物体是否平衡，并求滑动摩擦力。
先假设物体处于平衡，根据平衡方程求出物体平衡时需 要的摩擦力以及相应接触面间的正压力。再根据摩擦定 律求出相应于正压力的最大静摩擦力并与之比较。若满
足F≤Fmax这一关系，说明物体接触面能提供足够的摩擦
当仅有滑动趋势时，产生的摩擦力，称为静滑动摩擦力
静滑动摩擦力性质
1)静滑动摩擦力FS 的方向与滑动趋势相反，大小由平衡
条件确定；
0≤FS ≤Fmax （物体平衡范围）
2)只有当物体处于将动未动的平衡临界状态时,静滑动摩
擦力FS 达到最大值，即 FS =Fmax=f FN
f — 静滑动摩擦系数；
FN— 法向反力（一般也由平衡条件决定）。
摩擦角和自锁现象
1 摩擦角
FRA ---全约束力
物体处于临界平衡状态时，全约束 力和法线间的夹角---摩擦角
tan f
Fmax FN
fs FN FN
fs
全约束力和法线间的夹角的正切等于静 滑动摩擦系数．
摩擦锥
0 f
2 自锁现象
摩擦自锁的实例
1.粗糙斜面。当 a<m时,
不论W多大，物块A均保持 平衡－－摩擦自锁。
理论力学第5章(点的运动)
包括几何静力学、分析静力学
(2) 运动学: 研究点与刚体运动的几何性质。
包括位移、轨迹、速度、加速度。 (与力无关、也是变形体运动基础)
A B
F
C
B
刚体运动
C
变形(包含刚体位移和相对位移)
(3) 动力学: 研究物体所受力与运动间的关系。
包括质点系、刚体，变形体的动力效应。
第五章 点的运动学
§5-1 运动学的基本概念
速度
已知： OC AC BC l , MC a , t。 求：运动方程、轨迹、速度和加速度。
x l a cost ax v x 2 a y vy y l a sin t
2
加速度
a a a
F ( x, y) 0
二、点的速度v
又
r = xi + yj + zk
式中 v x 所以得
dr dx dy dz v i j k dt dt dt dt v = vx i + vy j + vz k
、v y
、v z
vx
dx dt
v
表明：“动点的速度在坐标轴上的投影，等于动点对应的位置 坐标对时间 t 的一阶导数”。 则速度的大小和方向余弦为
弧坐标的运动方程sf切向加速度表示速度大小的变化三点的加速度法向加速度表示速度方向的变化匀速运动v常数常数常数匀变速直线运动匀速圆周运动匀速直线运动或静止直线运动匀速运动圆周运动匀速运动直线运动匀速曲线运动匀变速曲线运动点作曲线运动画出下列情况下点的加速度方向
(1) 静力学: 研究物体所受力系的简化、平衡规律及其应用。
△r称为在△t时间内动点M的位移。
间间隔△t内的平均速度。以 v*表示。则： Δr v Δt 平均速度表示动点在△t内平均运动的快慢和运动方向。
(2) 运动学: 研究点与刚体运动的几何性质。
包括位移、轨迹、速度、加速度。 (与力无关、也是变形体运动基础)
A B
F
C
B
刚体运动
C
变形(包含刚体位移和相对位移)
(3) 动力学: 研究物体所受力与运动间的关系。
包括质点系、刚体，变形体的动力效应。
第五章 点的运动学
§5-1 运动学的基本概念
速度
已知： OC AC BC l , MC a , t。 求：运动方程、轨迹、速度和加速度。
x l a cost ax v x 2 a y vy y l a sin t
2
加速度
a a a
F ( x, y) 0
二、点的速度v
又
r = xi + yj + zk
式中 v x 所以得
dr dx dy dz v i j k dt dt dt dt v = vx i + vy j + vz k
、v y
、v z
vx
dx dt
v
表明：“动点的速度在坐标轴上的投影，等于动点对应的位置 坐标对时间 t 的一阶导数”。 则速度的大小和方向余弦为
弧坐标的运动方程sf切向加速度表示速度大小的变化三点的加速度法向加速度表示速度方向的变化匀速运动v常数常数常数匀变速直线运动匀速圆周运动匀速直线运动或静止直线运动匀速运动圆周运动匀速运动直线运动匀速曲线运动匀变速曲线运动点作曲线运动画出下列情况下点的加速度方向
(1) 静力学: 研究物体所受力系的简化、平衡规律及其应用。
△r称为在△t时间内动点M的位移。
间间隔△t内的平均速度。以 v*表示。则： Δr v Δt 平均速度表示动点在△t内平均运动的快慢和运动方向。
理论力学 第5章 小振动
A sin( 0 t )
2. 单自由度系统的小振动
三、复摆系统的自由振动 绕不通过质心的光滑水平轴摆动的刚体
d M mgl sin I 2 d t ( 5 )
d mgl I 2 dt
2
2
M l F
转动正向 O 向外
l
*C
d 2 0 2 dt
2. 单自由度系统的小振动
例2：已知 m, OA=AB=L, 求系统微振动固有频率 解：系统的动能和势能 1 1 1 1 2 2 2 2 T J o mv c J c mv B 2 2 2 2 xc 1.5L cos , yc 0.5L sin , xB 2L cos 1 2 2 2 ~ T ( mL 6mL2 sin 2 ) k 6g 2 3 ~ V 4mgL(1 cos ) m L 2 2 1 1~ 2 ~ 2 m mL mq T m (0) q 3 2 2 1 1~ 2 ~ 2 V (q) V " (0)q k q k 4mgL 2 2
3.1 多自由度系统小振动问题（推导）
ˆ 0 ˆ A ˆ 2M K
本征值问题（求本征值 2 和本征矢量 A ）
f ( 2 ) det k m 2 0
即
k11 m11 2 k21 m21 2 ks1 ms1 2
k12 m12 2
T ——周期，每振动一次所经历的时间。 T
2
0
f —— 频率，每秒钟振动的次数， f = 1 / T 。
0 —— 固有频率，振体在2秒内振动的次数。
反映振动系统的动力学特性，只与系统本身的固有参数有关。
2. 单自由度系统的小振动
2. 单自由度系统的小振动
三、复摆系统的自由振动 绕不通过质心的光滑水平轴摆动的刚体
d M mgl sin I 2 d t ( 5 )
d mgl I 2 dt
2
2
M l F
转动正向 O 向外
l
*C
d 2 0 2 dt
2. 单自由度系统的小振动
例2：已知 m, OA=AB=L, 求系统微振动固有频率 解：系统的动能和势能 1 1 1 1 2 2 2 2 T J o mv c J c mv B 2 2 2 2 xc 1.5L cos , yc 0.5L sin , xB 2L cos 1 2 2 2 ~ T ( mL 6mL2 sin 2 ) k 6g 2 3 ~ V 4mgL(1 cos ) m L 2 2 1 1~ 2 ~ 2 m mL mq T m (0) q 3 2 2 1 1~ 2 ~ 2 V (q) V " (0)q k q k 4mgL 2 2
3.1 多自由度系统小振动问题（推导）
ˆ 0 ˆ A ˆ 2M K
本征值问题（求本征值 2 和本征矢量 A ）
f ( 2 ) det k m 2 0
即
k11 m11 2 k21 m21 2 ks1 ms1 2
k12 m12 2
T ——周期，每振动一次所经历的时间。 T
2
0
f —— 频率，每秒钟振动的次数， f = 1 / T 。
0 —— 固有频率，振体在2秒内振动的次数。
反映振动系统的动力学特性，只与系统本身的固有参数有关。
2. 单自由度系统的小振动
理论力学第五章
vz z 4, a z 0 z
2 2 2 2 从而 v vx vy vz2 80m s, a ax a y az2 32m s2
dv at 0, an a 32 m/s 2 dt
v2 故 2.5m an
例 已知：椭圆规的曲柄OC 可绕定轴O 转动，其端点C 与规尺
AB 的中点以铰链相连接，而规尺A，B 两端分别在相互垂
直的滑槽中运动， OC AC BC l , MC a, ωt 求：① M 点的运动方程； ② 轨迹；
③ 速度；
④ 加速度。
解： 点M作曲线运动，取坐标系Oxy如图所示。
外啮合齿轮
分析齿轮上一点的运动
§ 5-3
自然法
自然法：利用点的运动轨迹建立弧坐标和自然轴系，利用它们 描述和分析点的运动的方法。 1.弧坐标 2.自然轴系
s f (t )
切向单位矢量
主法线单位矢量
n
b n
副法线单位矢量
曲线在P点的密切面形成
自然坐标轴的几何性质
l 2 a 2 2al cos 2 t vx (l a ) sin t cos(v , i ) v l 2 a 2 2al cos 2 t vy (l a) cos t cos(v , j ) v l 2 a 2 2al cos 2 t
加速度
y
v
M
2
A
a x 4 Rω 2 cos 2ωt x
a y 4 Rω sin 2ωt y
2
a
x
O
R
x y 大小 a 2 2 4Rω 2
ax cos (a,i ) cos 2ωt cos (π 2ωt) a 方向如图。 π ay cos (a,j ) sin 2ωt cos( 2ωt ) a 2
2 2 2 2 从而 v vx vy vz2 80m s, a ax a y az2 32m s2
dv at 0, an a 32 m/s 2 dt
v2 故 2.5m an
例 已知：椭圆规的曲柄OC 可绕定轴O 转动，其端点C 与规尺
AB 的中点以铰链相连接，而规尺A，B 两端分别在相互垂
直的滑槽中运动， OC AC BC l , MC a, ωt 求：① M 点的运动方程； ② 轨迹；
③ 速度；
④ 加速度。
解： 点M作曲线运动，取坐标系Oxy如图所示。
外啮合齿轮
分析齿轮上一点的运动
§ 5-3
自然法
自然法：利用点的运动轨迹建立弧坐标和自然轴系，利用它们 描述和分析点的运动的方法。 1.弧坐标 2.自然轴系
s f (t )
切向单位矢量
主法线单位矢量
n
b n
副法线单位矢量
曲线在P点的密切面形成
自然坐标轴的几何性质
l 2 a 2 2al cos 2 t vx (l a ) sin t cos(v , i ) v l 2 a 2 2al cos 2 t vy (l a) cos t cos(v , j ) v l 2 a 2 2al cos 2 t
加速度
y
v
M
2
A
a x 4 Rω 2 cos 2ωt x
a y 4 Rω sin 2ωt y
2
a
x
O
R
x y 大小 a 2 2 4Rω 2
ax cos (a,i ) cos 2ωt cos (π 2ωt) a 方向如图。 π ay cos (a,j ) sin 2ωt cos( 2ωt ) a 2
理论力学第五章
M Z Fxy M 0 Fxy Fxy d
0 OA 0
'
有两种特殊情况使力对轴之矩为零：
1 2
当力F与转 轴z平行时， 即F=Fz， Fxy=0，力对 z轴之矩 Mz(F)=0.
当力F与转 轴z相交时， 即d=0，力 对z轴之矩 Mz(F)=0.
概括为
当力与轴共面时，力对轴之矩为零。
力对轴之矩
力使物体绕该点转动效应的度量。
M O (F ) F d
M O (F ) =2⊿AOB=Fd ,
+
-
2倍⊿的面积。 在平面中：力对点的矩是代数量。
二、力对轴之矩
FZ对z轴 之矩为零。
Fx、Fy产生使 门绕z轴转动的 效应
力对轴之矩是力使物体绕该轴转动效应的度量，它等于力在垂 直于该轴的平面上的分力对轴与平面的交点之矩。
三、合力矩定理在力对轴之矩计算中的应用
将F分解为
Fx、Fy、Fz
各分力对 轴之矩
计算其代数和
M x F M x Fx M x Fy M x Fz M x Fx M y Fy M z Fz M y F M y Fx M y Fy M y Fz
R Fi
mO ( R) mO ( Fi )
rC R r1 F1 r2 F2 rn Fn
rC F1r1 F2 r2 Fn rn Fi ri R Fi
设 心 C的 标 重 坐 为 x C、y C、z C , 任 微 部 的 标 一 小 分 坐 x i、y i、z i , ， 即 对x、y、z轴 别 用 力 定 分 应 合 矩 理
Z F cosg F sin
理论力学第五章——点的运动
'
'
当Δt 0， Δv/Δt的极限称为点在瞬时t的加速度：
v dv d 2 x a lim 2 x t 0 t dt dt
5.1 点的直线运动
已知加速度或速度方程， 采用积分法 求运动方程 ，积 分常数由运动初始条件决定。 dv a dv adt dt v t dv adt
由于
dτ dτ ds dτ ds v n dt dt ds ds dt
所以
dv v a τ n dt
2
5.4 自然法
4 点的切向加速度和法向加速度
dv v a τ n dt
上式表明加速度矢量a是由两个分矢量组成：分矢量at 的方向永远沿轨迹的切线方向，称为切向加速度，它 表明速度代数值随时间的变化率；分矢量 an的方向永 远沿主法线的方向，称为法向加速度，它表明速度方 向随时间的变化率。
2 t 2
2
at tan | | 0.25 an
2
5.4 自然法
全加速度为aτ和an的矢量和
a at an
全加速度的大小和方向由下列二式决Leabharlann ： 大小：a at an
2
2
方向：
at an cos(a ,t ) , cos(a ,n ) a a
5.4 自然法
如果动点的切向加速度的代数值保持不变，则动 点的运动称为匀变速曲线运动。现在来求它的运动规 律。 at c
dτ τ j 1 lim lim n n ds s 0 s s 0 s
t"
5.4 自然法
3 点的速度
r s ds v lim lim t 0 t t 0 t dt
'
当Δt 0， Δv/Δt的极限称为点在瞬时t的加速度：
v dv d 2 x a lim 2 x t 0 t dt dt
5.1 点的直线运动
已知加速度或速度方程， 采用积分法 求运动方程 ，积 分常数由运动初始条件决定。 dv a dv adt dt v t dv adt
由于
dτ dτ ds dτ ds v n dt dt ds ds dt
所以
dv v a τ n dt
2
5.4 自然法
4 点的切向加速度和法向加速度
dv v a τ n dt
上式表明加速度矢量a是由两个分矢量组成：分矢量at 的方向永远沿轨迹的切线方向，称为切向加速度，它 表明速度代数值随时间的变化率；分矢量 an的方向永 远沿主法线的方向，称为法向加速度，它表明速度方 向随时间的变化率。
2 t 2
2
at tan | | 0.25 an
2
5.4 自然法
全加速度为aτ和an的矢量和
a at an
全加速度的大小和方向由下列二式决Leabharlann ： 大小：a at an
2
2
方向：
at an cos(a ,t ) , cos(a ,n ) a a
5.4 自然法
如果动点的切向加速度的代数值保持不变，则动 点的运动称为匀变速曲线运动。现在来求它的运动规 律。 at c
dτ τ j 1 lim lim n n ds s 0 s s 0 s
t"
5.4 自然法
3 点的速度
r s ds v lim lim t 0 t t 0 t dt
理论力学课件 第5章
• 2. 动滑动摩擦 • 当拉力F1超过静摩擦力的最大值时Fmax ，物 体将在水平面上滑动。此时物体受到的摩 擦力为动滑动摩擦力。动滑动摩擦也与物 体受到的压力FN成正比， • F = f FN • 如果拉力与动摩擦力相等F1 = f FN，物体作 匀速运动。 • 如果拉力大于动摩擦力F1 ＞ f FN，物体作加 速运动。
§5-2 摩擦角和自锁现象
• 1. 摩擦角 • 摩擦力也属于约束力。静摩擦力与法 向约束力（压力）的合力称为全约束 力。全约束力与法线的夹角的最大值 φf 称为摩擦角。
FRA FN Fs tan f Fmax FN f s FN FN fs
• 2. 自锁现象 • 如果摩擦力没有达到最大值Fs < Fmax ，则全 约束力在摩擦锥的内部。全约束力与法线 的夹角小于摩擦角， • 0<φ<φf 。 • 这时，如果全主动力(如重力、拉力的合力) 也在摩擦锥内部，无论全主动力有多大， 全约束力都能与全主动力平衡。此则自锁 现象。反之，全主动力在摩擦锥的外部， 无论这个全主动力多么小，全约束力都不 能平衡全主动力。物体比发生运动。
y
Fs f s FN 解得： F1max P
• 当水平力达到极小值时， • 要保证物体不能向下滑动。
F F
x
0 : F1 cos P sin Fs 0 0 : F1 sin P cos FN 0 sin f s cos cos f s sin
第五章 摩擦
• §5-1 滑动摩擦 • 1. 静滑动摩擦 • 物体放在粗糙的水平面上，对物体施 加一个水平拉力F1，此时物体受到一 个静摩擦力Fs，静摩擦力的方向与物 体的运动趋势方向相反。当拉力F1不 很大时，拉力F1与摩擦力Fs相等， F1 = Fs 。此时物体仍未运动。
理论力学 第五章 平面图形的几何性质
10
y
2)、求形心
xc
Ax
A
i ci
A1 xc1 A2 xc 2 A1 A2
C2
c(-20.3;34.7)
C1 80
35 1100 20.3(mm) 10 110 80 10
i ci
x
yc
A y
A
A1 y c1 A2 y c 2 A1 A2
60 1100 34.7(mm) 10 110 80 10
§5-3
极惯性矩
y
dA
定义：I p dA
2 A
I p：极惯性矩
极惯性矩恒为正 单位：长度4
x
O
圆截面
d
2
I p A dA
1、实心圆截面——
O
d
I P dA 2 d
2 2 A A
d 2 0
1 4 2 d d 32
y 10
A2 1200mm2 , xc 2 5mm, yc 2 60mm
2)、求形心
C2
120
c(19.7;39.7)
C1
A1 xc1 A2 xc 2 zc A A1 A2 45 700 5 1200 19.7mm) 700 1200
i ci
Ax
80
2 2 A A 2 A c 2 2 A A
y
I x I xc a 2 A I y I yc b A
2
yc xc
x
b
c
a
y
dA yc
xc
——平行移轴公式
o
x
•图形对任意轴的惯性矩，等于图形对于与该轴平 行的形心轴的惯性矩加上图形面积与两平行轴间距 平方的乘积；
y
2)、求形心
xc
Ax
A
i ci
A1 xc1 A2 xc 2 A1 A2
C2
c(-20.3;34.7)
C1 80
35 1100 20.3(mm) 10 110 80 10
i ci
x
yc
A y
A
A1 y c1 A2 y c 2 A1 A2
60 1100 34.7(mm) 10 110 80 10
§5-3
极惯性矩
y
dA
定义：I p dA
2 A
I p：极惯性矩
极惯性矩恒为正 单位：长度4
x
O
圆截面
d
2
I p A dA
1、实心圆截面——
O
d
I P dA 2 d
2 2 A A
d 2 0
1 4 2 d d 32
y 10
A2 1200mm2 , xc 2 5mm, yc 2 60mm
2)、求形心
C2
120
c(19.7;39.7)
C1
A1 xc1 A2 xc 2 zc A A1 A2 45 700 5 1200 19.7mm) 700 1200
i ci
Ax
80
2 2 A A 2 A c 2 2 A A
y
I x I xc a 2 A I y I yc b A
2
yc xc
x
b
c
a
y
dA yc
xc
——平行移轴公式
o
x
•图形对任意轴的惯性矩，等于图形对于与该轴平 行的形心轴的惯性矩加上图形面积与两平行轴间距 平方的乘积；
《理论力学》课件 第5章
因而 dBA/dt 0 ，于是得
vA vB
将上式再求一次导数，则得
aA aB
例5-1
如图5-4所示的曲柄滑道机构，当曲柄 OA 在平面上绕定轴 O 转动 时，通过滑槽连杆中的滑块 A 的带动，可使连杆在水平槽中沿直
线往复滑动。若曲柄 OA 的长为 r ，曲柄与 x 轴的夹角为 t，
其中 是常数，求此连杆在任一瞬时的速度及加速度。
根据上述结论，可作出截面上各点的加速度的分布图，在通过轴心的 直线上，各点的加速度按线性分布，将加速度矢的端点连成直线，此 直线通过轴心，如图5-10（b）所示。
（a）
图5-10
（b）
例5-3
如图5-11所示，一半径 R 0.2 m 的圆轮绕定轴O 的转动方程
为 t2 4t ， 单位为rad， t单位为s。求 t 1 s 时，轮
*
t
当 t 趋近于零时，刚体转动的瞬时角加速度为
lim * lim d
t 0
t0 t dt
刚体绕定轴转动的角加速度等于角速度对于时间的一阶导数，
或等于转角对于时间的二阶导数。
角加速度与角速度一样都是代数量，它的单位是 rad/s2
若 与 的符号相同，则角速度的绝对值随时间而增加，这 时称为加速转动；反之，若 与 的符号相反，则角速度
例
设有平动的刚体，在刚体上任取两点 A 和 B ，并连成一直线如
图5-3所示。运动开始时 AB 线在 A0B0 的位置；经过极短时间间 隔 t 之后，移至 A1B1 ；依次再继续移至 A2B2 ， ，AnBn 等。
首先证明这两个任意点的轨迹形状是完全 相同的，根据刚体的定义得知 A，B 两点间 的距离保持不变。 因此 AB A0B0 A1B1 A2B2 AnBn
理论力学PPT课件第5章 动量定理、质点系动量定理、质点系动量矩定理
y
A
o
G
B
x
2020年4月20日
15
偏心电机
e m2
F Oy
FOx
思考：偏心电机转动时，支座的动约束力为多大？
2020年4月20日
16
3.动量守恒与质心运动守恒
动量守恒 若：FRe＝0 则：p = 常矢量 若：FRex＝0 则：px = 常量
质心运动守恒（不动）
1) 若 FRe 0
ac 0
由动量矩定理：
dLOz dt
M
e Oz
d d t(2 W gr2A2 W gr2 BW gvC2 r)M W 2 r
2 W gr2A2 W gr2BW g2raCM 2 W r
2020年4月20日
49
2 W gr2A2 W gr2BW g2raCM 2 W r
补充运动学方程
aCrArB
2W graCW g2raCM2Wr
LA ri'm ivi' vi'— 相对速度
(3)绝对动量矩与相对动量矩的关系 LAL'AAC (mA)， v c为质心，
当AC＝0，即，动点为质心C时 LC＝LC —对质心的绝对与 量相 矩对 相动 等
2020年4月20日
34
3.刚体的动量矩（对定点A）
（1）平移刚体的动量矩
L A r i ' m iv c A (C v m c ) A P C
Mce 0,Lc守恒 .
O
FT
C
GV
2020年4月20日
52
思考：猴子爬绳比赛，已 m A 知 m B ,vA rv B.r
答：若不计绳与滑轮的质量，则 v1a v2a
若考虑绳与滑轮的质量，则 m AvArm BvBrJoω
A
o
G
B
x
2020年4月20日
15
偏心电机
e m2
F Oy
FOx
思考：偏心电机转动时，支座的动约束力为多大？
2020年4月20日
16
3.动量守恒与质心运动守恒
动量守恒 若：FRe＝0 则：p = 常矢量 若：FRex＝0 则：px = 常量
质心运动守恒（不动）
1) 若 FRe 0
ac 0
由动量矩定理：
dLOz dt
M
e Oz
d d t(2 W gr2A2 W gr2 BW gvC2 r)M W 2 r
2 W gr2A2 W gr2BW g2raCM 2 W r
2020年4月20日
49
2 W gr2A2 W gr2BW g2raCM 2 W r
补充运动学方程
aCrArB
2W graCW g2raCM2Wr
LA ri'm ivi' vi'— 相对速度
(3)绝对动量矩与相对动量矩的关系 LAL'AAC (mA)， v c为质心，
当AC＝0，即，动点为质心C时 LC＝LC —对质心的绝对与 量相 矩对 相动 等
2020年4月20日
34
3.刚体的动量矩（对定点A）
（1）平移刚体的动量矩
L A r i ' m iv c A (C v m c ) A P C
Mce 0,Lc守恒 .
O
FT
C
GV
2020年4月20日
52
思考：猴子爬绳比赛，已 m A 知 m B ,vA rv B.r
答：若不计绳与滑轮的质量，则 v1a v2a
若考虑绳与滑轮的质量，则 m AvArm BvBrJoω
理论力学第五章 点的运动和刚体的基本运动 [同济大学]
![理论力学第五章 点的运动和刚体的基本运动 [同济大学]](https://img.taocdn.com/s3/m/9038a70db52acfc788ebc909.png)
dv v2 τ n dt
a
r
O
`
v vτ
r
dv 2 v2 ) ( )2 dt ρ
tan
aτ an
1
例5-2 汽车以匀速度v=10m/s过拱桥，桥面曲线 y=4fx(L–x)/L2, f=1m,求车到桥最高点时的加速度。
解： aτ
例5-3 销钉A由导杆B带动沿固定圆弧槽运动。导杆B沿轴螺旋 立柱以不变的速度v0 =2m/s向上运动。试计算当θ=30° 时，销钉 A的切向和法向加速度。 解: 建立弧坐标s和直角坐标Oxy如图。 因 s=Rθ,
销钉A的加速度为
aτ v sin θ v0 θ cos θ
2 2 sin θ v0 12.32m/s 2 R cos3 θ
an
2 v2 v0 21.33m/s 2 R R cos 2 θ
例5-4
判别下图示曲线中加速度、速度矢量是否正确。
§5-4 刚体的基本运动平动，转动
则vＤ＝vＡ＝２rω
aＤn＝aＡn＝２rω２ aＤτ＝aＡτ＝２ra
0 dt
0
t
y x
θ θ0 ω0t
t
0 0
t
αdtdt
角加速度为常量：
两个独立方程
0 t,
1 θ θ0 ω0 t t 2 2
1 θ θ0 (ω0 ω)t , 2
t 0
'2 1 1 y " k y
切线
v r S M* + M
dτ s v lim n d t lim t 0 t t 0 s t
an
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
刚体做平面平行运动时，刚体中不在同一 直线上的任意三点到平面的距离相等，存 在三个约束条件，故刚体平面平行运动的 自由度为3
• 刚体的定点转动
若刚体上只有一个点固定不动，整个刚 体围绕此点转动，则此刚体做定点转动
刚体定点转动时，由于固 定点的3个坐标已经固定， 只剩下三个可以独立变化 的坐标变量，刚体定点转 动的故自由度为3
dT dW
• 三个定理所对应的守恒
动量守恒定律：刚体不受外力作用，或 外力相互抵消时，刚体的总动量守恒。 在某一方向力的分量为零，则在该方向 的动量分量守恒。
角动量守恒定律：刚体不受外力矩作用， 或外力矩相互抵消时，刚体的总角动量 动量守恒。在某一方向力矩的分量为零， 则在该方向的角动量分量守恒。
刚体做定轴转动时，刚体中的点（除转轴 上的点外）绕转轴做圆周运动，此时描述 刚体的运动只需要一个坐标变量，故刚体 绕定轴转动的自由度为1（描述刚体的转 动）
• 刚体的平面平行运动
若刚体内任意一点都平行于一固定平面 而运动，则此刚体做平面平行运动，刚 体中垂直于固定平面的直线上各点，其 运动状态完全相同，任何一个与固定平 面平行的刚体截面，其运动都可用来恰 当地代表刚体的运动
机械能守恒定律：作用于刚体的外力为 保守力时，刚体的总机械能守恒。刚体 只发生动能和势能的相互转换。
§5.4 刚体的定轴转动
刚体定轴转动的自由度为1
设量刚为体绕，转则轴角（速z轴度）为转：动r 的角&kr度变kr
刚体定轴转动的基本方程
质心定理：
m
d2rc dt 2
F (e)
F
FA
FB
刚体平动时的 动能
T
1 2
mvc2
1 2
mv2
刚体做定轴转动：设转轴为z轴，则
T
1 r
2
r L
1 2
J zz
2
1 2
I
2
其中 I Jzz x2 y2 dm r2dm
刚体平面平行运动
T
1 2
mvc2
1 2
I c 2
Ic 通过质心的转轴的转动动量
§5.3 刚体的动力学方程
• 刚体运动的动量定理
r 代表 距离转轴的垂直距离
刚体定点转动时的惯性是以张量 J 来度 量，刚体绕轴转动时的惯性则以转动惯 量 I 来度量，前者是张量，后者是标量
常见几何体的 转动惯量
I mR2 / 2
I 3mR2 / 2
（三）刚体的动能
• 在刚体中各质点与质心之间的距离恒定 不变，则刚体相对于质心的运动只可能 是围绕质点的转动，由此柯尼希定理变 为：
动量定理：
dP dt
N i1
Fi
F (e)
质心定理：
m
d2rc dt 2
F (e)
冲量定理：
P F(e)t I
• 刚体运动的角动量定理
对某一固定点的角动量定理：
d
dt
L
N i1
ri Fi
M
对质心的角动量定理：
d
dt
Lc
N i1
ri Fi M c
• 刚体运动的动能定理 刚体内任意两点间无相对位移，内力 不做功，外力对刚体所做的功等于刚 体动能的变化
刚体的平面平行运动可以看成为两种运 动的合成，即随刚体（或与之刚性联结） 的基点的平动，和绕通过基点并与运动 平面垂直的轴的转动！（通常取质心作 为基点）
三个坐标参量： xc , yc ,
质心的运动由质心定理确定；转动则由 转轴方向的角动量定理求解！
设质心的运动平面为 xy 平面，过质心 的转轴沿 z 方向，则由质心定理可得
• 例题：质量为M，半径为r的均质圆柱体 放在粗糙水平面上，柱的外端绕有轻绳 ，绳子跨过一个很轻的滑轮，并悬挂一 个质量m的物体。圆柱体做纯滚动，并 且圆柱体与滑轮间的绳子是水平的。求 绳子的张力T。
作业题
• 课后习题第五章 10，17， 21
角动量定理：
d dt
L
M
MA
MB
角动量方程的 z 分量方程为
I
d
dt
I
d2 dt 2
Mz
• 例题：一个质量m,长度L的细棒，绕着O 点在竖直平面内转动。棒的一端固定着 质量为M的质点。求：棒从水平位置静 止下落到最低点时候的角速度。
§5.5 刚体的平面平行运动
刚体的平面平行运动自由度为3
任意点的速度为
vi
ri
代入上面的式子，得角动量为
L
miri ri
mi ri2 ri ri
i
i
A (B C) B(C • A) C( A • B)
对于一固定坐标系有
ri
xi
i
ii
yj j
j
j
zk
k
kk
将上述两式代入角动量的表达式可得
L Lii Lj j Lkk
刚体平动时，刚体上各点的运动情况相 同，具有相同的速度和加速度，因此刚 体上任何一个质点的运动都可以代表刚 体的运动，故刚体平动的自由度为3（等 价于质点运动，3个坐标描述质心位置）
平动既可以是直线运动，也可以是曲线运动
• 刚体的定轴转动
刚体绕一固定轴线转动，称为刚体的定 轴转动，刚体在运动过程中如果有两点 固定不动，那么刚体的运动必然是定轴 转动，两固定点的连线就是转动轴（转 轴上的点都是固定不动的，其他的点则 围绕转轴做圆周运动）
Lz
J
zx
J xy J yy Jzy
r L
J
r
J xz x J yz y J zz z
J矩阵的每个分量均构成一个二阶张量， 称为刚体的惯量张量，J 矩阵称为惯量矩阵
惯量矩阵的对角元素
J J
xx yy
y2 z2 dm z2 x2 dm
J
zz
x2 y2 dm
J yx
i
mi xi yi
xydm
则角动量表达式可以写为
L J xx x J xyy J xz z i
J yx x J yyy J yz z j
J zx x J zyy J zz z k
采用矩阵表示，则角动量可以写为
Lx J xx
L Ly J yx
刚体的动能 = 刚体随质心运动的平动动能 + 刚体ห้องสมุดไป่ตู้质心转动的转动动能
刚体绕O点转动的动能
To
1 2
mi vi 2
1 2
mivi vi
To
1 2
mivi
ri
1
2
ri mivi
To
1 r
2
r L
1 r
2
J
r
1 2
(
J
2
xx x
J
yy
2 y
J
2
zz z
2J yzyz 2J zxzx 2J xyxy )
第五章：刚体力学
§5.1 刚体的运动
• 刚体、刚体运动及自由度
任何物体都可以看成是质点组，如果其中任 何两个质点之间的距离始终保持不变，这样 的物体（质点组）称作刚体
对于大多数固态物体来说，如果在运动过程 中，其大小和形变很小，即使受到拉伸或挤 压，变形也很小，则都可以近似为刚体
• 刚体的平动
在刚体中任意选定一条直线，如果刚体 运动时此直线始终保持平行，则这种运 动称为刚体的平动
刚体的内力不做功，当作用在刚体上的 外力是保守力时，刚体的总机械能守恒
T
V
1 2
mvc
2
1 2
I 2
V
E
讲解例题5.8
• 例题：质量m，半径R的匀质实心圆柱体 在倾角为 的斜面上作纯滚动。其所受 到的摩擦力大小为多少？圆柱体从静止 开始沿斜面滚下，其质心下降的垂直距 离为h时，这时质心的速度为多大？
m
d2 dt 2
rc
F
或
mmyxcc
Fx Fy
在质心坐标系中，刚体对过质心的轴做 定轴转动的角动量为
Lz I
则对质心轴的角动量定理的方程为：
d dt
Lz
I
d
dt
I
d2 dt 2
I&&
Mz
记
则
I M z
I M z
I 为刚体对过质心的转轴的转动惯量
为刚体转动时的角加速度
M z 为诸外力对质心的力矩之和的z分量
刚体绕 l 轴转动的角动量(选l 轴作为坐标 z 轴)
Ll
LeleJl eel l L
el
J
r
Ll 0
0
1
J xx J yx
J zx
J zzr Ir
J xy J yy J zy
J J
xz yz
0 0
r
J zz 1
• 转动惯量 I
I x2 y2 dm r2dm
引
J
xx
mi yi2 zi2
y2 z2 dm
入
记 号
J
yy
J
zz
i
mi
i
mi
i
zi2 xi2 xi2 yi2
z2 x2 dm x2 y2 dm
J
yz
J zy
mi yi zi yzdm
J
zx
J xz
i
mi zi xi
zxdm
i
J
xy
0
v
vA
a aA
定轴转动,取 基点A位于转 轴，则
vvaA0,arrA''
0
r'
平面平 行运动
v a
vA aA
r' r'