《大学物理简明教程》课后答案
大学物理简明教程_课后答案_1章

问题1.1 关于行星运动的地心说和日心说的根本区别是什么?答:地心说和日心说的根本区别在于描述所观测运动时所选取的参考系不同。
1.2 牛顿是怎样统一了行星运动的引力和地面的重力?答:用手向空中抛出任一物体,按照惯性定律,物体应沿抛出方向走直线,但是它最终却还会落到地面上。
这说明地球对地面物体都有一种吸引力。
平抛物体的抛速越大,落地时就离起点越远,惯性和地球吸引力使它在空中划出一条曲线。
地球吸引力也应作用于月球,但月球的不落地,牛顿认为这不过是月球下落运动曲线的弯曲度正好与地球表面的弯曲程度相同。
这样牛顿就把地球对地面物体的吸引力和地球对月球的吸引力统一起来了。
牛顿认为这种引力也作用在太阳和行星、行星与行星之间,称为万有引力。
并认为物体所受的重力就等于地球引力场的引力。
这样牛顿就统一了行星运动的引力和地面的重力。
1.3 什么是惯性? 什么是惯性系?答:任何物体都有保持静止或匀速直线运动状态的特性,这种特性叫惯性。
我们把牛顿第一定律成立的参考系叫惯性系。
而相对于已知惯性系静止或做匀速直线运动的参考系也是惯性系。
1.4 人推动车的力和车推人的力是作用力与反作用力,为什么人可以推车前进呢?答:人推动车的力和车推人的力是作用力与反作用力,这是符合牛顿第三定律的。
但这两两个力是分别作用在两个物体上的。
对于车这个研究对象来说,它就只受到人推动车的力(在不考虑摩擦力的情况下),所以人可以推车前进。
1.5 摩擦力是否一定阻碍物体的运动?答:不一定。
例如汽车前进时,在车轮与路面之间实际上存在着两种摩擦力:静摩擦和滚动摩擦。
前者是驱使汽车前进的驱动力,后者是阻碍汽车前进的阻力。
再如,拖板上放上一物体,拉动拖板,物体可以和拖板一起运动,其原因就是拖板给予了物体向前的摩擦力。
1.6 用天平测出的物体的质量,是引力质量还是惯性质量?两汽车相撞时,其撞击力的产生是源于引力质量还是惯性质量?1答:用天平测出的物体的质量和引力有关,是地球对物体和砝码的引力对天平刀口支撑点力矩平衡测出的质量,所以是引力质量。
大学物理简明教程课后习题参考答案-陈执平

∵
∴
由图中比例关系可知
矢量图
2-1质量为0.5kg的物体沿x轴作直线运动,在沿x方向的力 的作用下,t = 0时其位置与速度分别为x0 =5,v0 =2,求t = 1时该物体的位置和速度.(其中F以N为单位,t以s为单位,x0以m为单位,v0以m/s为单位)
分析当作用于物体的力是时间的函数时,由建立的运动方程积分可以求得速度.所求出的速度必定也是时间的函数,当还需要计算t时刻该物体的位置时,就应该利用速度的定义式 ,再积分求出位置的表示式.
(1)
如图所示,在距A为x远处取厚度为 的薄圆盘,半径为r,面积为 ,体积为 ,因 为一无穷小量,薄圆盘上电荷面密度 ,代入(1)式,得薄圆盘在A点产生的电场强度为
利用几何关系 ,对上式积分得圆锥体在A点的电场强度为
方向为沿对称轴向
5-4求真空中电荷面密度为 的无限大均匀带电平面的场强。
解:选取垂直于平面的圆柱面为高斯面。圆柱侧面上场强 与轴线平行,通过侧面电通量为零,而在两底面 上,场强方向与平面法线方向都一致。
分析由于木块与水平面间存在摩擦,子弹嵌入木块后与弹簧并不构成一个通常意义的弹簧振子,机械能不守恒,但是可以应用功能原理分析摩擦力作功与机械能的变化的关系.
解在子弹 和木块 碰撞的瞬间,因时间很短,木块的位置还未发生改变,因而还不受弹簧的作用,子弹和木块组成的系统水平方向无外力作用,水平方向动量守恒,设子弹质量为m1,速度为v10,木块质量为m2,子弹击中木块后,共同的速度为v2,得
1-1一质点在xy平面内运动,在 时它的位置矢量 ,经 后,其位移 m,求:(1) 时的位矢;(2)在Δt时间内质点的平均速度.
解(1)据题意,在 时刻,该质点的位矢为
大学物理简明教程课后习题以及它的答案

大学物理简明教程习题以及它的答案习题一1-1 解:(1)r ∆是位移的模,∆r 是位矢的模的增量,即r ∆12r r -=,12r r r ϖϖ-=∆; (2)t d d r 是速度的模,即t d d r ==v t sd d . t rd d 只是速度在径向上的分量.∵有rr ˆr =(式中r ˆ叫做单位矢),则t ˆrˆt r t d d d d d d r r r +=式中t rd d 就是速度径向上的分量,∴t r t d d d d 与r 不同如题1-1图所示. 题1-1图 (3)t d d v 表示加速度的模,即t v a d d ϖϖ=,t v d d 是加速度a 在切向上的分量.∵有ττϖϖ(v =v 表轨道节线方向单位矢),所以 t vt v t v d d d d d d ττϖϖϖ+= 式中dt dv 就是加速度的切向分量. (t t rd ˆd d ˆd τϖϖΘ与的运算较复杂,超出教材规定,故不予讨论) 1-2 解:后一种方法正确.因为速度与加速度都是矢量,在平面直角坐标系中,有j y i x r ϖϖϖ+=, j t y i t x t r a jty i t x t r v ϖϖϖϖϖϖϖϖ222222d d d d d d d d d d d d +==+==∴ 故它们的模即为222222222222d d d d d d d d ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=+=⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛=+=t y t x a a a t y t x v v v y x yx而前一种方法的错误可能有两点,其一是概念上的错误,即误把速度、加速度定义作22d d d d t r a t r v == 其二,可能是将22d d d d t r t r 与误作速度与加速度的模。
在1-1题中已说明t rd d 不是速度的模,而只是速度在径向上的分量,同样,22d d t r 也不是加速度的模,它只是加速度在径向分量中的一部分⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-=222d d d d t r t r a θ径。
《大学物理简明教程》课后习题答案(全)之欧阳数创编

《大学物理简明教程》习题解答时间:2021.03.02创作:欧阳数习题一1-1|r ∆|与r ∆有无不同?td d r 和td d r 有无不同?td d v 和td d v 有无不同?其不同在哪里?试举例说明.解:(1)r ∆是位移的模,∆r 是位矢的模的增量,即r ∆12r r -=,12r r r-=∆; (2)td d r 是速度的模,即t d d r ==v ts d d .tr d d 只是速度在径向上的分量.∵有r r ˆr =(式中r ˆ叫做单位矢),则t ˆrˆt r t d d d d d d r r r += 式中trd d 就是速度径向上的分量,∴t r t d d d d 与r 不同如题1-1图所示.题1-1图(3)td d v 表示加速度的模,即tv a d d=,tv d d 是加速度a 在切向上的分量.∵有ττ (v =v 表轨道节线方向单位矢),所以 式中dt dv就是加速度的切向分量.(t t r d ˆd d ˆd τ 与的运算较复杂,超出教材规定,故不予讨论) 1-2 设质点的运动方程为x =x (t ),y =y (t ),在计算质点的速度和加速度时,有人先求出r =22y x +,然后根据v =tr d d ,及a =22d d t r而求得结果;又有人先计算速度和加速度的分量,再合成求得结果,即v =22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛t y t x 及a =222222d d d d ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛t y t x你认为两种方法哪一种正确?为什么?两者差别何在? 解:后一种方法正确.因为速度与加速度都是矢量,在平面直角坐标系中,有j y i x r+=, 故它们的模即为而前一种方法的错误可能有两点,其一是概念上的错误,即误把速度、加速度定义作其二,可能是将22d d d d t r t r 与误作速度与加速度的模。
在1-1题中已说明trd d 不是速度的模,而只是速度在径向上的分量,同样,22d d t r也不是加速度的模,它只是加速度在径向分量中的一部分⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-=222d d d d t r t r a θ径。
《大学物理简明教程》课后习题答案(全)之欧阳法创编

《大学物理简明教程》习题解答习题一1-1|r ∆|与r ∆有无不同?td d r 和td d r 有无不同?td d v 和td d v 有无不同?其不同在哪里?试举例说明. 解:(1)r ∆是位移的模,∆r 是位矢的模的增量,即r ∆12r r -=,12r r r-=∆;(2)td d r 是速度的模,即t d d r ==v ts d d .tr d d 只是速度在径向上的分量.∵有r r ˆr =(式中r ˆ叫做单位矢),则t ˆr ˆt r t d d d d d d r rr += 式中trd d 就是速度径向上的分量,∴t r t d d d d 与r 不同如题1-1图所示.题1-1图(3)td d v 表示加速度的模,即tv a d d =,tv d d 是加速度a 在切向上的分量.∵有ττ (v =v 表轨道节线方向单位矢),所以 式中dt dv就是加速度的切向分量.(tt r d ˆd d ˆd τ 与的运算较复杂,超出教材规定,故不予讨论)1-2 设质点的运动方程为x =x (t ),y =y (t ),在计算质点的速度和加速度时,有人先求出r =22y x +,然后根据v =trd d ,及a =22d d t r而求得结果;又有人先计算速度和加速度的分量,再合成求得结果,即 v =22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛t y t x 及a =222222d d d d ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛t y t x你认为两种方法哪一种正确?为什么?两者差别何在?解:后一种方法正确.因为速度与加速度都是矢量,在平面直角坐标系中,有j y i x r +=, 故它们的模即为而前一种方法的错误可能有两点,其一是概念上的错误,即误把速度、加速度定义作其二,可能是将22d d d d t r t r 与误作速度与加速度的模。
在1-1题中已说明trd d 不是速度的模,而只是速度在径向上的分量,同样,22d d t r也不是加速度的模,它只是加速度在径向分量中的一部分⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-=222d d d d t r t r a θ径。
《大学物理简明教程》课后习题答案(全)之欧阳德创编
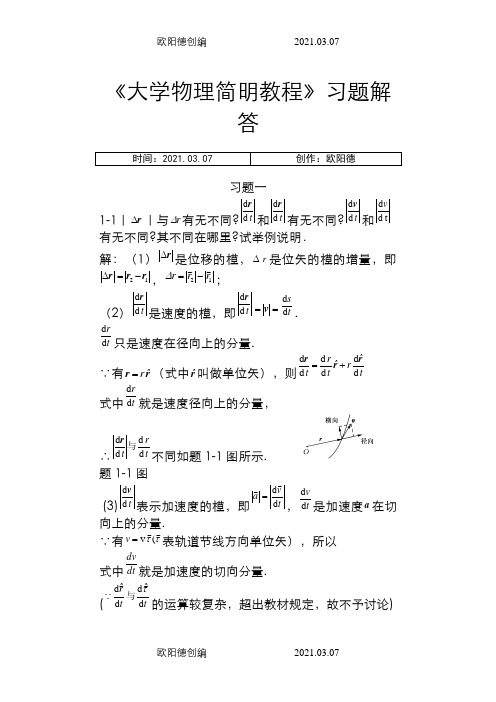
《大学物理简明教程》习题解答习题一1-1|r ∆|与r ∆有无不同?td d r 和td d r 有无不同?td d v 和td d v 有无不同?其不同在哪里?试举例说明.解:(1)r ∆是位移的模,∆r 是位矢的模的增量,即r ∆12r r -=,12r r r-=∆; (2)td d r 是速度的模,即t d d r ==v ts d d .tr d d 只是速度在径向上的分量.∵有r r ˆr =(式中r ˆ叫做单位矢),则t ˆr ˆt r t d d d d d d r rr += 式中trd d 就是速度径向上的分量,∴t r t d d d d 与r 不同如题1-1图所示.题1-1图(3)td d v 表示加速度的模,即tv a d d=,t vd d 是加速度a 在切向上的分量.∵有ττ (v =v 表轨道节线方向单位矢),所以 式中dt dv就是加速度的切向分量.(t t r d ˆd d ˆd τ 与的运算较复杂,超出教材规定,故不予讨论)1-2 设质点的运动方程为x =x (t ),y =y (t ),在计算质点的速度和加速度时,有人先求出r =22y x +,然后根据v =trd d ,及a =22d d t r而求得结果;又有人先计算速度和加速度的分量,再合成求得结果,即v =22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛t y t x 及a =222222d d d d ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛t y t x你认为两种方法哪一种正确?为什么?两者差别何在?解:后一种方法正确.因为速度与加速度都是矢量,在平面直角坐标系中,有j y i x r +=, 故它们的模即为而前一种方法的错误可能有两点,其一是概念上的错误,即误把速度、加速度定义作其二,可能是将22d d d d t r t r 与误作速度与加速度的模。
在1-1题中已说明trd d 不是速度的模,而只是速度在径向上的分量,同样,22d d t r也不是加速度的模,它只是加速度在径向分量中的一部分⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-=222d d d d t r t r a θ径。
《大学物理简明教程》课后习题答案(全)之欧阳科创编

《大学物理简明教程》习题解答习题一1-1|r ∆|与r ∆有无不同?td d r 和td d r 有无不同?td d v 和td d v 有无不同?其不同在哪里?试举例说明. 解:(1)r∆是位移的模,∆r 是位矢的模的增量,即r ∆12r r -=,12r r r-=∆;(2)td d r 是速度的模,即t d d r ==v ts d d .tr d d 只是速度在径向上的分量.∵有r r ˆr =(式中r ˆ叫做单位矢),则t ˆr ˆt r t d d d d d d r rr += 式中trd d 就是速度径向上的分量,∴t r t d d d d 与r 不同如题1-1图所示.题1-1图(3)td d v 表示加速度的模,即tv a d d=,tv d d 是加速度a 在切向上的分量.∵有ττ (v =v 表轨道节线方向单位矢),所以 式中dt dv就是加速度的切向分量.(t t r d ˆd d ˆd τ 与的运算较复杂,超出教材规定,故不予讨论)1-2 设质点的运动方程为x =x (t ),y =y (t ),在计算质点的速度和加速度时,有人先求出r =22y x +,然后根据v =trd d ,及a =22d d t r而求得结果;又有人先计算速度和加速度的分量,再合成求得结果,即v =22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛t y t x 及a =222222d d d d ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛t y t x你认为两种方法哪一种正确?为什么?两者差别何在? 解:后一种方法正确.因为速度与加速度都是矢量,在平面直角坐标系中,有j y i x r +=, 故它们的模即为而前一种方法的错误可能有两点,其一是概念上的错误,即误把速度、加速度定义作其二,可能是将22d d d d t r t r 与误作速度与加速度的模。
在1-1题中已说明t rd d 不是速度的模,而只是速度在径向上的分量,同样,22d d t r也不是加速度的模,它只是加速度在径向分量中的一部分⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-=222d d d d t r t r a θ径。
大学物理简明教程课后习题参考答案-陈执平

∴ 沿径向向外
(3)
∴
5-6真空中有一半径为 ,电量为 的均匀带电球体,求其球内、外各点的电场强度。
解:应用高斯定理计算电场分布.
(1)球体内的电场强度
球体体积为 ,均匀带电,电荷体密度 . 作半径为r 的球形高斯面S1,所包围的球体体积为 ,包围的电荷量为 ,设半径为r处的场强为 ,由高斯定理得
解:
系统初始角动量
物体到达棒端时系统的角动量
由 解得
4-3一细杆长为 、质量为 ,可绕垂直于一端的水平轴自由转动。杆原先处于平衡状态,现有一质量为 的小球沿光滑水平面飞来,恰与杆下端完全弹性碰撞,结果使杆上摆至 处,如图,求小球初速度。
解:小球和直杆系统角动量守恒
系统动能守恒
直杆重力矩作功
联立得
4-4一长 ,质量 的均匀细棒,静止平放于光滑水平面上,它可绕过其端点 且与面垂直的光滑定轴转动。现有一质量为 的小物块,在水平面内沿垂直于棒的方向与棒的另一端点 碰撞并弹回。若碰撞前后物块速率分别为 、 ,求碰撞后棒转动的角速度。
1-1一质点在xy平面内运动,在 时它的位置矢量 ,经 后,其位移 m,求:(1) 时的位矢;(2)在Δt时间内质点的平均速度.
解(1)据题意,在 时刻,该质点的位矢为
(2)在Δt时间内质点的平均速度为
1-3已知质点运动方程为 ,R为常量。求,t=0及 时质点的速度和加速度。
解:(1)
当t=0时,
当t=π/2时,
解由加速度的定义 ,应用牛顿第二定律,可得
分离变量:
两边积分得
由初始条件:t = 0时v=v0 =2,得 ,即
(1)
因 ,上式可写为
分离变量:
两边积分得
由初始条件:t = 0时x=x0 =5,得 ,即
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《大学物理简明教程》课后答案习题11-1 |r ∆|与r ∆ 有无不同?t d d r 和t d d r 有无不同? t d d v 和td d v 有无不同?其不同在哪里?试举例说明.解:(1)r ∆是位移的模,∆r 是位矢的模的增量,即r ∆12r r -=,12r r r-=∆;(2)t d d r 是速度的模,即t d d r ==v ts d d . trd d 只是速度在径向上的分量. ∵有r r ˆr =(式中r ˆ叫做单位矢),则tˆr ˆt r t d d d d d d rr r +=式中trd d 就是速度径向上的分量, ∴trt d d d d 与r 不同如题1-1图所示.题1-1图(3)t d d v 表示加速度的模,即t v a d d =,tv d d 是加速度a 在切向上的分量.∵有ττ(v =v 表轨道节线方向单位矢),所以tvt v t v d d d d d d ττ+= 式中dt dv就是加速度的切向分量. (tt r d ˆd d ˆd τ 与的运算较复杂,超出教材规定,故不予讨论)1-5 质点沿x 轴运动,其加速度和位置的关系为 a =2+62x ,a 的单位为2s m -⋅,x 的单位为 m. 质点在x =0处,速度为101s m -⋅,试求质点在任何坐标处的速度值. 解: ∵ xvv t x x v t v a d d d d d d d d ===分离变量: x x adx d )62(d 2+==υυ 两边积分得c x x v ++=322221 由题知,0=x 时,100=v ,∴50=c∴ 13s m 252-⋅++=x x v1-7 一质点沿半径为1 m 的圆周运动,运动方程为 θ=2+33t ,θ式中以弧度计,t 以秒计,求:(1) t =2 s 时,质点的切向和法向加速度;(2)当加速度的方向和半径成45°角时,其角位移是多少?解: t tt t 18d d ,9d d 2====ωβθω (1)s 2=t 时, 2s m 362181-⋅=⨯⨯==βτR a2222s m 1296)29(1-⋅=⨯⨯==ωR a n(2)当加速度方向与半径成ο45角时,有145tan ==︒na a τ即 βωR R =2亦即 t t 18)9(22= 则解得 923=t 于是角位移为rad 67.29232323=⨯+=+=t θ习题22-3 质点在流体中作直线运动,受与速度成正比的阻力kv (k 为常数)作用,t =0时质点的速度为0v ,证明(1) t 时刻的速度为v =t mk ev )(0-;(2) 由0到t 的时间内经过的距离为x =(k mv 0)[1-t m k e )(-];(3)停止运动前经过的距离为)(0kmv ;(4)证明当k m t =时速度减至0v 的e1,式中m 为质点的质量. 答: (1)∵ tvm kv a d d =-= 分离变量,得m tk v v d d -=即 ⎰⎰-=v v t mtk v v 00d d m kte v v -=ln ln 0∴ tm k e v v -=0(2) ⎰⎰---===tttm k m ke kmv t ev t v x 000)1(d d(3)质点停止运动时速度为零,即t →∞, 故有 ⎰∞-=='00d kmv t ev x tm k (4)当t=km时,其速度为 ev e v ev v km m k 0100===-⋅- 即速度减至0v 的e1.2-6 一颗子弹由枪口射出时速率为10s m -⋅v ,当子弹在枪筒内被加速时,它所受的合力为F =(bt a -)N(b a ,为常数),其中t 以秒为单位:(1)假设子弹运行到枪口处合力刚好为零,试计算子弹走完枪筒全长所需时间;(2)求子弹所受的冲量.(3)求子弹的质量. 解: (1)由题意,子弹到枪口时,有0)(=-=bt a F ,得ba t =(2)子弹所受的冲量⎰-=-=t bt at t bt a I 0221d )(将bat =代入,得 ba I 22=(3)由动量定理可求得子弹的质量202bv a v I m ==2-7 设N 67j i F -=合.(1) 当一质点从原点运动到m 1643k j i r++-=时,求F 所作的功.(2)如果质点到r 处时需0.6s ,试求平均功率.(3)如果质点的质量为1kg ,试求动能的变化.解: (1)由题知,合F为恒力,∴ )1643()67(k j i j i r F A++-⋅-=⋅=合J 452421-=--= (2) w 756.045==∆=t A P (3)由动能定理,J 45-==∆A E k2-8 如题2-18图所示,一物体质量为2kg ,以初速度0v =3m ·s -1从斜面A 点处下滑,它与斜面的摩擦力为8N ,到达B 点后压缩弹簧20cm 后停止,然后又被弹回,求弹簧的劲度系数和物体最后能回到的高度.解: 取木块压缩弹簧至最短处的位置为重力势能零点,弹簧原 长处为弹性势能零点。
则由功能原理,有⎪⎭⎫ ⎝⎛︒+-=-37sin 212122mgs mv kx s f r 222137sin 21kx s f mgs mv k r -︒+=式中m 52.08.4=+=s ,m 2.0=x ,再代入有关数据,解得-1m N 1390⋅=k题2-8图再次运用功能原理,求木块弹回的高度h '2o 2137sin kx s mg s f r -'='-代入有关数据,得 m 4.1='s , 则木块弹回高度m 84.037sin o ='='s h2-15 如题2-15图所示,一匀质细杆质量为m ,长为l ,可绕过一端O 的水平轴自由转动,杆于水平位置由静止开始摆下.求: (1)初始时刻的角加速度; (2)杆转过θ角时的角速度. 解: (1)由转动定律,有β)31(212ml mg= ∴ lg23=β(2)由机械能守恒定律,有22)31(21sin 2ωθml l mg =∴ lg θωsin 3=题2-15图习题33-7 试说明下列各量的物理意义. (1)kT 21 (2)kT 23 (3)kT i2 (4)RT i M M mol 2 (5)RT i 2 (6)RT 23解:(1)在平衡态下,分子热运动能量平均地分配在分子每一个自由度上的能量均为k 21T . (2)在平衡态下,分子平均平动动能均为kT 23.(3)在平衡态下,自由度为i 的分子平均总能量均为kT i2. (4)由质量为M ,摩尔质量为mol M ,自由度为i 的分子组成的系统的内能为RT iM M 2mol .(5) 1摩尔自由度为i 的分子组成的系统内能为RT i2. (6) 1摩尔自由度为3的分子组成的系统的内能RT 23,或者说热力学体系内,1摩尔分子的平均平动动能之总和为RT 23.3-11 1mol 氢气,在温度为27℃时,它的平动动能、转动动能和内能各是多少? 解:理想气体分子的能量RT iE 2υ= 平动动能 3=t 5.373930031.823=⨯⨯=t E J 转动动能 2=r 249330031.822=⨯⨯=r E J内能5=i 5.623230031.825=⨯⨯=i E J习题44-6 如题4-6图所示,一系统由状态a 沿acb 到达状态b 的过程中,有350 J 热量传入系统,而系统作功126 J .(1)若沿adb 时,系统作功42 J ,问有多少热量传入系统?(2)若系统由状态b 沿曲线ba 返回状态a 时,外界对系统作功为84 J ,试问系统是吸热还是放热?热量传递是多少?题4-6图解:由abc 过程可求出b 态和a 态的内能之差 A E Q +∆=224126350=-=-=∆A Q E Jabd 过程,系统作功42=A J26642224=+=+∆=A E Q J 系统吸收热量ba 过程,外界对系统作功84-=A J30884224-=--=+∆=A E Q J 系统放热4-7 1 mol 单原子理想气体从300 K 加热到350 K ,问在下列两过程中吸收了多少热量?增加了多少内能?对外作了多少功? (1)体积保持不变; (2)压力保持不变. 解:(1)等体过程由热力学第一定律得E Q ∆=吸热 )(2)(1212V T T R iT T C E Q -=-=∆=υυ 25.623)300350(31.823=-⨯⨯=∆=E Q J 对外作功 0=A(2)等压过程)(22)(1212P T T R i T T C Q -+=-=υυ 吸热 75.1038)300350(31.825=-⨯⨯=Q J )(12V T T C E -=∆υ 内能增加 25.623)300350(31.823=-⨯⨯=∆E J 对外作功 5.4155.62375.1038=-=∆-=E Q A J4-8 0.01 m 3氮气在温度为300 K 时,由0.1 MPa(即1 atm)压缩到10 MPa .试分别求氮气经等温及绝热压缩后的(1)体积;(2)温度;(3)各过程对外所作的功. 解:(1)等温压缩 300=T K 由2211V p V p = 求得体积 3211210101.0101-⨯=⨯==p V p V 3m 对外作功21112ln lnp pV p V V VRT A == 01.0ln 01.010013.115⨯⨯⨯⨯=31067.4⨯-=J(2)绝热压缩R C 25V =57=γ 由绝热方程 γγ2211V p V p = γγ/12112)(p V p V =1121/12112)()(V p pp V p V γγγ== 3411093.101.0)101(-⨯=⨯=m 由绝热方程γγγγ---=22111p T p T 得K 579)10(30024.04.1111212=⨯==--T p p T T γγγγ热力学第一定律A E Q +∆=,0=Q 所以 )(12molT T C M MA V --= RT M MpV mol=,)(2512111T T R RT V p A --=35105.23)300579(25300001.010013.1⨯-=-⨯⨯⨯⨯-=A J4-10 一卡诺热机在1000 K 和300 K 的两热源之间工作,试计算 (1)热机效率;(2)若低温热源不变,要使热机效率提高到80%,则高温热源温度需提高多少? (3)若高温热源不变,要使热机效率提高到80%,则低温热源温度需降低多少? 解:(1)卡诺热机效率 121T T -=η %7010003001=-=η (2)低温热源温度不变时,若%8030011=-=T η 要求 15001=T K ,高温热源温度需提高500K (3)高温热源温度不变时,若%80100012=-=T η 要求 2002=T K ,低温热源温度需降低100K习题88-1 质量为kg 10103-⨯的小球与轻弹簧组成的系统,按)SI ()328cos(1.0ππ+=x 的规律作谐振动,求:(1)振动的周期、振幅和初位相及速度与加速度的最大值;(2)最大的回复力、振动能量、平均动能和平均势能,在哪些位置上动能与势能相等? (3)s 52=t 与s 11=t 两个时刻的位相差;解:(1)设谐振动的标准方程为)cos(0φω+=t A x ,则知:3/2,s 412,8,m 1.00πφωππω===∴==T A 又 πω8.0==A v m 1s m -⋅ 51.2=1s m -⋅2.632==A a m ω2s m -⋅(2) N 63.0==m m a FJ 1016.32122-⨯==m mv E J 1058.1212-⨯===E E E k p当p k E E =时,有p E E 2=, 即)21(212122kA kx ⋅= ∴ m 20222±=±=A x (3) ππωφ32)15(8)(12=-=-=∆t t8-3 一质量为kg 10103-⨯的物体作谐振动,振幅为cm 24,周期为s 0.4,当0=t 时位移为cm 24+.求:(1)s 5.0=t 时,物体所在的位置及此时所受力的大小和方向; (2)由起始位置运动到cm 12=x 处所需的最短时间; (3)在cm 12=x 处物体的总能量.解:由题已知 s 0.4,m 10242=⨯=-T A ∴ 1s rad 5.02-⋅==ππωT又,0=t 时,0,00=∴+=φA x 故振动方程为m )5.0cos(10242t x π-⨯=(1)将s 5.0=t 代入得0.17m m )5.0cos(102425.0=⨯=-t x πN102.417.0)2(10103232--⨯-=⨯⨯⨯-=-=-=πωxm ma F方向指向坐标原点,即沿x 轴负向. (2)由题知,0=t 时,00=φ,t t =时 3,0,20πφ=<+=t v A x 故且 ∴ s 322/3==∆=ππωφt(3)由于谐振动中能量守恒,故在任一位置处或任一时刻的系统的总能量均为J101.7)24.0()2(10102121214223222--⨯=⨯⨯⨯===πωA m kA E8-5 图为两个谐振动的t x -曲线,试分别写出其谐振动方程.题4-8图解:由题4-8图(a),∵0=t 时,s 2,cm 10,,23,0,0000===∴>=T A v x 又πφ 即 1s rad 2-⋅==ππωT故 m )23cos(1.0ππ+=t x a 由题4-8图(b)∵0=t 时,35,0,2000πφ=∴>=v A x 01=t 时,22,0,0111ππφ+=∴<=v x又 ππωφ253511=+⨯= ∴ πω65= 故 m t x b )3565cos(1.0ππ+=8-6 有两个同方向、同频率的简谐振动,其合成振动的振幅为m 20.0,位相与第一振动的位相差为6π,已知第一振动的振幅为m 173.0,求第二个振动的振幅以及第一、第二两振动的位相差.题4-11图解:由题意可做出旋转矢量图如下.由图知01.02/32.0173.02)2.0()173.0(30cos 222122122=⨯⨯⨯-+=︒-+=A A A A A∴ m 1.02=A设角θ为O AA 1,则θcos 22122212A A A A A -+=即 01.0173.02)02.0()1.0()173.0(2cos 2222122221=⨯⨯-+=-+=A A A A A θ即2πθ=,这说明,1A 与2A 间夹角为2π,即二振动的位相差为2π. 习题99-5 沿绳子传播的平面简谐波的波动方程为y =0.05cos(10x t ππ4-),式中x ,y 以米计,t 以秒计.求:(1)波的波速、频率和波长;(2)绳子上各质点振动时的最大速度和最大加速度;(3)求x =0.2m 处质点在t =1s 时的位相,它是原点在哪一时刻的位相?这一位相所代表的运动状态在t =1.25s 时刻到达哪一点?解: (1)将题给方程与标准式)22cos(x t A y λππυ-=相比,得振幅05.0=A m ,频率5=υ1-s ,波长5.0=λm ,波速5.2==λυu 1s m -⋅.(2)绳上各点的最大振速,最大加速度分别为ππω5.005.010max =⨯==A v 1s m -⋅222max 505.0)10(ππω=⨯==A a 2s m -⋅(3)2.0=x m 处的振动比原点落后的时间为08.05.22.0==u x s 故2.0=x m ,1=t s 时的位相就是原点(0=x ),在92.008.010=-=t s 时的位相, 即 2.9=φπ.设这一位相所代表的运动状态在25.1=t s 时刻到达x 点,则825.0)0.125.1(5.22.0)(11=-+=-+=t t u x x m9-8 如题9-8图所示,设B 点发出的平面横波沿BP 方向传播,它在B 点的振动方程为t y π2cos 10231-⨯=;C 点发出的平面横波沿CP 方向传播,它在C 点的振动方程为)2cos(10232ππ+⨯=-t y ,本题中y 以m 计,t 以s 计.设BP =0.4m ,CP =0.5 m ,波速u =0.2m ·s -1,求:(1)两波传到P 点时的位相差;(2)当这两列波的振动方向相同时,P 处合振动的振幅;*(3)当这两列波的振动方向互相垂直时,P 处合振动的振幅.解: (1) )(2)(12BP CP ---=∆λπϕφφ)(BP CP u --=ωπ0)4.05.0(2.02=--=ππ题5-19图(2)P 点是相长干涉,且振动方向相同,所以321104-⨯=+=A A A P m(3)若两振动方向垂直,又两分振动位相差为0,这时合振动轨迹是通过Ⅱ,Ⅳ象限的直线,所以合振幅为33122211083.210222--⨯=⨯==+=A A A A m9-9 一驻波方程为y =0.02cos20x cos750t (SI),求:(1)形成此驻波的两列行波的振幅和波速;(2)相邻两波节间距离.解: (1)取驻波方程为 t u x A y πυπυ2cos 2cos2= 故知 01.0202.0==A m 7502=πυ,则πυ2750=, 202=uπυ ∴ 5.37202/7502202=⨯==πππυu 1s m -⋅ (2)∵314.01.020/2====πυπυυλu m 所以相邻两波节间距离 157.02==∆λx m9-11汽车驶过车站时,车站上的观测者测得汽笛声频率由1200Hz 变到了1000 Hz ,设空气中声速为330m ·s -1,求汽车的速率.解: 设汽车的速度为s v ,汽车在驶近车站时,车站收到的频率为 01υυsv u u -= 汽车驶离车站时,车站收到的频率为02υυs v u u +=联立以上两式,得:3010012001000120030021211=+-⨯=+-=υυυυυu 1s m -⋅。
