悬链线坐标计算
悬链线方程的推导
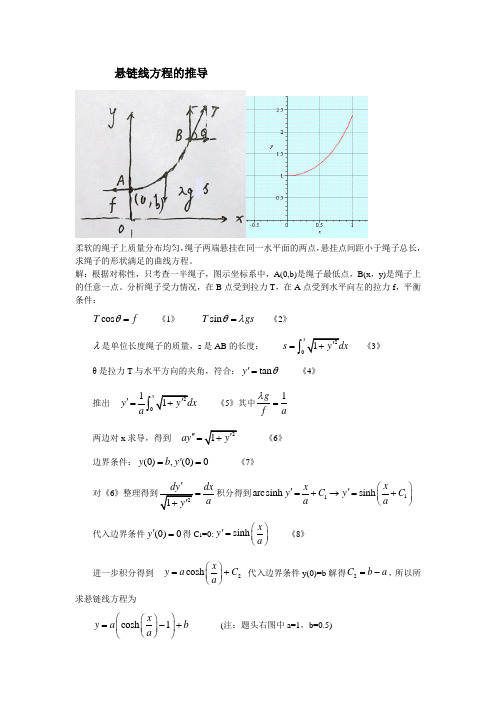
悬链线方程的推导
柔软的绳子上质量分布均匀,绳子两端悬挂在同一水平面的两点,悬挂点间距小于绳子总长,求绳子的形状满足的曲线方程。
解:根据对称性,只考查一半绳子,图示坐标系中,A(0,b)是绳子最低点,B(x ,y)是绳子上的任意一点。
分析绳子受力情况,在B 点受到拉力T ,在A 点受到水平向左的拉力f ,平衡条件:
cos T f θ= 《1》 sin T gs θλ= 《2》
λ是单位长度绳子的质量,s 是AB 的长度:
0s =⎰ 《3》
θ是拉力T 与水平方向的夹角,符合:tan y θ'= 《4》
推出
01y d x a '=⎰ 《5》其中1g f a
λ= 两边对x 求导,得到
a y
''= 《6》 边界条件:(0),(0)0y b y '== 《7》
对《6
dx a '
=积分得到1arcsinh x y C a '=+1sinh x y C a ⎛⎫'→=+ ⎪⎝⎭
代入边界条件(0)0y '=得C 1=0:sinh x y a ⎛⎫'= ⎪⎝⎭
《8》 进一步积分得到 2c o s h x y a C a ⎛⎫=+ ⎪⎝⎭
代入边界条件y(0)=b 解得2C b a =-,
所以所求悬链线方程为 cosh 1x y a b a ⎛⎫⎛⎫=-+ ⎪ ⎪⎝⎭⎝
⎭ (注:题头右图中a=1,b=0.5)。
悬链线长度计算

悬链线长度计算摘要:1.悬链线长度计算公式及原理2.悬链线长度的应用场景3.悬链线长度在工程实践中的重要性4.如何使用数学方法计算悬链线长度5.实例分析:不同形状的悬链线长度计算6.悬链线长度计算在实际工程中的案例分享7.总结与展望:悬链线长度计算的发展趋势与应用前景正文:悬链线长度计算在工程领域具有很高的实用价值,它可以应用于桥梁、电缆、塔架等各种工程结构的设计与优化。
本文将从悬链线长度的计算公式、应用场景、重要性等方面进行全面阐述,并通过实例分析与案例分享,让大家更好地理解和掌握悬链线长度的计算方法。
一、悬链线长度计算公式及原理悬链线长度计算的核心公式为:L = 2πε / γ,其中L表示悬链线长度,ε为悬链线的曲率半径,γ为悬链线的倾斜角度。
根据这一公式,我们可以计算出不同形状的悬链线长度。
二、悬链线长度的应用场景悬链线长度在工程实践中具有重要意义,它可以用于以下几个方面:1.桥梁结构设计:通过计算悬链线长度,可以确定桥梁的主跨长度,从而保证桥梁的稳定性和安全性。
2.电缆布线设计:在输电线路设计中,悬链线长度的计算有助于优化电缆的布设方式,降低电缆的张力,提高输电效率。
3.塔架结构设计:通过计算悬链线长度,可以确定塔架的结构形式和尺寸,确保塔架在风力等外力作用下的稳定性。
三、悬链线长度在工程实践中的重要性悬链线长度计算在工程实践中具有以下重要性:1.保证结构稳定性:准确计算悬链线长度,有助于工程结构在设计阶段就具备良好的稳定性。
2.优化结构形式:通过计算悬链线长度,可以优化结构形式,降低成本,提高工程效益。
3.提高设计质量:悬链线长度计算有助于发现问题,提前预防潜在安全隐患,提高设计质量。
四、如何使用数学方法计算悬链线长度1.确定悬链线的曲率半径:根据悬链线的形状,通过数学方法计算出曲率半径。
2.确定悬链线的倾斜角度:根据悬链线的形状和受力情况,通过数学方法计算出倾斜角度。
3.代入公式计算:将曲率半径和倾斜角度代入悬链线长度计算公式,得出结果。
悬链线方程
通常任何材料包括导线在内,都具有一定的刚性,但由于悬挂在杆塔上的一档导线相对较长,因此导线材料的刚性对其几何形状的影响很小,故在计算中假定:(1)导线为理想的柔索。
因此,导线只承受轴向张力(或拉力),任意一点的弯矩为零。
这样导线力学计算可应用理论力学中的柔索理论进行计算。
(2)作用在导线上的荷载均指同一方向,且沿导线均匀分布。
一、悬链线方程及曲线弧长1.悬链线方程为了分析方便,我们先从悬挂点等高,即相邻杆塔导线悬挂点无高差的情况讨论导线的应力及几何关系。
实际上,导线悬在空中的曲线形态,从数学角度用什么方程来描述是进行导线力学分析的前题。
由于假定视导线为柔索,则可按照理论力学中的悬链线关系来进行分析,即将导线架设在空中的几何形态视为悬链形态,而由此导出的方程式为悬链线方程。
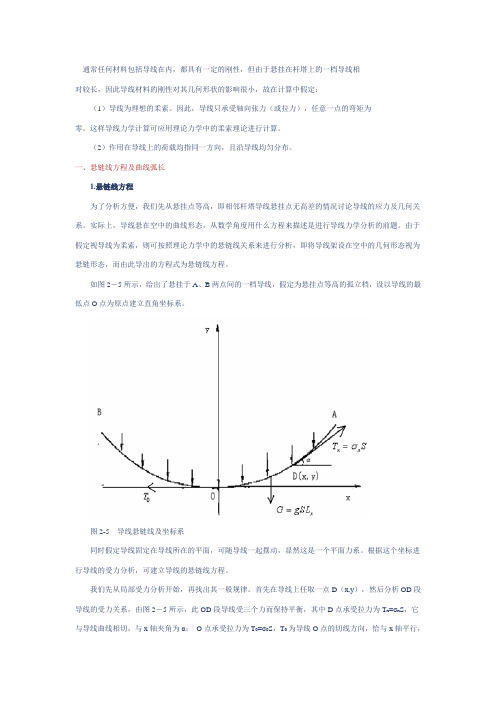
如图2-5所示,给出了悬挂于A、B两点间的一档导线,假定为悬挂点等高的孤立档,设以导线的最低点O点为原点建立直角坐标系。
图2-5导线悬链线及坐标系同时假定导线固定在导线所在的平面,可随导线一起摆动,显然这是一个平面力系。
根据这个坐标进行导线的受力分析,可建立导线的悬链线方程。
我们先从局部受力分析开始,再找出其一般规律。
首先在导线上任取一点D(x,y),然后分析OD段导线的受力关系,由图2-5所示,此OD段导线受三个力而保持平衡,其中D点承受拉力为T x=σx S,它与导线曲线相切,与x轴夹角为α;O点承受拉力为T0=σ0S,T0为导线O点的切线方向,恰与x轴平行,故又称水平张力;此外还有OD段导线自身的荷载为G=gSL x,其中L x为OD段导线的弧长。
将OD段导线的受力关系画为一个三角形表示,如图2-6所示,图2-6导线受力情况由静力学平衡条件可知,在平面坐标系中,其水平分力,垂直分力的代数和分别等于零。
或沿x轴或y轴上分力代数和分别等于零。
垂直方向分力G=T x sinα=gSL x;水平方向分为T0=T x cosα=σ0S。
悬链线方程
通常任何材料包括导线在内,都具有一定的刚性,但由于悬挂在杆塔上的一档导线相对较长,因此导线材料的刚性对其几何形状的影响很小,故在计算中假定:(1)导线为理想的柔索。
因此,导线只承受轴向张力(或拉力),任意一点的弯矩为零。
这样导线力学计算可应用理论力学中的柔索理论进行计算.(2)作用在导线上的荷载均指同一方向,且沿导线均匀分布.一、悬链线方程及曲线弧长1.悬链线方程为了分析方便,我们先从悬挂点等高,即相邻杆塔导线悬挂点无高差的情况讨论导线的应力及几何关系。
实际上,导线悬在空中的曲线形态,从数学角度用什么方程来描述是进行导线力学分析的前题。
由于假定视导线为柔索,则可按照理论力学中的悬链线关系来进行分析,即将导线架设在空中的几何形态视为悬链形态,而由此导出的方程式为悬链线方程。
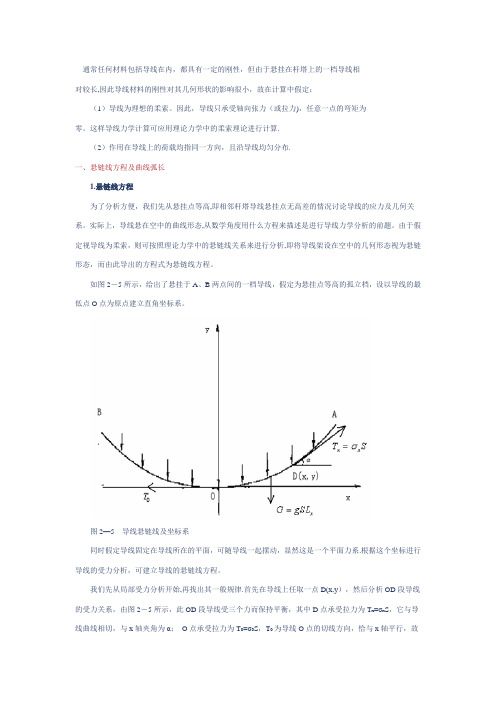
如图2-5所示,给出了悬挂于A、B两点间的一档导线,假定为悬挂点等高的孤立档,设以导线的最低点O点为原点建立直角坐标系。
图2—5导线悬链线及坐标系同时假定导线固定在导线所在的平面,可随导线一起摆动,显然这是一个平面力系.根据这个坐标进行导线的受力分析,可建立导线的悬链线方程。
我们先从局部受力分析开始,再找出其一般规律.首先在导线上任取一点D(x,y),然后分析OD段导线的受力关系,由图2-5所示,此OD段导线受三个力而保持平衡,其中D点承受拉力为T x=σx S,它与导线曲线相切,与x轴夹角为α;O点承受拉力为T0=σ0S,T0为导线O点的切线方向,恰与x轴平行,故又称水平张力;此外还有OD段导线自身的荷载为G=gSL x,其中L x为OD段导线的弧长。
将OD段导线的受力关系画为一个三角形表示,如图2-6所示,图2-6导线受力情况由静力学平衡条件可知,在平面坐标系中,其水平分力,垂直分力的代数和分别等于零.或沿x轴或y轴上分力代数和分别等于零。
垂直方向分力G=T x sinα=gSL x;水平方向分为T0=T x cosα=σ0S.其中σ0、T0为导线最低点的应力和张力,σx、T x为导线任一点的应力和张力,S、g为导线截面和比载.将上述二式相比,则可求得导线任意一点D的斜率为:(2—10)由微分学知识可知,曲线上任一点的导数即为切线的斜率。
悬链线坐标计算程序

悬链线坐标计算程序悬链线是一种理想化的模型,用于描述物体自身重力和张力平衡的关系。
在物理学和工程学中,悬链线常常被用于计算和分析各种结构的力学性质。
本文将介绍悬链线的坐标计算程序,以及它在实际问题中的应用。
我们来了解一下什么是悬链线。
悬链线是指在重力作用下,一个柔性、均匀且无质量的绳子所呈现的形状。
在悬链线的模型中,绳子的张力在各个点上都是相等的,同时满足重力和张力的平衡条件。
悬链线的形状是一个平滑曲线,通常被描述为一个无法解析求解的函数,因此需要使用数值计算方法来确定其坐标。
为了计算悬链线的坐标,我们可以使用迭代方法。
首先,我们假设绳子的初始形状为一条直线段。
然后,通过迭代计算,逐步调整绳子的形状,直到达到所期望的精度要求为止。
在每一步迭代中,我们根据当前绳子的形状,计算绳子上各个点的张力和重力分量,并根据平衡条件调整绳子的形状。
在实际计算中,我们可以将悬链线分成若干个小段,每个小段内的形状近似为一条直线。
然后,我们可以根据每个小段的起始点和长度,计算出小段的末端坐标,并将其作为下一个小段的起始点。
通过重复这个过程,我们可以逐步计算出悬链线上各个点的坐标。
悬链线的坐标计算程序可以使用各种编程语言来实现,例如Python、C++等。
在程序中,我们需要定义悬链线的长度、重力加速度等参数,并设置迭代的精度要求。
然后,我们可以使用循环结构来逐步计算悬链线的坐标,直到达到所要求的精度为止。
最后,我们可以将计算得到的悬链线坐标输出到文件或打印在屏幕上,以供进一步分析和应用。
悬链线的坐标计算程序在工程学和物理学中有着广泛的应用。
例如,在桥梁和吊塔的设计中,我们需要计算悬链线的形状和张力分布,以确定结构的稳定性和安全性。
此外,悬链线的模型还被用于分析电缆、输送带等柔性结构的力学性质,以及模拟绳索、链条等物体的运动和变形。
悬链线的坐标计算程序是一种重要的工具,用于分析和计算各种结构的力学性质。
通过迭代方法,我们可以逐步计算出悬链线上各个点的坐标,并通过这些坐标来分析和应用悬链线模型。
悬链线坐标计算程序

悬链线坐标计算程序悬链线是一种特殊的曲线,其形状类似于一条悬挂的链条。
在工程学和物理学中,悬链线的数学模型被广泛应用于桥梁、电线、杆塔等结构的设计和分析。
为了计算悬链线的坐标,可以编写一个简单的计算程序。
我们需要了解悬链线的一些基本概念。
悬链线是一条自由悬挂的曲线,在重力的作用下,曲线的形状会发生变化。
悬链线上的每个点都受到重力的作用,因此曲线的形状是由重力平衡条件决定的。
为了计算悬链线的坐标,我们可以采用数值计算的方法。
具体步骤如下:1. 假设悬链线的起始点坐标为(x0, y0),重力加速度为g。
选择合适的步长h。
2. 从起始点开始,依次计算曲线上的每个点的坐标。
假设当前点的坐标为(xi, yi)。
3. 根据重力平衡条件,计算当前点的斜率。
斜率的计算公式为:k = -g * (xi - x0) / (yi - y0)4. 根据斜率和步长h,计算下一个点的坐标。
下一个点的坐标可以通过以下公式计算:xi+1 = xi + hyi+1 = yi + k * h5. 重复步骤4,直到达到所需的终点。
通过编写一个悬链线坐标计算程序,我们可以方便地计算悬链线上任意点的坐标。
程序的基本框架如下:```pythondef catenary_coordinates(x0, y0, g, h, end):# 初始化起始点坐标xi = x0yi = y0# 计算悬链线上的每个点的坐标while xi <= end:# 计算斜率k = -g * (xi - x0) / (yi - y0)# 计算下一个点的坐标xi += hyi += k * h# 输出当前点的坐标print("悬链线上点({:.2f}, {:.2f})".format(xi, yi))# 主程序入口if __name__ == "__main__":# 设置悬链线的起始点坐标、重力加速度、步长和终点坐标x0 = 0.0y0 = 0.0g = 9.8h = 0.1end = 10.0# 调用悬链线坐标计算函数catenary_coordinates(x0, y0, g, h, end)```通过运行上述程序,我们可以得到悬链线上任意点的坐标。
求解悬链线拱坐标的优化算法

知拱轴线的弧线长度为 s 起点 横坐标为 z , , 求终点横坐标 z 3 影部分所示。如果在区间[ 1墨] 满足上 述条件则 调整步 长 ;) 墨一 , 不 已知上弦与下 弦的距离为 D及腹杆与拱轴线 交点横坐标 为 z , 腹 至原 步长 的 12 / 。重 复计算 上式 , 整 步长直 到满 足条 件 为止 。 调 杆垂直于拱轴线 , 求腹杆上下弦的交点坐标 ( ,t ,x ,b 。 Y)( bY ) 该方法的算法框图如图 3 示。 所
TANG W e i
Ab ta t Th o g i e o n i a c f me h ig e t n i s r c : r u h s e r c n a s n eo t s Xi n e Br es c i GUIXI h g wa n t e in d c me trs a c ig.t ea t o n — d o n — N ih y a d isd s o u n ee r h n g h u h r a a lz s t e c u e ftaf c ie tfe u n l a p n d i h ssc in fo h g wa ,v h c ,e v r n n n n g me t n d p o o e e— y e h a ss o r f ca cd n q e t h p e e t i e t m h y e i e n i me t d ma a e n ,a r p ssr l i r y n o r i l o a
提高求解速度。求横坐标使用牛顿迭代 法 , 如果 找到尽量接 近真 实解 的初始解可 以大幅提高计算性能 , 中对此进行 了分析 。 文
1 问题
若取坐标原点在拱顶 , z轴向左 , 向下 , Y轴 则拱轴线方程为 :
(完整版)悬链线知识点归纳总结

(完整版)悬链线知识点归纳总结1. 什么是悬链线?悬链线(catenary)是指理想情况下由均匀质地、可弯曲且自由悬挂的弦线形成的曲线形状。
在重力的作用下,悬链线形成一个平衡状态,其拉力在各点上的方向总是指向曲线的切线方向。
2. 悬链线的特性- 爱德蒙·哈利·觉斯(Edmond Halley)首先对悬链线进行了研究,并发现悬链线的特性可以由双曲余弦(hyperbolic cosine)函数表示。
- 悬链线是对称的,其左右两侧的曲线形状相同。
- 悬链线的曲率半径是变化的,最大曲率半径位于中央点处,逐渐减小,直至趋于无穷大。
- 悬链线是稳定的,任何一点受力后都会回到平衡状态。
3. 悬链线的应用领域悬链线主要应用于以下领域:- 建筑物和桥梁设计:悬链线可以用于确定建筑物和桥梁的最佳弧线形状,以承受安全荷载。
- 电线和电缆布置:悬链线形状可确保电线和电缆在自身重量下保持合适的张力。
- 自然科学研究:悬链线可以模拟自然界中的曲线形状,例如植物的枝干、动物的身体等。
4. 悬链线的计算方法计算悬链线的形状和参数可以使用以下方法:- 数值方法:通过计算机程序使用数值方法求解悬链线的方程。
- 解析方法:通过使用微积分和复杂方程推导出悬链线方程的解析解。
- 近似方法:对于特定情况,可以使用近似公式或经验公式估算悬链线的形状和参数。
5. 悬链线的例子以下是一些悬链线的实际例子:- 自由悬链线:没有外力作用,只受到重力拉力影响的悬链线。
例如,悬挂在两个支点上的灯泡线。
- 悬链桥:采用悬链线形状的桥梁。
例如,布鲁克林大桥。
- 高压电缆:电力输送中使用的悬链线形状的电缆。
6. 结论悬链线作为一种特殊的曲线形状,在建筑和电力等领域有着重要的应用。
了解悬链线的特性、计算方法和实际例子有助于我们更好地理解和运用它的优点。
