最新悬链线方程培训资料
悬挂链运输安全培训课件

悬挂链运输安全培训课件悬挂链运输安全培训课件悬挂链运输是一种常见的货物运输方式,广泛应用于工业生产和物流领域。
然而,由于悬挂链运输涉及到重物的悬挂和悬挂链的运行,存在一定的安全隐患。
为了提高悬挂链运输的安全性,减少事故发生的概率,我们需要进行相关的安全培训。
本次培训课件将重点介绍悬挂链运输的安全知识和操作技巧,帮助大家更好地理解和掌握悬挂链运输的安全要点。
一、悬挂链运输的基本原理悬挂链运输是利用链条将货物悬挂起来,通过链条的运动将货物从一个地方转移到另一个地方。
悬挂链通常由链环、链节和连接件组成,具有承重能力强、运输效率高的特点。
在悬挂链运输中,货物的安全悬挂和链条的平稳运行是保证运输安全的关键。
二、悬挂链运输的安全要点1. 货物悬挂安全:在进行悬挂链运输时,需要确保货物的悬挂安全。
首先,要选择适当的悬挂点,确保悬挂点能够承受货物的重量,并且悬挂点应固定可靠。
其次,要正确使用吊装工具,确保吊具与货物之间的连接牢固可靠。
最后,要注意货物的平衡悬挂,避免出现重心不稳导致的安全事故。
2. 链条运行安全:悬挂链的运行安全对于整个运输过程至关重要。
在链条运行过程中,需要注意链条的张紧度,确保链条与滑轮之间的配合良好。
此外,要定期检查链条的磨损情况,及时更换磨损严重的链条,避免链条断裂导致的事故发生。
3. 工作环境安全:悬挂链运输涉及到工作环境的安全。
在悬挂链运输过程中,需要确保工作环境的整洁和通风良好,避免因为杂物堆积或者空气不流通导致的安全事故。
此外,要注意工作人员的个人防护,佩戴好安全帽、防护眼镜等必要的防护用品。
三、悬挂链运输的事故案例分析为了更加深入地了解悬挂链运输的安全风险,我们将结合实际案例进行分析。
以下是两个悬挂链运输事故案例:1. 案例一:由于悬挂点选择不当,链条断裂导致货物掉落,造成人员伤亡。
分析发现,事故的主要原因是悬挂点的承重能力不足,没有进行合理的悬挂点评估。
2. 案例二:在悬挂链运输过程中,链条因长时间使用而磨损严重,导致链条断裂,造成货物损坏。
“建筑力学课件-悬链线”

这是一份关于建筑力学中悬链线的课件,您将了解什么是悬链线、它的性质 和应用,以及如何进行张力、拉力和弯矩的分析。
什么是悬链线?
悬链线是指一条自由悬挂在两个支点之间的线条,它受到自身重力的作用,形成独特的曲线形状。
悬链线与重力
悬链线是重力对自由悬吊物体产生的拉力与物体自身张力平衡的结果,形成 了一种稳定的结构。
3 动力响应与耐久性
悬链线在长期使用中需要考虑其动力响应和耐久性,以确保结构的安 全性。
悬链线的桥梁结构应用
桥梁设计
悬链线被广泛应用于桥梁结构,提供大跨度和美 观的设计方案。
索塔结构
通过悬挂式索塔结构,悬链线实现了桥梁的稳定 性和强度。
悬链线的杆件模型分析
悬链线可以通过简化为杆件模型进行力学分析,这种方法更易于计算和理解 结构的受力行为。
摩天大楼
悬链线原理可用于高层建筑,实现大跨度和 高稳定性。
悬链线的构造方法
1
图解法
2
通过计算和绘制受力图来确定悬链线
的形状和张力分布。
3
悬挂吊绳法
通过将绳索悬挂在支点上并逐渐加重, 使其形成悬链线形状。
数值模拟法
使用计算机模拟软件来进行悬链线的 构造和分析。
悬链线的典型问题
张力分析
如何确定悬链线上各点的张力大小和方向?
拉力分析
如何计算悬链线受到的外部拉力和重力的平衡?
弯矩分析
如何计算悬链线在不同位置的弯矩大小和分布?
无支点悬链线的分析方法
微分方程法
通过建立悬链线的微分方 程,并应用边界条件解得 悬链线的形状和受力状态。
有限元法
将悬链线离散为多个小段, 利用有限元分析方法计算 其受力和变形。
悬链线的实际解法 -回复

悬链线的实际解法-回复悬链线,也被称为悬臂悬链线,是指在一个绳子或链条的一端固定,另一端悬挂物体的情况下,求解该绳子或链条的形状和张力分布。
悬链线的实际解法,以悬链线的特性、方程的建立和解方程的方法为主题。
本文将一步一步回答有关悬链线的实际解法,并对解法进行详细的解释。
第一步:了解悬链线的特性悬链线的特点是其形状和张力分布在重力作用下达到平衡状态。
这意味着在整个线的长度上,每一点的受力都满足力的平衡方程。
在任何一段绳子或链条上,张力的大小和方向都是连续变化的。
第二步:建立悬链线的方程悬链线的形状可以通过建立方程来描述。
首先,我们假设悬链线的形状为一个函数y(x),其中x表示线的长度,y表示线的高度。
我们可以使用一些基本的物理原理,如受力平衡和力的投影等,来推导出悬链线的方程。
考虑悬链线上一小段dx的任意一点P,其坐标为(x,y)。
根据受力平衡,我们可以得到以下方程:1. 排除重力的作用下,绳子在x方向上的受力为零,即-T * sinα+ T * sin α+ T * dy/dx * cosα= 0。
2. 在y方向上,绳子的受力等于该点的重力,即-T * cosα+ T * cosα+ T * dy/dx * sinα= -dmg。
α表示绳子在该点的倾角,m表示单位长度的绳子或链条质量,g表示重力加速度。
根据三角函数的定义,我们有sinα= dy/ds,cosα= dx/ds,其中ds 表示线元的长度。
结合上面的方程,我们可以得到以下方程:-T * dy/ds * dx/ds + T * dy/ds * dx/ds + T * dy/ds * dy/dx = -dmg。
第三步:解方程现在我们可以解上述的方程,以得到悬链线的形状和张力分布。
为简化计算,我们可以将方程重新组织如下:-T * dx = -dy/ds * T * dx * sinα- dy/ds * T * dx * sinα- dy/dx * T * dy/ds * dx * sinα+ mg * ds。
悬链线长度计算

悬链线长度计算
(原创版)
目录
1.悬链线的定义与性质
2.悬链线计算公式
3.悬链线长度计算的实际应用
正文
一、悬链线的定义与性质
悬链线,又称为悬链曲线,是一种在数学和物理学中常见的曲线。
它是由两个固定的点以及一个沿着这两点连线方向作简谐振动的质点所形成的轨迹。
悬链线具有以下几个性质:
1.悬链线是一种特殊的正弦曲线,其方程可以用三角函数表示。
2.悬链线上的任意一点都在其相邻两点的连线上,且与这两点的距离之和为常数。
3.悬链线在数学和物理学中有广泛的应用,如在机械工程中,可用于计算悬链的长度。
二、悬链线计算公式
悬链线的计算公式较为复杂,一般通过微积分方法求解。
在悬链线长度计算中,通常采用以下公式:
L = 2π * sqrt((T/2π)^2 + (h/2)^2)
其中,L 表示悬链线的长度,T 表示振动周期,h 表示振动幅度。
三、悬链线长度计算的实际应用
悬链线长度计算在实际应用中有很多场景,下面以机械工程中的悬链线长度计算为例进行说明。
假设某机械设备上的悬链长度需要满足一定的运动范围要求,我们可以根据振动周期和振动幅度计算出悬链线的长度。
具体操作步骤如下:
1.根据机械设备的实际工作需求,确定振动周期和振动幅度。
2.利用悬链线长度计算公式,计算出悬链线的长度。
3.根据计算结果,设计出满足运动范围要求的悬链线。
通过以上步骤,我们可以确保悬链线在机械设备运行过程中能够满足其功能需求。
总之,悬链线长度计算在理论研究和实际应用中都具有重要意义。
悬链线方程
通常任何材料包括导线在内,都具有一定的刚性,但由于悬挂在杆塔上的一档导线相对较长,因此导线材料的刚性对其几何形状的影响很小,故在计算中假定:(1)导线为理想的柔索。
因此,导线只承受轴向张力(或拉力),任意一点的弯矩为零。
这样导线力学计算可应用理论力学中的柔索理论进行计算.(2)作用在导线上的荷载均指同一方向,且沿导线均匀分布.一、悬链线方程及曲线弧长1.悬链线方程为了分析方便,我们先从悬挂点等高,即相邻杆塔导线悬挂点无高差的情况讨论导线的应力及几何关系。
实际上,导线悬在空中的曲线形态,从数学角度用什么方程来描述是进行导线力学分析的前题。
由于假定视导线为柔索,则可按照理论力学中的悬链线关系来进行分析,即将导线架设在空中的几何形态视为悬链形态,而由此导出的方程式为悬链线方程。
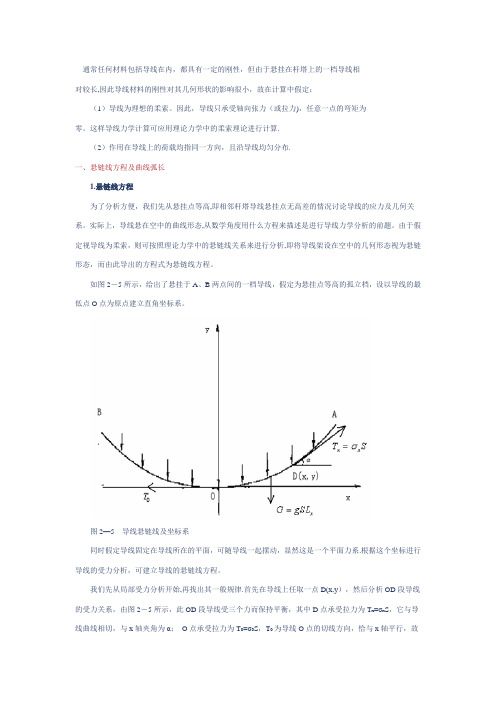
如图2-5所示,给出了悬挂于A、B两点间的一档导线,假定为悬挂点等高的孤立档,设以导线的最低点O点为原点建立直角坐标系。
图2—5导线悬链线及坐标系同时假定导线固定在导线所在的平面,可随导线一起摆动,显然这是一个平面力系.根据这个坐标进行导线的受力分析,可建立导线的悬链线方程。
我们先从局部受力分析开始,再找出其一般规律.首先在导线上任取一点D(x,y),然后分析OD段导线的受力关系,由图2-5所示,此OD段导线受三个力而保持平衡,其中D点承受拉力为T x=σx S,它与导线曲线相切,与x轴夹角为α;O点承受拉力为T0=σ0S,T0为导线O点的切线方向,恰与x轴平行,故又称水平张力;此外还有OD段导线自身的荷载为G=gSL x,其中L x为OD段导线的弧长。
将OD段导线的受力关系画为一个三角形表示,如图2-6所示,图2-6导线受力情况由静力学平衡条件可知,在平面坐标系中,其水平分力,垂直分力的代数和分别等于零.或沿x轴或y轴上分力代数和分别等于零。
垂直方向分力G=T x sinα=gSL x;水平方向分为T0=T x cosα=σ0S.其中σ0、T0为导线最低点的应力和张力,σx、T x为导线任一点的应力和张力,S、g为导线截面和比载.将上述二式相比,则可求得导线任意一点D的斜率为:(2—10)由微分学知识可知,曲线上任一点的导数即为切线的斜率。
悬链线方程的推导

1 悬链线方程的推导 锚链一端受到水平预张力()0T KN ,并在其均匀分布的自重力作用下产生下垂。
设锚链水中 单位重力为()/W KN m ,建立如图1所示的直角坐标系,并设锚链曲线对应的函数为()y f x =。
对于横坐标上0至x 这段锚链,长度为L ,则G wL =,顶端拉力为T ,该力倾角为θ,水平张力0T ,根据力学原理可知,T ,G 和0T 三力平衡。
可知0tan /G T θ=(图2). 图1图2假定该水平张力在锚链上处处相等,对于任意一段锚链L ,该平衡均成立,0tan wL T θ=,而tan dy dxθ=,对该式取微分,则有()()00tan x w d d L T θ===(1) 弧长微分ds=1)分离变量后并积分: 0tan d w dx T =⎰(2) 对式(2)积分后得到:10tan w sh x c T θ⎛⎫=+ ⎪⎝⎭(3)对式(3)再次分离变量后,得10w dy sh x c dx T ⎛⎫=+ ⎪⎝⎭(4)并积分,10w y sh x c dx T ⎛⎫=+ ⎪⎝⎭⎰(5)查积分公式可得:0120T w y ch x c c w T ⎛⎫=++ ⎪⎝⎭(6) 式(6)即为锚链悬链线的一般方程。
假设锚链末端拖地,并设拖地点为原点,则对于拖地点有,0,0,tan 0x y θ===,代入式(3)和(6),联立方程后,可解得:10c =,2T c w=,代入式(6)得: 001T w y ch x w T ⎛⎫=- ⎪⎝⎭(7) 式(5)即为拖地点为原点的悬链线一般方程。
而对于悬挂点为原点的悬链线方程,仅系数有所变化,如下式表示,推导过程不再叙述。
该方程对于有悬锤的悬链线更适用。
0,0,tan wL x y Tθ===,代入式(3),(6)可解得: 002cosh sinh wL T a T c w⎡⎤⎛⎫⎢⎥ ⎪⎝⎭⎣⎦=(8) 式(8)即是以悬挂点为原点的悬链线一般方程。
悬链线方程及曲线弧长
第二章导线应力弧垂分析第三节悬点等高时导线弧垂、线长和应力关系一、悬链线方程及曲线弧长1.悬链线方程为了分析方便,我们先从悬挂点等高,即相邻杆塔导线悬挂点无高差的情况讨论导线的应力及几何关系。
实际上,导线悬在空中的曲线形态,从数学角度用什么方程来描述是进行导线力学分析的前题。
由于假定视导线为柔索,则可按照理论力学中的悬链线关系来进行分析,即将导线架设在空中的几何形态视为悬链形态,而由此导出的方程式为悬链线方程。
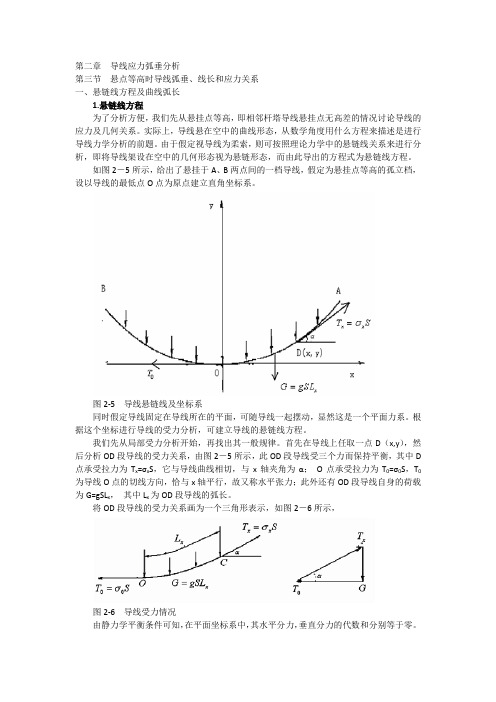
如图2-5所示,给出了悬挂于A、B两点间的一档导线,假定为悬挂点等高的孤立档,设以导线的最低点O点为原点建立直角坐标系。
图2-5导线悬链线及坐标系同时假定导线固定在导线所在的平面,可随导线一起摆动,显然这是一个平面力系。
根据这个坐标进行导线的受力分析,可建立导线的悬链线方程。
我们先从局部受力分析开始,再找出其一般规律。
首先在导线上任取一点D(x,y),然后分析OD段导线的受力关系,由图2-5所示,此OD段导线受三个力而保持平衡,其中D 点承受拉力为T x=σx S,它与导线曲线相切,与x轴夹角为α;O点承受拉力为T0=σ0S,T0为导线O点的切线方向,恰与x轴平行,故又称水平张力;此外还有OD段导线自身的荷载为G=gSL x,其中L x为OD段导线的弧长。
将OD段导线的受力关系画为一个三角形表示,如图2-6所示,图2-6导线受力情况由静力学平衡条件可知,在平面坐标系中,其水平分力,垂直分力的代数和分别等于零。
或沿x轴或y轴上分力代数和分别等于零。
垂直方向分力G=T x sinα=gSL x;水平方向分为T0=T x cosα=σ0S。
其中σ0、T0为导线最低点的应力和张力,σx、T x为导线任一点的应力和张力,S、g为导线截面和比载。
将上述二式相比,则可求得导线任意一点D的斜率为:(2-10)由微分学知识可知,曲线上任一点的导数即为切线的斜率。
式(2-10)是悬链曲线的微分方程。
我们要用坐标关系表示出导线受力的一般规律,还需要将不定量L x消去,因此,将式对x微分得:(微分学中弧长微分公式为dS2=(dx)2+(dy)2)将上式移项整理后,两端进行积分这是个隐函数,因此,再进行分离变量积分,查积分公式有:(2-11)再进行分离变量积分,有于是,导线任一点D的纵坐标为:(2-12)式(2-12)是悬链方程的普通形式,其中C1和C2为积分常数,其值可根据取坐标原点的位置及初始条件而定。
悬链线一般方程

悬链线一般方程悬链线是一种特殊的曲线,它的形状像一条被吊起的链子。
如果你在两个固定的点之间悬挂一根均质无弹力的链子,那么它所形成的曲线就是悬链线。
为了方便研究,我们通常把链子的质量看成无限小,而且只考虑在两个挂点处的张力作用。
下面我将为你介绍悬链线的方程和一些应用。
一、悬链线的方程悬链线的方程有多种推导方法,其中最常见的方法是利用牛顿-莱布尼茨公式和能量守恒定律。
经过推导,我们可以得到悬链线的一般方程如下:y = a * cosh(x/a)其中,y代表链子所在的位置的高度,x代表链子的长度,a则是一个常数,它与链子的张力、重力和挂点的距离有关。
二、悬链线的性质悬链线有一些特殊的性质:1. 它是对称的:悬链线在对称轴处呈现出对称性,即左右两侧的曲线完全相同。
2. 它是单峰的:悬链线的几何形状是单峰的,即它在中心位置最高,在两端位置最低。
3. 它是无穷光滑的:悬链线是无穷光滑的曲线,它不断变化,凸度不断改变。
三、悬链线的应用悬链线不仅仅是一个美妙的几何曲线,它还有一些重要的应用:1. 悬链桥的设计:悬链线的特殊性质使得它成为设计悬链桥的理想曲线。
悬链桥的主要结构是悬链线和桥塔,它可以承载大量的荷载和扭矩。
2. 物理学问题的解决:悬链线被广泛应用于物理学的许多问题中,如质点沿着悬链线的运动问题、悬链线的频率问题等等。
3. 工程结构的应用:悬链线的应用不仅限于桥梁和物理学问题,它还可以应用于建筑结构、电力电线杆、运动设备等领域中。
总之,悬链线是一条美妙的曲线,具有独特的性质和广泛的应用价值。
通过对悬链线的深入研究,我们可以更好地理解物理学问题,设计出更加牢固、高效的工程结构,创造出更加美好的未来。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
通常任何材料包括导线在内,都具有一定的刚性,但由于悬挂在杆塔上的一档导线相
对较长,因此导线材料的刚性对其几何形状的影响很小,故在计算中假定:
(1)导线为理想的柔索。
因此,导线只承受轴向张力(或拉力),任意一点的弯矩为
零。
这样导线力学计算可应用理论力学中的柔索理论进行计算。
(2)作用在导线上的荷载均指同一方向,且沿导线均匀分布。
一、悬链线方程及曲线弧长
1.悬链线方程
为了分析方便,我们先从悬挂点等高,即相邻杆塔导线悬挂点无高差的情况讨论导线的应力及几何关系。
实际上,导线悬在空中的曲线形态,从数学角度用什么方程来描述是进行导线力学分析的前题。
由于假定视导线为柔索,则可按照理论力学中的悬链线关系来进行分析,即将导线架设在空中的几何形态视为悬链形态,而由此导出的方程式为悬链线方程。
如图2-5所示,给出了悬挂于A、B两点间的一档导线,假定为悬挂点等高的孤立档,设以导线的最低点O点为原点建立直角坐标系。
图2-5导线悬链线及坐标系
同时假定导线固定在导线所在的平面,可随导线一起摆动,显然这是一个平面力系。
根据这个坐标进行导线的受力分析,可建立导线的悬链线方程。
我们先从局部受力分析开始,再找出其一般规律。
首先在导线上任取一点D(x,y),然后分析OD段导线的受力关系,由图2-5所示,此OD段导线受三个力而保持平衡,其中D点承受拉力为T x=σx S,它
与导线曲线相切,与x轴夹角为α;O点承受拉力为T0=σ0S,T0为导线O点的切线方向,恰与x轴平行,故又称水平张力;此外还有OD段导线自身的荷载为G=gSL x,其中L x为OD段导线的弧长。
将OD段导线的受力关系画为一个三角形表示,如图2-6所示,
图2-6导线受力情况
由静力学平衡条件可知,在平面坐标系中,其水平分力,垂直分力的代数和分别等于零。
或沿x轴或y轴上分力代数和分别等于零。
垂直方向分力G=T x sinα=gSL x;水平方向分为T0=T x cosα=σ0S。
其中σ0、T0为导线最低点的应力和张力,σx、T x为导线任一点的应力和张力,S、g为导线截面和比载。
将上述二式相比,则可求得导线任意一点D 的斜率为:
(2-10)
由微分学知识可知,曲线上任一点的导数即为切线的斜率。
式(2-10)是悬链曲线的微分方程。
我们要用坐标关系表示出导线受力的一般规律,还需要将不定量L x消去,因此,将式对x微分得:
(微分学中弧长微分公式为dS2=(dx)2+(dy)2)将上式移项整理后,两端进行积分
这是个隐函数,因此,再进行分离变量积分,查积分公式有:
(2-11)
再进行分离变量积分,有
于是,导线任一点D的纵坐标为:
(2-12)
式(2-12)是悬链方程的普通形式,其中C1和C2为积分常数,其值可根据取坐标原点的位置及初始条件而定。
如果将坐标原点于导线最低点处,则有下述初始条件:
x=0, dy/dx=tgα=0
代入式(2-11)则C1=0,将x=0,y=0,C1=0 代入式(2-12),,如此,求得坐标原点最低点O处的悬链方程为:
(2-13)
式中σ0—水平应力(即导线最低点应力),MPa;
g—导线的比载,N/m.mm2。
当坐标原点选在其它点(例如选在悬挂点处)时,悬链线方程的常数项将有所不同,可以得到不同的公式。
若式(2-13)中x代表档距的时候,则y即为导线的弧垂,因此悬链线方程描述了导线弧垂与应力、比载及档距之间的基本关系,此式称为精确式。
实际上导线的悬链线方程还可以从另一种方式进行推导,下面介绍如下:
由式,对其求导得:
变换为,为找原函数进行积分,
由积分式两边积分,
则有:变为指数形式为
这是个隐函数,为解出,对应有式:
将两式相减则有:
因为双曲正弦函数为:
双曲余弦函数为:
又因为:
最后积分有:
定积分常数,因在坐标原点则,其结果是一样的,即
在线路设计中,为了计算上的方便,一般不使用精确式方程,而是将其展开为泰勒级数形式。
将悬链线方程式(2-13)展开成无穷级数(在x=0点),可得:
(2-14)
2.曲线弧长(或弧长方程)
导线最低点O至任一点的曲线长度叫做弧长,用Lx表示。
将式(2-11)代入式(2-10)中,且积分常数C1=0,得导线的弧长方程为
(2-15)
根据式(2-15)可以计算一个档距内导线的曲线长度(也叫一档线长)将弧长方程式(2-15)展开成无穷级数可得:
(2-16)
一质量均匀分布的绳两端悬挂时绳子所表示的曲线为悬链线。
关于悬链线解析方程的求解,我很早就知道其方程为双曲余弦函数。
然而当时数学水平尚未满足要求。
后来学会关于双曲函数的相关内容后,又由于坚信绳中张力处处相等而推出悖论,本研究就此搁浅。
直到7
月初,我又想起了该曲线的方程求解问题。
需要说明的一点是,绳中张力处处相等要求绳子无质量、绷紧,对于悬链显然不适用。
但受力方向沿着绳是正确的,所以必须结合力的方向来求解。
假设一个无限长的质量均匀分布的绳子在重力作用下自然下垂。
设绳底端受到拉力为T0,线密度为ρ,重力加速度g。
如图所示建立直角坐标系,设绳对应的函数为y=f(x)
对于横坐标从0至x这一段的绳,设质量为m,长度L,受重力为G,受顶端拉力大小为T,该力倾斜角为θ
该段绳受三力平衡:T、G、T0,画出受力示意图,有G/T0=tanθ
由导数的几何意义,tanθ=dy/dx,而G=mg=ρgL,故ρgL/T0=dy/dx,ρgL=T0*dy/dx
对上式取微分,得ρg*dL=T0*d2y/dx,而dL=(dx2+dy2)1/2=[1+(dy/dx)2]1/2*dx,代入得
ρg[1+(dy/dx)2]1/2=T0*d2y/dx2=T0*d(dy/dx)/dx,令dy/dx=P,则
ρg(1+P2)1/2=T0*dP/dx,ρg/T0*dx=dP/(1+P2)1/2
对两侧取积分得∫ρg/T0*dx=∫dP/(1+P2)1/2
ρgx/T0=sinh-1P+C1,P=sinh(ρgx/T0-C1),dy/dx=sinh(ρgx/T0-C1)
当x=0时,dy/dx=0,代入得sinh(-C1)=0,C1=0,故dy=sinh(ρgx/T0)*dx
再次积分,得y=T0/ρg*cosh(ρgx/T0)+C2
当x=0时,y=0,故0=T0/ρg*cosh0+C2,C2=-T0/ρg
设k=T0/ρg,则y=kcosh(x/k)-k,若只考虑其形状可忽略常数项,故悬链线方程为
y=kcosh(x/k)-k,其中k=T0/ρg
关于双曲函数的一些说明:双曲正弦函数sinhx=(e x-e-x)/2,双曲余弦函数coshx=(e x+e-x)/2 由其定义可得d(sinhx)/dx=coshx,d(coshx)/dx=sinhx,cosh2x-sinh2x=1
其反函数分别为反双曲正弦函数sinh-1x=ln[x+(x2+1)1/2],反双曲余弦函数
cosh-1x=ln[x+(x2-1)1/2]
涉及的一步积分:在∫dP/(1+P2)1/2中,令P=sinht
∫dP/(1+P2)1/2=∫d(sinht)/(1+sinh2t)1/2=∫cosht*dt/cosht=∫dt=t+C=sinh-1P+C
比喻句拟人句练习
什么是比喻句:
就是打比方,用浅显、具体、生动的事物来代替抽象、难理解的事物。
一般有本体,喻体和比喻词组成,又有明喻、暗喻、隐喻之分。
比喻句的作用:
1、比喻说理浅显易懂,使人容易接受。
2、比喻叙事能化抽象为具体,使事物更加清楚明白。
3、比喻状物能使概括的东西形象化,给人深刻的印象。
比喻句中常用的比喻词:
像、是、好像、好似、如、有如、如同、彷佛、成了、变为…… 那么如何判断句式是否是比喻句呢,我们可以用“三看一比法”,一看有没有“本体”,二看有没有“比喻词”,三看有没有“喻体”。
“一比”就是把本体和喻体相比,看本质是否相同。
本质不同,那就是比喻句。
一、判断下列句子是不是比喻句,如果是,说说把什么比作什么。
1、这件文具好象是小明的。
( )
2、月亮像个大圆盘,高挂在夜空中。
( )
3、妈妈今天脸色很不好,看上去好象生病了似的。
( )
4、咆哮的洪水箱猛兽一般,把小村庄给淹没了。
( )
5、水底的鹅卵石像一颗颗晶莹剔透的宝石。
( )
6、姑娘有一颗金子一般的心。
( )
7、这句话仿佛一道温暖的阳光直射我的心田,抚慰了我受伤的心灵。
( )。
