悬链线微分方程的另一种解法_张养利
架空线悬链方程的积分普遍形式
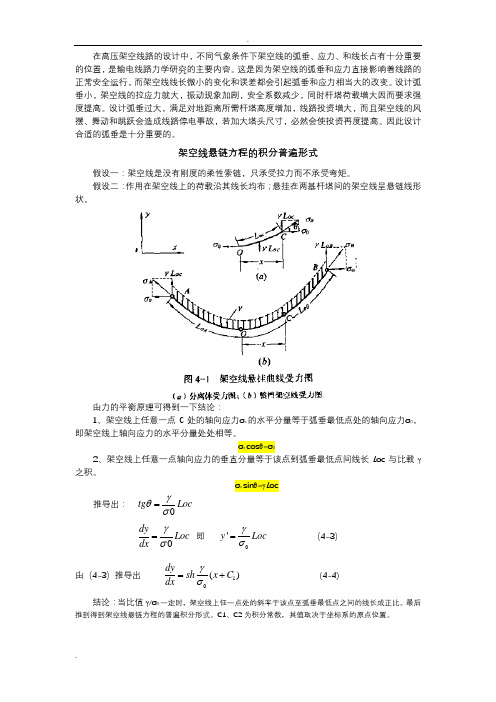
在高压架空线路的设计中,不同气象条件下架空线的弧垂、应力、和线长占有十分重要的位置,是输电线路力学研究的主要内容。
这是因为架空线的弧垂和应力直接影响着线路的正常安全运行,而架空线线长微小的变化和误差都会引起弧垂和应力相当大的改变。
设计弧垂小,架空线的拉应力就大,振动现象加剧,安全系数减少,同时杆塔荷载增大因而要求强度提高。
设计弧垂过大,满足对地距离所需杆塔高度增加,线路投资增大,而且架空线的风摆、舞动和跳跃会造成线路停电事故,若加大塔头尺寸,必然会使投资再度提高。
因此设计合适的弧垂是十分重要的。
架空线悬链方程的积分普遍形式假设一:架空线是没有刚度的柔性索链,只承受拉力而不承受弯矩。
假设二:作用在架空线上的荷载沿其线长均布;悬挂在两基杆塔间的架空线呈悬链线形状。
由力的平衡原理可得到一下结论:1、架空线上任意一点C 处的轴向应力σx 的水平分量等于弧垂最低点处的轴向应力σ0,即架空线上轴向应力的水平分量处处相等。
σx cos θ=σ02、架空线上任意一点轴向应力的垂直分量等于该点到弧垂最低点间线长L oc 与比载γ之积。
σx sin θ=γL oc推导出: 0tg Loc γθσ=dy Loc dx γσ= 即 0'y Loc γσ= (4-3) 由(4-3)推导出10()dy sh x C dx γσ=+ (4-4) 结论:当比值γ/σ0一定时,架空线上任一点处的斜率于该点至弧垂最低点之间的线长成正比。
最后推到得到架空线悬链方程的普遍积分形式。
C1、C2为积分常数,其值取决于坐标系的原点位置。
0(1)20y ch x C C σγγσ=++ (4-5)等高悬点架空线的弧垂、线长和应力等高悬点架空线的悬链方程等高悬点是指架空线的两个挂点高度相同。
由于对称性,等高悬点架空线的弧垂最低点位于档距中央,将坐标原点取在该点,如图:0(1)0y ch x σγγσ=- (4-6) 由上式可以看出,架空线的悬链线具体形状完全由比值σ0 /γ决定,即无论何种架空线、何种气象条件。
微分方程第二边界条件

微分方程第二边界条件一、什么是微分方程第二边界条件?在解微分方程时,我们常常需要给出两个边界条件,即在自变量的两个特定取值点上给出因变量的值。
这两个边界条件可以是函数值、导数值或者函数值与导数值的组合。
其中,微分方程第二边界条件指的是在自变量的第二个取值点上给出因变量的值。
微分方程第二边界条件在实际问题中有着广泛的应用。
下面我们将通过几个例子来说明。
1. 悬链线问题悬链线是指一根无质量、柔软的绳子自重下悬挂在两个固定点之间的形状。
我们可以通过微分方程来描述悬链线的形状,并通过给定的边界条件求解。
其中,微分方程的第二边界条件是绳子的一端固定在一个点上,即在该点上给出了绳子的位置。
2. 热传导问题热传导是指热量在物体中的传递过程。
我们可以通过热传导方程来描述物体内部的温度分布,并通过给定的边界条件求解。
其中,微分方程的第二边界条件是在物体的边界上给出了温度的变化情况。
3. 电容器充放电问题在电路中,电容器充放电是一个常见的问题。
我们可以通过电路方程和电容器的特性方程建立微分方程模型,并通过给定的边界条件求解。
其中,微分方程的第二边界条件是在充电或放电过程中给出了电容器的电压。
三、微分方程第二边界条件的意义微分方程第二边界条件的给定,可以帮助我们确定唯一的解。
在实际问题中,我们常常需要通过给定的边界条件来求解未知的物理量,例如温度、电压等。
微分方程第二边界条件的应用,可以帮助我们预测和解决各种实际问题。
四、总结微分方程第二边界条件在解微分方程时起着重要的作用。
通过给定的边界条件,我们可以确定微分方程的唯一解,从而解决实际问题。
无论是悬链线问题、热传导问题还是电容器充放电问题,微分方程第二边界条件都有着广泛的应用。
通过研究和理解微分方程第二边界条件的意义,我们可以更好地应用微分方程解决实际问题,推动科学技术的发展。
关于悬链形状的讨论

令 W0g/T0 =a,从上式中解得: f’(x) =1/2(eax - e-ax) = sh(ax) ……. ⒃ 那么,可以解出f(x)与x的关系: f(x) =1/a .ch(ax) +c1 ……. ⒄ 选取适当的坐标系,总能找到适当的坐标 系使得c1=0,因而: 1 ch(ax) (其中a=gW /T ) f(x) = a 0 0
对上式去微分,从而有: T0f’’(x) = S’W0g 也即: T0f’’(x) = W0g. √1+f’2(x) 对上式变形即的⑥式. 对方程⑥两边同取积分得: ln|f’(x)+√1+f’2(x)
……. ⒀ ……. ⒁
W0 x |= + c …….⒂ T0
考虑到初值条件f’(0)=0,c=0 ⒂可化为 ln|f’(x)+√1+f’2(x) |=
由上面的推导可知密度均匀的链在其自身 重力作用下所形成的形状是双区余弦函数的 形状,并且这条链的形状是关于轴对称的. f(x)的解析式中有一个待确定的常数T0(也 可以说是a).设链的长S.两悬点在坐标系上的 坐标分别是(x1,y1),(-x2,y2).其中x1,x2 y1,y2均大 于零,那么有: S =∫√1+f ’2(x) dx
关于悬链 形状的讨论
2003级物理学 2003级物理学 刘志勇、刘 晨 刘庆逊、刘加东
#前言 前言
这篇文章主要讨论两点间柔软悬链 在其自身重力作用下所形成的形状的讨 论及相关展开。这个题目也许可看成一 道数学应用题,但关键是为了了解悬链 的形状与哪些物理量有关。
首先,我们讨论一种相对简单的情形,即 悬链的线密度为一常量ω0。因而,建立坐 标,使Y轴通过悬链的最低点,并且设最低 点处悬链的张力为T0。可以肯定,其他物 理量确定后,T0为常数。
悬链线方程的求解及其应用

= 5. 70 kN 式中 f ——阻力系数, 取 0. 18
8 ——船体浸水面积, 1 500 m 2 v ——水流速度, 取 v = 1. 5 m s 波浪漂流阻力:
R 3=
3 4
k
ΘgB
(
1 4
H
1
3) 2co s0°× 10-
2 kN
= 0. 75 × 0. 7 × 104. 61 × 9. 8 × 15. 8
解: 通过程序进行计算, 并将计算过程汇总于表 3:
(3) 已知该浮船坞某锚链的挂链力 T = 1 623. 5 kN , 若要求沉石不产生上拔力, 求该链抛锚距离 x 的最小值。
19 © 1994-2006 China Academic Journal Electronic Publishing House. All rights reserved.
1 000
27 560
14 330
2
990
26 006
13 530
3
980
24 539
12 770
悬链长 L (m )
27 733 26 179 24 711
悬链重 G (t)
1 433 1 353 1 277
Β角 (°)
89164 89162 89159
是否满足 y= h
不满足 不满足
160. 76
选取锚重:
G = R 5= 8 963 5= 1 793 kg (取锚的抓重为 5;
实取 2 000 kg 斯贝克锚 2 只为首锚, 备用锚一只)
选取锚机: 5 46~ 48 电动锚机。
9. 554 9. 553 9. 553
46. 83 46. 82 46. 82
悬链线的实际解法 -回复

悬链线的实际解法-回复悬链线,也被称为悬臂悬链线,是指在一个绳子或链条的一端固定,另一端悬挂物体的情况下,求解该绳子或链条的形状和张力分布。
悬链线的实际解法,以悬链线的特性、方程的建立和解方程的方法为主题。
本文将一步一步回答有关悬链线的实际解法,并对解法进行详细的解释。
第一步:了解悬链线的特性悬链线的特点是其形状和张力分布在重力作用下达到平衡状态。
这意味着在整个线的长度上,每一点的受力都满足力的平衡方程。
在任何一段绳子或链条上,张力的大小和方向都是连续变化的。
第二步:建立悬链线的方程悬链线的形状可以通过建立方程来描述。
首先,我们假设悬链线的形状为一个函数y(x),其中x表示线的长度,y表示线的高度。
我们可以使用一些基本的物理原理,如受力平衡和力的投影等,来推导出悬链线的方程。
考虑悬链线上一小段dx的任意一点P,其坐标为(x,y)。
根据受力平衡,我们可以得到以下方程:1. 排除重力的作用下,绳子在x方向上的受力为零,即-T * sinα+ T * sin α+ T * dy/dx * cosα= 0。
2. 在y方向上,绳子的受力等于该点的重力,即-T * cosα+ T * cosα+ T * dy/dx * sinα= -dmg。
α表示绳子在该点的倾角,m表示单位长度的绳子或链条质量,g表示重力加速度。
根据三角函数的定义,我们有sinα= dy/ds,cosα= dx/ds,其中ds 表示线元的长度。
结合上面的方程,我们可以得到以下方程:-T * dy/ds * dx/ds + T * dy/ds * dx/ds + T * dy/ds * dy/dx = -dmg。
第三步:解方程现在我们可以解上述的方程,以得到悬链线的形状和张力分布。
为简化计算,我们可以将方程重新组织如下:-T * dx = -dy/ds * T * dx * sinα- dy/ds * T * dx * sinα- dy/dx * T * dy/ds * dx * sinα+ mg * ds。
第10讲 链形悬挂的状态方程及安装曲线

2 2 Tc1 Wx2lD Tcx W12lD t x (t1 ) 2 2 24 Z1 ES 24 Z x ES
Page 15
第10讲 链形悬挂的状态方程及安装曲线
课间休息!
Page 16
第10讲 链形悬挂的状态方程及安装曲线
10.4 半补偿链形悬挂状态方程起始条件的确定
简单悬挂安装曲线的绘制 第一步:确定接触悬挂的计算负载; 第二步:确定并计算当量跨距,取为5的 整倍数; 第三步:计算临界跨距; 第四步:确定起始条件; 第五步:利用状态方程,计算张力-温度 对照表; 第六步:计算接触线弛度与温度对照表。 注意:每一个实际跨距有一条弛度-温度曲线; 张力温度曲线是一个锚段一条 曲线。 第七步:根据张力温度对照表和弛度温度 对照表绘制安装曲线
2 2 Tc1 Wx2lD Tcx W12lD t x (t1 ) 24 Z12 ES 24 Z x2 ES
临界负载
链形悬挂承力索即将产生最大张力时的合成负载,承力索的最 大张力既可能出现在最大覆冰时,也可能出现在最低温度时。
t1 t min
W1 Wt min qo (1
承力索和接触线相互作用,承力索承受自重负载、附加负载、接触线自重负载 和附加负载。 在未补偿链形悬挂中,承力索和接触线的张力和弛度都是变化的。 在半补偿链形悬挂中,接触线张力为一常数,与温度变化无关。承力索的张力 和弛度随气象条件和接触线负载变化而变化,接触线弛度取决于承力索弛度的变化 在全补偿链形悬挂中,承力索和接触线的张力为一常数,其弛度也与温度无关
f Fcx Fc 0 h
= =
f ( Fcx Fc 0 )
(l 2 e ) 2 l2
4e(l e) ( Fcx Fco ) 1 l2
悬链线公式范文

悬链线公式范文悬链线曲线可以通过悬链线公式来描述,该公式是一种二次积分方程。
悬链线公式的推导可以追溯到17世纪,最早由数学家伽利略提出。
早期的研究主要关注两个重要参数,悬链线的弧长和张力。
在此基础上,经过长期的发展和改进,悬链线公式逐渐完善起来。
y = a * cosh(x/a)其中,y表示曲线上其中一点的纵坐标,x表示该点距离对称轴的横坐标,a是曲线的挂链长度。
这个公式可以用来计算悬链线上任意一点的位置。
在特定的条件下,可以通过解析法或数值计算的方法,确定悬链线上任意一点的坐标。
首先,我们考虑悬链线上其中一点的切线斜率。
根据物理学知识,悬链线上任意一点处切线的斜率等于该点处曲线的斜率。
而曲线的斜率可以通过曲线的微分方程来表示。
因此,我们可以通过微分方程计算出悬链线上其中一点的切线斜率。
接下来,我们将斜率表示为dy/dx的形式,并对其进行积分得到y关于x的函数表达式。
为了求解这个积分方程,我们使用变量代换来简化计算。
最后,我们对积分方程进行求解,得到了悬链线公式。
悬链线公式的应用非常广泛。
在物理学中,它可以用来描述悬链线的形状和张力分布。
在工程学中,悬链线公式可以应用于吊桥、电线杆、挂钟和索道等结构设计。
悬链线的形状对于这些结构的稳定性和载荷分布具有重要影响。
总之,悬链线公式是一种描述悬链线形状的数学公式。
它的推导过程比较复杂,需要运用高等数学知识。
悬链线公式的应用涵盖了物理学和工程学等领域,对于研究结构的稳定性和计算载荷分布非常重要。
悬链线方程课件ppt

【属于4-1】对于实腹拱
g 调整前拱轴系数: m
j
g
d
调整后拱轴系数:
g'
m g '
j '
d
gx –假载,一层均布荷载
'
g g g
m g g g '
j '
j
x
d
d
x
gx得符号当m’>m时为负;m’<m时为正
【属于4-1】对空腹拱
◎调整拱轴系数,使拱跨1/4点得拱轴线坐标y 1/4改变; ◎假载gx可用下式求:
4-5 主拱施工验算
保证施工中主拱得强度满足要求、稳定性可靠,防止倾 覆;合理确定施工加载程序,拱圈吊运过程构件内力, 各种临时措施,如吊点得位置,拱圈分段位置、辅助索 内力。
◎无支架施工得大、中跨径拱桥,需验算拱得纵、横向稳定 性;
3-2-1、 纵向稳定性
◎将拱圈换算为相当长度得压杆,按平均轴向力计算; 验算公式:
◎当主拱得长细比大于规范规定得数值时,按临界力控
制稳定;
临界平均轴向力
K1
NL Nj
4
~
5
N R A
b
/
荷载效应计算的平均轴向力
j
am
3-2-2、横向稳定性
2)整体浇筑,一般地区相当于降 低20℃,干燥地区30℃;分段 浇筑10~15℃;装配结构5~ 10℃;
3)考虑混凝土徐变影响,计算收 缩内力可采用0、45得 折减 系数;
2-6 拱脚变位引起得附加内力
1)拱脚相对水平位移 2)拱脚相对垂直位移 3)拱脚相对转角
三、主拱得强度及稳定性验算
*根据最不利情况得荷载内力组合,验算控制截面得强度及 拱得稳定性;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
[ 3 ] 王 敏 ,徐 勇勇 . 军队 大病 患者住 院费 用及 用药情 况统 计分 析 [ J] . 医学与社会 , 1998; ( 2): 11- 15.
故解为 y=
a 2
(
x
ea
+
e-
x a
)=
a ch
x a
1. 2 解法 2 由解法 1得到 启示 ,我 们也可以 采用双曲代 换
来去掉根号 ,
令
y
'=
sht ,则
y "=
ah t
dt dx
,
则方程
(
1)可化为
dt dx
=
1 a
,
t=
x a
+
C1
于是 y '=
sh (
x a
+
C1 )
由初始条件 y '( 0) = 0,得 C1= 0
则 ( 1)式化为±
t t2 -
dt 1dx
=
t a
或±
adt = dx 积分得 t2- 1,
x = ± a 1n (t+ t2 - 1)+ C1
( 4)
又由 dy = y 'dx = adt,得 y= at+ C2
( 5)
由 ( 4) ( 5)消去参数 t 得 y=
a 2
(
e±
x
a
a
+
e
x- a
令
y’
=
tant ,则
y "=
s ec2 t
dt dx
,
则 ( 1)式化为
s ect
dt dx
=
1 a
,积分得
x= a 1n( sect+ tant )+ C1
( 2)
又∵ dy = y’ d x= ta nt· asectdt ,积分得
y= a sect+ C2
( 3)
由 ( 2)、 ( 3)联立 ,消去参数 t ,得
[ 6 ] 林 杉 ,罗卫东 . 我院是如何做好大病统筹工作的 [ J ]. 解放 军医 院管理杂志 , 1998; ( 2): 162. 编辑 袁天峰
· 经验交流· 文章编号: 1000-2790( 2001) S041-01
悬链线微分方程的另一种解法
张 养利 ,王连昌 ,李文潮 ,张改英 (第四军医大 学生物
[ 4 ] 陈文亮 ,毛常学 et al . 关于军 队医疗保障制度改革目标模式的 探 讨 [ J] . 解放军卫勤杂志 , 1999; ( 2): 70- 72.
[ 5 ] 高 炜 ,高 昱 . 军队医院适应国家医疗制度 改革的必要性及 几 点设想 [ J] . 国防卫生论坛 , 1999; ( 3) : 20- 22.
医学工程系数学教研室 ,陕西 西安 710033)
关键词: 悬链线 ;微分方程 ;参数法 中图号: R311 文献标识 码: E
0 引言 在高 等数学 和数学 分析等 教材中 ,对悬 链线微 分
方程的解法一般都是作为“可降解的高阶微 分方程”之第二种
类型
y "= f ( x , y’ )型的 例子出 现 ,我 们介绍 悬链线 微分
41
同时 ,参照地方社会医疗保险的做法 ,将医疗保险经 费分为个人帐户和统筹基金 ,分别归包干家属的平时 门诊和住院大病使用 ,以便有效减少军费的补贴 ,控 制包干家属医疗费用的不断上涨 .
参考文献:
[ 1 ] 刘 信 , 马广学 . 军队医院“皇 粮”不足的成因 及对策 [ J] . 军 事 经济研究 , 1999; ( 9): 66- 70.
方程的另一种解法 参数法 ,供 大家参考 .
悬链线微分方程为:
y "=
1 a
1+ y’ 2
( 1)
y ( 0) = a, y’ ( 0) = 0,其中 a> 0
1 解法 1. 1 解 法 1 观 察方程 的形式 ,借 鉴求 函数积 分的 换元法 ,
引入参数 t,设法将 1+ y2化为三角函数有理式 ,不 妨用三角 代换 ,
于是
y '=
sh
x a
,积分得
y=
a ch
x a
+
C2 ,由
y( 0)=
a 得 C2=
0
故
y= aCh
x a
可见 ,用双典函 数代换较三角函数代换简明的多 .
1. 3 解 法 3 令 1+ y '2 = t , 则 y '= ± t2 - 1, y "= ±
t dt t2 - 1 dx
y=
a 2
(e
xa
a+
e
x
a
a )+
C2
收稿日期: 2001-10-30; 修回日期: 2001-11-10 作 者简 介: 张养 利 ( 1963-) ,女 (汉族 ) , 陕西 省户县 人 . 讲师 , 学 士 .
Tel. ( 029) 3374833
由初始条件 y ( 0) = a, y’ ( 0)= 0,得 C1= 0,C2= 0,
第四军医大学学报 ( J Four th M il M ed U niv ) 2001; 22( Suppl)
另外 ,对大病和高额医疗费用的管理 [6 ] ,也可参照地 方的相关做法 , 制定相应的规定 . 如我们在住院包 干家属的医疗费用分类分析中 ,医疗费用超过 1万元 的人数只占 0. 5% , 但其费用却占 15. 4% . 如采取对 大额消费万元以上的包干家属实行部分收费 ,影响范 围不会很大 ,若参照地方有关部门制定的部分贵重药 品和大病统筹不予负担的药品目录要求 ,规范药品使 用 ,建立“特种检查、特种治疗、贵重药品费用审批表” 等形式 ,协调解决大病医疗过程中出现的各种问题 , 都可有效限制超标准和过度医疗消费 . 4. 3 向军人家属军内医疗保险体制过渡 设立军内 医疗保险机构 ,将总部下拨的军人家属人员补助费、 门诊补助费和床位费 ,以及个人缴纳的保险费 (原包 干费 )统一管理 ,通过增加保险费 (相当于包干费 )的 筹措比例 ,达到使家属医疗保险经费的筹集 ,在人均 数量上高于全国同期城镇人口医疗消费平均水平 .
a )+
C2
由初始条件 y ( 0) = a, y’ ( 0)= 0,得 C1= 0,C2= 0
于是 y=
a
2
(
e±
x
Hale Waihona Puke aa+
e
xa
a
)
=
ach
x a
2 讨论 将以上解 法与教材中介绍的的解法 进行比较 ,可以 发现解 法 2中 用双曲 代换较 为简便 . 当然 ,悬 链线微 分方 程
可能还有其他的解法 ,有兴趣者不妨一试 . 编辑 何扬举
