飞机结构力学第四章
《结构力学》第四章 静定结构的位移计算 (3)

B EI
2
R 1
cos
( FP R
sin
)
Rd
0
EI
d
FPR3
2EI
FPk 1
A
B Bx 2 By 2
B kP
B
A M k M P ds B EI
2
(1)
(FPR sin
)
Rd
0
EI
R
O
FP R2 (
)
EI
(1)梁与刚架
三、结构的外力虚功
作用在结构上的外力可能是单个的集中力、力 偶、均布力,也可能是一个复杂的力系,为了 书写方便,通常将外力系的总虚功记为:
W = Fk × km
其中,Fk为作功的力或力系,称为广义力; km为广义力作功的位移,称为广义位移。 下面讨论几种常见广义力的虚功。
1) 集中力的虚功
Pk
k
M
4EIk
GAl 2
kP
若截面为矩形,则:A bh, I bh3 /12,k 6 l 1, 2
h / l 1 , 10
h/l 1 , 15
则:
Q kP
( h)2
Q
M kP
l
kP 25% kMP
对于粗短杆来说,剪 切变形产生的位移不可忽
Q
kP 1%
1
m
ds
第i根杆件静力状态上的力在位移状态的位移上所 作的虚功:
Vi
s FNk
mds
s FQk mds
s Mk
1
m
ds
整个杆件结构各个截面上的内力在位移状态的位 移上的所作的总虚功:
N
N
N
结构力学第四章习题参考解答

l
l
C
1 ql 4
2
1 2 ql 4
5 ql 4
A
M P图
1 2 ql 8
l 2
1
1 2 1 2 1 l l ql EI 3 8 2 2
ql 4 1 1 1 ql 4 EI 48 24 48 24EI
A
M图
1 2 3
4-3 试用图乘法求图示结构中B处的转角和C处的竖向 ql 位移。EI=常数。 2 q
(b)解:作 M图、M P图,
CV 1 1 1 2 l 2 l ql EI 2 4 2 3 2
1 1 1 2 1 2 ql l l EI 2 4 2 3
l
q
B
M 1
EI
A
在B点沿水平方向设单位力矩 M 1 。 故 M 1
1 1 qx3 M P qx x x 2 3 6l
l
MM P 1 qx3 ql 3 则 B dx dx EI EI 0 6l 24EI
l
q
4-2 试求桁架结点B的竖向位移,已知桁架各 杆的 EA 21 10 4 KN。
(c)求
BH、 B。
q qx x l
B
解:在B点沿水平方向设单位力 FP 1 。
q qx l x
故 M x 则
BH
1 1 qx3 M P qx x x 2 3 6l
l
EI
A
FP 1
MM P 1 x qx3 ql 4 dx dx EI EI 0 6l 30EI
BV FN FNP l EA
结构力学第四章 静定结构的影响线

第四章 静定结构的影响线
Last Edit: 2009.8.8
本章主要内容:
1 影响线的概念;
2 用静力法作静定梁的影响线;
3 用机动法作静定梁的影响线; 4 影响线的应用; 5 简支梁的包络图和绝对最大弯矩。 课后作业
2/72
4-1 影响线的概念
3/72
4-1 影响线的概念
一、移动荷载对结构的作用 固定荷载:荷载的位置是固定的
5/72
4-1 影响线的概念
二、解决移动荷载作用问题的途径 采用叠加原理(无论有几个FP)
A B
进一步采用单位力
—— 一个方向保持不变的单位荷载 FP=l在结构上移动时,对结构中某一 量值(反力,内力等)所产生的影响。
FP1 A
FA
FP2 B
x
结构力学 第四章 作业参考答案

结构力学 第四章习题 参考答案2005级4-1 图示抛物线拱的轴线方程24(fy x l l=−)x ,试求截面K 的内力。
解:(1) 求支座反力801155 kN 16AV AV F F ×=== 0805(5580)0.351500.93625 kN 16BV BV F F ×==−×+×== 0Mc 55880350 kN 4H F f ×−×===(2) 把及代入拱轴方程有:16m l =4m f =(16)16xy =−x (1)由此可得:(8)tan '8x y θ−==(2) 把截面K 的横坐标 ,代入(1),(2)两式可求得: 5m x ==>, 3.44m y =tan 0.375θ= 由此可得:20.56θ= 则有sin 0.351θ=,cos 0.936θ=最后得出截面k 处的内力为: (上标L 表示截面K 在作用力左边,R 则表示截面在作用力右边)055550 3.44103 kN m K H M M F y =−=×−×=i0cos sin 550.936500.35133.93 kN L sK s H F F F θθ=−=×−×= (5580)0.936500.35140.95 kN R sK F =−×−×==40.95 KN 0sin cos 550.351500.93666.1 kN L NK s H F F F θθ=+=×+×= (5580)0.351500.93638.03 kN R NK F =−×+×=4-2 试求拉杆的半圆三铰拱截面K 的内力。
解:(1)以水平方向为X 轴,竖直方向为Y 轴取直角坐标系,可得K 点的坐标为:2m6mK K x y =⎧⎪⎨==⎪⎩ (2)三铰拱整体分别对A ,B 两点取矩,由平衡方程可解得支座反力:0 20210500 20210500 2100A By B Ay x Ax M F M F F F ⎧=×−××⎪⎪=×+××⎨⎪=−×=⎪⎩∑∑∑=== => 5 kN ()20 kN () 5 kN ()Ay Ax By F F F =−⎧⎪=−⎨⎪=⎩向下向上向左(3)把拱的右半部分隔离,对中间铰取矩,列平衡方程可求得横拉杆轴力为:CN 0 105100MF =×−×∑=>N 5 kN F =(4)去如图所示的α角,则有:=>cos 0.6sin 0.8θθ=⎧⎨=⎩于是可得出K 截面的内力,其中:22(6)206525644 kN m 2K M ×=−+×−×−×=isK F (20265)sin 5cos 0.6 kN θθ=−×−×−×=− NK F (20265)cos 5sin 5.8 kN θθ=−−×−×−×=−13K M F r Fr ==(内侧受拉) K 截面作用有力,剪力有突变 且有01sin3032LSK 2F F F F =−=−×=− (2) 22R SK F FF F =−=(3)011sin30(326NKF F F F ==×=拉力)(4)4-4 试求图示三铰拱在均布荷载作用下的合理拱轴线方程。
《飞行器结构设计》课后答案第4章
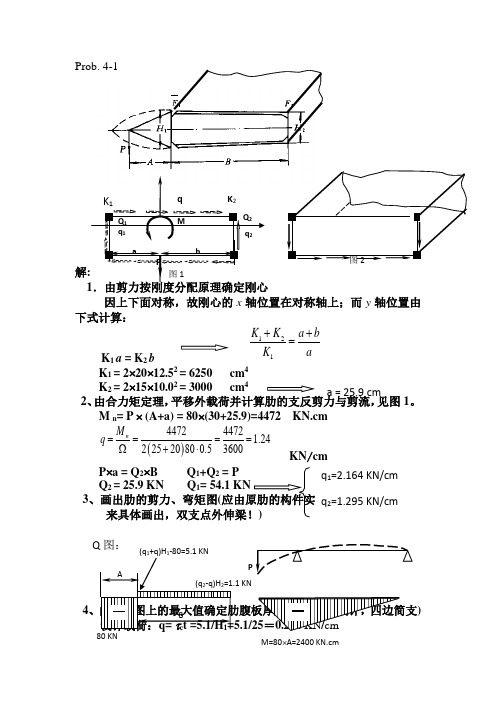
Prob. 4-1解: 1.由剪力按刚度分配原理确定刚心因上下面对称,故刚心的x 轴位置在对称轴上;而y 轴位置由下式计算:K 1 a = K 2 bK 1 = 2⨯20⨯12.52 = 6250 cm 4K 2 = 2⨯15⨯10.02 = 3000 cm 4 2、由合力矩定理,平移外载荷并计算肋的支反剪力与剪流,见图1。
M n = P ⨯ (A+a) = 80⨯(30+25.9)=4472 KN.cmKN /cmP ⨯a = Q 2⨯B Q 1+Q 2 = P Q 2 = 25.9 KN Q 13、画出肋的剪力、弯矩图(应由原肋的构件实际作用力图+支反力来具体画出,双支点外伸梁!)4、由剪力图上的最大值确定肋腹板厚度(抗剪型板设计,四边简支) 设计载荷:q= τc t =5.1/H 1=5.1/25=0.204 KN /cm121K K a bK a ++=()44724472 1.2422520800.53600n M q ====Ω+⋅q K 2 K 1 Q 2 Q 1 M q 2q 1 b a 图2 图1Pa = 25.9 cm q 1=2.164 KN/cm q 2=1.295 KN/cmQ 图:80 KN(q 2-q)H 2=1.1 KN M=80⨯A=2400 KN.cmAB公式: ,K=5.6+a /b =B/H 1=80/25=3.24 K= 5.97, E=70000 MPaδ = 3.3.899=3.4 mm5、由弯矩的最大值确定肋上下缘条的面积(上缘条受拉、下缘条受压,且力大小相等、方向相反):最大弯矩处的缘条内力: N = M max /H 1 = 2400/25=96 KN 上缘条面积由强度计算确定:A * σb = NA *=96000(N)/420 (MPa)=228.57 mm 2,应取 A *=228.57/0.9=253.97 mm 2 下缘条面积由压杆总体稳定性公式确定:(两端固支,K=4,注失稳的弯曲方向)(正方形) A * =A * == 516.78 mm 2 如按题目给出的受压失稳临界应力值(偏危险),可得: A * = 96000/280 = 342.86 mm 2 6、前梁腹板的厚度确定:前梁腹板的剪流:q q = q 1+q = 3.404 KN/cm 由公式粗算(不考虑立柱,a 很大)K= 5.6 + = 5.6mm (因厚度合适,可不考虑安装立柱)如考虑立柱,其间距取a = b =250 mm , 则 K=9.38mm7、后梁腹板的厚度确定:后梁腹板的剪流:q h = q 2 - q = 1.295-1.24= 0.055 KN/cmδ=()23.78/a b =22cr K EI P N l π==32**111212I ab A ==*cr A Nσ=δ=()23.78/a b 3.3δ== 2.8δ===1 mm可不再考虑立柱设计 。
结构力学第4章静定拱(f)

FH
FH
由边界条件
x 0, y 0 : x 0, y 0 :
A qc
B0
合理拱轴线的方程为
y qc (cosh x 1)
FH
§4-3 三铰拱的合理拱轴线
例4-3 试求三铰拱在垂直于拱轴线的均布荷载作用下的合理 拱轴线。
解:由图a,荷载为非竖向荷载。
思路:假定拱处于无弯矩状态,根据平衡 条件推求合理拱轴线方程。
Fi ai l
Fx 0 FAH FBH FH
相应简支梁
取左半拱为隔离体
MC 0
FH
FAV l1 F1(l1 a1) f
可 得
FAV FBV
FA0V FB0V
FH
M
0 C
f
三铰拱的反力只与 荷载及三个铰的位置有 关,与拱轴线形状无关;
推力FH 与拱高 f 成反比。
§4-2 三铰拱的计算
§4-2 三铰拱的计算
2、内力的计算
压力为正
任一截面的轴力等于该截面一 侧所有外力在该截面法线方向 上的投影代数和。
FN FAV sin FH cos F1 sin (FAV F1) sin FH cos FS0 sin FH cos
相应简支梁
§4-2 三铰拱的计算
2、内力的计算
区别拱与梁的主要标志:推力的存在与否。
§4-1 概述
拉杆拱: 拱两支座间的拉杆代替支座承受水平推力
拉杆做成折线形可获得较大空间
高跨比:f/l
平拱: 两拱趾在同一水平线上 斜拱: 两拱趾不在同一水平线上
§4-2 三铰拱的计算
1、支座反力的计算
由拱的整体平衡
M B 0 FAV
Fibi l
M A 0 FBV
结构力学-第4章影响线

影响线和包络图在该桥设计中的应用
详细阐述影响线和包络图在该桥设计中的应用过程,包括影响线和包络图的绘制、最不利位置的确定、最大内力的计 算等。
设计结果分析与评价
对该桥的设计结果进行分析和评价,包括结构安全性、经济性等方面的评估。同时,可以与其他设计方 案进行对比分析,以进一步验证影响线和包络图在工程设计中的有效性和优越性。
通过绘制建筑结构的包络图,可以找到结构在地震作用下的最大变形和位移,为结构的刚 度设计和稳定性分析提供依据。
影响线和包络图在建筑结构优化设计中的作用
利用影响线和包络图,可以对建筑结构进行优化设计,如调整结构布置、改变构件截面等 ,以提高结构的抗震性能和经济效益。
工程案例分析:某大桥设计过程剖析
工程背景介绍
结构优化设计
根据影响线的形状和分布,对结 构进行优化设计,以改善结构的 受力性能。
80%
工程实例分析
结合具体工程实例,利用影响线 理论进行结构分析和设计,验证 理论的正确性和实用性。
03
超静定结构影响线绘制与应用
超静定梁影响线绘制实例
实例一
实例三
一次超静定梁的影响线绘制。通过选取 基本体系和基本未知量,利用力法方程 求解多余未知力,并绘制影响线。
影响线用于确定桥梁结构在移动荷载作用下的最不利位置
通过绘制桥梁结构的影响线,可以确定移动荷载在桥梁上的最不利位置,从而进行结构分析和设 计。
包络图用于确定桥梁结构的最大内力
通过绘制桥梁结构的包络图,可以找到桥梁在移动荷载作用下的最大内力,为桥梁的强度设计和 稳定性分析提供依据。
影响线和包络图在桥梁优化设计中的作用
影响线在结构优化中的应用
结构力学第四章(荷载作用下位移计算公式)
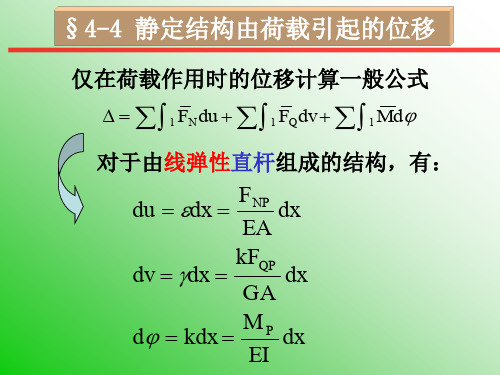
By
0l
MPM EI
ds
0 2
MPM EI
Rd
PR3
4EI
()
同理有:
Bx
PR3 2EI
()
三铰拱的分析同此类似,但一般要考
虑轴力对位移的贡献,也即
P
MM Pds EI
FN FNP ds EA
例 3:求对称桁架D点的竖向位移 Dy。图中
右半部各括号内数值为杆件的截面积A
2x6 2
3
AC段
0 x 2
80x qx 2
1 x 3
D
2720 9EI
()
例题:计算D处竖向位移,B处角位移?(EI为常数)
解:1.构造虚设状态
x
2.分别列出实际状态和虚拟状态中各杆的内力方程
x'
40kN 20kN/m
M
实际状态
虚拟状态
A
C
B
D
DB段
0 x2
P 轴向
FN FNP EA
kFQ FQP GA
MM P EI
ds
式中:
剪切 弯曲
E 弹性模量; G 剪切模量;
A 横截面积; I
截面惯性矩;
k 截面形状系数。如:对矩形截 面k=6/5;圆形截面k=10/9。
例 1:求刚架A点的竖向位移。
解:1.构造虚设状态
2.分别列出实际状态和虚拟状态中各杆的内力方程
x'
40kN 20kN/m
M
实际状态
虚拟状态
A
C
B
D
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4-14、(例题)图4-19示出某机身前段的计算模型。纵向有十根桁条,横向有八个隔框(在自身平面内几何不变),座舱内有三块板开洞。试判断此结构的静不定度数。
解:先不考虑座舱结构。机身是7段的笼式结构,第一段为静定结构,然后每增加一段就增加7度静不定,又因去掉一块蒙皮,所以机身段静不定度数是 。现在再分析座舱组成,由于有座舱,增加了4个空间节点,需要有12个约束,现用了12根杆和5块四边形板,共有17个约束。因此座舱部分静不定度数是 ,所以整个机身结构计算模型静不定度数为:
二、力法原理的应用
4-15、(例题)已知平面桁架几何尺寸、受载和支撑情况如图4-31所示,各杆Ef均相同。使用力法求解桁架各杆的内力。
解:(1)分析结构组成,计算静不定度数,确定多余约束力,解除多余约束,建立基本系统。
结构节点数 ,自由度数 。
有5根双铰杆,约束 ,所以 .
将1-3杆看作多余约束,1-3杆轴力 为多余约束力,令 ,切断1-3杆得静定的基本系统,如图4-31(b)所示。
第四章静不定结构的内力计算
一、结构静不定度数的判断
4-1、分析图4-2中所示的平面桁架结构的静不定度数,并指出哪些是多余约束。
解:结构1234567可以看成是以三角形桁架为基础,分别用两根不咋同一直线上的双铰杆逐次连接6、3、7、4而组成的简单桁架。结构本身是静定结构,此结构相对基础有三个自由度,N=3。现在用三个平面铰1、6、4将结构与基础相连,约束数C=2 3=6,所以K=C-N=3。
(2)求基本系统在外载荷作用下的内力状态<p>
(框里侧受压)
因结构与外载荷相对过刚框中心点的垂直轴对称,因此计算一半即可, 。
(3)求基本系统在 作用下的内力状态<1>、<2>。
(框里侧受压)
(框里侧受压)
(4)求解正则方程
①正则方程:
②求解正则方程系数
切口处弯矩 (与所设方向一致)
切口处轴力 (与所设方向相反)
此结构静不定度数为3,可将平面铰6的水平垂直约束和平面铰4的水平约束看成多余约束。
4-2、(例题):试分析图4-3中所示平面刚架的组成,计算多余约束数,吧并指出哪些约束是多余约束。
解:结构可看成是由杆件用刚节连接形成的平面刚架。这时一个闭合刚架,因此多余约束数K=3,多余约束是闭合刚架123任意截面上的轴力、剪力和弯矩。
(4)求解正则方程
①正则方程:
②求正则方程系数
(5)求解真正内力
结果标在图中(见4-32(d))或列于表中。
4-17、(例题)图中示出一半径为R的圆形刚框。在框的下部中点受到一垂直向下的力P作用,两侧支持剪流 。框截面弯曲刚度为EJ。
求:环形刚框的弯矩图。
注:只考虑刚框弯曲变形能的作用。
解:(1)分析结构组成,计算静不定度数,确定多余约束力,解除多余约束,建立基本系统。
解:(1)分析结构组成,计算静不定度数,确定多余约束及基本系统。
此结构为一边固定的四缘条盒段;因此静不定度数 。取四边形板1-2-6-5为多余约束, 。去掉板1-2-6-5得基本系统。
(2)求解基本系统在外载作用下的内力状态,<p>状态。见图4-32(b)。
(3)在基本系统上加单位力 ,求解内力状态<1>。见图4-32(c)。
将此结构固定在基础上,需要3个约束即可,现在用两个平面铰1、4与基础相连, ,可将铰4处y方向约束看成多余约束。
所以结构多余约束数 。
封闭刚架任意切面上的轴力,剪力和弯矩及铰支点4处y方向约束为多余约束。
4-3、判断图4-4中所示平面架的静不定度数,并指出多余约束力。
(1) ;杆5-6及1铰支点处xy方向约束视为多余约束;
见图4-31(b)。
(3)在基本系统上加单位力 ;求内力状态<1>
;
见图4-31(c)。
(4)求解正则方程
①正则方程 ;
②求解正则方程系数
编号
杆
长度
1
1-2
a
2
1-3
a
0
1
a
0
3
2-3
a
0
0
4
2-4
a
1
a
5
3-4
a
0
0
(5)求解真正内力
结果标在图上(见4-31(d))或列于表中。
4-16、(例题)空间四缘条盒式固定结构的受载及尺寸如图。 设 。求解:结构内力。
(1)、在任意载荷作用下,结构的组成。
(2)、在图中所示载荷作用下,结构的组成。
注:第(2)问中要利用对称性。
4-7、(例题)试分析图4-10(a)和(b)所示薄壁结构的静不定度数。设此两薄壁结构在1-2-3-4处蒙皮被开洞,而(b)结构的5、6节点处杆件被切断。
解:对于开洞和切口的结构,用增删构件法分析静不定度数最为方便。
(注意:节点6处不是十字节点,6点杆端杆力本来就是0,现在将杆子在6点切开,并不能减少未知力数,不能解除约束。)
4-8、试判断图4-11(1)-(6)所示平面薄壁结构的静不定度数。
(1) ;(2) ;(3) ;(4) ;(5) ;
(6)K=12;
4-9、(例题)图4-14中所示为一后掠机翼简化计算模型,其中间梁和肋均有腹板。试判断结构的静不定度数。
4-5、试分析图4-6中所示各刚架及混合杆系的静不定度数,并指出多余约束力。
(1) ;有一个封闭刚框,并且1铰支点处多余一个x方向的约束。
(2)
(3) ;有5个封闭刚框;
(4) ;有5个封闭刚框,并且有4根多余的双铰杆。
4-7、图4-7中示出一平面刚框,此刚框在结构上以x轴、y轴对称,A和B为两个平面铰。试分析:
解:单边相连的四缘条三角形盒段和矩形盒段均有一度静不定度数,而每增加一个双边相连的这种盒段就要增加三度静不定。因此,全结构的静不定度数为:
4-10、(例题)图4-15中所示的空间盒式薄壁结构的内部均有隔板,试判断其静不定度数。
解:以小矩形盒段为基础,基础是静定结构,然后将三角形盒段装在基础上增加静不定度数1,再将答的矩形盒段装在结构上,增加静不定度数1,因此整个结构的静不定度数为 。
(2) ;杆2-9、3-10、10-13的约束视为多余约束;
(3)
4-4、(例题)图4-5中所示为MD-82机身隔框简化计算模型。此框为一倒8字封闭刚框,框凹进处之间支撑一地板梁。地板梁与框式刚接。在地板梁和货仓壁之间有两根撑杆,撑杆两端用铰链与结构相连。
试分析此结构的静不定度数。
解:地板梁在框凹进处与框刚接,因此行程两个封闭刚框,静不定度数 ,两根撑杆是双铰杆,各为一个约束。所以结构静不定度数 。
(注意:分析此类结构组成可以以小矩形盒段或三角形盒段为基础开始增加结构单元,而不能以大矩形盒段为基础,因为将两个小盒段去掉,大矩形盒段是几何可变结构。)
4-11、图4-16中所示空间盒式薄壁结构的内部均有隔板,而蒙皮开口和支撑情况如图所示。试判断其静不定度数是多少。
(1) ;(2);(3) ;(4) ;(5) ;(6)
(5)求刚框真正弯矩:
画出刚框弯矩图,见图4-33(d)
(a)先分析图4-10(a)所示结构。若此平面格式薄壁结构不开洞,它有9个内部十字节点,即有9个多余约束。蒙皮1-2-3-4开洞后解除一个约束,所以此结构的静不定度数 。
(b)图4—10(b)所示结构若不开洞也不切开杆子,则有4个内部十字节点,有4个多余约束,而结构与基础通过2个平面铰和2根双铰杆相连 ,又多了3个约束,一共有多余约束 。现在蒙皮1-2-3-4开洞,十字节点5处杆子被切开,解除了2个约束,所以结构的静不定度数 。
注:也可将其余4根杆中任一杆看成多余约束,相应的轴力为多余约束力,切断多余约束杆,得到相应的静定基本系统。但切断1-3杆,或2-3杆,或3-4杆,得到的基本系统在P作用下,只有1-2,2-4杆有内力,比切断1-2杆或2-4杆得到的基本系统计算要简单。
(2)求解基本系统在外力作用下的内力状态<p>
;
;
环形刚框为 静不定结构。可将刚框任意一切口上的剪力、轴力和弯矩当作多余约束力。开口的刚框作为基本系统。
我们可利用结构对称性,因为结构与外载荷相对过刚框中心点的垂直轴对称,若把切口开在框上端对称面上(如图4-33(b)所示),切口处只有轴力和弯矩,可将静不定度数减少一度,成为 的静不定结构。取切口处轴力和弯矩为多余约束力,令 。框上端对称面开口刚框为基本系统。
(7) ;(8) ;(9) ;(10) 。
4-12、图4-17中所示空间盒式薄壁结构的内部均有隔板。试判断各结构的静不定度数是多少。
(1) ;(2) ;(3) ;(4) ;(5);(6) ;
4-13、图4-18中示出桁条式机翼计算模型,(1)图中大梁Ⅰ、Ⅳ和(2)图中大梁Ⅰ、Ⅴ沿纵向均有腹板,而中间的Ⅰ、Ⅱ、Ⅲ、Ⅳ沿纵向均无腹板,各肋在结构上与端肋结构相同,试判断其静不定度数。
