人教版中考专项复习全等三角形手拉手模型(word 版 无答案)
人教版数学八年级上册 综合专题2—全等三角形手拉手模型

长线交 CE 于 F 点.
证明重要结论:
C
① △ABD≌△ACE;
FD
② BD = CE;
③ BD 的延长线 BF⊥CE;
EA
B
解:∵△ABC、△ADE 都是等腰直角三角形, ∴ AB = AC,AD = AE. 在△ABD 和△ACE 中,
∴ △ABD≌△ACE(SAS). ∴ BD = CE. ∴ ∠ABD = ∠ACE. ∵ ∠BDC = ∠ABD + ∠BAC
E
① △ABD≌△ACE
② BD = CE
③ ∠BFC = ∠BAC = ∠DAE B
F D G
C
解:∵△ABC、△ADE 都是等腰三角形,
∴ AB = AC,AD = AE.
又∵∠BAC = ∠DAE,
A
∴∠BAC + ∠CAD =∠DAE +∠CAD,
即∠BAD = ∠CAE.
在△ABD 和△ACE 中
BE 交于点 O,AD 与 BC 交于点 P,BE 与 CD 交于点
Q,连接 PQ,则有以下五个结论: B ① AD = BE; ② PQ∥AE;
③ AP = BQ; ④ DE = DP;
⑤∠AOB = 60°.
P
OD Q
其中正确的结论有__①__②__③__⑤___.
A
C
E
=∠ACE + ∠BFC, ∴ ∠BFC = ∠BAC = 90°. ∴ BF⊥CE.
C FD
EA
B
练一练
2. 如图,△ABC、△ADE 都是等腰直角三角形,
∠BAC = ∠DAE = 90°,连接 BD、CE 交于点 F.
(1) 求证:BD = CE; (2) 求证:BD⊥CE. C
全等三角形之手拉手模型

全等三角形之手拉手模型专题
手拉手模型:
定义:所谓手拉手模型,是指有公共顶点的两个等腰三角形,顶角相等。
因为顶点相连的四条边,形象的可以看作两双手,所以通常称为手拉手模型。
基本模型:
例题:已知,△ABB'和△ACC'都是等腰三角形,AB=AB',AC=AC',且∠BAB'=∠CAC'。
共顶点的等腰直角三角形中的手拉手
变式精练1、下图,△ABC和△ADE是等腰直角三角形,∠BAC=∠DAE=90°,求证:⑴ BD=CE ⑵ BD⊥CE
共顶点的等边三角形中的手拉手
变式精练2:如图,点A为线段BD上一点,△ABC和△ADE均是等边三角形,求:(1)CD=BE (2)∠DAE+∠BFD=180° (3)∠BFA=∠DFA=60°
模型应用1:如图,分别以△ABC 的边AB、AC 同时向外作等腰直角三角形,其中AB =AE ,AC =AD,∠BAE =∠CAD=90°,点G为BC中点,点F 为BE 中点,
点H 为CD中点。
探索GF 与GH 的位置及数量关系并说明理由。
(选讲)模型应用2:如图,在五边形ABCDE中,∠ABC =∠AED =90°,∠BAC =∠EAD=α,F 为CD的中点。
求证:(1)BF=EF
课堂小测:
练习1:如图,两个正方形ABCD与DEFG,连结CE、AG,二者相交于点H。
求:(1)AG=CE (2)AG与CE之间的夹角为多少度?(3)HD平分∠AHE。
中考数学第四章 三角形 重难 微专项6 “手拉手”模型

故点F所经过的路径的长为3.
(3)取BC的中点H,当点M不与点D重合时,连接HN,
1
1
则BH= BC,∴BH= AB.
2
2
1
∵CD⊥AB,CA=CB,∴BD= AB,∴BH=BD.
2
重难·微专项6 “手拉手”模型
专项训练
∵△ABC,△BMN是等边三角形,
B的运动过程中,小亮以B为顶点作正方形BFGH,其中点F,G都在直线
AE上,如图(4).当点E到达点B时,点F,G,H与点B重合.则点H所经过的
路径长为
,点G所经过的路径长为
.
重难·微专项6 “手拉手”模型
专项训练
解:(1)∵△ABC,△BEF是等边三角形,
∴BA=BC,BE=BF,∠ABC=∠EBF=60°,
【答题关键点】
①当点P与点F重合时,可知AC垂直平分PE,结合点P
在△ABC的角平分线BD上,可知BP=PC,再结合三角函数即可求出BP
的长.
重难·微专项6 “手拉手”模型
例题
②连接AF,可证得BP∥EF,再由△BCP≌△ACE,可得△AFE为等边三
角形,进而可证得BP=EF,即可得证.
图(1)
图(2)
∴∠DCQ=∠BCE,CQ=CE.
∵∠PCB+∠QCD=∠PCQ,
∴∠PCB+∠BCE=∠PCQ=∠PCE.
重难·微专项6 “手拉手”模型
专项训练
= ,
在△QCP和△ECP中,ቐ∠ = ∠,
= ,
∴△QCP≌△ECP(SAS),
∴PQ=PE,
∴△APQ的周长=AQ+PQ+AP=AQ+PE+ AP=
专题3 全等模型——手拉手
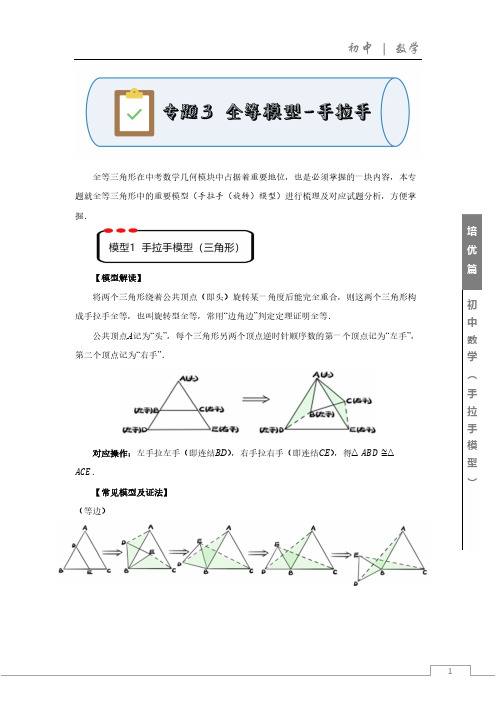
初中数学 ︵ 手拉手模型 ︶培优篇全等三角形在中考数学几何模块中占据着重要地位,也是必须掌握的一块内容,本专题就全等三角形中的重要模型(手拉手(旋转)模型)进行梳理及对应试题分析,方便掌握.【模型解读】将两个三角形绕着公共顶点(即头)旋转某一角度后能完全重合,则这两个三角形构成手拉手全等,也叫旋转型全等,常用“边角边”判定定理证明全等.公共顶点A 记为“头”,每个三角形另两个顶点逆时针顺序数的第一个顶点记为“左手”,第二个顶点记为“右手”.对应操作:左手拉左手(即连结BD ),右手拉右手(即连结CE ),得△ABD≅△ACE.【常见模型及证法】 (等边)初中数学 ︵ 手拉手模型 ︶培优篇 (等腰直角)(等腰)例1.如图,点O 是等边三角形ABC 内的一点,BOC ,将△BOC 绕点C 顺时针旋转60°得△ADC ,连接OD .(1)当100 时,ODA °; (2)当120时,ODA°;(3)若150 ,8OB ,4OC ,则OA 的长为 .初中数学 ︵ 手拉手模型 ︶培优篇 例2.已知△ABC 中,∠BAC =60°,以AB 和BC 为边向外作等边△ABD 和等边△BCE .(1)连接AE 、CD ,如图1,求证:AE =CD ;(2)若N 为CD 中点,连接AN ,如图2,求证:CE =2AN ;(3)若AB ⊥BC ,延长AB交DE 于M ,DB 3,则BM =_______(直接写出结果)初中数学 ︵ 手拉手模型 ︶培优篇 例3.两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来,则形成一组全等的三角形,把具有这个规律的图形称为“手拉手”图形.(1)问题发现:如图1,若△ABC 和△ADE 是顶角相等的等腰三角形,BC ,DE 分别是底边.求证:BD CE ;(2)解决问题:如图2,若△ACB 和△DCE 均为等腰直角三角形,∠ACB =∠DCE = 90°,点A ,D ,E 在同一条直线上,CM 为△DCE 中DE 边上的高,连接BE ,请判断∠AEB 的度数及线段CM ,AE ,BE 之间的数量关系并说明理由.图1 图2初中数学 ︵ 手拉手模型 ︶培优篇【模型解读】将两个多边形绕着公共顶点(即头)旋转某一角度后能完全重合,则这两个多边形构成手拉手全等,也叫旋转型全等,常用“边角边”判定定理证明全等.【常见模型及证法】如图,在任意△ABC 中,分别以AB 、AC 为边作正方形ABDE 、ACFG ,连接EC 、BG ,则△AEC ≌△ABG .例1.(1)作图发现:如图1,已知ΔABC ,小涵同学以AB 、AC 为边向ΔABC 外作等边ΔABD 和等边ΔACE ,连接BE 、CD .这时他发现BE 与CD的数量关系是.(2)拓展探究:如图2,已知ABC ,小涵同学以AB 、AC 为边向外作正方形ABFD 和正方形ACGE ,连接BE 、CD ,试判断BE 与CD 之间的数量关系,并说明理由.初中数学 ︵ 手拉手模型 ︶培优篇 例2.如图,ΔABD 和ΔACE 均为等边三角形,连接BE 、CD . (1)请判断:线段BE 与CD 的大小关系是 ;(2)观察图,当ΔABD 和ΔACE 分别绕点A 旋转时,BE 、CD 之间的大小关系是否会改变?(3)观察如图3和4,若四边形ABCD 、DEFG 都是正方形,猜想类似的结论是________,在如图中证明你的猜想.初中数学 ︵手拉手模型 ︶培优篇1.如图,在ABC 中,45,4,60ACB AB BAC ,D 是边BC 上的一个动点,连接AD ,并将线段AD 绕点A 逆时针旋转60 后得线段AD ,连接BD ,在点D 运动过程中,线段BD 长度的最小值是_________.初中数学 ︵ 手拉手模型 ︶培优篇(1)如图2,将△BDE 绕点B 逆时针旋转任意角度α,连接AD ,EC ,则线段EC 的关系是 ;(2)如图3,DE ∥BC ,连接AE ,判断△EAC 的形状,并求出EC 的长; (3)继续旋转△BDE ,当∠AEC =90°时,请直接写出EC 的长.初中数学 ︵ 手拉手模型 ︶培优篇 4.【问题发现】(1)如图1,△ABC 和△ADE 均为等边三角形,点B 、D 、E 在同一直线上,连接CE ,容易发现:①BEC 的度数为 ;②线段BD 、CE 之间的数量关系为 ;【类比探究】(2)如图2,△ABC 和△ADE 均为等腰直角三角形,∠BAC =∠DAE = 90°,点B ,D ,E 在同一直线上,连接CE ,试判断BEC 的度数以及线段BE 、CE 、DE 之间的数量关系,并说明理由;【问题解决】(3)如图3,90AOB ACB ,4OA ,8OB ,AC BC ,则2OC 的值为 .。
中考数学专题复习全等三角形之手拉手模型

中考数学专题复习全等三角形(手拉手模型)学校:___________姓名:___________班级:___________考号:___________ 评卷人 得分一、单选题1.如图,在ABC 中,90ABC ∠=︒,分别以AB ,AC 为边作等边ABD △和等边ACE ,连结DE ,若3AB =,5AC =,则ED =( )A .22B .23C .4D .322.如图,正ABC 和正CDE △中,B 、C 、D 共线,且3BC CD =,连接AD 和BE 相交于点F ,以下结论中正确的有( )个①60AFB ∠=︒ ①连接FC ,则CF 平分BFD ∠ ①3BF DF = ①BF AF FC =+ A .4 B .3C .2D .1评卷人 得分二、填空题 3.如图,ABC 是边长为5的等边三角形,BD CD =,120BDC ∠=︒.E 、F 分别在AB 、AC 上,且60EDF ∠=︒,则三角形AEF 的周长为______.评卷人得分三、解答题 4.(1)问题发现:如图1,ACB △和DCE 均为等腰直角三角形,90ACB DCE ∠=∠=︒,连接AD ,BE ,点A 、D 、E 在同一条直线上,则AEB ∠的度数为__________,线段AD 、BE之间的数量关系__________; (2)拓展探究:如图2,ACB △和DCE 均为等腰直角三角形,90ACB DCE ∠=∠=︒,连接AD ,BE ,点A 、D 、E 不在一条直线上,请判断线段AD 、BE 之间的数量关系和位置关系,并说明理由. (3)解决问题:如图3,ACB △和DCE 均为等腰三角形,ACB DCE α∠=∠=,则直线AD 和BE 的夹角为__________.(请用含α的式子表示)5.如图,已知点P 在矩形ABCD 外,①APB =90°,P A =PB ,点E 、F 分别在AD 、BC 上运动,且①EPF =45°,连接EF .(1)求证:①APE ①①BFP ; (2)若①PEF 是等腰直角三角形,求AEBF的值; (3)试探究线段AE 、BF 、EF 之间满足的等量关系,并证明你的结论.6.已知:如图,在①ABC中,AB=AC,在①ADE中,AD=AE,且①BAC=①DAE,连接BD,CE交于点F,连接AF.(1)求证:①ABD①①ACE;(2)求证:F A平分①BFE.7.【理解概念】当一个凸四边形的一条对角线把原四边形分成两个三角形.若其中有一个三角形是等腰直角三角形,则把这条对角线叫做这个四边形的“等腰直角线”,把这个四边形叫做“等腰直角四边形”,当一个凸四边形的一条对角线把原四边形分成两个三角形.若其中一个三角形是等腰直角三角形,另一个三角形是等腰三角形,则把这条对角线叫做这个四边形的“真等腰直角线”,把这个四边形叫做“真等腰直角四边形”.(1)【巩固新知】如图①,若AD=3,AD=DB=DC,BC=32,则四边形ABCD______(填“是”或“否”)真等腰直角四边形.(2)【深度理解】在图①中,如果四边形ABCD是真等腰直角四边形,且①BDC=90°,对角线BD是这个四边形的真等腰直角线,当AD=4,AB=3时,则边BC的长是______.(3)如图①,四边形ABCD与四边形ABDE都是等腰直角四边形,且①BDC=90°,①ADE=90°,BD>AD>AB,对角线BD、AD分别是这两个四边形的等腰直角线.求证:AC=BE.(4)【拓展提高】在图3中,已知:四边形ABCD是等腰直角四边形,对角线BD是这个四边形的等腰直角线.若BD正好是分得的等腰直角三角形的一条直角边,且AD=3,AB=4,①BAD=45°,求AC的长.8.如图,在等腰①ABC与等腰①ADE中,AB=AC,AD=AE,①BAC=①DAE=α,连接BD和CE相交于点P,交AC于点M,交AD于点N.(1)求证:BD=CE.(2)求证:AP平分①BPE.(3)若α=60°,试探寻线段PE、AP、PD之间的数量关系,并说明理由.9.在ABC中,90B∠=︒,D为BC延长线上一点,点E为线段AC,CD的垂直平分线的交点,连接EA,EC,ED.(1)如图1,当50BAC∠=︒时,则AED=∠_______°;(2)当60BAC∠=︒时,①如图2,连接AD,判断AED的形状,并证明;①如图3,直线CF与ED交于点F,满足CFD CAE∠=∠.P为直线CF上一动点.当PE PD-的值最大时,用等式表示PE,PD与AB之间的数量关系为_______,并证明.10.如图,在△ABC和△ADE中,AB=AC,AD=AE,①BAC=①DAE,连接BD,CE,BD与CE交于点O,BD与AC交于点F.(1)求证:BD=CE.(2)若①BAC=48°,求①COD的度数.(3)若G为CE上一点,GE=OD,AG=OC,且AG①BD,求证:BD①AC.11.如图,①ABC为等边三角形,点D为线段BC上一点,将线段AD以点A为旋转中心顺时针旋转60°得到线段AE,连接BE,点D关于直线BE的对称点为F,BE与DF 交于点G,连接DE,EF.(1)求证:①BDF=30°(2)若①EFD=45°,AC=3+1,求BD的长;(3)如图2,在(2)条件下,以点D为顶点作等腰直角①DMN,其中DN=MN=2,连接FM,点O为FM的中点,当①DMN绕点D旋转时,求证:EO的最大值等于BC.12.如图,在等腰直角三角形ABC和ADE中,AC=AB,AD=AE,连接BD,点M、N分别是BD,BC的中点,连接MN.(1)如图1,当顶点D在边AC上时,请直接写出线段BE与线段MN的数量关系是,位置关系是.(2)当①ADE绕点A旋转时,连接BE,上述结论是否依然成立,若成立,请就图2情况给出证明;若不成立,请说明理由.(3)当AC=8时,在①ADE绕点A旋转过程中,以D,E,M,N为顶点可以组成平行四边形,请直接写出AD的长.13.如图1,在①ABC中,AE①BC于E,AE=BE,D是AE上的一点,且DE=CE,连接BD,CD.(1)试判断BD与AC的位置关系和数量关系,并说明理由;(2)如图2,若将①DCE绕点E旋转一定的角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由;(3)如图3,若将(2)中的等腰直角三角形都换成等边三角形,其他条件不变.①试猜想BD与AC的数量关系,并说明理由;①你能求出BD与AC的夹角度数吗?如果能,请直接写出夹角度数;如果不能,请说明理由.14.如图,在等边三角形ABC右侧作射线,60CP ACPα∠=<︒,点A关于射线CP的对称点为点D,连接BD交CP于点E,连接,,AD CD AE.(1)用含α的式子表示BCD∠;(2)求BEC∠的度数;(3)试探究线段BD、AE、CE之间的数量关系,并证明.15.已知:①ABC与①BDE都是等腰三角形.BA=BC,BD=BE(AB>BD)且有①ABC=①DBE.(1)如图1,如果A、B、D在一直线上,且①ABC=60°,求证:①BMN是等边三角形;(2)在第(1)问的情况下,直线AE和CD的夹角是°;(3)如图2,若A、B、D不在一直线上,但①ABC=60°的条件不变则直线AE和CD 的夹角是°;(4)如图3,若①ACB=60°,直线AE和CD的夹角是°.16.如图1,在等边ABC 中,60,A AB AC ∠=︒=,点D ,E 分别在边,AB AC 上,AD AE =,连接DC ,点M ,P ,N 分别为,,DE DC BC 的中点.(1)观察猜想:图1中,线段PM 与PN 的数量关系是 ,MPN ∠= ;(2)探究证明:把ADE 绕点A 逆时针方向旋转到图2的位置,连接,,MN BD CE ,则上面题(1)中的两个结论是否依然成立,并说明理由;(3)拓展延伸:把ADE 绕点A 在平面内自由旋转,若4,10AD AB ==,请直接写出PMN 周长的最大值.17.已知,在①ABC 中,AB=AC ,(1)如图1,2,,ABC BDA αα∠=∠=若30α=︒,且点D 在CA 的延长线上时,求证:222CD BD AD =+;(2)如图2,2,,ABC BDA αα∠=∠=若30α=︒,试判断AD ,BD ,CD 之间的等量关系,并说明理由(3)如图3,若45,62,BDA ABC AD ∠=∠=︒=BD =5,求CD 的长.18.现有一块含30°角的直角三角板AOB,点N在其斜边AB上,点M在其最短直角边OA所在直线上.以MN为边作如图所示的等边①MNP.(1)如图1,当M在线段OA上时,证明:AM﹣AN=AP;(2)如图2当M在射线OA上时,试探究AM、AN、AP三者之间的数量关系并给出证明.19.正方形ABCD中,点E、F在BC、CD上,且BE=CF,AE与BF交于点G.(1)如图1,求证AE①BF;(2)如图2,在GF上截取GM=GB,①MAD的平分线交CD于点H,交BF于点N,连接CN,求证:AN+CN=2BN;(3)在(2)的条件下,若tan①AEB=3,S△CHN=95,求AB的长20.如图,在Rt ABC△中,90ABC∠=︒,点D在BC的延长线上,且BD AB=,过点B作BE AC⊥,与BD的垂线DE交于点E,连结AD,取AD中点O,连结OC,OE.(1)求证:ABC BDE△≌△.(2)求证:OC OE=.21.如图1,在①ABC中,AE①BC于E,AE=BE,D是AE上一点,且DE=CE,连接BD,CD.(1)判断BD与AC的位置关系和数量关系,并证明;(2)如图2,若将①DCE绕点E旋转一定的角度后,BD与AC的位置关系和数量关系是否发生变化?并证明;(3)如图3,将(2)中的等腰直角三角形都换成等边三角形,其他条件不变,求BD 与AC夹角的度数.22.正方形ABCD和正方形AEFG的边长分别为3和1,将正方形AEFG绕点A逆时针旋转.(1)当旋转至图1位置时,连接BE,DG,则线段BE和DG的关系为;(2)在图1中,连接BD,BF,DF,求在旋转过程中BDF的面积最大值;(3)在旋转过程中,当点G,E,D在同一直线上时,求线段BE的长.23.在平面直角坐标系中,A(a,0)、B(b,0),且a,b满足26930a a b-+++=,C、D两点分别是y轴正半轴、x轴负半轴上的两个动点;(1)如图1,若C(0,4),求△ABC的面积;(2)如图1,若C(0,4),BC=5,BD=AE,且∠CBA=∠CDE,求D点的坐标;(3)如图2,若∠CBA=60°,以CD为边,在CD的右侧作等边△CDE,连接OE,当OE最短时,求A,E两点之间的距离.24.在ABC中,AB=AC,点D是直线BC上一点(不与B,C重合),以AD为一边在AD的右侧作ADE,使AD=AE,①DAE=①BAC,连接CE.(1)(请直接写出你的结论)如图1,当点D在线段BC上:①如果①BAC=90°,则①BCE=°;①如果①BAC=100°,则①BCE=°;(2)设①BAC=α,①BCE=β.①如图2,当点D在线段BC上移动,则α、β之间有怎样的数量关系?请说明理由;①当点D在直线BC上移动,则α、β之间有怎样的数量关系?请画出图形,并直接写出你的结论.25.(1)问题:如图1,在Rt ①ABC 中,①BAC =90°,AB =AC ,D 为BC 边上一点(不与点B ,C 重合).连接AD ,过点A 作AE ①AD ,并满足AE =AD ,连接CE .则线段BD 和线段CE的数量关系是,位置关系是 ;(2)探索:如图2,当D 点为BC 边上一点(不与点B ,C 重合),Rt ①ABC 与Rt ①ADE 均为等腰直角三角形,①BAC =①DAE =90°,AB =AC ,AD =AE .试探索线段BD 、CD 、DE 之间满足的等量关系,并证明你的结论;(3)拓展:如图3,在四边形ABCD 中,①ABC =①ACB =①ADC =45°,若BD =3,CD =1,则线段AD 的长为26.已知:等腰Rt ABC 和等腰Rt ADE △中,AB AC =,AE AD =,90BAC EAD ∠=∠=︒.(1)如图1,延长DE 交BC 于点F ,若68BAE ∠=︒,则DFC ∠的度数为 ;(2)如图2,连接EC 、BD ,延长EA 交BD 于点M ,若90AEC ∠=︒,求证:点M 为BD 中点;(3)如图3,连接EC 、BD ,点G 是CE 的中点,连接AG ,交BD 于点H ,9AG =,5HG =,直接写出AEC △的面积.27.如图,点A,M,B在同一直线上,以AB为边,分别在直线两侧作等边三角形ABC和等边三角形ABD,连接CM,DM,过点M作MN=DM,交BC边于点G,交DB的延长线于点N.(1)求证:①BCM=①BDM;(2)求①CMN的度数;(3)求证:AM=BN.28.边长为4的正方形ABCD与边长为22的正方形CEFG如图1摆放,将正方形CEFG绕点C顺时针旋转,旋转角为α,连接BG,DE.(1)如图2,求证:①BCG①①DCE;(2)如图2,连接DG,BE,判断DG2+BE2否为定值.若是,求这个定值若不是,说明理由;(3)如图3,当点G恰好落在DE上时,求α的值.29.在ABC 中,90A ∠=︒,AB AC =.(1)如图1,ABC 的角平分线BD ,CE 交于点Q ,请判断“2QB QA =”是否正确;______(填“是”或“否”);(2)点P 是ABC 所在平面内的一点,连接PA ,PB 且2PB PA =. ①如图2,点P 在ABC 内,30ABP ∠=︒,求PAB ∠的大小;①如图3,点P 在ABC 外,连接PC ,设APC α∠=,BPC β∠=,求αβ+的值.30.在学习全等三角形知识时,数学兴趣小组发现这样一个模型:它是由两个共顶点且顶角相等的等腰三角形构成在相对位置变化的同时始终存在一对全等三角形通过资料查询,他们得知这种模型称为“手拉手模型”兴趣小组进行了如下探究:(1)如图1,两个等腰三角形ABC 和ADE 中,AB AC =,AE AD =,BAC DAE ∠=∠,连接BD 、CE ,如果把小等腰三角形的腰长看作小手,大等腰三角形的腰长看作大手,两个等腰三角形有公共顶点,类似大手拉着小手,这个就是“手拉手模型”,在这个模型中,和ADB △全等的三角形是______,此线BD 和CE 的数量关系是______.(2)如图2,两个等腰直角三角形ABC 和ADE 中,AB AC =,AE AD =,90BAC DAE ∠=∠=︒,连接BD 、CE ,两线交于点P ,请判断线段BD 和CE 的关系,并说明理由.参考答案:1.C 【解析】 【分析】在Rt △ABC 中可直接运用勾股定理求出BC ,然后结合“手拉手”模型证得△ABC ①①ADE ,即可得到DE =BC ,从而求解即可. 【详解】解:在Rt △ABC 中,AB =3,AC =5, ①由勾股定理得:BC =4,①ABD △和ACE 均为等边三角形, ①AB =AD ,AC =AE ,①BAD =①CAE =60°, ①①BAD -①CAD =①CAE -①CAD , 即:①BAC =①DAE , 在△ABC 和△ADE 中,AB AD BAC DAE AC AE =⎧⎪∠=∠⎨⎪=⎩①△ABC ①①ADE (SAS ), ①DE =BC =4, 故选:C . 【点睛】本题考查全等三角形的判定与性质,勾股定理的应用,掌握全等三角形的判定与性质,熟练运用勾股定理解三角形是解题关键. 2.A 【解析】 【分析】根据“手拉手”模型证明BCE ACD ≌,从而得到CBE CAD ∠=∠,再结合三角形的外角性质即可求解60AFB ACB ∠=∠=︒,即可证明①;作CM BE ⊥于M 点,CN AD ⊥于N 点,证明CEM CDN ≌,结合角平分线的判定定理即可证明①;利用面积法表示BCF △和DCF 的面积,然后利用比值即可证明①;利用“截长补短”的思想,在AD 上取点Q ,使得FC FQ =,首先判断出FCQ 为等边三角形,再结合“手拉手”模型推出BCF ACQ ≌即可证明①. 【详解】解:①①ABC 和CDE △均为等边三角形, ①60ACB ECD ∠=∠=︒,AC BC =,EC DC =, ①ACB ACE ECD ACE ∠+∠=∠+∠, ①BCE ACD ∠=∠, 在BCE 和ACD △中, BC AC BCE ACD EC DC =⎧⎪∠=∠⎨⎪=⎩①()BCE ACD SAS ≌, ①CBE CAD ∠=∠,①AFB CBE CDA ∠=∠+∠,ACB CDA CAD ∠=∠+∠, ①60AFB ACB ∠=∠=︒,故①正确;①如图所示,作CM BE ⊥于M 点,CN AD ⊥于N 点, 则90CME CND ∠=∠=︒, ①BCE ACD ≌, ①CEM CDN ∠=∠, 在CEM 和CDN △中, CME CND CEM CDN CE CD ∠=∠⎧⎪∠=∠⎨⎪=⎩①()CEM CDN AAS ≌, ①CM CN =,①CF 平分BFD ∠,故①正确; ①如图所示,作FP BD ⊥于P 点, ①1122BCFSBF CM BC FP ==,1122DCFS DF CN CD FP ==, ①11221122BCF DCFBF CM BC FP SSDF CN CD FP ==,①CM CN =, ①整理得:BF BCDF CD=, ①3BC CD =, ①33BF CDDF CD==, ①3BF DF =,故①正确;①如图所示,在AD 上取点Q ,使得FC FQ =, ①60AFB ACB ∠=∠=︒,CF 平分BFD ∠, ①120BFD ∠=︒,1602CFD BFD ∠=∠=︒,①FCQ 为等边三角形, ①60FCQ ∠=︒,CF CQ =, ①60ACB ∠=︒,①ACB ACF FCQACF ∠+∠=∠+∠, ①BCF ACQ ∠=∠, 在BCF △和ACQ 中, BC AC BCF ACQ CF CQ =⎧⎪∠=∠⎨⎪=⎩①()BCF ACQ SAS ≌, ①BF AQ =,①AQ AF FQ =+,FQ FC =, ①BF AF FC =+,故①正确; 综上,①①①①均正确; 故选:A .【点睛】本题考查等边三角形的判定与性质,全等三角形的判定与性质等,理解等边三角形的基本性质,掌握全等三角形中的辅助线的基本模型,包括“手拉手”模型,截长补短的思想等是解题关键.3.10【解析】【分析】延长AB到N,使BN=CF,连接DN,求出①FCD=①EBD=①NBD=90°,根据SAS证①NBD①①FCD,推出DN=DF,①NDB=①FDC,求出①EDF=①EDN,根据SAS证①EDF①①EDN,推出EF=EN,易得①AEF的周长等于AB+AC.【详解】解:延长AB到N,使BN=CF,连接DN,①①ABC是等边三角形,①①ABC=①ACB=60°,①BD=CD,①BDC=120°,①①DBC=①DCB=30°,①①ACD=①ABD=30°+60°=90°=①NBD,①在①NBD和①FCD中,BD DCNBD FCDBN CF=⎧⎪∠=∠⎨⎪=⎩,①①NBD①①FCD(SAS),①DN=DF,①NDB=①FDC,①①BDC=120°,①EDF=60°,①①EDB+①FDC=60°,①①EDB+①BDN=60°,即①EDF =①EDN ,在①EDN 和①EDF 中,DE DE EDF EDN DN DF =⎧⎪∠=∠⎨⎪=⎩,①①EDN ①①EDF (SAS ),①EF =EN =BE +BN =BE +CF ,即BE +CF =EF .①①ABC 是边长为5的等边三角形,①AB =AC =5,①BE +CF =EF ,①①AEF 的周长为:AE +EF +AF =AE +EB +FC +AF =AB +AC =10,故答案为:10.【点睛】本题考查了等边三角形性质和判定,等腰三角形的性质,三角形的内角和定理,全等三角形的性质和判定的综合运用.注意掌握辅助线的作法,注意掌握数形结合思想的应用.4.(1)90°,AD =BE ;(2)AD =BE ,AD ①BE ;(3)α【解析】【分析】(1)由已知条件可得AC BC =,CD CE =,进而根据①ACB −①DCB =①DCE −①DCB ,可得①ACD =①BCE ,证明①ACD ①①BCE (SAS ),即可求得AD =BE ;①BEC =①CDA =135°; (2)延长AD 交BE 于点F ,同理可得①ACD ①①BCE ,设①F AB =α,则①CAD =①CBE =45°-α,根据①ABE =45°+45°-α=90°-α,进而根据①AFB =180°-①F AB -①ABE =180°-α-(90°-α)=90°,即可求解;(3)延长BE 交AD 于点G ,方法同(2)证明①ACD ①①BCE ,进而根据三角形的内角和定理即可求得直线AD 和BE 的夹角. 【详解】(1)①ACB △和DCE 均为等腰直角三角形,90ACB DCE ∠=∠=︒,①AC BC =,CD CE =,①CDE =45°①①CDA =135°①①ACB −①DCB =①DCE −①DCB ,①①ACD =①BCE .在①ACD 和①BCE 中,AC BC ACD BCE CD CE ⎧⎪∠∠⎨⎪⎩===,①①ACD ①①BCE (SAS ),①①BEC =①ADC =135°,AD =BE∠①AEB =90°故答案为:90°,AD =BE(2)AD =BE ,AD ①BE ,理由如下,同理可得①ACD ①①BCE ,则AD =BE ,延长AD 交BE 于点F ,设①F AB =α,则①CAD =①CBE =45°-α①①ABE =45°+45°-α=90°-α①①AFB =180°-①F AB -①ABE =180°-α-(90°-α)=90°①AD ①BE(3)如图,延长BE 交AD 于点G ,①ACB △和DCE 均为等腰三角形,①AC BC =,CD CE =,①①ACB =①DCE =α,①①ACB +①ACE =①DCE +①ACE ,①①ACD =①BCE .在①ACD 和①BCE 中,AC BC ACD BCE CD CE ⎧⎪∠∠⎨⎪⎩===,①①ACD ①①BCE (SAS ),①①CBE =①CAD①ACB DCE α∠=∠=①①CBA =①CAB =()11180=9022αα︒-︒- ①①GAB +①GBA =()()CAD CAB ABC CBE ∠+∠+∠-∠,ABC CAB =∠+∠180α=︒-,①①AGB =180°-(①GAB +①GBA )α= ,即直线AD 和BE 的夹角为α.故答案为:α.【点睛】本题考查了等腰三角形的性质,三角形内角和定理,全等三角形的性质与判定,掌握旋转模型证明三角形全等是解题的关键.5.(1)见解析(2)12或2(3)线段AE,BF,EF之间满足的等量关系是AE2+BF2=EF2.证明见解析【解析】【分析】(1)根据矩形的性质和相似三角形的判定得出①APE①①BFP即可;(2)根据相似三角形的性质得出比例关系,分两种情况进行讨论解答即可;(3)利用全等三角形的判定和性质以及勾股定理解答即可.(1)①四边形ABCD是矩形,①①BAD=①ABC=90°.①①APB=90°,P A=PB,①①P AB=①PBA=45°.①①P AE=①P AB+①BAD=45°+90°=135°,①FBP=①PBA+①ABC=45°+90°=135°,①①P AE=①PBF.①①APE+①AEP=45°.①①EPF=45°,①APB=90°,①①APE+①BPF=45°.①①AEP=①BPF.①①APE①①BFP.(2)①①APE①①BFP,①AE AP EP BP BF PF==.①①PEF是等腰直角三角形,①EPF=45°,①可分为两种情况讨论:①当①PEF=90°,PE=EF时,则2.PF PE=.①12AE AP EPBP BF PF===.①12AE BP=,2BF AP=.①AP=BP,①11222BPAEBF AP==.①当①PFE=90°,PF=EF时,则2PE PF=.①2AE AP EPBP BF PF===.①2AE BP=,12BF AP=.①AP=BP,①2212AE BPBF AP⋅==.综上所述,AEBF的值为12或2.(3)线段AE,BF,EF之间满足的等量关系是AE2+BF2=EF2.证明:延长AB到G,使得BG=AE,连接PG,FG,①①PBA=45°,①①PBG=135°.①①P AE=135°,①①PBG=①P AE.①P A=PB,BG=AE,①①PBG①①P AE(SAS).①BG=AE,PG=PE,①BPG=①APE.①①APE+①BPF=①EPF=45°,①①BPG+①BPF=①EPF.即①GPF=①EPF.又①PF=PF,PG=PE,①①PGF①①PEF(SAS).①GF=EF.①①ABC=90°,①①GBF=90°.①由勾股定理得,BG2+BF2=GF2.①AE2+BF2=EF2.【点睛】此题主要考查了全等三角形的判定和性质,相似三角形的判定与性质,熟练掌握全等三角形的判定与性质和相似三角形的判定与性质是解本题的关键.6.(1)见解析(2)见解析【解析】【分析】(1)根据SAS证明结论即可;(2)作AM①BD于M,作AN①CE于N.由(1)可得BD=CE,S△BAD=S△CAE,然后根据角平分线的性质即可解决问题.(1)证明:①①BAC=①DAE,①①BAC+①CAD=①DAE+①CAD,即①BAD=①CAE,在①BAD和①CAE中,AB ACBAD CAEAD AE=⎧⎪∠=∠⎨⎪=⎩,①①BAD①①CAE(SAS);(2)证明:如图,作AM①BD于M,作AN①CE于N.由①BAD①①CAE,①BD=CE,S△BAD=S△CAE,①1122BD AM CE AN⋅⋅=⋅⋅,①AM=AN,①点A在①BFE平分线上,①F A平分①BFE.【点睛】本题考查全等三角形的判定和性质、三角形的面积,解题的关键是熟练掌握全等三角形的判定和性质,学会转化的思想,巧用等积法进行证明.7.(1)是(2)42或32(3)见解析(4)AC=34或41.【解析】【分析】(1)利用勾股定理的逆定理证明①BDC=90°,从而①BDC是等腰直角三角形,又因为①ABD是等腰三角形,即可得出结论;(2)由题意知①ABD是等腰三角形,当AD=BD=4时,由勾股定理得:BC=42,当BD=AB=3时,由勾股定理得:BC=32;(3)利用SAS证明①ADC①①EDB,得AC=BE;(4)分①BDC=90°和①DBC=90°,分别构造等腰直角三角形,利用(3)中全等进行转化,从而解决问题.(1)解:①AD=3,AD=DB=DC,①BD=CD=3,①BD2+CD2=18,BC2=(32)2=18,①BD2+CD2=BC2,①①BDC是等腰直角三角形,①①ABD是等腰三角形,①四边形ABCD是真等腰直角四边形,故答案为:是;(2)解:①对角线BD是这个四边形的真等腰直角线,①①ABD是等腰三角形,当AD=BD=4时,由勾股定理得:BC=2244+=42,当BD=AB=3时,由勾股定理得:BC=22+=32,33综上:BC=42或32,故答案为:42或32;(3)解:由题意知:①BDC和①ADE都是等腰直角三角形,①BD=CD,AD=DE,①BDC=①ADE=90°,①①ADC=①EDB,①①ADC①①EDB(SAS),①AC=BE;(4)解:由题意知:①BDC是等腰直角三角形,当①BDC=90°时,如图,作DE①AD,取DE=AD,连接AE,BE,由(3)同理得①ADC①①EDB(SAS),①AC=BE,①AD=3,①ADE是等腰直角三角形,①AE=32,①EAD=45°,①①DAB=45°,①①EAB=90°,由勾股定理得BE=()222232434AE AB+=+=,①AC=34;当①DBC=90°时,如图,同理可得AE=42,DE=AC=41,综上:AC=34或41.【点睛】本题主要考查了等腰直角三角形和等腰三角形的性质,全等三角形的判定与性质,勾股定理的应用,读懂题意,作辅助线构造全等三角形是解题的关键,注意问题设置的层次性.8.(1)见解析(2)见解析(3)PE=AP+PD,见解析【解析】【分析】(1)由“SAS”可证①BAD①①CAE,可得BD=CE;(2)由全等三角形的性质可得S△BAD=S△CAE,由三角形面积公式可得AH=AF,由角平分线的性质可得AP平分①BPE;(3)由全等三角形的性质可得①BDA=①CEA,由“SAS”可证①AOE①①APD,可得AO=AP,可证①APO是等边三角形,可得AP=PO,可得PE=AP+PD,即可求解.(1)证明:①①BAC=①DAE=α,①①BAD=①CAE,又①AB=AC,AD=AE,①①BAD①①CAE(SAS),①BD=CE;(2)证明:如图,过点A作AH①BD,AF①CE,①①BAD①①CAE,①S△BAD=S△CAE,BD=CE,①12BD×AH=12CE×AF,①AH=AF,又①AH①BD,AF①CE,①AP平分①BPE;(3)解:PE=AP+PD,理由如下:如图,在线段PE上截取OE=PD,连接AO,①①BAD①①CAE,①①BDA=①CEA,又①OE=PD,AE=AD,①①AOE①①APD(SAS),①AP=AO,①①BDA=①CEA,①PND=①ANE,①①NPD=①DAE=α=60°,①①BPE=180°-①NPD=180°-60°=120°,又①AP 平分①BPE ,①①APO =60°,又①AP =AO ,①①APO 是等边三角形,①AP =PO ,①PE =PO +OE ,①PE =AP +PD .【点睛】本题是三角形综合题,考查了全等三角形的判定和性质,直角三角形的性质,等边三角形的判定和性质以及角之间的关系,证明①BAD ①①CAE 是解本题的关键.9.(1)80;(2)AED 是等边三角形;(3)2PE PD AB -=.【解析】【分析】(1)根据垂直平分线性质可知AE EC ED ==,再结合等腰三角形性质可得EAC ECA ∠=∠,EDC ECD ∠=∠,利用平角定义和四边形内角和定理可得2AED ACB ∠=∠,由此求解即可; (2)根据(1)的结论求出260AED ACB ∠=∠=︒即可证明AED 是等边三角形;(3)根据利用对称和三角形两边之差小于第三边,找到当PE PD -的值最大时的P 点位置,再证明对称点D 与AD 两点构成三角形为等边三角形,利用旋转全等模型即可证明ACD ED D '≅,从而可知PE PD PE PD ED AC ''-=-==,再根据30°直角三角形性质可知2AC AB =即可得出结论.【详解】解:(1)①点E 为线段AC ,CD 的垂直平 分线的交点,①AE EC ED ==,①EAC ECA ∠=∠,EDC ECD ∠=∠,①EAC EDC ACE ECD ACD ∠+∠=∠+∠=∠,①360EAC EDC ACD AED ∠+∠+∠+∠=︒,①2360ACD AED ∠+∠=︒,①180ACD ACB ∠+∠=︒,①2AED ACB ∠=∠,①在ABC 中,90B ∠=︒,50BAC ∠=︒,①40ACB ∠=︒,①280AED ACB ∠=∠=︒,故答案为:80︒.(2)①结论:AED 是等边三角形.证明:①在ABC 中,90B ∠=︒,60BAC ∠=︒,①30ACB ∠=︒,由(1)得:260AED ACB ∠=∠=︒,AE EC ED ==,①AED 是等边三角形.①结论:2PE PD AB -=.证明:如解图1,取D 点关于直线AF 的对称点D ,连接PD 、PD ';①PD PD '=,①PE PD ED ''-≤,等号仅P 、E 、D 三点在一条直线上成立,如解图2,P 、E 、D 三点在一条直线上,由(1)得:CAE EDC ACD ∠+∠=∠,又①CFD CAE ∠=∠,①CFD CDE ACD ∠+∠=∠,又①180ACD ACB ∠+∠=︒,180CFD CDE PCD ∠+∠+∠=︒,①30PCD ACB ∠=∠=︒,①点D 、点D 是关于直线AF 的对称点,①CD CD '=,260D CD PCD '∠=∠=︒,①D CD '△是等边三角形,①CD DD '=,60CDD '∠=︒,①AED 是等边三角形,①AD ED =,60ADE ∠=︒,①ADC D DA D DA EDD '''∠+∠=∠+∠,①ADC EDD '∠=∠,在ACD △和ED D '中,AD ED ADC EDD CD D D '=⎧⎪∠=∠⎨='⎪⎩,①ACD ED D '≅(SAS )①AC ED '=,①PD PD '=,①PE PD PE PD ED AC ''-=-==,在ABC 中,90B ∠=︒,30ACB ∠=︒,①2AC AB =,①2PE PD AB -=【点睛】 本题是三角形综合题,主要考查了等腰三角形、等边三角形的性质和判定,全等三角形性质和判定等知识点,解题关键是利用对称将PE PD -转化为三角形三边关系找到P 的位置,并证明对称点D 与AD 两点构成三角形为等边三角形.10.(1)见解析;(2)132°;(3)见解析【解析】【分析】(1)根据①BAC =①DAE ,推出①BAD =①CAE ,从而结合“SAS ”证明△BAD ①①CAE ,即可得出结论;(2)根据外角定理推出①COD =①OBC +①BCA +①ACE ,结合全等三角形的性质推出①COD =①ABC +①BCA ,最后在△ABC 中利用内角和定理求解即可;(3)连接AO ,根据题意确定△ADO ①△AEG ,得到①OAD =①GAE ,AO =AG ,再结合题干条件推出△AOC 为等腰三角形,以及①BOA =①BOC ,从而根据“三线合一”证明即可.【详解】(1)证:①①BAC =①DAE ,①①BAC +①CAD =①DAE +①CAD ,即:①BAD =①CAE ,在△BAD 和△CAE 中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩①△BAD ①①CAE (SAS ),①BD =CE ;(2)解:①①COD =①OBC +①BCO ,①BCO =①BCA +①ACE ,①①COD =①OBC +①BCA +①ACE ,①△BAD ①①CAE ,①①ABD =①ACE ,①①COD =①OBC +①BCA +①ABD =①ABC +①BCA ,①①BAC =48°,①①ABC +①BCA =180°-48°=132°,①①COD =132°;(3)证:如图所示,连接AO ,①△BAD ①①CAE ,①①ADO =①AEG ,在△ADO 和△AEG 中,E A ADO A G E E D G D A O =⎧⎪⎨⎪∠==⎩∠①△ADO①△AEG(SAS),①①OAD=①GAE,AO=AG,①①AOG=①AGO,①①OAD+①DAG=①GAE+①DAG,即:①OAG=①DAE,①①DAE=①BAC,①①BAC=①OAG,在△ABF和△COF中,①BAC=180°-①ABD-①AFB,①BOC=180°-①ACE-①CFO,由(2)知①ABD=①ACE,①①AFB=①CFO,①①BAC=①BOC,①①BOC=①OAG,①AG①BD,①①BOA=①OAG,①①BOA=①BOC,①AO=AG,AG=CO,①AO=CO,即:△AOC为等腰三角形,①①BOA=①BOC,①OF①AC,①BD①AC.【点睛】本题考查全等三角形的判定与性质,等腰三角形的判定与性质等,掌握全等三角形的判定与性质,熟悉“手拉手”模型的证明是解题关键.11.(1)见解析;(2)2;(3)见解析【解析】【分析】(1)由①ABC是等边三角形,可得①ABC=60°,由D、F关于直线BE对称,得到BF=BD,则①BFD=①BDF,由三角形外角的性质得到①BFD+①BDF=①ABD,则①BDF=①BFD=30°;(2)设BG x=,由D、F关于直线BE对称,得到①BGD=①BGF=90°,EF=ED,EG=DG,由含30度角的直角三角形的性质和勾股定理得2BD x=,3DG x=,证明①EAB①①DAC得到3CD BE EG BG GD BG x x==-=-=-,再由31BC AC==+,得到2331BD CD x x x+=+-=+,由此求解即可;(3)连接OG,先求出2MD=,证明OG是三角形DMF的中位线,得到112OG DM==,再根据两点之间线段最短可知13OE EG OG≤+=+,则OE的最大值等于BC.【详解】解:(1)①①ABC是等边三角形,①①ABC=60°,①D、F关于直线BE对称,①BF=BD,①①BFD=①BDF,①①BFD+①BDF=①ABD,①①BDF=①BFD=30°;(2)设BG x=,①D、F关于直线BE对称,①①BGD=①BGF=90°,EF=ED,①①EDG=EFG=45°,①EG=DG,①①BDG=30°,①22BD BG x==,①223DG BD BG x=-=,由旋转的性质可得AE =AD ,①EAD =①BAC =60°,①①EAB +①BAD =①CAD +①BAD ,即①EAB =①DAC ,又①AB =AC ,①①EAB ①①DAC (SAS ),①3CD BE EG BG GD BG x x ==-=-=-,①31BC AC ==+,①2331BD CD x x x +=+-=+,①1x =,①22BD x ==;(3)如图所示,连接OG ,①在等腰直角三角形DMN 中,2DN MN ==,①222MD DN MN =+=,①D 、F 关于直线BE 对称,①G 为DF 的中点,又①O 为FM 的中点,①OG 是三角形DMF 的中位线,①112OG DM ==, 由(2)可得3EG =,根据两点之间线段最短可知13OE EG OG ≤+=+,①OE 的最大值等于BC .【点睛】本题主要考查了等边三角形的性质,轴对称的性质,全等三角形的性质与判定,勾股定理,含30度角的直角三角形性质,三角形中位线定理,两点之间线段最短等等,解题的关键在于能够熟练掌握轴对称的性质和等边三角形的性质.12.(1)MN =12BE ;MN ①BE ;(2)成立,理由见解析;(3)81313或855【解析】【分析】(1)延长MN 交AB 于点G ,根据三角形的中位线定理证明//MN AB ,1122MN CD BE ==,再由平行线的性质证明90NGB A ∠=∠=︒,则MN BE ⊥;(2)(1)中的结论依然成立,连接CD ,由等腰直角三角形的性质推出相应的线段相等和角相等,证明CAD BAE ∆≅∆,先证明CD BE ⊥,再证明MN BE ⊥;由三角形的中位线定理证明12MN BE =; (3)以D ,E ,M ,N 为顶点的四边形为平行四边形分两种情况,即AD 在ABC ∆的内部、AD 、AE 都在ABC ∆的外部,此时C 、D 、E 三点在同一条直线上,且2CD BE DE ==,再根据CD BE ⊥,得到直角三角形,由勾股定理列方程求AD 的长.【详解】解:(1)如图1,延长MN 交AB 于点G ,M 、N 分别是BD 、BC 的中点,//MN CD ∴,且12MN CD =, 90NGB A ∴∠=∠=︒,MN BE ∴⊥.AC AB =,AD AE =,CD BE ∴=,12MN BE ∴=; 故答案为:12MN BE =,.MN BE ⊥ (2)成立,理由如下:∴如图2,连接并延长CD 交BE 于点H ,延长NM 交BE 于点G ,90CAB DAE ∠=∠=︒,90CAD BAE DAB ∴∠=∠=︒-∠,AC AB =,AD AE =,()CAD BAE SAS ∴∆∆≌, CD BE ∴=,ACD ABE ∠=∠,点M 、N 分别是BD 、BC 的中点,//MN CD ∴,12MN CD =, 12MN BE ∴=; 90BCH CBH BCH ABE ABC BCH ACD ABC ACB ABC ∠+∠=∠+∠+∠=∠+∠+∠=∠+∠=︒, 90CHB ∴∠=︒,CD BE ∴⊥,90NGB CHB ∴∠=∠=︒;MN BE ∴⊥.(3)如图3,AD 在ABC ∆内部,AE 在ABC ∆的外部,且四边形DEMN 是平行四边形,由(2)得,CD BE ⊥,//MN CD ,1122MN CD BE ==,∵四边形DEMN 是平行四边形, //DE MN ,DE MN =,C ∴、D 、E 三点在同一条直线上,90BEC ∴∠=︒,222DE AD =,2DE AD ∴=,2222CD BE MN DE AD ∴====,8AC =,22288128BC ∴=+=, 由222CE BE BC +=得,22(222)(22)128AD AD AD ++=,解得81313AD =; 如图4,AD 、AE 都在ABC ∆的外部,且四边形DENM 是平行四边形,设BE 交AC 于点O ,90CAD BAE CAE ∠=∠=︒+∠,AC AB =,AD AE =,()CAD BAE SAS ∴∆∆≌,CD BE ∴=,M 、N 分别为BD 、BC 的中点,//MN CD ∴,四边形DENM 是平行四边形,//DE MN ∴,∴点E 在CD 上,ACD ABE ∠=∠,COE AOB ∠=∠,90ACE COE ABE AOB ∴∠+∠=∠+∠=︒,90BEC ∴∠=︒,M 、N 分别是BD 、BC 的中点,1122MN CD BE ∴==, 22BE CD MN DE ∴===,2DE AD =,22BE CD AD ∴==,由222CE BE BC +=得,22(222)(22)128AD AD AD -+=,解得855AD =, 综上所述,AD 的长为81313或855. 【点睛】 本题主要考查平行四边形的性质、等腰直角三角形的性质、三角形的中位线、勾股定理及二次根式的运算,熟练掌握平行四边形的性质、等腰直角三角形的性质、三角形的中位线、勾股定理及二次根式的运算是解题的关键.13.(1)BD =AC ,BD ①AC ,理由见解析;(2)不变,理由见解析;(3)①BD =AC ,理由见解析;①能,60°或120°.【解析】【分析】(1)延长BD 交AC 于F ,根据“SAS ”判定BED AEC ≌,根据全等三角形的性质,即可求证;(2)根据“SAS ”判定BED AEC ≌,根据全等三角形的性质,即可求证;(3)①根据“SAS ”判定BED AEC ≌,根据全等三角形的性质,即可求证;①设AC 与BD 交于点F ,根据全等三角形的性质,即可求证.【详解】(1)BD =AC ,BD ①AC ,理由:延长BD 交AC 于F .①AE ①BC ,①①AEB =①AEC =90°,在①BED 和①AEC 中BE AE BED AEC DE EC =⎧⎪∠=∠⎨⎪=⎩①()BED AEC SAS ≌,①BD =AC ,①DBE =①CAE ,①①BED =90°,①①EBD +①BDE =90°,①①BDE =①ADF ,①①ADF +①CAE =90°,①①AFD =180°﹣90°=90°,①BD ①AC ;(2)不发生变化,理由是:①①BEA =①DEC =90°,①①BEA +①AED =①DEC +①AED ,①①BED =①AEC ,在①BED 和①AEC 中,BE AE BED AEC DE EC =⎧⎪∠=∠⎨⎪=⎩①①BED ①①AEC (SAS ),①BD =AC ,①BDE =①ACE ,①①DEC =90°,①①ACE +①EOC =90°,①①EOC =①DOF ,①①BDE +①DOF =90°,①①DFO =180°﹣90°=90°,①BD ①AC ;(3)①①①BEA =①DEC =90°,①①BEA +①AED =①DEC +①AED ,①①BED =①AEC ,在①BED 和①AEC 中, BE AE BED AEC DE EC =⎧⎪∠=∠⎨⎪=⎩①①BED ①①AEC (SAS ),①BD =AC ,①能.设AC 与BD 交于点F ,如下图:理由:①①ABE 和①DEC 是等边三角形,①AE =BE ,DE =EC ,①EDC =①DCE =60°,①BEA =①DEC =60°,①①BEA +①AED =①DEC +①AED ,①①BED =①AEC ,在①BED 和①AEC 中,BE AE BED AEC DE EC =⎧⎪∠=∠⎨⎪=⎩,①①BED ①①AEC (SAS ),①①BDE =①ACE ,BD =AC .①()180DFC BDE EDC DCF ∠=︒-∠+∠+∠180()ACE EDC DCF ︒-∠+∠+∠=180(6060)︒-︒+︒= 60=︒,即BD 与AC 所成的角的度数为60°或120°.【点睛】此题考查了全等三角形的判定与性质,解题的关键是掌握全等三角形的判定方法与性质. 14.(1)602BCD α∠=︒+;(2)60︒;(3)2BD AE CE =+,证明见解析【解析】【分析】(1)根对称性可知PC 垂直平分AD ,ACP DCP α∠=∠=,则2ACD α∠=,根据ABC 是等边三角形,则60BCA ∠=︒,即可求得BCD ∠;。
中考数学常见几何模型手拉手模型(从全等到相似)

专题03 手拉手模型(从全等到相似)全等三角形与相似三角形在中考数学几何模块中占据着重要地位。
相似三角形与其它知识点结合以综合题的形式呈现,其变化很多,难度大,是中考的常考题型。
如果大家平时注重解题方法,熟练掌握基本解题模型,再遇到该类问题就信心更足了.本专题就手拉手模型进行梳理及对应试题分析,方便掌握。
模型1.手拉手模型(全等模型)【模型解读】将两个三角形绕着公共顶点(即头)旋转某一角度后能完全重合,则这两个三角形构成手拉手全等,也叫旋转型全等,常用“边角边”判定定理证明全等。
【常见模型及证法】(等腰)(等边)(等腰直角)公共顶点A记为“头”,每个三角形另两个顶点逆时针顺序数的第一个顶点记为“左手”,第二个顶点记为“右手”。
对应操作:左手拉左手(即连结BD),右手拉右手(即连结CE),得ABD ACE 1.(2022·青海·中考真题)两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来,则形成一组全等的三角形,把具有这个规律的图形称为“手拉手”图形.(1)问题发现:如图1,若ABC 和ADE 是顶角相等的等腰三角形,BC ,DE 分别是底边.求证:BD CE =;(2)解决问题:如图2,若ACB △和DCE 均为等腰直角三角形,90ACB DCE ∠=∠=︒,点A ,D ,E 在同一条直线上,CM 为DCE 中DE 边上的高,连接BE ,请判断∠AEB 的度数及线段CM ,AE ,BE 之间的数量关系并说明理由.图1 图2【答案】(1)见解析 (2)90DCE ∠=︒;2AE AD DE BE CM =+=+【分析】(1)先判断出∠BAD =∠CAE ,进而利用SAS 判断出△BAD ∠∠CAE ,即可得出结论; (2)同(1)的方法判断出△BAD ∠∠CAE ,得出AD =BE ,∠ADC =∠BEC ,最后用角的差,即可得出结论.【解析】(1)证明:∠ABC 和ADE 是顶角相等的等腰三角形,∠AB AC =,AD AE =,BAC DAE ∠=∠,∠BAC CAD DAE CAD ∠-∠=∠-∠,∠BAD CAE ∠=∠. 在BAD 和CAE 中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,∠()BAD CAE SAS ≌△△,∠BD CE =.(2)解:90AEB =︒∠,2AE BE CM =+,理由如下:由(1)的方法得,≌ACD BCE ,∠AD BE =,ADC BEC ∠∠=,∠CDE △是等腰直角三角形,∠45CDE CED ∠=∠=︒,∠180135ADC CDE ∠=︒-∠=︒,∠135BEC ADC ∠=∠=︒,∠1354590AEB BEC CED ∠=∠-∠=︒-︒=︒.∠CD CE =,CM DE ⊥,∠DM ME =.∠90DCE ∠=︒,∠DM ME CM ==,∠2DE CM =.∠2AE AD DE BE CM =+=+.【点睛】此题是三角形综合题,主要考查了全等三角形的判定和性质,等腰三角形,等边三角形,等腰直角三角形的性质,判断出△ACD ∠∠BCE 是解本题的关键.2.(2022·黑龙江·中考真题)ABC 和ADE 都是等边三角形.(1)将ADE 绕点A 旋转到图①的位置时,连接BD ,CE 并延长相交于点P (点P 与点A 重合),有PA PB PC +=(或PA PC PB +=)成立;请证明.(2)将ADE 绕点A 旋转到图②的位置时,连接BD ,CE 相交于点P ,连接P A ,猜想线段P A 、PB 、PC 之间有怎样的数量关系?并加以证明;(3)将ADE 绕点A 旋转到图③的位置时,连接BD ,CE 相交于点P ,连接P A ,猜想线段P A 、PB 、PC 之间有怎样的数量关系?直接写出结论,不需要证明.【答案】(1)证明见解析 (2)图②结论:PB PA PC =+,证明见解析 (3)图③结论:PA PB PC +=【分析】(1)由△ABC 是等边三角形,得AB =AC ,再因为点P 与点A 重合,所以PB =AB ,PC =AC ,P A =0,即可得出结论;(2)在BP 上截取BF CP =,连接AF ,证明BAD CAE ≌(SAS ),得ABD ACE ∠=∠,再证明CAP BAF ≌△△(SAS ),得CAP BAF ∠=∠,AF AP =,然后证明AFP 是等边三角形,得PF AP =,即可得出结论;(3)在CP 上截取CF BP =,连接AF ,证明BAD CAE ≌(SAS ),得ABD ACE ∠=∠,再证明BAP CAF ≌△△(SAS ),得出CAF BAP ∠=∠,AP AF =,然后证明AFP 是等边三角形,得PF AP =,即可得出结论:PA PB PF CF PC +=+=.(1)证明:∠∠ABC 是等边三角形,∠AB =AC ,∠点P 与点A 重合,∠PB =AB ,PC =AC ,P A =0,∠PA PB PC +=或PA PC PB +=;(2)解:图②结论:PB PA PC =+证明:在BP 上截取BF CP =,连接AF ,∠ABC 和ADE 都是等边三角形,∠AB AC =,AD AE =,60BAC DAE ∠=∠=︒∠BAC CAD DAE CAD ∠+∠=∠+∠,∠BAD CAE ∠=∠,∠BAD CAE ≌(SAS ),∠ABD ACE ∠=∠,∠AC =AB ,CP =BF , ∠CAP BAF ≌△△(SAS ),∠CAP BAF ∠=∠,AF AP =,∠CAP CAF BAF CAF ∠+∠=∠+∠,∠60FAP BAC ∠=∠=︒,∠AFP 是等边三角形,∠PF AP =,∠PA PC PF BF PB +=+=;(3)解:图③结论:PA PB PC +=,理由:在CP 上截取CF BP =,连接AF ,∠ABC 和ADE 都是等边三角形,∠AB AC =,AD AE =,60BAC DAE ∠=∠=︒∠BAC BAE DAE BAE ∠+∠=∠+∠,∠BAD CAE ∠=∠,∠BAD CAE ≌(SAS ),∠ABD ACE ∠=∠,∠AB =AC ,BP =CF ,∠BAP CAF ≌△△(SAS ),∠CAF BAP ∠=∠,AP AF =,∠BAF BAP BAF CAF ∠+∠=∠+∠,∠60FAP BAC ∠=∠=︒,∠AFP 是等边三角形,∠PF AP =,∠PA PB PF CF PC +=+=,即PA PB PC +=.【点睛】本题考查等边三角形的判定与性质,全等三角形的判定与性质,熟练掌握等边三角形的判定与性质、全等三角形的判定与性质是解题的关键.3.(2022·吉林·九年级期末)如图①,在ABC 中,90C ∠=︒,6AC BC ==,点D ,E 分别在边AC ,BC 上,且2CD CE ==,此时AD BE =,AD BE ⊥成立.(1)将CDE △绕点C 逆时针旋转90︒时,在图②中补充图形,并直接写出BE 的长度;(2)当CDE △绕点C 逆时针旋转一周的过程中,AD 与BE 的数量关系和位置关系是否仍然成立?若成立,请你利用图③证明,若不成立请说明理由;(3)将CDE △绕点C 逆时针旋转一周的过程中,当A ,D ,E 三点在同一条直线上时,请直接写出AD 的长度.【答案】(1)补充图形见解析;22BE =;(2)AD BE =,AD BE ⊥仍然成立,证明见解析;(3)51AD =-或51=+AD .【分析】(1)根据旋转作图的方法作图,再根据勾股定理求出BE 的长即可;(2)根据SAS 证明E ACD BC ≅∆∆得AD =BE ,∠1=∠2,再根据∠1+∠3+∠4=90°得∠2∠3+∠4=90°,从而可得出结论;(3)分两种情况,运用勾股定理求解即可.【详解】解:(1)如图所示,根据题意得,点D 在BC 上,∠BCE ∆是直角三角形,且BC =6,CE =2由勾股定理得,2222(2)(6)22BE CE BC =+=+=;(2)AD BE =,AD BE ⊥仍然成立. 证明:延长AD 交BE 于点H ,∠90ACB DCE ∠=∠=︒,ACD ACB BCD ∠=∠-∠,BCE DCE BCD ∠=∠-∠,∠ACD BCE ∠=∠,又∠CD CE =,AC BC =,∠ACD BCE ≅△△,∠AD BE =,12∠=∠,在Rt ABC 中,13490∠+∠+∠=︒,∠23490∠+∠+∠=︒,∠90AHB ∠=︒,∠AD BE ⊥.(3)①当点D 在AC 上方时,如图1所示,同(2)可得ACD BCE ≅△△∠AD =BE同理可证BE AE ⊥在Rt △CDE 中,2CD CE ==∠DE =222CD CE +=在Rt △ACB 中,6AC BC ==∠2223AB AC BC =+=设AD =BE =x ,在Rt △ABE 中,222BE AE AB +=∠222(2)(23)x x ++=解得,51x =-∠ 51AD =-②当点D 在AC 下方时,如图2所示,同(2)可得ACD BCE ≅△△∠AD =BE同理可证BE AE ⊥在Rt △CDE 中,2CD CE ==∠DE =222CD CE +=在Rt △ACB 中,6AC BC ==∠2223AB AC BC =+=设AD =BE =x ,在Rt △ABE 中,222BE AE AB +=∠222(2)(23)x x +-=解得,5+1x =∠ 51=+AD .所以,AD 的值为51-或5+1【点睛】本题考查了旋转的性质,全等三角形的判定与性质,勾股定理等知识,熟练解答本题的关键.模型2.手拉手模型(旋转相似模型)【模型解读与图示】旋转放缩变换,图中必有两对相似三角形.1.(2022·四川达州·中考真题)某校一数学兴趣小组在一次合作探究活动中,将两块大小不同的等腰直角三角形ABC 和等腰直角三角形CDE ,按如图1的方式摆放,90ACB ECD ∠=∠=︒,随后保持ABC 不动,将CDE △绕点C 按逆时针方向旋转α(090α︒<<︒),连接AE ,BD ,延长BD 交AE 于点F ,连接CF .该数学兴趣小组进行如下探究,请你帮忙解答:(1)【初步探究】如图2,当ED BC ∥时,则α=_____;(2)【初步探究】如图3,当点E ,F 重合时,请直接写出AF ,BF ,CF 之间的数量关系:_________; (3)【深入探究】如图4,当点E ,F 不重合时,(2)中的结论是否仍然成立?若成立,请给出推理过程;若不成立,请说明理由.(4)【拓展延伸】如图5,在ABC 与CDE △中,90ACB DCE ∠=∠=︒,若BC mAC =,CD mCE =(m 为常数).保持ABC 不动,将CDE △绕点C 按逆时针方向旋转α(090α︒<<︒),连接AE ,BD ,延长BD 交AE 于点F ,连接CF ,如图6.试探究AF ,BF ,CF 之间的数量关系,并说明理由.【答案】(1)45︒(2)2BF AF CF =+(3)2BF AF CF =+仍然成立,理由见解析(4)21BF m FC mAF =++【分析】(1)根据等腰直角三角形的性质,可得AC BC ⊥,根据题意可得AC ED ⊥,根据等原三角形的性质可得AC 平分ECD ∠,即可得45ACE ∠=︒,根据旋转的性质可知ECA α∠=;(2)证明ACE ≌BCD △,可得AE DB =,根据等腰直角三角形可得2ED CE =,由BE BD ED =+,即可即可得出2BF AF CF =+;(3)同(2)可得ACE ≌BCD △,过点C ,作CH FC ⊥,交BF 于点H ,证明FEC HDC ≌,AFC △≌BHC △,可得BH AF =,即可得出2BF AF CF =+;(4)过点C 作CG CF ⊥,交BF 于点G ,证明ACE BCD △∽△,可得BG mAF =,GC mFC =,在Rt FCG 中,勾股定理可得21FG m FC =+,即可得出21BF m FC mAF =++.(1)等腰直角三角形ABC 和等腰直角三角形CDE ,90ECD ∴∠=︒,AC BC ⊥ED BC ∥ED AC ∴⊥45ACE α∴∠==︒故答案为:45︒(2)90∠=∠=︒ACB ECD ACE ACD ACD BCD ∴∠+∠=∠+∠ACE BCD ∴∠=∠ 在ACE 与BCD △中,AC BC ACE BCD EC DC =⎧⎪∠=∠⎨⎪=⎩ ACE ≌BCD △∴AE DB =BE BD ED ∴=+ 又2ED CE =2BE AE CE ∴=+,E F 重合,2BF AF CF ∴=+故答案为:2BF AF CF =+ (3)同(2)可得ACE ≌BCD △AE DB ∴=,EAC DBC ∠=∠过点C ,作CH FC ⊥,交BF 于点H ,则90ECF FCD FCD DCH ∠+∠=∠+∠=︒,∴ECF DCH ∠=∠, 在FEC 与HDC △中,FEC HDC EC CD ECF DCH ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴FEC HDC ≌, FC CH ∴=,CFH ∴是等腰直角三角形,2FH FC ∴=,CH FC =,90,90FCH ACF ACH ACB BCH ACH ∴∠=∠+∠=︒∠=∠+∠=︒,ACF BCH ∴∠=∠,在AFC △与BHC △中,FC HC ACF BCH AC BC =⎧⎪∠=∠⎨⎪=⎩,∴AFC △≌BHC △,BH AF ∴=,2BF FH BH CF AF ∴=+=+,即2BF AF CF =+,(4)过点C 作CG CF ⊥,交BF 于点G ,BC mAC =,CD mCE =,BC CDAC CE ∴=,AC BC EC DC∴=, ACE BCD α∠=∠=,ACE BCD ∴△△∽,CBG CAF ∴∠=∠,FCA ACG GCB ACG ∠+∠=∠+∠,∴FCA GCB ∠=∠,AFC BGC ∴∽,BG GC BC AF FC AC∴==m =, BG mAF ∴=,GC mFC =, Rt FCG 中,2221FG FC CG m FC =+=+,∴21BF FG GB m FC mAF =+=++,即21BF m FC mAF =++.【点睛】本题考查了等腰直角三角形的性质,旋转的性质,全等三角形的性质与判定,相似三角形的性质与判定,掌握全等三角形的性质与判定,相似三角形的性质与判定是解题的关键.2.(2022·山东烟台·中考真题)(1)【问题呈现】如图1,∠ABC 和∠ADE 都是等边三角形,连接BD ,CE .求证:BD =CE .(2)【类比探究】如图2,∠ABC 和∠ADE 都是等腰直角三角形,∠ABC =∠ADE =90°.连接BD ,CE .请直接写出BD CE的值.(3)【拓展提升】如图3,∠ABC 和∠ADE 都是直角三角形,∠ABC =∠ADE =90°,且AB BC =AD DE =34.连接BD ,CE .①求BD CE的值;②延长CE 交BD 于点F ,交AB 于点G .求sin∠BFC 的值.【答案】(1)见解析(2)22(3)①35;②45 【分析】(1)证明△BAD ∠∠CAE ,从而得出结论; (2)证明△BAD ∠∠CAE ,进而得出结果;(3)①先证明△ABC ∠∠ADE ,再证得△CAE ∠∠BAD ,进而得出结果; ②在①的基础上得出∠ACE =∠ABD ,进而∠BFC =∠BAC ,进一步得出结果. (1)证明:∠∠ABC 和△ADE 都是等边三角形, ∠AD =AE ,AB =AC ,∠DAE =∠BAC =60°, ∠∠DAE ﹣∠BAE =∠BAC ﹣∠BAE ,∠∠BAD =∠CAE ,∠∠BAD ∠∠CAE (S A S ),∠BD =CE ; (2)解:∠∠ABC 和∠ADE 都是等腰直角三角形,12AB AB AE AC ∴==,∠DAE =∠BAC =45°,∠∠DAE ﹣∠BAE =∠BAC ﹣∠BAE , ∠∠BAD =∠CAE ,∠∠BAD ∠∠CAE ,1222BD AB CE AC ∴===; (3)解:①34AB AD AC DE ==,∠ABC =∠ADE =90°, ∠∠ABC ∠∠ADE ,∠∠BAC =∠DAE ,35AB AD AC AE ==, ∠∠CAE =∠BAD ,∠∠CAE ∠∠BAD ,35BD AD CE AE ∴== ; ②由①得:∠CAE ∠∠BAD ,∠∠ACE =∠ABD ,∠∠AGC =∠BGF ,∠∠BFC =∠BAC ,∠sin∠BFC 45BC AC ==. 【点睛】本题考查了等腰三角形的性质,全等三角形的判定和性质,相似三角形的判定和性质等知识,解决问题的关键是熟练掌握“手拉手”模型及其变形. 3.(2022·山东·东营市一模)【提出问题】(1)如图1,在等边∠ABC 中,点M 是BC 上的任意一点(不含端点B 、C ),连结AM ,以AM 为边作等边∠AMN ,连结CN .求证:∠ABC =∠ACN .【类比探究】(2)如图2,在等边∠ABC 中,点M 是BC 延长线上的任意一点(不含端点C ),其它条件不变,(1)中结论∠ABC =∠ACN 还成立吗?请说明理由.【拓展延伸】(3)如图3,在等腰∠ABC 中,BA =BC ,点M 是BC 上的任意一点(不含端点B 、C ),连结AM ,以AM 为边作等腰∠AMN ,使顶角∠AMN =∠ABC .连结CN .试探究∠ABC 与∠ACN 的数量关系,并说明理由.【答案】(1)证明见解析;(2)成立,理由见解析;(3)∠ABC=∠CAN,理由见解析.【分析】(1)利用SAS可证明∠BAM∠∠CAN,继而得出结论.(2)也可以通过证明∠BAM∠∠CAN,得出结论,和(1)的思路完全一样.(3)首先得出∠BAC=∠MAN,从而判定∠ABC∠∠AMN,得到AB ACAM AN=,根据∠BAM=∠BAC﹣∠MAC,∠CAN=∠MAN﹣∠MAC,得到∠BAM=∠CAN,从而判定∠BAM∠∠CAN,得出结论.【详解】解:(1)证明:∠∠ABC、∠AMN是等边三角形,∠AB=AC,AM=AN,∠BAC=∠MAN=60°.∠∠BAM=∠CAN.∠在∠BAM和∠CAN中,AB ACBAM CANAM AN=⎧⎪∠=∠⎨⎪=⎩,∠∠BAM∠∠CAN(SAS).∠∠ABC=∠ACN.(2)结论∠ABC=∠ACN仍成立.理由如下:∠∠ABC、∠AMN是等边三角形,∠AB=AC,AM=AN,∠BAC=∠MAN=60°.∠∠BAM=∠CAN.∠在∠BAM和∠CAN中,AB ACBAM CANAM AN=⎧⎪∠=∠⎨⎪=⎩,∠∠BAM∠∠CAN(SAS),∠∠ABC=∠ACN.(3)∠ABC=∠ACN.理由如下:∠BA=BC,MA=MN,顶角∠ABC=∠AMN,∠底角∠BAC=∠MAN,∠∠ABC∠∠AMN,∠AB ACAM AN=,又∠∠BAM=∠BAC﹣∠MAC,∠CAN=∠MAN﹣∠MAC,∠∠BAM=∠CAN,∠∠BAM∠∠CAN,∠∠ABC=∠ACN.4.(2022·山西长治·九年级期末)问题情境:如图1,在∠ABC中,AB=6,AC=5,点D,E 分别在边AB,AC上,且∥DE BC.数学思考:(1)在图1中,BDCE的值为 ;(2)图1中∠ABC 保持不动,将∠ADE 绕点A 按逆时针方向旋转到图2的位置,其它条件不变,连接BD ,CE ,则(1)中的结论是否仍然成立?并说明理由;(3)拓展探究:在图2中,延长BD ,分别交AC ,CE 于点F ,P ,连接AP ,得到图3,探究∠APE 与∠ABC 之间有何数量关系,并说明理由;(4)若将∠ADE 绕点A 按逆时针方向旋转到图4的位置,连接BD ,CE ,延长BD 交CE 的延长线于点P ,BP 交AC 于点F ,则(3)中的结论是否仍然成立,若成立,请说明理由;若不成立,请直接写出∠APE 与∠ABC 之间的数量关系.【答案】(1)65(2)(1)中结论仍然成立,理由见解析(3)∠APE =∠ABC ,理由见解析(4)结论不成立,∠APE +∠ABC =180°,理由见解析 【分析】(1)根据平行线分线段成比例定理求解即可;(2)根据旋转的性质得到∠BAD =∠CAE ,由(1)可证明∠BAD ∠∠CAE ,从而可证∠APE +∠ABC得到65BD AB CE AC ==;(3)由(2)可证∠ABD =∠ACE ,证明∠AFB ∠∠PFC 和∠AFP ∠∠BFC 即可得到结论;(4)证明∠ABD =∠ACE ,推出A 、B 、C 、P 四点共圆即可得到结论;(1)解:∠∥DE BC ,∠BD CE AB AC=,∠65BD AB CE AC ==;(2)解:中结论仍然成立,理由如下: ∠旋转的性质,∠∠ADE =∠ABC ,∠AED =∠ACB , ∠∠ADE ∠∠ABC ,∠AD AE AB AC=,在图2中,由旋转的性质可知,∠BAC =∠DAE ,∠∠BAD =∠CAE ,∠∠BAD ∠∠CAE ,∠65BD AB CE AC ==; (3)解:∠APE =∠ABC ,理由如下: 由(2)得∠BAD ∠∠CAE ,∠∠ABD =∠ACE , 又∠∠AFB =∠PFC ,∠∠AFB ∠∠PFC ,∠AF BFBAC BPC PF CF ==,∠∠,∠AF PF BF CF=,又∠∠AFP =∠BFC ,∠∠AFP ∠∠BFC ,∠∠CBF =∠P AF ,∠∠APE =∠ACE +∠P AF ,∠ABC =∠ABF +∠CBF ,∠∠APE =∠ABC ; (4)解:(3)结论不成立,∠APE +∠ABC =180°,理由如下: 由(2)知,∠BAD ∠∠CAE ,∠∠ABD =∠ACE , ∠A 、B 、C 、P 四点共圆,∠∠APE +∠ABC =180°.【点睛】本题主要考查了平行线分线段成比例,旋转的性质,相似三角形的性质与判定,圆内接四边形的性质等等,熟练掌握相关三角形的性质与判定是解题的关键.课后专项训练:1.(2022·湖南·中考真题)如图,点O 是等边三角形ABC 内一点,2OA =,1OB =,3OC =,则AOB ∆与BOC ∆的面积之和为( )A .34B .32C .334D .3【答案】C【分析】将AOB ∆绕点B 顺时针旋转60︒得BCD ∆,连接OD ,得到BOD 是等边三角形,再利用勾股定理的逆定理可得90COD ∠=︒,从而求解.【详解】解:将AOB ∆绕点B 顺时针旋转60︒得BCD ∆,连接OD ,OB OD ∴=,60BOD ∠=︒,2CD OA ==,BOD ∴∆是等边三角形, 1OD OB ∴==,∵()2222134OD OC +=+=,2224CD==,222OD OC CD ∴+=,90DOC ∴∠=︒, AOB ∴∆与BOC ∆的面积之和为23133113424BOC BCD BOD CODSSSS+=+=⨯+⨯⨯=.故选:C .【点睛】本题主要考查了等边三角形的判定与性质,勾股定理的逆定理,旋转的性质等知识,利用旋转将AOB ∆与BOC ∆的面积之和转化为BOCBCDSS+,是解题的关键.2.(2022·四川宜宾·中考真题)如图,ABC 和ADE 都是等腰直角三角形,90BAC DAE ∠=∠=︒,点D 是BC 边上的动点(不与点B 、C 重合),DE 与AC 交于点F ,连结CE .下列结论:①BD CE =;②DAC CED ∠=∠;③若2BD CD =,则45CF AF =;④在ABC 内存在唯一一点P ,使得PA PB PC ++的值最小,若点D 在AP 的延长线上,且AP 的长为2,则23CE =+.其中含所有正确结论的选项是( )A .①②④B .①②③C .①③④D .①②③④【答案】B【分析】证明BAD CAE ≌,即可判断①,根据①可得ADB AEC ∠=∠,由180ADC AEC ∠+∠=︒可得,,,A D C E四点共圆,进而可得DAC DEC ∠=∠,即可判断②,过点A 作AG BC ⊥于G ,交ED 的延长线于点H ,证明FAH FCE ∽,根据相似三角形的性质可得45CF AF =,即可判断③,将APC △绕A 点逆时针旋转60度,得到AB P ''△,则APP '是等边三角形,根据当,,,B P P C ''共线时,PA PB PC ++取得最小值,可得四边形ADCE 是正方形,勾股定理求得DP , 根据CE AD AP PD ==+即可判断④. 【详解】解:ABC 和ADE 都是等腰直角三角形,90BAC DAE ∠=∠=︒,,,AB AC AD AE BAD CAE ∴==∠=∠BAD CAE ∴△≌△BD CE ∴=故①正确;BAD CAE ≌ADB AEC ∴∠=∠180ADC AEC ∴∠+∠=︒,,,A D C E ∴四点共圆, CD CD =DAC DEC ∴∠=∠故②正确;如图,过点A 作AG BC ⊥于G ,交ED 的延长线于点H ,BAD CAE ≌,45,45ACE ABD ACB ∴∠=∠=︒∠=︒ 90DCE ∴∠=︒FC AH ∴∥2BD CD =,BD CE =1tan 2DC DEC CE ∴∠==,13CD BC = 设6BC a =,则2DC a =,132AG BC a ==,24EC DC a ==则32GD GC DC a a a =-=-= FC AH ∥1tan 2GD H GH ∴==22GH GD a ∴==325AH AG GH a a a ∴=+=+= AH ∠CE ,FAH FCE ∴∽CF CE AF AH ∴=4455CF a AF a ∴==则45CF AF =;故③正确 如图,将ABP 绕A 点逆时针旋转60度,得到AB P ''△,则APP '是等边三角形,PA PB PC PP P B PC B C '''+++∴'+=≥,当,,,B P P C ''共线时,PA PB PC ++取得最小值, 此时180********CPA APP '∠=-∠=︒-=︒︒︒,180********APB AP B AP P ∠=∠=︒-∠=︒-︒='''︒, 360360*********BPC BPA APC ∠=︒-∠-∠=︒-︒-︒=︒,此时120APB BPC APC ∠=∠=∠=︒,AC AB AB '==,AP AP '=,APC AP B ''∠=∠, AP B APC ''∴≌, PC P B PB ''∴==, 60APP DPC '∠=∠=︒,DP ∴平分BPC ∠, PD BC ∴⊥,,,,A D C E 四点共圆,90AEC ADC ∴∠=∠=︒,又AD DC BD ==,BAD CAE ≌, AE EC AD DC ∴===,则四边形ADCE 是菱形, 又90ADC ∠=︒,∴四边形ADCE 是正方形,9060150B AC B AP PAC P AP ''''∠=∠+∠+∠=︒+︒=︒,则'B A BA AC ==,()1180152B ACB B AC '''∠=∠=︒-∠=︒,30PCD ∠=︒,3DC PD ∴=,DC AD =,2AP =,则()312AP AD DP DP =-=-=,23131DP ∴==+-, 2AP =,33CE AD AP PD ∴==+=+,故④不正确,故选B .【点睛】本题考查了旋转的性质,费马点,圆内接四边形的性质,相似三角形的性质与判定,全等三角形的性质与判定,勾股定理,解直角三角形,正方形的性质与判定,掌握以上知识是解题的关键. 3.(2022·湖北·襄阳市樊城区青泥湾中学九年级阶段练习)如图,已知AOB 和MON 都是等腰直角三角形(22OA <OM =ON ),∠AOB =∠MON =90°.(1)如图①,连接AM,BN,求证:AOM∠BON;(2)若将MON绕点O顺时针旋转,①如图②,当点N恰好在AB边上时,求证:22220BN AN N+=;②当点A,M,N在同一条直线上时,若OB=4,ON =3,请直接写出线段BN的长.【答案】(1)见解析;(2)①见解析;②46322+或46322-.【分析】(1)利用SAS定理证明AOM BON≌即可;(2)①连接AM,证明AOM BON≌,即可证2222BN AN ON=+;②当点N在线段AM上时,连接BN,在Rt ANB中构造勾股定理的等量关系;当点M在线段AN上时,同理即可求得.(1)证明:90AOB MON︒∠=∠=,MON AON AOB AON∴∠+∠=∠+∠,即AOM BON∠=∠.MON和AOB是等腰直角三角形,,OM ON OA OB∴==,AOM BON∴≌(SAS) .(2)解:①证明:如图,连接AM.90AOB MON︒∠=∠=,MON AON AOB AON∴∠-∠=∠-∠,即AOM BON∠=∠.MON和AOB是等腰直角三角形,,,45OM ON OA OB OAB OBA︒∴==∠=∠=,.()AOM BON SAS∴≌45,MAO OBA AM BN︒∴∠=∠==,90MAN︒∴∠=,222AM AN MN∴+=.MON是等腰直角三角形,222MN ON∴=,2222BN AN ON=∴+.②46322+或46322-.∠△AOB和△MON都是等腰直角三角形,OB=4,ON =3,∠42,32AB MN==.当点N在线段AM上时,如图,连接BN,设BN x=,由(1)可知AOM BON≌.∠OAM OBN∠=∠,AM BN x==.∠NAB ABN OAM OAB ABN OBN ABN OAB∠+∠=∠+∠+∠=∠+∠+∠18090OBA OAB AOB =∠+∠=︒-∠=︒,∠()18090ANB NAB ABN ∠=︒-∠+∠=︒,∠ANB 是直角三角形,222+=AN BN AB . 又∠32AN AM MN BN MN x =-=-=-,∠222(32)(42)x x -+=, 解得:1246324632,22x x +-+==(舍去)∠46322BN +=;当点M 在线段AN 上时,如图,连接BN ,设BN x =,由(2)①可知AOM BON ≌. ∠OAM OBN ∠=∠,AM BN x ==.∠NAB ABN OAM OAB ABN OBN ABN OAB ∠+∠=∠+∠+∠=∠+∠+∠18090OBA OAB AOB =∠+∠=︒-∠=︒,∠()18090ANB NAB ABN ∠=︒-∠+∠=︒,∠ANB 是直角三角形,222+=AN BN AB . 又∠32AN AM MN BN MN x =+=+=+,∠222(32)(42)x x ++=, 解得: 1246324632,22x x ---==(舍去)∠46322BN -=综上所述:BN 的长为46322+或46322-.【点睛】本题主要考查全等三角形的判定与性质、等腰直角三角形的性质,三点共线分类讨论,对几何题目的综合把握是解题关键. 4.(2022·山西朔州·九年级期末)综合与实践问题情境:在数学课上老师出了这样一道题:如图1,在ABC 中6AB AC ==,30BAC ∠=︒,求BC 的长.(1)探究发现:如图2,勤奋小组经过思考后,发现:把ABC 绕点A 顺时针旋转90︒得到ADE ,连接BD ,BE ,利用直角三角形的性质即可求解,请你根据勤奋小组的思路,求BC 的长; (2)探究拓展:如图3,缜密小组的同学在勤奋小组的启发下,把ABC 绕点A 顺时针旋转120︒后得到ADE ,连接BD ,CE 交于点F ,交AB 于点G ,请你判断四边形ADFC 的形状并证明;(3)奇异小组的同学把图3中的BGF 绕点B 顺时针旋转,在旋转过程中,连接AF ,发现AF 的长度在不断变化,直接写出AF 的最大值和最小值.【答案】(1)BC 的长是3632-,见解析;(2)四边形ADFC 是菱形,见解析; (3)AF 的最大值是63,AF 的最小值是1263-,见解析.【分析】(1)过点B 作BH DE ⊥交DE 的延长线于点H .由旋转性质进一步得AEB △是等边三角形, EBH △是等腰直角三角形,ABD △是等腰直角三角形,45BDA ∠=︒,在Rt EBH △中由勾股定理,1832HE HB ===,在Rt BDH 中,62BD =.在Rt BDH 中,求得36=DH ,进而得解;(2)利用旋转的性质得到相关结论,进一步证明四边形ADFC 是平行四边形.又有AD AC =,得证四边形ADFC 是菱形;(3)作AH ∠BD 于点H ,则90AHB ∠=︒,利用解直角三角形求得BF 的长,分两种情况进行分析,即可得解. (1)解:如图4,延长CB 、DE 交于点H .∠ABC 绕点A 顺时针旋转90︒得到ADE ∠ABC ADE △≌△,90CAE BAD ∠=∠=︒,∠H =90°, ∠AB AD ==6,AC AE ==6,DAE BAC ∠=∠,DE BC =∠6AB AC ==,30BAC ∠=︒∠∠ABC 是等腰三角形,60∠=∠-∠=︒BAE CAE BAC ∠180752-=︒∠∠=︒BAC ABC , ∠=6AE AB = ∠AEB △是等边三角形∠6BE AB ==,60ABE ∠=︒∠18045∠=︒-∠-∠=︒EBH ABE ABC ∠EBH △是等腰直角三角形∠HE HB =.∠AD AB =,90DAB ∠=︒.∠ABD △是等腰直角三角形,45BDA ∠=︒.在Rt EBH △中,由勾股定理,得222+=HE HB BE .∠2226+=HE HB =36.∠HE 2=HB 2=18∠1832HE HB ===.在BDH 中,90H ∠=︒,30∠=∠-∠=∠=︒-∠BDH EDA BDA ABC BDA .在Rt BDH 中,1322==BH BD .∠62BD =. 在Rt BDH 中,tan ∠=BH BDH DH ,∠3233=DH , ∠36=DH .∠3632=-=-DE DH EH .∠DE BC =,∠BC 的长是3632-.(2)解:四边形ADFC 是菱形.理由如下:∠ABC 绕点A 顺时针旋转120︒得到ADE ,AB AC =,30BAC ∠=︒,∠ABC ADE △≌△,120∠=∠=︒BAD CAE .∠AC AE =,AB AD =,30BAC DAE ∠=∠=︒.∠AC AE AB AD ===.∠∠ACE 是等腰三角形∠180302︒-∠=︒∠=∠=CAE ACE AEC .同理可得:30ABD ADB ∠=∠=︒.∠180752-=︒∠∠=︒BAC ACB .∠45∠=∠-∠=︒BCG ACB ACE ,105∠=∠+∠=︒FBC ABC ABF .∠在BFC △中,18030∠=︒-∠-∠=︒BFG FBC BCG .∠∠=∠BFG ACF ,∠=∠BFG ADB .∠∥DB AC ,∥FC AD .∠四边形ADFC 是平行四边形.∠AD AC =,∠四边形ADFC 是菱形.(3)如图5,作AH ∠BD 于点H ,则90AHB ∠=︒∠ABC 绕点A 顺时针旋转120︒得到ADE , ∠ABC ADE △≌△,120BAD ∠=︒∠AB AD ==6∠∠ABD 是等腰三角形∠BH =DH =12BD ∠180302BAD ABD ADB ︒-∠∠=∠==︒ .在Rt △ABH 中,∠AHB =90°,∠ABH =30°, AB =6∠cos cos30BH ABH AB==︒∠∠BH =33∠BD =2 BH =63 由(2)知四边形ADFC 是菱形∠DF =AD =6 ∠BF =BD -DF =63-6当BGF 绕点B 顺时针旋转,在旋转过程中,当旋转到A 、B 、F 第一次三点共线时,如图6,∠=BF ''BF此时AF 有最小值,此时AF =AF ''=AB -BF ''=AB -BF =6-(63-6)=12-63 当旋转到A 、B 、F 第二次三点共线时,如图7,BGF ''△≌△BGF ,∠=BF 'BF 此时AF 有最大值,此时AF =AB +BF '=AB +BF =6+63-6=63故AF 的最大值是63,AF 的最小值是1263-【点睛】本题以图形的变换——旋转为载体考查了全等三角形的性质和判定,菱形的判定,线段长度的最值问题等知识点,综合性较强,准确作出辅助线是解题的关键.5.(2022·湖北武汉·八年级期末)已知ABC中,∠BAC=60°,以AB和BC为边向外作等边ABD和等边BCE.(1)连接AE、CD,如图1,求证:AE=CD;(2)若N为CD中点,连接AN,如图2,求证:CE=2AN(3)若AB∠BC,延长AB交DE于M,DB=2,如图3,则BM=_______(直接写出结果)【答案】(1)见解析(2)见解析(3)22【分析】(1)先判断出∠DBC=∠ABE,进而判断出∠DBC∠∠ABE,即可得出结论;(2)先判断出∠ADN∠∠FCN,得出CF=AD,∠NCF=∠AND,进而判断出∠BAC=∠ACF,即可判断出∠ABC∠∠CF A,即可得出结论;(3)先判断出∠ABC∠∠HEB(ASA),得出22=,再判断出∠ADM∠∠HEMBH AC==,AB EH(AAS),得出AM=HM,即可得出结论.(1)解:∠∠ABD和∠BCE是等边三角形,∠BD=AB,BC=BE,∠ABD=∠CBE=60°,∠∠ABD+∠ABC=∠CBE+∠ABC,∠∠DBC=∠ABE,∠∠ABE∠∠DBC(SAS),∠AE=CD;(2)解:如图,延长AN使NF=AN,连接FC,∠N为CD中点,∠DN=CN,∠∠AND=∠FNC,∠∠ADN∠∠FCN(SAS),∠CF=AD,∠NCF=∠AND,∠∠DAB=∠BAC=60°∠∠ACD +∠ADN=60°∠∠ACF=∠ACD+∠NCF=60°,∠∠BAC=∠ACF,∠∠ABD 是等边三角形,∠AB =AD ,∠AB =CF ,∠AC =CA ,∠∠ABC ∠∠CF A (SAS ),∠BC =AF ,∠∠BCE 是等边三角形,∠CE =BC =AF =2AN ;(3)解: ∠∠ABD 是等边三角形,∠2AB AD DB ===,∠BAD =60°,在Rt ∠ABC 中,∠ACB =90°-∠BAC =30°,∠222AC AB ==,如图,过点E 作EH // AD 交AM 的延长线于H ,∠∠H =∠BAD =60°,∠∠BCE 是等边三角形,∠BC =BE ,∠CBE =60°,∠∠ABC =90°,∠∠EBH =90°-∠CBE =30°=∠ACB ,∠∠BEH =180°-∠EBH -∠H =90°=∠ABC ,∠∠ABC ∠∠HEB (ASA ),∠22BH AC ==,AB EH =,∠AD =EH ,∠∠AMD =∠HME ,∠∠ADM ∠∠HEM (AAS ),∠AM =HM ,∠()()1111122222BM AM AB AH AB AB BH AB BH AB BH AB =-=-=+-=-=- ∠22BH =,2AB =,∠22BM =.故答案为:22. 【点睛】此题是三角形综合题,主要考查了等边三角形的性质,含30°角的直角三角形的性质,全等三角形的判定和性质,构造出全等三角形是解本题的关键.6.(2022·湖南·长沙市湘郡培粹实验中学八年级阶段练习)如图1,在Rt ∠ABC 中,∠B =90°,AB =BC =4,点D ,E 分别为边AB ,BC 上的中点,且BD =BE =2.(1)如图2,将∠BDE 绕点B 逆时针旋转任意角度α,连接AD ,EC ,则线段EC 与AD 的关系是;(2)如图3,DE∠BC,连接AE,判断∠EAC的形状,并求出EC的长;(3)继续旋转∠BDE,当∠AEC=90°时,请直接写出EC的长.【答案】(1)EC=AD,EC∠AD(2)等腰三角形,10(3)151【分析】(1)延长CE交AD于F,交AB于O,证明∠ABD∠∠CBE(SAS),得∠BCE=∠BAD,CE=AD,再由∠AOF=∠BOC,可得∠AFC=∠ABC=90°,即可得到结论;(2)设DE与AB的交点为H,可得AB是DE的垂直平分线,利用勾股定理可求出AE的长,由(1)知CE=AD,从而得出答案;(3)分当点E在BC上方时和当点E在BC下方时,分别画图,利用勾股定理计算即可.(1)EC与AD垂直且相等,理由如下:延长CE交AD于F,交AB于O,∠∠BDE和△ABC都是等腰直角三角形,∠BD=BE,AB=BC,∠DBE=∠ABC=90°,∠∠ABD=∠CBE,∠∠ABD∠∠CBE(SAS),∠∠BCE=∠BAD,CE=AD,∠∠AOF=∠BOC,∠∠AFE=∠ABC=90°,∠AD∠CE,∠故答案为:EC=AD,EC∠AD;(2)设DE与AB的交点为H,∠DE∠BC,∠∠AHE=∠ABC=90°,∠BD=BE,∠AB是DE的垂直平分线,∠AD =AE ,由(1)知AD =CE ,∠AE =CE ,∠∠ACE 是等腰三角形, ∠BE =2,∠BH =HE =1,∠AH =AB ﹣BH =4﹣1=3,在Rt △AHE 中,由勾股定理得:AE =2210AH HE +=,∠CE =AE =10;(3)如图4,当点E 在BC 上方时,过点B 作BG ∠DE 于G ,∠∠AEC =90°,CE ∠AD ,∠A 、E 、D 三点共线,∠AG =2215AB BG -=,∠AD =AG +DG =151+,∠CE =AD =15+1;如图,当点E 在BC 下方时,同理可得CE =CG ﹣GE =15﹣1.综上:CE =15+1或15﹣1.【点睛】本题主要考查了等腰直角三角形的判定与性质,全等三角形的判定与性质,旋转的性质,勾股定理等知识,根据前面探索的结论解决新的问题是解题的关键.7.(2022·广东·惠州一中八年级期中)ABC 为等边三角形,4AB =,AD BC ⊥于点D .E 为线段AD 上一点,3AE =.以AE 为边在直线AD 右侧构造等边AEF .连结CE ,N 为CE 的中点.(1)如图1,EF 与AC 交于点G ,①连结NG ,求线段NG 的长;②连结ND ,求DNG ∠的大小.(2)如图2,将AEF 绕点A 逆时针旋转,旋转角为α.M 为线段EF 的中点.连结DN 、MN .当30120α︒<<︒时,猜想DNM ∠的大小是否为定值,并证明你的结论.【答案】(1)①72;②120︒;(2)120DNM ∠=︒,证明见解析 【分析】(1)①根据等边三角形的性质,AD BC ⊥,可得60,30AEF EAG ∠=︒∠=︒,NG 是Rt EGC △斜边EC 上的中线,勾股定理在Rt EDC 中可求得EC 的长,进而求得NG 的长;②根据①的结论可得NG NC ND ==,根据120NGC NCG NCD NDC ∠+∠+∠+∠=︒=GND ∠,即可求得GND ∠的度数; (2)连接,BE FC ,证明BAE CAF ≌,进而可得ABE ACF ∠=∠,则120EBC BCF ABC ABE ACB ACF ABC ACB ∠+∠=∠-∠+∠+∠=∠+∠=︒,进而根据D 为BC的中点,N 为EC 的中点,M 为EF 的中点,根据三角形中位线定理可得,DN BE MN CF ∥∥,进而可得MNE DNE ∠+∠=FCE DCE ∠+∠120=︒【详解】(1)①ABC 是等边三角形,4,AB AD BC =⊥222,23DB DC AD AC DC ∴===-=,60BAC ∠=︒3AE =3ED AD AE ∴=-=AEF 是等边三角形,60AEG ∴∠=︒1302DAG DAB CAB ∠=∠=∠=︒90EGC ∴∠=︒ N 为CE 的中点()22221117322222NG EC DE DC ∴==+=+= ②如图,连接DN ,11,22NG EC NC DN EC ===NG NC ND ∴== ==NGC NCG NCD NDC ∴∠∠∠∠,()2=2120NGC NCG NCD NDC NCD NCG BCA ∴∠+∠+∠+∠=∠+∠=︒NGC NCG NCD NDC GNE DNE GND ∠+∠+∠+∠=∠+∠=∠120GND ∴∠=︒;(2)120DNM ∠=︒,理由如下,如图,连接,BE FC ABC,AEF 为等边三角形,,AB AC AE AF ∴==,60BAE BAC CAE CAE ∠=∠+∠=︒+∠60CAF CAE EAF CAE ∠=∠+∠=︒+∠BAE CAF ∴∠=∠BAE CAF ∴△≌△∴ABE ACF ∠=∠则120EBC BCF ABC ABE ACB ACF ABC ACB ∠+∠=∠-∠+∠+∠=∠+∠=︒D 为BC 的中点,N 为EC 的中点,M 为EF 的中点,DN BE MN CF ∴∥∥,MNE FCE EBC NDC ∴∠=∠∠=∠END NDC NCD ∠=∠+∠∴DNM DNE MNE NDC ACB ACN ECF∠=∠+∠=∠+∠+∠+∠=∠+∠+∠=∠+∠=︒120EBC ACB ACF EBC BCFDNM∴∠=︒120【点睛】本题考查了等边三角形的性质,勾股定理,三线合一,直角三角形斜边上的中线等于斜边的,勾股定理,中位线定理,三角形全等的性质与判定,旋转的性质,综合运用以上知识是解题的关键.8.(2022•新乡中考模拟)在△ABC中,CA=CB=m,在△AED中,DA=DE=m,请探索解答下列问题.【问题发现】(1)如图1,若∠ACB=∠ADE=90°,点D,E分别在CA,AB上,则CD 与BE的数量关系是,直线CD与BE的夹角为;【类比探究】(2)如图2,若∠ACB=∠ADE=120°,将△AED绕点A旋转至如图2所示的位置,则CD与BE之间是否满足(1)中的数量关系?说明理由.【拓展延伸】(3)在(1)的条件下,若m=2,将△AED绕点A旋转过程中,当B,E,D 三点共线.请直接写出CD的长.【分析】(1)根据等腰直角三角形的性质得到AB=AC=m,AE=AD=m,计算即可;(2)过点C作CH⊥AB于H,延长CD、BE交于点F,根据直角三角形的性质得到AB=AC,AE=AD,证明△CAD∽△BAE,根据相似三角形的性质解答即可;(3)分点E在线段BD上、点D在线段BE上两种情况,根据相似三角形的性质计算即可.【解答】解:(1)∵∠ACB=∠ADE=90°,CA=CB,DA=DE,∴∠A=∠B=∠DEA=45°,∴AB=AC=m,AE=AD=m,∴CD=AC﹣AD=m,BE=AB﹣AE=m,∴BE=CD,∵∠A=45°,∴直线CD与BE的夹角为45°,故答案为:BE=CD,45°;(2)不满足,BE=CD,直线CD与BE的夹角为30°,理由如下:如图2,过点C作CH⊥AB于H,延长CD、BE交于点F,∵CA=CB,∴AH=HB,∵∠ACB=∠ADE=120°,CA=CB,DA=DE,∴∠CAB=∠CBA=30°,∠DAE=∠DEA=30°,∴AC=2CH,∠CAD=∠BAE,由勾股定理得:AH=AC,∴AB=AC,同理可得:AE=AD,∴=,∵∠CAD=∠BAE,∴△CAD∽△BAE,∴==,∠ACD=ABE,∴BE=CD,∠F=∠CAB=30°,∴BE=CD,直线CD与BE的夹角为30°;(3)如图3,点E在线段BD上,∵m=2,∴AD=DE=1,AB=2,由勾股定理得:BD==,∴BE=BD﹣DE=﹣1,∴CD=BE=,如图4,点D在线段BE上,BE=BD+DE=+1,∴CD=BE=,综上所述:当B,E,D三点共线.CD的长为或.【点评】本题考查的是相似三角形的判定和性质、直角三角形的性质、等腰三角形的性质,掌握相似三角形的判定定理和性质定理是解题的关键.9.(2022•虹口区期中)如图,在△ABC和△ADE中,△BAD=△CAE,△ABC=△ADE.(1)求证:△ABC△△ADE;(2)判断△ABD与△ACE是否相似?并证明.【分析】(1)由△BAD=△CAE,可得△BAC=△DAE,又有△ABC=△ADE,即可得出相似;(2)有(1)中可得对应线段成比例,又有以对应角相等,即可判定其相似.【解答】证明:(1)△△BAD=△CAE,△△BAC=△DAE,。
全等三角形单元复习全等三角形复习课(“手拉手”模型)-2024-2025学年人教版八年级上学期

(2)如图2,在(1)的条件下,若点E在BC边上,请说明DB⊥BC;
(3)如图3,在四边形ABCD中,∠ABC=∠ADC=90°,AB=CB,连接BD,AC,BD=
7cm,求四边形ABCD的面积.(友情提示:在图3中,∠BAD+∠BCD=180°)
A
D
图1
图2
图3
B
图4
∴∠BAD=∠CAE
等角-公共角 得 新等角
=
在△ABD 和△ACE中,ቐ∠BAD =∠CAE
=
∴△ABD≌△ACE(SAS)
活动二:推理论证,抽象模型
变式3:
如图,若△ABC和△ADE变为等边三角形, 即∠BAC=∠DAE=60°
其他条件不变,结论△ABD≌△ACE还成立吗?请说明理由.
人教版八年级数学上册
第十二章《全等三角形》:
全等三角形复习课(“手拉手”模型)
活动一:创设情境,感知模型
问题1.如图,已知:△ABC和△ADE是等腰直角三角形,
∠BAC=∠DAE=90°,AB=AC,AD=AE,
________,
求证:△ABD≌△ACE .
活动二:推理论证,抽象模型
变式1.如图,已知:△ABC和△ADE是等腰直角三角形,
特殊到一般
模型思想
手拉手模型
条件:AB=AC, AD=AE, ∠BAC=∠DAE.
结论:△ABD≌△ACE
总结:共顶点,等线段,等夹角,得全等,找全等,回初始.
活动四:学以致用,运用模型
1.问题背景:某数学兴趣小组在课外托管延时服务中进行如下探究活动:把两个等腰直角三角
形的直角顶角顶点重合,
(1)如图1,在△ABC、△ADE中,∠BAC=∠DAE=°,AB=AC,AD=AE,连接BD,
中考复习讲义: 全等中的“一线三等(直)角”与“手拉手”模型(部分无答案)

全等中的“一线三等(直)角”与“手拉手”模型
一、何为一线三等(直)角模型
我们先来研究最特殊的一线三直角.
如图,当∠CAB=∠CBE=∠BDE=90°,CB=BE时,△CAB≌△BDE.证明略.一般的,当∠CAB=∠CBE=∠BDE,(钝角或锐角),CB=BE时,同样有
△CAB≌△BDE.
可能有些同学对证明过程有疑虑,
其实不难,利用外角.
∠C+∠CAB=∠CBD=∠CBE+∠EBD
∵∠CAB=∠CBE,∴∠C=∠EBD,下略.
当然,这里还有引申结论,如CA+DE=AD等.
即便CB与BE不等,这两个三角形也是初三学习相似时的重要模型.
本讲,我们主要研究最特殊的一线三直角.
二、一线三直角典型例题
例1:
分析:
这里的背景是正方形,则其邻边相等,加上∠COA=90°,则可以构造一线三直角模型.
解答:
变式:
已知点P的坐标为(3,4),O为原点,连结OP,将线段OP绕点P按顺时针方向旋转90°得线段PQ,则点Q的坐标为________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1页/共1页 全等三角形--------手拉手模型
例题1、在直线ABC 的同一侧作两个等边三角形△ABD 和△BCE ,连接AE 与CD ,证明:
(1) △ABE ≌△DBC (2) AE=DC (3) AE 与DC 的夹角为60。
(4) △AGB ≌△DFB (5) △EGB ≌△CFB
(6) BH 平分∠AHC (7) GF ∥AC
变式练习1、如果两个等边三角形△ABD 和△BCE ,连接AE 与CD ,证明:
(1) △ABE ≌△DBC (2) AE=DC
(3) AE 与DC 的夹角为60。
(4) AE 与DC 的交点设为H,BH 平分∠
AHC
变式练习2:如果两个等边三角形△ABD 和△
BCE ,连接AE 与CD ,证明:
(1) △ABE ≌△DBC
(2) AE=DC
(3) AE 与DC 的夹角为60。
AHC (4)AE 与DC 的交点设为H,BH 平分∠例题2:如图,两个正方形ABCD 和DEFG ,连接AG 与CE ,二者相交于H 问:(1)△ADG ≌△CDE 是否成立?
(2)AG 是否与CE 相等?
(3)AG 与CE 之间的夹角为多少度?
(4)HD 是否平分∠AHE ?
例题3:如图两个等腰直角三角形ADC 与EDG ,连接AG ,CE,二者相交于H. 问 (1)△ADG ≌△CDE 是否成立?
(2)AG 是否与CE 相等?
(3)AG 与CE 之间的夹角为多少度? (4)HD 是否平分∠AHE ?
例题4:两个等腰三角形ABD 与BCE ,其中
AB=BD,CB=EB,∠ABD=∠CBE=a 连接AE 与CD. 问(1)△ABE ≌△DBC 是否成立?
(2)AE 是否与CD 相等?
(3)AE 与CD 之间的夹角为多少度? (4)HB 是否平分∠AHC ? H
F G E D
A B C E B
D
A C H E
B D A
C H G A
D C
E
H D A
B C
E。
