EXCEL常用面积、体积计算公式
EXCEL常用面积体积计算公式

EXCEL常用面积体积计算公式在Excel中,可以使用各种公式来计算面积和体积。
以下是一些常用的公式和方法,可以帮助你在Excel中进行这些计算。
一、面积计算公式:1.长方形面积计算:面积=长度*宽度2.正方形面积计算:面积=边长*边长3.圆形面积计算:面积=PI(*半径*半径4.椭圆面积计算:面积=PI(*长轴半径*短轴半径5.三角形面积计算:面积=底边长度*高/26.梯形面积计算:面积=(上底+下底)*高/27.平行四边形面积计算:面积=底边长度*高度8.菱形面积计算:面积=对角线1长度*对角线2长度/2二、体积计算公式:1.立方体体积计算:体积=边长*边长*边长2.正方体体积计算:体积=边长*边长*边长3.圆柱体体积计算:体积=PI(*半径*半径*高4.圆锥体体积计算:体积=PI(*半径*半径*高/35.球体体积计算:体积=4*PI(*半径*半径*半径/36.椭球体体积计算:体积=4/3*PI(*长半轴*短半轴*短半轴在Excel中,可以使用这些公式来进行面积和体积的计算。
以下将详细介绍如何在Excel中使用这些公式进行计算。
步骤1:打开Excel并创建一个新的工作表。
步骤2:在一个单元格中输入数据,例如长方形的长度和宽度。
步骤3:选择一个单元格来计算面积或体积,然后输入公式。
公式可以插入/粘贴或手动键入。
公式中的单元格引用应与你输入的数据单元格相对应。
步骤4:按下回车键,Excel将计算并显示结果。
例如,假设你输入了一个长方形的长度和宽度,分别为A1和B1单元格。
你想要计算该长方形的面积。
在C1单元格,你可以输入公式=A1 * B1,然后按下回车键。
Excel将根据你所提供的长度和宽度来计算面积,并在C1单元格显示结果。
除了基本的面积和体积计算公式之外,Excel还提供了许多其他功能和公式,可以帮助你进行更复杂的计算。
例如,你可以使用SUM函数计算多个区域的总面积或体积,可以使用IF函数根据特定条件计算不同的公式,以及使用ROUND函数对结果进行舍入等等。
excel几何数学公式大全详解

文章标题:深度剖析Excel中的几何数学公式在Excel这个常见的电子表格软件中,数学公式扮演着至关重要的角色。
特别是在处理几何数学方面,Excel提供了多种功能强大的公式和工具,帮助用户轻松进行各种几何计算和分析。
本文将从简单到复杂、由浅入深地探讨Excel中的几何数学公式,为您全面解读和详细解释这些公式的使用方法和实际应用场景。
1. Excel中的基本几何数学公式在Excel中,最基本的几何数学公式包括计算面积、周长、体积等内容。
对于二维几何图形,例如矩形、三角形、圆形等,可以通过简单的公式来实现计算。
以矩形面积为例,可以使用“=长*宽”来计算矩形的面积。
而对于三维几何图形,例如立方体、圆柱体等,可以通过类似的方法来计算体积和表面积。
这些基本公式为我们在Excel中进行几何计算提供了方便快捷的工具。
2. Excel中的几何函数除了基本的几何公式外,Excel还提供了丰富的几何函数,可以更加灵活地进行几何计算。
通过使用PI()函数,可以在计算圆的面积和周长时直接引用数学常数π,简化公式的书写。
而通过SUM()函数和AVERAGE()函数,可以方便地对多个几何图形的面积或体积进行求和和平均值的计算。
这些几何函数的应用极大地提高了我们在Excel中处理几何数学的效率和精度。
3. Excel中的图形绘制与数据分析除了简单的几何计算外,Excel还提供了丰富的图形绘制和数据分析功能,帮助用户更直观地理解和展示几何问题。
通过使用Excel的图表功能,可以将几何图形的数据绘制成直观的图表和图形,更好地展现问题的分布和变化趋势。
通过数据透视表和条件格式化等功能,可以对几何数据进行更深入的分析和挖掘,了解图形的特性和规律。
4. 个人观点与总结Excel作为一款强大的电子表格软件,提供了丰富的几何数学公式和功能,满足了我们在几何计算和分析方面的多样化需求。
通过熟练掌握和灵活运用这些公式和功能,我们可以更加高效地处理几何数学问题,提高工作和学习的效率。
EXCEL计算器与常用面积、体积计算公式
序号 图形 名称
正 方 形
图
式
参数代号
a
参数值
4
名称
面积A 对角线d 边长a A=a d=2
2
计算公式
1
d a a 2 3 6 4
1/2
*a
a=d/21/2 A=a*b d=(a2+b2)1/2 b=A/a
面积A 对角线d 边长b
2
长 方 形
Байду номын сангаас
b A
3
平 行 四 边 形
b h A a b h
10
r
5
体积V
V=π r2(h1+h)/2
11
正 六 角 柱
a
8
表面积S
S=5.1962a +6ah
2
h
75
体积V
V=2.5981a h
2
a 正 方 角 锥 台
0.3 表面积S S=a +b +2(a+b)h1
2 2
12
12
正 方 角 锥 台
表面积S b h1(斜边 高) h 1.95 表面积S 2.16
求表面积
4.7556
求表面积
3.51234
求体积
314
求表面积
523.3333333
求体积
7.021253449 7.021253449 2.093333333
求侧面积 求侧面积
1.94198275
求侧面积
0.26376
求体积
20
求面积
0
已知面积、边b,求高 度
0
求面积
#DIV/0! 0
实用:EXCEL计算器、面积、体积计算公式

公 式 F=1/2×r×L =0.008727×r×a 2.094393 1.0472
m2
公式
L=r×a×π /180
2.094393 m
公式
高:h 角度:a 弓宽:e 半径:r 常数:
0.30 60 0.3 1.5
0.0174
m 面积:F m 弓宽:e m 半径:r
m 弓高:h 弧长:L
公式 公式 公式 公式
18.97466 m2 5.854933 m3
筒节高:H 2
直径:D 1.5
锥度: 常数: 常数: 常数: 常数:
90 1.075 1.11 0.123 0.131
m 面积F m 体积V
公式 公式
M=π *Dh+1.078D2+1.11D2 V=π /4*D2*H+0.123*D2+0.131*D3
1 正六角柱 2 正方锥台 3球 4 圆锥 5 截头圆锥 6 缺球 7 封头贮罐 8 90°锥底贮罐
9 60°锥底贮罐
10 球底 11 封头 12 正方形 13 长方形 14 平行四边形
已知参数
高:h
2m
边长:a 2 m
常数: 2.59*2.598×a2
M1=6×a×h
M=S+M1
M=2*π *R×h F=π ×D2×h F=2×π ×r×h =π ×d×h M′=π ×(D-d) V=π ×h×(r2-r2)
25.13272 25.13272 m2 18.84954 18.84954 m2
1.570795 m2 5.497783 m3
28 斜底截圆柱
长边高:h 1.5
短边高:h1 1.3
4.712385 7.024809 m2 0.31831 m3
EXCEL计算器与常用面积体积计算公式

EXCEL计算器与常用面积体积计算公式Excel是一款功能强大的电子表格软件,其中涵盖了许多常用的计算功能,包括面积和体积的计算。
在Excel中,我们可以使用各种公式来计算不同形状的物体的面积和体积。
下面是一些常用的面积和体积计算公式及其在Excel中的应用。
1.矩形的面积矩形的面积可以通过长度和宽度的乘积来计算。
在Excel中,可以使用乘法运算符“*”来计算矩形的面积。
例如,假设我们要计算一个矩形的面积,其长度为10米,宽度为5米。
我们可以在Excel中的一个单元格中输入以下公式来计算面积:=10*52.正方形的面积正方形的面积可以通过边长的平方来计算。
在Excel中,可以使用乘法运算符“*”和指数运算符“^”来计算正方形的面积。
例如,假设我们要计算一个正方形的面积,其边长为8米。
我们可以在Excel中的一个单元格中输入以下公式来计算面积:=8^2或=8*83.圆的面积圆的面积可以通过半径的平方乘以π(圆周率)来计算。
在Excel 中,可以使用乘法运算符“*”、指数运算符“^”和PI函数来计算圆的面积。
例如,假设我们要计算一个圆的面积,其半径为5米。
我们可以在Excel中的一个单元格中输入以下公式来计算面积:=5^2*PI(或=5*5*PI1.长方体的体积长方体的体积可以通过长度、宽度和高度的乘积来计算。
在Excel中,可以使用乘法运算符“*”来计算长方体的体积。
例如,假设我们要计算一个长方体的体积,其长度为10米,宽度为5米,高度为3米。
我们可以在Excel中的一个单元格中输入以下公式来计算体积:=10*5*32.正方体的体积正方体的体积可以通过边长的立方来计算。
在Excel中,可以使用乘法运算符“*”和指数运算符“^”来计算正方体的体积。
例如,假设我们要计算一个正方体的体积,其边长为8米。
我们可以在Excel中的一个单元格中输入以下公式来计算体积:=8^3或=8*8*83.圆柱体的体积圆柱体的体积可以通过底面积乘以高度来计算。
EXCEL自动求得常用面积体积计算公式

EXCEL自动求得常用面积体积计算公式在Excel中,我们可以利用函数和公式来自动计算常用的面积和体积。
以下是一些常见的公式和函数:1. 计算矩形面积:矩形的面积可以通过长度和宽度的乘积来计算。
在Excel中,您可以使用乘法运算符(*)来计算矩形的面积。
例如,如果A1包含长度,B1包含宽度,则可以在C1中输入公式=A1*B1来计算面积。
2. 计算圆的面积:圆的面积可以通过半径的平方乘以π来计算。
在Excel中,您可以使用PI(函数和乘法运算符来计算圆的面积。
例如,如果A1包含半径,则可以在B1中输入公式=PI(*A1^2来计算圆的面积。
3. 计算三角形的面积:三角形的面积可以通过底边乘以高度再除以2来计算。
在Excel中,您可以使用乘法运算符和除法运算符来计算三角形的面积。
例如,如果A1包含底边,B1包含高度,则可以在C1中输入公式=A1*B1/2来计算三角形的面积。
4. 计算立方体的体积:立方体的体积可以通过长度、宽度和高度的乘积来计算。
在Excel中,您可以使用乘法运算符来计算立方体的体积。
例如,如果A1包含长度,B1包含宽度,C1包含高度,则可以在D1中输入公式=A1*B1*C1来计算立方体的体积。
5. 计算圆柱体的体积:圆柱体的体积可以通过底面积乘以高度来计算。
在Excel中,您可以使用圆的面积公式和乘法运算符来计算圆柱体的体积。
例如,如果A1包含半径,B1包含高度,则可以在C1中输入公式=PI(*A1^2*B1来计算圆柱体的体积。
除了上述的常见计算公式外,还可以利用Excel中的其他函数和工具来求解更复杂的面积和体积计算。
例如,使用SUM函数来计算多边形的面积,使用IF函数进行逻辑判断,使用条件格式化来可视化结果等等。
Excel是一个功能强大的工具,通过熟练运用,您可以轻松完成各种面积和体积的计算任务。
EXCEL自动求得常用面积体积计算公式
EXCEL自动求得常用面积体积计算公式Excel是一款功能强大的电子表格软件,可以用于各种计算和数据分析任务。
在面积和体积计算方面,Excel提供了许多自动计算公式,可以帮助用户快速计算各种图形的面积和体积。
本文将介绍Excel中常用的面积和体积计算公式,并提供一些实际应用示例。
矩形是最简单的几何形状之一,其面积和体积可以通过以下公式计算:面积(A)=长(L)×宽(W)体积(V)=长(L)×宽(W)×高(H)在Excel中,可以使用乘法运算符“*”来计算面积和体积。
例如,如果矩形的长为10,宽为5,高为3,可以使用以下公式计算面积和体积:面积:=10*5体积:=10*5*3圆是一种常见的二维和三维几何形状,其面积和体积可以通过以下公式计算:面积(A)=π×半径(R)^2体积(V)=4/3×π×半径(R)^3在Excel中,可以使用内置的PI函数(=PI()来获取圆周率π的值,并使用幂运算符“^”来计算面积和体积。
例如,如果圆的半径为5,可以使用以下公式计算面积和体积:面积:=PI(*5^2体积:=4/3*PI(*5^3三角形是另一个常见的二维几何形状,其面积可以通过以下公式计算:面积(A)=1/2×底边(B)×高(H)在Excel中,可以使用除法运算符“/”来计算面积。
例如,如果三角形的底边为10,高为8,可以使用以下公式计算面积:面积:=1/2*10*8由于三角形是一个二维形状,没有体积的概念。
正方形是一种特殊的矩形,其面积可以通过以下公式计算:面积(A)=边长(S)^2在Excel中,可以使用幂运算符“^”来计算面积。
例如,如果正方形的边长为6,可以使用以下公式计算面积:面积:=6^2由于正方形是一个二维形状,没有体积的概念。
以上是常见的几何形状的面积和体积计算公式。
除了这些基本的公式之前,在Excel中还可以使用一些其他功能来进行更复杂的计算,并将计算结果应用于实际问题中。
EXCEL常用面积、体积计算公式
已知直径D,求V、A。
已知球半径 r与冠高h,求V、A。
已知球半径 r与冠半弦a,求V、A。
长边 a∥c,高度为 h。
Am为棱柱体中截面,但Am≠ (A1+A2)/2。
Am为棱柱体中截面,但Am≠ (A1+A2)/2。
坡道长度为 l,宽度为 a,纵坡为 i, 边坡坡比均为 1:n。
a
a
b n h
A1
9
台 体
A2 a2
h
a1 a2 A1 A2 R
D
10
截 头 圆 柱
α h2 h1
h1
7
斜径(D)
D=sqrt((h2-h1)^2+4*R^2)
10.198
10
截 头 圆 柱
h1 R
h2
9
体积(V) 体积(V)
V=pi()*R^2*(h1+h2)/2 V=4*pi()*r^3/3 A=4*pi()*r^2 D=2*r V=pi()*D^3/6 A=pi()*D^2 V=pi()*h^2*(3*r-h)/3 As=2*pi()*r*h V=pi()*h*(a^2+r^2-r*sqrt(r^2-a^2))/3 As=2*pi()*r*(r-sqrt(r^2-a^2))
h
12
a
10 侧面积(As)
a
h
6 5 体积(V) V=(2*a+c)*b*h/6 75.000 6 5 4 4 体积(V) V=l*(A1+4*Am+A2)/6 12.000 4
13
契 形 体
h
b c
b
a
l/2
l/2
h A1
A2 Am
EXCEL面积体积计算公式
EXCEL面积体积计算公式Excel是一款功能强大的电子表格软件,可以进行各种数学计算。
在Excel中,我们可以使用不同的公式来计算面积和体积。
首先,我们来介绍如何计算面积。
面积是一个平面上的量,通常用平方单位表示,比如平方米、平方厘米等。
1.矩形的面积计算:矩形的面积计算公式为:面积=长×宽。
假设矩形的长为A1单元格,宽为B1单元格,那么可以在C1单元格输入公式“=A1*B1”来计算矩形的面积。
2.圆的面积计算:圆的面积计算公式为:面积= π × 半径的平方。
假设圆的半径为A1单元格,可以在B1单元格输入公式“=PI( * A1^2”来计算圆的面积。
其中,PI(是Excel内置的π值。
3.三角形的面积计算:三角形的面积计算公式为:面积=底边长度×高/2、假设三角形的底边长度为A1单元格,高为B1单元格,可以在C1单元格输入公式“=A1*B1/2”来计算三角形的面积。
接下来,我们来介绍如何计算体积。
体积是一个立体的量,通常用立方单位表示,比如立方米、立方厘米等。
1.矩形长方体的体积计算:矩形长方体的体积计算公式为:体积=长×宽×高。
假设矩形长方体的长为A1单元格,宽为B1单元格,高为C1单元格,可以在D1单元格输入公式“=A1*B1*C1”来计算矩形长方体的体积。
2.圆柱体的体积计算:圆柱体的体积计算公式为:体积=π×半径的平方×高。
假设圆柱体的半径为A1单元格,高为B1单元格,可以在C1单元格输入公式“=PI(*A1^2*B1”来计算圆柱体的体积。
3.球体的体积计算:球体的体积计算公式为:体积=4/3×π×半径的立方。
假设球体的半径为A1单元格,可以在B1单元格输入公式“=4/3*PI(*A1^3”来计算球体的体积。
以上是一些常见的面积和体积计算公式,你可以根据实际需求和具体应用场景,灵活运用Excel中的数学公式进行计算。
测绘常用EXCEL计算公式
测绘常用EXCEL计算公式测绘工作是一个涉及测量、分析和计算的专业领域,其中计算部分经常使用Excel来完成。
下面是一些测绘常用的Excel计算公式。
1. 坐标转换公式:在测绘中,坐标转换是一个重要的任务,可以使用Excel来进行坐标的转换。
常见的公式包括:-直角坐标转换为极坐标:可以使用公式"=ATAN2(Y/X)"来计算。
-极坐标转换为直角坐标:可以使用公式"=X*COS(Y)"和"=X*SIN(Y)"来计算。
2.距离和角度计算:在测绘中,经常需要计算两点之间的距离和角度。
下面是常用的公式:-距离计算:可以使用公式"=SQRT((X2-X1)^2+(Y2-Y1)^2)"来计算两点之间的直线距离。
-角度计算:可以使用公式"=ATAN2(Y2-Y1,X2-X1)"来计算两点之间的方位角。
3.曲线元素计算:在道路和铁路设计中,经常需要计算曲线元素,如曲线半径、切线长度和切线偏角。
下面是一些公式:-曲线半径计算:可以使用公式"=L^2/24R"来计算曲线半径,其中L为曲线长度,R为曲线反曲率。
-切线长度计算:可以使用公式"=R*TAN(A/2)"来计算切线长度,其中R为曲线半径,A为切线偏角。
-切线偏角计算:可以使用公式"=2*ATAN(L/(2*R))"来计算切线偏角,其中L为切线长度,R为曲线半径。
4.面积和体积计算:在土地测量和容积测量中,需要计算面积和体积。
下面是常见的计算公式:-面积计算:可以使用公式"=SUMPRODUCT(($A:$A=B1)*($C:$C=C1)*($D:$D=D1)*($E:$E-E1))"来计算条件下的面积,其中B1、C1和D1为条件,E1为面积值。
-体积计算:可以使用公式"=SUMPRODUCT(($A:$A=B1)*($C:$C=C1)*($D:$D=D1)*($E:$E-E1)*($F:$F-F1))"来计算条件下的体积,其中B1、C1、D1为条件,E1为面积值,F1为高度值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
已知直径D,求V、A。
已知球半径 r与冠高h,求V、A。
已知球半径 r与冠半弦a,求V、A。
长边 a∥c,高度为 h。
Am为棱柱体中截面,但Am≠ (A1+A2)/2。
Am为棱柱体中截面,但Am≠ (A1+A2)/2。
坡道长度为 l,宽度为 a,纵坡为 i, 边坡坡比均为 1:n。
h
4 弓 形
h
3
弧长(l) 弦长(c)
c α r
c 15
面积(A) 弧长(l) 矢高(h)
R 角 缘 面 积
60
5
α
R
α (°) 50
面积(A)
A=R^2*(tan(α /2)-pi()*α /360)
107.911
b
6 椭 圆
a
6
面积(A)
A=PI()*a*b
75.398
6
椭 圆 b 4 周长(S) S≈pi()*sqrt(2*(a^2+b^2)-(a-b)^2/22) 32.010
h
12
a
10 侧面积(As)
a
h
6 5 体积(V) V=(2*a+c)*b*h/6 75.000 6 5 4 4 体积(V) V=l*(A1+4*Am+A2)/6 12.000 4
13
契 形 体
h
b c
b
a
l/2
l/2
h A1
A2 Am
14
棱 柱 体
A2 Am
A1
14
棱 柱 体
l
体积(V)
V=l*(A1+4*Am+A2)/6
628.319 904.779 452.389 12.000 904.779 452.389 904.779 376.991 1256.637 628.319
r
6
表面积(A) 直径(D) 体积(V)
r
11 球
D
D
12 表面积(A)
r 球 冠 r
c a h
10 6
体积(V) 侧面积(As) 体积(V)
弧长(l)
l
r
15 面积(A) A=(l*r-c*(r-h))/2 l=2*r*asin(c/(2*r)) c=2*sqrt(h*(2*r-h)) A=(l*r-c*(r-h))/2 l=2*r*asin(c/(2*r)) h=r-sqrt(r^2-c^2/4) 36.788 19.305 18.000 20.382 15.708 2.010
已知边数n,边长s,求A,R,r
已知边数n,外接圆R,求A,s
r为扇形半径。
已知弧长 l,求面积A与圆心角α
已知弧长 l,求面积A与圆心角α
已知圆心角α ,求面积A与弧长l
r为扇形半径。
已知矢高h,求面积A、弧长l、弦长c。
已知弦长c,求面积A、弧长l、矢高h。
已知半径R,弧心角α ,求角缘面积A。
长轴 a
短轴 b
长轴 a
短轴 b
b 为抛物线半开口宽。
多边形边数n,台体高度h。
已知上、下边长a1、a2,求As、V。
已知上.下面积A1.A2,求As、V
已知圆柱半径R,截高h1、h2,求截面 α 、D、与体积V。
已知圆柱半径R,截高h1、h2,求截面 α 、D、与体积V。
已知半径 r,求V、A、D。
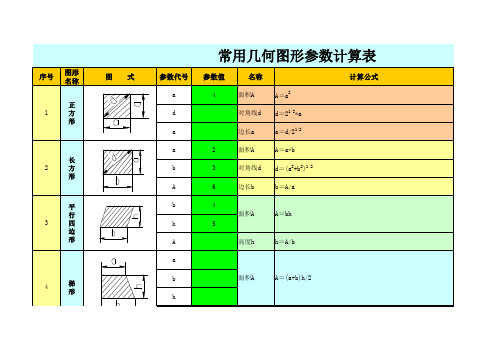
常用几何图形参数计算表
序号 图形名称 图
B
任 意 三 角 形
式
参数 代号
a b
参数值
3
名
称
A=b*h/2
计算公式
计算值
17.500 6.495 21.787° 38.213° 120.000° 60.000° 120.000° 0.176 0.260 0.225 0.000 0.000
面积(A) 5 7 7 7.5 圆心角(α ) β n 6 内角(β ) R s R 0.26 面积(A) 外接圆(R) 内切圆(r) 面积(A) β =180-α =180*(n-2)/n A=n*s*r/2 R=(s/2)/sin(α /2) r=(s/2)/tan(α /2) A=n*R^2*sin(α /2)*cos(α /2) s=2*R*sin(α /2) 角度(°) A=sqrt((s*(s-a)*(s-b)*(s-c)) ∠A=acos((b^2+c^2-a^2)/(2*b*c)) ∠B=acos((a^2+c^2-b^2)/(2*a*c)) ∠C=acos((b^2+a^2-c^2)/(2*a*b)) α =360/n
a a
7 椭 圆 角 缘 a 8 面积(A) b 4 A=a*b*(1-pi()/4) 6.867
b
8
抛 物 线
a1
b
b
a
5 面积(A) A=4/3*a*b 20.000 3 7 5 3 4 100 体积(V) V=h*(A1+A2+sqrt(A1*A2))/6 280.669 125 5 倾角(α ) α =atan((h2-h1)/2/R) 11.310° 上面积(A1) 下面积(A2) 侧面积(As) 体积(V) A1=n*a1^2/tan(pi()/n)/4 A2=n*a2^2/tan(pi()/n)/4 As=n*(a1+a2)*h1/2 V=h*(A1+A2+sqrt(A1*A2))/6 32.705 58.143 125.113 112.046
12.000
l n
3 1 0.05 体积(V) 13 50 V=i^2*l^2*(3*a+2*n*i*l*(1-n*I))*(1/in)/6Βιβλιοθήκη h1:ni
l
15
路 基 坡 道
i
a
1:n
1:n
i
865.885
a
a l
备
注
a、b、c为三角形的三条边长。
h为b边上的高。 s=(a+b+c)/2
n为正多边形边数
a
a
b n h
A1
9
台 体
A2 a2
h
a1 a2 A1 A2 R
D
10
截 头 圆 柱
α h2 h1
h1
7
斜径(D)
D=sqrt((h2-h1)^2+4*R^2)
10.198
10
截 头 圆 柱
h1 R
h2
9
体积(V) 体积(V)
V=pi()*R^2*(h1+h2)/2 V=4*pi()*r^3/3 A=4*pi()*r^2 D=2*r V=pi()*D^3/6 A=pi()*D^2 V=pi()*h^2*(3*r-h)/3 As=2*pi()*r*h V=pi()*h*(a^2+r^2-r*sqrt(r^2-a^2))/3 As=2*pi()*r*(r-sqrt(r^2-a^2))
c
1
h
a
c
A
b
C
h s
2
正 n 边 形
r α
S
l
R
0 边长(s)
r
9 面积(A) A=l*r/2 27.000
3
扇 形
l
6
3
扇 形
l
6 圆心角(α ) 面积(A) α =l/r A=0.008727*α *r^2 l=0.01745*α *r 38.197° 95.426 21.206
r α
α (°) 135
