利用同位角判断两直线平行 优秀教案
利用同位角判定两直线平行优秀教案

2.2 探索直线平行的条件(1)【学习主题】探索直线平行的条件【学习课时】1课时【课标要求】1 认识同位角2 理解平行线的概念,掌握:两直线被第三条直线所截,如果同位角相等,那么这两直线平行。
3掌握基本事实:过直线外一点有且仅有一条直线与已知直线平行;平行于同一直线的两条直线平行【学习目标】1 通过观察认识同位角2通过“转动木条”活动,掌握并运用“同位角相等,两直线平行”的公理,进一步提升空间观念和逻辑推理能力。
3 借助三角尺会做过已知直线外一点画这条直线的平行线,发现平行线性质,发展有条理表达能力。
【评价任务】1完成任务12完成练习1、2、33完成达标检测4 完成达标检测【资源与建议】1本节内容是北师大版七年级下册第二章相交线和平行线的第二节,本节内容借助几何直观,发展合情推理,为今后的几何证明奠定了基础。
2本节内容从工人订木条情景,提出直线平行问题,通过木条操作,直观认识“同位角相等,两直线平行”,再根据“同位角相等,两直线平行”画平行线的过程中,发现平行线性质。
3 本节重点是平行线判定公理“同位角相等,两直线平行”,难点是掌握平行线判定公理。
通过任务二可以突破重点,通过任务三可以突破难点。
一、学习准备1 一般地,在同一平面内,两条直线的位置关系有两种:_____ 和______2 对顶角性质:对顶角__________二、学习新知(一)任务一:认识同位角(1)如图,直线a、b与c相交,观察图中∠1与∠2,它们有怎样的位置关系?与∠2是____角,它们是由直线___和直线_____,被直线1_____截成的.(2)认识同位角:两直线被第三条直线所截,如果两个角在被截线的同侧,在截线的同旁,那么这两个角叫做__________.思考:图1中的同位角有哪些?图1(3)如图2,已知直线a,b被直线c所截,那么∠1的同位角是()A ∠5B ∠2C ∠3D ∠4图2(4)判断图3 ∠1,,2是否为同位角?图3(任务二):判定定理观察归纳:2∠与的大小满足________时,木条a和木条b平行?1∠平行判定1:两条直线被第三条直线所截,如果同位角_____,那么这两直线______简称:_________________________________________(公理)如图②,可表述为:____________∴()___________练习1:如图所示1 (已知)∠1∠=2∴()____//_____2 (已知)∠=2∠3∴()_____//____练习2:如图, ∠1=∠2=55º,直线AB,CD 平行吗?说明你的理由.练习3:如图,已知1152651=∠=∠, 直线BC 与DF 平行吗? 为什么?任务三:平行线公理(PO3)完成教材45页想一想,做一做:(1)你能过直线AB 外一点C 画直线AB 的平行线吗?能画出几条?(2)如图,分别过点C,D 画直线AB 的平行线EF,GH,那么EF,GH 有怎样的位置关系?1 平行线公理:过直线外一点有_____________条直线与这条直线平行。
利用同位角判断两直线平行 教学设计

二、学情分析
1、学生的知识技能基础:学生在七年级上册《平面图形及其位置关系》一章中,已经 结合丰富的现实情景,直观认识了两条直线的平行关系,了解了平行线的定义,会借助方格 纸、利用直尺、三角板用多种方法画平行线,经历了在操作活动中探索图形性质的过程,初 步掌握了平行线的有关性质,并用自己的语言加以描述,初步具有了有条理地思考与表达的 能力,为本章的深入学习奠定了基础。
三、教学重难点
重点:会辨认同位角,并掌握“同位角相等,两直线平行”。
难点:将实际问题转化为数学问题以及对同位角的认知。
四、教学策略设计
1.在智慧教室环境下,恰到好处的运用利用交互式电子白板的视频播放、动画展示、文 字书写、信息反馈等功能,以学生自主学习、展示的方式为主,教师点拨为辅,在师生互动, 生机互动中完成学习,在潜移默化中突破重难点。
4、本节课提供给学生的探究的时间和空间不够充分。
《探索直线平行的条件第 1 课时》教学设计
一、教学目标
1、知识技能:经历探索直线平行条件的过程,掌握利用同位角相等判别直线平行的结 论,并能解决一些问题。
2、数学思考:会识别由“三线八角”构成的同位角,会用三角尺过已知直线外一点画 这条直线的平行线。
3、问题解决:经历观察、操作、想象、推理、交流等活动,体会利用操作、归纳获得 数学结论的过程,进一步发展空间想象、推理能力和有条理表达的能力。
3、组织个别学生补充回答自己的 发现:只有当∠1=∠2 时,两条直 线平行,他们是同位角。
4角相 等,两直线平行,并出示几何语言 和图形语言的表达。
3、个别学生补充回答自己的发现
利用同位角判断两直线平行-北师大版七年级数学下册教案

利用同位角判断两直线平行-北师大版七年级数学下册教案一、教学目标1.了解同位角概念。
2.学会利用同位角判断两条直线是否平行。
二、教学重难点1.重点:同位角的概念和运用。
2.难点:如何判断两直线是否平行。
三、教学过程1. 导入环节教师通过引导问题,让学生思考同位角的概念:如果两根杆子之间的角度一样,我们叫它们同位角。
同学们是否发现了类似同位角的例子?2. 新知呈现教师通过多媒体展示同位角的图像,并让学生观察并思考:•几何图形中同位角的特点是什么?•同位角的度数是否相等?接着,老师引出判断两直线是否平行的方法:当两个交错内角或同位角相等的时候,则两直线是平行的。
3. 知识拓展教师引导学生做同位角的应用练习,让学生能够熟练运用同位角判断两直线是否平行。
例如:上图中,如何判断两直线是否平行?A. ∠1=∠2,因此AB∥DE;B. ∠2=∠3,因此DE∥FG;C. ∠4=∠5,因此BC∥FG。
4. 实践演练教师布置练习题目,让学生自主完成。
例如:5. 总结归纳教师引导学生回顾同位角的定义、判断两直线是否平行的方法,并让学生自己总结并口头表述。
6. 课后作业教师布置课后作业,要求学生完成同位角的习题,并写出解题步骤和答案。
四、教学评价教师在课程结束后,可以通过课堂问答、小组讨论等形式进行学生评价。
例如:1.请你总结一下同位角判断两直线是否平行的方法。
2.如果给你一个图形,请你用同位角的知识判断两条直线是否平行。
五、教学反思教师可以根据学生的表现和反馈,对本节课的教学效果进行总结和反思,并根据需要进行适当的调整和改进。
利用同位角判断两直线平行-北师大版七年级数学下册教案

利用同位角判断两直线平行-北师大版七年级数学下册教案一、教学目标1.理解同位角的概念及判定两线段平行的方法;2.掌握同位角的性质并能正确运用于实际问题中。
二、教学重点1.同位角的概念;2.利用同位角判断两直线平行的方法。
三、教学难点能够正确理解同位角的判定方法及运用于实际问题中。
四、教学过程1.导入同位角在我们的生活中很常见。
例如,电视机的四个角的角度必须一样,否则我们就会感觉画面歪曲,失去美观。
正因为同位角的重要性,我们需要学会如何判断两条直线是否平行。
2.讲解同位角的概念:具有相同顶点的两个角是同位角,如图1所示。
图1同位角有以下两个重要性质:1.同位角相等的两条直线平行,如图2所示。
图22.在平行线上,同位角相等,如图3所示。
图3由此,我们可以运用同位角的性质,来判断两条直线是否平行。
3.练习(1) 例题1在图4中,求∠A、∠B、∠C、∠D的度数,如果∠A=∠C,判断AB与CD是否平行。
图4解:∠A=70°,∠C=70°,∠D=180°-70°=110°,∠B=180°-70°-110°=∠C。
根据同位角的性质,若∠A=∠C,则线段AB与CD平行。
(2) 例题2在图5中,若∠1=60°,∠3=120°,判断AC和BD是否平行。
图5解:因为∠1和∠3不是同位角,不能直接判断AC和BD是否平行。
由于∠1和∠2是同位角,∠3和∠2是同位角,所以∠1=∠2,∠3=∠2。
根据同位角的性质,若∠2=∠4,则线段BD与AC平行。
因为∠2=∠4=60°,所以BD与AC平行。
4.归纳总结同位角的概念及性质。
5.拓展学习同位角的应用很广泛,例如在建筑设计、绘画等方面都有应用。
如果同位角的性质运用得好,不仅可以美化环境,也可以解决工程设计中的问题,是应用数学中很重要的一部分。
五、课堂练习请手写一组例题进行练习。
北师大版七年级数学下册《2.2 第1课时 利用同位角判定两条直线平行》教案

北师大版七年级数学下册《2.2 第1课时利用同位角判定两条直线平行》教案一. 教材分析《2.2 第1课时利用同位角判定两条直线平行》这一课时主要让学生掌握利用同位角判定两条直线平行的方法。
教材通过引入实际生活中的情境,让学生观察和分析同位角的变化规律,从而得出结论。
本节课的内容是学生学习几何的基础知识,对于培养学生的空间观念和逻辑思维能力具有重要意义。
二. 学情分析学生在进入七年级之前,已经学习了角的分类、角的度量等基础知识,对于观察和分析角的变化有一定的经验。
但是,对于利用同位角判定两条直线平行的方法,他们可能还没有完全理解和掌握。
因此,在教学过程中,教师需要引导学生观察和分析同位角的变化规律,通过实践操作,使学生逐步理解和掌握这一方法。
三. 教学目标1.让学生了解同位角的概念,能够识别同位角。
2.引导学生观察和分析同位角的变化规律,掌握利用同位角判定两条直线平行的方法。
3.培养学生的空间观念和逻辑思维能力。
四. 教学重难点1.重点:同位角的概念,利用同位角判定两条直线平行的方法。
2.难点:观察和分析同位角的变化规律,灵活运用同位角判定两条直线平行。
五. 教学方法1.采用情境导入法,通过实际生活中的情境,引发学生的兴趣和好奇心。
2.采用观察和分析法,让学生通过观察和分析同位角的变化规律,得出结论。
3.采用实践操作法,让学生通过实际操作,巩固所学知识。
4.采用小组合作学习法,让学生在小组内进行讨论和交流,培养学生的合作能力。
六. 教学准备1.准备一些实际生活中的情境图片,用于导入和演示。
2.准备一些滑动板和直尺,用于学生实践操作。
3.准备一些练习题,用于巩固所学知识。
七. 教学过程1.导入(5分钟)利用情境图片,引导学生观察和分析同位角的变化规律,引发学生的兴趣和好奇心。
2.呈现(10分钟)介绍同位角的概念,引导学生观察和分析同位角的变化规律,让学生通过实践操作,体验和理解同位角的含义。
3.操练(10分钟)让学生分组进行实践操作,利用同位角判定两条直线平行。
北师大版数学七年级下册《利用同位角判断两直线平行》教学设计1

北师大版数学七年级下册《利用同位角判断两直线平行》教学设计1一. 教材分析《利用同位角判断两直线平行》是北师大版数学七年级下册第五章《几何图形》的一部分。
本节课的主要内容是让学生掌握同位角的定义,并利用同位角判断两直线是否平行。
这一内容是学生学习直线、射线、线段等基本几何概念之后的进一步拓展,对于学生理解和掌握几何知识体系具有重要意义。
二. 学情分析学生在进入七年级下册之前,已经学习了直线、射线、线段等基本几何概念,对于这些概念的理解和运用已经有一定的基础。
但是,对于利用同位角判断两直线平行的方法,他们可能还没有接触过,因此需要通过本节课的学习来掌握。
同时,学生对于几何图形的认知还处于初步阶段,需要通过大量的实践活动来提高。
三. 教学目标1.知识与技能目标:让学生掌握同位角的定义,学会利用同位角判断两直线是否平行。
2.过程与方法目标:通过观察、操作、思考、交流等活动,培养学生空间想象能力和逻辑思维能力。
3.情感态度与价值观目标:激发学生学习数学的兴趣,培养他们勇于探索、积极思考的精神。
四. 教学重难点1.教学重点:同位角的定义,利用同位角判断两直线平行。
2.教学难点:如何引导学生理解和运用同位角判断两直线平行的方法。
五. 教学方法1.情境教学法:通过设置情境,让学生在实际问题中感受和理解同位角的概念。
2.互动教学法:引导学生通过观察、操作、思考、交流等活动,共同探讨和解决问题。
3.实践教学法:让学生通过实际操作,加深对同位角的理解,提高运用能力。
六. 教学准备1.准备一些关于直线、射线、线段的图片,用于导入和新课的教学。
2.准备一些实际的例子,用于讲解和练习同位角判断两直线平行的方法。
3.准备黑板和粉笔,用于板书和标注。
七. 教学过程1.导入(5分钟)利用图片展示直线、射线、线段等基本几何概念,引导学生回顾和复习。
然后,提出问题:“如何判断两条直线是否平行?”引发学生的思考,为新课的学习做好铺垫。
初中数学北师大版七年级下册《利用同位角判定两条直线平行》教学设计
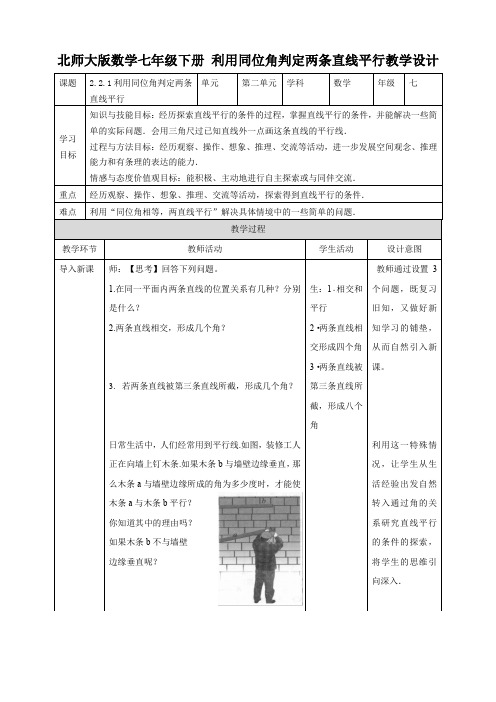
北师大版数学七年级下册利用同位角判定两条直线平行教学设计师:【思考】回答下列问题。
1.在同一平面内两条直线的位置关系有几种?分别是什么?2.两条直线相交,形成几个角?3.若两条直线被第三条直线所截,形成几个角?日常生活中,人们经常用到平行线.如图,装修工人正在向墙上钉木条.如果木条b与墙壁边缘垂直,那么木条a与墙壁边缘所成的角为多少度时,才能使木条a与木条b平行?你知道其中的理由吗?如果木条b不与墙壁边缘垂直呢?【做一做】 如图,三根木条相交成 ∠1,∠2,固定木条b ,c ,转动木条 a .如图,在木条 a 的转动过程中,观察∠2的变化以及它与∠1的大小关系,你发现木条 a 与木条b 的位置关系发生了什么变化?木条a 何时与木条b 平行?【思考】木条a 何时与木条b 平行?【思考】改变上图中∠1的大小,按照上面的方式再做一做.∠1与∠2的大小满足什么关系时,木条a 与木条b 平行?与同伴进行交流.【思考】观察∠1 与∠2的位置,你能发现什么特点?具有∠1与∠2这样位置关系的角称为同位角 。
想一想:什么样的角叫做同位角?两直线被第三条直线所截,位于两条直线(被截线)ACBDl13752486同一方、且在第三直线(截线)同一侧的两个角,(位置相同的一对角)叫做同位角.图中还有类似于∠1与∠2的同位角吗?将其特殊位置抽象成几何图形:由上面的操作过程,你能发现判定两直线平行的方法吗?现在你能说明其中的理由吗?如果木条b不与墙壁边缘垂直呢?【想一想】你能借助三角尺画平行线吗?小明按如下方法画出了两条平行线,请说明其中的道理.【探究】怎样用三角尺和直尺画平行线?.一放;二靠;三推;四画由前面我们已经知道平行线的画法:你能过直线AB 外一点P 画直线AB的平行线吗?能画出几条?你能得到什么结论?师:在图中,分别过点C,D画直线AB的平行线EF,GH,那么EF与GH有怎样的位置关系?【想一想】你能得到什么结论?。
利用同位角判定两条直线平行 【一等奖教案】 表格版

2.2探索直线平行的条件第1课时利用同位角判定两条直线平行1.理解并掌握同位角的概念,能够判定同位角并确定其个数;2.能够运用同位角相等判定两直线平行;(重点,难点)3.理解并掌握平行公理及其推论,能够运用其解决实际问题.一、情境导入数学来源于生活,生活中处处有数学,观察下面的图片,你发现了什么?以上的图片中都有直线平行,这将是我们这节课学习的内容.二、合作探究探究点一:同位角【类型一】判断同位角下列图形中,∠1和∠2不是同位角的是()解析:选项A、B、D中,∠1与∠2在截线的同侧,并且在被截线的同一方向,是同位角,即在图中可找到形如“F”的模型;选项C中,∠1与∠2没有公共直线,不是同位角.故选C.方法总结:判断两个角是否是同位角的有效方法——描图法:①把两个角在图中“描画”出来;②找到两个角的公共直线;③观察所描的角,判断所属“字母”类型是否为“F”型.【类型二】数同位角的个数,l2被l3所截,则同位角共有()如图,直线lA.1对B.2对C.3对D.4对解析:图中同位角有:∠1和∠5,∠2和∠6,∠3和∠7,∠4和∠8共4对.故选D.方法总结:数同位角的个数时,应从各个方向逐一观察,避免重复或漏数.探究点二:利用同位角判定两直线平行如图,直线AB、CD分别与EF相交于点G、H,已知∠1=70°,∠2=70°,试说明:AB∥CD.解析:要说明AB∥CD,可转化为说明∠1与其同位角相等,这由∠2的对顶角容易证出.解:因为∠2=∠EHD(对顶角相等),又因为∠2=70°,所以∠EHD=70°.因为∠1=70°,所以∠EHD=∠1,所以AB∥CD(同位角相等,两直线平行).方法总结:本题考查的是平行线的判定,熟知“同位角相等,两直线平行”是解答此题的关键.探究点三:平行公理及其推论【类型一】应用平行公理及其推论进行判断有下列四种说法:(1)过直线外一点有且只有一条直线与这条直线平行;(2)同一平面内,过一点能且只能作一条直线与已知直线垂直;(3)直线外一点与直线上各点连接的所有线段中,垂线段最短;(4)平行于同一条直线的两条直线平行.其中正确的个数是()A.1个B.2个C.3个D.4个解析:根据平行公理、垂线的性质进行判断.(1)过直线外一点有且只有一条直线与这条直线平行,正确;(2)同一平面内,过一点能且只能作一条直线与已知直线垂直,正确;(3)直线外一点与直线上各点连接的所有线段中,垂线段最短,正确;(4)平行于同一条直线的两条直线平行,正确.正确的有4个.故答案为D.方法总结:平行线公理和垂线的性质两者比较相近,特别注意,对于平行公理中,必须是过直线外一点可以作已知直线的平行线,过直线上一点不能做已知直线的平行线.但垂线的性质中,无论点在平面内何处都能作出已知直线的唯一垂线.【类型二】应用平行公理进行推论论证四条直线a,b,c,d互不重合,如果a∥b,b∥c,c∥d,那么直线a,d的位置关系为________.解析:由于a∥b,b∥c,根据平行公理的推论得到a∥c,而c∥d,所以a∥d.故答案为a∥d.方法总结:平行公理的推论是证明两条直线相互平行的理论依据.【类型三】平行公理推论的实际应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 平行线与相交线
2.2.1探索直线平行的条件
教学目标 知识与技能
1.经历探索直线平行条件的过程,掌握利用同位角相等判别直线平行的结论,并能解决一些问题。
2.会识别由“三线八角”构成的同位角,会用三角尺过已知直线外一点画这条直线的平行线。
过程与方法
3.经历观察、操作、想象、推理、交流等活动,体会利用操作、归纳获得数学结论的过程,进一步发展空间想象、推理能力和有条理表达的能力。
情感态度与价值观
4.使学生在积极参与探索、交流的数学活动中,体验数学与实际生活的密切联系,激发学生的求知欲,感受与他人合作的重要性。
教学过程
第一环节:巧妙设疑,复习引入
问题1:在同一平面内两条直线的位置关系有几种?分别是什么?
学生很容易回答出“在同一平面内两条直线的位置关系有两种,分别是相交和平
行”,再进一步针对相交和平行分别提出问题2、3。
问题2:如图,两条直线相交所构成的四个角中分别有何关系?
借助两条直线相交的基本图形复习“两线四角”的关系,为探索“三线八角” 的关系奠定基础。
问题3:什么叫两条直线平行?
复习平行线的定义:在同一平面内,不相交的两条直线叫做平行线。
A
B
D
C
O
A
C B
D l
1
2 3 4 6
7 5
8
问题4:观察下面每幅图中的直线a,b ,它们分别平行吗?你能验证吗?
教师引入:三组直线看上去似乎不平行,其实它们分别都是平行的,这是由于背景造成的视觉误差,所以按照平行线的定义仅凭观察来判断直线的平行关系是不够的,这就需要进一步寻求证据,本节课老师将和同学们一起来——探索直线平行的条件,由此引入新课。
第二环节:预习引入 新知预热
1.比较课前同学们制作的工具,看看哪一组做的工具比较好, 教师提问:此工具是有几条线组成,其中小于平角的角有几个。
老师简要介绍此工具的用处:我们把这个工具称之为平行线分析器,我们将借助这个工具进行平行线的学习,不要看他构造简单,他对探究分析平行线是很有帮助的。
2.由∠1与∠2的位置关系引出对“三线八角”的认识与同位角的概念。
如图,直线AB ,CD 被直线l 所截,构成了八个角,具有∠1与∠2
这样位置关系的角,可以看作是在被截直线的同一侧,在截线的同一旁, 相对位置是相同的,我们把这样的角称为同位角。
问题:图中还有其他的同位角吗? 3.练习(独立思考,小组合作,集体交流) (1)(2016海珠期末)如图,同位角是( ) A .∠1和∠2
B .∠3和∠4
C .∠2和∠4
D .∠1和∠4
(2)下列图形中,∠1和∠2是同位角的是( )
第三环节:联系实际,积极探索
活动内容:1.引入实际问题:如课本彩图,装修工人正在向墙上钉木条。
如果木条b 与墙壁边缘垂直,那么木条a 与墙壁边缘所夹角是多少度时,才能使木条a 与木条b 平行?学生根据自己的生活经验自然会得到:木条a 也与墙壁边缘垂直时,才能使木条a 与木条b 平行。
在此基础上提出两个问题:
问题1:实际问题中在判断两根木条平行时,借助了墙壁作为参照,你能将上述问题抽象为数学问题吗?你能用我们制作的平行线分析器来比划这个实际情景吗?试着画出图形,并结合图形说明。
学生回答:如图,把墙壁看作直线c,直线b 与直线c 垂直时, 只有当直线a 也与直线c 垂直时,才能得到直线a 平行于直线b 。
问题2:
1.图中的直线b 与直线c 不垂直,直线a 应满足什么条件才能与直线b 平行呢?请你利用自己制作的工具亲自动手操作。
2.综上探索,引导学生归纳出两直线平行的条件:同位角相等,两直线平行。
第四环节:画图延生 巩固新知 1.教师通过课件演示介绍平行线的画法
a
c
b
2.学生模仿教师画法并且说明理由
3.层层巩固,续探新知 议一议:
问题1:你还记得怎样用移动三角板的方法画两条平行线吗?你能用这种方法过已知直线AB 外一点P 画它的平行线吗?请说出其中的道理。
问题2:分别过点C 、D 画直线AB 的平行线EF 、GH , EF 与GH 有怎样的位置关系?
你有什么发现?与同伴交流.
结论:1.过直线外一点有且只有一条直线与这条直线平行。
2.平行于同一条直线的两条直线互相平行。
第五环节:巩固练习
1.如图,∠1 =∠2 =55°,∠3等于多少度?直线AB 、CD 平行吗? 说明你的理由。
变式1:如图,∠1=∠2=55°,∠3等于多少度?直线AB ,CD 平行吗?说明你的理由.
变式2:如图,∠1=55°,∠2=125°,∠3等于多少度?直线AB ,CD 平行吗?说明你的理由.
A
B
P
. 议一议 2
议一议1
E F
2 C
A
3 B 1
D
E F
2 C
A 3
B
1
D
E F
2
C
A
3
B
1
D
变式1
变式2
C
D
C
B
A 54
3
21 2.按要求完成下列各题 (1)如图, ∠1=70°,在给出的下列条件中,能判定AB ∥ CD 的条件的是( )
A.∠2= 70°
B. ∠3= 110°
C.∠4= 70° D .∠5= 70°
(2)如图,∠1=65°,∠B =65°,可以判断______∥_____,理由是_________________. (3)∠3=30°,当∠ABE =______时,就
能使 BE ∥CD ?
第六环节:拓展延伸,迁移运用
2.如图,在屋架上要加一根横梁DE ,已知∠B=32°,要使BC,则∠ADE 必须等于多少度?为什么? 第六环节:总结反思,布置作业 总结反思
问题1:本节课你认为自己解决的最好的问题是什么? 问题2:本节课你有哪些收获?
问题3:通过今天的学习,你想进一步探究的问题是什么? 布置作业
习题2.1 A 组1、2、3题 B 组 1、2题
3E
D
C
B
A
1
D
C
B
A
第1题图
第2题图 第3题图。
