自动控制原理标准实验报告
自动控制原理实验报告

自动控制原理实验报告一、实验目的。
本实验旨在通过实际操作,加深对自动控制原理的理解,掌握PID控制器的调节方法,并验证PID控制器的性能。
二、实验原理。
PID控制器是一种常见的控制器,它由比例环节(P)、积分环节(I)和微分环节(D)三部分组成。
比例环节的作用是根据偏差的大小来调节控制量的大小;积分环节的作用是根据偏差的累积值来调节控制量的大小;微分环节的作用是根据偏差的变化率来调节控制量的大小。
PID控制器通过这三个环节的协同作用,可以实现对被控对象的精确控制。
三、实验装置。
本次实验所使用的实验装置包括PID控制器、被控对象、传感器、执行机构等。
四、实验步骤。
1. 将PID控制器与被控对象连接好,并接通电源。
2. 调节PID控制器的参数,使其逐渐接近理想状态。
3. 对被控对象施加不同的输入信号,观察PID控制器对输出信号的调节情况。
4. 根据实验结果,对PID控制器的参数进行调整,以达到最佳控制效果。
五、实验结果与分析。
经过实验,我们发现当PID控制器的比例系数较大时,控制效果会更为迅速,但会引起超调;当积分系数较大时,可以有效消除稳态误差,但会引起响应速度变慢;当微分系数较大时,可以有效抑制超调,但会引起控制系统的抖动。
因此,在实际应用中,需要根据被控对象的特性和控制要求,合理调节PID控制器的参数。
六、实验总结。
通过本次实验,我们深刻理解了PID控制器的工作原理和调节方法,加深了对自动控制原理的认识。
同时,我们也意识到在实际应用中,需要根据具体情况对PID控制器的参数进行调整,以实现最佳的控制效果。
七、实验心得。
本次实验不仅让我们在理论知识的基础上得到了实践锻炼,更重要的是让我们意识到掌握自动控制原理是非常重要的。
只有通过实际操作,我们才能更好地理解和掌握知识,提高自己的实际动手能力和解决问题的能力。
八、参考文献。
[1] 《自动控制原理》,XXX,XXX出版社,2010年。
[2] 《PID控制器调节方法》,XXX,XXX期刊,2008年。
自动控制原理实验报告五个实验

自动控制原理实验专业班级姓名学号实验时间:2010.10—2010.11一、实验目的和要求:通过自动控制原理实验牢固地掌握《自动控制原理》课的基本分析方法和实验测试手段。
能应用运算放大器建立各种控制系统的数学模型,掌握系统校正的常用方法,掌握系统性能指标同系统结构和参数之间的基本关系。
通过大量实验,提高动手、动脑、理论结合实际的能力,提高从事数据采集与调试的能力,为构建系统打下坚实的基础。
二、实验仪器、设备(软、硬件)及仪器使用说明自动控制实验系统一套计算机(已安装虚拟测量软件---LABACT)一台椎体连接线 18根典型环节实验(一)、实验目的:1、了解相似性原理的基本概念。
2、掌握用运算放大器构成各种常用的典型环节的方法。
3、掌握各类典型环节的输入和输出时域关系及相应传递函数的表达形式,熟悉各典型环节的参数(K、T)。
4、学会时域法测量典型环节参数的方法。
(二)、实验内容:1、用运算放大器构成比例环节、惯性环节、积分环节、比例积分环节、比例微分环节和比例积分微分环节。
2、在阶跃输入信号作用下,记录各环节的输出波形,写出输入输出之间的时域数学关系。
3、在运算放大器上实现各环节的参数变化。
(三)、实验要求:1、仔细阅读自动控制实验装置布局图和计算机虚拟测量软件的使用说明书。
2、做好预习,根据实验内容中的原理图及相应参数,写出其传递函数的表达式,并计算各典型环节的时域输出响应和相应参数(K、T)。
3、分别画出各典型环节的理论波形。
5、输入阶跃信号,测量各典型环节的输入和输出波形及相关参数。
(四)、实验原理实验原理及实验设计:1.比例环节: Ui-Uo的时域响应理论波形:传递函数:比例系数:时域输出响应:2.惯性环节: Ui-Uo的时域响应理论波形:传递函数:比例系数:时常数:时域输出响应:3.积分环节: Ui-Uo的时域响应理论波形:传递函数:时常数:时域输出响应:4.比例积分环节: Ui-Uo的时域响应理论波形:传递函数:比例系数:时常数:时域输出响应:5.比例微分环节: Ui-Uo的时域响应理论波形:传递函数:比例系数:时常数:时域输出响应:6.比例积分微分环节: Ui-Uo的时域响应理论波形:传递函数:比例系数:时常数:时域输出响应:(五)、实验方法与步骤2、测量输入和输出波形图。
自动控制原理实验报告(一、二阶系统的电子模拟及时域响应的动态测试等三个实验)

自动控制原理实验报告作者姓名学科专业机械工程及自动化班级学号X X年10月27日实验一一、二阶系统的电子模拟及时域响应的动态测试一、实验目的1、了解一、二阶系统阶跃响应及其性能指标与系统参数之间的关系。
2、学习在电子模拟机上建立典型环节系统模型的方法。
3、学习阶跃响应的测试方法。
二、实验内容1、建立一阶系统的电子模型,观测并记录在不同时间常数T时的跃响应曲线,并测定其过渡过程时间TS。
2、建立二阶系统的电子模型,观测并记录在不同阻尼比ζ时的跃响应曲线,并测定其超调量σ%及过渡过程时间TS。
三、实验原理1、一阶系统阶跃响应性能指标的测试系统的传递函数为:()s()1C s KR s Ts φ=+()=模拟运算电路如下图:其中21R K R =,2T R C =;在实验中,始终保持21,R R =即1K =,通过调节2R 和C 的不同取值,使得T 的值分别为0.25,0.5,1。
记录实验数据,测量过度过程的性能指标,其中按照经验公式取3s t T=2、二阶系统阶跃响应性能指标的测试系统传递函数为:令ωn=1弧度/秒,则系统结构如下图:二阶系统的模拟电路图如下:在实验过程中,取22321,1R C R C ==,则442312R R C R ζ==,即4212R C ζ=;在实验当中取123121,1R R R M C C F μ===Ω==,通过调整4R 取不同的值,使得ζ分别为0.25,0.5,1;记录所测得的实验数据以及其性能指标,其中经验公式为3.5%100%,s net σζω=⨯=.四、试验设备:1、HHMN-1型电子模拟机一台。
2、PC机一台。
3、数字万用表一块。
4、导线若干。
五、实验步骤:1、熟悉电子模拟机的使用,将各运算放大器接成比例器,通电调零。
2、断开电源,按照实验说明书上的条件和要求,计算电阻和电容的取值,按照模拟线路图搭接线路,不用的运算放大器接成比例器。
3、将D/A输出端与系统输入端Ui连接,将A/D1与系统输出端UO连接(此处连接必须谨慎,不可接错)。
实验报告-自动控制原理
________________________________________________________________________________
〖分析பைடு நூலகம்:______________________________________________________________________
_______________________________________________________________________________
说明:特征参数为比例增益K和微分时间常数T。
1)R2=R1=100KΩ, C2=0.01µF,C1=1µF;特征参数实际值:K=______,T=________。
波形如下所示:
2)R2=R1=100KΩ, C2=0.01µF,C1=0.1µF;特征参数实际值:K= 1,T=0.01。
波形如下所示:
四、实验心得体会
实验报告
班级
姓名
学号
所属课程
《自动控制原理》
课时
2
实践环节
实验3控制系统的稳定性分析
地点
实字4#318
所需设备
电脑、工具箱
一、实验目的
1.观察系统的不稳定现象。
2.研究系统开环增益和时间常数对稳定性的影响
3.学习用MATLAB仿真软件对实验内容中的电路进行仿真。
2、实验步骤
_______________________________________________________________________________
自动控制实验报告(全)

自动控制原理实验报告册院系:班级:学号:姓名:目录实验五采样系统研究 (3)实验六状态反馈与状态观测器 (9)实验七非线性环节对系统动态过程的响应 (14)实验五 采样系统研究一、实验目的1. 了解信号的采样与恢复的原理及其过程,并验证香农定理。
2. 掌握采样系统的瞬态响应与极点分布的对应关系。
3. 掌握最少拍采样系统的设计步骤。
二、实验原理1. 采样:把连续信号转换成离散信号的过程叫采样。
2. 香农定理:如果选择的采样角频率s ω,满足max 2ωω≥s 条件(max ω为连续信号频谱的上限频率),那么经采样所获得的脉冲序列可以通过理想的低通滤波器无失真地恢复原连续信号。
3. 信号的复现:零阶保持器是将采样信号转换成连续信号的元件,是一个低通滤波器。
其传递函数:se Ts--14. 采样系统的极点分布对瞬态响应的影响:Z 平面内的极点分布在单位圆的不同位置,其对应的瞬态分量是不同的。
5. 最小拍无差系统:通常称一个采样周期为一拍,系统过渡过程结束的快慢常采用采样周期来表示,若系统能在最少的采样周期内达到对输入的完全跟踪,则称为最少拍误差系统。
对最小拍系统时间响应的要求是:对于某种典型输入,在各采样时刻上无稳态误差;瞬态响应最快,即过渡过程尽量早结束,其调整时间为有限个采样周期。
从上面的准则出发,确定一个数字控制器,使其满足最小拍无差系统。
三、实验内容1. 通过改变采频率s s s T 5.0,2.0,01.0=,观察在阶跃信号作用下的过渡过程。
被控对象模拟电路及系统结构分别如下图所示:图中,1)(/)()(==z E z U z D ,系统被控对象脉冲传递函数为:T T Ts e z e s s e Z z U z Y z G -----=⎥⎦⎤⎢⎣⎡+-==)1(4141)()()( 系统开环脉冲传递函数为:T T w e z e Z G z D z G ----===)1(4)()()(系统闭环脉冲传递函数为:)(1)()(z G z G z w w +=Φ在Z 平面内讨论,当采样周期T 变化时对系统稳定性的影响。
自控原理实验报告

一、实验目的1. 理解并掌握自动控制原理的基本概念和基本分析方法。
2. 掌握典型环节的数学模型及其在控制系统中的应用。
3. 熟悉控制系统的时间响应和频率响应分析方法。
4. 培养实验操作技能和数据处理能力。
二、实验原理自动控制原理是研究控制系统动态性能和稳定性的一门学科。
本实验主要涉及以下几个方面:1. 典型环节:比例环节、积分环节、微分环节、惯性环节等。
2. 控制系统:开环控制系统和闭环控制系统。
3. 时间响应:阶跃响应、斜坡响应、正弦响应等。
4. 频率响应:幅频特性、相频特性等。
三、实验内容1. 典型环节的阶跃响应- 比例环节- 积分环节- 比例积分环节- 比例微分环节- 比例积分微分环节2. 典型环节的频率响应- 幅频特性- 相频特性3. 二阶系统的阶跃响应- 上升时间- 调节时间- 超调量- 峰值时间4. 线性系统的稳态误差分析- 偶然误差- 稳态误差四、实验步骤1. 典型环节的阶跃响应- 搭建比例环节、积分环节、比例积分环节、比例微分环节、比例积分微分环节的实验电路。
- 使用示波器观察并记录各个环节的阶跃响应曲线。
- 分析并比较各个环节的阶跃响应曲线,得出结论。
2. 典型环节的频率响应- 搭建比例环节、积分环节、比例积分环节、比例微分环节、比例积分微分环节的实验电路。
- 使用频率响应分析仪测量各个环节的幅频特性和相频特性。
- 分析并比较各个环节的频率响应特性,得出结论。
3. 二阶系统的阶跃响应- 搭建二阶系统的实验电路。
- 使用示波器观察并记录二阶系统的阶跃响应曲线。
- 计算并分析二阶系统的上升时间、调节时间、超调量、峰值时间等性能指标。
4. 线性系统的稳态误差分析- 搭建线性系统的实验电路。
- 使用示波器观察并记录系统的稳态响应曲线。
- 计算并分析系统的稳态误差。
五、实验数据记录与分析1. 典型环节的阶跃响应- 比例环节:K=1,阶跃响应曲线如图1所示。
- 积分环节:K=1,阶跃响应曲线如图2所示。
自动控制原理实验报告根轨迹分析法

相关根轨迹知识
根轨迹的概念 根轨迹是开环系统某一参数从零变化到无穷大时, 闭环系 统特征根在 s 平面上变化的轨迹。 增设零、极点对根轨迹的影响 (1)增加开环零点对根轨迹的影响 第一,加入开环零点,改变渐近线的条数和渐近线的倾角; 第二,增加开环零点,相当于增加微分作用,使根轨迹向左 移动或弯曲,从而提高了系统的相对稳定性。系统阻尼增加,过 渡过程时间缩短; 第三,增加的开环零点越接近坐标原点,微分作用越强,系 统的相对稳定性越好。 (2)增加开环极点对根轨迹的影响 第一,加入开环极点,改变渐近线的条数和渐近线的倾角; 第二,增加开环极点,相当于增加积分作用,使根轨迹向右 移动或弯曲,从而降低了系统的相对稳定性。系统阻 尼减小,过渡过程时间加长;
-4-
五、实验过程
第一题 Gc=1:
Gc=s+5:
Gc=(s+2)(s+3):
-5-
Gc=1/(s+5):
第二题 第 一 步 : 在 MATLAB 的 命 令 窗 口 中 键 入 “ num=[1 3];den=[1 2 0];rlocus(num,den)” ,得图如下:
第二步: 第三步:
第三题 第一步:由已知条件 ts(△=2%)≤4s,超调量≤40%得
s ( s 2)
1 。作 s5
确定系统具有最大的超调量时的根轨迹增益,并作时域 仿真验证;(2)确定系统阶跃响应无超调时的根轨迹取值 范围,并作时域仿真验证 3、已知一单位反馈系统的开环传递函数为 ss 0.8试加入一 个串联超前校正控制(其中,|z|<|p|) ,使得闭环系统 的 ts(△=2%)≤4s,超调量≤40%。
-7-
本为图标的切线与 K 的横坐标的交点所得的纵坐标再减去延迟时间。 随后按图慢慢调整数值,一定要有耐心。 第二题中,Step 的属性不能忘改,否则横轴(0,1)处恒为 1。 分母出 S 前的系数必须小于 1(阻尼比小于 1) ,之后改改分子,调整 调整 S 前的系数并保持 S^2 前的系数不变 (因为分子分母都可约分) , 曲线即可得出。
自动控制原理实验报告
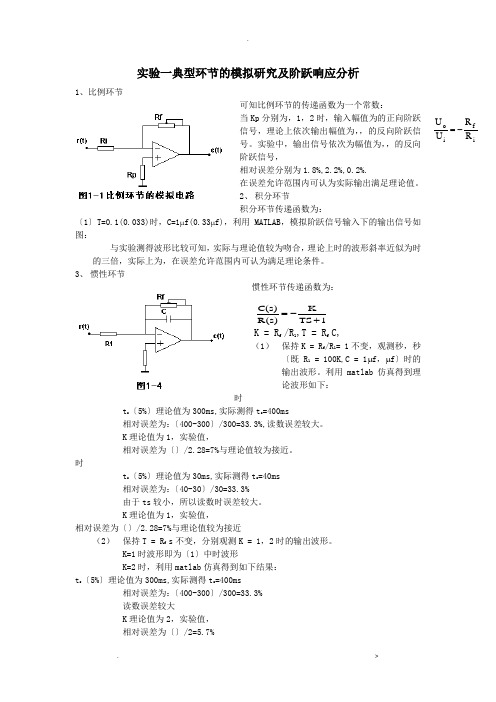
实验一典型环节的模拟研究及阶跃响应分析1、比例环节可知比例环节的传递函数为一个常数:当Kp 分别为,1,2时,输入幅值为的正向阶跃信号,理论上依次输出幅值为,,的反向阶跃信号。
实验中,输出信号依次为幅值为,,的反向阶跃信号,相对误差分别为1.8%,2.2%,0.2%.在误差允许范围内可认为实际输出满足理论值。
2、 积分环节积分环节传递函数为:〔1〕T=0.1(0.033)时,C=1μf(0.33μf),利用MATLAB ,模拟阶跃信号输入下的输出信号如图:与实验测得波形比较可知,实际与理论值较为吻合,理论上时的波形斜率近似为时的三倍,实际上为,在误差允许范围内可认为满足理论条件。
3、 惯性环节惯性环节传递函数为:K = R f /R 1,T = R f C,(1) 保持K = R f /R 1= 1不变,观测秒,秒〔既R 1 = 100K,C = 1μf ,μf 〕时的输出波形。
利用matlab 仿真得到理论波形如下:时t s 〔5%〕理论值为300ms,实际测得t s =400ms 相对误差为:〔400-300〕/300=33.3%,读数误差较大。
K 理论值为1,实验值,相对误差为〔〕/2.28=7%与理论值较为接近。
时t s 〔5%〕理论值为30ms,实际测得t s =40ms 相对误差为:〔40-30〕/30=33.3% 由于ts 较小,所以读数时误差较大。
K 理论值为1,实验值,相对误差为〔〕/2.28=7%与理论值较为接近(2) 保持T = R f s 不变,分别观测K = 1,2时的输出波形。
K=1时波形即为〔1〕中时波形K=2时,利用matlab 仿真得到如下结果:t s 〔5%〕理论值为300ms,实际测得t s =400ms相对误差为:〔400-300〕/300=33.3% 读数误差较大K 理论值为2,实验值, 相对误差为〔〕/2=5.7%if i o R RU U -=1TS K)s (R )s (C +-=与理论值较为接近。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电子科技大学自动化工程学院标准实验报告(实验)课程名称自动控制原理电子科技大学教务处制表电子科技大学实验报告学生姓名:音学学号:2014070902029 指导教师:实验地点:C2 507 实验时间:实验室名称:实验项目名称:系统认识与系统测试实验学时:4实验原理:实验原理图如下:被测试系统是指:由控制部分,电动机,反馈电位器组成的部分。
在该实验中要求:1 测试输入(外部、计算机)信号与输出角度信号之间的关系(曲线)。
2 测试反馈电位器的输出电压与角度信号之间的关系(曲线)。
实验电路图实验目的:1了解开环系统的工作状态,掌握闭环系统反馈极性的判别方法及其影响。
2 掌握系统相关数据的测试方法。
实验容:1 测试输入(外部、计算机)信号与输出角度信号之间的关系(曲线)。
2 测试反馈电位器的输出电压与角度信号之间的关系(曲线)。
实验器材:XZ-IIC型实验仪计算机自动控制原理实验仪万用表实验步骤:1 将系统接为单位负反馈系统,适当选取K值(约等于3)。
2 在-5V-+5V围间隔0.5V调整R的输出电压(用万用表监测),读出对应的输出角度值(可用计算机读出)。
3 断开系统输入,用手转动电机,在-150°-+150°间每隔10°选取一测试值用万用表监测反馈电位器的输出电压并作好记录。
(用计算机监测给定角度)实验数据及结果分析:实验机号20054409计算机的给定电压与系统输出角度的关系:给定电压-3-2.5-2-1.5-1-0.500.51 1.5 2.03 2.53输出角度-110-90.4-77.2-53.9-39.4-2201735.555.567.890.4107.6横轴-计算机的给定电压纵轴-系统输出角度系统输出角度与反馈电压间的关系:输出角度-150-140-130-120-110-100-90-80-70-60反馈电压-4.29-4-3.71-3.42-3.-2.801-2.51-2.29-1.94-1.658-50-40-30-20-1001020304050 -1.366-1.-0.8-0.52-0.23300.3460.6280.915 1.196 1.483607080901001101201301.772.052 2.338 2.628 2.9133.201 3.824.11横轴-系统输出角度纵轴-反馈电压外部输入电压与系统输出角度的关系:外部输入电压-3-2.5-2-1.5-1-0.500.51 1.52 2.53输出角度-115-86-76-48-36-2001636536885107横轴-外部输入电压纵轴-输出角度实验结论::报告评分:指导教师签字:实验项目名称:随动系统的时域特性分析实验学时:2实验原理:图21 实验系统方块图该实验主要研究系统前向增益K与系统反馈增益H的变化,对系统时域指标的影响。
由于本系统负载摆杆有一限位挡杆,不能连续转动,不宜做系统开环实验,故只做闭环实验。
1)系统前向增益K与系统性能的关系系统输入为单位阶跃信号(refi=1v),先固定反馈增益H为1,设置不同前向增益K=0.3,0.5, 1, 1.5 , 2 , 2.5 , 3(前向增益K首次设置为1),观察并记录其不同的输出响应曲线。
并注意观察对稳态控制精度的影响。
2)系统反馈增益H与系统性能的关系系统输入为单位阶跃信号(refi=1v),先固定前向增益K为1,设置不同反馈增益H=0.5, 1, 1.5 , 2 , 2.5 , 3(反馈增益H首次设置为1),观察记录其输出响应曲线。
并注意观察稳态值及对稳态控制精度的影响。
实验目的:了解系统频域分析方法。
分析并掌握前向增益和反馈增益对系统稳定性的影响,并观察对稳态控制精度的影响。
实验容:1设置不同前向增益K=0.3,0.5, 1, 1.5 , 2 , 2.5 , 3(前向增益K首次设置为1),观察并记录其不同的输出响应曲线2设置不同反馈增益H=0.5, 1, 1.5 , 2 , 2.5 , 3(反馈增益H首次设置为1),观察记录其输出响应曲线。
实验器材(设备、元器件):XZ-IIC型实验仪计算机(或自动控制原理实验仪、示波器、万用表)实验步骤:1.首先打开DSP.EXE文件,得到PC操作界面;2.接着点击菜单项“文件(F)”—“设置(S)”,或者第二个快捷键得到设置对话框“ESPSetting”,选择其运行模式为“控制模式”,点击“OK”按扭;3. 然后点击菜单项“实验(E)”—“2:随动系统的稳定性分析”,随之出现的“随动系统的稳定性分析”参数设置对话框(如图22)中有三个参数可供选择:参考输入REFI、前向增益K和反馈增益H,设置好参数后点击“OK”按扭;实验数据及结果分析:实验机号20054409k=0.3 h=1 稳态值:44.5 ,46.9 ,47.9k=0.5 h=1 稳态值:35.8 ,35.7 ,35.8k=1 h=1 稳态值:34.1,34.4,34.8k=1.5 h=1 稳态值:35.1 ,35.0 ,35.0k=2 h=1k=3 h=1h=0.5 k=1 稳态值:77.2 ,75.9 ,75.2h=1.5 k=1 稳态值:24.3 ,24.2 ,24.0h=2 k=1 稳态值:18.2 ,17.5 ,16.8h=2.5 k=1 稳态值:14.9 ,14.2 ,14.8h=3 k=1实验结论:1报告评分:指导教师签字:实验项目名称:随动系统的频率特性测试及分析实验学时:4实验原理:系统原理图如下,图25 实验原理简图固定反馈增益H为1,由先验知识可以知道,此随动系统具有低通特性,且频带较窄。
实验时:输入信号采用正弦信号,频率从0.1Hz到6.0Hz(不同的电机可能会有较小的差异)开始时每隔0.1Hz变化,2.0HZ后间隔可增大,选择适当的输入信号的幅值,只要计算输出与输入信号的幅值之比即可。
记录输入、输出信号幅值比及相应的频率,从而分析其幅频特性。
实验目的:1.了解系统频域分析方法;了解系统频域指标与时域指标的关系。
2.掌握系统频率特性的测试方法,进一步理解频率特性的物理意义;3.根据闭环幅频特性求出被测系统相应的开环传递函数。
实验容:1.记录在不同频率下系统的输入,输出数据。
2.作出闭环系统的幅频特图,并分析求得其相应的传递函数(等效为二阶系统)。
3.实验时应如何选择实验频率及频率间隔?实验器材(设备、元器件):XZ-IIC型实验仪计算机(或自动控制原理实验仪、示波器、信号发生器)。
实验步骤:1 首先打开DSP.EXE文件,得到PC操作界面;2 接着点击菜单项“文件(F)”—“设置(S)”,或者第二个快捷键得到设置对话框“ESP Setting”,选择其运行模式为“控制模式”,点击“OK”按扭;3 然后点击菜单项“实验(E)”—“4:随动系统的频率特性及分析”,随之出现的“随动系统的频率特性及分析”参数设置对话框(如图26)中有两个参数可供选择:正弦输入信号的幅值A和角频率w,选择好参数后点击“OK”按扭;图26 随动系统的频率特性及分析参数设置4 点击菜单项“文件(F )”—“开始(K )”或者第一个快捷键,开始实验;5 如需进行多次实验重复上述(3)、(4)步骤即可。
实验数据及结果分析:实验机号20054409输入电压=0.5sin(ωt) 与 输出角度间的关系:角频率 0.10.20.30.40.50.60.70.80.91817 161815 16 16.5 17.5 1615161715 1817 16.5 15.517输出角度平均值 16.516.5 16.5 16.5 16.5 16.5 16.5 16.5 16.5 频率 0.6281.256 1.8842.5123.143.7684.3965.5.6521 1.52 2.53 3.5 3.6 3.7 3.8 18 15 20 25 32 28 30 30 35 1515 15 20 1825 25 28.53016.5 15 17.5 22.5 25 26.5 27.5 29.25 32.5 6.289.42 12.56 15.7 18.84 21.98 22.608 23.236 23.8643.8 3.9 44.1 4.2 4.3 4.4 4.5 4.6 35 37 40 50 60 110 140 130 115 30 32 35 42 58 100 140 125 110 32.5 34.5 37.5 46 59 105 140 127.5 112.5 23.864 24.492 25.12 25.748 26.376 27.004 27.632 28.26 28.8884.7 4.8 4.9 55.5 6 7 8 100 80 75 65 50 35 20 15 95 75 65 60 40 25 15 10 97.5 77.5 70 62.5 45 30 17.5 12.5 29.516 30.144 30.772 31.4 34.54 37.68 43.96 50.24曲线图如下:由实验数据并结合实验二的结果可得: Amax=4; A(0)≈0.5; ωn ≈8 根据公式 Mr=Amax/A(0); ξ=22^111Mr -- 可求得ξ=0.0707所求二阶系统为 G(s)=6413.12^64++S S其对应的开环益传递函数为)13.1(64+S S报告评分:指导教师签字:实验项目名称:随动系统的PID 校正实验学时:2 实验原理:图27 实验系统结构简图该实验主要观察PID 校正网络各参数变化,对系统时域指标的影响,了解其作用规律。
所加校正网络为:ST ST K2111++T 1为微分环节时间常数 T 2为一阶积分环节时间常数观察校正网络参数变化对系统性能的影响。
实验中参数选取如下:k=1 ;T 2=0.0167 分别取T 1=0.01,0.05,0.1,1 k=1 ;T 1=0.1 分别取T 2=0.001,0.01,0.167,1.67 记录系统的输出曲线、超调量、调节时间Ts 。
实验目的:1.了解线性系统最常用的校法。
2.了解PID校正网络参数变化对系统的影响。
3.掌握校正的概念,了解其PID校正对系统时域指标的作用规律。
实验容:1.记录系统不同结构参数校正下对应的输出响应曲线;2.分析不同的校正参数对系统各项性能指标的影响;实验器材(设备、元器件):XZ-IIC型实验仪计算机(或自动控制原理实验仪、示波器、万用表)实验步骤:1.首先打开DSP.EXE文件,得到PC操作界面;2.接着点击菜单项“文件(F)”—“设置(S)”,或者第二个快捷键得到设置对话框“ESP Setting”,选择其运行模式为“控制模式”,点击“OK”按扭;3.然后点击菜单项“实验(E)”—“5:随动系统的校正”,随之出现的“随动系统的校正”参数设置对话框(如图28)中有四个参数可供选择:参考输入REFI和前向增益K,及两个校正环节参数T1和T2,设置好参数数值后点击“OK”按扭;图28 随动系统的校正参数设置对话框4.点击菜单项“文件(F)”—“开始(K)”或者第一个快捷键,从而开始实验;5. 如需进行多次实验,重复上述(3)、(4)步骤即可。
