线性规划案例
线性规划应用案例分析

线性规划应用案例分析线性规划是一种在数学和运营管理中常见的优化技术。
它涉及到在一组线性不等式约束下,最大化或最小化一个线性目标函数。
这种技术可以应用于许多不同的领域,包括供应链管理、资源分配、投资组合优化等。
本文将探讨几个线性规划应用案例,以展示其在实际问题中的应用和价值。
某制造公司需要计划生产三种产品,每种产品都需要不同的原材料和生产时间。
公司的目标是最大化利润,但同时也受到原材料限制、生产能力限制以及每种产品市场需求限制的约束。
通过使用线性规划,该公司能够找到最优的生产计划,即在满足所有约束条件下,最大化利润。
某物流公司需要计划将货物从多个产地运输到多个目的地。
公司的目标是最小化运输成本,但同时也受到运输能力、货物量和目的地需求的约束。
通过使用线性规划,该公司能够找到最优的运输方案,即在满足所有约束条件下,最小化运输成本。
某投资公司需要将其资金分配给多个不同的投资项目。
每个项目都有不同的预期回报率和风险水平。
公司的目标是最大化回报率,同时也要保证投资风险在可接受的范围内。
通过使用线性规划,该公司能够找到最优的投资组合,即在满足所有约束条件下,最大化回报率。
这些案例展示了线性规划在实践中的应用。
然而,线性规划的应用远不止这些,它还可以用于诸如资源分配、时间表制定、路线规划等问题。
线性规划是一种强大的工具,可以帮助决策者解决复杂的问题并找到最优解决方案。
线性规划是一种广泛应用的数学优化技术,适用于在多种资源限制下寻求最优解。
这种技术涉及到各种领域,包括工业、商业、运输、农业、金融等,目的是在给定条件下最大化或最小化线性目标函数。
下面我们将详细讨论线性规划的应用。
线性规划是一种求解最优化问题的数学方法。
它的基本思想是在一定的约束条件下,通过线性方程组的求解,求得目标函数的最优解。
这里的约束条件通常表现为一组线性不等式或等式,而目标函数则通常表示为变量的线性函数。
工业生产:在工业生产中,线性规划可以用于生产计划、物料调配、人力资源分配等方面。
线性规划应用案例

线性规划应用案例线性规划是一种在约束条件下寻找最优解的数学优化方法。
它在实际应用中广泛使用,涉及许多领域和行业。
本文将介绍两个典型的线性规划应用案例:运输问题和产能规划问题。
一、运输问题运输问题是线性规划最早发展起来的一个领域,它是指如何在各个供应地和需求地之间运输商品,以使得总运输成本最小。
一个典型的运输问题可以描述为:有m个供应地和n个需求地,每个供应地和需求地之间有一个固定的运输成本和一个固定的供应和需求量。
问题是如何确定每对供需地之间的运输量,以使得总运输成本最小。
举例来说,假设有三个供应地A、B、C,三个需求地X、Y、Z。
运输成本如下表所示:\begin{array}{ c c c c c c }&X&Y&Z&供应量\\A&10&12&8&100\\B&6&8&7&200\\C&9&10&11&300\\需求量&150&175&125&\\\end{array}求解此问题的线性规划模型如下:目标函数:minimize \quad Z = 10x_{11} + 12x_{12} + 8x_{13} + 6x_{21} + 8x_{22} + 7x_{23} + 9x_{31} + 10x_{32} + 11x_{33}约束条件:x_{11} + x_{12} + x_{13} \leq 100x_{21} + x_{22} + x_{23} \leq 200x_{31} + x_{32} + x_{33} \leq 300x_{11} + x_{21} + x_{31} \geq 150x_{12} + x_{22} + x_{32} \geq 175x_{13} + x_{23} + x_{33} \geq 125x_{ij} \geq 0, i = 1,2,3 \quad j = 1,2,3其中x_{ij}表示从供应地i到需求地j的运输量。
线性规划案例5

问题描述:
靠近某河流有两个化工厂(见图1-1),流经第一化工厂的河流流量为每天500万立方米,在两个工厂之间有一条流量为每天200万立方米的支流。
化工厂1每天排放含有某种有害物质的工业污水2万立方米,化工厂2每天排放的工业污水为1.4万立方米。
从化工厂1排出的污水流到化工厂2前,有20%可自然净化。
根据环保要求,河流中工业污水的含量应不大于0.2%。
因此两个工厂都需处理一部分工业污水。
化工厂1处理污水的成本是1000元/万立方米,化工厂2处理污水的成本是800元/万立方米。
问:
在满足环保要求的条件下,每厂各应处理多少工业污水,使两个工厂处理工业污水的总费用最小。
(一)线性规划

(一)线性规划
案例分析1
例1.10飞乐公司经营一个回收中心,专门混合三种废弃原材料C、P和h,以生产三
种不同规格的产品abd。
根据混合过程中各种材料的比例,产品可分为不同等级(见表
1.12)。
尽管混合不同等级的产品时允许一定的流动性,各等级产品中各种材料的最大值
和最小值必须符合下列质量标准的规定(最大值和最小值根据材料重量占该等级产品总重
量的比例确定)。
在两种更高级的产品中,一种特定材料的比例是固定的。
规格要求、单价、原材料数量、每天可供原材料单价见表1.12、表1.13。
工厂应该如何安排生产以实
现利润最大化?表1.12
产品名称abd
本规范要求原料C不小于50%,原料P不大于25%,原料C不小于25%,原料P不大于50%
不限
单价(元/公斤)
503525
回收中心可以定期从某些渠道收集所需的固体废物,从而获得处理能力,保持稳定运行。
表1.13显示了中心每天可以收集的每种材料的数量和单价。
表1.13
原料名称
cph
最大日供应量(千克)
10010060
单价(元/公斤)
652535
飞乐公司是格陵兰组织的全资子公司,格陵兰组织是一家专门从事环境相关业务的组织。
管理层决定在表1.12和表1.13所列的限制范围内,有效地向各级产品分配各种材料,以使每周的总利润最大化。
线性规划应用案例
市场营销应用案例一:媒体选择在媒体选择中应用线性规划的目的在于帮助市场营销经理将固定的广告预算分配到各种广告媒体上,可能的媒体包括报纸、杂志、电台、电视和直接邮件。
在这些媒体中应用线性规划,目的是要使宣传范围、频率和质量最大化。
对于应用中的约束条件通常源于对公司政策、合同要求及媒体的可用性。
在下面的应用中,我们将介绍如何应用线性规划这一工具来建立模型进而解决媒体选择问题。
REL发展公司正在私人湖边开发一个环湖社区。
湖边地带和住宅的主要市场是距离开发区100英里以内的所有中上收入的家庭。
REL公司已经聘请BP&J 来设计宣传活动。
考虑到可能的广告媒体和要覆盖的市场,BP&J建议将第一个月的广告局限于5种媒体。
在第一个月末,BP&J将依据本月的结果再次评估它的广告策略。
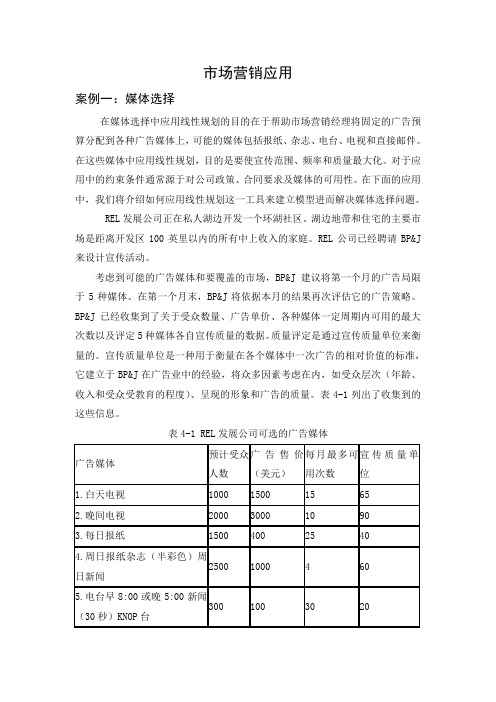
BP&J已经收集到了关于受众数量、广告单价、各种媒体一定周期内可用的最大次数以及评定5种媒体各自宣传质量的数据。
质量评定是通过宣传质量单位来衡量的。
宣传质量单位是一种用于衡量在各个媒体中一次广告的相对价值的标准,它建立于BP&J在广告业中的经验,将众多因素考虑在内,如受众层次(年龄、收入和受众受教育的程度)、呈现的形象和广告的质量。
表4-1列出了收集到的这些信息。
表4-1 REL发展公司可选的广告媒体REL发展公司提供给BP&J第一个月广告活动的预算是30000美元。
而且,REL公司对BP&J如何分配这些资金设置了如下限制:至少要使用10次电视广告,达到的受众至少要有50000人,并且电视广告的费用不得超过18000美元。
应当推荐何种广告媒体选择计划呢?案例二:市场调查公司开展市场营销调查以了解消费者个性特点、态度以及偏好。
专门提供此种信息的市场营销调查公司,经常为客户机构开展实际调查。
市场营销调查公司提供的典型服务包括涉及计划、开展市场调查、分析收集数据、提供总结报告和对客户提出意见。
线性规划 实际案例

线性规划是一种数学优化模型,用于解决在有一些约束条件下,如何使一个目标函数达到最优解的问题。
线性规划广泛应用于许多实际案例中,其中一些常见的案例如下:
1.生产规划:在生产过程中,企业可能需要在有限的生产资源和需求的限制下,决策
生产的数量、成本、产品组合等,以使生产效益最大化。
这就需要用到线性规划模
型来解决。
2.交通规划:在城市规划过程中,市政部门可能需要决策道路的建设、扩建、维护等,
以满足城市交通需求,并考虑到道路建设的成本和环境影响等因素。
这时候可以使
用线性规划模型来解决。
3.财务规划:在进行财务管理时,企业或个人可能需要在有限的资金和资产的限制下,
决策投资、储蓄、借贷等,以使财务效益最大化。
这时候可以使用线性规划模型来
解决。
4.供应链管理:在供应链管理过程中,企业可能需要决策采购、生产、运输、库存等
各个环节,以保证供应链的流畅运行并达到最优的效益。
这时候可以使用线性规划
模型来解决。
这些都是线性规划在实际案例中的应用,线性规划能够帮助企业和组织在有限的条件下,有效地规划和决策,并取得较好的效益。
线性规划案例(2)

饮食规划问题分析摘要本案例旨在解决一个与饮食规划相关的管理问题。
通过应用线性规划方法,我们将建立一个模型来帮助一个人根据营养需求和食材成本,制定最佳的饮食计划。
问题描述希望根据自己的营养需求,在预算限制下制定每日的饮食计划。
1确保摄入足够的蛋白质、碳水化合物、脂肪和维生素,并且希望最小化食材的总成本。
2已知不同食材的营养含量和价格,确定每种食材的最佳购买量,以满足所需的营养需求并节约成本。
模型的构建1. 变量定义:- Xi:购买的食材i的数量(单位:克)2. 目标函数:Minimize: ∑(i) Pi * Xi其中,Pi表示食材i的价格(单位:货币单位/克)3. 约束条件:蛋白质约束:∑(i) Ni * Xi ≥P碳水化合物约束:∑(i) Ci * Xi ≥C脂肪约束:∑(i) Fi * Xi ≥ F维生素约束:∑(i) Vi * Xi ≥V预算约束:∑(i) Pi * Xi ≤ B非负约束:Xi ≥0为了模拟数据,我们将使用一个简化的饮食规划问题来说明。
假设我们有以下食材和相关参数:4 变量确定鸡胸肉:价格0.3 货币单位/克,蛋白质含量20g/100g,碳水化合物含量0g/100g,脂肪含量2g/100g,维生素含量0g/100g米饭:价格0.1 货币单位/克,蛋白质含量7g/100g,碳水化合物含量28g/100g,脂肪含量0.3g/100g,维生素含量0g/100g鸡蛋:价格0.2 货币单位/克,蛋白质含量13g/100g,碳水化合物含量1.1g/100g,脂肪含量10g/100g,维生素含量0.2g/100g个人营养需求:蛋白质需求:每日需要摄入至少50g碳水化合物需求:每日需要摄入至少150g脂肪需求:每日需要摄入至少30g维生素需求:每日需要摄入至少0.5g预算限制:每日食材购买总成本不超过10 货币单位5建立线性规划模型(1)变量定义:X1:购买的鸡胸肉数量(单位:克)X2:购买的米饭数量(单位:克)X3:购买的鸡蛋数量(单位:克)(2)目标函数:Minimize: 0.3 * X1 + 0.1 * X2 + 0.2 * X3(3)约束条件:蛋白质约束:20/100 * X1 + 7/100 * X2 + 13/100 * X3 ≥50碳水化合物约束:0/100 * X1 + 28/100 * X2 + 1.1/100 * X3 ≥150脂肪约束:2/100 * X1 + 0.3/100 * X2 + 10/100 * X3 ≥30维生素约束:0/100 * X1 + 0/100 * X2 + 0.2/100 * X3 ≥0.5预算约束:0.3 * X1 + 0.1 * X2 + 0.2 * X3 ≤10非负约束:X1 ≥0, X2 ≥0, X3 ≥06 模型的spss求解与分析我们将根据上述数据和模型构建的线性规划模型来进行分析。
线性规划应用案例分析

通过整理,得到以下模型:
15
例6.(续)
目标函数:Max z = -15x11+25x12+15x13-30x21+10x22-40x31-10x33 约束条件: s.t. 0.5 x11-0.5 x12 -0.5 x13 ≥ 0 (原材料1不少于50%) -0.25x11+0.75x12 -0.25x13 ≤ 0 (原材料2不超过25%)
标准汽油
表 4
辛烷数
蒸汽压力(g/cm2)
库存量(L)
1
2 3 4
107.5
93.0 87.0 108.0
7.11×10-2
11.38 ×10-2 5.69×10-2 28.45 ×10-2 蒸汽压力(g/cm2)
380000
265200 408100 130100 产量需求
表 4 7
---
6
飞机汽油 辛烷数 1 2 不小于91 不小于100
0.75x21-0.25x22 -0.25x23 ≥ 0 (原材料1不少于25%)
-0.5 x21+0.5 x22 -0.5 x23 ≤ 0 (原材料2不超过50%)
x11+
x21 +
x31 ≤ 100
(供应量限制)
x12+
x13+
x22 +
x23 +
x32 ≤ 100
x33 ≤ 60
(供应量限制)
约束条件: 从第1个表中有:
x11≥0.5(x11+x12+x13)
x12≤0.25(x11+x12+x13)
x21≥0.25(x21+x22+x23) x22≤0.5(x21+x22+x23)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a 11 a 12
A
a 21
am
1
a 22 am2
为系数矩阵。
a 1 n
a 2n
a mn
第12页
规范形式
min c x
Ax b
s .t .
x
0
第13页
标准形 式
min c x
Ax b
s
.t
.
x
0
第14页
概
念
可行解(或可行点):满足所有约束条件的向量x (x1, x2, xn) 可行集(或可行域):所有的可行解的全体
第17页
不等式变等 式
a i1 x 1 a i 2 x 2 a in x n b i
a i1 x 1 a i 2 x 2 a in x n s i b i , s i 0
或
a i1 x 1 a i 2 x 2 a in x n b i
松弛变量
a i1 x 1 a i 2 x 2 a in x n s i b i , s i 0
❖目标转换
求最大可以等价成求负的最小
maxcx mi ncx
❖ 约束转换 ❖ 实例
第16页
约束转换 ❖等式变不等式
ai1 x1 ai2 x2 ainxn bi
ai1 x1 ai2 x2 ainxn bi ai1 x1 ai2 x2 ainxn bi
❖ 不等式变等式
❖ 不等式变不等式
可控因素:每天生产三种产品的数量,分别设为 x1 , x2 , x3 目标:每天的生产利润最大
利润函数 3x1 5x2 4x3 受制条件:
每天原料的需求量不超过可用量: 原料P1 : 2x1 3x2 1500 原料P2 :2 x2 4x3 800 原料P3 : 3 x1 2 x2 5 x3 2000
蕴含约束:数量非负xij 0;i 1,2, j 1,2,3,4
第9页
模 型
24
min
cij xij
i1 j1
xi1 xi2 xi3 xi4 ai ;i 1,2
s.t. x1j x2 j bj ; j 1,2,3,4
xij 0;i 1,2, j 1,2,3,4
第10页
一般形 式
注
释
x j ; j 1 , 2 ,..., n 为 待 定 的 决 策 变 量 , c (c1 ,c 2 , ,c n ) 为 价 值 向 量 , c j ; j 1 , 2 ,..., n 为 价 值 系 数 , b ( b 1 , b 2 ,..., b m ) 为 右 端 向 量 , 矩阵
蕴含约束:产量为非负数
x1 , x2 , x3 0
第5页
模 型
max 3 x1 5 x 2 4 x 3 2x1 3x2 1500
s.t. 2 x2 4 x3 800
3x1 2x2 5x3 2000 x1, x2 , x3 0
第6页
计算结 果
OBJECTIVE FUNCTION VALUE
2675.000
VARIABLE VALUE
REDUCED COST
X1
375.000000
0.000000
X2
250.000000
0.000000
X3
75.000000
0.000000
ROW SLACK OR SURPLUS DUAL PRICES
1)
0.000000
1.050000
2)
0.000000
第3页
生产计划问题
某工厂用三种原料生产三种产品,已知的条件如表 2.1.1所示,试制订总利润最大的生产计划
单位产品所需原 产品Q1 产品
料数量(公斤)
Q2
原料P1
23
原料P2
02
原料P3
32
单位产品的利润 3
5
(千元)
产品 Q3
原料可用量 (公斤/日)
0 1500
4
800
5 2000
4
第4页
问题分 析
剩余变量
x 1 a i 2 x 2 a in x n b i
a i1 x 1 a i 2 x 2 a in x n b i
或
a i1 x 1 a i 2 x 2 a in x n b i
a i1 x 1 a i 2 x 2 a in x n b i
目标函数
minz c1 x1 c2 x2 cn xn
ai1 x1 ai2 x2 ainxn bi ;i 1,2,...,p
s.t.axij1
x1
0;
ai2 x2 ainxn j 1,2,...,q
bi ;i
p 1,...,m
xj无 限 制; j 1,2,...,q
约束条件
第11页
运筹学课 件
运
决
筹
胜
帷
线性规划
千
幄
里
之
之
中
Linear
外
Programming
第1页
线性规 划
线性规划问题 可行区域与基本可行解 单纯形算法 初始可行解 对偶理论 灵敏度分析 计算软件 案例分析
第2页
线性规划问 题
线性规划实例
生产计划问题 运输问题
线性规划模型
一般形式 规范形式 标准形式 形式转换 概念
第19页
例2.1.3 把问题转化为标准形
0.625000
3)
0.000000
0.300000
第7页
运 输问 题
一个制造厂要把若干单位的产品从两个仓库Ai;i 1,2 发送到零售点Bj;j 1,2,3,4,仓库 Ai 能供应的产品数量为 ai;i 1,2,零售点Bj 所需的产品的数量为bj;j 1,2,3,4。 假设供给总量和需求总量相等,且已知从仓库 Ai 运一个单 位产品往Bj 的运价为cij 。问应如何组织运输才能使总运费 最Ai 小?
D {x Ax b, x 0}
最优解:在可行域中目标函数值最大(或最小)的可行解,最优解的全体 称为最优解集合 O {x Dc x c y,y D }
最优值:最优解的目标函数值
v c x, x O
第15页
模型转换
❖变量转换
令 自 由 变 量 xjx j x j , 其 中 x j,x j为 非 负 变 量
第8页
问题分析
可控因素:从仓库Ai 运往Bj 的产品数量 设为xij;i 1,2, j 1,2,3,4 目标:总运费最小
24
费用函数ci j xi j i1 j1
受控条件: 从仓库运出总量不超过可用总量,运入零售点的数量不低于需求量。 由于总供给量等于总需求量,所以都是等号。即
xi1 xi2 xi3 xi4 ai ;i 1,2 x1j x2j bj ; j 1,2,3,4
