运筹学线性规划案例

第五章运筹学线性规划在管理中的应用案例

第五章线性规划在管理中的应用某企业停止了生产一些已经不再获利的产品，这样就产生了一部分剩余生产力。

管理层考虑将这些剩余生产力用于新产品Ⅰ、Ⅱ、Ⅲ的生产。

可用的机器设备是限制新产品产量的主要因素，具体数据如下表：司的利润最大化。

1、判别问题的线性规划数学模型类型。

2、描述该问题要作出决策的目标、决策的限制条件以及决策的总绩效测度。

3、建立该问题的线性规划数学模型。

4、用线性规划求解模型进行求解。

5、对求得的结果进行灵敏度分析（分别对最优解、最优值、相差值、松驰/剩余量、对偶价格、目标函数变量系数和常数项的变化范围进行详细分析）。

6、若销售部门表示，新产品Ⅰ、Ⅱ生产多少就能销售多少，而产品Ⅲ最少销售18件，请重新完成本题的1-5。

解：1、本问题是资源分配型的线性规划数学模型。

2、该问题的决策目标是公司总的利润最大化，总利润为：+ +决策的限制条件：8x1+ 4x2+ 6x3≤500 铣床限制条件4x1+ 3x2≤350 车床限制条件3x1+ x3≤150 磨床限制条件即总绩效测试（目标函数）为：max z= + +3、本问题的线性规划数学模型max z= + +S．T．8x1+ 4x2+ 6x3≤5004x1+ 3x2≤3503x1+ x3≤150x1≥0、x2≥0、x3≥04、用Excel线性规划求解模板求解结果：最优解（50，25，0），最优值：30元。

5、灵敏度分析目标函数最优值为: 30变量最优解相差值x1 50 0x2 25 0x3 0 .083约束松弛/剩余变量对偶价格1 0 .052 75 03 0 .033目标函数系数范围:变量下限当前值上限x1 .4 .5 无上限x2 .1 .2 .25x3 无下限.25 .333常数项数范围:约束下限当前值上限1 400 500 6002 275 350 无上限3 150（1）最优生产方案：新产品Ⅰ生产50件、新产品Ⅱ生产25件、新产品Ⅲ不安排。

线性规划应用案例分析

线性规划应用案例分析线性规划是一种在数学和运营管理中常见的优化技术。

它涉及到在一组线性不等式约束下，最大化或最小化一个线性目标函数。

这种技术可以应用于许多不同的领域，包括供应链管理、资源分配、投资组合优化等。

本文将探讨几个线性规划应用案例，以展示其在实际问题中的应用和价值。

某制造公司需要计划生产三种产品，每种产品都需要不同的原材料和生产时间。

公司的目标是最大化利润，但同时也受到原材料限制、生产能力限制以及每种产品市场需求限制的约束。

通过使用线性规划，该公司能够找到最优的生产计划，即在满足所有约束条件下，最大化利润。

某物流公司需要计划将货物从多个产地运输到多个目的地。

公司的目标是最小化运输成本，但同时也受到运输能力、货物量和目的地需求的约束。

通过使用线性规划，该公司能够找到最优的运输方案，即在满足所有约束条件下，最小化运输成本。

某投资公司需要将其资金分配给多个不同的投资项目。

每个项目都有不同的预期回报率和风险水平。

公司的目标是最大化回报率，同时也要保证投资风险在可接受的范围内。

通过使用线性规划，该公司能够找到最优的投资组合，即在满足所有约束条件下，最大化回报率。

这些案例展示了线性规划在实践中的应用。

然而，线性规划的应用远不止这些，它还可以用于诸如资源分配、时间表制定、路线规划等问题。

线性规划是一种强大的工具，可以帮助决策者解决复杂的问题并找到最优解决方案。

线性规划是一种广泛应用的数学优化技术，适用于在多种资源限制下寻求最优解。

这种技术涉及到各种领域，包括工业、商业、运输、农业、金融等，目的是在给定条件下最大化或最小化线性目标函数。

下面我们将详细讨论线性规划的应用。

线性规划是一种求解最优化问题的数学方法。

它的基本思想是在一定的约束条件下，通过线性方程组的求解，求得目标函数的最优解。

这里的约束条件通常表现为一组线性不等式或等式，而目标函数则通常表示为变量的线性函数。

工业生产：在工业生产中，线性规划可以用于生产计划、物料调配、人力资源分配等方面。

管理运筹学-线性规划案例《食用调和油生产计划》

食用调和油生产计划案例1.问题的提出调和油又称高合油，它是根据使用需要，将两种以上经精炼的油脂（香味油除外）按比例调配制成的食用油。

其原料常选用精炼大豆油、菜籽油、花生油、葵花籽油、棉籽油等，还可配有精炼过的米糠油、玉米胚油、油茶籽油、红花籽油、小麦胚油等特种油酯。

调和油是是目前市场上比较常见的食用油类之一，以其油色澄清、透明，味道香醇可口，营养较纯种食用油更加丰富均衡，逐渐成为市场上的主流。

在调和油制作成本上，厂家可根据配方，以一定的加工工艺将几种油脂混合配制，取代了传统的纯种油脂，从而大大降低了成本和市面价格，更加迎合消费者追求“物美价廉”的消费心理，为企业带来了效益。

但在调和油的生产过程中，伴随着原料的采购、贮存、加工，都必然要有一定资金和设备上的投入。

当然，除了这些必须具备的，以为了保证调和油质量的程序外，如何降低相关原料和设备所受社会和市场因素引起的价格升高，原料过长时间保养带来的负经济利润，从而实现企业生产成本降低，成为生产厂家不得不考虑的一个问题。

2.问题分析在上述的问题中，存在着一个不争的事实。

价格会随着社会和市场的因素的影响而产生变化，其关系即为“经济函数”（通过广泛地进行市场调查并且采集足够的统计资料，分析确定各宗经济变量之间的函数关系）。

而大量低价采购原料又会带来贮存和保鲜方面成本的升高。

相应关系式可概括为：生产成本=原料价格*数量+贮存保鲜费用+加工费（加工成本+工人工资）+机器折损费+产品维护费用。

3.题目要求食油厂精炼两种类型的原料油——菜籽油和花生油，并将精制油混合得到一种调和油产品。

生产流程如下图所示：菜籽油原料油来自两个产地，而花生原料油来自另外三个产地。

据预测，这5种原料油菜籽油1採購菜籽油2採購花生油1採購花生油2採購花生油3採購的价格从一至六月分别为：表1 五种原料油的价格（元/吨）成品调和油售价为11000元/吨。

菜籽油和花生油需要由不同的生产线来精炼。

运筹学线性规划案例

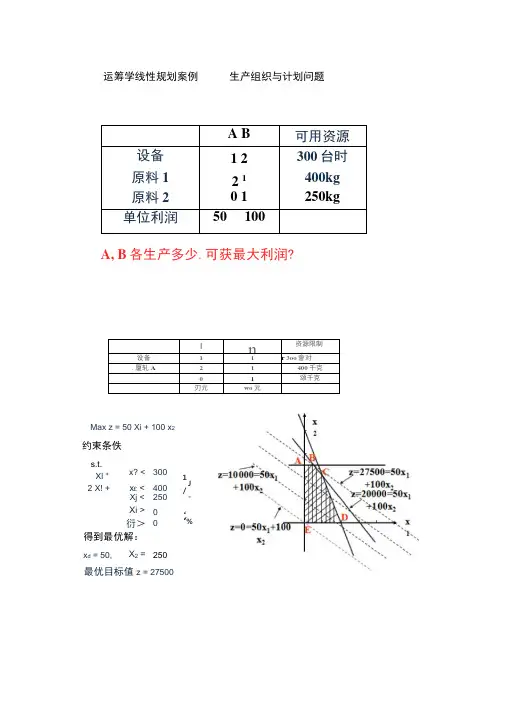
运筹学线性规划案例生产组织与计划问题A B可用资源设备原料1 原料2 1 2 2 1 0 1 300台时 400kg 250kg单位利润50 100A, B 各生产多少.可获最大利润?In 资源限制设备 1 1r 3oo 會对.厦轧A2 1 400千克 0 1 颂千克刃元wo 元Max z = 50 Xi + 100 x 2 s.t.Xl + x? < 300 2 X! + x £< 400 Xj < 250Xi > 0衍＞ 0得到最优解：x d = 50, X 2 = 250 约束条佚 J - %1/ i fI t / J A B 最优目标值z = 27500目标函数：Max z= 50x1 + 100x2 线性规划模型=约束条件：s.t. xi+ X2 < 3002 Xj+ 勺 W 400 x2 W 250X], x2 $ 0•建模过程1. 理解要解决的问题，了解解题的目标和条件；2. 定义决策变量(X】，X2,…，Xn),每一组值表示一个方案；3. 用决策变量的线性函数形式写出目标函数，确定最大化或最小化目标；4. 用一组决策变量的等式或不等式表示解决问题过程中必须遵循的约束条件• 一般形式目标函数：Max (Min) z = c】x^ + c? x?+…约束条件：s.t. dll X1 + 62X2+ …+dln Xn W ( =, D ) bl02］衍 + 022七+…+匕5石 W ( =?) b2dml X] + 如2 旳+ …+ dmn % W ( =?) b mXj , X],・••，X n 0(1) 分别取决策变量X】,X2为坐标向量建立直角坐标系。

在直角坐标系里，图上任意一点的坐标代表了决策变量的一组值，题中的每个约束条件都代表一个半平面。

(2) 对每个不等式(约束条件)，先取其等式在坐标系中作直线，然后确定不等式所决定的半平面。

运筹学应用案例

运筹学应用案例运筹学是一门应用数学，研究如何在资源有限的情况下，最优地组织和管理这些资源。

运筹学的应用范围非常广泛，涉及到各个领域。

以下是一个关于运筹学应用的实际案例。

某公司是一家制造业企业，主要生产产品A和产品B。

这家公司有两个生产车间和一个物流中心，每个车间配备了不同的生产设备。

公司的目标是最大化利润。

产品A在车间1中生产，车间1的生产设备可以在一小时内生产5个单位的产品A。

产品B在车间2中生产，车间2的生产设备可以在一小时内生产4个单位的产品B。

物流中心负责将产品A和产品B运送到市场，物流中心的运输能力为每小时20个单位。

同时，公司还面临一个资源的限制，即每天生产的产品A和产品B的总数不能超过400个单位。

另外，公司还有一个库存的限制，即每天生产的产品A和产品B的总数不能超过600个单位。

为了系统地解决这个问题，公司决定使用运筹学的方法进行决策。

首先，公司需要确定目标函数。

由于公司的目标是最大化利润，所以可以将目标函数定义为利润函数。

假设公司每个单位的产品A的利润为10美元，每个单位的产品B的利润为8美元。

那么公司的目标函数可以定义为：Z=10A+8B。

然后，公司需要确定约束条件。

根据资源的限制，可以得到以下约束条件：A≤5×小时数（车间1的生产能力）B≤4×小时数（车间2的生产能力）A+B≤400（每天生产的总数限制）A+B≤600（库存的限制）20A+20B≤600（物流中心的运输能力）接下来，公司需要确定变量的取值范围。

由于产量和库存数量为实数，所以可以将A和B的取值范围定义为非负实数。

最后，公司需要使用线性规划算法来求解最优解。

线性规划算法可以通过求解目标函数的最大值来找到最优解。

在这个案例中，可以使用单纯形法来求解最优解。

通过使用运筹学的方法，公司可以得到最优的生产和运输计划，以最大化利润。

对于公司而言，这个案例展示了如何在资源有限的情况下，通过合理的规划和管理，实现最优的生产和销售策略。

运筹学教学案例：Cases1(线性规划案例答案1)

2.1a) In this case, we have two decision variables: the number of Family Thrillseekers we should assemble and the number of Classy Cruisers we should assemble. We also have the following three constraints:1. The plant has a maximum of 48,000 labor hours.2. The plant has a maximum of 20,000 doors available.3. The number of Cruisers we should assemble must be less than or equal to 3,500.4567D Resources Used=SUMPRODUCT(B6:C6,Production)=SUMPRODUCT(B7:C7,Production)1011FTotal Prof it=SUMPRODUCT(UnitProf it,Production)Rachel’s plant should assemble 3,800 Thrillseekers and 2,400 Cruisers to obtain a maximum profit of $26,640,000.b) In part (a) above, we observed that the Cruiser demand constraint was not binding.Therefore, raising the demand for the Cruiser will not change the optimal solution.The marketing campaign should not be undertaken.c) The new value of the right-hand side of the labor constraint becomes 48,000 *1.25 = 60,000 labor hours. All formulas and Solver settings used in part (a)remain the same.Rachel’s plant should now assemble 3,250 Thrillseekers and 3,500 Cruisers to achieve a maximum profit of $30,600,000.d) Using overtime labor increases the profit by $30,600,000 – $26,640,000 =$3,960,000. Rachel should therefore be willing to pay at most $3,960,000 extra for overtime labor beyond regular time rates.e) The value of the right-hand side of the Cruiser demand constraint is 3,500 * 1.20= 4,200 cars. The value of the right-hand side of the labor hour constraint is48,000 * 1.25 = 60,000 hours. All formulas and Solver settings used in part (a) remain the same. Ignoring the costs of the advertising campaign and overtimelabor,Rachel’s plant should produce 3,000 Thrillseekers and 4,000 Cruisers for amaximum profit of $32,400,000. This profit excludes the costs of advertising and using overtime labor.f) The advertising campaign costs $500,000. In the solution to part (e) above, weused the maximum overtime labor available, and the maximum use of overtime labor costs $1,600,000. Thus, our solution in part (e) required an extra $500,000 + $1,600,000 = $2,100,000. We perform the following cost/benefit analysis:Profit in part (e): $32,400,000Advertising and overtime costs: $ 2,100,000$30,300,000We compare the $30,300,000 profit with the $26,640,000 profit obtained in part (a) and conclude that the decision to run the advertising campaign and use overtime labor is a very wise, profitable decision.g) Because we consider this question independently, the values of the right-handsides for the Cruiser demand constraint and the labor hour constraint are the same as those in part (a). We now change the profit for the Thrillseeker from $3,600 to $2,800 in the problem formulation. All formulas and Solver settings used in part(a) remain the same.Rachel’s plant should assemble 1,875 Thrillseekers and 3,500 Cruiser s to obtain a maximum profit of $24,150,000.h) Because we consider this question independently, the profit for the Thrillseekerremains the same as the profit specified in part (a). The labor hour constraint changes. Each Thrillseeker now requires 7.5 hours for assembly. All formulas and Solver settings used in part (a) remain the same.Rachel’s plant should assemble 1,500 Thrillseekers and 3,500 Cruisers for amaximum profit of $24,300,000.i) Because we consider this question independently, we use the problem formulationused in part (a). In this problem, however, the number of Cruisers assembled has to be strictly equal to the total demand. The formulas used in the problemformulation remain the same as those used in part (a).The new profit is $25,650,000, which is $26,640,000 – $25,650,000 = $990,000 less than the profit obtained in part (a). This decrease in profit is less than$2,000,000, so Rachel should meet the full demand for the Cruiser.j) We now combine the new considerations described in parts (f), (g), and (h). In part (f), we decided to use both the advertising campaign and the overtime labor.The advertising campaign raises the demand for the Cruiser to 4,200 sedans, and the overtime labor increases the labor hour capacity of the plant to 60,000 labor hours. In part (g), we decreased the profit generated by a Thrillseeker to $2,800.In part (h), we increased the time to assemble a Thrillseeker to 7.5 hours. The formulas and Solver settings used for this problem are the same as those used in part (a).Rachel’s plant should assemble 2,120 Thrillseekers and 4,200 Cruisers for amaximum profit of $28,616,000 – $2,100,000 = $26,516,000.。

运筹学线性规划灵敏度分析教学案例

2020/8/1
多个资源系数同时变动分析
例如，将 1 个小时的用工时间从3车间移到2车间，对总利润产生什么影响？
总利润增加 3650 - 3600 = 50 元，而目标系数未变，所以最优解肯定发生变化，
2020/8/1
百分之百法则
如果约束右端值同时变动，计算出每一变动占允许变动量的的百分比，如果所有的百分比之和不超过100%，那么，影子价格依然有效；否则，就无法确定。
2020/8/1
灵敏度分析的概念
LP 问题的系数有 aij、bi 、 cj，这些系数往往是估计值或预测值。
市场条件变化， cj 值就会变化；工艺条件和技术水平改变， aij 就变化； bi 是根据资源投入后的经济效果决定的一种选择，市场供应条件发生变化时，亦会改变。
提出问题:
• 当 LP 问题的系数有一个或几个发生变化时，已求得的最优解会有什么变化； • 这些系数在什么范围内变化时，LP 问题的最优解不会变化。
再改变参数
最优解变了
2020/8/1
那么，保持最优解不变的价值系数允许变化范围？
改变最优解的临界值是什么呢？
敏感性报告
在“规划求解结果”中选定“敏感性报告”。得到一个工作表：
2020/8/1
敏感性报告
最优解
目标函数系数
“递减成本” --- 表示目标函数的系数必须改变多少，才能使决策变量有正数解。 “允许的增量”和“允许的减量” --- 给出最优解不变的范围。如门的系数范围： 0≤c1≤750；窗的系数范围：c2≥200
2020/8/1
资源数量变化的分析
考虑只有一个右段值 bi 改变：2 车间可用工时由原来的 12小时增加到 13 小时，最优解如何变化呢？再变化呢？

运筹学案例分析

运筹学案例分析⼀.案例描述西兰物业公司承担了正⼤⾷品在全市92个零售店的⾁类、蛋品和蔬菜的运送业务，运送业务要求每天4点钟开始从总部发货，必须在7:30前送完货（不考虑空车返回时间）。

这92个零售点每天需要运送货物吨，其分布情况为：5千⽶以内为A区，有36个点，从总部到该区的时间为20分钟；10千⽶以内5千⽶以上的为B区，有26个点，从总部到该区的时间为40分钟；10千⽶以上的为C区，有30个点，从总部到该区的时间为60分钟；A区各点间的运送的时间为5分钟，B区各点间的运送时间为10分钟，C区各点间的运送时间为20分钟，A区到B区的运送时间为20分钟，B区到C 区的运送时间为20分钟，A区到C区的运送时间为40分钟。

每点卸货、验收时间为30分钟。

该公司准备购买规格为2吨的运送车辆，每车购价5万元。

请确定每天的运送⽅案，使投⼊的购买车辆总费⽤为最少。

⼆.案例中关键因素及其关系分析关键因素：1.⾸先针对⼀辆车的运送情况作具体分析，进⽽推⼴到多辆车的运送情况；2.根据案例中的关键点“零售点每天需要运送货物吨”及“规格为2吨的运送车辆”可知就⼀辆车运送⽽⾔，可承担4个零售点的货物量；3.根据案例中的“运送业务要求每天4点钟开始从总部发货，必须在7:30前送完货（不考虑空车返回时间）”可知每天货物运送的总时间为210分钟，超过该时间的运送⽅案即为不合理；4.如下表以套裁下料的⽅法列出所有可能的下料防案，再逐个分析。

三、模型构建1、决策变量设置设已穷举的12个⽅案中⽅案i所需的车辆数为决策变量Xi （i=1，2…12），即：⽅案1的运送车台数为X1；⽅案2的运送车台数为X2；⽅案3的运送车台数为X3；⽅案4的运送车台数为X4；⽅案5的运送车台数为X5；⽅案6的运送车台数为X6；⽅案7的运送车台数为X7；⽅案8的运送车台数为X8；⽅案9的运送车台数为X9；⽅案10的运送车台数为X10；⽅案11的运送车台数为X11；⽅案12的运送车台数为X12。

运筹学案例——QSB解线性规划应用题

问题描述：某电视机工厂生产四种型号的特用电视机：Ⅰ型——轻便黑白，Ⅱ型——正规黑白，Ⅲ型——轻便彩色，Ⅳ型——正规彩色。

各型号每台所需组装时间、调试时间、销售收入以及该厂组装调试能力如表2.47所示。

表2.47但现在显像管紧缺，每月最多只能进货180只，其中彩色显像管不超过100只。

令1x 、2x 、3x 、4x 一次表示各型号每月计划产量。

现工厂需拟定使目标总销售收入z 为最大的生产计划。

（1）写出该问题的数字模型，对于约束条件依下列次序：组装时间、调试时间、显像管数、彩色显像管数，并引入松弛变量，使之为等式。

（2）用单纯形法求解得终表如图2.48所示。

表2.48BCBXbB 1-4 6 8 10 0 0 0 01x 2x3x 4x5x6x7x8x0 8x50 -0.2 0 0.2 0 0.1 -0.50 1 6 2x 125 0.51 00 0.25 -0.750 0 0 7x5 0.3 0 0.2 0 -0.15 0.25 1 0 104x 500.2 0 0.8 1 -0.1 0.5 0 0jσ-10 -0.5-0.5试分别回答：（1）最优生产是什么？是否还有其他最优生产计划？为什么？（2）组装时间的影子价格是多少？（3）若外厂可调剂增加80小时的调试时间，但每小时需付0.4（百元），这样Ⅰ Ⅱ Ⅲ Ⅳ 工厂能力（h ）组装时间调试时间 8 2 10 2 12 4 15 5 2000 500 售价（百元）46810的调剂值得吗？能增加多少收入？（4）若Ⅰ型机售价由4（百元）增加到4.5（百元），最优计划会改变吗？如果增加到5.5（百元）呢？说明理由。

（5）写出本问题的对偶模型，并指出其最优解。

解：建立模型：由该问题，可建立如下模型：设Ⅰ型、Ⅱ型、Ⅲ型、Ⅳ型分别生产1x 台、2x 台、3x 台、4x 台，则可列出目标函数及线性约束条件： MaxZ=41x +62x +83x +104x81x +102x +123x +154x ≤200021x +22x +43x +54x ≤5001x +2x +3x +4x ≤1803x +4x ≤100ix ≥0 （i=1、2、3、4）将该模型进行标准化，则引入松弛变量5x 、6x 、7x 、8x ，则变为：MaxZ=41x +62x +83x +104x81x +102x +123x +154x +5x ≤200021x +22x +43x +54x +6x ≤5001x +2x +3x +4x +7x ≤1803x +4x +8x ≤100ix ≥0 （i=1、2、3、4、……7、8）第1步：启动子程序“Linear and Integer Programming ”。

运筹学分析方法及应用案例

运筹学分析方法及应用案例运筹学是一门研究如何通过使用数学、统计学和计算机科学等工具来解决决策问题的学科。

其应用领域广泛，包括生产、物流、供应链管理、交通网络优化、人员调度等。

运筹学分析方法可以通过建立数学模型，优化决策方案，并通过模拟和数据分析来评估方案的效果。

下面将介绍运筹学分析方法及其应用案例。

一种常见的运筹学分析方法是线性规划。

线性规划可以用于在给定约束条件下优化目标函数的值。

一个典型的应用是生产计划问题。

假设一个公司有多个产品和多个生产资源，线性规划可以帮助确定如何安排生产以最大化利润或最小化成本。

举个例子，一个公司生产产品A和产品B，有两个生产线和一定数量的原材料。

每生产一个单位的A需要2个单位的原材料和2个单位的生产时间，每生产一个单位的B需要1个单位的原材料和4个单位的生产时间。

每个生产线每天的工作时间为8个小时，而每天的原材料供应量为10个单位。

公司希望确定每个产品在每个生产线上的产量以最大化总利润。

我们可以建立一个线性规划模型来解决这个问题。

假设x1和x2分别代表在两个生产线上生产产品A的产量，y1和y2分别代表在两个生产线上生产产品B的产量。

目标函数为最大化总利润，可以表示为：Maximize 3x1 + 4x2 + 2y1 + 3y2约束条件包括每个生产线的工作时间和原材料供应量：2x1 + x2 ≤82x1 + 4x2 ≤82y1 + 3y2 ≤10并且x1、x2、y1、y2都不能小于零。

通过求解这个线性规划模型，我们可以得到最优解，即在每个生产线上生产产品A和产品B的最佳产量，从而实现最大利润。

除了线性规划，运筹学还有其他分析方法，如整数规划、动态规划、网络优化等。

这些方法可以应用于不同的决策问题，解决实际的运营和管理挑战。

另一个应用案例是供应链网络优化。

供应链管理面临的一个关键问题是如何确定最优的物流网络来实现成本最小化和服务水平最大化。

运筹学可以帮助优化供应链网络的设计和运作。

线性规划应用案例分析

通过整理，得到以下模型：
15
例6．（续）
目标函数：Max z = -15x11+25x12+15x13-30x21+10x22-40x31-10x33 约束条件： s.t. 0.5 x11-0.5 x12 -0.5 x13 ≥ 0 （原材料1不少于50%） -0.25x11+0.75x12 -0.25x13 ≤ 0 （原材料2不超过25%）
标准汽油
表 4
辛烷数
蒸汽压力(g/cm2)
库存量(L)
1
2 3 4
107.5
93.0 87.0 108.0
7.11×10-2
11.38 ×10-2 5.69×10-2 28.45 ×10-2 蒸汽压力(g/cm2)
380000
265200 408100 130100 产量需求
表 4 7
---
6
飞机汽油辛烷数 1 2 不小于91 不小于100
0.75x21-0.25x22 -0.25x23 ≥ 0 （原材料1不少于25%）
-0.5 x21+0.5 x22 -0.5 x23 ≤ 0 （原材料2不超过50%）
x11+
x21 +
x31 ≤ 100
(供应量限制）
x12+
x13+
x22 +
x23 +
x32 ≤ 100
x33 ≤ 60
(供应量限制）
约束条件：从第1个表中有：
x11≥0.5(x11+x12+x13)
x12≤0.25(x11+x12+x13)
x21≥0.25(x21+x22+x23) x22≤0.5(x21+x22+x23)

运筹学线性规划建模

线性规划建模应用举例
线性规划问题的三要素：决策变量线性目标函数线性约束条件
例 1．(下料问题) 现要做 100 套钢架，每套用长为 2.9m，2.1m 和 2.5m
的原钢各一根。已知原料长 7.4m，问应如何下料，使用的原材料最省。
解：套截方案，如表
下料数方案
(根)
1
长度 m
2.9
1
2.1
设备 Ⅰ
A1
5
A2
7
B1
6
B2
4
B3
7
原材料（元/件） 0.25
单价（元/件）
1.25
产品 Ⅱ
10 9 8 0.35 2.00
有效台使用费
Ⅲ
时用（元）
-
6000
300
12
10000 321
-
4000
250
11
7000
783
-
4000
200
0.50
2,80
目标函数：
maxZ (1.25 0.25)(x1 x2 ) (2.00 0.35)(x5 x6 ) (2.80 0.50)x7 300(5x1 10x5)/ 6000 321(7x2 9x6 12x7 )/ 10000 250 (6x3 8x5 8x6 ) / 4000 783 (4x4 11x7 ) / 7000 2007 (x1 x2 x3 x4 )/ 4000
格、各种设备有效台时以及满负荷操作时设备使用费如表示：
设备
产品
有效台时使用费用
ⅠⅡ
Ⅲ
（元）
A1
5 10
-
6000
300
A2
7
9
12

运筹学案例2 (3)

Automobile Alliance是一家大型的汽车制造公司。

他将产品分为三类：家用卡车、家用小型轿车以及家用中型和豪华轿车。

位于底特律和密执安交界处的一家工厂装配两种中型和豪华轿车。

第一种车型，Family Thrillseeker，是一种四门轿车，装有乙烯树脂座椅、塑料内饰、标准配置，省油性能出色。

购买这种车对于生活不是十分富裕的中产家庭来说是一个明智的选择。

每一辆Family Trillseeker为公司带来中等水平的3600美元的利润。

第二种车型，Classy Cruiser，是一种双门豪华车，配有真皮座椅、选装配置、木质内饰以及导航能力。

它定位于较高层次的中产阶级，每一辆Classy Cruiser 能够为公司带来5400美元的可观利润。

装配厂经理Rachel Rosencrantz目前正在为下一个月制定生产计划。

具体地说就是她要决定Family Thrilseeker和Classy Cruiser各需要生产多少能够使得公司的利润最大。

她知道工厂每个月有48000工时的生产能力，装配一辆Family Trillseeker需要他6个工时，一辆Classy Cruiser需要10.5工时。

由于工厂只是一个装配厂，装配这两种车所需的所有零件都不在厂里制造，而从密执安附近区域的其他工厂运来。

例如轮胎、转向轮、车窗、座椅以及车门都来自与不同的供应厂。

Rachel知道下一个月她只能从车门供应厂得到20000扇车门。

最近的一场罢工迫使这家供应厂停产了几天，下个月将无法完成生产计划。

Family Trillseeker和Classy Cruiser都是用相同的车门。

另外根据公司新近的对葛总车型的月需求预测，Classy Cruiser的产量限制在3500辆。

在装配厂生产能力范围内，Family Thrillseeker的生产没有限制。

（1）建立线性规划模型并求解，确定Family Trillseeker和Classy Cruiser各应当装配多少？（2）营销部得知他们可以花费500000美元进行一个广告活动，使得下个月对Classy Cruiser的需求增加20%。

运筹学线性规划

其次线性规划模型必须满足如下两个要求： ① 目标函数必须是决策变量的线性函数； ② 约束条件必须是含决策变量的线性等式或不等式。
运筹学建模步骤: 识别问题定义决策变量
建立约束条件建立目标函数
整理课件
2.2 线性规划模型的一般形式和标准形式
2.2.1 线性规划的一般模型
为了讨论一般的线性规划问题的求解。我们先给出线性规划模型的一般形式如下：
max(或min)z CX
n
s.t. j1
Pj x j
(或，或)b
X 0
其中
x1
a1j b1
Xx2,Cc1 c2 cn,Pj a2j,bb2
xn
amj bm
整理课件
用矩阵的记号可以将线性规划模型一般形式写成：
max(或min)z CX
AX (或，或)b s.t.X 0
其中 X, C, b 同上，而矩阵 A 是由各约束条件的系数（技术
养分
饲料
A
B
C
M
0.5
0.2
0.3
D
价格
0
300
N
0.1
0.3
0.4
0.2
200
每头日需 10
5
8
7
答案：设购买M饲料x1，N饲料x2
Min Z=300 x1 +200x2 0.5 x1 +0.1x2≥10
0.2x1 +0.3x2 ≥5
s.t.
0.3x1 +0.4x2 ≥8
0.2x2 ≥7
x1 , x2≥0 整理课件
x1 2 x2 5
s.t.
2
4
x1 x1
x2 4 3x2 9

运筹学中的线性规划理论与应用

运筹学中的线性规划理论与应用线性规划是运筹学中的一种重要工具，被广泛应用于经济、管理、工程等领域。

它的核心思想是通过建立数学模型，以线性目标函数和线性约束条件为基础，以最优化为目标，找到最佳的决策方案。

在本文中，我将讨论线性规划的基本概念和理论，并介绍其在实际应用中的案例。

一、线性规划的基本概念和理论线性规划主要研究如何分配有限资源以达到最优化的利益。

在线性规划中，决策变量、目标函数和约束条件是构建数学模型的三个基本要素。

1. 决策变量决策变量是指在问题中需要做决策的变量，通常表示为一个向量。

例如，在生产计划中，决策变量可以表示为不同产品的生产数量。

2. 目标函数目标函数是指在线性规划中需要最大化或最小化的目标指标。

目标函数通常是由决策变量线性组合而成的。

3. 约束条件约束条件是指在线性规划中限制决策变量取值范围的条件。

约束条件通常是由一系列线性不等式或等式组成的。

在线性规划问题中，通过将目标函数和约束条件转化为数学表达式，可以建立一个数学模型。

这个模型可以通过一系列数学方法求解，以达到最优化的目标。

二、线性规划在实际应用中的案例线性规划在现代管理和决策中有着广泛的应用。

以下是几个典型的案例。

1. 生产计划在生产计划中，线性规划可以用于确定不同产品的生产数量，以最大化利润或满足市场需求。

2. 配送问题在物流配送中，线性规划可以用于合理安排不同配送点的货物数量和时间，以最小化配送成本。

3. 投资组合在金融领域，线性规划可以用于确定不同投资项目的投资比例，以最大化收益或降低风险。

4. 网络流问题在网络建设中，线性规划可以用于确定网络中各节点之间的流量分配，以最大化网络传输效率。

这些案例只是线性规划在实际应用中的冰山一角。

在现代运筹学和管理科学中，线性规划以其简单、有效和灵活的特点，成为了决策分析的重要工具。

总结：线性规划是运筹学中的一种重要工具，通过建立数学模型，以线性目标函数和约束条件为基础，以最优化为目标，解决实际决策问题。

运筹学大m法例题详解

运筹学大m法例题详解一、标题解释大M法是运筹学中常用的一种优化方法，主要用于求解线性规划问题。

大M法是通过引入一个乘常数向量M，将原问题转化为标准型，从而更容易求解。

M中的每个元素M(i,j)称为大M元素，对应于原问题中约束条件中的右侧元素。

二、实例分析【例题1】求以下线性规划问题的最优解：Maxz=3x+4ys.t.x+y-6<=03x-y-3M(1,1)<=0x-y-M(2,2)<=0x,y>=0解：1.将目标函数和第一个约束条件转化为标准型：Maxz=3x+4y=3(M(1,1)+M(2,2))x+4(M(2,2)-M(1,1))y+6M(1,2)2.将第二个约束条件转化为标准型：3x-y-M(1,1)<=0(其中M(1,1)=M(2,2)+3*z')-y-M(2,2)<=0(其中z'为约束条件的等式右侧向量在第一个约束下的元素个数)将第二个约束中的-y变为-z*x+M(2,2)+z*y（此处需要乘上大M元素和系数z'），再将M进行转置。

注意在加M之前要处理一些元素（即上三角部分的元素和下三角部分非负的元素），这是因为在大M法中要求矩阵的对称部分必须是正定的。

处理完之后得到一个新的矩阵A和向量b。

3.对A和b进行求解，得到最优解x*和y*。

【例题2】求以下非线性规划问题的最优解：Minf(x,y)=x^2+y^2+x*ys.t.x+y-6<=0(这里假设目标函数中x和y的系数都是正数，即f(x,y)是凸函数)x>=0y>=0解：将目标函数转化为标准型：Minz=x^2+y^2*z'(z为权重系数)得$x=M^(-1)*(z\timesy-b')$$y=(6/y^2)-z\times(6/y^2)$，其中$M$为$\left\{\begin{matrix}\frac{1}{z_1}&\frac{6}{z_2}\\\frac{6}{z_1}&\frac{z_2}{y}\\\end{matrix}\right.$矩阵的逆矩阵，$b'$为约束条件的等式右侧向量在目标函数下标为$j$的元素的权重。

四个运筹学案例

1、年度配矿计划优化——线性规划j（单位：万吨）2 约束条件：包括三部分1）供给（资源）约束：x1 ≤70 x2≤7 x3≤17 x4≤23 x5≤3 x6≤9.5 x7≤1 x8≤15.4 x9≤ 2.7 x10≤7.6 x11≤13.5 x12≤2.7 x13≤1.2 x14≤7.22）品位约束3）非负约束： x j ≥ 0 j = 1,2,3, … ,143 目标函数：此题目要求“效益最佳”有一定的模糊性，由于配矿后的混合矿石将作为后面工序的原料而产生利润，故在初始阶段，可将目标函数选作配矿总量的极大化。

三、计算结果及分析1 计算结果利用单纯形法可得出该问题的最优解为：x1 = 31.121 x2 = 7 x3 = 17 x4 = 23 x5 = 3 x6 = 9.5 x7 = 1 x8 = 15.4 x9 = 2.7 x10 = 7.6 x11 = 13.5 x12 = 2.7 x13 = 1.2 x14 = 7.2 最优值：Z* = 141.921（万吨）2 分析与讨论1）计算结果是否可被该公司接受？——回答是否定因为：①在最优解中，除第1个采矿点有富裕外，其余13个采矿点的出矿量全部参与了配矿。

而矿点1在配矿以后尚有富余量 70 －31.12 ＝38.879 （万吨），但矿点1的矿石品位仅为37.16%，属贫矿。

②该公司花费了大量人力、物力、财力后，在矿点1生产的贫矿中却有近39万吨矿石被闲置，而且在大量积压的同时，还会对环境造成破坏，作为该公司的负责人或公司决策者是难以接受这样的生产方案的。

———原因何在？出路何在？2）解决问题的思路经过分析后可知：在矿石品位T Fe 及出矿量都不可变更的情况下，只能把注意力集中在混合矿石的品位T Fe 要求上。

——不难看出，降低T Fe 的值，可以使更多的低品位矿石参与配矿。

问题：T Fe 的值有可能降低吗？在降低T Fe 的值，使更多的贫矿入选的同时，会产生什么影响？——以上问题就属于运筹学的灵敏度分析（优化后分析）3）经调查，以及与现场操作人员、工程技术人员、管理人员学习、咨询，拟定了三个T Fe 的新值：44％、43％、42％3 变动参数之后再计算，结果如下表所示：∑==+++++++++++++14114131211109875432145.0502.04073.05692.05271.04022.0408.04834.05141.064996.04200.04700.0400.05125.03716.0j jx x x x x x x x x x x x x x x ∑==141max j jx zFe境的破坏，故不予以考虑。

运筹学线性规划案例

运筹学线性规划案例线性规划是运筹学中的一个重要分支，它主要研究如何利用数学模型来解决最优化问题。

在实际应用中，线性规划可以帮助企业做出最佳的决策，使资源得到最大化利用。

本文将通过一个实际案例来介绍线性规划的应用，以便读者更好地理解和掌握这一方法。

假设某公司生产两种产品A和B，它们分别需要机器加工和人工装配。

公司拥有的机器和人工资源分别为每周80小时和60人天。

产品A每单位需要机器加工2小时，人工装配3人天；产品B每单位需要机器加工3小时，人工装配2人天。

每单位产品A的利润为2000元，产品B的利润为3000元。

现在的问题是，如何安排生产计划，才能使得利润最大化呢？首先，我们可以将该问题建立成数学模型。

假设x1和x2分别表示生产产品A 和B的单位数，则该问题可以表示为：Max Z=2000x1+3000x2。

约束条件为：2x1+3x2≤80。

3x1+2x2≤60。

x1≥0，x2≥0。

接下来，我们可以通过线性规划的方法来求解最优解。

在这里，我们不妨使用单纯形法来进行求解。

首先，我们将约束条件转化成标准形式，得到：2x1+3x2+s1=80。

3x1+2x2+s2=60。

x1≥0，x2≥0。

然后，我们构造初始单纯形表，并进行单纯形法的迭代计算。

最终得到最优解为x1=20，x2=10，此时利润最大为80000元。

通过这个简单的案例，我们可以看到线性规划在实际中的应用。

通过建立数学模型和运用线性规划方法，我们可以很好地解决类似的最优化问题，使得资源得到最大化利用，从而帮助企业做出更加科学合理的决策。

总之，线性规划作为运筹学中的重要方法，具有广泛的应用前景。

通过不断地学习和实践，我们可以更好地掌握线性规划的原理和方法，为实际问题的解决提供更加科学的支持。

希望本文的案例能够帮助读者更好地理解线性规划的应用，从而在实际工作中能够更好地运用这一方法，取得更好的效果。

线性规划算法的应用案例

线性规划算法的应用案例线性规划是应用最广泛的数学优化方法之一，也是一种非常有效的运筹学技术。

它的基本思想是将问题建模成一组线性方程和线性不等式的组合，通过寻找最优解来实现目标最大化或最小化。

线性规划算法广泛应用于制造业、金融、物流和交通等领域，以下将介绍几个重要的应用案例。

1. 生产计划和调度线性规划算法可以用于制造业的生产计划和调度。

例如，在一家造纸厂中，有若干个可用的生产线、仓库和运输车辆，需要考虑原材料的成本、工人的人工费用、工厂的能耗费用以及运输的成本等因素，制定出最佳的生产计划和调度方案。

对于这类问题，可以将目标函数设置为生产成本最小化或产出效率最大化，约束条件包括原材料的库存量、生产线的容量和物流的时间窗口等。

通过使用线性规划算法，可以得到最佳的生产计划和调度方案，使得企业的生产效率和盈利能力得到提升。

2. 市场营销和广告投放线性规划算法可以帮助企业制定最佳的市场营销和广告投放方案。

例如，在一家快递公司中，需要制定如何调整价格策略、开拓市场份额、投放广告等方案，以达到最大化利润或最小化成本的目标。

对于这类问题，可以将目标函数设置为销售额最大化或成本最小化，约束条件包括市场份额的限制、广告投放预算的限制等。

通过使用线性规划算法，可以得到最佳的市场营销和广告投放方案，提高企业的营销效率和市场竞争力。

3. 交通运输和物流配送线性规划算法可以用于交通运输和物流配送领域。

例如，在一个物流中心中，需要规划配送路线和运输车辆的分配，以最小化交通堵塞和物流成本的影响。

对于这类问题，可以将目标函数设置为运输成本最小化或配送效率最大化，约束条件包括车辆数量的限制、货物配送时间的限制等。

通过使用线性规划算法，可以得到最佳的路线规划和车辆分配方案，提高企业的配送效率和物流运转效率。

4. 金融投资和风险管理线性规划算法可以用于金融投资和风险管理领域。

例如，在一个投资银行中，需要制定最佳的投资组合和股票交易策略，以最大化收益和降低风险。