矩形的性质与判定三
矩形的判定和性质
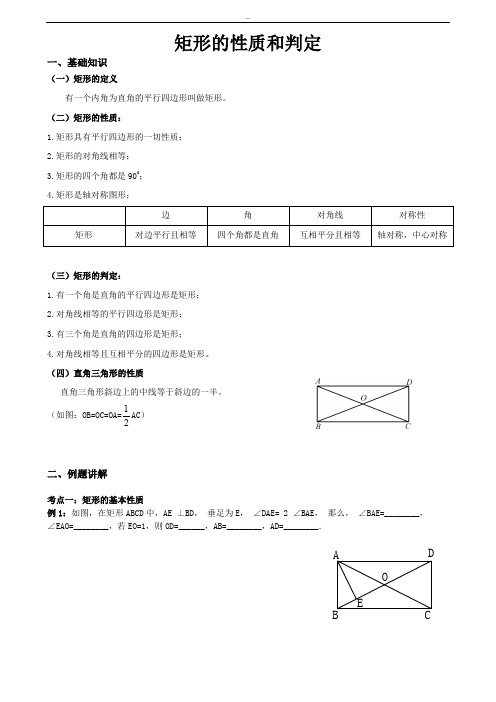
矩形的性质和判定一、基础知识(一)矩形的定义有一个内角为直角的平行四边形叫做矩形。
(二)矩形的性质:1.矩形具有平行四边形的一切性质;2.矩形的对角线相等;3.矩形的四个角都是900; 4.矩形是轴对称图形;边 角 对角线 对称性 矩形对边平行且相等四个角都是直角互相平分且相等轴对称,中心对称(三)矩形的判定:1.有一个角是直角的平行四边形是矩形;2.对角线相等的平行四边形是矩形;3.有三个角是直角的四边形是矩形;4.对角线相等且互相平分的四边形是矩形。
(四)直角三角形的性质直角三角形斜边上的中线等于斜边的一半。
(如图:OB=OC=OA=21AC )二、例题讲解考点一:矩形的基本性质例1:如图,在矩形ABCD 中,AE•⊥BD ,•垂足为E ,•∠DAE=•2•∠BAE ,•那么,•∠BAE=________, ∠EAO=________,若EO=1,则OD=______,AB=________,AD=________.AEDCBO练习 1:矩形ABCD中, ,对角线AC与BD相交于点O,BC的长为6,△OBC的周长是15,求矩形的对角线的长度.练习2:如图,在矩形ABCD中,CE⊥BD,E为垂足,∠DCE∶∠ECB=3∶1,求∠ACD.例2:如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线长是13cm,那么矩形的周长是多少?练习1:矩形ABCD中, ,对角线AC与BD相交于点O,已知矩形ABCD的面积是12cm2,AB=4cm,求矩形的对角线长。
例3:如图,在矩形ABCD 中,相邻两边AB 、BC 分别长15cm 和25cm ,内角∠BAD 的角平分线与边BC 交于点E .试求BE 与CE 的长度.练习1:如图,在矩形ABCD 中,E 是边AD 上的一点.试说明△BCE 的面积与矩形ABCD 的面积之间的关系.例4:(2009年广西钦州)已知:如图1,在矩形ABCD 中,AF =BE .求证:DE =CF ;ADCB 图1F E练习1:如图,矩形ABCD 中,E 为AD 中点,∠BEC 为直角,矩形ABCD 的周长是20,求AD 、AB 的长。
矩形的性质和判定

矩形的性质和判定【知识梳理】一、定义:有一个是直角的平行四边形是矩形。
二、性质:①矩形的四个角都是直角②矩形的对角线相互平分且相等③矩形既是中心对称图形又是轴对称图形,有两条对称轴④矩形的面积S=长×宽三、判定:①有一个角是直角的平行四边形是矩形;②有三个角是直角的四边形是矩形;③对角线相等的平行四边形是矩形;④对角线相等且互相平分的四边形是矩形。
四、矩形与平行四边形的区别与联系:①相同点1、两组对边分别平行2、两组对边分别相等3、两组对角分别相等4、对角线相互平分②区别1、有一个角是直角的平行四边形矩形2、对角线相互平分且相等【例题精讲】考点1 矩形的性质【例1】已知:如图,在矩形ABCD中,BE=CF,求证:AF=DE。
【例2】如图,在矩形ABCD 中,,E F 分别是,BC AD 上的点,且BE DF =。
求证:ABE ∆≌CDF ∆。
【例3】如图,矩形ABCD 的两条对角线相交于点O ,60AOB ∠=︒,2AB =,则矩形的对角线AC 的长是( ) A .2 B .4 C .23 D .43【变式1】下列性质中,矩形具有而平行四边形不一定具有的是( ) A 、对边相等 B 、对角相等 C 、对角线相等 D 、对边平行【变式2】矩形ABCD 的对角线AC 、BD 交于O ,如果ABC ∆的周长比AOB ∆的周长大10cm ,则边AD 的长是 。
【变式3】如图,矩形ABCD 沿AE 折叠,使D 点落在BC 边上的F 点处,如果60BAF ∠=︒,则DAE ∠= 。
FED CBA考点2 矩形的判定【例4】如图,在△ABC 中,AB=AC ,D 为BC 中点,四边形ABDE 是平行四边形。
求证:四边形ADCE 是矩形。
【例5】如图,在平行四边形ABCD 中,E 是CD 的中点,△ABE 是等边三角形,求证:四边形ABCD 是矩形。
ODC BAD EFCAB【变式6】如图11,已知E 是ABCD 中BC 边的中点,连接AE 并延长AE 交DC 的延长线于点F 。
矩形的性质和判定

矩形的性质和判定基础知识点1、矩形的性质和判定:定 义矩 形有一个内角是直角的平行四边形。
性质边对边平行,对边相等。
角 四个角相等,都是直角。
对角线互相平分,相等。
判定有一个角是直角的平行四边形是矩形。
有三个角是直角的四边形是矩形。
对角线相等的平行四边形是矩形。
2、在直角三角形中,斜边的中线等于斜边的一半。
3、矩形是轴对称图形,对称轴是对边中点的连线所在的直线。
例题剖析例1、 已知矩形ABCD 中,AB=2BC ,点E 在边DC 上,且AE=AB ,求∠EBC 的度数.【变式练习】矩形ABCD 中,AC 与BD 交于O 点,BE ⊥AC 于E ,CF ⊥BD 于F ,•求证:BE=CF .【变式练习】在矩形ABCD 中,AC ,BD 是对角线,过顶点C 作BD•的平行线与AB 的延长线相交于点E ,求证:△ACE 是等腰三角形.例2、折叠矩形ABCD 纸片,先折出折痕BD ,再折叠使A 落在对角线BD 上A ′位置上,折痕为DG ,AB=2,BC=1。
求AG 的长。
GA`DCBA【变式练习】如图,将矩形ABCD 沿对角线BD 折叠,使点C 落在F 的位置,BF 交AD 于E ,AD=8,AB=4,求△BED 的面积。
EDC BAF例3、在△ABC中,∠ABC=90°,BD是△ABC的中线,延长BD到E,•使DE=BD,连结AE,CE,求证:四边形ABCE是矩形.【变式练习】在△ABC中,AB=AC,D为BC中点,四边形ABDE是平行四边形。
求证:四边形ADCE是矩形。
例4、已知:如图,在△ABC中,AB=AC,点D为BC中点,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.求证:四边形ADCE为矩形.【变式练习】(2011•青岛)在▱ABCD中,E、F分别是AB、CD的中点,连接AF、CE.(1)求证:△BEC≌△DFA;(2)连接AC ,当CA=CB 时,判断四边形AECF 是什么特殊四边形?并证明你的结论【变式练习】E 为□ABCD 外一点,AE ⊥CE,BE ⊥DE ,求证:□ABCD 为矩形例5、□ABCD 中,AE 、BF 、CG 、DH 分别是各内角的平分线,E 、F 、G 、H 为它们的交点, 求证:四边形EFGH 的矩形。
矩形的判定和性质
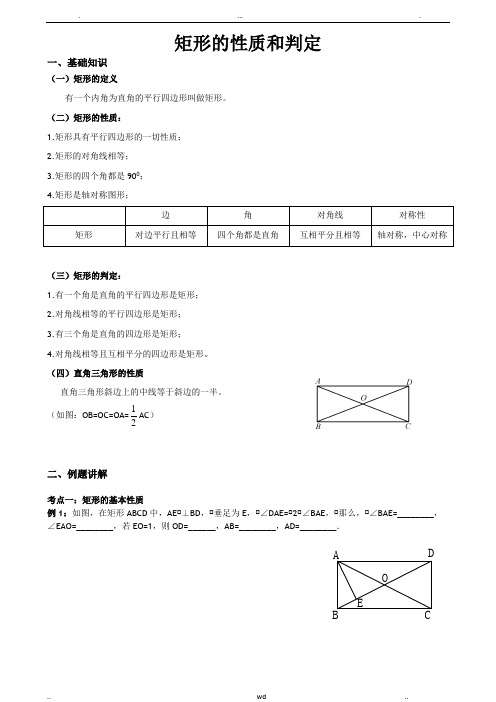
矩形的性质和判定一、基础知识(一)矩形的定义有一个内角为直角的平行四边形叫做矩形。
(二)矩形的性质:1.矩形具有平行四边形的一切性质;2.矩形的对角线相等;3.矩形的四个角都是900;4.矩形是轴对称图形;边 角 对角线 对称性 矩形对边平行且相等四个角都是直角互相平分且相等轴对称,中心对称(三)矩形的判定:1.有一个角是直角的平行四边形是矩形;2.对角线相等的平行四边形是矩形;3.有三个角是直角的四边形是矩形;4.对角线相等且互相平分的四边形是矩形。
(四)直角三角形的性质直角三角形斜边上的中线等于斜边的一半。
(如图:OB=OC=OA=21AC )二、例题讲解考点一:矩形的基本性质例1:如图,在矩形ABCD 中,AE•⊥BD ,•垂足为E ,•∠DAE=•2•∠BAE ,•那么,•∠BAE=________, ∠EAO=________,若EO=1,则OD=______,AB=________,AD=________.AEDCBO练习1:矩形ABCD中, ,对角线AC与BD相交于点O,BC的长为6,△OBC的周长是15,求矩形的对角线的长度.练习2:如图,在矩形ABCD中,CE⊥BD,E为垂足,∠DCE∶∠ECB=3∶1,求∠ACD.例2:如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线长是13cm,那么矩形的周长是多少?练习1:矩形ABCD中, ,对角线AC与BD相交于点O,已知矩形ABCD的面积是12cm2,AB=4cm,求矩形的对角线长。
例3:如图,在矩形ABCD中,相邻两边AB、BC分别长15cm和25cm,内角∠BAD的角平分线与边BC 交于点E.试求BE与CE的长度.练习1:如图,在矩形ABCD中,E是边AD上的一点.试说明△BCE的面积与矩形ABCD的面积之间的关系.例4:(2009年广西钦州)已知:如图1,在矩形ABCD中,AF=BE.求证:DE=CF;AD CB图1F E练习1:如图,矩形ABCD中,E为AD中点,∠BEC为直角,矩形ABCD的周长是20,求AD、AB的长。
1.2 矩形的性质与判定(三)

课堂小结
1、说说你的收获。 2、说说你的困惑。 3、说说你的方法。
独立 作业
▪课本: P 18-19页
▪预习: P20-21
1 、 2、 3
如图,四边形ABCD中,对角线相交于点O,E、F、G、 H分别是AD,BD, BC,AC的中点。 (1)求证:四边形EFGH是平行四边形; (2)当四边形ABCD满足一个什么条件时,四边形 EFGH是矩形?并证明你的结论。
复习导入
2. 如图2,四边形ABCD是平行四边形,添加一 有一个角是直角 个条件 ,可使它成为矩形。
例3 如图1-14,在矩形ABCD中,AD=6,对角线 AC与BD交于点O,AE⊥BD,垂足为E,ED=3BE. 求AE的长. 解∵ 四边形ABCD是矩形, 1 ∴AO=BO=DO= 2 BD (矩形的对角线相等且互相平分). ∠BAD=90°(矩形的四个都是直角). ∵ED=3BE,∴BE=OE. 又∵ AE⊥BD,∴AB=AO. ∴AB=AO=BO.
1 2
例4 如图1-15,在△ABC中,AB=AC,AD为∠BAC 的平分线,AN为△ABC外角∠CAM的平分线, CE⊥AN,垂足为E.求证:四边形ADCE是矩形. 证明:∵AD平分∠BAC,AN平分∠CAM, 1 ∴∠CAD= 1 ∠BAC,∠CAN= ∠CAM. 2 2 ∴∠DAE=∠CAD +∠CAN 1 = 2 (∠BAC+∠CAM) 1 = 2 ×180° =90°.
第一章 特殊平行四边形
1.2 矩形的性质
矩形对边平行且相等;
B
C
角
矩形的四个角都是直角;
矩形的对角线相等且平分;
对角线
直角三角形的性质定理:
直角三角形斜边上的中线等于斜边的一半.
1.2矩形的性质与判定第3课时(教案)

在上完这节关于矩形的性质与判定的课程后,我对自己教学过程中的优点和不足之处进行了一些思考。首先,我觉得在引入新课的部分,通过提问学生日常生活中的例子,成功引起了他们的兴趣,这有助于提高学生们在课堂上的参与度。然而,我也发现有些学生在理解矩形判定方法时遇到了困难,这让我意识到需要针对这部分内容进行更深入的解释和练习。
3.重点难点解析:在讲授过程中,我会特别强调矩形的性质和判定方法这两个重点。对于难点部分,如矩形的证明和判定方法的选择,我会通过举例和比较来帮助大家理解。
(三)实践活动(用时10分钟)
1.分组讨论:学生们将分成若干小组,每组讨论一个与矩形相关的实际问题,如矩形的桌面如何计算面积。
2.实验操作:为了加深理解,我们将进行一个简单的实验操作,如用直尺和量角器测量矩形物体的边长和角度,验证矩形的性质。
(二)新课讲授(用时10分钟)
1.理论介绍:首先,我们要了解矩形的基本概念。矩形是一种特殊的平行四边形,具有对边平行且相等,对角相等,四个角都是直角的特点。它是平面几何中非常重要的一种图形,广泛应用于日常生活和建筑等领域。
2.案例分析:接下来,我们来看一个具体的案例。通过分析矩形桌面,了解矩形的性质如何帮助我们计算桌面的面积和周长。
在理论介绍环节,我尝试用简洁明了的语言阐述矩形的概念和性质,并通过案例进行分析,使学生能够更好地理解矩形在实际中的应用。但在讲授过程中,我发现自己可能过于注重性质的记忆,而忽略了让学生通过实际操作来感受这些性质。在未来的教学中,我打算增加更多动手操作的环节,让学生在实践中学习和理解。
实践活动的设计原本是为了让学生们将理论知识应用到实际中,但在执行过程中,我发现学生们的讨论并不充分,可能是因为我对讨论主题的引导不够明确。在接下来的课程中,我会尝试提供更具指导性的问题,帮助学生更深入地进行讨论。
矩形的定义性质与判定

矩形的定义性质与判定
1.矩形的定义:有一个角是直角的平行四边形叫做矩形.
2.矩形的性质
矩形是特殊的平行四边形,它具有平行四边形的所有性质,•还具有自己独特的性质:
①边的性质:对边平行且相等.
②角的性质:四个角都是直角.
③对角线性质:对角线互相平分且相等.
④对称性:矩形是中心对称图形,也是轴对称图形.
直角三角形斜边上的中线等于斜边的一半.
直角三角形中,30°角所对的直角边等于斜边的一半.
3.矩形的判定
判定①:有一个角是直角的平行四边形是矩形.
判定②:对角线相等的平行四边形是矩形.
判定③:有三个角是直角的四边形是矩形.。
矩形的性质与判定(第3课时)

二.课堂检测:
1.下列关于矩形的说法中正确的是:()
A.矩形的对角线互相垂直平分
B.矩形的对角线相等且互相平分
C.对角线相等的四边形是矩形
D.对角线互相平分的四边形是矩形
2.矩形具有而菱形不具有的性质是()
A.两组对边分别平行B.对角线相等
C.对角线互相平分D。两组对角分别相等
3.课本18页习题1.6的第一题
南大里初中初三学案(1课时)
执教者
学科
学习内容
时间
4.课本19页习题ห้องสมุดไป่ตู้.6的第3题。
柴江丽
数学
矩形的判定与性质(第3课时)
2015.09.11
【学习目标】:1.理解矩形的定义,掌握矩形的性质与判定。(重点)
2.能运用矩形的性质和判定进行简单的计算与证明.(难点)。
【学习过程】::
一.复习旧知:矩形有哪些性质?(学生回答)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.2矩形的性质与判定(3)
学习目标:
1.对矩形的性质与判定定理进行巩固应用。
2.提升学生应用能力和证明能力。
3.重点性质定理和判定定理的正确使用。
学习内容:
一、知识梳理
1.矩形的定义:
2. 矩形的性质: 边: 角: 对角线:
对称性:
3. 矩形的判定:
4.如图1,矩形ABCD 的两条对角线相交于点O ,已知∠AOD=
120°,AB=2.5cm ,则∠DAO= ,AC= cm ,
ABCD S 矩形_______。
5. 如图2,四边形ABCD 是平行四边形,添加一个条
件 ,可使它成为矩形。
二、典例分析:
例1. 如图1-14,在矩形ABCD 中,AD=6,对角线AC
与BD 交于点O ,AE ⊥BD ,垂足为E ,ED=3BE.求AE 的长.
变式:如图,在矩形ABCD中,对角线AC与BD交于点O,
过A点做BD的垂线,垂足为E,∠EAD=3∠BAE.求∠EAO
的度数
例2 如图1-15,在△ABC中,AB=AC,AD为∠BAC的平分线,AN为△ABC外角∠CAM的平分线,CE⊥AN,垂足为E.求证:四边形ADCE是矩形.
证明:
三、拓展延伸
在例题2中,若连接DE,交AC于点F(如图1-16)
(1)试判断四边形ABDE的形状,并证明你的结论. (2)线段DF与AB有怎样的关系?请证明你的结论.
四、巩固练习:
1.已知:如图,四边形ABCD是由两个全等的等边三角
形ABD和CBD组成,M、N分别是BC和AD的中点.
求证:四边形BMDN是矩形.
2.在矩形ABCD中,对角线AC与BD交于点O,∠ACB=300,BD=4. 求矩形ABCD 的面积。
3.在△ABC中,AB=AC,D为BC中点,四边形ABDE
是平行四边形。
求证:四边形ADCE是矩形。
五、课堂小结:
说说你的收获、困惑。
六、当堂检测:
1.矩形的面积是60,一边长为5,则他的一条对角线长为。
2.若一个直角三角形的两条直角边分别为5和12.则斜边上的中线等于
3.矩形的一条对角线长为8cm,两条对角线的一个夹角为1200,则矩形的面积为,矩形的周长为
4.矩形的周长为14cm,对角线长为5cm,则它的面积为
5.(提高题)在矩形ABCD中,AB=3,AD=4,P是AD上不
与A和D 重合的一个懂点,过点P分别做AC和BD的垂
线,垂足为E、F。
求PE+PF的值。
七:布置作业:必做同步P12 1.2.3.4.
以下选做:P13 5.6
如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别
是AD,BD, BC,AC的中点。
(1)求证:四边形EFGH是平行四边形;
(2)当四边形ABCD满足一个什么条件时,四边形EFGH是菱形?并证明你的结论。
课后反思:
1.灵活处理教材,在精不在多
对于本节课的知识,不能机械地照搬教材内容,应该视各班学生情况而定,对教材内容进行再加工,灵活运用,使教材内容得到升华。
也不应加大习题量,题目在精不在多,扎实的讲解和学习比大量练习要有效果的多。
把关注学生能力的培养提到首位,达到本节课所要完成的真正目标。
2.分层次教学
对于不同层次的学生,在课堂上的要求要有所不同。
在同一题目中,通过一题多问或者一题多解等形式,可以使优生有所突破,也可以让学困生受到关注,获得解题的成就感,这就对我们的备课和选题提出了更高的要求。
3.充分给学生以时间
本课时,是综合运用的一节课,应给予学生充分的时间和空间展示自己,不仅有利于提高学生的积极性,更有利于教师发现学生的独到见解和新思维、新想法,同时还能让教师发现学生存在的问题,这对于课堂教学是非常有利的。
