矩形的性质与判定练习题

合集下载

(完整版)矩形的性质和判定

矩形的性质和判定一．填空题（共12小题）1．如图，矩形ABCD中，∠ABC的平分线交AD边于点E，点F是CD的中点，连接EF．若AB=8，且EF平分∠BED，则AD的长为．题1 题3 题42．若矩形的一条对角线与一边的夹角是40°，则两条对角线相交所成的锐角是．3．如图，在矩形ABCD中，AB=，E是BC的中点，AE⊥BD于点F，则CF的长是．4．如图，在矩形ABCD中，M为BC边上一点，连接AM，过点D作DE⊥AM，垂足为E．若DE=DC=1，AE=2EM，则BM的长为．5．如图，在矩形ABCD中，∠ABC的平分线交AD于点E，连接CE．若BC=7，AE=4，则CE= ．题5 题6 题76．如图，在矩形ABCD中，对角线AC、BD相交于点O，点E、F分别是AO、AD 的中点，若AB=6cm，BC=8cm，则EF= cm．7．如图，连接四边形ABCD各边中点，得到四边形EFGH，还要添加条件，才能保证四边形EFGH是矩形．8．如图，在四边形ABCD中，对角线AC、BD相交于点O，且AO=CO，BO=DO，要使四边形ABCD为矩形，则需添加的条件为（填一个即可）．题8 题11 题129．已知四边形ABCD为平行四边形，要使得四边形ABCD为矩形，则可以添加一个条件为．10．木匠做一个矩形木框，长为80cm，宽为60cm，对角线的长为100cm，则这个木框（填“合格”或“不合格”）11．如图，在四边形ABCD中，已知AB∥DC，AB=DC，在不添加任何辅助线的情况下，请补充一个条件，使四边形ABCD成为矩形，这个条件是．12．如图，在平行四边形ABCD中，延长AD到点E，使DE=AD，连接EB，EC，DB 请你添加一个条件，使四边形DBCE是矩形．二．解答题（共6小题）13．如图，在▱ABCD中，∠BAD的平分线交CD于点E，交BC的延长线于点F，连接BE，∠F=45°．（1）求证：四边形ABCD是矩形；（2）若AB=14，DE=8，求sin∠AEB的值．14．如图，AD是等腰△ABC底边BC上的高．点O是AC中点，延长DO到E，使OE=OD，连接AE，CE．（1）求证：四边形ADCE的是矩形；（2）若AB=17，BC=16，求四边形ADCE的面积．15．如图，四边形ABCD中，AB∥DC，∠B=90°，F为DC上一点，且FC=AB，E 为AD上一点，EC交AF于点G．（1）求证：四边形ABCF是矩形；（2）若EA=EG，求证：ED=EC．16．如图，在▱ABCD中，AE⊥BC于点E点，延长BC至F点使CF=BE，连接AF，DE，DF．（1）求证：四边形AEFD是矩形；（2）若AB=6，DE=8，BF=10，求AE的长．17．平行四边形ABCD中，过点D作DE⊥AB于点E，点F在CD上，CF=AE，连接BF，AF．（1）求证：四边形BFDE是矩形；（2）若AF平分∠BAD，且AE=3，DE=4，求矩形BFDE的面积．矩形的性质和判定解析一．填空题（共12小题）1．如图，矩形ABCD中，∠ABC的平分线交AD边于点E，点F是CD的中点，连接EF．若AB=8，且EF平分∠BED，则AD的长为12 ．【分析】根据两直线平行，内错角相等求出∠AEB=∠EBC，再求出∠ABE=∠EBC，根据等角对等边可得AE=AB，然后根据AD=AE+ED代入数据计算即可得解．【解答】解：∵矩形ABCD中，∴AD∥BC，∴∠AEB=∠EBC，∵∠ABC的平分线交AD边于点E，∴∠ABE=∠EBC，∴∠ABE=∠AEB，∴AB=AE=8，同理得出ED=DF=DC=4，∴AD=AE+ED=8+4=12，故答案为：12．2．若矩形的一条对角线与一边的夹角是40°，则两条对角线相交所成的锐角是80°．【分析】因为两条对角线相交所成的锐角只有一个，直接应用三角形的内角和定理求解即可．【解答】解：由矩形的对角线相等且互相平分，所构成的三角形为等腰三角形，利用等边对等角，所以另一底角为40°，两条对角线相交所成的钝角为：180°﹣40°×2=100°故它们所成锐角为：180°﹣100°=80°．故答案为80．3．如图，在矩形ABCD中，AB=，E是BC的中点，AE⊥BD于点F，则CF的长是．【分析】根据四边形ABCD是矩形，得到∠ABE=∠BAD=90°，根据余角的性质得到∠BAE=∠ADB，根据相似三角形的性质得到BE=1，求得BC=2，根据勾股定理得到AE==，BD==，根据三角形的面积公式得到BF==，过F作FG⊥BC于G，根据相似三角形的性质得到CG=，根据勾股定理即可得到结论．【解答】解：∵四边形ABCD是矩形，∴∠ABE=∠BAD=90°，∵AE⊥BD，∴∠AFB=90°，∴∠BAF+∠ABD=∠ABD+∠ADB=90°，∴∠BAE=∠ADB，∴△ABE∽△ADB，∴，∵E是BC的中点，∴AD=2BE，∴2BE2=AB2=2，∴BE=1，∴BC=2，∴AE==，BD==，∴BF==，过F作FG⊥BC于G，∴FG∥CD，∴△BFG∽△BDC，∴==，∴FG=，BG=，∴CG=，∴CF==．故答案为：．4．如图，在矩形ABCD中，M为BC边上一点，连接AM，过点D作DE⊥AM，垂足为E．若DE=DC=1，AE=2EM，则BM的长为．【分析】由AAS证明△ABM≌△DEA，得出AM=AD，证出BC=AD=3EM，连接DM，由HL证明Rt△DEM≌Rt△DCM，得出EM=CM，因此BC=3CM，设EM=CM=x，则BM=2x，AM=BC=3x，在Rt△ABM中，由勾股定理得出方程，解方程即可．【解答】解：∵四边形ABCD是矩形，∴AB=DC=1，∠B=∠C=90°，AD∥BC，AD=BC，∴∠AMB=∠DAE，∵DE=DC，∴AB=DE，∵DE⊥AM，∴∠DEA=∠DEM=90°，在△ABM和△DEA中，，∴△ABM≌△DEA（AAS），∴AM=AD，∵AE=2EM，∴BC=AD=3EM，连接DM，如图所示：在Rt△DEM和Rt△DCM中，，∴Rt△DEM≌Rt△DCM（HL），∴EM=CM，∴BC=3CM，设EM=CM=x，则BM=2x，AM=BC=3x，在Rt△ABM中，由勾股定理得：12+（2x）2=（3x）2，解得：x=，∴BM=；故答案为：．5．如图，在矩形ABCD中，∠ABC的平分线交AD于点E，连接CE．若BC=7，AE=4，则CE= 5 ．【分析】首先证明AB=AE=CD=4，在Rt△CED中，根据CE=计算即可．【解答】解：∵四边形ABCD是矩形，∴AD∥BC，AB=CD，BC=AD=7，∠D=90°，∴∠AEB=∠EBC，∵∠ABE=∠EBC，∴AB=AE=CD=4，在Rt△EDC中，CE===5．故答案为56．如图，在矩形ABCD中，对角线AC、BD相交于点O，点E、F分别是AO、AD 的中点，若AB=6cm，BC=8cm，则EF= 2.5 cm．【分析】根据勾股定理求出AC，根据矩形性质得出∠ABC=90°，BD=AC，BO=OD，求出BD、OD，根据三角形中位线求出即可．【解答】解：∵四边形ABCD是矩形，∴∠ABC=90°，BD=AC，BO=OD，∵AB=6cm，BC=8cm，∴由勾股定理得：BD=AC==10（cm），∴DO=5cm，∵点E、F分别是AO、AD的中点，∴EF=OD=2.5cm，故答案为：2.5．7．如图，连接四边形ABCD各边中点，得到四边形EFGH，还要添加AC⊥BD 条件，才能保证四边形EFGH是矩形．【分析】根据三角形的中位线平行于第三边，HG∥BD，EH∥AC，根据平行线的性质∠EHG=∠1，∠1=∠2，根据矩形的四个角都是直角，∠EFG=90°，所以∠2=90°，因此AC⊥BD．【解答】解：∵G、H、E分别是BC、CD、AD的中点，∴HG∥BD，EH∥AC，∴∠EHG=∠1，∠1=∠2，∴∠2=∠EHG，∵四边形EFGH是矩形，∴∠EHG=90°，∴∠2=90°，∴AC⊥BD．故还要添加AC⊥BD，才能保证四边形EFGH是矩形．8．如图，在四边形ABCD中，对角线AC、BD相交于点O，且AO=CO，BO=DO，要使四边形ABCD为矩形，则需添加的条件为∠DAB=90°（填一个即可）．【分析】根据对角线互相平分线的四边形为平行四边形可得四边形ABCD是平行四边形，添加条件∠DAB=90°可根据有一个角是直角的平行四边形是矩形进行判定．【解答】解：可以添加条件∠DAB=90°，∵AO=CO，BO=DO，∴四边形ABCD是平行四边形，∵∠DAB=90°，∴四边形ABCD是矩形，故答案为：∠DAB=90°．9．已知四边形ABCD为平行四边形，要使得四边形ABCD为矩形，则可以添加一个条件为∠BAD=90°．【分析】根据矩形的判定方法：已知平行四边形，再加一个角是直角填空即可．【解答】解：∵四边形ABCD是平行四边形，∠BAD=90°，∴四边形ABCD是矩形，故答案为：∠BAD=90°（答案不唯一）．10．木匠做一个矩形木框，长为80cm，宽为60cm，对角线的长为100cm，则这个木框合格（填“合格”或“不合格”）【分析】只要算出桌面的长与宽的平方和是否等于对角线的平方，如果相等可得长、宽、对角线构成的是直角三角形，由此可得到每个角都是直角，根据矩形的判定：有三个角是直角的四边形是矩形，可得此桌面合格．【解答】解：解：∵802+602=10000=1002，即：AD2+DC2=AC2，∴∠D=90°，同理：∠B=∠BCD=90°，∴四边形ABCD是矩形，故答案为合格．11．如图，在四边形ABCD中，已知AB∥DC，AB=DC，在不添加任何辅助线的情况下，请补充一个条件，使四边形ABCD成为矩形，这个条件是∠A=90°．【分析】根据有一个角是90°的平行四边形是矩形，即可解决问题．【解答】解：∵AB∥DC，AB=DC，∴四边形ABCD是平行四边形，∴当∠A=90°时，四边形ABCD是平行四边形．故答案为∠A=90°．（填∠B=90°或∠C=90°或∠D=90°也可以）12．如图，在平行四边形ABCD中，延长AD到点E，使DE=AD，连接EB，EC，DB 请你添加一个条件EB=DC ，使四边形DBCE是矩形．【解答】解：添加EB=DC．理由如下：∵四边形ABCD是平行四边形，∴AD∥BC，且AD=BC，∴DE∥BC，又∵DE=AD，∴DE=BC，∴四边形DBCE为平行四边形．又∵EB=DC，∴四边形DBCE是矩形．故答案是：EB=DC．二．解答题（共6小题）13．如图，在▱ABCD中，∠BAD的平分线交CD于点E，交BC的延长线于点F，连接BE，∠F=45°．（1）求证：四边形ABCD是矩形；（2）若AB=14，DE=8，求sin∠AEB的值．【分析】（1）欲证明四边形ABCD是矩形，只需推知∠DAB是直角；（2）如图，过点B作BH⊥AE于点H．构建直角△BEH．通过解该直角三角形可以求得sin∠AEB的值．在Rt△BCE中，由勾股定理得．在Rt △AHB中，BH=AB•sin45°=7．所以通过解Rt△BHE得到：sin∠AEB=．【解答】（1）证明：∵四边形ABCD是平行四边形，∴AD∥BC．∴∠DAF=∠F．∵∠F=45°，∴∠DAE=45°．∵AF是∠BAD的平分线，∴∠EAB=∠DAE=45°．∴∠DAB=90°．又∵四边形ABCD是平行四边形，∴四边形ABCD是矩形．（2）解：如图，过点B作BH⊥AE于点H．∵四边形ABCD是矩形，∴AB=CD，AD=BC，∠DCB=∠D=90°．∵AB=14，DE=8，∴CE=6．在Rt△ADE中，∠DAE=45°，∴∠DEA=∠DAE=45°．∴AD=DE=8．∴BC=8．在Rt△BCE中，由勾股定理得．在Rt△AHB中，∠HAB=45°，∴BH=AB•sin45°=7．∵在Rt△BHE中，∠BHE=90°，∴sin∠AEB=．14．如图，AD是等腰△ABC底边BC上的高．点O是AC中点，延长DO到E，使OE=OD，连接AE，CE．（1）求证：四边形ADCE的是矩形；（2）若AB=17，BC=16，求四边形ADCE的面积．【分析】（1）根据平行四边形的性质得出四边形ADCE是平行四边形，根据垂直推出∠ADC=90°，根据矩形的判定得出即可；（2）求出DC，根据勾股定理求出AD，根据矩形的面积公式求出即可．【解答】（1）证明：∵点O是AC中点，∴AO=OC，∵OE=OD，∴四边形ADCE是平行四边形，∵AD是等腰△ABC底边BC上的高，∴∠ADC=90°，∴四边形ADCE是矩形；（2）解：∵AD是等腰△ABC底边BC上的高，BC=16，AB=17，∴BD=CD=8，AB=AC=17，∠ADC=90°，由勾股定理得：AD===15，∴四边形ADCE的面积是AD×DC=15×8=120．15．如图，四边形ABCD中，AB∥DC，∠B=90°，F为DC上一点，且FC=AB，E 为AD上一点，EC交AF于点G．（1）求证：四边形ABCF是矩形；（2）若EA=EG，求证：ED=EC．【分析】（1）由条件可先证得四边形ABCF为平行四边形，再由∠B=90°可证得结论；（2）利用等腰三角形的性质可求得∠EAG=∠EGA=∠FGC，再利用直角三角形的性质可求得∠D=∠ECD，可证得ED=EC．【解答】证明：（1）∵AB∥CD，且FC=AB，∴四边形ABCF为平行四边形，∵∠B=90°，∴四边形ABCF是矩形；（2）∵EA=EG，∴∠EAG=∠EGA=∠FGC，∵四边形ABCF为矩形，∴∠AFC=∠AFD=90°，∴∠D+∠DAF=∠FGC+∠ECD=90°，∴∠D=∠ECD，∴ED=EC．16．如图，在▱ABCD中，AE⊥BC于点E点，延长BC至F点使CF=BE，连接AF，DE，DF．（1）求证：四边形AEFD是矩形；（2）若AB=6，DE=8，BF=10，求AE的长．【分析】（1）先证明四边形AEFD是平行四边形，再证明∠AEF=90°即可．（2）证明△ABF是直角三角形，由三角形的面积即可得出AE的长．【解答】（1）证明：∵CF=BE，∴CF+EC=BE+EC．即 EF=BC．∵在▱ABCD中，AD∥BC且AD=BC，∴AD∥EF且AD=EF．∴四边形AEFD是平行四边形．∵AE⊥BC，∴∠AEF=90°．∴四边形AEFD是矩形；（2）解：∵四边形AEFD是矩形，DE=8，∴AF=DE=8．∵AB=6，BF=10，∴AB2+AF2=62+82=100=BF2．∴∠BAF=90°．∵AE⊥BF，∴△ABF的面积=AB•AF=BF•AE．∴AE===．17．平行四边形ABCD中，过点D作DE⊥AB于点E，点F在CD上，CF=AE，连接BF，AF．（1）求证：四边形BFDE是矩形；（2）若AF平分∠BAD，且AE=3，DE=4，求矩形BFDE的面积．【分析】（1）根据有一个角是90度的平行四边形是矩形即可判定．（2）首先证明AD=DF，求出AD即可解决问题．【解答】证明：（1）∵四边形ABCD是平行四边形，∴AB=CD，AB∥CD，∴DF∥BE，∵CF=AE，∴DF=BE，∴四边形BFDE是平行四边形，∵DE⊥AB，∴∠DEB=90°，∴四边形BFDE是矩形．（2）∵AB∥CD，∴∠BAF=∠AFD，∵AF平分∠BAD，∴∠DAF=∠AFD，∴AD=DF，在Rt△ADE中，∵AE=3，DE=4，∴AD==5，∴矩形的面积为20．18．在▱ABCD中，过点D作DE⊥AB于点E，点F在CD上，CF=AE，连接BF，AF．（1）求证：四边形BFDE是矩形；（2）若AD=DF，求证：AF平分∠BAD．【分析】（1）先证明四边形BFDE是平行四边形，再证明∠DEB=90°即可．（2）欲证明AF平分∠BAD，只要证明∠DAF=∠BAF即可．【解答】证明：（1）∵四边形ABCD是平行四边形，∴AB=CD，AB∥CD，即BE∥DF，∵CF=AE，∴DF=BE，∴四边形BFDE是平行四边形，∵DE⊥AB，∴∠DEB=90°，∴四边形BFDE是矩形．（2）由（1）可知AB∥CD，∴∠BAF=∠AFD，∵AD=DF，∴∠DAF=∠AFD，∴∠BAF=∠DAF，即AF平分∠BAD．。

初一下册矩形的性质与判定练习题含答案

矩形：有一个角是直角的平行四边形叫做矩形，也说是长方形。

矩形的性质：矩形的四个角都是直角；矩形的对角线相等；矩形的对角线相等且互相平分。

特别提示：直角三角形斜边上的中线等于斜边的一半矩形具有平行四边形的一切性质。

矩形的判定方法有一个角是直角的平行四边形是矩形；对角线相等的平行四边形是矩形有三个角是直角的四边形是矩形【例题】专题一：矩形的性质矩形的性质性质1. 矩形的四个角都是直角。

几何语言：∵四边形ABCD 是矩形；∴∠BAD=∠ABC=∠BCD=∠ADC=90°性质2. 矩形的对角线相等且平分。

几何语言：∵四边形ABCD 是矩形；∴OA=OC=OB=OD=D B 21AC 21==性质3. 对边平行且相等几何语言：∵四边形ABCD 是矩形；∴AD=BC ， AD ∥BC 或者 AB=CD ， AB ∥CD3. 直角三角形的一个性质：直角三角形斜边上的中线等于斜边的一半。

几何语言：∵ 在Rt △ABC 中，OA=OC （OB 是AC 边上的中线）∴ OB=21AC在直角三角形中，30角所对的直角边等于斜边的一半。

矩形具有平行四边形的一切性质。

1．如图，矩形ABCD 中，BE ⊥AC 于E ，DF ⊥AC 于F ，若AE=1，EF ＝2，则FC ＝，AB ＝。

FEADBFC ＝1，AB ＝2.2．只用一把刻度尺检查一张四边形纸片是否是矩形，下列操作中最为恰当的是（）A. 先测量两对角线是否互相平分，再测量对角线是否相等 CB. 先测量两对角线是否互相平分，再测量是否有一个直角C. 先测量两组对边是否相等，再测量对角线是否相等D. 先测量两组对边是否互相平行，再测量对角线是否相等3.已知：如图3-32，矩形ABCD 中，对角线AC 、BD 相交于点O ，AC = 10cm ，∠ACB = 30°, 则∠AOB = °，AD = cm ；60 534.如图，将矩形纸片ABCD 沿对角线AC 折叠，使点B 落在点E 处，求证：EF =DF .5.如图，在Rt ⊿ABC 中，∠C = 90，AC = AB ，AB = 30，矩形 DEFG 的一边DE 在AB 上，顶点G 、F 分别在AC 、BC 上，若 DG ：GF = 1：4，则矩形DEFG 的面积是 100 ；专题二：矩形的判定图3-32OBACDABCDF G矩形的判定方法方法1：矩形的定义：有一个角是直角的平行四边形叫做矩形。

矩形的性质与判定练习题

1、矩形具有而一般平行四边形不具有的性质是 ( ) A. 对角相等B. 对边相等C. 对角线相等D. 对角线互相平分2、能够判断一个四边形是矩形的条件是 ( )A ．对角线相等B ．对角线垂直C ．对角线互相平分且相等 D ．对角线垂直且相等．3、下列命题中正确的是（） A ．对角线相等的四边形是矩形 B ．对角相等且有一个角是直角的四边形是矩形C ．有一个角是直角的四边形是矩形 D ．内角都相等的四边形是矩形4、下列条件中，不能判定四边形ABCD 为矩形的是（）． A ．AB ∥CD ，AB=CD ，AC=BD B ．∠A=∠B=∠D=90 C ．AB=BC ，AD=CD ，且∠C=90°D ．AB=CD ，AD=BC ，∠A=90°5、已知一矩形的周长是24cm ，相邻两边之比是1:2，那么这个矩形的面积是 __________B ． 32cm 2C ．48cm 26、两条平行线被第三条直线所截，两组内错角的平分线相交所成的四边形是_________7、若矩形的一条角平分线分一边为3cm 和5cm 两部分，则矩形的周长为（）cm. A ．22 B ．26 C ．22或26 D ．28 8、在矩形ABCD 中，∠AOD=130°，则∠ACB=__ _. 9、在矩形ABCD 中，对角线AC ，BD 相交于点O ，若对角线AC=10cm ，•边BC=•8cm ，•则△ABO 的周长为________．10、已知矩形的一条对角线长是8cm ，两条对角线的一个交角为60°，则矩形的周长为______.11、矩形ABCD 的两条对角线相交于O,∠AOB ＝60o,AB ＝8,则矩形对角线的长________．12、在矩形ABCD 中, 对角线交于O 点，AB=0.6, BC=0.8, 那么△AOB 的面积为_________; 周长为_________.13、矩形的两条对角线夹角为60°，一条对角线与短边的和为15，则短边的长是，对角线长是 . 14、矩形ABCD 的对角线相交于点O ，AC=2AB ，则△COD 为________三角形.15、矩形ABCD 中，S 矩形ABCD =24 cm 2，若BC=6 cm ，则对角线AC 的长是________ cm.16、矩形ABCD 被两条对角线分成四个小三角形，如果四个小三角形的周长的和是86cm ，对角线是13cm ，那么矩形的周长是_________.17、在矩形ABCD 的边AB 上有一点E ，且CE=DE ，若AB=2AD ，则∠ADE= .18、在△ABC 中, AM 是中线, ∠BAC=90︒, AB=6cm, AC=8cm, 那么AM 的长为____________.19、已知直角三角形的周长为14，斜边上的中线长为3．则直角三角形的面积为 .20、一个矩形周长是12cm, 对角线长是5cm, 那么它的面积为___________.21、直角三角形斜边上的高与中线分别是5cm 和6cm ，则它的面积为 .22、在Rt △ABC 中，BD 为斜边AC 上的中线，若∠A=35°，那么∠DBC= .23、若一直角三角形斜边上的中线与斜边上的高所夹锐角为34°，则这个直角三角形的较小内角是度． 24、如图,在矩形ABCD 中，M 是BC 中点，且MA ⊥MD ．•若矩形ABCD•的周长为48cm ，•则矩形ABCD 的面积为_______cm 2．第24题第27题第22题25、如果一个矩形较短的边长为5cm ．两条对角线所夹的角为60°，则这个矩形的面积是_____cm 2.26、矩形一个角的平分线分矩形一边成2cm 和3cm ，则这个矩形的面积为 .27、如图，在矩形ABCD 中，已知AB=8cm ，BC=10cm ，折叠矩形的一边AD ，使点D 落在BC 边的点F 处，折痕为AE ，则CE 的长为．28、已知：如图，矩形ABCD 中，E 在DC 上，AB=AE=2BC ，则 ∠EBC= .29、如图，矩形ABCD 中，AC 与BD 交于O 点，BE ⊥AC 于E ，CF ⊥BD 于F.求证：BE=CF.30、已知，如图，矩形ABCD 的对角线AC 、BD 相交于点O ，E 、F 、G 、H 分别是OA 、OB 、OC 、OD 的中点，顺次连结E、F 、G 、H 所得的四边形EFGH 是矩形吗？说明理由.31、如图，矩形ABCD 中，AB=2 cm , BC=3 cm . M 是BC 的中点，求D 点到AM 的距离.32、已知，如图，□ABCD 中，AC ，BD 交于O ，AE ⊥BC 于E ，EO 交AD 于F ．求证：四边形AECF 是矩形．33、已知，如图，△ABC 中，∠C=90°，AC=BC ，AD=DB ，PE ⊥AC ，PF⊥BC ．求证：DE=DF ．34、已知，如图，矩形ABCD 中，BE 平分∠ABC 交DC 于E ，EF ⊥AE 交BC 于F ．求证：AE=EF ．35、如图，将矩形纸片折叠，先折出折痕(对角线)BD ，再折使AD 边与对角线BD 重合，A 点落到A ’处，得折痕DG ，若AB=2，BC=1，求AG 的长.36、已知，如图，矩形ABCD 中，E 是BC 上一点，DF ⊥AE 于F ．若AE=BC ，求证：CE=FE ．37、如图，矩形ABCD 的两边AB=3，BC=4，P 是AD 上任一点，PE ⊥AC 于点E ，PF ⊥BD 于点F 。

矩形的性质与判定习题及答案

由题意得：AE＝CF＝t
AE＝CF＝t
∵点G、H分别是矩形ABCD的边AB、 EF＝5﹣2（5﹣t）＝2t-5
DC的中点，
∴ BG 1 AB，CH 1 CD
2
2
∴2t-5=4 ∴t＝4.5
又∵AB=CD,AB∥CD
综上，当t为0.5秒或4.5秒时，
∴BG∥CH，BG=CH
四边形EGFH为矩形
∴四边形BCHG为平行四边形
2
2
4
∴ 13 PE PF 15
4
∴ PE PF 60 13
（1）矩形的面积公式是S=长×宽（两邻边的乘积）
（2）过矩形对角线交点O的任一直线平分矩形ABCD的面积
（3）矩形ABCD对角线AC、BD相交于点O，则
①△ABO≌△CDO，△AOD≌△COB
△ABO，△CDO，△AOD，△COB都是等腰三角形
1
2
证明：（1）∵四边形ABCD是矩形，在△AEG与△CFH中
∴AB＝CD，AB∥CD，AD∥BC， ∠B＝90°
∴∠1＝∠2 ∵G、H分别是AB、DC的中点 ∴AG＝BG，CH＝DH ∴AG＝CH
AG CH
1
2
AE CF
∴△AEG≌△CFH（SAS）
∴EG＝FH
∵AE＝CF
又∵GF＝HE
②△ABD≌△CDB≌△BAC≌△DCA
△ABD，△CDB，△BAC，△DCA都是直角三角形
③S△ABO
=S△BCO
=S△CDO
=S△AOD
=
1 4
S矩形ABCD
例4．如图，O是矩形ABCD的对角线的交点，E、F、G、 H分别是OA、OB、OC、OD上的点，且AE＝BF＝CG ＝DH．（1）求证：四边形EFGH是矩形；（2）若E、F、G、H分别是OA、OB、OC、OD的中点，且DG⊥AC，OF＝2cm，求矩形ABCD的面积．

矩形的性质与判定典型例题

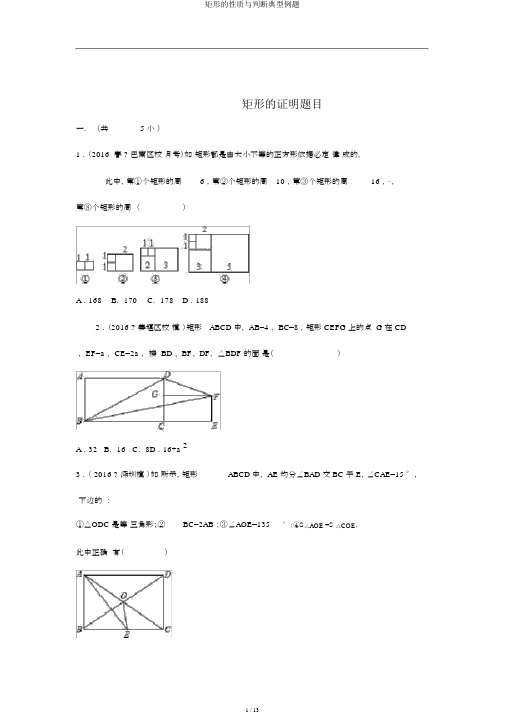
_矩形的证明题目一．（共 5 小）1 ．（2016 春 ? 巴南区校月考）如矩形都是由大小不等的正方形依据必定律成的，此中，第①个矩形的周 6 ，第②个矩形的周10 ，第③个矩形的周16 ，⋯，第⑧个矩形的周（）A ．168 B． 170 C． 178 D ．1882 ．（2016 ? 姜堰区校模）矩形ABCD 中， AB=4 ， BC=8 ，矩形 CEFG 上的点 G 在 CD， EF=a ， CE=2a ，接 BD 、 BF、 DF，△BDF 的面是（）2A ．32 B． 16 C． 8D ．16+a3 ．（ 2016 ? 深圳模）如所示，矩形ABCD 中， AE 均分∠BAD 交 BC 于 E，∠CAE=15 °，下边的：①△ODC 是等三角形；②BC=2AB ；③∠AOE=135°；④S△AOE=S△COE，此中正确有（）_ A．1 个 B．2 个C．3 个 D．4 个4 ．（2015 ? 十堰一模）如，在矩形ABCD 中， E， F 分是AB ， CD 上的点， AE=CF ，接 EF，BF，EF 与角AC 交于点 O，且 BE=BF ，∠BEF=2 ∠BAC ，FC=2 ， AB 的（）A．8B．8C．4 D ．65 ．（2015 ? 露台模）如，矩形ABCD 中， BC=1 ，接 AC 与 BD 交于点 E1， E1作 E1F1⊥ BC 于 F1，接 AF1交 BD 于 E2， E2作 E2F2⊥ BC 于 F2，接 AF2交 BD 于 E3，E3作 E3 F3⊥ BC 于 F3，⋯，以此推，BF n（此中 n 正整数）的（）A．B．C．D．二．解答（共25 小）6 ．（2015 ? 岩）如， E， F 分是矩形 ABCD 的 AD ， AB 上的点，若EF=EC ，且 EF⊥EC．（ 1 ）求： AE=DC ；（2 ）已知 DC=，求BE的．7 ．（ 2015 ? 玉林）如图，在矩形ABCD 中， AB=5 ，AD=3 ，点 P 是 AB 边上一点（不与 A ，B 重合），连结 CP，过点 P 作 PQ⊥ CP 交 AD 边于点 Q ，连结 CQ ．（1 ）当△CDQ ≌△CPQ 时，求 AQ 的长；（2 ）取 CQ 的中点 M ，连结 MD ， MP ，若 MD ⊥MP ，求 AQ 的长．8 ．（2015 ? 石家庄二模）已知：如下图，四边形ABCD 是矩形，分别以BC、 CD 为一边作等边△EBC 和等边△FCD ，点 E 在矩形上方，点 F 在矩形内部，连结AE、 EF．（1 ）求∠ECF 的度数；（2 ）求证： AE=FE ．9 ．（2015 春 ? 巴南区校级期末）如图，在矩形ABCD 中， E 是 BC 的中点，将△ ABE 沿 AE 折叠后获得△ AFE，点 F 在矩形 ABCD 内部，延伸AF 交 CD 于点 G．（1 ）猜想线段GF 与 GC 有何数目关系？并证明你的结论；（2 ）若 AB=3 ， AD=4 ，求线段GC 的长．10 ．（ 2015 秋 ? 开江县期末）已知，四边形ABCD 是长方形， F 是 DA 延伸线上一点，CF 交 AB 于点 E， G 是 CF 上一点，且 AG=AC ，∠ACG=2 ∠GAF ．（1 ）若∠ACB=60 °，求∠ECB 的度数．（2 ）若 AF=12cm ， AG=6.5cm ，求△AEF 中 EF 边上的高？11 ．（ 2015 春 ? 宜兴市校级期中）定义：如图①，在△ABC 中， CD 是 AB 边上的中线，那么△ACD 和△BCD 是“友善三角形” ，而且 S△ACD =S △BCD．应用：如图②，在矩形 ABCD 中，AB=4 ， BC=6 ，点 E 在 AD 上，点 F 在 BC 上， AE=BF ， AF 与 BE 交于点 O ．（1）求证：△ AOB 和△AOE 是“友善三角形” ；（2）连结 OD ，若△AOE 和△DOE 是“友善三角形” ，求四边形 CDOF 的面积．12 ．（ 2015 春 ? 汕头校级期中）如下图，在矩形ABCD 中， AB=12 ，AC=20 ，两条对角线订交于点O ．以 OB、 OC 为邻边作第 1 个平行四边形 OBB 1 C，对角线订交于点A1，再以 A 1B1、 A 1C 作第 2 个平行四形 A 1B1C1C，角订交于点O 1；再以 O 1B1、O1C1 作第3个平行四形O 1B1B2C1⋯依此推．（1 ）求矩形ABCD 的面；（ 2 ）求第 1 个平行四形 OBB 1 C 的面是第 2个平行四形 A 1B1C1C 是第 3 个平行四形OB 1B2C 的面是（3 ）第n 个平行四形的面是．13 ．（ 2015 春 ? 青山区期中）如 1 ，已知 AB ∥CD ，AB=CD ，∠A= ∠D ．（ 1 ）求：四形 ABCD 矩形；（ 2 ）E 是 AB 的中点， F AD 上一点，∠ DFC=2 ∠BCE．①如 2 ，若 FAD 中点， DF=1.6 ，求 CF 的度：②如 2 ，若 CE=4 ，CF=5 ， AF+BC=，AF=．14 ．（ 2015 春 ? 富顺县校级月考）矩形ABCD 中， AB=3 ， AD=4 ；P 是 AD 上的随意一点，过 P 作 PE⊥ OA ， PF⊥ OD ，求 PE+PF 的值？15 ．（ 2015 春 ? 启东市校级月考）如图，已知矩形ABCD 中，过点 C 引∠A 的均分线AM 的垂线，垂足为M ， AM 交 BC 于 E，连结 MB ， MD ．（1）求证： BE=DC ；（2）求证：∠ MBE= ∠MDC ．（3 ）假如 AB=6 ，AD=10，则四边形ABMD面积=．16 ．（ 2014 ? 丹东一模）（1 ）如图 1 ，四边形ABCD 是矩形， E 为 AD 上一点，且BE=ED ，P 为对角线BD 上一点， PF⊥ BE 于点 F，PG⊥ AD 于点 G．判断 PF、PG 和 AB 的数目关系并说明原因．（2 ）如图 2 ，当四边形ABCD 变成平行四边形，其余条件不变，若∠ABC=60 °，判断 PF、PG 和 AB 的数目关系并说明原因．（3 ）如图 3 ，当四边形ABCD 知足∠ABD=90 °，AB=3 ，BD=4 ，其余条件不变，判断PF、PG 和 AB 的数目关系并说明原因．_17 ．（ 2014 ? 南岸区一模）如图，在矩形ABCD中，点E是AD边上一点，点 F 是CB 延伸线上一点，连结EF交 AB于点G，且DE=BF．AE的垂直均分线MN交AE于点N 、交EF 于点 M ．若∠AFG=2 ∠BFG=45 °，AF=2 ．（1 ）求证： AF=CE ；（2 ）求△CEF 的面积．18 ．（ 2014 春 ? 涪陵区期末）如图，矩形ABCD 中， AB=8 ， AD=10 ．（1）求矩形 ABCD 的周长；（2）E 是 CD 上的点，将△ ADE 沿折痕 AE 折叠，使点 D 落在 BC 边上点 F 处．①求DE 的长；②点 P 是线段 CB 延伸线上的点，连结PA，若△PAF 是等腰三角形，求PB 的长．（3 ）M是 AD上的动点，在DC上存在点N ，使△MDN沿折痕MN折叠，点 D 落在BC 边上点T 处，求线段CT长度的最大值与最小值之和．_ 19 ．（ 2014春 ? 郯城县期末）如图 1 ，在平面直接坐标系中，矩形OABC的极点A、C的坐标分别为（10 ，0）、（0，4 ），点D 5 的等腰三角形时，求点 P 的坐标．是OA的中点，点P 在2 、图BC3上运动，当△ ODP是腰长为20 ．（ 2013 秋 ? 渝中区校级期末）如图，点AE，交 CD 于点 F， G 是 AF 的中点，再连结（1 ）求证：∠ DEA=2 ∠AEB ；（2 ）若 BC=2AB ，求∠AED 的度数．E 是矩形 ABCD 的边 BC 延伸线上一点，连结DG 、DE ，且 DE=DG ．21 ．（ 2014 春 ? 宜昌校级期末）在矩形ABCG 中，点 D 是 AG 的中点，点 E 是 AB 上一点，DE⊥ DC ，CE 交 BD 于 F，（1）求证： ED 均分∠ AEC；（2）当∠BEC=60 °，且AE=1 时，求矩形 ABCG 的面积；（3）当 BE=BC ，求证： BD 均分∠CDE．_ 22 ．（ 2014 春 ? 沂水县期末）数学学习老是如数学知识自己的生长历史同样，常常发源于猜测中的发现，我们所发现的不必定对，可是当利用我们已有的知识作为推理的前提论证以后，当所发现的在逻辑上没有矛盾以后，就能够作为新的推理的前提，数学中称之为定理．（1 ）试试证明：等腰三角形的研究中借助折纸发现：直角三角形斜边上的中线等于斜边的一半．可是当时并未说明这个结论的合理．此刻我们学些了矩形的判断和性质以后，就能够解决这个问题了．如图 1 若在 Rt △ABC 中 CD 是斜边 AB 的中线，则，你能用矩形的性质说明这个结论吗？请说明．（2 ）迁徙运用：利用上述结论解决以下问题：①如图 2所示，四边形 ABCD 中，∠BAD=90 °，∠DCB=90 °，EF 分别是 BD 、AC 的中点，请你说明EF 与 AC 的地点关系．②如图 3所示， ? ABCD 中，以 AC 为斜边作 Rt △ACE，∠AEC=90 °，且∠BED=90 °，试说明平行四边形 ABCD 是矩形．23 ．（ 2014 春 ? 金川区校级期中）如图，在正方形ABCD 的边 BC 上任取一点 M ，过点 C作 CN ⊥ DM 交 AB 于 N ，设正方形对角线交点为O ，试确立 OM 与 ON 之间的关系，并说明原因．_24 ．（2014 春 ? 合川区校级期中）如图，在矩形ABCD 中，点 E 为 CD 上一点，将△ BCE 沿BE 翻折后点 C 恰巧落在AD 边上的点 F 处，过 F 作 FH ⊥ BC 于 H ，交 BE 于 G，连结 CG．（1）求证：四边形 CEFG 是菱形；（2）若 AB=8 ， BC=10 ，求四边形 CEFG 的面积．25 ．（ 2014 春 ? 仙桃期中）矩形 ABCD 绕点 A 顺时针旋转至矩形AEFG ，使 B 点正好落在CD 上的点 E 处，连 BE．（1 ）求证：∠ BAE=2 ∠CBE；（2 ）如图 2，连 BG 交 AE 于 M ，点 N 为 BE 的中点，连M N 、AF，尝试究AF 与 MN的数目关系，并证明你的结论．26 ．（ 2014 春 ? 青县校级期中）如图 1，在四边形ABCD 中， AB ∥CD ，∠BCD=90 °，AB=AD=10cm ，BC=8cm ．点 P 从点 A 出发，以每秒3cm 的速度沿线段AB 方向向 B 运_动，点 Q 从点同时发，当点D 出发，以每秒2cm 的速度沿线段DC 方向向点CP 运动到点 B 时， P、Q 同时运动停止，设运动时间为运动．已知动点t 秒．P、Q（1）求 CD 的长；（2）当 t 为什么值时，四边形 PBQD 为平行四边形？（3 ）在运动过程中，能否存在四边形BCQP 是矩形？若存在，恳求出t 的值；若不存在，请说明原因．27 ．（ 2013 ? 遵义）如图，将一张矩形纸片ABCD 沿直线 MN 折叠，使点 C 落在点 A 处，点 D 落在点 E处，直线 MN交BC于点M，交AD于点N．（1 ）求证：CM=CN；（2 ）若△CMN的面积与△ CDN的面积比为3：1，求的值．28 ．（ 2013 ? 郑州模拟）（1 ）如图 1 ，已知矩形ABCD 中，点 E 是 BC 上的一动点，过点E 作 EF⊥ BD 于点 F， EG⊥ AC 于点 G， CH ⊥ BD 于点 H ，试证明 CH=EF+EG ；_（2 ）若点 E 在 BC 的延伸线上，如图 2 ，过点 E 作 EF⊥ BD 于点 F，EG⊥ AC 的延伸线于点G， CH ⊥ BD 于点 H ，则 EF、EG、CH 三者之间拥有如何的数目关系，直接写出你的猜想；（3 ）如图 3 ， BD 是正方形 ABCD 的对角线， L 在 BD 上，且 BL=BC ，连结 CL，点 E 是CL 上任一点， EF⊥BD 于点 F，EG⊥BC 于点 G，猜想 EF、EG、BD 之间拥有如何的数目关系，直接写出你的猜想；（4 ）察看图 1 、图2 、图 3 的特征，请你依据这一特征结构一个图形，使它仍旧拥有EF、EG、 CH 这样的线段的关系，并知足（1）或（ 2 ）的结论，写出有关题设的条件和结论．29 ．（ 2013 ? 重庆模拟）如图，矩形ABCD 中，点 E 为矩形的边CD 上随意一点，点P 为线段 AE 中点，连结 BP 并延伸交边 AD 于点 F，点 M 为边 CD 上一点，连结 FM ，且∠1= ∠2 ．（1 ）若 AD=2 ， DE=1 ，求 AP 的长；（2 ）求证： PB=PF+FM ．30 ．（2013 ? 南岸区校级模拟）如图，在矩形ABCD 中，点 M 、N 在线段 AD 上，∠MBC=∠NCB=60 °，点E、 F 分别为线段 CN 、BC 上的点，连结EF 并延伸，交MB 的延伸线于点G， EF=FG ．（1）点 K 为线 BM 的中点，若线段 AK=2 ， MN=3 ，求矩形 ABCD 的面积；（2 ）求证： MB=NE+BG ．_。

专题1.2 矩形的性质与判定(能力提升)(解析版)

专题1.2 矩形的性质与判定（能力提升）（解析版）一、选择题。

1．（2022春•遵化市期末）如图，矩形ABCD中，对角线AC，BD交于点O，若∠AOB＝60°，BD＝8，则DC长为（）A．4B．4C．3D．5【答案】B。

【解答】解：由矩形对角线相等且互相平分可得AO＝BO＝＝4，即△OAB为等腰三角形，又∠AOB＝60°，∴△OAB为等边三角形．故AB＝BO＝4，∴DC＝AB＝4．故选：B．2．（2021秋•沂水县期末）下列各图是由若干个正方形和长方形组成的，其中能表示等式（a+b）2＝a2+2ab+b2的是（）A．B．C．D．【答案】B。

【解答】解：对于等式（a+b）2＝a2+2ab+b2，可看作边长为（a+b）的正方形由一个边长为a的正方形、一个边长为b的正方形和一个长宽为a、b的矩形组成．故选：B．3．（2022•海曙区校级模拟）如图，矩形ABCD中，AB＝8cm，AD＝6cm，EF是对角线BD 的垂直平分线，则EF的长为（）A．cm B．cm C．cm D．8cm【答案】C。

【解答】解：∵EF是BD的垂直平分线，∴OB＝OD，∵∠OBF＝∠ODE，∠BOF＝∠DOE，∴△BOF≌△DOE，则OE＝OF，∵∠OBF＝∠ABD，∴△BOF∽△BAD∴＝，∵BD＝＝10cm，∴BO＝5cm，∴FO＝5×cm＝cm，∴EF＝2FO＝cm．故选：C．4．（2021春•洛南县期末）如图，在四边形ABCD中，对角线AC，BD相交于点O，且OA ＝OC，OB＝OD．若要使四边形ABCD为矩形，则可以添加的条件是（）A．∠AOB＝60°B．AC＝BD C．AC⊥BD D．AB＝BC【答案】B。

【解答】解：∵OA＝OC，OB＝OD，∴四边形ABCD是平行四边形，∵AC＝BD，∴四边形ABCD是矩形．故B选项符合题意，由∠AOB＝60°无法判断平行四边形ABCD是矩形．故A选项不符合题意，由AC⊥BD无法判断平行四边形ABCD是矩形．故C选项不符合题意，由AB＝BC无法判断平行四边形ABCD是矩形．故D选项不符合题意，故选：B．5．（2022春•黔南州期末）如图，在△ABC中，∠C＝90°，AC＝8，BC＝6，点P为斜边AB上一动点，过点P作PE⊥AC于E，PF⊥BC于点F，连接EF，则线段EF的最小值为（）A．24B．3.6C．4.8D．5【答案】C。

矩形的性质与判定习题

1、如图，在菱形ABCD中，AB=5，∠BCD=120°，则△ABC的周长等于（）A．20 B．15 C.10 D． 52、顺次连接矩形四边中点得到的四边形一定是（）A．正方形B．矩形C．菱形 D.平行四边形3、如图，菱形ABCD中，AB＝2，∠A＝120º，点P、Q、K分别为线段BC、CD、BD上任意一点，则PK＋QK的最小值为………………………………………………（）A．1 B． C．2 D．＋14、如图，将一个长为，宽为的矩形纸片先按照从左向右对折，再按照从下向上的方向对折，沿所得矩形两邻边中点的连线（虚线）剪下（如图（1）），再打开，得到如图（2）所示的小菱形的面积为（）A. B. C. D.（1）（2）5、如图，在菱形中，，∠，则对角线等于（）A.20B.15C.10D.56、从菱形的钝角顶点向对角的两条边作垂线，垂足恰好是该边的中点，则菱形的内角中钝角的度数是（）A.150°B. 135°C. 120°D. 100°7、如图5所示，有一个利用四边形的不稳定性制作的菱形晾衣架．已知其中每个菱形的边长为20cm，墙上悬挂晾衣架的两个铁钉A、B之间的距离为20cm，则∠1等于( )A.90°Ｂ.60°Ｃ.45°Ｄ.30°8、菱形的周长为4，两个相邻的内角的度数之比为1：2，则较短的对角线长为（）A．2 B． C．1 D．9、如图所示，在平面直角坐标系中，菱形MNPO的顶点P的坐标是（3，4），则顶点M、N的坐标分别是（）A．M（5，0），N（8，4） B．M（4，0），N（8，4）C．M（5，0），N（7，4） D．M（4，0），N（7，4）10、如图，在平面直角坐标系中，菱形ABCD的顶点C的坐标为（-1，0），点B的坐标为（0，2），点A在第二象限．直线与x轴、y轴分别交于点N、M．将菱形ABCD沿x轴向右平移m个单位，当点D落在△MON的内部时（不包括三角形的边），则m的值可能是（）A.1B.2C.4D.811、如右上图，小红在作线段AB的垂直平分线时，是这样操作的：分别以点A，B为圆心，大于线段AB长度一半的长为半径画弧，相交于点C，D，则直线CD即为所求。

矩形的性质及判定专项练习

矩形的性质及判定专项练习
矩形的判定方法（1）：有3个内角是的四边形是矩形
例1 已知：如图，平行四边形ABCD的四个内角的平分线分别相交于点E，F，G，H，求证：四边形EFGH 是矩形。

练习已知：如图，在四边形ABCD中，O为边AB的中点，且∠AOD=∠BOC．求证：四边形ABCD是矩形．
矩形的判定方法（2）：有 1个内角是直角的形是矩形
例2如图，已知在四边形ABCD中，AC DB
交于O，E、F、G、H分别是四边的中点，求证：四边形EFGH是矩形．B
A C
D
O
练习在平行四边形ABCD 中，对角线AC 、BD 相交于O ，EF 过点O ，且AF ⊥BC ，求证：四边形AFCE 是矩形
矩形的判定方法（3）：对角线的平行四边形是矩形
例3已知：如图，在Y ABCD 中，以AC 为斜边作Rt △ACE ，且∠BED 为直角．求证：•四边形ABCD 是矩形．
练习如图，在△ABC 中，O 是AC 上一个动点，过点O 作直线MN ∥BC ，设MN 交∠BCA 的角平分线于点E ，交∠BCA 的外角平分线于点F 。

（1）求证：EO=FO ；（2）当点O 运动到何处时，四边形AECF 是矩形？并证明你的结论；
B A
C E
D O F
E O N M C B A。

矩形的性质与判定练习(含答案)

．
17．在四边形 ABCD 中，对角线 AC ， BD 交于点 O ，OA OC ，OB OD ，添加一个条件
使四边形 ABCD 是矩形，那么所添加的条件可以是
（写出一个即可）．
18．如图，在矩形 ABCD 中，对角线 AC 与 BD 相交于点 O ，CE BD ，垂足为点 E ，CE 5 ，
A．5
B． 5 3
C．10
D．10 3
7．如图，延长矩形 ABCD 的边 BC 至点 E ，使 CE BD ，连接 AE ，如果 ADB 38 ，则 E 的值是 ( )
A． 19
B． 18
C． 20
D． 21
8．如图，在矩形 ABCD 中，对角线 AC 、 BD 交于 O ， BC 2 ， AE BD ，垂足为 E ，
．
24．如图，已知 BEFG 是长方形， A 为 EB 延长线上一点， AF 交 BG 于点 C ， D 为 AC 上一点，且 AD BD BF ，若 BFG 60 ，则 AFG 的度数为．
B．②③
3．下列对矩形的判定中，正确的个数有 (
C．③④ )
D．②④
（1）对角线相等的四边形是矩形；
（2）对角线互相平分且相等的四边形是矩形；
（3）有一个角是直角的四边形是矩形；
（4）有四个角是直角的四边形是矩形；
（5）四个角都相等的四边形是矩形；
（6）对角线相等，且有一个直角的四边形是矩形；
（7）一组邻边垂直，一组对边平行且相等的四边形是矩形；
A． 12 5
B． 24 5
C． 18 5
D．5
11．如图所示，矩形 ABCD 中， AE 平分 BAD 交 BC 于 E ，CAE 15 ，则下面的结论中正确的有 ( ) ① ODC 是等边三角形； ② BC 2 AB ； ③ AOE 135 ； ④ SAOE SCOE ．

矩形的性质和判定典型试题综合训练(含解析)完美打印版

矩形的性质和判定典型试题综合训练（含解析）一．选择题（共15小题）1．矩形具有而平行四边形不一定具有的性质是（）A．对角相等B．对边相等C．对角线相等D．对角线互相平分2．已知平行四边形ABCD，AC、BD是它的两条对角线，那么下列条件中，能判断这个平行四边形为矩形的是（）A．∠BAC=∠DCA B．∠BAC=∠DAC C．∠BAC=∠ABD D．∠BAC=∠ADB3．下列关于矩形的说法中正确的是（）A．对角线相等的四边形是矩形B．矩形的对角线相等且互相平分C．对角线互相平分的四边形是矩形D．矩形的对角线互相垂直且平分4．如图，平行四边形ABCD的对角线AC与BD相交于点O，要使它成为矩形，需再添加的条件是（）A．AO=OC B．AC=BD C．AC⊥BD D．BD平分∠ABC5．下列图形是用矩形纸片来折出阴影部分为等腰三角形，其中正确的有（）A．1个B．2个C．3个D．4个6．如图，EF过矩形ABCD对角线的交点O，且分别交AD、BC于点E、F已知AB=3，BC=4，则图中阴影部分的面积是（）A．3 B．4 C．6 D．127．如图，过矩形ABCD的对角线BD上一点K分别作矩形两边的平行线MN与PQ，那么图中矩形AMKP 的面积S1与矩形QCNK的面积S2的关系是（）A．S1＞S2B．S1=S2C．S1＜S2D．S1=2S28．如图，四边形ABCD和四边形AEFC是两个矩形，点B在EF边上，若矩形ABCD和矩形AEFC的面积分别是S1、S2的大小关系是（）A．S1＞S2B．S1=S2C．S1＜S2D．3S1=2S29．如图，矩形ABCD中，AB=12，BC=13，以B为圆心，BA为半径画弧，交BC于点E，以D为圆心，DA 为半径画弧，交BC于点F，则EF的长为（）A．3 B．4 C．D．510．如图，长方形ABCD中，M为CD中点，分别以点B、M为圆心，以BC长、MC长为半径画弧，两弧相交于点P．若∠PMC=110°，则∠BPC的度数为（）A．35°B．45°C．55°D．65°11．已知：线段AB，BC，∠ABC=90°．求作：矩形ABCD．以下是甲、乙两同学的作业：对于两人的作业，下列说法正确的是（）A．两人都对B．两人都不对C．甲对，乙不对D．甲不对，乙对12．如图，将矩形纸片ABCD沿直线EF折叠，使点C落在AD边的中点C′处，点B落在点B′处，其中AB=9，BC=6，则FC′的长为（）A．B．4 C．4.5 D．513．如图，P是矩形ABCD的边AD上一个动点，PE⊥AC于E，PF⊥BD于F，当P从A向D运动（P与A，D不重合），则PE+PF的值（）A．增大B．减小C．不变D．先增大再减小14．如图，矩形ABCD中，AB=4，BC=6，P是CD边上的中点，E是BC边上的一动点，点M、N分别是AE、PE的中点，则线段MN长为（）A．2B．3 C．D．15．如图，矩形ABCD的面积为20cm2，对角线交于点O；以AB、AO为邻边做平行四边形AOC1B，对角线交于点O1；以AB、AO1为邻边做平行四边形AO1C2B；…；依此类推，则平行四边形AO4C5B的面积为（）A．cm2B．cm2C．5cm2D．cm2二．填空题（共12小题）16．如图，在平行四边形ABCD中，延长AD到点E，使DE=AD，连接EB，EC，DB请你添加一个条件，使四边形DBCE是矩形．17．如图，矩形ABCD的对角线AC，BD相交于点O，分别过点C，D作BD，AC的平行线，相交于点E．若AD=6，则点E到AB的距离是．18．如图，连接四边形ABCD各边中点，得到四边形EFGH，还要添加条件，才能保证四边形EFGH 是矩形．19．如图，在矩形ABCD中，∠ABC的平分线交AD于点E，连接CE．若BC=7，AE=4，则CE=．20．如图，在矩形ABCD中，AD=4，AB=3，MN∥BC分别交AB、CD于点M、N，在MN上任取两点P、Q，那么图中阴影部分的面积是．21．如图，在矩形ABCD中，AD=6，AB=4，点E、G、H、F分别在AB、BC、CD、AD上，且AF=CG=2，BE=DH=1，点P是直线EF、GH之间任意一点，连接PE、PF、PG、PH，则△PEF和△PGH的面积和等于．22．如图矩形ABCD中，AB=8cm，CB=4cm，E是DC的中点，BF=BC，则四边形DBFE的面积为cm2．23．已知：Rt△ABC中，∠C=90°，AC=3，BC=4，P为AB上任意一点，PF⊥AC于F，PE⊥BC于E，则EF 的最小值是．24．如图，在平面直角坐标系中，矩形OABC的顶点B的坐标为（10，4），点D是OA的中点，点P在边BC上运动，当△ODP是等腰三角形时，点P的坐标为．25．如图，把矩形ABCD沿EF翻折，点B恰好落在AD边的B′处，若AE=2，DE=6，∠EFB=60°，则矩形ABCD的面积是．26．如图，矩形ABCD中，O为AC中点，过点O的直线分别与AB、CD交于点E、F，连结BF交AC于点M，连结DE、BO．若∠COB=60°，FO=FC，则下列结论：①FB垂直平分OC；②△EOB≌△CMB；③DE=EF；④S△AOE：S△BCM=2：3．其中一定成立的结论有（将正确结论的序号填在横线上）27．如图，矩形ABCD中，AD=，F是DA延长线上一点，G是CF上一点，且∠ACG=∠AGC，∠GAF=∠F=20°，则AB=．三．解答题（共7小题）28．如图，在△ABC中，AB=AC，D为边BC的中点，四边形ABDE是平行四边形，AC，DE相交于点O．（1）求证：四边形ADCE是矩形；（2）若∠AOE=60°，AE=2，求矩形ADCE对角线的长．29．如图，在▱ABCD中，AC⊥BC，过点D作DE∥AC交BC的延长线于点E，连接AE交CD于点F．（1）求证：四边形ADEC是矩形；（2）在▱ABCD中，取AB的中点M，连接CM，若CM=5，且AC=8，求四边形ADEC的面积．30．如图，O为△ABC内一点，把AB、OB、OC、AC的中点D、E、F、G依次连接形成四边形DEFG．（1）四边形DEFG是什么四边形，请说明理由；（2）若四边形DEFG是矩形，点0所在位置应满足什么条件？说明理由．31．△ABC中，点O是AC边上一个动点，过点O作直线MN∥BC，设MN交∠BCA的平分线于E，交∠DCA的平分线于点F．（1）求证：EO=FO；（2）当点O运动到何处时，四边形AECF是矩形？并证明你的结论．32．如图，在▱ABCD中，点P是AB边上一点（不与A，B重合），CP=CD，过点P作PQ⊥CP，交AD边于点Q，连结CQ．（1）若∠BPC=∠AQP，求证：四边形ABCD是矩形；（2）在（1）的条件下，当AP=2，AD=6时，求AQ的长．33．如图，在△ABC中，AB=AC，AD平分∠BAC，CE∥AD且CE=AD．（1）求证：四边形ADCE是矩形；（2）若△ABC是边长为4的等边三角形，AC，DE相交于点O，在CE上截取CF=CO，连接OF，求线段FC 的长及四边形AOFE的面积．34．已知：如图1，矩形ABCD中，AB=6，BC=8，E、F、G、H分别是AB、BC、CD、DA四条边上的点（且不与各边顶点重合），设m=EF+FG+GH+HE，探索m的取值范围．（1）如图2，当E、F、G、H分别是AB、BC、CD、DA四边中点时，m=．（2）为了解决这个问题，小贝同学采用轴对称的方法，如图3，将整个图形以CD为对称轴翻折，接着再连续翻折两次，从而找到解决问题的途径，求得m的取值范围．①请在图3中补全小贝同学翻折后的图形；②m的取值范围是．矩形的性质和判定典型试题综合训练参考答案与试题解析一．选择题（共15小题）1．矩形具有而平行四边形不一定具有的性质是（）A．对角相等B．对边相等C．对角线相等D．对角线互相平分【分析】矩形的对角线互相平分且相等，而平行四边形的对角线互相平分，不一定相等．【解答】解：矩形的对角线相等，而平行四边形的对角线不一定相等．故选：C．2．已知平行四边形ABCD，AC、BD是它的两条对角线，那么下列条件中，能判断这个平行四边形为矩形的是（）A．∠BAC=∠DCA B．∠BAC=∠DAC C．∠BAC=∠ABD D．∠BAC=∠ADB【分析】由矩形和菱形的判定方法即可得出答案．【解答】解：A、∠BAC=∠DCA，不能判断四边形ABCD是矩形；B、∠BAC=∠DAC，能判定四边形ABCD是菱形；不能判断四边形ABCD是矩形；C、∠BAC=∠ABD，能得出对角线相等，能判断四边形ABCD是矩形；D、∠BAC=∠ADB，不能判断四边形ABCD是矩形；故选：C．3．下列关于矩形的说法中正确的是（）A．对角线相等的四边形是矩形B．矩形的对角线相等且互相平分C．对角线互相平分的四边形是矩形D．矩形的对角线互相垂直且平分【分析】根据矩形的性质和判定定理逐个判断即可．【解答】解：A、对角线相等的平行四边形才是矩形，故本选项错误；B、矩形的对角线相等且互相平分，故本选项正确；C、对角线互相平分的四边形是平行四边形，不一定是矩形，故本选项错误；D、矩形的对角线互相平分且相等，不一定垂直，故本选项错误；故选B．4．如图，平行四边形ABCD的对角线AC与BD相交于点O，要使它成为矩形，需再添加的条件是（）A．AO=OC B．AC=BD C．AC⊥BD D．BD平分∠ABC【分析】根据矩形的判定定理（对角线相等的平行四边形是矩形）推出即可．【解答】解：添加的条件是AC=BD，理由是：∵AC=BD，四边形ABCD是平行四边形，∴平行四边形ABCD是矩形，故选：B．5．下列图形是用矩形纸片来折出阴影部分为等腰三角形，其中正确的有（）A．1个B．2个C．3个D．4个【分析】根据等腰三角形的定义，即可一一判断．【解答】解：如图图1中，∵∠1=∠3，∠2=∠3，∴∠1=∠2，∴BA=BC，∴△ABC是等腰三角形．图3中，同法可证∠1=∠2，∴BA=BC，∴△ABC是等腰三角形．图4中，△ABC是等腰直角三角形，故选C．6．如图，EF过矩形ABCD对角线的交点O，且分别交AD、BC于点E、F已知AB=3，BC=4，则图中阴影部分的面积是（）A．3 B．4 C．6 D．12【分析】由全等三角形的判定得到△OFB≌△OED，将阴影部分的面积转化为规则的几何图形的面积进行计算．【解答】解：在矩形ABCD中，OB=OD，∠FBO=∠EDO，∴在△OFB与△OED中，∴△FBO≌△EDO，∴S阴影部分=S△ABO=S矩形=×3×4=3．故选A．7．如图，过矩形ABCD的对角线BD上一点K分别作矩形两边的平行线MN与PQ，那么图中矩形AMKP 的面积S1与矩形QCNK的面积S2的关系是（）A．S1＞S2B．S1=S2C．S1＜S2D．S1=2S2【分析】根据矩形的性质，可知△ABD的面积等于△CDB的面积，△MBK的面积等于△QKB的面积，△PKD的面积等于△NDK的面积，再根据等量关系即可求解．【解答】解：∵四边形ABCD是矩形，四边形MBQK是矩形，四边形PKND是矩形，∴△ABD的面积=△CDB的面积，△MBK的面积=△QKB的面积，△PKD的面积=△NDK的面积，∴△ABD的面积﹣△MBK的面积﹣△PKD的面积=△CDB的面积﹣△QKB的面积=△NDK的面积，∴S1=S2．故选：B．8．如图，四边形ABCD和四边形AEFC是两个矩形，点B在EF边上，若矩形ABCD和矩形AEFC的面积分别是S1、S2的大小关系是（）A．S1＞S2B．S1=S2C．S1＜S2D．3S1=2S2【分析】由于矩形ABCD的面积等于2个△ABC的面积，而△ABC的面积又等于矩形AEFC的一半，所以可得两个矩形的面积关系．【解答】解：矩形ABCD的面积S=2S△ABC，而S△ABC=S矩形AEFC，即S1=S2，故选B．9．如图，矩形ABCD中，AB=12，BC=13，以B为圆心，BA为半径画弧，交BC于点E，以D为圆心，DA为半径画弧，交BC于点F，则EF的长为（）A．3 B．4 C．D．5【分析】连接DF，在Rt△CDF中，求出CF，再求出CE即可解决问题．【解答】解：连接DF．∵四边形ABCD是矩形，∴AB=CD=BE=12，DA=BC=DF=13，∠C=90°，∴CF===5，∵EC=BC﹣BE=13﹣12=1，∴EF=CF﹣CE=4．故选B．10．如图，长方形ABCD中，M为CD中点，分别以点B、M为圆心，以BC长、MC长为半径画弧，两弧相交于点P．若∠PMC=110°，则∠BPC的度数为（）A．35°B．45°C．55°D．65°【分析】根据三角形内角和定理和等腰三角形两底角相等求出∠MCP，然后求出∠BCP，再根据等腰三角形两底角相等和三角形内角和定理求解即可．【解答】解：∵以B、M为圆心，分别以BC长、MC长为半径的两弧相交于P点，∴BP=BC，MP=MC，∵∠PMC=110°，∴∠MCP=（180°﹣∠PMC）=（180°﹣110°）=35°，在长方形ABCD中，∠BCD=90°，∴∠BCP=90°﹣∠MCP=90°﹣35°=55°，∴∠BCP=∠BPC=55°．故选C．11．已知：线段AB，BC，∠ABC=90°．求作：矩形ABCD．以下是甲、乙两同学的作业：对于两人的作业，下列说法正确的是（）A．两人都对B．两人都不对C．甲对，乙不对D．甲不对，乙对【分析】先由两组对边分别相等的四边形是平行四边形得出四边形ABCD是平行四边形，再根据有一个角是直角的平行四边形是矩形判断甲的作业正确；先由对角线互相平分的四边形是平行四边形得出四边形ABCD是平行四边形，再根据有一个角是直角的平行四边形是矩形判断乙的作业也正确．【解答】解：由甲同学的作业可知，CD=AB，AD=BC，∴四边形ABCD是平行四边形，又∵∠ABC=90°，∴▱ABCD是矩形．所以甲的作业正确；由乙同学的作业可知，CM=AM，MD=MB，∴四边形ABCD是平行四边形，又∵∠ABC=90°，∴▱ABCD是矩形．所以乙的作业正确；故选A．12．如图，将矩形纸片ABCD沿直线EF折叠，使点C落在AD边的中点C′处，点B落在点B′处，其中AB=9，BC=6，则FC′的长为（）A．B．4 C．4.5 D．5【分析】设FC′=x，则FD=9﹣x，根据矩形的性质结合BC=6、点C′为AD的中点，即可得出C′D的长度，在Rt△FC′D中，利用勾股定理即可找出关于x的一元一次方程，解之即可得出结论．【解答】解：设FC′=x，则FD=9﹣x，∵BC=6，四边形ABCD为矩形，点C′为AD的中点，∴AD=BC=6，C′D=3．在Rt△FC′D中，∠D=90°，FC′=x，FD=9﹣x，C′D=3，∴FC′2=FD2+C′D2，即x2=（9﹣x）2+32，解得：x=5．故选D．13．如图，P是矩形ABCD的边AD上一个动点，PE⊥AC于E，PF⊥BD于F，当P从A向D运动（P与A，D不重合），则PE+PF的值（）A．增大B．减小C．不变D．先增大再减小【分析】首先过A作AG⊥BD于G．利用面积法证明PE+PF=AG即可．【解答】解：如图，过A作AG⊥BD于G，则S△AOD=×OD×AG，S△AOP+S△POD=×AO×PF+×DO×PE=×DO×（PE+PF），∵S△AOD=S△AOP+S△POD，四边形ABCD是矩形，∴OA=OD，∴PE+PF=AG，∴PE+PF的值是定值，故选C．14．如图，矩形ABCD中，AB=4，BC=6，P是CD边上的中点，E是BC边上的一动点，点M、N分别是AE、PE的中点，则线段MN长为（）A．2B．3 C．D．【分析】连接AP，根据矩形的性质求出AP的长度，再根据三角形的中位线平行于第三边并且等于第三边的一半可得MN=AP，问题得解．【解答】解：连接AP，∵矩形ABCD中，AB=DC=4，P是CD边上的中点，∴DP=2，∴AP==2，连接AP，∵M，N分别是AE、PE的中点，∴MN是△AEP的中位线，∴MN=AP=．故选D．15．如图，矩形ABCD的面积为20cm2，对角线交于点O；以AB、AO为邻边做平行四边形AOC1B，对角线交于点O1；以AB、AO1为邻边做平行四边形AO1C2B；…；依此类推，则平行四边形AO4C5B的面积为（）A．cm2B．cm2C．5cm2D．cm2【分析】根据矩形的对角线互相平分，平行四边形的对角线互相平分可得下一个图形的面积是上一个图形的面积的，然后求解即可．【解答】方法一：解：设矩形ABCD的面积为S=20cm2，∵O为矩形ABCD的对角线的交点，∴平行四边形AOC1B底边AB上的高等于BC的，∴平行四边形AOC1B的面积=S，∵平行四边形AOC1B的对角线交于点O1，∴平行四边形AO1C2B的边AB上的高等于平行四边形AOC1B底边AB上的高的，∴平行四边形AO1C2B的面积=×S=，…，依此类推，平行四边形AO4C5B的面积===（cm2）．故选：B．二．填空题（共12小题）16．如图，在平行四边形ABCD中，延长AD到点E，使DE=AD，连接EB，EC，DB请你添加一个条件EB=DC，使四边形DBCE是矩形．【分析】利用平行四边形的判定与性质得到四边形DBCE为平行四边形，结合“对角线相等的平行四边形为矩形”来添加条件即可．【解答】解：添加EB=DC．理由如下：∵四边形ABCD是平行四边形，∴AD∥BC，且AD=BC，∴DE∥BC，又∵DE=AD，∴DE=BC，∴四边形DBCE为平行四边形．又∵EB=DC，∴四边形DBCE是矩形．故答案是：EB=DC．17．如图，矩形ABCD的对角线AC，BD相交于点O，分别过点C，D作BD，AC的平行线，相交于点E．若AD=6，则点E到AB的距离是9．【分析】连接EO，延长EO交AB于H．只要证明四边形ADEO是平行四边形，推出OE=AD，再证明OH 是△ADB的中位线，可得OE=AD，延长即可求出EH解决问题．【解答】解：连接EO，延长EO交AB于H．∵DE∥OC，CE∥OD，∴四边形ODEC是平行四边形，∵四边形ABCD是矩形，∴OD=OC，∴四边形ODEC是菱形，∴OE⊥CD，∵AB∥CD，AD⊥CD，∴EH⊥AB，AD∥OE，∵OA∥DE，∴四边形ADEO是平行四边形，∴AD=OE=6，∵OH∥AD，OB=OD，∴BH=AH，∴OH=AD=3，∴EH=OH+OE=3+6=9，故答案为9．18．如图，连接四边形ABCD各边中点，得到四边形EFGH，还要添加AC⊥BD条件，才能保证四边形EFGH是矩形．【分析】根据三角形的中位线平行于第三边，HG∥BD，EH∥AC，根据平行线的性质∠EHG=∠1，∠1=∠2，根据矩形的四个角都是直角，∠EFG=90°，所以∠2=90°，因此AC⊥BD．【解答】解：∵G、H、E分别是BC、CD、AD的中点，∴HG∥BD，EH∥AC，∴∠EHG=∠1，∠1=∠2，∴∠2=∠EHG，∵四边形EFGH是矩形，∴∠EHG=90°，∴∠2=90°，∴AC⊥BD．故还要添加AC⊥BD，才能保证四边形EFGH是矩形．19．如图，在矩形ABCD中，∠ABC的平分线交AD于点E，连接CE．若BC=7，AE=4，则CE=5．【分析】首先证明AB=AE=CD=4，在Rt△CED中，根据CE=计算即可．【解答】解：∵四边形ABCD是矩形，∴AD∥BC，AB=CD，BC=AD=7，∠D=90°，∴∠AEB=∠EBC，∵∠ABE=∠EBC，∴AB=AE=CD=4，在Rt△EDC中，CE===5．故答案为520．如图，在矩形ABCD中，AD=4，AB=3，MN∥BC分别交AB、CD于点M、N，在MN上任取两点P、Q，那么图中阴影部分的面积是6．【分析】用矩形的面积减去△ADQ和△BCP的面积求解即可．【解答】解：∵四边形ABCD为矩形，∴AD=BC=4．S阴影=S矩形ABCD﹣S△BPC﹣S△ADQ=AB•CB﹣BC•MB AD•AM=4×3﹣4×BM﹣×4×AM=12﹣2MB﹣2AM=12﹣2（MB+AM）=12﹣2×3=6．故答案为：6．21．如图，在矩形ABCD中，AD=6，AB=4，点E、G、H、F分别在AB、BC、CD、AD上，且AF=CG=2，BE=DH=1，点P是直线EF、GH之间任意一点，连接PE、PF、PG、PH，则△PEF和△PGH的面积和等于7．【分析】连接EG，FH，根据题目数据可以证明△AEF与△CGH全等，根据全等三角形对应边相等可得EF=GH，同理可得EG=FH，然后根据两组对边相等的四边形是平行四边形可得四边形EGHF是平行四边形，所以△PEF和△PGH的面积和等于平行四边形EGHF的面积的一半，再利用平行四边形EGHF的面积等于矩形ABCD 的面积减去四周四个小直角三角形的面积即可求解．【解答】解：∵在矩形ABCD中，AD=6，AB=4，AF=CG=2，BE=DH=1，∴AE=AB﹣BE=4﹣1=3，CH=CD﹣DH=4﹣1=3，∴AE=CH，在△AEF与△CGH中，，∴△AEF≌△CGH（SAS），∴EF=GH，同理可得，△BGE≌△DFH，∴EG=FH，∴四边形EGHF是平行四边形，∵△PEF和△PGH的高的和等于点H到直线EF的距离，∴△PEF和△PGH的面积和=×平行四边形EGHF的面积，平行四边形EGHF的面积=4×6﹣×2×3﹣×1×（6﹣2）﹣×2×3﹣×1×（6﹣2），=24﹣3﹣2﹣3﹣2，=14，∴△PEF和△PGH的面积和=×14=7．故答案为：7．22．如图矩形ABCD中，AB=8cm，CB=4cm，E是DC的中点，BF=BC，则四边形DBFE的面积为10cm2．【分析】本题主要考查矩形的性质，找出题里面的等量关系求解即可．【解答】解：AB=8cm，CB=4cm，E是DC的中点，BF=BC，∴CE=4，CF=3．∴四边形DBFE的面积=8×4﹣8×4÷2﹣4×3÷2=10cm2．23．已知：Rt△ABC中，∠C=90°，AC=3，BC=4，P为AB上任意一点，PF⊥AC于F，PE⊥BC于E，则EF 的最小值是 2.4．【分析】根据已知得出四边形CEPF是矩形，得出EF=CP，要使EF最小，只要CP最小即可，根据垂线段最短得出即可．【解答】解：连接CP，如图所示：∵∠C=90°，PF⊥AC于F，PE⊥BC于E，∴∠C=∠PFC=∠PEC=90°，∴四边形CEPF是矩形，∴EF=CP，要使EF最小，只要CP最小即可，当CP⊥AB时，CP最小，在Rt△ABC中，∠C=90°，AC=3，BC=4，由勾股定理得：AB=5，由三角形面积公式得：×4×3=×5×CP，∴CP=2.4，即EF=2.4，故答案为：2.4．24．如图，在平面直角坐标系中，矩形OABC的顶点B的坐标为（10，4），点D是OA的中点，点P在边BC上运动，当△ODP是等腰三角形时，点P的坐标为（2，4）或（3，4）或（8，4）或（2.5，4）．【分析】分为三种情况：①OP=OD时，②DO=DP时，③OP=PD时，根据点B的坐标，根据勾股定理和等腰三角形的性质即可求出答案．【解答】解：∵B的坐标是（10，4），四边形OCBA是矩形，∴OC=AB=4，∵D为OA中点，∴OD=AD=5，∵P在BC上，∴P点的纵坐标是4，以O为圆心，以OD为半径作弧，交BC于P，如图1所示：此时OP=OD=5，由勾股定理得：CP=3，即P的坐标是（3，4）；由勾股定理得：CP=3，即P的坐标是（3，4）；以D为圆心，以OD为半径作弧，交BC于P、P′，如图2所示：此时DP=OD=DP′=5，由勾股定理得：DM=DN=3，即P的坐标是（2，4），P′的坐标是（8，4）；③作OD的垂直平分线交BC于P，如图3所示：此时OP=DP，P的坐标是（2.5，4）；故答案为：（2，4）或（3，4）或（8，4）或（2.5，4）．25．如图，把矩形ABCD沿EF翻折，点B恰好落在AD边的B′处，若AE=2，DE=6，∠EFB=60°，则矩形ABCD的面积是16．【分析】由把矩形ABCD沿EF翻折，点B恰好落在AD边的B′处，∠EFB=60°，易证得△EFB′是等边三角形，继而可得△A′B′E中，B′E=2A′E，则可求得B′E的长，然后由勾股定理求得A′B′的长，继而求得答案．【解答】解：在矩形ABCD中，∵AD∥BC，∴∠DEF=∠EFB=60°，∵把矩形ABCD沿EF翻折点B恰好落在AD边的B′处，∴∠EFB=∠EFB′=60°，∠B=∠A′B′F=90°，∠A=∠A′=90°，AE=A′E=2，AB=A′B′，在△EFB′中，∵∠DEF=∠EFB=∠EB′F=60°∴△EFB′是等边三角形，Rt△A′EB′中，∵∠A′B′E=90°﹣60°=30°，∴B′E=2A′E，而A′E=2，∴B′E=4，∴A′B′=2，即AB=2，∵AE=2，DE=6，∴AD=AE+DE=2+6=8，∴矩形ABCD的面积=AB•AD=2×8=16．故答案为：16．26．如图，矩形ABCD中，O为AC中点，过点O的直线分别与AB、CD交于点E、F，连结BF交AC于点M，连结DE、BO．若∠COB=60°，FO=FC，则下列结论：①FB垂直平分OC；②△EOB≌△CMB；③DE=EF；④S△AOE：S△BCM=2：3．其中一定成立的结论有①③④（将正确结论的序号填在横线上）【分析】①正确．只要证明BO=BC，OF=FO即可解决问题；②错误．可以证明△EOB≌△FCB，由此即可判断；③正确．只要证明△DEF是等边三角形即可．④正确．只要证明S△BCM=S△ACB，S△AOE=S△AOB=S即可；△ABC【解答】解：∵四边形ABCD是矩形，∴∠ABC=∠DCB=90°，OA=OC，∴OB=OA=OB，∵∠COB=60°，∴△BOC是等边三角形，∴∠OCB=60°，∴∠DCA=30°，∵FO=FC，BO=BC，∴BF垂直平分OC，故①正确，∴∠FBC=∠OBE=30°，∴∠FOC=∠FCO=30°，∴∠FOB=90°，∵CD∥AB，∴∠FCO=∠EAO，∵∠FOC=∠AOE，OA=OC，∴△FOC≌△EOA，∴OE=OF，∴BF=BE，∵∠BOE=∠BCF=90°，∠EBO=∠CBF，∴△EBO≌△FBC，故②错误，∵DF∥EB，DF=BE，∴四边形DEBF是平行四边形，∴∠EDF=∠FBE=60°，∵∠DFE=180°﹣∠CFO=60°，∴△EDF是等边三角形，∴DE=EF，故③正确，易知CM=AC，AE=CF=BF=BE，∴S△BCM=S△ACB，S△AOE=S△AOB=S△ABC，∴S△AOE：S△BCM=2：3．故④正确，故答案为①③④27．如图，矩形ABCD中，AD=，F是DA延长线上一点，G是CF上一点，且∠ACG=∠AGC，∠GAF=∠F=20°，则AB=．【分析】根据三角形的一个外角等于与它不相邻的两个内角的和可得∠AGC=∠GAF+∠F=40°，再根据等腰三角形的性质求出∠CAG，然后求出∠CAF=120°，再根据∠BAC=∠CAF﹣∠BAF求出∠BAC=30°，再根据直角三角形30°角所对的直角边等于斜边的一半可得AC=2BC=2AD，然后利用勾股定理列式计算即可得解．【解答】解：由三角形的外角性质得，∠AGC=∠GAF+∠F=20°+20°=40°，∵∠ACG=∠AGC，∴∠CAG=180°﹣∠ACG﹣∠AGC=180°﹣2×40°=100°，∴∠CAF=∠CAG+∠GAF=100°+20°=120°，∴∠BAC=∠CAF﹣∠BAF=120°﹣90°=30°，在Rt△ABC中，AC=2BC=2AD=2，由勾股定理，AB===．故答案为：．三．解答题（共7小题）28．如图，在△ABC中，AB=AC，D为边BC的中点，四边形ABDE是平行四边形，AC，DE相交于点O．（1）求证：四边形ADCE是矩形；（2）若∠AOE=60°，AE=2，求矩形ADCE对角线的长．【分析】（1）根据四边形ABDE是平行四边形和AB=AC，推出AD和DE相等且互相平分，即可推出四边形ADCE是矩形．（2）根据∠AOE=60°和矩形的对角线相等且互相平分，得出△AOE为等边三角形，即可求出AO的长，从而得到矩形ADCE对角线的长．【解答】（1）证明：∵四边形ABDE是平行四边形，∴AB=DE，又∵AB=AC，∴DE=AC．∵AB=AC，D为BC中点，∴∠ADC=90°，又∵D为BC中点，∴CD=BD．∴CD∥AE，CD=AE．∴四边形AECD是平行四边形，又∴∠ADC=90°，∴四边形ADCE是矩形．（2）解：∵四边形ADCE是矩形，∴AO=EO，∵∠AOE=60°∴△AOE为等边三角形，∴AO=AE=2，∴AC=2OA=4．29．如图，在▱ABCD中，AC⊥BC，过点D作DE∥AC交BC的延长线于点E，连接AE交CD于点F．（1）求证：四边形ADEC是矩形；（2）在▱ABCD中，取AB的中点M，连接CM，若CM=5，且AC=8，求四边形ADEC的面积．【分析】（1）利用平行四边形的性质可得AD∥BC，结合条件可先证得四边形ADEC为平行四边形，结合AC⊥BC，可证得结论；（2）由直角三角形的性质可求得AB的长，在Rt△ABC中，由勾股定理可求得BC的长，再利用矩形的性质可求得AD的长，结合AC可求得矩形ADEC的面积．【解答】（1）证明：∵四边形ABCD是平行四边形，∴AD∥BC．又∵DE∥AC，∴四边形ADEC是平行四边形．又∵AC⊥BC，∴∠ACE=90°．∴四边形ADEC是矩形；（2）解：∵AC⊥BC，∴∠ACB=90°．∵M是AB的中点，∴AB=2CM=10．∵AC=8，∴BC==6．又∵四边形ABCD是平行四边形，∴BC=AD．又∵四边形ADEC是矩形，∴EC=AD．∴EC=BC=6．∴矩形ADEC的面积=6×8=48．30．如图，O为△ABC内一点，把AB、OB、OC、AC的中点D、E、F、G依次连接形成四边形DEFG．（1）四边形DEFG是什么四边形，请说明理由；（2）若四边形DEFG是矩形，点0所在位置应满足什么条件？说明理由．【分析】（1）可用三角形中位线定理求解，易知DG、EF分别是△ABC和△BOC的中位线，那么DG、EF 都平行且相等于BC，即DG与EF平行且相等，由此可证得四边形DEFG是平行四边形．（2）连接OA，则DE∥OA∥GF；若四边形DEFG是矩形，则DG和DE互相垂直；因此OA和BC也互相垂直，由此可判断出O点所处的位置．【解答】解：（1）四边形DEFG是平行四边形．理由如下：∵D、G分别是AB、AC的中点，∴DG是△ABC的中位线；∴DG∥BC，且DG=BC；同理可证：EF∥BC，且EF=BC；∴DG∥EF，且DG=EF；故四边形DEFG是平行四边形；（2）O在BC边的高上（且不与点A和垂足重合）理由如下：连接OA；∵把AB、OB、OC、AC的中点D、E、F、G依次连接形成四边形DEFG．∴DE∥OA∥GF，EF∥BC，∵O点在BC边的高上，∴AO⊥BC，∴AO⊥EF，∵DE∥OA，∴DE⊥EF，∴四边形DEFG是矩形．31．△ABC中，点O是AC边上一个动点，过点O作直线MN∥BC，设MN交∠BCA的平分线于E，交∠DCA的平分线于点F．（1）求证：EO=FO；（2）当点O运动到何处时，四边形AECF是矩形？并证明你的结论．【分析】（1）由于CE平分∠BCA，那么有∠1=∠2，而MN∥BC，利用平行线的性质有∠1=∠3，等量代换有∠2=∠3，于OE=OC，同理OC=OF，于是OE=OF；（2）OA=OC，那么可证四边形AECF是平行四边形，又CE、CF分别是∠BCA及其外角的角平分线，易证∠ECF是90°，从而可证四边形AECF是矩形．【解答】（1）解：当点O运动到AC中点时，四边形AECF是矩形；理由如下：如图所示：∵CE平分∠BCA，∴∠1=∠2，又∵MN∥BC，∴∠1=∠3，∴∠3=∠2，∴EO=CO，同理，FO=CO，∴EO=FO；（2）解：∵OA=OC，∴四边形AECF是平行四边形，∵CF是∠BCA的外角平分线，∴∠4=∠5，又∵∠1=∠2，∴∠1+∠5=∠2+∠4，又∵∠1+∠5+∠2+∠4=180°，∴∠2+∠4=90°，∴平行四边形AECF是矩形．32．如图，在▱ABCD中，点P是AB边上一点（不与A，B重合），CP=CD，过点P作PQ⊥CP，交AD边于点Q，连结CQ．（1）若∠BPC=∠AQP，求证：四边形ABCD是矩形；（2）在（1）的条件下，当AP=2，AD=6时，求AQ的长．【分析】（1）证出∠A=90°即可；（2）由HL证明Rt△CDQ≌Rt△CPQ，得出DQ=PQ，设AQ=x，则DQ=PQ=6﹣x，由勾股定理得出方程，解方程即可．【解答】（1）证明：∵∠BPQ=∠BPC+∠CPQ=∠A+∠AQP，又∠BPC=∠AQP，∴∠CPQ=∠A，∵PQ⊥CP，∴∠A=∠CPQ=90°，∴四边形ABCD是矩形；（2）解：∵四边形ABCD是矩形∴∠D=∠CPQ=90°，在Rt△CDQ和Rt△CPQ中，，∴Rt△CDQ≌Rt△CPQ（HL）），∴DQ=PQ，设AQ=x，则DQ=PQ=6﹣x在Rt△APQ中，AQ2+AP2=PQ2 ∴x2+22=（6﹣x）2，解得：x=∴AQ的长是．33．如图，在△ABC中，AB=AC，AD平分∠BAC，CE∥AD且CE=AD．（1）求证：四边形ADCE是矩形；（2）若△ABC是边长为4的等边三角形，AC，DE相交于点O，在CE上截取CF=CO，连接OF，求线段FC 的长及四边形AOFE的面积．【分析】（1）根据平行四边形判定得出平行四边形，再根据矩形判定推出即可；（2）分别求出AE、OH、CE、CF的长，再求出三角形AEC和三角形COF的面积，即可求出答案．【解答】（1）证明：∵CE∥AD且CE=AD，∴四边形ADCE是平行四边形，∵在△ABC中，AB=AC，AD平分∠BAC，∴AD⊥BC（等腰三角形三线合一性质），∴∠ADC=90°，∴四边形ADCE是矩形；（2）解：∵△ABC是等边三角形，边长为4，∴AC=4，∠DAC=30°，∴∠ACE=30°，AE=2，CE=2，∵四边形ADCE为矩形，∴OC=OA=2，∵CF=CO，∴CF=2，过O作OH⊥CE于H，∴OH=OC=1，∴S四边形AOFE=S△AEC﹣S△COF=×2×2﹣×2×1=2﹣1．34．已知：如图1，矩形ABCD中，AB=6，BC=8，E、F、G、H分别是AB、BC、CD、DA四条边上的点（且不与各边顶点重合），设m=EF+FG+GH+HE，探索m的取值范围．（1）如图2，当E、F、G、H分别是AB、BC、CD、DA四边中点时，m=20．（2）为了解决这个问题，小贝同学采用轴对称的方法，如图3，将整个图形以CD为对称轴翻折，接着再连续翻折两次，从而找到解决问题的途径，求得m的取值范围．①请在图3中补全小贝同学翻折后的图形；②m的取值范围是20≤m＜28．【分析】（1）利用勾股定理求出矩形对角线的长度，再利用三角形中位线的性质得出EH=BD，EF=AC，FG=BD，HG=AC，进而求出即可；（2）①利用轴对称图形的性质得出答案即可；②利用两点之间线段最短以及三角形三边关系得出m的取值范围即可．【解答】解：（1）如图2，连接AC，BD，∵在矩形ABCD中，AB=6，BC=8，∴AC=BD==10，∵E、F、G、H分别是AB、BC、CD、DA四边中点，∴EH，EF，FG，HG，分别是△ABD，△ABC，△BCD，△ACD的中位线，∴EH=BD，EF=AC，FG=BD，HG=AC，∴m=EF+FG+GH+HE=AC+BD=10+10=20；（2）①如图3所示（虚线可以不画），②由图形可知，四边形的周长即折线HM的长，由两点之间线段最短可知，折线HM≥20，即周长不小于20；又由题可知，四边形周长小于矩形ABCD的周长，即周长小于28，故20≤m＜28．故答案为：20；20≤m＜28．。

矩形的性质和判定同步练习及答案

矩形的性质和判定一．填空题1．如图，矩形ABCD中，∠ABC的平分线交AD边于点E，点F是CD的中点，连接EF．若AB=8，且EF平分∠BED，则AD的长为．题1 题3 题42．若矩形的一条对角线与一边的夹角是40°，则两条对角线相交所成的锐角是．3．如图，在矩形ABCD中，AB=，E是BC的中点，AE⊥BD于点F，则CF的长是．4．如图，在矩形ABCD中，M为BC边上一点，连接AM，过点D作DE⊥AM，垂足为E．若DE=DC=1，AE=2EM，则BM的长为．5．如图，在矩形ABCD中，∠ABC的平分线交AD于点E，连接CE．若BC=7，AE=4，则CE= ．题5 题6 题76．如图，在矩形ABCD中，对角线AC、BD相交于点O，点E、F分别是AO、AD的中点，若AB=6cm，BC=8cm，则EF= cm．7．如图，连接四边形ABCD各边中点，得到四边形EFGH，还要添加条件，才能保证四边形EFGH是矩形．8．如图，在四边形ABCD中，对角线AC、BD相交于点O，且AO=CO，BO=DO，要使四边形ABCD 为矩形，则需添加的条件为（填一个即可）．题8 题11 题129．已知四边形ABCD为平行四边形，要使得四边形ABCD为矩形，则可以添加一个条件为．10．木匠做一个矩形木框，长为80cm，宽为60cm，对角线的长为100cm，则这个木框（填“合格”或“不合格”）11．如图，在四边形ABCD中，已知AB∥DC，AB=DC，在不添加任何辅助线的情况下，请补充一个条件，使四边形ABCD成为矩形，这个条件是．12．如图，在平行四边形ABCD中，延长AD到点E，使DE=AD，连接EB，EC，DB请你添加一个条件，使四边形DBCE是矩形．二．解答题13．如图，在▱ABCD中，∠BAD的平分线交CD于点E，交BC的延长线于点F，连接BE，∠F=45°．（1）求证：四边形ABCD是矩形；（2）若AB=14，DE=8，求sin∠AEB的值．14．如图，AD是等腰△ABC底边BC上的高．点O是AC中点，延长DO到E，使OE=OD，连接AE，CE．（1）求证：四边形ADCE的是矩形；（2）若AB=17，BC=16，求四边形ADCE的面积．15．如图，四边形ABCD中，AB∥DC，∠B=90°，F为DC上一点，且FC=AB，E为AD上一点，EC交AF于点G．（1）求证：四边形ABCF是矩形；（2）若EA=EG，求证：ED=EC．16．如图，在▱ABCD中，AE⊥BC于点E点，延长BC至F点使CF=BE，连接AF，DE，DF．（1）求证：四边形AEFD是矩形；（2）若AB=6，DE=8，BF=10，求AE的长．17．平行四边形ABCD中，过点D作DE⊥AB于点E，点F在CD上，CF=AE，连接BF，AF．（1）求证：四边形BFDE是矩形；（2）若AF平分∠BAD，且AE=3，DE=4，求矩形BFDE的面积．矩形的性质和判定解析一．填空题（共12小题）1．如图，矩形ABCD中，∠ABC的平分线交AD边于点E，点F是CD的中点，连接EF．若AB=8，且EF平分∠BED，则AD的长为12 ．【分析】根据两直线平行，内错角相等求出∠AEB=∠EBC，再求出∠ABE=∠EBC，根据等角对等边可得AE=AB，然后根据AD=AE+ED代入数据计算即可得解．【解答】解：∵矩形ABCD中，∴AD∥BC，∴∠AEB=∠EBC，∵∠ABC的平分线交AD边于点E，∴∠ABE=∠EBC，∴∠ABE=∠AEB，∴AB=AE=8，同理得出ED=DF=DC=4，∴AD=AE+ED=8+4=12，故答案为：12．2．若矩形的一条对角线与一边的夹角是40°，则两条对角线相交所成的锐角是80°．【分析】因为两条对角线相交所成的锐角只有一个，直接应用三角形的内角和定理求解即可．【解答】解：由矩形的对角线相等且互相平分，所构成的三角形为等腰三角形，利用等边对等角，所以另一底角为40°，两条对角线相交所成的钝角为：180°﹣40°×2=100°故它们所成锐角为：180°﹣100°=80°．故答案为80．3．如图，在矩形ABCD中，AB=，E是BC的中点，AE⊥BD于点F，则CF的长是．【分析】根据四边形ABCD是矩形，得到∠ABE=∠BAD=90°，根据余角的性质得到∠BAE=∠ADB，根据相似三角形的性质得到BE=1，求得BC=2，根据勾股定理得到AE==，BD==，根据三角形的面积公式得到BF==，过F作FG⊥BC于G，根据相似三角形的性质得到CG=，根据勾股定理即可得到结论．【解答】解：∵四边形ABCD是矩形，∴∠ABE=∠BAD=90°，∵AE⊥BD，∴∠AFB=90°，∴∠BAF+∠ABD=∠ABD+∠ADB=90°，∴∠BAE=∠ADB，∴△ABE∽△ADB，∴，∵E是BC的中点，∴AD=2BE，∴2BE2=AB2=2，∴BE=1，∴BC=2，∴AE==，BD==，∴BF==，过F作FG⊥BC于G，∴FG∥CD，∴△BFG∽△BDC，∴==，∴FG=，BG=，∴CG=，∴CF==．故答案为：．4．如图，在矩形ABCD中，M为BC边上一点，连接AM，过点D作DE⊥AM，垂足为E．若DE=DC=1，AE=2EM，则BM的长为．【分析】由AAS证明△ABM≌△DEA，得出AM=AD，证出BC=AD=3EM，连接DM，由HL证明Rt △DEM≌Rt△DCM，得出EM=CM，因此BC=3CM，设EM=CM=x，则BM=2x，AM=BC=3x，在Rt△ABM中，由勾股定理得出方程，解方程即可．【解答】解：∵四边形ABCD是矩形，∴AB=DC=1，∠B=∠C=90°，AD∥BC，AD=BC，∴∠AMB=∠DAE，∵DE=DC，∴AB=DE，∵DE⊥AM，∴∠DEA=∠DEM=90°，在△ABM和△DEA中，，∴△ABM≌△DEA（AAS），∴AM=AD，∵AE=2EM，∴BC=AD=3EM，连接DM，如图所示：在Rt△DEM和Rt△DCM中，，∴Rt△DEM≌Rt△DCM（HL），∴EM=CM，∴BC=3CM，设EM=CM=x，则BM=2x，AM=BC=3x，在Rt△ABM中，由勾股定理得：12+（2x）2=（3x）2，解得：x=，∴BM=；故答案为：．5．如图，在矩形ABCD中，∠ABC的平分线交AD于点E，连接CE．若BC=7，AE=4，则CE= 5 ．【分析】首先证明AB=AE=CD=4，在Rt△CED中，根据CE=计算即可．【解答】解：∵四边形ABCD是矩形，∴AD∥BC，AB=CD，BC=AD=7，∠D=90°，∴∠AEB=∠EBC，∵∠ABE=∠EBC，∴AB=AE=CD=4，在Rt△EDC中，CE===5．故答案为56．如图，在矩形ABCD中，对角线AC、BD相交于点O，点E、F分别是AO、AD的中点，若AB=6cm，BC=8cm，则EF= cm．【分析】根据勾股定理求出AC，根据矩形性质得出∠ABC=90°，BD=AC，BO=OD，求出BD、OD，根据三角形中位线求出即可．【解答】解：∵四边形ABCD是矩形，∴∠ABC=90°，BD=AC，BO=OD，∵AB=6cm，BC=8cm，∴由勾股定理得：BD=AC==10（cm），∴DO=5cm，∵点E、F分别是AO、AD的中点，∴EF=OD=，故答案为：．7．如图，连接四边形ABCD各边中点，得到四边形EFGH，还要添加AC⊥BD 条件，才能保证四边形EFGH是矩形．【分析】根据三角形的中位线平行于第三边，HG∥BD，EH∥AC，根据平行线的性质∠EHG=∠1，∠1=∠2，根据矩形的四个角都是直角，∠EFG=90°，所以∠2=90°，因此AC⊥BD．【解答】解：∵G、H、E分别是BC、CD、AD的中点，∴HG∥BD，EH∥AC，∴∠EHG=∠1，∠1=∠2，∴∠2=∠EHG，∵四边形EFGH是矩形，∴∠EHG=90°，∴∠2=90°，∴AC⊥BD．故还要添加AC⊥BD，才能保证四边形EFGH是矩形．8．如图，在四边形ABCD中，对角线AC、BD相交于点O，且AO=CO，BO=DO，要使四边形ABCD 为矩形，则需添加的条件为∠DAB=90°（填一个即可）．【分析】根据对角线互相平分线的四边形为平行四边形可得四边形ABCD是平行四边形，添加条件∠DAB=90°可根据有一个角是直角的平行四边形是矩形进行判定．【解答】解：可以添加条件∠DAB=90°，∵AO=CO，BO=DO，∴四边形ABCD是平行四边形，∵∠DAB=90°，∴四边形ABCD是矩形，故答案为：∠DAB=90°．9．已知四边形ABCD为平行四边形，要使得四边形ABCD为矩形，则可以添加一个条件为∠BAD=90°．【分析】根据矩形的判定方法：已知平行四边形，再加一个角是直角填空即可．【解答】解：∵四边形ABCD是平行四边形，∠BAD=90°，∴四边形ABCD是矩形，故答案为：∠BAD=90°（答案不唯一）．10．木匠做一个矩形木框，长为80cm，宽为60cm，对角线的长为100cm，则这个木框合格（填“合格”或“不合格”）【分析】只要算出桌面的长与宽的平方和是否等于对角线的平方，如果相等可得长、宽、对角线构成的是直角三角形，由此可得到每个角都是直角，根据矩形的判定：有三个角是直角的四边形是矩形，可得此桌面合格．【解答】解：解：∵802+602=10000=1002，即：AD2+DC2=AC2，∴∠D=90°，同理：∠B=∠BCD=90°，∴四边形ABCD是矩形，故答案为合格．11．如图，在四边形ABCD中，已知AB∥DC，AB=DC，在不添加任何辅助线的情况下，请补充一个条件，使四边形ABCD成为矩形，这个条件是∠A=90°．【分析】根据有一个角是90°的平行四边形是矩形，即可解决问题．【解答】解：∵AB∥DC，AB=DC，∴四边形ABCD是平行四边形，∴当∠A=90°时，四边形ABCD是平行四边形．故答案为∠A=90°．（填∠B=90°或∠C=90°或∠D=90°也可以）12．如图，在平行四边形ABCD中，延长AD到点E，使DE=AD，连接EB，EC，DB请你添加一个条件EB=DC ，使四边形DBCE是矩形．【解答】解：添加EB=DC．理由如下：∵四边形ABCD是平行四边形，∴AD∥BC，且AD=BC，∴DE∥BC，又∵DE=AD，∴DE=BC，∴四边形DBCE为平行四边形．又∵EB=DC，∴四边形DBCE是矩形．故答案是：EB=DC．二．解答题（共6小题）13．如图，在▱ABCD中，∠BAD的平分线交CD于点E，交BC的延长线于点F，连接BE，∠F=45°．（1）求证：四边形ABCD是矩形；（2）若AB=14，DE=8，求sin∠AEB的值．【分析】（1）欲证明四边形ABCD是矩形，只需推知∠DAB是直角；（2）如图，过点B作BH⊥AE于点H．构建直角△BEH．通过解该直角三角形可以求得sin ∠AEB的值．在Rt△BCE中，由勾股定理得．在Rt△AHB中，BH=AB•sin45°=7．所以通过解Rt△BHE得到：sin∠AEB=．【解答】（1）证明：∵四边形ABCD是平行四边形，∴AD∥BC．∴∠DAF=∠F．∵∠F=45°，∴∠DAE=45°．∵AF是∠BAD的平分线，∴∠EAB=∠DAE=45°．∴∠DAB=90°．又∵四边形ABCD是平行四边形，∴四边形ABCD是矩形．（2）解：如图，过点B作BH⊥AE于点H．∵四边形ABCD是矩形，∴AB=CD，AD=BC，∠DCB=∠D=90°．∵AB=14，DE=8，∴CE=6．在Rt△ADE中，∠DAE=45°，∴∠DEA=∠DAE=45°．∴AD=DE=8．∴BC=8．在Rt△BCE中，由勾股定理得．在Rt△AHB中，∠HAB=45°，∴BH=AB•sin45°=7．∵在Rt△BHE中，∠BHE=90°，∴sin∠AEB=．14．如图，AD是等腰△ABC底边BC上的高．点O是AC中点，延长DO到E，使OE=OD，连接AE，CE．（1）求证：四边形ADCE的是矩形；（2）若AB=17，BC=16，求四边形ADCE的面积．【分析】（1）根据平行四边形的性质得出四边形ADCE是平行四边形，根据垂直推出∠ADC=90°，根据矩形的判定得出即可；（2）求出DC，根据勾股定理求出AD，根据矩形的面积公式求出即可．【解答】（1）证明：∵点O是AC中点，∴AO=OC，∵OE=OD，∴四边形ADCE是平行四边形，∵AD是等腰△ABC底边BC上的高，∴∠ADC=90°，∴四边形ADCE是矩形；（2）解：∵AD是等腰△ABC底边BC上的高，BC=16，AB=17，∴BD=CD=8，AB=AC=17，∠ADC=90°，由勾股定理得：AD===15，∴四边形ADCE的面积是AD×DC=15×8=120．15．如图，四边形ABCD中，AB∥DC，∠B=90°，F为DC上一点，且FC=AB，E为AD上一点，EC交AF于点G．（1）求证：四边形ABCF是矩形；（2）若EA=EG，求证：ED=EC．【分析】（1）由条件可先证得四边形ABCF为平行四边形，再由∠B=90°可证得结论；（2）利用等腰三角形的性质可求得∠EAG=∠EGA=∠FGC，再利用直角三角形的性质可求得∠D=∠ECD，可证得ED=EC．【解答】证明：（1）∵AB∥CD，且FC=AB，∴四边形ABCF为平行四边形，∵∠B=90°，∴四边形ABCF是矩形；（2）∵EA=EG，∴∠EAG=∠EGA=∠FGC，∵四边形ABCF为矩形，∴∠AFC=∠AFD=90°，∴∠D+∠DAF=∠FGC+∠ECD=90°，∴∠D=∠ECD，∴ED=EC．16．如图，在▱ABCD中，AE⊥BC于点E点，延长BC至F点使CF=BE，连接AF，DE，DF．（1）求证：四边形AEFD是矩形；（2）若AB=6，DE=8，BF=10，求AE的长．【分析】（1）先证明四边形AEFD是平行四边形，再证明∠AEF=90°即可．（2）证明△ABF是直角三角形，由三角形的面积即可得出AE的长．【解答】（1）证明：∵CF=BE，∴CF+EC=BE+EC．即 EF=BC．∵在▱ABCD中，AD∥BC且AD=BC，∴AD∥EF且AD=EF．∴四边形AEFD是平行四边形．∵AE⊥BC，∴∠AEF=90°．∴四边形AEFD是矩形；（2）解：∵四边形AEFD是矩形，DE=8，∴AF=DE=8．∵AB=6，BF=10，∴AB2+AF2=62+82=100=BF2．∴∠BAF=90°．∵AE⊥BF，∴△ABF的面积=AB•AF=BF•AE．∴AE===．17．平行四边形ABCD中，过点D作DE⊥AB于点E，点F在CD上，CF=AE，连接BF，AF．（1）求证：四边形BFDE是矩形；（2）若AF平分∠BAD，且AE=3，DE=4，求矩形BFDE的面积．【分析】（1）根据有一个角是90度的平行四边形是矩形即可判定．（2）首先证明AD=DF，求出AD即可解决问题．【解答】证明：（1）∵四边形ABCD是平行四边形，∴AB=CD，AB∥CD，∴DF∥BE，∵CF=AE，∴DF=BE，∴四边形BFDE是平行四边形，∵DE⊥AB，∴∠DEB=90°，∴四边形BFDE是矩形．（2）∵AB∥CD，∴∠BAF=∠AFD，∵AF平分∠BAD，∴∠DAF=∠AFD，∴AD=DF，在Rt△ADE中，∵AE=3，DE=4，∴AD==5，∴矩形的面积为20．18．在▱ABCD中，过点D作DE⊥AB于点E，点F在CD上，CF=AE，连接BF，AF．（1）求证：四边形BFDE是矩形；（2）若AD=DF，求证：AF平分∠BAD．【分析】（1）先证明四边形BFDE是平行四边形，再证明∠DEB=90°即可．（2）欲证明AF平分∠BAD，只要证明∠DAF=∠BAF即可．【解答】证明：（1）∵四边形ABCD是平行四边形，∴AB=CD，AB∥CD，即BE∥DF，∵CF=AE，∴DF=BE，∴四边形BFDE是平行四边形，∵DE⊥AB，∴∠DEB=90°，∴四边形BFDE是矩形．（2）由（1）可知AB∥CD，∴∠BAF=∠AFD，∵AD=DF，∴∠DAF=∠AFD，∴∠BAF=∠DAF，即AF平分∠BAD．。

矩形性质与判定练习题

矩形性质与判定练习题1、已知矩形的一条对角线长是8cm ，两条对角线的一个交角为60°，则矩形的周长为______2、矩形的一内角平分线把矩形的一条边分成3和5两部分，则该矩形的周长是___________.3、形的两条对角线的夹角是60°，一条对角线与矩形短边的和为15，那么矩形对角线的长为_______，短边长为_______.4、一个矩形周长是12cm ，对角线长是5cm ，那么它的面积为_______________5、在△ABC 中，AM 是中线, ∠BAC=090，AB=6cm ，AC=8cm ，那么AM 的长为____________.6、如图所示，将△ABC 绕AC 的中点O 顺时针旋转180°得到△CDA ，添加一个条件______，使四边形ABCD 为矩形。

第6题第7题第9题7、（2013江西）如图，矩形ABCD 中，点E 、F 分别是AB 、CD 的中点，连接DE 和BF ，分别取DE 、BF 的中点M 、N ，连接AM ，CN ，MN ，若AB=4，BC=面积为___________。

8、如图所示，将矩形ABCD 绕点A 顺时针旋转到矩形AB ′C ′D ′的位置，旋转角为α00(090)α<<若01110∠=，则α=（）A 、020B 、030C 、040D 、0509、（2004•黑龙江）如图，矩形ABCD 中，AB=3，BC=4，如果将该矩形沿对角线BD 折叠，那么图中阴影部分的面积是___________。

10、菱形具有而矩形不一定具有的性质是（）A 、对角线互相垂直B 、对角线相等C 、对角线互相平分D 、对角互补第11题第12题11、如图：长方形纸片ABCD 中，AD=4cm ，AB=10cm ，按如图的方式折叠，使点B 与点D 重合．折痕为EF ，则DE 长为___________。

12、图所示，矩形ABCD 中，AE ⊥BD 于E ，∠BAE=30°，BE=1cm ，那么DE 的长为_____13、□ABCD 的对角线AC 与BD 相交于点O ，（1）若AB=AD ，则□ABCD 是形；（2）若AC=BD ，则□ABCD 是形；（3）若∠ABC是直角，则□ABCD是形；（4）若∠BAO=∠DAO，则□ABCD是形。

矩形的性质与判定练习题

矩形的性质与判定练习题1．如图，矩形ABCD 中，AB=3，BC=3，AE ⊥BD 于E ，则EC=（）A ． 27B ． 25C ． 215D ． 221 2．下列说法：①矩形是轴对称图形，两条对角线所在的直线是它的对称轴；②两条对角线相等的四边形是矩形；③有两个角相等的平行四边形是矩形；④两条对角线相等且互相平分的四边形是矩形；⑤两条对角线互相垂直平分的四边形是矩形．其中，正确的有（）A ．1个B ．2个C ．3个D ．4个3．如图，在△ABC 中，AB=3，AC=4，BC=5，P 为边BC 上一动点，PE ⊥AB 于E ，PF ⊥AC 于F ，则EF 的最小值为（）A ．2B ．2.2C ．2.4D ．2.54．如图∠BOP=∠AOP=15°，PC ∥OB ，PD ⊥PB 于D ，PC=2，则PD 的长度为（）A ．4 B ．3 C ．2 D ．15．下列说法中，错误的是（）A ．矩形的四个内角都相等 B ．四个内角都相等的四边形是矩形 C ．菱形的对角线互相垂直D ．对角线互相垂直的四边形是菱形6．如图，在△ABC 中，AB=3，AC=4，BC=5，P 为边BC 上一动点，PE ⊥AB 于E ，PF ⊥AC 于F ，M 为EF 中点，则AM 的最小值为（）A ． 45 B ． 25 C ． 35 D ． 56 7．在梯形ABCD 中，AD ∥BC ，若CD=2，∠C=60°，∠B=90°，则AB=（）A ．4 B ．2 C ． 3 D ．38．如图，在△ABC 中，AB=6，AC=8，BC=10，P 为边BC上一动点（且点P 不与点B 、C 重合），PE ⊥AB 于E ，PF ⊥AC于F ．则EF 的最小值为（）A ．4B ．4.8C ．5.2D ．69．如图是一把30°的三角尺，外边AC=8，内边与外边的距离都是2，那么EF 的长度是（）A ．4 B ．43 C ．2.5 D ．6-2310．下列命题错误的是（）A ．平行四边形的对边相等 B ．两组对边分别相等的四边形是平行四边形 C ．对角线相等的四边形是矩形 D ．矩形的对角线相等11．△ABC 中，AB=AC=5，BC=6，点D 是BC 上的一点，那么点D 到AB 与AC 的距离的和为（）A ．5 B ．6 C ．4 D ．524 12．（2013•河北区二模）已知下列命题中：（1）矩形是轴对称图形，且有两条对称轴；（2）两条对角线相等的四边形是矩形；（3）有两个角相等的平行四边形是矩形；（4）两条对角线相等且互相平分的四边形是矩形．其中正确的有（）A ．4个 B ．3个 C ．2个 D ．1个13．如图，在梯形ABCD 中，AD ∥BC ，∠BCD=90°，BC=2AD ，F 、E 分别是BA 、BC 的中点，则下列结论不正确的是（）A ．△ABC 是等腰三角形 B ．四边形EFAM 是菱形 C ．S △BEF = 21S △ACD D ．DE 平分∠CDF 14．（2012•冷水江市三模）下列关于矩形的说法中正确的是（）A ．矩形的对角线互相垂直且平分 B ．矩形的对角线相等且互相平分C ．对角线相等的四边形是矩形D ．对角线互相平分的四边形是矩形15．直角梯形ABCD 中，AD ∥BC ，AB ⊥BC ，AD=2．BC=DC=5，P 在BC 上运动，则PA+PD 取最小值时，△APD 边AP 上的高是多少（）A ． 17174 B ．17178 C ． 17177 D ． 81717 16．如图，四边形ABCD 中，AC=a ，BD=b ，且AC 丄BD ，顺次连接四边形ABCD 各边中点，得到四边形A 1B 1C 1D 1，再顺次连接四边形A 1B 1C 1D 1各边中点，得到四边形A 2B 2C 2D 2…，如此进行下去，得到四边形A n B n C n D n ．下列结论正确的有（）①四边形A 2B 2C 2D 2是矩形； ②四边形A 4B 4C 4D 4是菱形；③四边形A 5B 5C 5D 5的周长是4ba + ④四边形A n B n C n D n 的面积是12+n abA ．①②B ．②③C ．②③④D ．①②③④17.如图，△ABC 中，AC 的垂直平分线分别交AC 、AB 于点D 、F ，BE ⊥DF 交DF 的延长线于点E ，已知∠A=30°，BC=2，AF=BF ，则四边形BCDE 的面积是（）A ．23B ．33C ．4D ．4318.．下列关于矩形的说法，正确的是（） A ．对角线相等的四边形是矩形 B ．对角线互相平分的四边形是矩形 C ．矩形的对角线互相垂直且平分 D ．矩形的对角线相等且互相平分19．下列命题中，正确的是（）A ．等腰梯形的对角线相等 B ．矩形的对角线互相垂直平分 C ．有两个角为直角的四边形是矩形 D ．对角线互相垂直的四边形是菱形20.下列说法正确的是（）A ．有两个角为直角的四边形是矩形 B ．矩形的对角线互相垂直 C ．等腰梯形的对角线相等 D ．对角线互相垂直的四边形是菱形21．时钟的表面为圆形，在它的圆周上有12个用于表示整点的等分点．以这些等分点为顶点的矩形共有（）A ．6个B ．12个C ．15个D ．18个22．四边形ABCD 中，∠BAD=90°，DC ⊥AC ，AC 交BD 于点O ，AO=AB ，过B 作BN ∥CD 交AC 于E ，交AD 于N ，下列结论：①∠NBD=21 ∠ADC ；②CD+BE=AD ；③若AO=2CO ，则BE=CD ；④S △ABD =S △ADC ，其中正确的个数是（）A ．1个B ．2个C ．3个D ．4个23．如图，四边形ABCD 中，对角线AC ⊥BD ，且AC=8，BD=4，各边中点分别为A 1、B 1、C 1、D 1，顺次连接得到四边形A 1B 1C 1D 1，再取各边中点A 2、 B 2、C 2、D 2，顺次连接得到四边形A 2B 2C 2D 2，…，依此类推，这样得到四边形A n B n C n D n ，则四边形A n B n C n D n 的面积为（）A ．n 216 B ． 128-n C ．421-n D ．不确定 24．下列各组条件中，能判定四边形ABCD 为矩形的是（）A ．∠A+∠B=90°B ．AB ∥CD ，AB=CD ，AC=BDC ．AB ∥CD ，AD=BC ，AC=BD D ．AC=BD ，∠A=90°25．顺次连接四边形ABCD 的四条边的中点，得到一个矩形，那么（）A ．AC=BDB ．AC ⊥BD C ．AB=CD D ．AB ⊥CD26．在四边形ABCD 中，∠A=60°，AB ⊥BC ，CD ⊥AD ，AB=4cm ，CD=2cm ，求四边形ABCD 的周长（）A ．10+23 B ．8+25 C ．8+35 D ．10+2531．如图，在△ABC 中，AB=8，BC=6，AC=10，D 为边AC 上一动点，DE ⊥AB 于点E ，DF ⊥BC 于点F ，则EF 的最小值为（）A ．2.4 B ．3C ．4.8D ．532．等腰梯形的一内角为45°，高等于上底，下底为9，那么梯形的面积为（）A ．27 B ．18 C ．36 D ．2433．下列命题：（1）两条对角线相等的四边形是矩形（2）圆心角相等则所对的弦也相等．（3）两条对角线互相平分的四边形是平行四边形（4）垂直于弦的直径平分这条弦．其中真命题的个数是（） A ．3B ．2C ．1D ．034．比较左、右两图的阴影部分面积，可以得到因式分解公式（）A ．a 2-b 2=（a+b ）（a-b ）B ．（a+b ）2=a2+2ab+b2 C．（a-b）2=a2-2ab+b2 D．a2-ab=a（a-b）35．取四边形ABCD的各边中点E、F、G、H，依次连接EFGH得到四边形EFGH，现知四边形EFGH是菱形，则四边形ABCD的对角线（）A．相等B．相等且平分C．垂直D．垂直且平分36．如图，矩形ABCD中，AB＞AD，AN平分∠DAB，DM⊥AN于点M，CN⊥AN于点N，G为MN的中点，GH⊥MN交CD于点H，且DM=a，GH=b，则CN的值为（用含a、b的代数式表示）（）A．2a+b B．a+2b C．a+b D．2a+2b37．下列说法正确的是（）A．矩形的对角线互相平分B．平行四边形的对角线相等C．有一个角是直角的四边形是矩形D．对角线相等的四边形是矩形39．已知1个四边形的对角线互相垂直，且两条对角线的长度分别是8和10，那么顺次连接这个四边形的四边中点所得的四边形的面积是（）A．40 B．202C．20 D．10240．在四边形ABCD中，∠A=60°，∠ABC=∠ADC=90°，BC=2，CD=11，自D作DH⊥AB 于H，则DH的长是（）A．7.5 B．7 C．6.5 D．5.5。

矩形的判定和性质经典习题

O F E D C B AO D C B A ON M D C B A [矩形的判定和性质]重点内容: ①具有的一切性质；②内角都是直角；③对角线相等；④全等三角形的个数；⑤等腰三角形的个数；⑥对称轴的条数；⑦斜边中线定理；⑧平方等式；⑨两种面积计算方法；⑩有一个直角的→矩形；⑾有三个直角的四边形→矩形；⑿对角线相等的→矩形.基础练习1.在矩形ABCD 中, 对角线交于O 点，AB=0.6, BC=0.8, 那么△AOB 的面积为_______________; 周长为_______________.2.一个矩形周长是12cm, 对角线长是5cm, 那么它的面积为__________________.3.在△ABC 中, AM 是中线, ∠BAC=90︒, AB=6cm, AC=8cm, 那么AM 的长为___________.4.如图, 矩形ABCD 对角线交于O 点, EF 经过O 点, 那么图中全等三角形共有_________对.5.在矩形ABCD 中, AB=3, BC=4, P 为形内一点, 那么PA+PB+PC+PD 的最小值为_________.6.在矩形ABCD 内有一点Q, 满足QA=1, QB=2, QC=3, 那么QD 的长为________________.7.如图, 矩形ABCD 的对角线交于O 点, 若3那么∠BDC 的大小为________.8.如图, 矩形ABCD 对角线交于O 点, 且满足AM=BN, 给出以下结论: ①MN //DC; ②∠DMN=∠MNC; ③OMDONCSS=. 其中正确的是______________.9.一个平行四边形的四个内角的角平分线相交围成的四边形的形状是________________. 10.如图, 在矩形ABCD 中, AE 平分∠BAD, ∠CAE=15︒, 那么∠BOE 的度数为_________.P HD C B AE D C B AF E D C B A FE D C B A O ED C B A 二. 解题技巧1.在矩形ABCD 中，∠A 和∠B 的平分线交边CD 于点M 和N ，若M 、N 是CD 的三等分点，那么AB ：BC 的值为___________________.2.如图, 在矩形ABCD 中,DE ⊥AC 于点E,BC=, CD=2, 那么BE=_______________________.3.如图, 在矩形ABCD 中, AP=DC, PH=PC, 求证: PB 平分∠CBH.4.如图, 矩形ABCD 的周长为16cm, DE=2cm, 若△CEF 是等腰直角三角形, 那么这个三角形的面积为______________.三．简答题1.如图, 在矩形ABCD 中, AD=12, AB=7, DF 平分∠ADC, AF ⊥EF, (1)求EF 长; (2)在平面上是否存在点Q, 使得QA=QD=QE=QF? 若存在, 求出QA 的长; 若不存在, 说明理由.2.一个四边形满足: 它的每个顶点到其它三个顶点的距离之和相等, 试判断这个四边形的形状.3.已知矩形ABCD ，试问：当边AB 和BC 满足什么条件时, 在边CD 上一定存在点P, 使得PA ⊥PB?二巩固练习基本知识点：矩形的性质及判定，直角三角形斜边中线定理.1.矩形的一内角平分线把矩形的一条边分成3和5两部分，则该矩形的周长是___________.2.矩形的两条对角线的夹角是60°，一条对角线与矩形短边的和为15，那么矩形对角线的长为_______，短边长为_______.3.若一个直角三角形的两条直角边分别为5和12，则斜边上的中线等于 .4.如图，E 为矩形ABCD 对角线AC 上一点，DE ⊥AC 于E ，∠ADE: ∠EDC=2:3,则∠BDE 为_______.5.矩形的两邻边分别为4㎝和3㎝，则其对角线为㎝，矩形面积为 cm 2. 6.若矩形的一条对角线与一边的夹角是40°，则两条对角线相交所成的锐角是__________. 7.矩形具有一般平行四边形不具有的性质是（）A. 对边相互平行B. 对角线相等C. 对角线相互平分D. 对角相等8.矩形具备而平行四边形不具有的性质是（）A．对角线互相平分 B．邻角互补 C．对角相等 D．对角线相等9.在下列图形性质中，矩形不一定具有的是（）A．对角线互相平分且相等 B．四个角相等C．是轴对称图形 D．对角线互相垂直平分10.如图，四边形ABCD中，∠ABC=∠ADC=90°，M、N分别是AC、BD•的中点，那么MN⊥BD成立吗？试说明理由．11.如图，在矩形ABCD中，AB=3，BC=4，如果将该矩形沿对角线BD重叠，求图中阴影部分的面积.12.如图，已知在四边形ABCD中，AC DB⊥交于O，E、F、G、H分别是四边的中点，求证：四边形EFGH是矩形．13. 如图，平行四边形ABCD中，AQ、BN、CN、DQ分别是DAB∠、ABC∠、BCD∠、CDA∠的平分线，AQ与BN交于P，CN与DQ交于M，求证：四边形PQMN是矩形．★14.如图矩形ABCD中，延长CB到E，使CE AC=，F是AE中点．求证：BF DF⊥．CCDABEHGOFEDCBANMQPDCBAAFD★15. 如图，矩形ABCD中，CE BD⊥于E，AF平分BAD∠交EC于F，求证：CF BD=．DABCEF。

矩形的性质与判定经典例题练习

矩形第一课时1、矩形的定义2、矩形的性质 1)边 2）角 3）对角线4）对称性3.已知矩形ABCD 中，S 矩形ABCD =24 cm 2，若BC =6 cm ，则对角线AC 的长是________ cm.练一练： 1、矩形的两条对角线把矩形分成个等腰三角形．2、矩形具有而平行四边形不具有的性质是（）A ．对角线互相平分B ．两组对边分别相等C ．相邻两角互补D ．对角线相等3.已知E 是矩形ABCD 的边BC 的中点，那么S △AED =________S 矩形ABCD （）A.21B.41C.51D.61 4.在矩形ABCD 的边AB 上有一点E ，且CE =DE ，若AB =2AD ，则∠ADE 等于（）A.45°B.30°C.60°D.75°【探究三】直角三角形斜边上的中线性质1、根据矩形对角线性质可得到直角三角形斜边上的中线性质：练一练：1、已知直角三角形的周长为14，斜边上的中线长为3．则直角三角形的面积为（） A ．5B ．6C ．7D ．82、如果一个直角三角形斜边上的中线与斜边上的高所夹的锐角为34°，那么这个直角三角形的较小的内角是度．精讲精练例1、如图，在矩形ABCD 中，AC 、BD 相较于点O ，AE 平分BAD ∠交BC 于E ，若15CAE ∠=︒,求BOE ∠的度数。

变式：已知矩形ABCD 中，如图2，对角线AC 、BD 相交于O ，AE ⊥BD 于E ，若∠DAE ∶∠BAE =3∶1，则∠EAC =________.例题2、如图，已知BD 、CE 是ABC 的两条高，M 、N 分别是BC 、DE 的中点，MN 与DE 有怎样的位置关系。

请证明。

例题3.如图，周长为68的矩形ABCD 被分成7个全等的矩形，则矩形ABCD 的面积为（）A.98B.196C.280D.284三、用中学习： 1．（2013•老河口市模拟）由10块相同的长方形地砖拼成面积为1.6m 2的矩形ABCD （如图），则矩形ABCD 的周长为多少？2.矩形的一内角平分线把矩形的一条边分成3和5两部分，则该矩形的周长是（）A.16B.22C.26D.22或263.矩形的两条对角线的夹角是60°，一条对角线与矩形短边的和为15，那么矩形对角线的长为_______，短边长为_______.O N M D CBA 4.矩形ABCD 的周长是56 cm ，它的两条对角线相交于O ，△AOB 的周长比△BOC 的周长少 4 cm ，则AB =_______，BC =_______.5、矩形是轴对称图形，它有______条对称轴．6、在矩形ABCD 中，对角线AC ，BD 相交于点O ，若对角线AC=10cm ，•边BC=•8cm ，•则△ABO 的周长为________．7、如图2，根据实际需要，要在矩形实验田里修一条公路（•小路任何地方水平宽度都相等），则剩余实验田的面积为________．（1） (2)8、在矩形ABCD 中, 对角线交于O 点，AB=0.6, BC=0.8, 那么△AOB 的面积为_______________; 周长为_______9、一个矩形周长是12cm, 对角线长是5cm, 那么它的面积为__________________.10.在△ABC 中, AM 是中线, ∠BAC=90︒, AB=6cm, AC=8cm, 那么AM 的长为_____________________.11.在矩形ABCD 中, AB=3, BC=4, P 为形内一点, 那么PA+PB+PC+PD 的最小值为______12.如图, 矩形ABCD 对角线交于O 点, 且满足AM=BN, 给出以下结论: ①MN //DC; ②∠DMN=∠MNC; ③OMD ONC S S =. 其中正确的是______________.13、已知，如图，矩形ABCD 的对角线AC ，BD 相交于点O ，E ，F 分别是OA ，OB 的中点．（1）求证：△ADE ≌△BCF ；（2）若AD=4cm ，AB=8cm ，求OF 的长．14、如图，在矩形ABCD 中，已知AB=8cm ，BC=10cm ，折叠矩形的一边AD ，使点D 落在BC 边的中点F 处，折痕为AE ，求CE 的长．矩形的判定典型例题及练习归纳矩形的三种判定方法：精讲精练例1、已知：如图，ABCD 的四个内角的平分线分别相交于点E 、F 、G 、H 。

矩形的性质与判定综合练

矩形的性质和判定综合练习一．选择题1．下列四个命题中，正确的是（）A．对角线相等的四边形是矩形 B．有一个角是直角的四边形是矩形C．两组对边分别相等的四边形是矩形 D．四个角都相等的四边形是矩形2．四边形ABCD的对角线AC，BD，下面给出的三个条件中，选取两个，能使四边形ABCD是矩形，①AC，BD互相平分；②AC⊥BD；③AC＝BD，则正确的选法是（）A．①②B．①③C．②③D．以上都可以3．如图，在等腰直角△ABC中，AB＝BC，点D是△ABC内部一点，DE⊥BC，DF⊥AB，垂足分别为E，F，若CE＝3DE，5DF＝3AF，DE＝2.5，则AF＝（）A．8 B．10 C．12.5 D．154．如图，矩形ABCD中，点E是BC上一动点，连接AE、DE，以AE、DE为边作▱AEDF，当点E从点B运动到点C的过程中，▱AEDF的面积（）A．先变小后变大 B．先变大后变小C．保持不变 D．一直变大5．如图，矩形ABCD中，对角线AC，BD相交于点O，AE平分∠BAD交BC于点E，∠CAE＝15°，则∠AOE的度数为（）A．120° B．135°C．145° D．150°6．如图，在锐角△ABC中，延长BC到点D，点O是AC边上的一个动点，过点O作直线MN∥BC，MN 分别交∠ACB、∠ACD的平分线于E，F两点，连接AE、AF，在下列结论中：①OE＝OF；②CE＝CF；③若CE＝12，CF＝5，则OC的长为6；④当AO＝CO时，四边形AECF是矩形．其中正确的是（）A．①④ B．①② C．①②③ D．②③④二．解答题7．如图．平行四边形ABCD中，AD＝2AB，M、N分别为AD、BC的中点，AN、BM交于点P，CM、DN交于点Q．求证：（1）四边形ABNM为菱形；（2）四边形PNQM为矩形．8．如图，菱形ABCD的对角线AC，BD相交于点O，E是AD的中点，点F，G在AB上，EF⊥AB，OG∥EF．（1）求证：四边形OEFG是矩形；（2）若AD＝20，EF＝8，求OE和BG的长．9.如图，在矩形ABCD中，AB=2，BC=5，E、P分别在AD、BC上，且DE=BP=1，AP、BE相交于点H，CE、DP相交于点F.(1)判断△BEC的形状，并说明理由;(2)判断四边形EFPH是什么特殊四边形，并证明你的判断.（选做题）如图，在菱形ABCD中，对角线AC，BD交于点O，过点A作AE⊥BC于点E，延长BC到点F，使CF ＝BE，连接DF．（1）求证：四边形AEFD是矩形；（2）连接OE，若AD＝10，EC＝4，求OE的长度．。