矩形的性质和判定
矩形的判定和性质
矩形的性质和判定一、基础知识(一)矩形的定义有一个内角为直角的平行四边形叫做矩形。
(二)矩形的性质:1.矩形具有平行四边形的一切性质;2.矩形的对角线相等;3.矩形的四个角都是900; 4.矩形是轴对称图形;边 角 对角线 对称性 矩形对边平行且相等四个角都是直角互相平分且相等轴对称,中心对称(三)矩形的判定:1.有一个角是直角的平行四边形是矩形;2.对角线相等的平行四边形是矩形;3.有三个角是直角的四边形是矩形;4.对角线相等且互相平分的四边形是矩形。
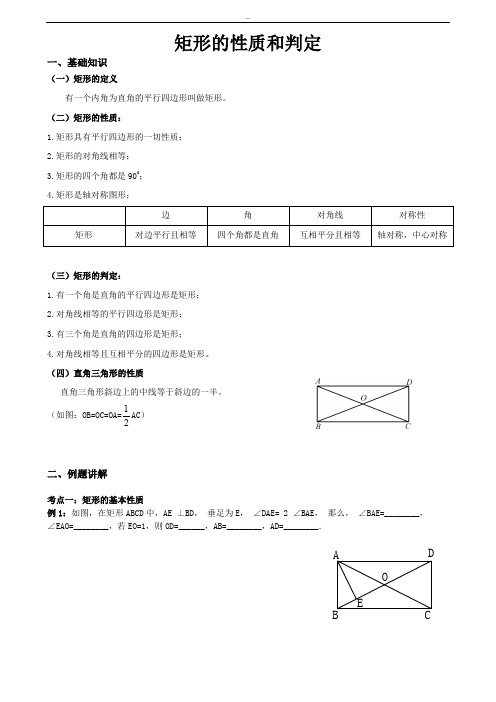
(四)直角三角形的性质直角三角形斜边上的中线等于斜边的一半。
(如图:OB=OC=OA=21AC )二、例题讲解考点一:矩形的基本性质例1:如图,在矩形ABCD 中,AE•⊥BD ,•垂足为E ,•∠DAE=•2•∠BAE ,•那么,•∠BAE=________, ∠EAO=________,若EO=1,则OD=______,AB=________,AD=________.AEDCBO练习 1:矩形ABCD中, ,对角线AC与BD相交于点O,BC的长为6,△OBC的周长是15,求矩形的对角线的长度.练习2:如图,在矩形ABCD中,CE⊥BD,E为垂足,∠DCE∶∠ECB=3∶1,求∠ACD.例2:如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线长是13cm,那么矩形的周长是多少?练习1:矩形ABCD中, ,对角线AC与BD相交于点O,已知矩形ABCD的面积是12cm2,AB=4cm,求矩形的对角线长。
例3:如图,在矩形ABCD 中,相邻两边AB 、BC 分别长15cm 和25cm ,内角∠BAD 的角平分线与边BC 交于点E .试求BE 与CE 的长度.练习1:如图,在矩形ABCD 中,E 是边AD 上的一点.试说明△BCE 的面积与矩形ABCD 的面积之间的关系.例4:(2009年广西钦州)已知:如图1,在矩形ABCD 中,AF =BE .求证:DE =CF ;ADCB 图1F E练习1:如图,矩形ABCD 中,E 为AD 中点,∠BEC 为直角,矩形ABCD 的周长是20,求AD 、AB 的长。
矩形的性质与判定习题及答案

由题意得:AE=CF=t
AE=CF=t
∵点G、H分别是矩形ABCD的边AB、 EF=5﹣2(5﹣t)=2t-5
DC的中点,
∴ BG 1 AB,CH 1 CD
2
2
∴2t-5=4 ∴t=4.5
又∵AB=CD,AB∥CD
综上,当t为0.5秒或4.5秒时,
∴BG∥CH,BG=CH
四边形EGFH为矩形
∴四边形BCHG为平行四边形
2
2
4
∴ 13 PE PF 15
4
∴ PE PF 60 13
(1)矩形的面积公式是S=长×宽(两邻边的乘积)
(2)过矩形对角线交点O的任一直线平分矩形ABCD的面积
(3)矩形ABCD对角线AC、BD相交于点O,则
①△ABO≌△CDO,△AOD≌△COB
△ABO,△CDO,△AOD,△COB都是等腰三角形
1
2
证明:(1)∵四边形ABCD是矩形, 在△AEG与△CFH中
∴AB=CD,AB∥CD,AD∥BC, ∠B=90°
∴∠1=∠2 ∵G、H分别是AB、DC的中点 ∴AG=BG,CH=DH ∴AG=CH
AG CH
1
2
AE CF
∴△AEG≌△CFH(SAS)
∴EG=FH
∵AE=CF
又∵GF=HE
②△ABD≌△CDB≌△BAC≌△DCA
△ABD,△CDB,△BAC,△DCA都是直角三角形
③S△ABO
=S△BCO
=S△CDO
=S△AOD
=
1 4
S矩形ABCD
例4.如图,O是矩形ABCD的对角线的交点,E、F、G、 H分别是OA、OB、OC、OD上的点,且AE=BF=CG =DH. (1)求证:四边形EFGH是矩形; (2)若E、F、G、H分别是OA、OB、OC、OD的中点 ,且DG⊥AC,OF=2cm,求矩形ABCD的面积.
矩形的性质与判定知识点

矩形的性质与判定知识点矩形是我们日常生活中最常见的几何形状之一,因为它有很多明显的性质和特点,所以在数学、物理等领域中也被广泛应用。
本文旨在介绍矩形的性质与判定知识点,以帮助读者更好地理解和应用矩形。
一、矩形的基本定义和性质在几何学中,矩形是一个四边形,其中对角线相等,且所有内角均为直角。
它的两条对边平行且长度相等,两条相邻边的内角均为90度。
由此可以得到矩形的以下基本性质:1. 对角线相等设矩形的两条对角线为AC和BD,则AC=BD,即对角线相等。
2. 边角关系设矩形的边长为a和b,则它的周长为C=2a+2b,面积为S=ab。
3. 内角和由于矩形的内角均为90度,因此它的任意两个内角的和均为180度。
4. 三角函数关系设矩形的一条边长为a,另一条边长为b,则其对角线长为D=sqrt(a^2+b^2)。
根据三角函数关系,可得矩形各角的正切值和余切值:tanA=a/b,tanB=b/a,cotA=b/a,cotB=a/b。
二、矩形的性质扩展除了以上基本性质外,矩形还有一些特殊的性质,它们在具体的数学问题中往往会有实际的应用。
下面介绍一些常见的扩展性质。
1. 中线定理设矩形ABCD的对角线AC和BD相交于点O,线段AB与线段CD交于点E,线段AD与线段BC交于点F。
则OE、OF为矩形的中线,且OE=OF=1/2AC。
证明:由于AC=BD,因此OC=OD。
又由于AB∥CD,因此∠OAB=∠OCD,∠OBA=∠OCB。
因此三角形OAB和OCD,三角形OBA和OCB均为全等三角形,故OA=OC,OB=OD。
又因为OE是线段AB上的中线,OF是线段AD上的中线,因此OE=1/2AB=1/2CD,OF=1/2AD=1/2BC。
因此OE=OF=1/2AC。
2. 对称性质设矩形ABCD的对角线AC和BD相交于点O,则AO=CO,BO=DO。
由此可知,点O是矩形的对称中心。
证明:因为AC=BD,所以OC=OD,且三角形AOC和COD的第一边、第三边、第五边相等,因此它们一定全等。
初中数学矩形的性质与判定

初中数学矩形的性质与判定
矩形是平面几何中最基本的图形之一,它是一个由四条直线构成的平行四边形,两个对角
线相等,对角线分别叫做矩形的两个直角边。
由以上定义可知,矩形是一种特殊的平行四
边形,所以,矩形的性质有如下一些:
一、矩形的四边相等
矩形的四条边是相等的,不管你横向测量,还是纵向测量,都得到相同的长度。
二、矩形的两个对角线相等
即矩形对角线是相等的,并且垂直于矩形的四边。
三、矩形有四个顶点
矩形有四个定点,分布在矩形的每个角,两个对角上。
判定矩形:
我们可以根据以上性质来判定一个图形是否是矩形:
1、检查四边,如果四边相等,则可以推断它可能是矩形;
2、测量对角线的长度,如果两条对角线长度相等,且垂直于矩形的四边,则可以确认它
是矩形;
3、查看顶点,如果有四个顶点,则它就是矩形。
综上所述,矩形是一种平行四边形,有四边相等,两个对角线相等,且垂直于矩形的四边,有四个顶点的特殊图形。
我们可以根据矩形的性质和判定规则,很容易判断出一个平行四
边形是否是矩形。
矩形的性质与判定

矩形的周长计算与性质
矩形的周长计算:
• 两倍的长加上两倍的宽 • 对角线的和
矩形的周长性质:
• 周长大于等于零 • 周长是一个常数
矩形在实际问题中的应用案例
建筑设计中的矩形框架:
• 节省材料 • 结构稳定
电子元件中的矩形封装:
• 方便安装 • 散热性能好
04
矩形与其他图形的关系与转化
矩形与平行四边形的关系与转化
矩形的性பைடு நூலகம்与判定
CREATE TOGETHER
DOCS
01
矩形的定义与基本性质
矩形的定义及其几何特征
矩形的定义:
• 有四个角都是直角的四边形 • 对边平行且相等
矩形的几何特征:
• 对边平行且相等 • 四个角都是直角 • 对角线相等且互相平分
矩形的实际应用:
• 建筑设计中的矩形框架 • 电子元件中的矩形封装
• 矩形可以通过对角线平移转化为正方形 • 正方形可以通过对角线折叠转化为矩形
矩形与长方形的关系与转化
矩形与长方形的关系:
• 矩形是长方形的一种特殊情况 • 长方形是特殊的矩形
矩形与长方形的转化:
• 矩形可以通过对角线平移转化为长方形 • 长方形可以通过对角线折叠转化为矩形
05
矩形在几何解题中的策略与方法
矩形的对边平行且相等
矩形的对边平行且相等的性质:
• 对角线互相平分 • 对角线相等
矩形的对边平行:
• 同一列的边平行 • 同一行的边平行
矩形的对边相等:
• 同一列的边相等 • 同一行的边相等
矩形的四个角都是直角
矩形的角:
• 四个角都是直角 • 直角的角度为90度
矩形的直角性质:
矩形的性质和判定

〖知识梳理〗知识点1:矩形的概念与性质1.概念:有一个角是的平行四边形叫做矩形。
2.矩形的性质(1)矩形是特殊的平行四边形,所以具有平行四边形的一切性质(2)矩形性质定理1:矩形的四个角都是。
(3)矩形性质定理2:矩形的对角线。
(如图,在矩形ABCD中,AC,BD相交于点O,由性质2有AO=BO=CO=DO=21AC=21BD.因此可以得到直角三角形的一个性质:直角三角形斜边上的中线等于斜边的一半.)3.矩形的性质也可以从边、角、线及对称性来分析(如右图分析)边:角:线:对称性:【例1】已知:如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4cm,求矩形对角线的长.【例2】已知:如图,矩形ABCD,AB长8 cm ,对角线比AD边长4 cm.求AD的长及点A到BD的距离AE的长.学习目标1、掌握矩形的概念与性质,应用矩形的性质计算和证明。
2、理解矩形的判定定理,能够有理有据地推理证明及精准的书写表达.知识点2:矩形的判定1、(定义)矩形判定定理1:有一个角是直角的平行四边形式矩形。
2、矩形判定定理2:有三个角是的四边形是矩形。
3、矩形判定定理3:对角线的平行四边形是矩形。
【例3】已知:如图,O是矩形ABCD对角线的交点,AE平分∠BAD,∠AOD=120°,求∠AEO的度数.【例4】如图,四边形ABCD是平行四边形,AC=BD.求证:四边形ABCD是矩形【例5】如图,在ABCD中,DE⊥AB,DF⊥CD,垂足分别为E,F. 求证(1)△ADE≌△CBF(2)四边形BFDE为矩形【例6】1.(填空)(1)矩形的定义中有两个条件:一是,二是.(2)已知矩形的一条对角线与一边的夹角为30°,则矩形两条对角线相交所得的四个角的度数分别为、、、.(3)已知矩形的一条对角线长为10cm,两条对角线的一个交角为120°,则矩形的边长分别为cm,cm,cm,cm.2.(选择)(1)下列说法错误的是().(A)矩形的对角线互相平分(B)矩形的对角线相等(C)有一个角是直角的四边形是矩形(D)有一个角是直角的平行四边形叫做矩形(2)矩形的对角线把矩形分成的三角形中全等三角形一共有().(A)2对(B)4对(C)6对(D)8对〖课堂练习〗一、选择题1.若矩形ABCD的邻边长分别是1,2,则BD的长是( )A. 3 B.3 C. 5 D.2 52.如图,在矩形ABCD中,E是BC边的中点,且AE平分∠BAD,CE=2,则CD的长是( ) A.2 B.3 C.4 D.53.下列说法不正确的是( )A.矩形的四个内角都是直角B.矩形的对角线相等且互相平分C.矩形既是轴对称图形,又是中心对称图形D.矩形的对角线互相垂直4.如图5所示,在矩形ABCD中,对角线AC,BD相交于点O,若OA=2,则BD的长为( ) A.4 B.3 C.2 D.1图 65.2019·海口如图6,矩形ABCD的对角线AC与BD相交于点O,∠ADB=30°,AB=4,则OC等于( ) A.5 B.4 C.3.5 D.3二、填空题6.如图2,将矩形ABCD沿对角线BD折叠,使点C和点C′重合,若AB=2,则C′D的长为________.27.如图7所示,已知矩形ABCD的周长为56,O为对角线的交点,△BOC与△AOB的周长之差为4,则AB=________,BC=________.78.如图8,在矩形ABCD中,E为BC的中点,且∠AED=90°,AD=10,则AB的长为________.8三、解答题9.如图,四边形ABCD是矩形,E是AD的中点,F是BC的中点.求证:△ABF≌△CDE.10.如图,在矩形ABCD中,BF=CE.求证:AE=DF.11.如图,在ABCD中,AB=6,BC=8,AC=10.(1)求证:四边形ABCD是矩形.(2)求BD的长.12.已知:如图,在△ABC中,∠ACB=90°,D是AB的中点,DE,DF分别是△ADC,△BDC的角平分线.求证:四边形DECF是矩形.13.如图,在△ABC中,AB=AC,点F在CA的延长线上,AD,AE分别平分∠BAC和∠BAF,BE⊥AE,垂足为E.求证:(1)DA⊥AE;(2)四边形ADBE是矩形.。
矩形定义、性质、判定
矩形定义、性质、判定
•矩形:
是一种平面图形,矩形的四个角都是直角,同时矩形的对角线相等,而且矩形所在平面内任一点到其两对角线端点的距离的平方和相等。
•矩形的性质:
1.矩形的4个内角都是直角;
2.矩形的对角线相等且互相平分;
3.矩形所在平面内任一点到其两对角线端点的距离的平方和相等;
4.矩形既是轴对称图形,也是中心对称图形(对称轴是任何一组对边中点的连线),它至少有两条对称轴。
对称中心是对角线的交点。
5.矩形是特殊的平行四边形,矩形具有平行四边形的所有性质
6.顺次连接矩形各边中点得到的四边形是菱形
•矩形的判定:
①定义:有一个角是直角的平行四边形是矩形
②定理1:有三个角是直角的四边形是矩形
③定理2:对角线相等的平行四边形是矩形
④对角线互相平分且相等的四边形是矩形
矩形的面积:S矩形=长×宽=ab。
•黄金矩形:
宽与长的比是(√5-1)/2(约为0.618)的矩形叫做黄金矩形。
黄金矩形给我们一协调、匀称的美感。
世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计。
如希腊的巴特农神庙等。
矩形的性质与判定
∴四边形DEMN是平行四边形.
∵BD=2AB,BD=2BO,∴AB=OB.又∵M是AO的中点,∴BM⊥AO. ∴∠AMB=∠EMN=90°. ∴四边形DEMN是矩形. ∵AB=5,DN=BM=EM=4,∴AM=3=MO. ∴MN=6. ∴矩形DEMN的面积为6×4=24.
理由如下: ∵△ABC 是等腰三角形且 AD⊥BC,
A
E N
∴BD = CD,
F
又∵ADCE是矩形,∴AE = CD,AE∥CD,
∴BD=AE, BD∥AE,
B
D
C
∴四边形 ABDE 是平行四边形.
探究新知
A 直角三角形斜边上的中
线等于斜边的一半。 B
符号语言:
∵ Rt△ABC,O是AC的中点
∴
BO=
(2)当AB=DC时,求证:AEFD是矩形.
B (2)证明:∵四边形ABED和四边形AFCD都是平行四边形,
E
F
C
∴DE=AB,AF=DC.
又AB=DC,
∴DE=AF.
又∵四边形AEFD是平行四边形,
A
D
四边形 判定 条件
平行四边形 有一个角是直角
对角线相等
B
O
C
判定菱形的常见思路:
四条边都相等
四边形 判定 平行四边形 一组邻边相等
条件
对角线互相垂直
菱形
随堂练习
1. 已知:如图,四边形 ABCD 由两个全等的等边三角形 ABD 和 CBD 组 成,M,N 分别是 BC 和 AD 的中点. 求证:四边形BMDN是矩形.
1.2.1矩形的性质和判定(教案)
(1)在解决矩形相关问题时,能够灵活运用矩形的性质,如求矩形的周长、面积等。
(2)在给定条件下,能够准确判定一个四边形是否为矩形,例如,当知道一个四边形有一个直角且对边平行时,能判定它为矩形。
2.教学难点
-矩形性质的理解与应用:难点在于学生需要深入理解矩形性质的内涵,并在实际问题中灵活应用。
五、教学反思
在上完这节关于矩形的性质和判定的课程后,我思考了一些问题。首先,我发现学生们在理解矩形性质方面相对容易,他们能够通过观察日常生活中的矩形物体,如桌子、书本等,来形象地理解这些性质。然而,对于判定矩形的方法,尤其是综合运用多个条件进行判定时,学生们似乎遇到了一些困难。
我意识到,可能需要更多的实际例子和练习来帮助学生巩固这些判定方法。在接下来的课程中,我打算设计一些更具挑战性的问题,让学生们通过小组合作解决,这样可以提高他们在实际情境中运用知识的能力。
-矩形判定的综合运用:难点在于学生需要将判定方法综合运用,解决较复杂的几何问题。
举例解释:
(1)难点在于如何引导学生从已知条件中发现矩形性质的应用,例如,在求解矩形对角线长度时,需要运用到对角线互相平分的性质。
(2)当面对一个复杂的四边形,学生需要综合运用判定方法,如对角线相等且互相平分,来判断它是否为矩形。这时,学生可能会在判定过程中出现困惑,如何将不同判定方法相结合,是教学的难点。
3.成果展示:每个小组将向全班展示他们的讨论成果和实验操作的结果。(四)学生小组Fra bibliotek论(用时10分钟)
1.讨论主题:学生将围绕“矩形在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法,并与其他小组成员进行交流。
2.引导与启发:在讨论过程中,我将作为一个引导者,帮助学生发现问题、分析问题并解决问题。我会提出一些开放性的问题来启发他们的思考。
小学数学知识归纳矩形的性质与判定
小学数学知识归纳矩形的性质与判定矩形是小学数学中常见的几何形状之一,它具有特定的性质和判定方法。
本文将详细介绍矩形的性质与判定,旨在帮助小学生全面了解和掌握矩形的知识。
一、矩形的性质1. 边与角矩形的四条边两两平行,两组对边相等。
矩形的四个角都是直角,即每个角都是90度。
2. 对角线矩形的对角线互相垂直且相等。
对角线是由矩形的两个非邻边所组成的线段,它们相交于矩形的中心点。
3. 对边的关系矩形的两条邻边相等,两条对边相等但不相交。
这意味着,如果一边的长度确定了,那么对边的长度也就确定了。
4. 周长和面积矩形的周长等于其所有边的长度之和,即P=2(a+b),其中a和b分别表示矩形的两条邻边的长度。
矩形的面积等于邻边的长度之积,即S=a*b。
二、矩形的判定方法1. 边长判定判定一个四边形是否为矩形,可以先检查其四条边是否两两平行。
如果四边互相平行且相邻边长度相等,则可以确定该四边形是矩形。
2. 直角判定对于四边形的角度判定,可以使用直角定理。
直角定理指出,如果一个四边形的四个角都为直角(90度),那么该四边形就是矩形。
三、矩形的应用举例1. 长方形长方形是一种特殊的矩形,其中两对对边相等且所有角均为直角。
在日常生活中,许多物体的形状可以近似看作长方形,例如书桌、门窗等。
2. 正方形正方形也是一种特殊的矩形,它的四个角都是直角且四条边相等。
正方形具有较为均匀的分布和轻便的特点,常见于方形小盒子、棋盘等物体。
四、总结矩形作为小学数学中的重要内容,其性质和判定方法需要小学生们仔细学习和理解。
矩形具有特定的边与角、对角线、对边关系、周长与面积等性质,使用边长判定和直角判定方法可以快速判断矩形。
长方形和正方形是矩形的特殊情况,它们在日常生活中的应用广泛。
通过学习矩形的性质与判定,小学生们可以更好地应用数学知识解决实际问题,培养逻辑思维和几何思维能力。
同时,深入理解矩形的知识有助于打下数学基础,为后续学习其他几何形状奠定坚实的基础。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
矩形教学设计
教学目标
知识与技能
1.能用综合法来证明矩形的性质定理和判定定理以及相关结论.
2.能运用矩形的性质进行简单的证明与计算
过程与方法
体会在证明过程中所运用的归纳、类比、转化等数学思想方法.
情感、态度与价值观
学生通过观察发现生活中的矩形,在探索和运用矩形的过程中感受到数学的乐趣
重点难点
重点:矩形的性质;矩形的判定。
难点:矩形的性质和判定的综合运用。
教学方法
观察、总结、讨论分析。
教学过程
一、回顾旧知,温故新知
1.平行四边形有哪些特征?
2.有几种方法可以判别四边形为平行四边形?
3.四边形具有稳定性吗?
二、创设情境,导入新课
出示多媒体
1.引入
我们已经知道平行四边形是特殊的四边形,因此平行四边形除具有四边形的
性质外,还有它的特殊性质,同样对于平行四边形来说有特殊情况即特殊的平行
四边形,这堂课我们就来研究一种特殊的平行四边形—— 矩形
2.知识讲解
观察
A
B
C
D
A
B C
D
一个角变成直角
分析:(1)矩形的形成过程是平行四边形的一个角由量变到质变的变化过程.
(2)矩形只比平行四边形多一个条件:“一个角是直角”,不能用“四个角都是
直角的平行四边形是矩形”来定义矩形.
定义:有一个角是直角的平行四边形是矩形
矩形与平形四边形之间的关系
(3)矩形是特殊的平行四边形,具有平行四边形的一切性质(共性),还具有它
自己特殊的性质(个性)
(4)从边、角、对角线方面,观察或度量猜想矩形的特殊性质.
①边:对边分别平行且相等(与平行四边形相同),邻边互相垂直
②角:四个角都是直角(性质1)
③对角线:相等且互相平分
三、例题讲解
已知:如图,四边形ABCD是矩形.
求证:∠A=∠B=∠C=∠D=90°.
分析:由矩形的定义,利用对角相等,邻角互补可使问题得证.
证明: ∵ 四边形ABCD是矩形,
∴∠A=90°,四边形ABCD是平行四边形.
∴∠C=∠A=90°, ∠B=180°-∠A=90°,
∠D=180°-∠A=90°.
∴四边形ABCD是矩形.
【定理】矩形的四个角都是直角.
跟踪练习
已知:如图,AC,BD是矩形ABCD的两条对角线.
求证: AC=BD.
分析:根据矩形的性质,可转化为
全等三角形(SAS)来证明.
证明:∵ 四边形ABCD是矩形,
∴AB=DC,∠ABC=∠DCB=90°.
∵BC=CB,
∴△ABC≌△DCB(SAS).
∴AC=DB.
【定理】矩形的两条对角线相等.
练一练:
平行四边形
矩形
A B C D
O
D B C A
如图在矩形ABCD中①AB∥_____,
AB=_____;AD∥____,AD=_____.
②∠BAD=∠______=∠_____=∠______=90°
③AC=_____= 2AO =2______=2_____=2______.
问:在Rt△ABC中,斜边AC上的中线是_____,它与斜边的关系是_____=____AC.
问:是不是所有的三角形都有这样的性质?
【推论】直角三角形斜边上的中线等于斜边的一半
例题:已知:如图,在□ABCD中,对角线AC=BD.
求证:四边形ABCD是矩形.
分析:要证明□ABCD是矩形,只要证明
有一个角是直角即可.
证明: ∵四边形ABCD是平行四边形.
∴AB=CD,AB∥CD.∵AC=DB,BC=CB,
∴ △ABC≌△DCB.∴∠ABC=∠DCB.
∵∠ABC+∠DCB=180°.∴∠ABC=90°.
∴平行四边形ABCD是矩形.
【定理】对角线相等的平行四边形是矩形.
练一练
1.已知:如图,在四边形ABCD中, ∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
分析:利用同旁内角互补,两直线平行来
证明四边形是平行四边形,可使问题得证.
证明:∵ ∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°.
∴AD∥BC,AB∥CD.
∴四边形ABCD是平行四边形.
∴四边形ABCD是矩形.
【定理】有三个角是直角的四边形是矩形.
2.填空
⑴有三个角是直角的四边形是_______
⑵有一个角是直角的_____________是矩形.
⑶对角线_______的平行四边形是矩形
⑷对角线互相平分且相等的四边形是_______
⑸有一个角是直角,且对角线_______________的四边形是矩形.
随堂练习
A
BC
D
O
B D C
A
D
B
C
A
1.(2010·巴中中考)如图所示,已知□ABCD,下列条件:①AC=BD,②AB=AD,
③∠1=∠2,④AB⊥BC中,能说明□ABCD是矩形的有 (填写序号).
解析:根据对角线相等的平行四边形是矩形;矩形的定义.
答案:① ④
2.(2010·益阳中考)如图,在△ABC中,AB=AC=8,AD是底边上的高,E为
AC中点,则DE= .
解析:根据直角三角形斜边上的中线等于斜边的一半可得,DE等于AC的一
半,所以DE=4.
答案:4
3.(2010·聊城中考)如图,在等边△ABC中,点D是BC边的中点,以AD
为边作等边△ADE.
(1)求∠CAE的度数;
(2)取AB边的中点F,连结CF、CE,
试证明四边形AFCE是矩形.
解析:(1)在等边△ABC中,
∵点D是BC边的中点,
∴∠DAC=30º,又∵△ADE是等边三角形,
∴∠DAE=60º,
∴∠CAE=30º
(2)在等边△ABC中,∵F是AB边的中点,D是BC边的中点,∴CF=AD,
∠CFA=90º,又∵AD=AE,∴AE=CF,由(1)知∠CAE=30º,∴∠EAF=60º+30
º=90º,∴∠CFA=∠EAF,∴CF∥AE,∵AE=CF,∴四边形AFCE是平行四边形,
又∵∠CFA=90º,∴四边形AFCE是矩形.
4.已知:如图,四边形ABCD是由两个全等的正三角形ABD和BCD组成的,M、
N•分别为BC、AD的中点.
求证:四边形BMDN是矩形.
2
1
D
C
B
A
E
F
D
A
BC
证明:在正△ABD和正△BCD中 ,M、N•分别为BC、AD的中点
∴BN⊥AD,DM ⊥ BC,∠DBC=60°
∠BND= ∠DMB=90°,∠NBD=30°
∴ ∠NBM=90°
四边形BMDN是矩形
5.已知:如图,AC,BD是矩形ABCD的两条对角线,AC,BD相交于点O,∠
AOD=120°,AB=2.5cm.求矩形对角线的长.
解析:∵四边形ABCD是矩形,
∴AC=BD,且
∴OA=OD,
∵∠AOD=120°,
∴∠ODA=∠OAD=
∵∠DAB=90°,
∴BD=2AB=2×2.5=5(cm).
你认为本题还可以怎样解?
本课小结
通过本课时的学习,需要我们掌握:
1.矩形的特有性质:
(1)矩形的四个角都是直角;
(2)矩形的对角线相等;
(3)推论:直角三角形斜边上的中线等于斜边的一半.
2.矩形的判定定理:
(1)定义:有一个角是直角的平行四边形是矩形;
(2)对角线相等的平行四边形是矩形;
(3)有三个角是直角的四边形是矩形。
作业
习题19.3 1. 2. 3(1)。
D B C A
O
