第2讲 计量资料的基本统计分析方法
计量的统计分析 PPT
将原始数据采用划记法或计算机汇
总，得到各个组段的观察单位数
（频数），列成频数表。
计量的统计分析
6
表2-2 某地140名正常男子红细胞数的频数表
累计频 数：某 一指定 组段及 前面各 组段的 频数之 和。
累计频数 除以总各频组频数分别 数的比除值以总频数的 称为累比计值称为频率。 频率。各它组频率之和 描述了应累为100％。 计频数频在率描述了各 全体中组所频数在全体 占的比中重所。占的比重。
正偏态分布：长尾向右延伸
0.5
3.5
6.5
9.5 12.5 15.5 18.5 21.5 24.5 27.5 30.5 33.5 36.5 39.5 42.5 45.5 48.5 51.5 54.5 57.5
计量的统计分析
11
三、频数表的用途
1.作为陈述资料的形式，可代替原始资料，便 于进一步分析 2.便于观察数据的分布类型 3.便于发现资料中某些远离群体的特大或特小 的可疑值 4.当样本含量比较大时，可用各组段的频率作 为概率的估计值
熟悉：百分位数。
计量的统计分析
2
计量资料的统计描述
方法计有量两资类料：（measurement data):对每个
1. 统观计察图对表象的观察指标用定量方法测定 主其要数是值频大数小分所布得表的、资频料数，分一布般图有度量
（直衡方单图位）。
2. 选用适当的统计指标 集中趋势指标、变异程度指标
计量的统计分析
如何有效地组织、整理和表达数据的信息？
计量的统计分析
5
一、频数表 (Frequency Tabl区间内出现的频数。 确定组数k 通常选择在8～15之间
确定组距 确定组段 列表划记
2.计量资料的统计描述
2021/8/3
22
(100X)%
PX
百分位数示意图
2021/8/3
23
PXLXifX X(nX%fL)
Lx Px所在组段的下限
ix Px所在组段的组距
fx Px所在组段的频数
fL 该组段之前的累计频数
n 总例数
2021/8/3
24
百分位数例
利用上表，求P50，P25，P75
P 5 01 43 4 0 7 1 2 5% 0 0 3 5 1.4 9(c 2 4)m
2021/8/3
35
4.标准差 standard deviation
符号： σ—总体标准差
S —样本标准差
计算： （x）2
N
S （xx）2
n1
意义：标准差越大，观察值的变异就越大
，数据越分散，均数的代表性越差；反之
，资料越集中，均数的代表性越好。
适用条件：对称分布、正态分布资料
2021/8/3
算术均数 几何均数 中位数
2021/8/3
12
第二节 描述集中趋势的指标
算数均数（mean） 简称均数 适用条件：对称分布，尤其是正态分布或近似正态分布
x 表示：总体均数用μ表示；样本均数用 表示
意义：描述一组同质资料的平均水平。 计算方法：
直接法 间接法（频数表法）
2021/8/3
13
1、 算 术 均 数 ( arithm etic m ean)
2021/8/3
32
2、四分位数间距 quantile range 符号： Q（中间一半观察值的极差） 计算 ：Q=P75-P25
下四分位数： QL P25
上四分位数： QU P75
计量资料的统计描述
分 层 抽 样
整 群 抽 样
样
7
概率抽样、非概率抽样
• 概率抽样：每个对象被抽中的概率是已知/可计算的，其样本统计量是参数估计 和计算误差的基础；
• 等概率抽样：随机抽样 • 不等概率抽样：多单位被抽取的概率不同，可能会得到更有效的估计量 • 非概率抽样：抽样概率未知/无法计算，按主观、有目的、为方便进行抽样； • 不能计算抽样误差，或一般按简单随机抽样计算误差。配额抽样、滚雪球/识别
计量资料的统计描述
1
统计学中的几个基本概念
1、同质与变异 2、总体与样本 3、普查与抽样 4、参数与误差 5、频率与概率（小概率事件）
2
1. 同 质 与 变 异
• 同质（homogeneity）
指事物某方面的性质、影响条件或背景相同或相 近
• 变异（variation）
同质个体间的差异。来源于一些未加控制或无法控制的甚至不明原因的因素。 是统计学存在的基础。
M
X
8＋X
2
8＋1 2
2 （X 4＋X5）2 （14＋15）2 14.5(天)
42
百分位数
• 将N个观察值从小到大依次排列，再分成100等份，对应于X%位的数值即为PX。 中位数是百分位的特殊形式P50 。同样还有四分位数、十分位数等。
TG
31
第二节 计量资料的常用统计指标
一、集中趋势的描述－平均值
平均值是一组数据典型或有代表性的值。由于这样典型 的值趋向于落在根据数据大小排列的数据的波峰位置， 因此可以用于度量集中位置。
常用几种平均值：
1.算术均数 2.几何均数 3.中位数
32
1.算术均数（均数）
• 意义：一组性质相同的观察值在数量上的平均水平。 • 表示： （总体） X（样本） • 计算：直接法、频数表法 • 特征： ∑（X- X）=0 • 注意：应用于正态分布或近似正态分布，才能求均数，
计量资料的统计学方法
计量资料的统计学方法
首先，计量资料的统计学方法包括描述统计和推断统计。
描述
统计用于总结和展示数据的特征，包括均值、中位数、标准差、频
数分布等。
这些统计量可以帮助我们了解数据的集中趋势、离散程
度和分布形态。
推断统计则用于从样本数据中推断总体的特征，包
括参数估计和假设检验。
参数估计可以帮助我们对总体参数（如均值、比例）进行估计，而假设检验则可以帮助我们对总体参数的假
设进行检验。
其次，计量资料的统计学方法还包括回归分析和方差分析。
回
归分析用于研究自变量和因变量之间的关系，可以帮助我们预测因
变量的取值。
常见的回归分析包括简单线性回归和多元线性回归。
方差分析则用于比较多个总体均值是否相等，可以帮助我们判断不
同组别之间的差异是否显著。
此外，计量资料的统计学方法还包括相关分析和时间序列分析。
相关分析用于研究两个变量之间的相关关系，可以帮助我们了解它
们之间的相关性强弱和方向。
时间序列分析则用于研究时间序列数
据的特征和规律，包括趋势、季节性和周期性等，可以帮助我们进
行未来的预测和规划。
综上所述，计量资料的统计学方法涵盖了描述统计、推断统计、回归分析、方差分析、相关分析和时间序列分析等多个方面，可以
帮助我们全面深入地理解和解释数据的特征和规律。
在实际应用中，研究者可以根据具体问题的特点和要求选择合适的统计方法进行分
析和解释。
统计学第二章计量资料的统计描述
02
统计数据整理与展示方法
数据清洗与预处理技巧
80%
缺失值处理
根据数据的分布情况和实际背景 ，选择合适的缺失值填充方法， 如均值、中位数、众数等。
100%
异常值处理
采用箱线图、散点图等方法识别 异常值，并根据实际情况选择删 除、替换或保留。
分类
根据测量水平的不同，计量资料可分为离散型和连续型两类。离 散型数据只能取整数值，如人口数、医院床位数等；连续型数据 则可以取实数范围内的任何值，如身高、体重等。
计量资料特点分析
数值性
计量资料以数值形式表示，具有数量化的特点，便 于进行数学运算和统计分析。
连续性
连续型计量资料在实数范围内可以取任意值，数据 分布的连续性使得统计推断更为精确。
06
统计图表在数据可视化中应用
常见统计图表类型介绍
条形图（Bar Chart）
用于展示分类数据之间的比较，横轴表示分类，纵轴表示数量或比例。
折线图（Line Chart）
用于展示时间序列数据或连续性数据的趋势变化，横轴表示时间或类 别，纵轴表示数量或比例。
散点图（Scatter Plot）
用于展示两个变量之间的关系，横轴和纵轴分别表示两个变量，点的 位置表示变量的取值。
一组观察值中出现次数最多的数。
计算方法
应用场景
中位数计算需先将数据排序，然后取中间 位置的数；众数计算则是统计各数值出现 的次数，取出现次数最多的数。
适用于各种类型的数据，尤其适用于偏态 分布数据。中位数和众数对极端值不敏感 ，因此能较好地反映数据的集中趋势。
不同集中趋势指标比较
算术平均数、中位数和 众数都是描述数据集中 趋势的指标，但各有特 点。
第2讲 计量资料的基本统计分析方法
149 138 156
148
165 148 149
158
160 139 135
163
119 168 148
138
174 160 138
156
137 120 133
134
152 151 150
140
154 121 132
152
140 146 153
132
122 135 140
148
133 145 145 146 123 140
常用指标：算术均数、中位数等。
（一）算术均数(mean)
1. 定义：简称均数，符号为 数记为μ）。定义公式为
x （相应的总体均
x x n
2.均数的应用与特点
算术均数适合于对称分布的资料 ,如分布均匀的 小样本数据或近似正态分布的大样本数据； 算术均数容易受极端值的影响。
（二）中位数（median）
中位数将变量值一分为二，一半比它小，一半比它大。符号为
将一组变量值按大小顺序排列，位次居中的变量值即为中位数。
M、 M d 。
1. 中位数的计算
x( n 1 ) / 2 Md xn / 2 x1 n / 2 2 n为奇数 n为偶数
2. 中位数的应用与特点
中位数将频数等分为二，所以中位数适合各种类型 的资料，尤其适合于大样本偏态分布的资料。 由于中位数总处在居中的位置上，因而它不受特大 或特小值的影响。
3.16228 4.74342 2.91548
丙组 3 乙组 2 甲组 1
0 20 24 28 32 36 40
（三）方差与标准差的应用
方差或标准差属同类变异指标，它们多用来描 述均匀分布或近似正态分布的资料，大、小样本均 可，其中以标准差的应用最广，通常与均数结合使 用。比如在许多医学研究报告中常用
2计量资料统计分析
(
xxi2
( x)2
xi )2 n
x2 (
x)2 n
n 1
n 1n 1
n 1
式中n－1称为自由度
（四）标准差
1、直接法：
S (x x)2
n 1
x2
( x)2
n
n 1
例：三组同年龄、同性别儿童的体重（kg） 甲组 26 28 30 32 34 乙组 24 27 30 33 36 丙组 26 29 30 31 34
5
3.85
125
96.15
156~
3
2.31
128
98.46
160~164
2
1.54
130
100.00
合计
130 100.00
—
—
二、集中趋势指标
包括：算术均数、几何均数、中位数 意义：
1. 反映一组同质变量值的平均 水平或分布的集中位置。
2. 作为一组资料的代表值，便 于组间的分析比较。
（一）算术均数
G
lg
1
lg
10
lg
100
lg
1000 5
lg
10000
lg
100000
lg 13 1000
5个人的平均血清抗体效价为1：1000
2、加权法
G
lg
1
f lg f
x
lg 1
f1
lg
x1
f2 f1
lg x2 f2 fk
fk
lg
xk
3、几何均数的应用
计量资料的统计分析
4.25
4.5 〜
4.75
5.0 〜
5.25
5.5 〜
5.75
6.0 〜
6.25
6.5 〜
6.75
7.0 〜
7.25
合计
f
fx
3 9.75
6 22.50
20 85.00
22 104.50
31 162.75
26 149.50
18 112.50
5 33.75
1 7.25
132 687.50
fx2 31.69 84.38 361.25 496.38 854.44 859.62 703.12 227.81 52.56 3671.25
本例可将各抗体效价的倒数代入公式，求平均效价数的倒数。
G lg 1 lg10 lg 20 lg 40 lg 80 lg160 lg 11.6522 45
6
该6份血清的平均抗体效价为1:45。
3、中位数
M ,P50 (注意与百分位数的关系) 一组按大小排列的资料中处于中间位置的数
值. 适用于任何分布的计量资料，但较粗糙。
=57.8（小时）
p 95
48
12 12
164
95 100
146
情景资料
1、如果1、2班的平均身高均为160cm，是否 可以认为二个班的身高情况没有差别？
2、可以用哪些指标反映身高的变异程度？哪 个最合适？为什么？
3、计算本班身高的变异程度？ 4、举例说明，什么情况下需要计算变异系数？
描述本班身高变异程度时是否需要用该指标？
x f1xx f 2 x2 f k xk fx
f1 f2 fk
f
=687.50/132=5.21mmol/L
2计量资料的统计描述指标介绍
2计量资料的统计描述指标介绍计量资料的统计描述指标是对数据集合进行概括和描述的方法，可帮助我们了解数据的分布、集中趋势和离散程度，以及可能存在的异常值。
常用的统计描述指标包括均值、中位数、众数、极差、标准差、方差、四分位数和百分位数等。
1. 均值（Mean）：均值是一组数据的总和除以数据的个数。
均值可以反映数据的集中程度，但容易受到异常值的影响。
2. 中位数（Median）：中位数是一组数据按大小排序后，位于中间位置的数值。
中位数可以反映数据的中间位置，不受异常值的影响。
3. 众数（Mode）：众数是一组数据中出现次数最多的数值。
众数可以反映数据集中的特点。
4. 极差（Range）：极差是一组数据的最大值与最小值之差。
极差可以反映数据的全面分布。
5. 标准差（Standard Deviation）：标准差测量数据的离散程度。
标准差越大，数据的离散程度越大。
6. 方差（Variance）：方差是标准差的平方。
方差可以反映数据的离散程度，但单位是原数据的平方。
7. 四分位数（Quartiles）：四分位数将一组数据按大小排序后，分为四等分，分位点分别是Q1（25%分位点）、Q2（中位数）和Q3（75%分位点）。
四分位数可以帮助我们了解数据集的分布情况。
8. 百分位数（Percentiles）：百分位数是将一组数据按大小排序后，分为100等分，每个等分对应一个百分位数。
百分位数可以帮助我们了解数据的分布情况，例如第75百分位数表示排在该位置的数据值大约有75%的数据小于它。
这些统计描述指标都是通过对数据进行运算得出的，可以帮助我们了解数据的分布情况和特点。
在实际应用中，我们可以根据具体的问题选取适当的统计描述指标进行分析，帮助我们更好地理解数据。
同时，还需要注意统计描述指标的局限性，例如均值容易受到异常值的影响，中位数和众数不能反映数据的离散程度等，因此在使用时需要结合具体情况进行综合分析。
计量资料的统计描述
4.66 4.28 3.83 4.20 5.24 4.02 4.33 3.76 4.81 4.17 3.96 3.27
4.61 4.26 3.96 4.23 3.76 4.01 4.29 3.67 3.39 4.12 4.27 3.61
4.98 4.24 3.83 4.20 3.71 4.03 4.34 4.69 3.62 4.18 4.26 4.36
M
x
n
2
x
n
2
1
2
4
百分位数(percentile)
0%
PX
M 即50％分位数就是中位数
100%
27
1.直接计算法
28
例2-9 对某医院细菌性痢疾治愈者的住院天数统计， 119名患者的住院天数从小到大的排列如下， 试求第5百分位数和第99百分位数
患 者 1 2 3 4 5 6 7 8 116 117 118 119 住院天数 1 1 2 2 2 3 4 4 39 40 40 42
3.77 4.20 4.36 3.07 4.89 3.97 4.28 3.64 4.66 4.04 4.55 4.25
4.63 3.91 4.41 3.52 5.03 4.01 4.30 4.19 4.75 4.14 4.57 4.26
4.56 3.79 3.89 4.21 4.95 3.98 4.29 3.67 4.69 4.12 4.56 4.26
第一篇 基本统计方法
1
第二章 计量资料的统计描述
Descriptions of Measurement Data
2
Chapt 2
Frequency distribution
Description of central tendency
第2章计量资料的统计描述 PPT课件
计量资料的统计描述第一节频数分布(frequency distribution)一、频数表的编制P11 例2.1该资料未进行任何加工整理，称为原始资料(raw data)。
1. 频数表的编制步骤（1）求极差（range）：即最大值与最小值之差，又称为全距。
本例极差：R=5.46－3.07=2.39（×1012/L）（2）决定组数、组段和组距：根据研究目的和样本含量n确定。
组距=极差/拟分组数，通常分8-15个组，为方便计，组距参考极差的十分之一, 再略加调整。
本例：i= R /10=2.39/10=0.239≈0.20。
（3）列出组段：第一组段的下限略小于最小值，最后一个组段上限必须包含最大值，其它组段上限值忽略。
（4）划记计数：用划记法将所有数据归纳到各组段，得到各组段的频数。
2.频数表的图示及分析⏹频数分布如右图所示；⏹频数分布的分析： 频数分布的类型 频数分布的特征1020304050F r e q u e n c y33.2 3.4 3.6 3.844.2 4.4 4.6 4.855.2 5.4 5.6RBC3. 频数表的用途(1)揭示资料的分布类型：属对称分布，还是不对称。
(2)观察资料的分布特征：①集中趋势(central tendency):变量值集中位置(location)。
本例在组段“4.2～”。
—平均水平指标②离散趋势(tendency of dispersion):变量值围绕集中位置的分布情况。
离“中心”位置越远，频数越小；且围绕“中心”左右对称。
—变异程度指标(3)发现资料有无可疑值：特大或特小值。
(4)便于进一步统计处理。
(5)陈述资料的一种形式。
第二节集中趋势的描述寻找集中的位置(central location），平均（average）反映了定量资料的集中位置，不同分布类型的资料，要用不同的平均数反映，常用的有：1. 算术均数(arithmetic mean)，简称均数 (mean)2. 几何均数(geometric mean)3.中位数 (median)4. 众数（mode）5.调和均数(harmonic mean)6.截尾均数（censored mean)1.均数（mean ）符号表示： 表示样本均数， 总体均数 12nx x x X x nn+++∑==1123123k k ik if X fX fX f X fX x f f f f f ++++∑==++++∑适用条件：对称分布，尤其是正态或近似正态分布的资料(正态分布后述)。
计量资料的统计方法
计量资料的统计方法计量资料那可是科研和实际工作中的常客呀！到底啥是计量资料呢？简单说就是用数字表示的资料，像身高、体重、血压啥的。
那计量资料的统计方法有哪些呢？首先就是参数检验啦！比如t 检验、方差分析。
这就好比在数字的海洋里找规律，t 检验就像是个小侦探，专门比较两组数据有没有差异。
咱想想，要是两组人的身高不一样，t 检验就能告诉咱这差异是真的不一样呢，还是只是偶然呢？方差分析呢，就更厉害了，能同时比较多组数据。
这就像一场数字大比拼，看看哪一组更厉害。
那做这些统计的时候有啥注意事项呢？可得注意数据的正态性和方差齐性。
要是数据不正态或者方差不齐，那可就麻烦啦！这就像盖房子，地基不牢可不行。
咱得先检查检查数据是不是符合要求，不然得出的结果可就不靠谱喽。
计量资料统计方法安全不？稳定不？那当然啦！只要咱按照正确的方法来，就像走在平坦的大路上，稳稳当当的。
这些方法都是经过无数科学家验证过的，放心用就行。
那计量资料统计方法都用在啥场景呢？那可多了去了。
比如医学研究中，比较不同药物的疗效；工程领域里，分析不同材料的性能。
这就像一把万能钥匙，能打开很多知识的大门。
优势也很明显呀，能给出精确的结果，让咱心里有数。
咱来举个实际案例吧！比如说研究两种减肥方法的效果，咱就可以用计量资料的统计方法。
测量一群人的体重，一部分人用方法A，一部分人用方法B，最后看看两组人的体重变化有没有差异。
哇塞，这多直观呀！结果一出来，咱就知道哪种方法更好啦。
所以说呀，计量资料的统计方法真的超棒！它就像一个神奇的魔法棒，能让我们从一堆数字中找到有用的信息。
咱可得好好掌握这些方法，让它们为我们的工作和研究服务。
第二章 计量资料的统计描述PPT课件
12.1
120
85.8
5.20~ 13 5.30
9.3
133
95.1
5.40~
4 5.50
2.913798.0Fra bibliotek5.60~
2 5.70
1.4
139
99.4
5.80~6.00 1 5.90
0.7
140
合计 140
140
100.0 10
100.0
表2-3 某地140名正常男子红细胞数的频数表
红细胞数
3.80～ 4.00～ 4.20～ 4.40～ 4.60～ 4.80～ 5.00～ 5.20～ 5.40～ 5.60～ 5.80～ 6.00 合计
13
三、频数分布的两个重要特征:
1.集中趋势(central tendency): 指变量值的集中位置所在。
2. 离散趋势(tendency of dispersion): 指变量值围绕集中位置的分布情况。
14
四、频数分布的类型:
1. 对称分布: 各组段的频数以频数最多组 段为中心(集中位置在中间), 左右两侧大体对称。
6
4.49 4.22 4.71 5.21 4.94 4.68 5.17 4.91 5.02 4.76
一、频数表的编制 1、确定组数k ：通常选择8 ~15之间。若
资料在100例以上,一般取10组左右; 若例数 较少, 组数相应减少。以能显示数据的分 布规律为宜。 2、计算极差(全距)，确定组距 i ：
第二章
计量资料的统计描述
1
概述
1
点击输入简要文字内容，文字内容需概括精炼，不用多余 的文字修饰，言简意赅的说明分项内容……
2
点击输入简要文字内容，文字内容需概括精炼，不用多余 的文字修饰，言简意赅的说明分项内容……
2.计量资料(定量资料)的统计描述资料
2018/10/28
11
1. 频数表的编制步骤
（3）列表划记
计算出每个组段的 频率
每组的频数 样本含量
2018/10/28
12
1. 频数表的编制步骤
（3）列表划记
计算出每个组段的 累计频率 =本组段的频率+上 一组段的累计频率
2018/10/28
13
1. 频数表的编制步骤
2018/10/28
14
观察值不能有0。因为0不能去对数，不能与任何其他数呈倍
数关系。 观察值不能同时有正值和负值。若全是负值，计算是可以把 负号去掉，得出结果后再加上负号。 同一组资料求得的几何均数小于算术均数。
2018/10/28
41
2.几何均数
若一组数值变量资料为偏态分布，变量为x，令y=lgx后， 变量y服从正态分布，请问变量x为什么样的偏态分布资料？
2.绘制频数分布直方图
绘制频数分布直方图 坐标轴
横坐标：变量值即研究指标，无需从0开始，以单位尺度 划分。 纵坐标：为频数f，必须从0开始（f为每一组段内的人数）
直条
直条的宽度：组距 直条的高度：每一组段的频数
累计
2018/10/28
15
2.绘制频数分布直方图
2018/10/28
最 大 值
2018/10/28
5
第一节 数值变量资料的频数分布
1. 频数表的编制步骤 （1）求数据的极差: 极差（range）是全部数
据中的最大值与最小值之差，它描述了数据的变 异幅度。
公式：R＝XMax－XMin 例8.1： XMax =5.59
XMin =3.60
R=5.59-3.60=1.99
统计学课件第二章统计计量
06
Excel在统计计量中的应用
数据输入与整理
数据输入
在Excel中输入数据，包括数值 型、文本型、日期型等多种类型
的数据。
数据整理
对数据进行排序、筛选、分类汇、异常值、重复值等 问题，保证数据质量。
描述性统计功能
02
01
03
集中趋势度量
计算均值、中位数、众数等，反映数据的集中趋势。
饼图
用于展示分类数据的占比情况，将一个圆饼按照不同分类的 比例进行切割，通过扇形的面积来表示不同类别的数据占比 。
折线图与散点图
折线图
用于展示时间序列数据或连续变量的变化趋势，横轴表示时间或自变量，纵轴表 示因变量，通过折线的起伏来表示数据的变化情况。
散点图
用于展示两个连续变量之间的关系，横轴和纵轴分别表示两个变量，通过点的分 布来表示变量之间的关系。
布更尖峭，小于0则表示更平坦。
03
箱线图
通过最小值、下四分位数、中位数、上四分位数和最大值五个数值来概
括数据分布的中心位置和散布范围，同时可以通过异常值的识别来判断
数据分布的离群情况。
04
推论性统计方法
参数估计
01
02
03
点估计
用样本统计量来估计总体 参数的方法，如样本均值、 样本比例等。
区间估计
性水平，进行假设检验。
结果解读
根据检验结果，判断两组数 据是否存在显著差异，并给
出相应的解释和结论。
实战演练：使用Excel进行统计计量
数据输入与整理
在Excel中输入需要分析的数据 ，并进行必要的整理和清洗。
图表绘制
利用Excel的图表功能，绘制直方 图、折线图、散点图等图表，直 观展示数据的分布和趋势。
计量资料分析方法ppt课件
样本分别来自总体
X
~
N
(1,
2 1
)、Y
~
N
(2
,
2 2
)。
2. 总体均数配对比较的统计假设
记差值的总体均数为 d： d 1 2 (1) 双侧检验：H0 : 1 2 H1 : 1 2
H0 : d 0 H1 : d 0
(2) 单侧(右侧、左侧)检验：
1. 加载数据分析工具
(1) 依次单击“工具”、“加载宏”； (2) 单击“数据分析”选项左边的复选框； (3) 单击对话框中“确定”。
2. 选择配对比较 T 检验工具
(1) 依次单击“工具”、“数据分析”； (2) 在数据分析工具选项框中，选择
“t-检验：平均值的成对二样本分析”； (3) 单击对话框中“确定”。
若 |t| t (n 1)， 则 P 。 2
拒绝 H 0，接受 H 1。反之，不能拒绝 H 0。
2. 单侧检验的分析方法 (1)查表，确定 T 分布单侧界值 t (n 1)。
(2)比较统计量的值和单侧界值。
若 | t | t (n 1) ， 则 P 。
拒绝 H0，接受 H1。反之，不能拒绝 H0。 9
2. T 检验对样本资料的要求：
X ~ N (1,12 ),
Y
~
N
(
2
,
2 2
)
25
二、检验的目的和统计假设
1. 双侧检验的目的和统计假设
(1)目的：判断总体均数 1与2是否有差异。
(2)统计假设： H0 : 1 2 H1 : 1 2
2. 单侧检验的目的和统计假设
(1)右侧检验目的：判断 1是否大于 2。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
135
127 134 141 121 143 139
146
132 143 150 143 140 140
158
155 128 152 130 140 125
137
134 147 125 141 147 147
153
138 137 147 150 130 129
142
139 142 144 128 141 149
定义：将观察单位按某种属性或类别分组计数， 分组汇总得到各组观察单位数称为计数资料。 特点：计数排列是无序分组，同组各观察单位之
间没有量的差别，但各组间有质的不同，各组互不
相容。
二项分类和多项分类
各战期战士破伤风病死率比较
战期 第一战期 第二战期 第三战期 合计 死亡人数 28 7 12 47 存活人数 14 16 10 40 合计 42 23 22 87
24
三组均数 均为30
第二讲 计量资料的基本统计分析方法
Quantitative data Statistical Analysis
胆管癌患者部分指标
编号 性别 年龄（岁） 部位 分化程度 分期 肝转移 （1） （2） （3） （4） （5） （6） （7） 1 2 3 4 5 … 男 女 女 女 男 … 61 58 63 71 59 … 上 中 上 下 上 … 低分化 高分化 高分化 中分化 高分化 … Ⅰ Ⅱ Ⅳ Ⅱ Ⅲ … 阳性 阴性 阴性 阳性 阴性 … PCNA 指数 （8） 52 89 93 78 85 … 生存时间(月) （9） 14 20 19 5 35 …
中位数将变量值一分为二，一半比它小，一半比它大。符号为
将一组变量值按大小顺序排列，位次居中的变量值即为中位数。
M、 M d 。
1. 中位数的计算
x( n 1 ) / 2 Md xn / 2 x1 n / 2 2 n为奇数 n为偶数
2. 中位数的应用与特点
中位数将频数等分为二，所以中位数适合各种类型 的资料，尤其适合于大样本偏态分布的资料。 由于中位数总处在居中的位置上，因而它不受特大 或特小值的影响。
常用指标：算术均数、中位数等。
（一）算术均数(mean)
1. 定义：简称均数，符号为 数记为μ）。定义公式为
x （相应的总体均
x x n
2.均数的应用与特点
算术均数适合于对称分布的资料 ,如分布均匀的 小样本数据或近似正态分布的大样本数据； 算术均数容易受极端值的影响。
（二）中位数（median）
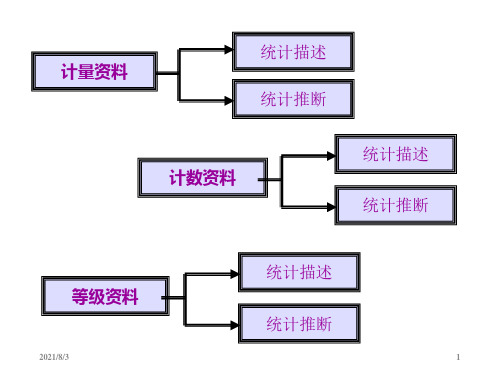
3.等级资料（或半定量资料，有序分类变量）
ranked data，semi-quantitative data， ordinal category data
定义：将观察单位按某个指标量的大小分成等级或
某种属性的不同程度分成等级后分组计数，分类汇总各
组的观察单位数称为等级资料。
特点：等级是有序分组。同计数资料的区别是：属
140
154 121 132
152
140 146 153
132
122 135 140
148
133 145 145 146 123 140
135
127 134 141 121 143 139
146
132 143 150 143 140 140
158
155 128 152 130 140 125
137
134 147 125 141 147 147
计量资料的统计描述 Statistical Description
某市110名健康男性工人的血红蛋白量(g/L)
118
149 138 156
148
165 148 149
158
160 139 135
163
119 168 148
138
174 160 138
156
137 120 133
134
152 151 150
统计资料的分类
1.计量资料（或定量变量） measurment data ，quantitative data，
定义：测定每个观察单位的某项指标量的大小， 所得的资料称为计量资料。其变量值是定量的，一 般带有度量衡或其它单位。 特点：每个观察单位的观察值之间有量的区别。
某市110名健康男性工人的血红蛋白量(g/L)
变异指标
变异指标——又称离散指标，用以描述一组计量 资料各观察值之间参差不齐的程度。
变异指标越大，观察值之间差异愈大，说明平均
数的代表性就越差；反之亦然。
三组同性别、同年龄儿童体重
甲组 乙组 26 24 28 27 30 30 32 33 34 36
丙组
丙组 3
乙组 2 甲组 1
26
29
30
31
153
138 137 147 150 130 129
142
139 142 144 128 141 149
155
131 119 131 142 126 142
114
142 139 162 150 151 154
147
135 131 138 107 149 151
平均数指标
平均数(average) 是描述一群同质变量值集中位置的特征值， 用以说明同类现象或事物数量的中等水平（集中趋势）。
118
149 138 156
148
165 148 149
158
160 139 135
163
119 168 148
138
174 160 138
156
137 120 133
134
152 151 150
140
154 121 132
152
140 146 153
132
122 135 140
148
133 145 145 146 123 140
155
131 119 131 142 126 142
114
142 139 162 150 151 154
147
135 131 138 107 149 151
2.计数资料（或定性变量，无序分 类变量）
enumeration data， qualitative data， unordered category data
性的分组有程度的差别，各组按一定顺序排列；与计量
资料的区别是：每个观察单位未确切定量，所以又称为 半定量资料。
ቤተ መጻሕፍቲ ባይዱ
某地居民体内核黄素营养状况调查结果
季节 缺乏 夏季 冬季 5 11
营养状况 不足 7 9 适宜 8 2 合计 20 22
*核黄素营养状况评价标准：缺乏为<400μg，不足为 400~1000μg，适宜为>1000μg。