平移与旋转导学案
平移和旋转(导学案)-2022-2023学年数学三年级上册

平移和旋转(导学案)一、知识点概述本单元主要内容是平移和旋转。
平移是指在平面上沿着一定方向和距离将图形移动到新的位置,而旋转是指绕定点旋转一定角度改变图形的方向。
本单元将带领同学们探究平移和旋转的基本概念、性质和应用。
二、学习目标1.了解平移和旋转的基本概念;2.掌握平移和旋转的基本性质;3.能够运用平移和旋转的知识解决简单问题。
三、重点难点1.平移、旋转的基本概念;2.平移、旋转的基本性质。
四、教学过程1.引入新知识通过展示一些具有平移和旋转的图形,引导同学们了解平移和旋转的基本概念,并带领同学们感受平移和旋转对于图形的影响。
2.学习平移的基本概念和性质平移是指将一个图形按照一个方向和一个距离移动到另一个位置上。
简单来说,就是将图形整体上下左右移动。
学生可以动手自己移动物品,感受平移的过程。
平移的基本性质有:•平移前后图形相似;•平移前后图形面积不变;•平移前后图形周长不变。
3.学习旋转的基本概念和性质旋转是指沿着一个定点按照一个角度旋转图形。
在学习旋转之前,可以先引导学生认识旋转涉及到的一些基本术语:定点、旋转角、旋转方向。
旋转的基本性质有:•旋转前后图形相似;•旋转前后图形面积不变;•旋转前后图形周长不变;•旋转角等于旋转后的图形与旋转前的图形的对应角的差。
4.练习与拓展为巩固同学们的学习成果,可以设置一些练习题目,让同学们在实践中掌握平移和旋转的基本应用技巧。
5.复习与总结在学习结束之前,带领同学们进行本单元的总结和复习。
通过回顾本单元的主要知识点和难点,以及运用所学知识解决实际问题的经历,巩固同学们对于平移和旋转的理解与运用。
五、学习评估为了检验学生对于平移和旋转知识的掌握,可以通过一些小测验和测试题目来进行学习评估。
根据测试结果,及时调整教学计划,提高同学们的学术水平。
六、教学反思教学中,我们应该注重让学生从实践中感悟知识,注重让学生动手进行实验和操作,提高学生的学习兴趣和参与度。
鼓励同学们自己发现问题和解决问题,有利于激发同学们的思考和创新意识,使得学生能够更好的掌握平移和旋转的基本概念和性质。
平移和旋转【导学案】苏教版三年级上册数学

平移和旋转(导学案)导学目标1.了解平移的概念和基本特征;2.了解旋转的概念和基本特征;3.掌握常见的平移和旋转的变换方式。
知识回顾在前面的学习中,我们学习了数学中的几何图形变换,包括镜像和翻转。
这些变换都是通过改变图形的位置和形状来达到的。
今天我们要学习两种新的几何图形变换,即平移和旋转。
平移概念平移是指将图形沿着一个方向移动一段距离,同时保持其形状和大小不变的操作。
基本特征对于一个图形来说,它的平移有以下基本特征:1.平移后的图形与原图形大小和形状相同;2.平移沿着一个固定的方向进行;3.平移后的图形与原图形之间的距离和方向相同。
变换方式平移变换有两种方式,即向左平移和向右平移。
向左平移:将图形沿着指定方向向左移动一段距离。
向右平移:将图形沿着指定方向向右移动一段距离。
旋转概念旋转是指将图形沿着一个中心点旋转一定角度,同时保持其形状和大小不变的操作。
基本特征对于一个图形来说,它的旋转有以下基本特征:1.旋转后的图形与原图形大小和形状相同;2.旋转的中心点是固定的;3.旋转的角度范围为0到360度。
变换方式旋转变换有两种方式,即顺时针旋转和逆时针旋转。
顺时针旋转:将图形沿着指定角度顺时针旋转。
逆时针旋转:将图形沿着指定角度逆时针旋转。
课后练习1.用手绘制一个长方形,对其进行向左平移、向右平移、顺时针旋转和逆时针旋转操作;2.思考一下,平移和旋转操作分别可以用来做哪些应用呢?通过学习本课程,我们了解了平移和旋转的概念、基本特征和变换方式,并进行了简单的练习。
希望同学们能够在以后的练习中善于运用这些知识,体会到它们在数学中的应用价值。
旋转与平移导学案

云阳县海峡小学课堂教学导学案(二)主备人:王、胡、谭备课组长:王审批人:谢厚元课题:旋转与平移班级:三年级学生姓名:导学目标:能感知、区别、举例平移与旋转的现象。
导学重难点:感知平移与旋转的现象,并会直观地区别这两种常见现象。
能说出生活中各种平移与旋转现象,感受数学与日常生活的紧密联系。
导学过程一、自主学习观察第62页、63页的教学情景图。
1.说说图中哪些现象是旋转?哪些现象是平移?()是旋转。
()是平移。
2.生活中你还见过哪些现象是旋转?哪些现象是平移?()是旋转。
()是平移。
二、同伴互学1.举例说明什么是旋转?什么是平移?﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍2.在旋转现象中,你发现了什么?在平移现象中,你发现了什么?﹍﹍﹍﹍﹍﹍﹍﹍﹍3.我们如何判断物体的运动是旋转还是平移?﹍﹍﹍﹍﹍﹍﹍﹍﹍三、展示交流(展示、交流时声音洪亮、学会倾听)1. 物体或图形沿着()线移动的运动现象叫平移。
物体或图形绕着()移动的运动现象叫旋转。
2.判断哪些是平移现象现象在()里划√, 哪些是旋转现象在()里划○荡秋千()推拉门窗()直升飞机的螺旋桨()翻书()拧螺丝()开门()四、达标训练判断下面的物体运动是平移(√)还是旋转(×)升旗时的运动()钟表中指针的运动()火车在直轨道上的运动()在算盘上拨珠()电梯的运动()风扇叶片的运动()光盘在电脑的运动()行驶的汽车的反向盘的运动()光盘在电脑里的运动()五、反思提升总结、评价:今天的学习,我学会了()我在()方面表现很好,在哪方面表现不够。
以后我要注意的是()。
总体表现(优良差)愉悦指数(高兴一般痛苦)。
《平移和旋转》导学案
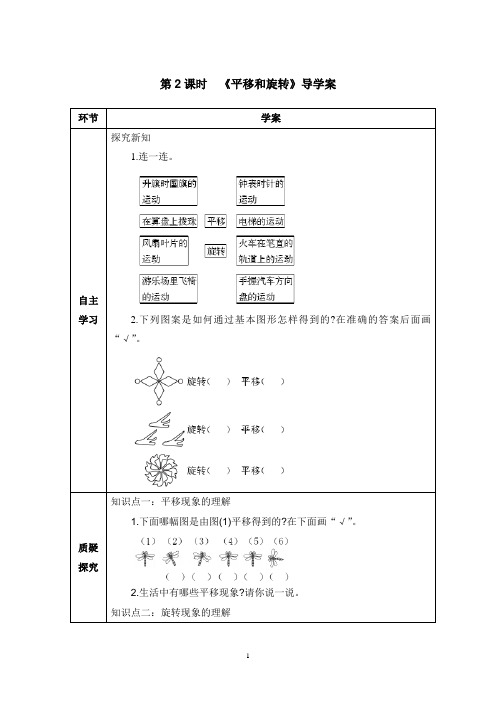
第2课时《平移和旋转》导学案
环节学案
自主
学习
探究新知
1.连一连。
2.下列图案是如何通过基本图形怎样得到的?在准确的答案后面画
“√”。
质疑
探究
知识点一:平移现象的理解
1.下面哪幅图是由图(1)平移得到的?在下面画“√”。
2.生活中有哪些平移现象?请你说一说。
知识点二:旋转现象的理解
1.下面的图形( )是由其中一个图形旋转与组合得到。
2.生活中有哪些旋转现象?请你说一说。
实践
应用
一、随堂练习
1.在括号里填上“平移”或“旋转”。
2.把通过右边的图形平移后得到的图形涂上红色,旋转后得到的图形
涂上绿色。
二、拓展练习
接着往下画。
自我
总结
通过今天的学习,我学会了:
我的问题是:。
平移与旋转的应用(导学案)- 五年级下册数学 人教版

平移与旋转的应用(导学案)- 五年级下册数学人教版一、教学目标1. 知识与技能:理解平移与旋转的概念,掌握平移与旋转的基本性质,能运用平移与旋转进行图形变换。
2. 过程与方法:通过观察、操作、分析,培养学生的空间观念和动手操作能力。
3. 情感态度价值观:激发学生对数学的兴趣,培养学生的合作意识和创新精神。
二、教学重点与难点1. 教学重点:理解平移与旋转的概念,掌握平移与旋转的基本性质。
2. 教学难点:运用平移与旋转进行图形变换,解决实际问题。
三、教学过程1. 导入新课通过生活中的实例,如推拉门、风车等,让学生初步感知平移与旋转现象,激发学生的学习兴趣。
2. 探究平移与旋转的性质(1)平移的性质引导学生观察平移现象,如推拉窗、抽屉等,总结平移的性质:图形平移后,形状、大小不变,位置发生变化。
(2)旋转的性质引导学生观察旋转现象,如风车、地球仪等,总结旋转的性质:图形旋转后,形状、大小不变,位置发生变化。
3. 活动与实践(1)小组合作,探究平移与旋转在生活中的应用,如平移应用在推拉门、抽屉等,旋转应用在风车、地球仪等。
(2)学生展示成果,交流分享。
4. 巩固练习设计练习题,让学生运用平移与旋转的性质解决问题,巩固所学知识。
5. 小结引导学生回顾本节课所学内容,总结平移与旋转的性质及应用。
四、作业布置1. 完成课后练习题。
2. 观察生活中平移与旋转现象,举例说明。
五、教学反思本节课通过观察、操作、分析,让学生理解平移与旋转的概念,掌握平移与旋转的基本性质。
在教学过程中,注重培养学生的空间观念和动手操作能力,激发学生对数学的兴趣。
同时,通过小组合作、交流分享,培养学生的合作意识和创新精神。
在今后的教学中,要注意以下几点:1. 加强对平移与旋转性质的讲解,让学生充分理解。
2. 设计更多的生活实例,让学生感受平移与旋转在实际生活中的应用。
3. 注重培养学生的观察、操作、分析能力,提高学生的数学素养。
4. 激发学生的学习兴趣,让学生在轻松愉快的氛围中学习数学。
五年级下册数学导学案-1.4 旋转和平移|冀教版

五年级下册数学导学案-1.4 旋转和平移 | 冀教版一、教学目标1.理解旋转和平移的概念。
2.能够进行简单的旋转和平移操作。
3.能够在平面直角坐标系中表示图形的旋转和平移。
二、教学重点1.旋转和平移的概念。
2.图形的旋转和平移操作。
3.平面直角坐标系中图形旋转和平移的表示。
三、教学难点1.熟练掌握平面直角坐标系中图形的旋转和平移表示。
2.能够对复杂图形进行旋转和平移操作。
四、教学过程1. 导入新知1.引出今天的主题:旋转和平移。
2.通过日常生活中的例子(如:转盘转动,门关上)让学生了解旋转和平移的概念。
2. 理解旋转的概念1.引导学生回忆圆的相关知识。
2.将一张纸片放在桌子上,让学生观察纸片上的图形随着旋转的角度的变化。
3.让学生发现图形旋转不改变图形的大小和形状,仅是方向不同。
3. 理解平移的概念1.让学生观察一张纸片,并让他们在纸片上画一个图形。
2.让学生尝试将图形移动到纸片上的其他位置。
3.让学生发现图形平移时形状大小不变,仅是位置发生了变化。
4. 图形的旋转和平移操作1.将一张格子纸放在桌子上,让学生在格子纸上画一个简单的几何图形(如正方形)。
2.让学生尝试将图形旋转和平移到不同的位置。
3.引导学生思考,当图形旋转和平移时需要考虑哪些因素(如旋转中心点和平移的位移)。
5. 平面直角坐标系中的图形旋转和平移表示1.引导学生回忆平面直角坐标系的相关知识。
2.让学生在平面直角坐标系中表示图形的旋转和平移操作。
3.引导学生思考如何通过旋转和平移来构造新的图形。
五、作业布置1.完成教师布置的相关练习题。
2.对平面直角坐标系中图形的旋转和平移进行总结,并能够对复杂图形进行旋转和平移操作。
六、教学总结通过本节课的学习,我们掌握了旋转和平移的概念,能够进行简单的旋转和平移操作,并且能够在平面直角坐标系中表示图形的旋转和平移。
在今后的学习中,我们将会进一步掌握如何通过旋转和平移来构造新的图形。
平移与旋转导学案

《平移和旋转》导学案
苏教版第五册第80-82页
主备人:黄素玉审核人:班级:组别:小主人:学习时间:2014年月日
学习目标
1.结合同学们的生活经验和实例,初步感知、辨别平移和旋转现象。
(重点)
2.能用自己的方式表示平移和旋转。
3.通过联系生活经验,体会平移和旋转的特点,培养空间观念。
(难点)
预习案
1.认真阅读课本第80页和第81页,试着找一找生活中的平移现象和旋转现象,把它写下来。
2.在不明白的地方画上标记,准备课上讨论质疑。
合作探究案
探究一:感知平移现象
1.像()、()、()这些物体的运动都可以看成是平移。
我可以用自己的方式表示这些运动。
我发现:平移是沿着线移动。
2.我还见过这些平移现象。
3.试一试:把数学书放在课桌的左上角,接着把它平移到课桌的右上角,再依次平移到右下角和左下角。
探究二:感知旋转现象
1.像()、()、()这些物体的运动都可以看成是旋转。
我可以用手势表示这些运动。
我发现:旋转是围绕着一个转动。
2.我还见过这些旋转现象。
3.试一试:在转盘上把指针从A点旋转到指向B点,再继续旋转到指向C 点或D点。
达标检测案
挑战一:下面 的运动是平移, 的运动是旋转。
挑战二:1.把红棋子先向东平移3格,再向南平移3格,然后画下来。
2.把黄棋子先向北平移4格,再向西平移4格。
然后画下来。
总结评价我最棒:
今天的学习我知道了 。
我想提醒同学们 。
第四单元《平移与旋转》(导学案)青岛版三年级上册数学

第四单元《平移与旋转》(导学案)青岛版三年级上册数学
一、学习目标
1.掌握平移和旋转的概念;
2.学会平移和旋转的操作方法;
3.了解平移和旋转在日常生活中的应用。
二、学习重点
1.平移和旋转的概念;
2.平移和旋转的操作方法。
三、学习难点
1.理解平移和旋转的含义;
2.熟练掌握平移和旋转的操作方法。
四、学习内容
1. 平移
(1) 概念
平移是指将一个图形按照一定的方向和距离移动到另一个位置的操作。
(2) 操作方法
平移的操作方法如下:
1.用直尺连接图形上需要移动的点与移动的终点,标出直线的方向和距离;
2.将直尺按照标出的方向和距离移动到新的位置;
3.将图形沿着直尺的方向移动到新的位置。
2. 旋转
(1) 概念
旋转是指将一个图形围绕某一点按一定角度旋转后得到的图形。
(2) 操作方法
旋转的操作方法如下:
1.在图形中选择一个点作为旋转中心;
2.用直尺连接旋转中心和图形上需要旋转的点,标出旋转的方向;
3.用量角器测量旋转的角度;
4.将图形围绕旋转中心按照测得的角度旋转。
3. 应用
平移和旋转在日常生活中有很多应用,例如:
1.舞蹈中的身体旋转;
2.地图中的地图平移和旋转;
3.动漫中角色的行走和转头等。
五、学习方法
1.逐步理解平移和旋转的概念;
2.反复练习平移和旋转的操作方法;
3.积极探究和应用平移和旋转的相关知识。
六、课后作业
1.完成练习册中与平移和旋转相关的练习;
2.自行寻找一些日常生活中的平移和旋转的例子,写出相关的说明。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
15.1.1图形的平移◆随堂检测1、下列几种运动属于平移的是()(1)水平运输带上的砖的运动;(2)啤酒生产线上的啤酒通过压盖机前后的运动;(3)升降机上下做机械运动;(4)足球场上足球的运动A.一种 B.两种 C.三种 D.四种2、下列图形中,由原图平移得到的图形是()原图 A. B. C.D.3、在如图所示的四个汽车标志图案中,能用平移变换来分析其形成过程的图案是( )A. B. C . D.4、如图所示,△ABC平移后成为△EFB,下列说法正确的个数有:()①线段AC的对应线段是BE;②点B的对应点是点C;③点B的对应点是点F;④平移的距离是线段CF的长度。
A1个B2个C3个D4个5、卷帘门上有A、B两点,(B点在A点下方)当A点向上移1m,那么B点向移动了 m。
O平移到了点o ,你能作出平移后的圆吗?O ∙ O '◆ 典例分析ABC ∆平移后得到△DEF ,如图所示,若∠A=80O ,∠E=60O ,你知道∠C 的度数吗?说明理由。
◆课下作业●拓展提高1、火车在笔直的铁路上开动,火车头以100千米/时的速度前进了半小时,则车尾走的路程是( )A 、100千米B 、50千米C 、200千米D 、无法计算2、将线段AB 平移1cm,得到的线段是A /B /,则A 到点A /的距离是 。
3、如图所示,在等边三角形ABC 中,D 、E 、F 分别是边BC 、AC 、AB 的中点,图中有两个小等边三角形,其中△FBD 可以看成是由△AFE 平移而得到,则平移的方向是 ,平移的距离为 。
4、△DEF 是把△ABC 水平向左平移3.5cm 得到,你能作出△ABC 吗?DE F5、如图所示,长方形ABCD ,对角线AC,BD 相交于O,DE ∥AC,CE ∥BD,那么△EDC 可以看作由 平移得到的,平移的距离是线段 的长度。
●体验中考1、(2009年广东广州)将图1所示的图案通过平移后可以得到的图案是( )2、(2009年青海)如图,请借助直尺按要求画图: (1)平移方格纸中左下角的图形,使点1P 平移到点2P 处. (2)将点1P 平移到点3P 处,并画出将原图放大为两倍的图形.15.1.2平移的特征◆随堂检测1、在下面的六幅图案中,平移(1)可得到(2)、(3)、(4)、(5)、(6)中的哪个图案?2、在下列说法中,①四边形在平移过程中,对应线段一定相等;②四边形在平移过程中,对应线段一定平行;③四边形在平移过程中,周长不变;④四边形在平移过程中,面积不变,、其中正确的是:( )A 、①②③B 、①②③④C 、②③④D 、①③④ 3、平移不改变图形的 和 ,只改变图形的4、小明把自己的左手手印和右手手印按在同一张白纸上,左手手印 (填能或不能)通过平移与右手手印完全重合。
5、将线段AB 向右平移3cm 得到线段CD ,如果AB=5 cm ,则CD= cm.6、将∠ABC 向上平移10cm 得到∠EFG ,如果∠ABC=52°,则∠EFG= °,BF= cm.◆典例分析如图,已知Rt △ABC 中,∠C=90°,BC=4,AC=4,现将△ABC 沿CB 方向平移到△A ’B ’C ’的位置。
(1)若平移距离为3,求△ABC 与△A ’B ’C ’的重叠部分的面积; (2)若平移距离为x (),求△ABC 与△A ’B ’C ’的重叠部分的面积y ,并写出y 与x 的关系式。
●拓展提高1、下图中,ABC ∆平移到了'C 'B 'A ∆位置,下列结论不成立的是 ( )A .'C 'B BC =B .'C C ∠=∠C .'A A ∠=∠D .'C 'A AB =2、如图,△ABC 沿着点A 到A 1的方向平移到△A 1B 1C 1的位置,如果AB=5cm,BC=4cm ,∠A=60O∠B=50O,则∠C 1= ,B 1C 1= .3、 将面积为30cm 2的等腰直角三角形ABC 向下平移20cm ,得到△MNP ,则△MNP 是 三角形,它的面积是 cm 2.4、如图,在长方形ABCD 中,对角线AC 与BD 相交于点 O ,画出AOB 平移后的三角形,其平移方向为射线AD 的方向,平移的距离为线段AD 的长.5、如图,由三角形ABC 平移得到的三角形有几个?6、△ABC 经过平移后得到△DEF,(1)指出平移的方向和距离; (2)写出图中相等的线段和平行的线段(包括虚线); (3)写出图中相等的角。
●体验中考1、(2009年,广东)将线段AB 平移1cm ,得到线段///,A A B A 到点则点 的距离是 2.(2009年福建宁德)在如图所示的四个汽车标志图案中,能用平移变换来分析其形成过程的图案是( )ABA. B. C . D.15.2.1图形的旋转◆随堂检测1、如右图,甲图案可以看作是乙图案通过怎样变换而得到?()A.先按逆时针旋转90°再平移;B.先按逆时针旋转90°再作轴对称图C.先平移再作轴对称;D.先平移再作逆时针旋转90°2.将字母“T”按顺时针方向旋转90°后的图形是()3、现象中属于旋转的有( )个①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.A.2B.3C.4D.54、如图,线段MO绕点O旋转900得到线段NO,在这个旋转过程中,旋转中心是,旋转角是,它等于度.(第4题)(第5题)5、如图,长方形ABCD是长方形EFGD绕旋转中心________•沿_______•旋转______度得到的,对角线AC与EG的关系是________,理由是_________.◆典例分析如图,将△ABC绕点A旋转得到△AEF,指出图中的旋转中心、旋转角度及对应线段、对应角。
分析:旋转角是连结对应点与旋转中心所形成的角,而对应线段是对应点所在的线段,对应角则由对应点所形成的角,因此关键是要分清楚是谁的对应点。
◆课下作业●拓展提高1、如图1,在正方形ABCD 中有一点P ,把⊿ABP 绕点B 旋转到⊿CQB , 连接PQ ,则⊿PBQ 的形状是( )(A )等边三角形 (B )等腰三角形 (C )直角三角形 (D )等腰直角三角形(第1题) (第2题) (第3题)2.如图,把菱形ABOC 绕点O 顺时针旋转得到菱形DFOE ,则下列角中不是旋转角的为( )A .∠BOFB .∠AODC .∠COED .∠ AOF3、如图,ABO ∆绕点O 旋转450后得到DCO ∆,则点B 的对应点是_____;线段OB 的对应线段是____;线段AB 的对应线段是____;∠A 的对应角是_____;∠B 的对应角是_____;旋转中心是_____;旋转的角度是______.△AOB 的边OB 的中点M 的对应点在 .4、图中的两个等腰三角形是全等的,且∠AOD=45°,OB=4㎝,OA= 1㎝.怎样将右边的三角形变为左边的三角形? DM第4题5、如图,△ABC 是等边三角形,D 是BC 上一点,△ABD 经过旋转后到达△ACE 的位置。
(1)旋转中心是哪一点?(2)旋转了多少度?(3)如果M 是AB 的中点,那么经过上述旋转后,点M 转到了什么位置?6、如图,四边形CDEF 旋转后能与正方形ABCD 重合,那么图形所在平面上可以作为旋转中心的点共有几个?●体验中考1、(2009年,陕西)如图,∠AOB =90°,∠B =30°,△A ’OB ’可以看作是由△AOB 绕点O 顺时针旋转α角度得到的,若点A ’在AB 上,则旋转角α的大小可以是( ) A 、30° B 、45° C 、60° D 、90°(第1题) (第2题)2、如图,把△ABC 绕点C 顺时针旋转35°,得到△A ′B ′C ,A ′B ′交AC 于点D ,如果∠A ′DC=90°,那么∠A 的度数是多少? EDE15.2.2旋转的特征◆随堂检测1、你玩过万花筒吗?它是由三块等宽等长的玻璃片围成的。
下图是看到的万花筒的一个图形,图中所有的小三角形均是全等的等边三角形,其中的菱形AEFG可以看成是把菱形ABCD 以A为中心()A.顺时针旋转600得到B.顺时针旋转1200得到C.逆时针旋转600得到D.逆时针旋转1200得到2、如图,在△ABC中,∠B=900,∠C=3001800,点C落在C1处,则C C1的长为()A.24B.4C .32D.523、如图所示,图形①经过变化成图形②,图形②经过图①图②图③4、如图,△ABC绕点C旋转后得到△CDE,则∠A= ,∠B= ,AB= , AC=5、如图,△ABC中,∠ACB=1200,将它绕着点C旋转300后得到△DCE,则∠ACE=∠A+∠E=16、如图,△ABC绕O点旋转后,顶点A的对应点为点A′,•试确定顶点B、C对应点的位置,以及旋转后的三角形.◆典例分析如图所示,△ACD和△BCE都是等边三角形,△DCB经过旋转后得到△ACE。
⑴指出旋转中心是哪一点?⑵旋转了多少度?⑶图中还存在是旋转关系的三角形吗?◆课下作业●拓展提高1、下列关于图形旋转特征的说法不正确的是()A.对应线段相等B.对应角相等C.图形的形状与大小都保持不变D.旋转中心平移了一定的距离2、如图所示,在四边形ABCD中,AB=AD, ∠BAD=∠BCD=O90,AH⊥BC于H,AH=5,则四边形ABCD的面积是()A.15 B.20 C.25 D.无法确定3、如图,边长为1的正方形ABCD绕点A 逆时针旋转300到正方形A 1B 1C 1D 1,图中阴影部分的面积为( ) A .21 B .33 C .1 -33 D .1 -434、将等边△ABC 绕着点A 按某个方向旋转400后得到△ADE(点B 与点D 是对应点),则∠BAE 的度数为_____.5、如图,在Rt △ABC 中,∠ACB=90°,∠A=35°,以直角顶点C•为旋转中心,将△ABC 旋转到△A ′B ′C 的位置,其中A ′、B ′分别是A 、B 的对应点,且点B 在斜边A ′B ′上,直角边CA ′交AB 于D ,求∠BDC 的度数.6、如图,点P 为正方形ABCD 内一点,且PA=1,PB=2,PC=3.试求∠APB 的度数.(提示:可将△ABP 绕点B 顺时针方向旋转90°得△BP ′C ,连PP ′,从而求出∠PP ′C 的度数).●体验中考1、(2009年,泸州)如图l ,P 是正△ABC 内的一点,若将△BCP 绕点B 旋转到△BAP ’,则∠PBP ’的度数是( )A 、45°B 、60°C 、90°D 、120°2、(2008年,长沙)如图所示,等边△ABC 中,D 是AB 边上的动点(不与A 、B 重合),以CD AC为一边,向上作等边△EDC 。
