您的位置：360文档中心› 先序遍历的非递归算法 C语言

先序遍历的非递归算法 C语言

合集下载

一种二叉树非递归遍历算法的C语言实现

一种二叉树非递归遍历算法的C语言实现

Ｔ ｅ ｌ ： ＋ ８ ６ — ５ ５ １ － ６ ５ ６ ９ ０ ９ ６ ３ ６ ５ ６ ９ ０ ９ ６ ４
一
种 二 叉树 非 递 归 遍历 算 法 的 Ｃ语 言实 现
龚 佳 ， 袁 赘 ， 刘 远 军
（ 邵阳学院 信息工程系 ， 湖南 邵阳 ４ ２ ２ ０ ０ ４ ）
摘要 ： 针对二叉树 的链 式存储 结构 ， 分析 了二叉树 的各种遍 历算法 ， 探 讨 了递 归算 法的递推 消除问题 ， 提 出了一种改进的 非递归遍 历算法并用Ｃ语言 予以实现。
收 稿 日期 ： ２ ０ １ ３ — １ １ — １ ５
ｍｅ ｎｔ ｅ ｄ ｉ ｎ Ｃ ｌ ａ ｎｇ ｕａ ｇｅ ． Ｋｅ ｙ ｗｏ ｒ ｄｓ ：ｂｉ ｎａ ｙ ｒ ｔ ｒ ｅ ｅ ； ｔ ｒ ａ ｖｅ ｒ ｓ ａ ｌ ａ ｌ ｇ ｏｒ ｉ ｔ ｈ ｍ； ｎｏｎ— — ｒ ｅ ｃ ｕ ｒ ｓ ｉ ｖｅ ；Ｃ ｌ ａ ｎｇ ｕａ ｇｅ
ＧＯＮＧ Ｊ ｉ ａ ， Ｙ ＵＡ Ｎ Ｙ ｕ ｎ ， Ｌ Ｉ Ｕ Ｙ ｕ ｎ － ｊ ｔ ｉ ｎ
（ Ｉ ｎ ｆ ｏ ｒ ｍａ ｔ ｉｐ ａ ｒ ｔ ｍｅ ｎ ｔ ， Ｓ ｈ ａ ｏ ｙ ａ ｎ ｇ Ｕｎ ｉ ｖ ｅ ｒ ｓ ｉ ｔ ｙ ， Ｓ ｈ ａ ｏ ｙ ａ ｎ ｇ ４ ２ ２ ０ ０ ４ ， Ｃ ｈ ｉ ｎ ａ ）
一
个结点 至少 由３ 个 域组成 ， 即数据域 、 左子结点域和右子结点域 （ 如图１ 所示 ） 。
图１
为了更好 的对树结构进行计算和处理 ， 我们 可以加上一个 双亲结点域（ 如 图２ 所示 ） 。
！ｆ ｌ ！ ！
图２
Ｌ
＿
！ Ｉ ！ 二 ！ Ｊ
Ｉ Ｄ ａ ｔ ｅ

c语言红黑树遍历序算法

c语言红黑树遍历序算法

c语言红黑树遍历序算法红黑树是一种自平衡的二叉查找树，它具有良好的平衡性能，能够保持在较低的高度范围内。

在C语言中，我们可以使用递归或者非递归的方式来实现红黑树的遍历。

下面我将分别介绍中序遍历、前序遍历和后序遍历的算法。

1. 中序遍历算法：中序遍历的顺序是先遍历左子树，然后访问根节点，最后遍历右子树。

在C语言中，我们可以使用递归实现中序遍历：c.void inOrderTraversal(struct Node root) {。

if (root != NULL) {。

inOrderTraversal(root->left);printf("%d ", root->data);inOrderTraversal(root->right);}。

}。

2. 前序遍历算法：前序遍历的顺序是先访问根节点，然后遍历左子树，最后遍历右子树。

同样可以使用递归实现前序遍历：c.void preOrderTraversal(struct Node root) {。

if (root != NULL) {。

printf("%d ", root->data);preOrderTraversal(root->left);preOrderTraversal(root->right);}。

}。

3. 后序遍历算法：后序遍历的顺序是先遍历左子树，然后遍历右子树，最后访问根节点。

同样可以使用递归实现后序遍历：c.void postOrderTraversal(struct Node root) {。

if (root != NULL) {。

postOrderTraversal(root->left);postOrderTraversal(root->right);printf("%d ", root->data);}。

}。

另外，以上是使用递归实现的遍历算法，也可以使用非递归的方式来实现，利用栈来辅助实现遍历。

广度优先遍历非递归算法

广度优先遍历非递归算法

广度优先遍历非递归算法
广度优先遍历（BFS）是一种图的遍历算法，用来遍历图中所有的节点。

以下是广度优先遍历的非递归算法：
1. 创建一个队列，用来存放待访问的节点。

2. 将起始节点放入队列中。

3. 创建一个集合，用来存放已经访问过的节点。

4. 将起始节点加入到已访问节点的集合中。

5. 循环执行以下步骤，直到队列为空为止：
5.1. 从队列中取出一个节点。

5.2. 访问该节点。

5.3. 获取该节点的所有相邻节点。

5.4. 对于每个相邻节点，如果它没有被访问过，则将其加入到队列和已访问节点的集合中。

通过以上步骤，可以按广度优先的顺序遍历整个图。

这种非递归算法利用队列的先进先出（FIFO）特性，保证了相邻节点的访问顺序是按照它们与起始节点的距离逐渐增加的顺序进行的，从而实现了广度优先遍历。

c语言fibonacci数列非递归

c语言fibonacci数列非递归

c语言fibonacci数列非递归Fibonacci数列是一个经典的数学问题，它的前两项是0和1，而后续项是前两项的和。

数列的前几项是：0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...在C语言中，我们可以使用非递归的方法来生成Fibonacci数列。

非递归的方法更高效，因为它不会遇到递归调用所带来的额外开销。

下面我将详细介绍如何使用非递归方法生成Fibonacci数列，并给出相应的C语言代码。

算法思路：1. 为了生成Fibonacci数列，我们需要一个数组来存储数列的值。

由于我们不知道数列的长度，所以我们需要选择一个足够大的数组来存储数列的值。

在这里，我们选择一个包含1000个元素的整型数组来存储数列的值。

2. 数列的第一个和第二个元素是已知的，所以我们在数组中分别存储0和1。

3. 接下来，我们使用一个循环从第三个元素开始生成数列的值。

循环从3一直到1000进行遍历，以确保数组足够大，同时也为了保证我们能生成至少1000个数。

4. 在每次循环中，我们将前两个元素的和存储到第三个元素中，然后将前两个元素的值更新为当前元素和前一个元素。

5. 最后，我们通过循环遍历生成的数列，并将其打印出来。

下面是相应的C语言代码：c#include<stdio.h>int main() {int fibonacci[1000];int i;fibonacci[0] = 0;fibonacci[1] = 1;for (i = 2; i < 1000; i++) {fibonacci[i] = fibonacci[i-1] + fibonacci[i-2];}for (i = 0; i < 1000; i++) {printf("%d ", fibonacci[i]);}return 0;}在上述代码中，我们使用一个整型数组`fibonacci`来存储Fibonacci数列的值。

c语言二叉树的先序,中序,后序遍历

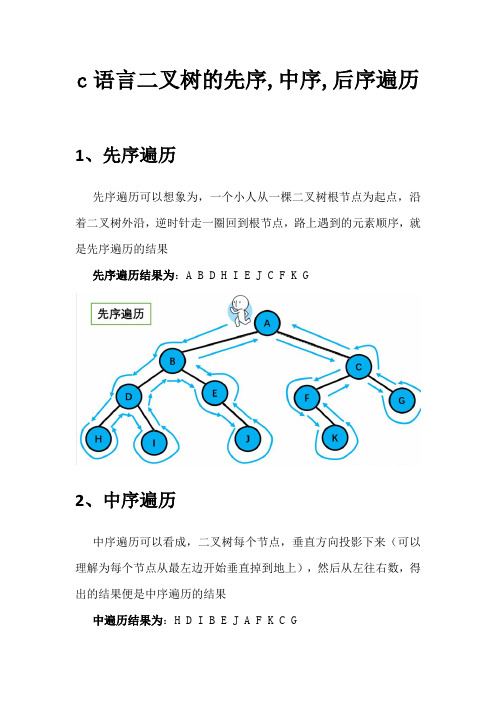
c语言二叉树的先序,中序,后序遍历

c语言二叉树的先序,中序,后序遍历1、先序遍历先序遍历可以想象为，一个小人从一棵二叉树根节点为起点，沿着二叉树外沿，逆时针走一圈回到根节点，路上遇到的元素顺序，就是先序遍历的结果先序遍历结果为：A B D H I E J C F K G2、中序遍历中序遍历可以看成，二叉树每个节点，垂直方向投影下来（可以理解为每个节点从最左边开始垂直掉到地上），然后从左往右数，得出的结果便是中序遍历的结果中遍历结果为：H D I B E J A F K C G3、后序遍历后序遍历就像是剪葡萄，我们要把一串葡萄剪成一颗一颗的。

还记得我上面提到先序遍历绕圈的路线么？（不记得翻上面理解）就是围着树的外围绕一圈，如果发现一剪刀就能剪下的葡萄（必须是一颗葡萄）（也就是葡萄要一个一个掉下来，不能一口气掉超过1个这样），就把它剪下来，组成的就是后序遍历了。

后序遍历中，根节点默认最后面后序遍历结果：H I D J E B K F G C A4、口诀先序遍历：先根再左再右中序遍历：先左再根再右后序遍历：先左再右再根这里的根，指的是每个分叉子树（左右子树的根节点）根节点，并不只是最开始头顶的根节点，需要灵活思考理解5、代码展示#include<stdio.h>#include<stdlib.h>typedef struct Tree{int data; // 存放数据域struct Tree *lchild; // 遍历左子树指针struct Tree *rchild; // 遍历右子树指针}Tree,*BitTree;BitTree CreateLink(){int data;int temp;BitTree T;scanf("%d",&data); // 输入数据temp=getchar(); // 吸收空格if(data == -1){ // 输入-1 代表此节点下子树不存数据，也就是不继续递归创建return NULL;}else{T = (BitTree)malloc(sizeof(Tree)); // 分配内存空间T->data = data; // 把当前输入的数据存入当前节点指针的数据域中printf("请输入%d的左子树: ",data);T->lchild = CreateLink(); // 开始递归创建左子树printf("请输入%d的右子树: ",data);T->rchild = CreateLink(); // 开始到上一级节点的右边递归创建左右子树return T; // 返回根节点}}// 先序遍历void ShowXianXu(BitTree T) // 先序遍历二叉树{if(T==NULL) //递归中遇到NULL，返回上一层节点{return;}printf("%d ",T->data);ShowXianXu(T->lchild); // 递归遍历左子树ShowXianXu(T->rchild); // 递归遍历右子树}// 中序遍历void ShowZhongXu(BitTree T) // 先序遍历二叉树{if(T==NULL) //递归中遇到NULL，返回上一层节点{return;}ShowZhongXu(T->lchild); // 递归遍历左子树printf("%d ",T->data);ShowZhongXu(T->rchild); // 递归遍历右子树}// 后序遍历void ShowHouXu(BitTree T) // 后序遍历二叉树{if(T==NULL) //递归中遇到NULL，返回上一层节点{return;}ShowHouXu(T->lchild); // 递归遍历左子树ShowHouXu(T->rchild); // 递归遍历右子树printf("%d ",T->data);}int main(){BitTree S;printf("请输入第一个节点的数据:\n");S = CreateLink(); // 接受创建二叉树完成的根节点printf("先序遍历结果: \n");ShowXianXu(S); // 先序遍历二叉树printf("\n中序遍历结果: \n");ShowZhongXu(S); // 中序遍历二叉树printf("\n后序遍历结果: \n");ShowHouXu(S); // 后序遍历二叉树return 0;}。

汉诺塔问题非递归算法c语言

汉诺塔问题非递归算法c语言

汉诺塔问题非递归算法c语言汉诺塔问题是一个经典的数学问题，也是一个常见的编程练习题。

在这个问题中，有三根柱子和一些圆盘，圆盘的大小不一，从小到大依次叠放在一根柱子上。

目标是将所有的圆盘从一根柱子移动到另一根柱子，移动过程中要保证大的圆盘在小的圆盘上面。

同时，每次只能移动一个圆盘，且不能把一个大的圆盘放在一个小的圆盘上面。

在解决汉诺塔问题时，通常采用递归算法。

但是递归算法的效率并不高，因为每次递归都会产生额外的函数调用，增加了系统的开销。

因此，我们可以通过非递归的方式来解决汉诺塔问题，提高算法的效率。

以下是一个用C语言实现的汉诺塔问题的非递归算法：```c#include <stdio.h>#include <stdlib.h>typedef struct {int n;char start, end, temp;} StackNode;typedef struct {StackNode data[100];int top;} Stack;void push(Stack *s, StackNode node) {s->data[s->top++] = node;}StackNode pop(Stack *s) {return s->data[--s->top];}void hanoi(int n, char start, char end, char temp) {Stack s;s.top = 0;StackNode node;node.n = n;node.start = start;node.end = end;node.temp = temp;push(&s, node);while (s.top > 0) {node = pop(&s);if (node.n == 1) {printf("Move disk 1 from %c to %c\n", node.start, node.end); } else {StackNode node1, node2, node3;node1.n = node.n - 1;node1.start = node.temp;node1.end = node.end;node1.temp = node.start;push(&s, node1);node2.n = 1;node2.start = node.start;node2.end = node.end;node2.temp = node.temp;push(&s, node2);node3.n = node.n - 1;node3.start = node.start;node3.end = node.end;node3.temp = node.temp;push(&s, node3);}}}int main() {int n;printf("Enter the number of disks: "); scanf("%d", &n);hanoi(n, 'A', 'C', 'B');return 0;}```在这个非递归算法中，我们使用了一个栈来模拟递归的过程。

c语言判断回文(递归法,非递归法)

c语言判断回文(递归法,非递归法)
return isPalindrome(i-2);//循环直至判断出该字符串是否为回文数 } else {
return 0; } } int main() { int n; printf("输入一串字符以判断是否为回文。\n"); scanf("%s",&a); n=strlen(a); if(isPalindrome(n)) printf("输入的是回文。\n"); else printf("输入的不是回文。\n"); }
编写程序判断一个字符串是否为回文，要求使用递归方法实现。
代码： #include<stdio.h> #include<string.hindrome(int i) {
int m; m=strlen(a); if(i<=1) return 1; if(a[m-i]==a[i-1]) {
编写程序判断一个字符串是否为回文，要求使用非递归方法实现。
代码： #include<stdio.h> #include<string.h> #include<stdlib.h> void main() {
char ch[100]; //存放键入的字符串 int i,j; printf("输入一串字符以判断是否为回文。\n"); scanf("%s",ch); //接受键入的字符串 i=0; j=strlen(ch)-1; while(i<j) if(ch[i]==ch[j]) {i++; j--; } else break; if(i>=j) printf("输入的是回文。\n"); else printf("输入的不是回文。\n"); }

先序遍历的非递归算法

先序遍历的非递归算法

数据结构1、先序遍历的非递归算法。

用c语言写。

void PreOrderUnrec(Bitree t){SqStack s;StackInit(s);p=t;while (p!=null || !StackEmpty(s)){while (p!=null) //遍历左子树{visite(p->data);push(s,p);p=p->lchild;}//endwhileif (!StackEmpty(s)) //通过下一次循环中的内嵌while实现右子树遍历{ p=pop(s);p=p->rchild;}//endif}//endwhile}//PreOrderUnrec/////////////////////////////////#include "stdio.h"#include "stdlib.h"#include "string.h"#define null 0struct node{char data;struct node *lchild;struct node *rchild;};//先序,中序建树struct node *create(char *pre,char *ord,int n){struct node * head;int ordsit;head=null;if(n<=0){return null;}else{head=(struct node *)malloc(sizeof(struct node)); head->data=*pre;head->lchild=head->rchild=null;ordsit=0;while(ord[ordsit]!=*pre){ordsit++;}head->lchild=create(pre+1,ord,ordsit);head->rchild=create (pre+ordsit+1,ord+ordsit+1,n-ordsit-1); return head;}}//中序递归遍历void inorder(struct node *head){if(!head)return;else{inorder(head->lchild );printf("%c",head->data );inorder(head->rchild );}}//中序非递归遍历void inorder1(struct node *head) {struct node *p;struct node *stack[20];int top=0;p=head;while(p||top!=0){while (p){stack[top++]=p;p=p->lchild ;}p=stack[--top];printf("%c ",p->data );p=p->rchild ;}}/////////////////////////////////////////////////////////////////// ////////////////////二叉树前序、中序、后序三种遍历的非递归算法1.先序遍历非递归算法void PreOrderUnrec(Bitree *t){Stack s;StackInit(s);Bitree *p=t;while (p!=NULL || !StackEmpty(s)){while (p!=NULL) //遍历左子树{visite(p->data);push(s,p);p=p->lchild;}if (!StackEmpty(s)) //通过下一次循环中的内嵌while实现右子树遍历{p=pop(s);p=p->rchild;}//endif}//endwhile}2.中序遍历非递归算法void InOrderUnrec(Bitree *t){Stack s;StackInit(s);Bitree *p=t;while (p!=NULL || !StackEmpty(s)){while (p!=NULL) //遍历左子树{push(s,p);p=p->lchild;}if (!StackEmpty(s)){p=pop(s);visite(p->data); //访问根结点p=p->rchild; //通过下一次循环实现右子树遍历}//endif }//endwhile}3.后序遍历非递归算法typedef enum{L,R} tagtype;typedef struct{Bitree ptr;tagtype tag;}stacknode;typedef struct{stacknode Elem[maxsize];int top;}SqStack;void PostOrderUnrec(Bitree t) {SqStack s;stacknode x;StackInit(s);p=t;do{while (p!=null) //遍历左子树{x.ptr = p;x.tag = L; //标记为左子树push(s,x);p=p->lchild;}while (!StackEmpty(s) && s.Elem[s.top].tag==R){x = pop(s);p = x.ptr;visite(p->data); //tag为R,表示右子树访问完毕,故访问根结点} if (!StackEmpty(s)){s.Elem[s.top].tag =R; //遍历右子树p=s.Elem[s.top].ptr->rchild;}}while (!StackEmpty(s));}//PostOrderUnrec二。

C语言实现二叉树的前序遍历

C语言实现二叉树的前序遍历

C语言实现二叉树的前序遍历二叉树是一种非线性数据结构，由节点和边组成。

每个节点最多有两个子节点，分别称为左子节点和右子节点。

二叉树可以用递归或迭代的方法进行前序、中序和后序遍历。

在本文中，我们将重点介绍如何使用递归方法实现二叉树的前序遍历。

前序遍历是指首先访问根节点，然后按照左子树->右子树的顺序遍历二叉树。

在实际编程中，我们可以通过递归的方式来遍历每个节点。

首先，让我们定义二叉树的节点结构。

```c//定义二叉树节点结构struct TreeNodeint val; // 节点值struct TreeNode* left; // 左子节点指针struct TreeNode* right; // 右子节点指针};```接下来，让我们实现二叉树的前序遍历函数。

```c//二叉树的前序遍历函数void preorderTraversal(struct TreeNode* root)if (root == NULL) { // 如果根节点为空，则返回return;}//首先打印根节点的值printf("%d ", root->val);//然后递归遍历左子树preorderTraversal(root->left);//最后递归遍历右子树preorderTraversal(root->right);```首先，我们判断根节点是否为空。

如果为空，表示已经遍历到叶子节点，直接返回。

然后，我们打印当前节点的值。

接下来，我们递归调用前序遍历函数，遍历左子树和右子树。

接下来，我们可以通过构建一个简单的二叉树来测试我们的前序遍历函数。

```c//创建一个二叉树用于测试前序遍历struct TreeNode* createTestTrestruct TreeNode* root = (structTreeNode*)malloc(sizeof(struct TreeNode)); // 创建根节点root->val = 1;root->left = (struct TreeNode*)malloc(sizeof(struct TreeNode)); // 创建左子节点root->left->val = 2;root->left->left = NULL;root->left->right = NULL;root->right = (struct TreeNode*)malloc(sizeof(struct TreeNode)); // 创建右子节点root->right->val = 3;root->right->left = NULL;root->right->right = NULL;return root;```在主函数中，我们创建一个测试二叉树，并调用前序遍历函数进行遍历。

关于树的各种C语言代码

关于树的各种C语言代码

集合了树的各种算法，已经运行过，本人亲自所写，先序，后序，等全包括#include<stdio.h>#include<malloc.h>#define Max 100typedef int Status;typedef struct BiTNode{char data;struct BiTNode *lchild,*rchild;}BiTNode,*BiTree;int count;Status CreatBiTree(BiTree *bt) /*1.按先序遍历序列创造二叉树的二叉链表*/ {char ch;getchar();scanf("%c",&ch);if (ch == ' '){*bt = NULL;}else{*bt = (BiTree)malloc(sizeof(BiTNode));(*bt)->data = ch;printf("\n\t请输入%c结点的左孩子:",(*bt)->data);CreatBiTree(&((*bt)->lchild));printf("\n\t请输入%c结点的右孩子:",(*bt)->data);CreatBiTree(&((*bt)->rchild));}return 1;}void PreOrder(BiTree bt) /*2.先序遍历二叉树*/{if (bt != NULL){printf("%c\n",bt->data);PreOrder(bt->lchild);PreOrder(bt->rchild);}}void InOrder(BiTree bt) /*3.中序遍历二叉树*/{if (bt != NULL){InOrder(bt->lchild);printf("%c\n",bt->data);InOrder(bt->rchild);}}void PostOrder(BiTree bt) /*4.后序遍历二叉树*/{if (bt != NULL){PostOrder(bt->lchild);PostOrder(bt->rchild);printf("%c\n",bt->data);}}void PreOrderLeaf(BiTree bt) /*5.输出所有的叶子结点*/{if (bt != NULL){if ((bt->lchild == NULL) && (bt->rchild == NULL)){printf("%c\n",bt->data);}PreOrderLeaf(bt->lchild);PreOrderLeaf(bt->rchild);}}Status Leaf(BiTree bt) /*6.统计叶子结点数目，即度为零的结点数目*/ {if (bt == NULL){count = 0;}else if ((bt->lchild == NULL) && (bt->rchild == NULL)){count = 1;}else{count = Leaf(bt->lchild) + Leaf(bt->rchild);}return count;}void Degree1Node(BiTree bt) /*7.输出度为一的结点*/{if (bt != NULL){if (((bt->lchild != NULL) || (bt->rchild != NULL))&& (!((bt->lchild != NULL) && (bt->rchild != NULL)))) {printf("%c\n",bt->data);}Degree1Node(bt->lchild);Degree1Node(bt->rchild);}}void Degree2Node(BiTree bt) /*8.输出度为二的结点*/{if ( bt != NULL){if ((bt->lchild != NULL) && (bt->rchild != NULL)){printf("%c\n",bt->data);}Degree2Node(bt->lchild);Degree2Node(bt->rchild);}}Status CountNode(BiTree bt) /*9.统计二叉树中结点的总数*/{if (bt == NULL){return 0;}else{count++;CountNode(bt->lchild);CountNode(bt->rchild);return count;}}Status TreeDepth(BiTree bt) /*10.求二叉树的深度*/{int ldep, rdep;if (bt == NULL){return 0;}else{ldep = TreeDepth(bt->lchild);rdep = TreeDepth(bt->rchild);if (ldep > rdep){return (ldep +1);}else{return (rdep + 1);}}}void PrintTree(BiTree bt, int nlayer) /*11.按树状打印二叉树*/ {if (bt == NULL) /*如果是空则直接退出函数*/{return;}PrintTree(bt->rchild,nlayer + 1);for ( int i = 0; i < nlayer; i++){printf("----");}printf("%c\n",bt->data);PrintTree(bt->lchild,nlayer + 1);}void PreOrderTree(BiTree bt) /*12.非递归先序遍历*/BiTree Stack[Max];BiTree p = bt;int top = 0;while (p != NULL || top != 0){if (p != NULL){printf("%c",p->data);top++;Stack[top] = p;p = p->lchild;}else{p = Stack[top];top--;p = p->rchild;}}}void InOrderTree(BiTree bt) /*13.非递归中序遍历*/ {BiTree Stack[Max];BiTree p = bt;int top = 0;do{while (p != NULL){top++;Stack[top] = p;p = p->lchild;}if (top != 0){p = Stack[top];top--;printf("%c",p->data);p = p->rchild;}}while ((p != NULL) || (top != 0));void PostOrderTree(BiTree bt) /*14.非递归后序遍历*/ {BiTree p, q;int top = 0;BiTree Stack[Max];q = NULL;p = bt;while ((p != NULL) || (top != 0)){while (p != NULL){top++;Stack[top] = p;p = p->lchild;}if (top > 0){p = Stack[top];if ((p->rchild == NULL) || (p->rchild == q)){printf("%c",p->data);q = p;p = NULL;top--;}else{p = p->rchild;}}}}void LayerOrder(BiTree bt) /*15.层次遍历*/{int front,rear;BiTree Q[Max];front = 0;rear = front;BiTree r, s, p;r = s = p = bt;if (p == NULL) return;Q[rear] = p;rear++;while (front != rear){s = r = Q[front];printf("%c",Q[front]->data);front++;if (r->lchild){Q[rear] = r->lchild;rear++;}if (s->rchild){Q[rear] = s->rchild;rear++;}}}int main(){BiTree bt;int choice;int i,j,k;int nlayer = 1;printf("请用数字选择操作：\n");printf("1.按先序序列创建二叉树（二叉链表）\n");printf("2.递归先序遍历二叉树\n");printf("3.递归中序遍历二叉树\n");printf("4.递归后序遍历二叉树\n");printf("5.输出叶子结点（即度为零的结点）\n");printf("6.统计叶子结点数目\n");printf("7.输出度为一的结点\n");printf("8.输出度为二的结点\n");printf("9.统计二叉树中结点总数\n");printf("10.求二叉树的高度（即深度）\n");printf("11.按树状打印二叉树\n");printf("12.非递归先序遍历二叉树\n");printf("13.非递归中序遍历二叉树\n");printf("14.非递归后序遍历二叉树\n");printf("15.层次遍历二叉树\n");printf("0.则退出\n");while (1){printf("请输入你要执行的操作(0-15):");scanf("%d",&choice);if (choice == 0){break;}else switch (choice){case 1 : printf("\n请输入按先序建立二叉树的结点序列：");printf("\n说明：逐个输入，输入空格代表后继结点为空，按回车输入下一个结点。

《数据结构(C语言描述)》-马秋菊-源代码和习题参考答案

《数据结构(C语言描述)》-马秋菊-源代码和习题参考答案

习题配套第一章2．C、A、B、B、A、A、D3．D={A,B,C,E,F,G,H,I,J};R={<A,B>,<A,C>,<A,E>,<B,F>,<B,G>,<E,H>,<E,I>,<E,J>,<H,I>,<I,J>}题1-3图4．顺序、链式、索引、哈希。

*5．解：100n2>2n n至少要多大6.Ｏ(n)、Ｏ(n)、Ｏ(n)、Ｏ(n)、(5)当n>m，Ｏ(n),当m>n，Ｏ(m)7．n!2100>lgn>n1/2>n3/2>(3/2)n>2n>n lgn>n n第二章1．×、√、×、√、√2．AAD4．顺序表void Delete_SeqListx(SeqList *L,ElemType x)/*删除表中值为x元素*/{inti,j;for(i=1;i<=L->length;i++){if(L->elem[i]==x){for(j=i;j<=L->length-1;j++)L->elem[j]=L->elem[j+1];L->length--;}/*向上移动*/}O(n2)链表void del_link(LinkList H，int x)/*删除数据域为x的结点*/ {LNode *p，*q;p=H;q=H->next;while(q!=NULL){if(q->data==x){p->next=q->next;free(q);q=p->next;}else{p=q;q=q->next;}}}O(n)5．int Delete_SeqListx(SeqList *L,int i,int k)/*删除表中删除自第i个结点开始的k个结点*/{intj;if(i<1||k<0||i+k-1>L->length)/*检查空表及删除位置的合法性*/{printf(＂不存在第i个元素＂);return ERROR;}for(j=i;j<=L->length-k;j++)L->elem[j]=L->elem[j+k]; /*向上移动*/L->length-=k;Return OK;/*删除成功*/}O(n)6．void Delete_SeqListx(SeqList *L,ElemType x)/*将表中值为x元素换成y*/{inti,j;for(i=1;i<=L->length;i++){if(L->elem[]==x){L->elem[i]=y;}/* */}O(n)7．写一算法在循环单链表上实现线性表的CList_length(L)运算。

2010年硕士研究生入学考试“数据结构与C语言程序设计”试题与答案

2010年硕士研究生入学考试“数据结构与C语言程序设计”试题与答案

13．C 语言规定，简单变量做实参时，它和对应的形参之间的数据传递方式是 A．单向值传递 B．地址传递 C．由实参传给形参，再由形参传回给实参 D．由用户指定传递方式 14．C 语言规定，函数返回值的类型是由 A．return 语句中的表达式的类型所决定 B．调用该函数时的主函数的类型所决定 。
3
C．调用该函数时系统临时决定 D．在定义该函数时所指定的函数的类型所决定 15．下面给出的 4 个定义语句中，与 int *p[5]; 等价的是 。 A．int p[5]; B．int *p; C．int *(p[5]); 16．若有以下定义和语句，则值为 1002 的表达式是 。 struct s{ int age; int num; }; static struct s a[3]={1001,20,1002,19,1003,21},*ptr; ptr=a; A．ptr++->num B．(ptr++)->age C．(*ptr).num D．(*++ptr).age 17．若要通过下面的程序段使得指针变量指向一个存储整型变量的动态存储单元，则程序段中的空 。 白处(横线上方)应该是 int *ptr; ptr= malloc(sizeof(int)); A．int B．int * C．(int *) D．(*int ) 。 18．下面关于宏的叙述中，错误的是 A．宏名无类型，其参数也无类型 B．宏定义不是 C 语句，不必在行的末尾加分号 C．宏替换只是字符替换 D．宏定义命令必须写在文件的开头 。 19．下列关于 C 语言文件操作的叙述中，正确的是 A．对文件的操作必须是先打开文件 B．对文件的操作必须是先关闭文件 C．对文件操作之前必须先测试文件是否已打开，然后再打开文件 D．对文件的操作无顺序要求 20．使用 fopen( )函数以文本方式打开或者建立可读写文件。要求：若指定文件不存在，则建立一 个文件，并使文件指针指向其开头；若指定文件存在，则打开该文件，并将文件指针指向其结尾。下列 。 “文件使用方式”中，正确的是 A．“r+” B．“ a+” C．“ w+” D．“a”

c语言常见排序算法

c语言常见排序算法

常见的C语言排序算法有以下几种：
1. 冒泡排序（Bubble Sort）：比较相邻的元素，如果前一个元素大于后一个元素，则交换它们的位置，重复这个过程直到整个序列有序。

2. 插入排序（Insertion Sort）：将未排序的元素逐个插入到已排序序列中的正确位置，直到整个序列有序。

3. 选择排序（Selection Sort）：每次从未排序的元素中选择最小的元素，将其放到已排序序列的末尾，重复这个过程直到整个序列有序。

4. 快速排序（Quick Sort）：选择一个基准元素，将序列分成两部分，一部分小于等于基准元素，一部分大于基准元素，然后对两部分递归地进行快速排序。

5. 归并排序（Merge Sort）：将序列分成两部分，分别对两部分进行归并排序，然后将两个有序的子序列合并成一个有序的序列。

6. 堆排序（Heap Sort）：将序列构建成一个最大堆，然后将堆顶元素与堆末尾元素交换，重复这个过程直到整个序列有序。

7. 希尔排序（Shell Sort）：将序列按照一定的间隔分成若干个子序列，对每个子序列进行插入排序，然后逐渐减小间隔直到间隔为1，最后对整个序列进行插入排序。

8. 计数排序（Counting Sort）：统计序列中每个元素出现的次数，然后按照元素的大小顺序将它们放入一个新的序列中。

9. 基数排序（Radix Sort）：按照元素的个位、十位、百位等依次进行排序，直到所有位数都排完为止。

以上是常见的C语言排序算法，每种算法都有其特点和适用场景，选择合适的排序算法可以提高排序效率。

数据结构(C语言描述)(第2版 李学刚拓展训练 (3)[3页]

数据结构(C语言描述)(第2版 李学刚拓展训练 (3)[3页]

单元4 拓展训练一、单项选择题1．在一棵度为3的树中，度为3的结点个数为2，度为2的结点个数为1，则度为0的结点个数为（）。

A．4 B．5 C．6 D．7 2．在一棵度为3的树中，度为2的结点个数是2，度为0的结点个数是7，则度为3的结点个数是（）。

A．1 B．2 C．3 D．4 3．在具有n个结点的带双亲指针的二叉链表中，共有（）个指针域用来指示结点的左、右孩子或双亲。

A．n+1 B．n+2 C．2n-1 D．2n-2 4．在具有n个结点的带双亲指针的二叉链表中，共有（）个指针域为空。

A．n+1 B．n+2 C．2n-1 D．2n-2 5．n（≥2）个结点二叉树的前序和后序序列正好相反，则该二叉树一定是（）的二叉树。

A．只有两个结点B．高度等于其结点数C．任一结点无左孩子D．任意结点无右孩子6．n（≥2）个结点二叉树的前序和后序序列正好相反，则该二叉树的形态描述错误的是（）。

A．没有度为2的结点B．高度等于nC．只有一个叶结点D．只有1度结点7．一棵树T采用双亲链表存储，parent是双亲指针，若T.nodes[i]. parent =j （j≥0），则（）。

A．T.nodes[i]是 T.nodes[j]的双亲B．T.nodes[j]是 T.nodes[i]的双亲C．T.nodes[i]与T.nodes[j]互为双亲D．不确定8．一棵树T采用孩子兄弟链表存储，如果某个结点的最左孩子和右邻兄弟的指针域均为空，则该结点一定是（）。

A．叶子结点B．最左孩子结点C．最右孩子结点D．叶子结点且是最右孩子结点9．已知一棵树的前序序列为ABCDEF，后序序列为CEDFBA，则对该树进行层次遍历得到的序列为（）。

A．ABCDEF B．ABCEFD C．ABFCDE D．ABCDFE 10．已知一棵完全二叉树有64个叶子结点，则该树可能达到的最大深度为（）。

A ．7B ．8C ．9D ．1011．设深度为k 的二叉树上只有度为0和度为2的结点，则这类二叉树上所含结点总数最少（ ）个。

浅析一种二叉树非递归遍历算法的C语言实现论文.doc

浅析一种二叉树非递归遍历算法的C语言实现论文.doc

浅析一种二叉树非递归遍历算法的C语言实现论文一种二叉树非递归遍历算法的C语言实现论文导读：本论文是一篇关于一种二叉树非递归遍历算法的C语言实现的优秀论文范文,对正在写有关于递归论文的写有一定的参考和指导作用,摘要：针对二叉树的链式存储结构，分析了二叉树的各种遍历算法，探讨了递归算法的递推消除理由，提出了一种改善的非递归遍历算法并用C语言予以实现。

关键词：二叉树；遍历算法；非递归；C语言实现1009-3044（2014）01-0223-031 概述树形结构是一种非常常见的数据结构，而二叉树又是其中最重要的一种树形结构。

二叉树的遍历是指按照一定的规则和次序将二叉树中的每一个结点都访问一次，既不能重复，也不能漏掉。

一般而言，对二叉树的遍历有前序遍历、中序遍历、后序遍历和按层遍历等几种方式。

在具体的算法设计上，以上遍历方式一般采取递归算法来实现，该文将探讨采用非递归算法来实现二叉树的遍历。

2 二叉树的数据结构描述二叉树作为一种非线性结构，每个结点最多有一个双亲结点和两个子结点。

二叉树可以采用顺序存储结构和链式存储结构。

对于完全二叉树而言，采用顺序存储是非常方便并且节省空间的，但是对于大部分的非完全二叉树而言，采用顺序存储将导致空间浪费严重且结构混乱、效率低下。

因此，更多的时候，大家都更愿意用链式存储结构来表示二叉树，这样结构更加清晰，尤其是对于一种二叉树非递归遍历算法的C语言实现由写论文的好帮手.zbjy.提供,.左右子树的描述和双亲节点的描述更加方便。

该文中拟采用链式结构来表示二叉树。

用链式存储结构来表示二叉树，一个结点至少由3个域组成，即数据域、左子结点域和右子结点域（如图1所示）。

3 二叉树的遍历及递归算法实现3.1 二叉树的遍历二叉树的遍历就是一个不漏的访问树中的每个结点，同时也不能重复。

所谓“访问”，就是指对结点的数据域进行某种操作，比如说读取、删除、更新、求该节点深度等等。

对于二叉树中的任意一个部分，都可以把它看作三部分，根节点、左子树、右子树，我们用D表示访问跟结点，用L表示遍历左子树，用R表示遍历右子树，则共有以下6种遍历方式[1]。

c语言中序非递归遍历求树的高度

c语言中序非递归遍历求树的高度

C语言是一种广泛应用于系统程序设计和应用软件开发的高级编程语言。

在C语言中，常常需要对树进行遍历操作，以求取树的高度。

其中，序非递归遍历是一种常用的遍历方式。

本文将针对C语言中对树进行序非递归遍历求树的高度进行详细的讲解。

一、序非递归遍历1.序非递归遍历是一种在树的遍历过程中不使用递归的方式。

通过借助栈这一数据结构来完成遍历操作。

2.在序非递归遍历中，我们首先将树的根节点入栈，然后循环执行以下步骤：a.将栈顶节点弹出，并输出该节点的值；b.将该节点的右子节点入栈（如果存在的话）；c.将该节点的左子节点入栈（如果存在的话）。

3.直到栈为空为止，遍历结束。

二、求树的高度1.树的高度是指树中从根节点到叶节点的最长路径的节点数。

求树的高度是树的常见操作之一。

2.在进行序非递归遍历的过程中，我们可以借助一个变量来记录树的高度。

具体做法如下：a.在栈中入栈的使用一个额外的变量记录当前节点的高度；b.每次遇到叶子节点时，将该节点的高度与之前记录的最大高度进行比较，并更新最大高度。

3.遍历结束后，最大高度即为树的高度。

三、C语言实现以下是C语言实现序非递归遍历求树高度的示例代码：```c#include <stdio.h>#include <stdlib.h>// 树的节点结构typedef struct Node {int data;struct Node* left;struct Node* right;} Node;// 栈的结构typedef struct Stack {Node* data[100]; // 假设栈的最大容量为100 int top;} Stack;// 初始化栈void init(Stack* s) {s->top = -1;}// 入栈void push(Stack* s, Node* node) {s->data[++(s->top)] = node;}// 出栈Node* pop(Stack* s) {return s->data[(s->top)--];}// 判断栈是否为空int isEmpty(Stack* s) {return s->top == -1;}// 求树高度int getHeight(Node* root) {Stack s;init(s);int maxHeight = 0;Node* curr = root;Node* prev = NULL;while (curr != NULL || !isEmpty(s)) { if (curr != NULL) {push(s, curr);if (s.top + 1 > maxHeight) { maxHeight = s.top + 1;}curr = curr->left;} else {curr = pop(s);curr = curr->right;}}return maxHeight;}// 主函数int m本人n() {// 构建一棵树（这里用简单的示例，实际情况中树的构建可能更加复杂）Node* root = (Node*)malloc(sizeof(Node));root->data = 1;root->left = (Node*)malloc(sizeof(Node));root->left->data = 2;root->left->left = NULL;root->left->right = NULL;root->right = (Node*)malloc(sizeof(Node));root->right->data = 3;root->right->left = NULL;root->right->right = NULL;printf("树的高度为：d\n", getHeight(root));return 0;}四、总结通过以上的讲解和示例代码，我们详细地介绍了C语言中如何利用序非递归遍历求树的高度。

先序遍历的非递归算法C语言

先序遍历的非递归算法C语言

先序遍历的非递归算法C语言先序遍历是二叉树遍历的一种方式，它的遍历顺序是根节点、左子树、右子树。

非递归算法利用栈的数据结构来实现。

具体算法步骤如下：1.定义一个栈，用于存储节点。

2.将根节点入栈。

3.当栈不为空时，执行步骤4-6，否则结束遍历。

4.弹出栈顶节点，并访问该节点。

5.若该节点有右孩子，将右孩子入栈。

6.若该节点有左孩子，将左孩子入栈。

7.返回步骤3下面是使用C语言实现先序遍历的非递归算法的示例代码：```c#include <stdio.h>#include <stdlib.h>//定义二叉树节点结构typedef struct TreeNodeint data;struct TreeNode* left;struct TreeNode* right;} TreeNode;//定义栈结构typedef struct StackTreeNode* data[100]; // 栈的最大容量int top; // 栈顶指针} Stack;Stack* createStacStack* stack = (Stack*)malloc(sizeof(Stack)); stack->top = -1;return stack;void push(Stack* stack, TreeNode* node)stack->data[++stack->top] = node;TreeNode* pop(Stack* stack)return stack->data[stack->top--];int isEmpty(Stack* stack)return stack->top == -1;//先序遍历的非递归算法void preorderTraversal(TreeNode* root)if (root == NULL)return;}Stack* stack = createStack(; // 创建栈push(stack, root); // 根节点入栈while (!isEmpty(stack))TreeNode* node = pop(stack); // 弹出栈顶节点printf("%d ", node->data); // 访问节点//右孩子先入栈，保证左孩子会在右孩子之前被访问if (node->right != NULL)push(stack, node->right);}//左孩子入栈if (node->left != NULL)push(stack, node->left);}}free(stack); // 释放栈的内存int mai//构建二叉树TreeNode* root = (TreeNode*)malloc(sizeof(TreeNode)); root->data = 1;TreeNode* node2 = (TreeNode*)malloc(sizeof(TreeNode)); node2->data = 2;TreeNode* node3 = (TreeNode*)malloc(sizeof(TreeNode)); node3->data = 3;TreeNode* node4 = (TreeNode*)malloc(sizeof(TreeNode)); node4->data = 4;TreeNode* node5 = (TreeNode*)malloc(sizeof(TreeNode)); node5->data = 5;root->left = node2;root->right = node3;node2->left = node4;node2->right = NULL;node3->left = NULL;node3->right = node5;node4->left = NULL;node4->right = NULL;node5->left = NULL;node5->right = NULL;//先序遍历printf("先序遍历结果：");preorderTraversal(root);//释放二叉树的内存free(root);free(node2);free(node3);free(node4);free(node5);return 0;```以上代码实现了二叉树先序遍历的非递归算法。

C++二叉树的先序，中序，后序遍历

C++二叉树的先序，中序，后序遍历

C++⼆叉树的先序，中序，后序遍历三种遍历⽅式都分为递归与⾮递归的⽅式。

三种遍历⽅式的递归思想相同。

后序遍历⾮递归⽅法分为两种，具体见代码。

构造⽅式：1 #include<iostream>2 #include<stack>3using namespace std;45 typedef struct BiTNode{6char data;7int lvisited,rvisited;//左、右孩⼦是否访问过，1表⽰已访问（此项只在后序⾮递归2算法中需要）8struct BiTNode *lchild,*rchild;9 }BiTNode,*BiTree;1011void InitBiTree(BiTree &T)//构造空⼆叉树12 {13 T=NULL;14 }15void CreateBiTree(BiTree &T)//⽣成⼆叉树16 {17char ch;18 cin>>ch;19if(ch=='0')//0代表空20 T=NULL;21else22 {23 T=(BiTree)malloc(sizeof(BiTNode));//⽣成根结点24if(!T)25 {26 cout<<"⽣成结点错误！"<<endl;27return;28 }29 T->data=ch;30 T->lvisited=0;31 T->rvisited=0;32 CreateBiTree(T->lchild);33 CreateBiTree(T->rchild);34 }35 }三种遍历⽅式代码：1void PreOrder(BiTree T)//先序递归遍历2 {3if(T!=NULL)4 {5 cout<<T->data<<"";6 PreOrder(T->lchild);7 PreOrder(T->rchild);8 }9 }10void SqlPreOrder(BiTree T)//先序⾮递归遍历11 {12 stack<BiTree> s;13 BiTree p=T;14while(p || !s.empty())15 {16if(p)17 {18 cout<<p->data<<"";19 s.push(p);20 p=p->lchild;21 }22else23 {24 p=s.top();25 p=p->rchild;26 s.pop();27 }28 }29 }30313233void InOrder(BiTree T)//中序递归遍历34 {35if(T!=NULL)36 {37 InOrder(T->lchild);38 cout<<T->data<<"";39 InOrder(T->rchild);40 }41 }42void SqInOrder(BiTree T)//中序⾮递归遍历43 {44 stack<BiTree> s;45 BiTree p=T;46while(p || !s.empty())47if(p)48 {49 s.push(p);50 p=p->lchild;51 }52else53 {54 p=s.top();55 cout<<p->data<<"";56 s.pop();57 p=p->rchild;58 }59 }60616263void PostOrder(BiTree T)//后序递归遍历64 {65if(T!=NULL)66 {67 PostOrder(T->lchild);68 PostOrder(T->rchild);69 cout<<T->data<<"";70 }71 }7273//后序⾮递归遍历1思路：因为后序⾮递归遍历⼆叉树的顺序是先访问左⼦树，再访问后⼦树，最后 74//访问根结点。

先序遍历的非递归算法

先序遍历的非递归算法

先序遍历的非递归算法先序遍历是二叉树的一种遍历方式，它的步骤是先访问根节点，然后递归地先序遍历左子树，最后递归地先序遍历右子树。

在非递归算法中，我们使用栈来辅助实现遍历。

首先，我们创建一个空栈，将根节点压入栈中。

然后进入循环，循环条件是栈不为空。

在循环中，首先将栈顶元素出栈并访问，然后将其右子节点（如果存在）压入栈中，再将其左子节点（如果存在）压入栈中。

这样可以保证在遍历的过程中，左子树总是先于右子树被访问。

详细的步骤如下：1.创建一个空栈，将根节点压入栈中。

2.进入循环，循环条件为栈不为空。

在循环中执行以下步骤：1.弹出栈顶元素并访问。

2.如果存在右子节点，将右子节点压入栈中。

3.如果存在左子节点，将左子节点压入栈中。

3.循环结束后，遍历完成。

下面是使用非递归算法实现先序遍历的代码：```pythonclass TreeNode:def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightdef preorderTraversal(root):if not root:return []stack = [] # 创建空栈result = [] # 用于存储遍历结果stack.append(root) # 将根节点压入栈中while stack: # 当栈不为空时循环node = stack.pop( # 弹出栈顶元素并访问result.append(node.val)if node.right: # 如果存在右子节点，将右子节点压入栈中stack.append(node.right)if node.left: # 如果存在左子节点，将左子节点压入栈中stack.append(node.left)return result#测试代码#创建二叉树root = TreeNode(1)root.left = TreeNode(2)root.right = TreeNode(3)root.left.left = TreeNode(4)root.left.right = TreeNode(5)#执行先序遍历并输出结果result = preorderTraversal(root)print(result)```运行上述代码可以得到先序遍历的结果：[1,2,4,5,3]。

用C语言编写二叉树的建立与遍历

用C语言编写二叉树的建立与遍历

用C语言编写二叉树的建立与遍历1．对题目要有需求分析在需求分析中，将题目中要求的功能进行叙述分析，并且设计解决此问题的数据存储结构，设计或叙述解决此问题的算法。

给出实现功能的一组或多组测试数据，程序调试后，将按照此测试数据进行测试的结果列出来。

如果程序不能正常运行，写出实现此算法中遇到的问题和改进方法；2．对题目要有相应的源程序源程序要按照写程序的规则来编写。

要结构清晰，重点函数的重点变量，重点功能部分要加上清晰的程序注释。

(注释量占总代码的四分之一)程序能够运行，要有基本的容错功能。

尽量避免出现操作错误时出现死循环；3．最后提供的主程序可以象一个应用系统一样有主窗口，通过主菜单和分级菜单调用课程设计中要求完成的各个功能模块，调用后可以返回到主菜单，继续选择其他功能进行其他功能的选择。

二叉树的建立与遍历[问题描述]建立一棵二叉树，并对其进行遍历（先序、中序、后序），打印输出遍历结果。

[基本要求]从键盘接受输入，以二叉链表作为存储结构，建立二叉树，并对其进行遍历（先序、中序、后序），将遍历结果打印输出。

以下是我的数据结构实验的作业：肯定好用，里面还包括了统计树的深度和叶子数！记住每次做完一个遍历还要重新输入你的树哦！#include "stdio.h"#include "string.h"#define NULL 0typedef struct BiTNode{char data;struct BiTNode *lchild,*rchild;}BiTNode,*BiTree;BiTree Create(BiTree T){char ch;ch=getchar();if(ch=='#')T=NULL;else{if(!(T=(BiTNode *)malloc(sizeof(BiTNode))))printf("Error!");T->data=ch;T->lchild=Create(T->lchild);T->rchild=Create(T->rchild); }return T;}void Preorder(BiTree T){if(T){printf("%c",T->data); Preorder(T->lchild); Preorder(T->rchild);}}int Sumleaf(BiTree T){int sum=0,m,n;if(T){if((!T->lchild)&&(!T->rchild)) sum++;m=Sumleaf(T->lchild);sum+=m;n=Sumleaf(T->rchild);sum+=n;}return sum;}void zhongxu(BiTree T){if(T){zhongxu(T->lchild);printf("%c",T->data); zhongxu(T->rchild);}}void houxu(BiTree T){if(T){houxu(T->lchild);houxu(T->rchild);printf("%c",T->data);}}int Depth(BiTree T){int dep=0,depl,depr;if(!T) dep=0;else{depl=Depth(T->lchild);depr=Depth(T->rchild);dep=1+(depl>depr?depl:depr);}return dep;}main(){BiTree T;int sum,dep;T=Create(T);Preorder(T);printf("\n");zhongxu(T);printf("\n");houxu(T);printf("\n");sum=Sumleaf(T);printf("%d",sum);dep=Depth(T);printf("\n%d",dep);}在Turbo C的环境下，先按Ctrl+F9运行程序，此时就是建立二叉树的过程，例如输入序列ABC##DE#G##F###（其中的“#”表示空，并且输入过程中不要加回车，因为回车也有对应的ASCII码，是要算字符的，但是输入完之后可以按回车退出），然后再按ALT+F5显示用户界面，这时候就能够看到结果了。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Preorder(p);printf("\n");
}
if(* BT==NULL) * BT=p;
else
{
if(k==1) s[top]->left=p;
else s[top]->right=p;
}
}
else {printf("二叉树广义表字符串有错!\n");exit(1);}
}
i++;
}
}
void Preorder(struct BTreeNode * BT)
p=p->left;
}
if(top!=-1)
{
p=s[top];
top--;
p=p->right;
}
}
}
void main()
{
struct BTreeNode * p;
char * a="A(B(C),D(E(F,G),H(,I)))";
InitBTree(&p);
CreatBTree(&p,a);
{
* BT=NULL;
}
void CreatBTree(struct BTreeNode * * BT,char * a)
{
struct BTreeNode * p;
struct BTreeNode * s[MS];
int top=-1;
int k;
int i=0;
* BT=NULL;
while(a[i])
exit(1);
}
top--;break;
case ',' : k=2;break;
default :
if((a[i]>='a'&&a[i]<='z')||(a[i]>='A'&&a[i]<='Z'))
{
p=malloc(sizeof(struct BTreeNode));
p->data=a[i];p->left=p->right=NULL;
{
structBTreeNode * s[10];
int top=-1;
structBTreeNode * p=BT;
printf("先序遍历结点的访问序列为:\n");
while(top!=-1||p!=NULL)
{
while(p!=NULL)
{
top++;
s[top]=p;
printf("%c",p->data);
先序遍历的非递归算法
#include<stdio.h>
#include<stdlib.h>
#define MS 10
struct BTreeruct BTreeNode * left;
struct BTreeNode * right;
};
void InitBTree(struct BTreeNode * * BT)
{
switch(a[i])
{
case ' ':break;
case '(':
if(top==MS-1)
{
printf("栈空间太小，需增加MS的值!\n");
exit(1);
}
top++;s[top]=p;k=1;
break;
case ')':
if(top==-1)
{
printf("二叉树广义表字符串有错!\n");
相关文档
最新文档