数字信号的基带传输
通信原理 第6章_数字信号的基带传输

功率谱密度为:
T P(f) S
Sa2
fT
(S
)
S
4
2
0.6 0.4 0.25 0.2
0
2.0
单极性不归零
1.5
P= 0.5
1.0
0.5
0.4 0.8 1.2 1.6 2.0 f/fb
0
双极性不归零 P= 0.5
0.4 0.8 1.2 1.6 2.0 f/fb
0.12
0.08 0.0625
0.04
单极性归零 0.0507 半占空P= 0.5
1
Sa2 (m
)
(
f
16
2
16 m
2
mfs )
TS Sa2 (fTS ) 1 ( f ) 1 Sa2 (m ) ( f
16
2 16
16 m奇数
2
mfs )
4、双极性归零码
∵ g1(t)= Gτ(t), g2(t)= - Gτ(t),τ=TS /2,
∴
,G2(f)=- G1(f)
且当信源等概 p=1/2时,单双极性归零码的
差分码或相对码(Differential encoding): 差分码又称为相对码,特征是:不用电平的绝对值 而用电平的相对变化传0、1符号。
原始代码 1 1 0 1 0 0 1
传号差分码
“1变0不变”,
TS
空号差分码
“0变1不变”
TS
多电平波形
0 0 0 1 0 1 10 0 0 1 1 11
Ts Ts
习题6-1
设二进制符号序列为110010001110,试以 矩形脉冲为例,分别画出相应的单极性波 形,双极性波形,单极性归零波形,双极 性归零波形,二进制差分波形及八电平波 形。
数字信号的基带传输

B 2
H(ω)
0 -
ω0
0
B 2
ω
(a)低通滤波器
(b)带通滤波器
A H ( ) 0
0 B other
A H ( ) 0
B B 0 0 2 2 other
15
无失真系统是否为线性系统?
(1)是否具有齐次性?
幅度。
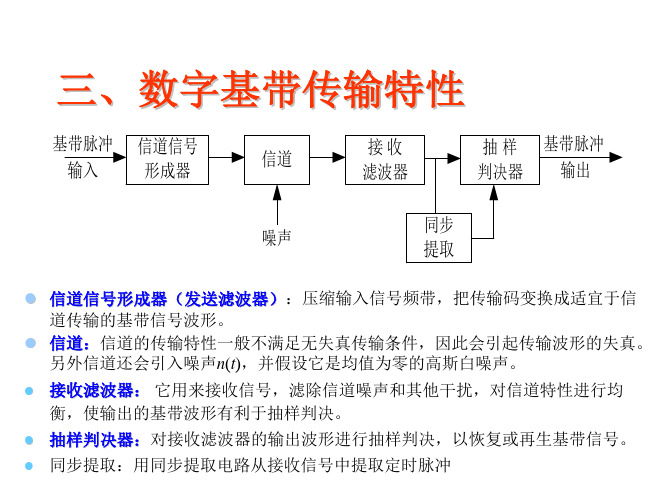
(4) 时隙(Slot):一个时隙一个数据位逐个进行。 码元
5
基本概念
二、基带传输与频带传输
数字基带信号:未经调制的数字信号,它所占据的频谱是从零
频或很低频率开始的。
基带传输:将数字基带信号通过基带信道(传递函数为低通型)传
输 —— 信号频谱不搬移,直接传送。
同轴电缆,双绞线 频带信号:数字基带信号经正弦波调制的带通信号 频带传输:将数字带通信号通过带通信道传输
振幅失真:
是信号各个频率分量的振幅值随频率发生了不同变化。
由传输设备和线路引起的衰损造成的
延迟失真:
是信号各频率分量的传播速度不一致所造成的失真。
12
基本概念
三、信号通过系统 3、无失真系统
如果信号通过系统后各个频率分量的振幅和延迟改变 都是相同的,则称信号不失真。能够使信号不失真的系 统称为不失真系统。
假定通过系统前的信号为X(t),通过系统后的信号为Y(t),
不失真系统只能导致信号如下改变:
Y (t ) kX (t t 0 )
13
系统对信号的作用如下:
输入信号
系统
输出信号
Y ( ) X ( ) H ( )
不失真系统信号输出:
X(t )
h(t )
6-数字信号的基带传输-3
x(t)
y(t)
信道
C( ω)
n(t)
接收滤波器
+
成型网络
R( ω)
判决 {an}
S(t)
基带传输模型
数字基带传输模型
z {an}为发送滤波器的输入符号序列,二进制时符号an的取 值为0、+1、-1,此序列对应的基带信号x(t):
∞
∑ x(t) = anδ (t − nTs ) n=−∞
z 此信号激励发送滤波器产生信号y(t):
(3)传输二进制码元时,求信息频带利用率ηb。
解 (1)将该系统的传递函数H(f)以2f0为间隔切割,然后分段 沿f轴平移到[-f0,f0]区间内进行叠加,如图6-19(b)所示。 叠加后的传输特性为
H
(
f
)
=
⎪⎧1, f ≤ ⎪⎩⎨0 ,其它
f
0
由于叠加后的传输特性符合等效理想低通特性,所以该系
统能够实现无码间串扰的传输。
z 则接收滤波器的输出信号S(t):
∞
∑ S(t) = ans(t − nT ) + nR (t) n=−∞
式中,s(t)与S(ω)互为傅里叶变换对;
∫ s(t) = 1 ∞ S(ω)e jωtdω
2π −∞
nR(t)为n(t)通过接收滤波器后的波形 S(t)送入抽样判决电路,进行抽样判决。
数字基带传输模型
z 抽样判决器:对接收滤波器的输出波形进行抽样判决,以恢复或再生基带信号。 z 同步提取:用同步提取电路从接收信号中提取定时脉冲
基带系统各点波形:
(a)
(b) (c)
(d )
(e) (f)
(g)
输入信号 t 码型变换后
第五章数字信号的基带传输

第五章 数字信号的基带传输基带传输系统频带传输系统(调制传输系统)数字基带信号:没有经过调制的原始数字信号。
(如各种二进制码PCM 码,M ∆码等)数字调制信号:数字基带信号对载波进行调制形成的带通信号。
5.1、基带信号的码型一、数字基带信号的码型设计原则:1. 对传输频带低端受限的信道,线路传输的码型的频谱中应该不含有直流分量;2.信号的抗噪声能力强;3.便于从信号中提取位定时信息;4.尽量减少基带信号频谱中的高频分量,节省传输频带、减小串扰; 5.编译码设备应尽量简单。
二、数字基带信号的常用码型。
1、单极性不归零码NRZ (Non Return Zero )脉冲宽度τ等于码元宽度T特点:(1)有直流,零频附近的低频分量一般信道难传输。
(2)收端判决门限与信号功率有关,不方便。
(3)要求传输线一端接地。
(4)不能用滤波法直接提取位定时信号。
2、双极性非归零码(BNRZ )T =τ,有正负电平特点:不能用滤波直接提取位定时信号。
⎩⎨⎧数字通信系统3、单极性归零码(RZ)τ<T特点:(1)可用滤波法提取位同步信号(2)NRZ的缺点都存在4、双极性归零码(BRZ)特点:(1)整流后可用滤波提取位同步信号(2)NRZ的缺点都不存在5、差分码电平跳变表1,电平不变表0 称传号差分码电平跳变表0,电平不变表1 称空号差分码特点:反映相邻代码的码元变化。
6、传号交替反转码(AMI)τ)归零码表0用零电平表示,1交替地用+1和-1半占空(T5.0=示。
优点:(1)“0”、“1”不等概时也无直流(2)零频附近低频分量小(3)整流后即为RZ码。
缺点:连0码多时,AMI整流后的RZ码连零也多,不利于提取高质量的位同步信号(位同频道抖动大)应用:μ律一、二、三次群接口码型:AMI加随机化。
7、三阶高密度双极性码()3HDBHDB3码编码步骤如下。
①取代变换:将信码中4个连0码用取代节000V或B00V代替,当两个相邻的V码中间有奇数个1码时用000V代替4个连0码,有偶数个1码时用B00V代替4个连0码。
第5章 数字信号的基带传输系统

HDB3码: -1000 -V +1000 +V -1 +1 -B00 -V +1 —1
虽然HDB3码的编码规则比较复杂,但译码比较简单。从上述 原理看出,每一个破坏符号V总是与前一非“0”符号同极性(包括
B符号在内),故从收到的符号序列中可以容易地找到破坏点V,
从而断定V符号及其前面的3个符号必是连“0”符号,然后恢复4个
一、单极性不归0二进制脉冲序列的功率谱密度数字 基带信号单个波形的频谱:
(设“1”、“0”码等概率出现,码元宽度)。
19
天津电子信息职业技术学院
20
天津电子信息职业技术学院
二、单极性归零二进制码序列的功率谱密度:
g1(t)
g2 (t )
A
Ts 2 Ts
2Ts 3Ts t
(a) 单极性归0二进制序列
6
天津电子信息职业技术学院
占空比指的是脉冲宽度τ与码元宽度Tb之比τ/Tb。单极性RZ码 的占空比为50%。
4.双极性归零(RZ)码 双极性归零码的构成原理与单极性归零码相同,如图5-1d)。 每一个码元被分成两个相等的间隔,“1”码是在前一个间隔为正 电平而后一个间隔回到零电平,而“0”码则是在前一个间隔内为 负电平而后一个间隔回到零电平。
1
1…
AMI码: +100 —1 +1000 -1 +1 -1 …
第5章数字信号的基带传输

(5.2 - 23)
Pu
(
f
)
lim
N
(2N
1)P(1 P) G1( f (2N 1)Ts
)
G2
(
f
)
2
fs P(1 P) G1( f ) G2 ( f ) 2
(5.2 - 24)
交变波的的功率谱Pu(f)是连续谱,它与g1(t)和g2(t)的 频谱以及出现概率P有关。根据连续谱可以确定随机
抽样判决器
在传输特性不理想及噪声背景下,在规定时刻 (由位定时脉冲控制)对接收滤波器的输出波形 进行抽样判决,以恢复或再生基带信号。而用来 抽样的位定时脉冲则依靠同步提取电路从接收信 号中提取,位定时的准确与否将直接影响判决效 果。
(a)基带信号; (b)码型变换后; (c) 对 (a) 进 行 了 码 型 及波形的变换,适合 在信道中传输的波形;
m
fs )
(5.2 - 28)
(1) g(t)为单极性不归零矩形脉冲
g
(t)
1,
0,
t Ts 2
其它
G(
f
)
Ts
s
in
f
f Ts Ts
Ts Sa(
f
Ts )
m 有直流分量
m 0 : G(m fs ) TsSa(m ) 0 离散谱均为零,因而无定时信号。
g2(t+ 4Ts) g1(t+ 3Ts) g1(t+ 2Ts) g2(t+Ts)
g (t) g1 (t)
g2(t- 2Ts)
g2(t-Ts)
(a)
-Ts O Ts
t
2
2
v(t)
(b)
-Ts -Ts O Ts Ts
数字信号的基带传输

,图
5 - 4(c)画出了
ut ut
下面我们根据式(5.2 - 5)和式(5.2 - 8), 分别求出稳
态波 V t 和交变波 ut 的功率谱,然后根据式(5.2 -
6)的关系,将两者的功率谱合并起来就可得到随机基
带脉冲序列 S t 的频谱特性。
1. V的功t 率谱密度
Pv f
由于 是以 为周期的周期信号,
另一种比较简单的方法是以随机过程功率谱的原始定义为出发点,求出数字随机序列的 功率谱公式。
设二进制的随机脉冲序列如图 5 - 4(a)所示,其中,假设
表示“0”码, 表示“1”码。 和 在实际中可以是任意的脉冲,但为了便于在
图上g1区分t ,这里我们把
g画2成宽t 度为Ts的方波,把 g1 画t 成宽度g为2 Tst的三角波。
g
t
A t
2
0 t 其它值
T 22
T
22
其频谱为:G
A
Sa
2
4 2
2 4
此双极性信号的功率谱密度为:
PS
1 TS
G 2
1 TS
A2
2
Sa2
2
A2TS 4
Sa2
TS
4
近似带宽可视为:
BS
4
TS
2 2 1 TS
TS 2
8 4
TS
TS
4 8
TS
TS
(2) 若 g t 为单极性信号,则:
数字基带信号是随机的脉冲序列,没有确定的频谱函数, 所以只能用功率谱来描述它 的频谱特性。方法有二:
1:由随机过程的相关函数去求随机 过程的功率(或能量)谱密度就是一种典型 的分析广义平稳随机过程的方法。但这 种计算方法比较复杂。
基带传输的三种调制方式

基带传输的三种调制方式在通信领域中,基带传输是指将数字信号直接传输到信道上的一种方式。
为了能够在信道上传输数字信号,需要对其进行调制处理。
基带传输的调制方式有三种:振幅调制(AM)、频率调制(FM)和相位调制(PM)。
下面将逐一介绍这三种调制方式的原理和特点。
1. 振幅调制(AM)振幅调制是将数字信号的振幅与载波的振幅进行调制,以实现信号的传输。
在振幅调制中,载波的频率和相位保持不变,只调制其振幅。
当数字信号为1时,振幅调制会使得载波的振幅增大;当数字信号为0时,振幅调制会使得载波的振幅减小。
通过这种方式,可以将数字信号转换为模拟信号,便于在信道上传输。
振幅调制的优点是实现简单,对信道的要求较低。
然而,由于调制信号是通过改变载波的振幅来传输信息的,因此容易受到噪声的干扰,信号的可靠性较低。
2. 频率调制(FM)频率调制是将数字信号的频率与载波的频率进行调制。
在频率调制中,载波的振幅和相位保持不变,只调制其频率。
当数字信号为1时,频率调制会使得载波的频率增加;当数字信号为0时,频率调制会使得载波的频率减小。
通过这种方式,可以将数字信号转换为模拟信号,便于在信道上传输。
频率调制的优点是抗干扰能力较强,信号的可靠性较高。
然而,频率调制的实现相对复杂,对信道的要求也较高。
3. 相位调制(PM)相位调制是将数字信号的相位与载波的相位进行调制。
在相位调制中,载波的振幅和频率保持不变,只调制其相位。
当数字信号为1时,相位调制会使得载波的相位发生变化;当数字信号为0时,相位调制会使得载波的相位保持不变。
通过这种方式,可以将数字信号转换为模拟信号,便于在信道上传输。
相位调制的优点是调制过程简单,对信道的要求较低。
然而,相位调制容易受到相位偏移和多径效应的影响,导致信号失真。
总结起来,振幅调制、频率调制和相位调制是基带传输中常用的调制方式。
每种调制方式都有其独特的优点和适用场景。
振幅调制简单易实现,适用于对信号可靠性要求不高的场景;频率调制抗干扰能力较强,适用于抗干扰能力要求较高的场景;相位调制实现简单,适用于对信道要求不高的场景。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实训三数字信号的基带传输
一、实验目的
1.掌握基带信号的功率谱密度方法。
2.掌握数字基带传输系统的误码率计算。
3.理解码间干扰和信道噪声对眼图的影响。
4.理解匹配滤波器的原理。
二、实验内容
1.基带信号采用不归零矩形脉冲或升余弦滚降波形,基带信号的功率谱密度分析。
2.误码率的计算:A/σ和误码率之间的性能曲线。
3.眼图的生成。
4.匹配滤波器。
三.实验结果
1.基带信号采用矩形脉冲和根号升余弦信号波形的功率谱。
(1)二进制不归零矩形脉冲的时域波形与功率谱(对应的m 文件为rectpul.m)。
012345678910
-1
1
时间
幅度2012210178 黄亮平
-5-4-3-2-1012345
01
2
3
频率功率
双极性矩形脉冲信号的功率谱密
度(2)二进制滚降系数为1的升余弦信号的时域波形和功率谱(对应的m 文件为rcos.m)。
0102030405060708090100
-1
1
时间
幅度2012210178 黄亮平 滚降系数为1的基带信号波形
00.51 1.52 2.53 3.5
x 104
00.1
0.2
0.3
0.4
升余弦信号功率谱2、误码率的计算
随机产生10^6个二进制信息数据,采用双极性码,映射为±A。
随机产生高斯噪声(要求A/σ为0~12dB),叠加在发送信号上,直接按判决规则进行判决,然后与原始数据进行比较,统计出错的数据量,与发送数据量相除得到误码率。
画出A/σ和误码率之间的性能曲线,并与理论误码率曲线相比较(对应的m 文件为bercompared.m)。
0246
81012
10
101010
1010
2012210178 黄亮平 误码率仿真曲线与理论曲线的比较
A/sigma b e r
3.绘制波形和眼图
(1)设基带信号波形为滚降系数为1的升余弦波形,符号周期Ts,试绘出不同滚降系数a=1,0.75,0.5,0.25时的时域脉冲波形(对应的m 文件为diffrcosa.m)。
02468101214161820
0.5
1
2012210178 黄亮平 滚降信号波形 a=1
02468101214161820
0.5
1
滚降信号波形 a=0.75
02468101214161820
0.5
1
2012210178 黄亮平 滚降信号波形 a=0.5
02468101214161820
0.5
1
滚降信号波形 a=0.25
(2)随机生成一系列二进制序列,滚降系数a=1,画出多个信号的升余弦波形(对应的m 文件为multicossignals.m)。
0102030405060708090100
-1.5-1
-0.5
0.5
1
1.5
时间幅度2012210178 黄亮平 滚降系数为1的基带信号波形
0102030405060708090100
-1.5-1
-0.5
0.5
1
1.5时间幅度2012210178 黄亮平 滚降系数为1的基带信号波形
0102030405060708090100
-1.5-1
-0.5
0.5
1
1.5时间幅度2012210178 黄亮平 滚降系数为1的基带信号波形
(3)通过高斯白噪声信道,选择a=1的升余弦波形,分别绘制出无噪声干扰以及信噪比为30,20,10,0dB 时的眼图(对应的m 文件为eyes.m)。
<1>无噪声干扰时的眼图:
-2-1.5-1-0.50
0.51 1.52
-1.5-1
-0.5
0.5
1
1.5Time A m p l i t u d e 2012210178 黄亮平 无噪声时的眼图
<2>SNR=30dB 时的眼图:
-2-1.5-1-0.50
0.51 1.52
-1.5-1
-0.5
0.5
1
1.5Time A m p l i t u d e 2012210178 黄亮平 SNR=30dB 的眼图
<3>SNR=20dB 时的眼图:
-2-1.5-1-0.50
0.51 1.52
-1.5-1
-0.5
0.5
1
1.5Time A m p l i t u d e <4>SNR=10dB 时的眼图:
-2-1.5-1-0.50
0.51 1.52-2.5-2
-1.5
-1
-0.5
00.51
1.5
2
2.5
Time A m p l i t u d e 2012210178 黄亮平 SNR=10dB 的眼图
<5>SNR=0dB 时的眼图:
-2-1.5-1-0.50
0.51 1.52
-6
-4
-2
2
4
6
Time A m p l i t u d e 四.实验中遇到的问题
1.编程过程中基带信号的功率谱密度只能显示正频部分,后来利用频谱的对称性将频谱反折得到双边功率谱密度。
2.绘制理论误码率曲线时公式推导不正确,导致最后仿真曲线与理论曲线相差较大。
3.本次实验编程过程中计算功率谱密度及误码率均需要运用for 循环,由于对MATLAB 中循环语句的误解,导致编程时思路中断,不时出现语法错误。
