模拟试卷三
2020年安徽省中考数学模拟试卷(三)

2020年安徽省中考数学模拟试卷(三)一、选择题(本大题共10小题,每小题4分,满分40分)1.(4分)6-的绝对值的相反数是()A.6-B.6C.16D.16-2.(4分)计算3a a÷,结果是()A.a B.2a C.3a D.4a3.(4分)下列几何体是由4个相同的小正方体搭成的,其中左视图和俯视图相同的是( )A.B.C.D.4.(4分)设a为正整数,且371a a<<+,则a的值为()A.5B.6C.7D.85.(4分)已知:如图,////AB CD EF,50ABC∠=︒,150CEF∠=︒,则BCE∠的值为( )A.50︒B.30︒C.20︒D.60︒6.(4分)计算222211111a a a aa a a-+-÷-+-+的正确结果为()A.11a+B.1C.2D.1a-7.(4分)我国南宋数学家杨辉曾提出这样一个问题:“直田积(矩形面积),八百六十四(平方步),只云阔(宽)不及长一十二步(宽比长少12步),问阔及长各几步.“如果设矩形田地的长为x步,那么同学们列出的下列方程中正确的是()A.(12)864x x+=B.(12)864x x-=C.212864x x+=D.2128640x x+-=8.(4分)如图,ABCD 中,AC BC ⊥,3BC =,4AC =,则B ,D 两点间的距离是()A .213B .62C .10D .559.(4分)二次函数2y ax bx c =++的图象如图所示,反比例函数ay x=与正比例函数y bx =在同一坐标系中的大致图象可能是( )A .B .C .D .10.(4分)如图1,已知平行四边形ABCD 中,点E 是AB 边上的一动点(与点A 不重合),设AE x =,DE 的延长线交CB 的延长线于点F ,设BF y =,且y 与x 之间的函数关系图象如图2所示,则下面的结论中不正确的是( )A .2AD =B .当1x =时,6y =C .若AD DE =,则1BF EF ==D .若2BF BC =,则43AE =二、填空题(本大题共4小题,每小题5分,满分20分)11.(5分)港珠澳大桥是世界最长的跨海大桥,其中主体工程“海中桥隧”长达35.578公里,整个大桥造价超过720亿元人民币.720亿用科学记数法可表示为 元.12.(5分)二十四节气列入联合国教科文组织人类非物质文化遗产代表作名录.太阳运行的轨道是一个圆形,古人将之称作“黄道”,并把黄道分为24份,每15度就是一个节气,统称“二十四节气”.这一时间认知体系被誉为“中国的第五大发明”.如图,指针落在惊蛰、春分、清明区域的概率是 .13.(5分)如图,已知四边形ABCD 内接于O ,AD 是直径,120ABC ∠=︒,3CD =,则弦AC = .14.(5分)如图,抛物线2286y x x =-+-与x 轴交于点A ,B ,把抛物线在x 轴及其上方的部分记作1C ,将1C 向右平移得2C ,2C 与x 轴交于点B ,D ,若直线y x m =+与1C ,2C 共有3个不同的交点,则m 的取值范围是 .三、(本大题共2小题,每小题8分,满分16分) 15.(8分)计算:201()|22|2cos45(3)2π-----︒+-16.(8分)定义一种新运算:观察下列式: 131437=⨯+=3(1)34111-=⨯-= 5454424=⨯+=4(3)44313-=⨯-=(1)请你想一想:a b = ; (2)若a b ≠,那么a b ba (填入“=”或“≠” )(3)若(2)3ab -=,请计算()(2)a b a b -+的值.四、(本大题共2小题,每小题8分,满分16分)17.(8分)2019年2月24日,华为发布旗下最新款折叠屏手机MateX ,如图是这款手机的示意图,当两块折叠屏的夹角为30︒时(即30)ABC ∠=︒,测得AC 之间的距离为40mm ,此时45CAB ∠=︒.求这款手机完全折叠后的宽度AB 长是多少?(结果保留整数,参考数据:2 1.414≈,3 1.732≈,6 2.449)≈18.(8分)已知:在平面直角坐标系中,ABC ∆的三个顶点的坐标分别为(5,4)A ,(0,3)B ,(2,1)C .(1)画出ABC ∆关于原点成中心对称的△111A B C ,并写出点1C 的坐标; (2)画出将111A B C 绕点1C 按顺时针旋转90︒所得的△221A B C .五、(本大题共2小题,每小题10分,满分20分)19.(10分)如图,在圆O中,弦8AB=,点C在圆O上(C与A,B不重合),连接CA、⊥,垂足分别是点D、E.CB,过点O分别作OD AC⊥,OE BC(1)求线段DE的长;(2)点O到AB的距离为3,求圆O的半径.20.(10分)为了增强学生体质,某校对学生设置了体操、球类、跑步、游泳等课外体育活动,为了了解学生对这些项目的喜爱情况,在全校范围内随机抽取了若干名学生,对他们最喜爱的体育项目(每人只选一项)进行了问卷调查,将数据进行了统计并绘制成了如图所示的频数分布直方图和扇形统计图(均不完整).(1)在这次问卷调查中,一共抽查了多少名学生?(2)补全频数分布直方图,求出扇形统计图中“体操”所对应的圆心角度数;(3)估计该校1200名学生中有多少人喜爱跑步项目.六、(本题满分12分)21.(12分)如图,一次函数的图象与y 轴交于(0,8)C ,且与反比例函数(0)k y x x=>的图象在第一象限内交于(3,)A a ,(1,)B b 两点. (1)求AOC ∆的面积;(2)若2224a ab b -+=,求反比例函数和一次函数的解析式.七、(本题满分12分)22.(12分)攀枝花得天独厚,气候宜人,农产品资源极为丰富,其中晚熟芒果远销北上广等大城市.某水果店购进一批优质晚熟芒果,进价为10元/千克,售价不低于15元/千克,且不超过40元/千克.根据销售情况,发现该芒果在一天内的销售量y (千克)与该天的售价x (元/千克)之间的数量满足如下表所示的一次函数关系. 销售量y (千克) ⋯32.5 35 35.5 38⋯售价x (元/千克)⋯27.5 25 24.5 22⋯(1)某天这种芒果的售价为28元/千克,求当天该芒果的销售量.(2)设某天销售这种芒果获利m 元,写出m 与售价x 之间的函数关系式,如果水果店该天获利400元,那么这天芒果的售价为多少元? 八、(本题满分14分)23.(14分)如图1,在锐角ABC ∆中,D 、E 分别是AB 、BC 的中点,点F 在AC 上,且满足AFE A ∠=∠,//DM EF 交AC 于点M . (1)证明:DM DA =;(2)如图2,点G 在BE 上,且BDG C ∠=∠,求证:DEG ECF ∆∆∽; (3)在图2中,取CE 上一点H ,使得CFH B ∠=∠,若3BG =,求EH 的长.2020年安徽省中考数学模拟试卷(三)参考答案与试题解析一、选择题(本大题共10小题,每小题4分,满分40分)1.(4分)6-的绝对值的相反数是()A.6-B.6C.16D.16-【解答】解:6-的绝对值为6,6的相反数为6-,6∴-的绝对值的相反数是6-.故选:A.2.(4分)计算3a a÷,结果是()A.a B.2a C.3a D.4a【解答】解:32a a a÷=.故选:B.3.(4分)下列几何体是由4个相同的小正方体搭成的,其中左视图和俯视图相同的是( )A.B.C.D.【解答】解:A、左视图第一层两个小正方形,俯视图第一层一个小正方形,故A不符合题意;B、左视图和俯视图相同,故B符合题意;C、左视图第一层两个小正方形,俯视图第一层一个小正方形,故C不符合题意;D、左视图是一列两个小正方形,俯视图一层三个小正方形,故D不符合题意;故选:B.4.(4分)设a为正整数,且371a a<+,则a的值为()A.5B.6C.7D.8【解答】解:363749∴6377<<,a 为正整数,且371a a <<+,6a ∴=.故选:B .5.(4分)已知:如图,////AB CD EF ,50ABC ∠=︒,150CEF ∠=︒,则BCE ∠的值为()A .50︒B .30︒C .20︒D .60︒【解答】解:////AB CD EF ,50ABC BCD ∴∠=∠=︒,180CEF ECD ∠+∠=︒; 18030ECD CEF ∴∠=︒-∠=︒, 20BCE BCD ECD ∴∠=∠-∠=︒.故选:C .6.(4分)计算222211111a a a a a a a-+-÷-+-+的正确结果为( )A .11a + B .1 C .2D .1a-【解答】解:原式2(1)(1)111111(1)(1)(1)a a a a a a a a a-+=⨯-+=-+=+--.故选:B .7.(4分)我国南宋数学家杨辉曾提出这样一个问题:“直田积(矩形面积),八百六十四(平方步),只云阔(宽)不及长一十二步(宽比长少12步),问阔及长各几步.“如果设矩形田地的长为x 步,那么同学们列出的下列方程中正确的是( ) A .(12)864x x +=B .(12)864x x -=C .212864x x +=D .2128640x x +-=【解答】解:设矩形田地的长为x 步,那么宽就应该是(12)x -步. 根据矩形面积=长⨯宽,得:(12)864x x -=. 故选:B .8.(4分)如图,ABCD 中,AC BC ⊥,3BC =,4AC =,则B ,D 两点间的距离是()A .213B .62C .10D .55【解答】解:过D 作DE BC ⊥,ABCD 中,AC BC ⊥, //AD CE ∴, DE BC ⊥, //AC DE ∴,∴四边形ACED 是平行四边形,3CE AD BC ∴===,连接BD ,在Rt BDE ∆中,222264213BD BE DE =+=+=, 故选:A .9.(4分)二次函数2y ax bx c =++的图象如图所示,反比例函数ay x=与正比例函数y bx =在同一坐标系中的大致图象可能是( )A .B .C .D .【解答】解:二次函数2y ax bx c =++的图象开口方向向下, 0a ∴<,对称轴在y 轴的右边, a ∴、b 异号,即0b >.∴反比例函数ay x=的图象位于第二、四象限, 正比例函数y bx =的图象位于第一、三象限. 观察选项,C 选项符合题意. 故选:C .10.(4分)如图1,已知平行四边形ABCD 中,点E 是AB 边上的一动点(与点A 不重合),设AE x =,DE 的延长线交CB 的延长线于点F ,设BF y =,且y 与x 之间的函数关系图象如图2所示,则下面的结论中不正确的是( )A .2AD =B .当1x =时,6y =C .若AD DE =,则1BF EF == D .若2BF BC =,则43AE =【解答】解:ABCD 为平行四边形//AD BC ∴,//AB DCF ADF ∴∠=∠,FBE A ∠=∠ BFE ADE ∴∆∆∽∴BF BEAD AE=设AB a =,AD b = 则BE AB AE a x =-=-∴y a xb x -=aby b x∴=- 图象过点(2,2),(4,0) 4a ∴=,2b =故A 正确; 4a =,2b =82y x∴=- ∴当1x =时,6y =,故B 正确;若AD DE =,则A AED ∠=∠A FBE ∠=∠,AED FEB ∠=∠ FBE FEB ∴∠=∠ BF EF ∴=∴若AD DE =,则总有BF EF =,它们并不总等于1,故C 不正确;若2BF BC =, BF BEAD AE=∴24BC AEBC AE-=解得43AE =故D 正确. 故选:C .二、填空题(本大题共4小题,每小题5分,满分20分)11.(5分)港珠澳大桥是世界最长的跨海大桥,其中主体工程“海中桥隧”长达35.578公里,整个大桥造价超过720亿元人民币.720亿用科学记数法可表示为 107.210⨯ 元. 【解答】解:720亿10720000000007.210==⨯. 故答案为:107.210⨯.12.(5分)二十四节气列入联合国教科文组织人类非物质文化遗产代表作名录.太阳运行的轨道是一个圆形,古人将之称作“黄道”,并把黄道分为24份,每15度就是一个节气,统称“二十四节气”.这一时间认知体系被誉为“中国的第五大发明”.如图,指针落在惊蛰、春分、清明区域的概率是18.【解答】解:如图,此转盘被平分成了24等份,其中惊蛰、春分、清明有3份,∴指针落在惊蛰、春分、清明的概率是:31248=. 故答案为:1813.(5分)如图,已知四边形ABCD 内接于O ,AD 是直径,120ABC ∠=︒,3CD =,则弦AC = 33 .【解答】解:四边形ABCD 内接于O , 18060D B ∴∠=︒-∠=︒,AD 是直径,90ACD ∴∠=︒, tan 33AC CD D ∴==故答案为:3314.(5分)如图,抛物线2286y x x =-+-与x 轴交于点A ,B ,把抛物线在x 轴及其上方的部分记作1C ,将1C 向右平移得2C ,2C 与x 轴交于点B ,D ,若直线y x m =+与1C ,2C 共有3个不同的交点,则m 的取值范围是1538m -<<-.【解答】解:令22860y x x =-+-=, 即2430x x -+=, 解得1x =或3, 则点(1,0)A ,(3,0)B ,由于将1C 向右平移2个长度单位得2C , 则2C 解析式为22(4)2(35)y x x =--+, 当1y x m =+与2C 相切时, 令212(4)2y x m y x =+==--+, 即21215300x x m -++=, △18150m =--=, 解得1158m =-, 当2y x m =+过点B 时, 即203m =+,23m =-,当1538m -<<-时直线y x m =+与1C 、2C 共有3个不同的交点, 故答案是:1538m -<<-.三、(本大题共2小题,每小题8分,满分16分) 15.(8分)计算:201()22|2cos45(3)2π----︒+-【解答】解:原式422213=-+=.16.(8分)定义一种新运算:观察下列式: 131437=⨯+=3(1)34111-=⨯-= 5454424=⨯+=4(3)44313-=⨯-=(1)请你想一想:a b = 4a b + ; (2)若a b ≠,那么a b ba (填入“=”或“≠” )(3)若(2)3ab -=,请计算()(2)a b a b -+的值. 【解答】解:(1)根据定义可知:4a b a b =+;(2)4a b a b =+,4b a b a =+,a b ≠,ab ba ∴≠;(3)(2)3a b -=,423a b ∴-=, 2 1.5a b ∴-=,()(2)a b a b ∴-+4()(2)a b a b =-++ 63a b =-3(2)a b =- 4.5=.故答案为:4a b +;≠.四、(本大题共2小题,每小题8分,满分16分)17.(8分)2019年2月24日,华为发布旗下最新款折叠屏手机MateX ,如图是这款手机的示意图,当两块折叠屏的夹角为30︒时(即30)ABC ∠=︒,测得AC 之间的距离为40mm ,此时45CAB ∠=︒.求这款手机完全折叠后的宽度AB 长是多少?(结果保留整数,参考数据:2 1.414≈,3 1.732≈,6 2.449)≈【解答】解:过点C 作CD AB ⊥于点D , 40AC mm =,45A ∠=︒,40202()2CD AD mm ∴===,30B ∠=︒,2402()BC CD mm ∴==,∴由勾股定理可知:206()BD mm =,AB AD BD ∴=+202206=+77()mm ≈,18.(8分)已知:在平面直角坐标系中,ABC ∆的三个顶点的坐标分别为(5,4)A ,(0,3)B ,(2,1)C .(1)画出ABC ∆关于原点成中心对称的△111A B C ,并写出点1C 的坐标; (2)画出将111A B C 绕点1C 按顺时针旋转90︒所得的△221A B C .【解答】解:(1)如图所示,△111A B C 即为所求,其中点1C 的坐标为(2,1)--.(2)如图所示,△221A B C 即为所求.五、(本大题共2小题,每小题10分,满分20分)19.(10分)如图,在圆O 中,弦8AB =,点C 在圆O 上(C 与A ,B 不重合),连接CA 、CB ,过点O 分别作OD AC ⊥,OE BC ⊥,垂足分别是点D 、E .(1)求线段DE 的长;(2)点O 到AB 的距离为3,求圆O 的半径.【解答】解:(1)OD 经过圆心O ,OD AC ⊥, AD DC ∴=,同理:CE EB =,DE ∴是ABC ∆的中位线,12DE AB ∴=, 8AB =,4DE ∴=.(2)过点O 作OH AB ⊥,垂足为点H ,3OH =,连接OA ,OH 经过圆心O ,12AH BH AB ∴==, 8AB =,4AH ∴=,在Rt AHO ∆中,222AH OH AO +=, 5AO ∴=,即圆O 的半径为5.20.(10分)为了增强学生体质,某校对学生设置了体操、球类、跑步、游泳等课外体育活动,为了了解学生对这些项目的喜爱情况,在全校范围内随机抽取了若干名学生,对他们最喜爱的体育项目(每人只选一项)进行了问卷调查,将数据进行了统计并绘制成了如图所示的频数分布直方图和扇形统计图(均不完整).(1)在这次问卷调查中,一共抽查了多少名学生?(2)补全频数分布直方图,求出扇形统计图中“体操”所对应的圆心角度数; (3)估计该校1200名学生中有多少人喜爱跑步项目. 【解答】解:(1)45%80÷=,即在这次问卷调查中,一共抽查了80名学生; (2)喜爱游泳的学生有:8025%20⨯=(人), 补全的频数分布直方图如右图所示,扇形统计图中“体操”所对应的圆心角度数是:103604580︒⨯=︒;(3)10120015080⨯=(人), 答:该校1200名学生中有150人喜爱跑步项目.六、(本题满分12分)21.(12分)如图,一次函数的图象与y 轴交于(0,8)C ,且与反比例函数(0)k y x x=>的图象在第一象限内交于(3,)A a ,(1,)B b 两点. (1)求AOC ∆的面积;(2)若2224a ab b -+=,求反比例函数和一次函数的解析式.【解答】解:(1)作AD y ⊥轴于D ,(3,)A a , 3AD ∴=,一次函数的图象与y 轴交于(0,8)C , 8OC ∴=,11831222AOC S OC AD ∆∴==⨯⨯=;(2)(3,)A a ,(1,)B b 两点在反比例函数(0)ky x x=>的图象上,3a b ∴=,4, 22216a ab b ∴-+=,2223(3)16a a a a ∴-+=, 整理得,24a =, 0a >, 2a ∴=,(3,2)A ∴, 326k ∴=⨯=,设直线的解析式为y mx n =+,∴832n m n =⎧⎨+=⎩,解得:28m n =-⎧⎨=⎩,∴一次函数的解析式为28y x =-+, ∴反比例函数和一次函数的解析式分别为6y x=和28y x =-+. 七、(本题满分12分)22.(12分)攀枝花得天独厚,气候宜人,农产品资源极为丰富,其中晚熟芒果远销北上广等大城市.某水果店购进一批优质晚熟芒果,进价为10元/千克,售价不低于15元/千克,且不超过40元/千克.根据销售情况,发现该芒果在一天内的销售量y (千克)与该天的售价x (元/千克)之间的数量满足如下表所示的一次函数关系.(1)某天这种芒果的售价为28元/千克,求当天该芒果的销售量.(2)设某天销售这种芒果获利m 元,写出m 与售价x 之间的函数关系式,如果水果店该天第21页(共23页)获利400元,那么这天芒果的售价为多少元?【解答】解:(1)设该一次函数解析式为(0)y kx b k =+≠,则 25352238k b k b +=⎧⎨+=⎩, 解得160k b =-⎧⎨=⎩, 60(1540)y x x ∴=-+,∴当28x =时,32y =,答:芒果售价为28元/千克时,当天该芒果的销售量为32千克;(2)由题易知2(10)(60)(10)70600m y x x x x x =-=-+-=-+-, 当400m =时,则270600400x x -+-=,解得,120x =,250x =,1540x ,20x ∴=,答:这天芒果的售价为20元.八、(本题满分14分)23.(14分)如图1,在锐角ABC ∆中,D 、E 分别是AB 、BC 的中点,点F 在AC 上,且满足AFE A ∠=∠,//DM EF 交AC 于点M .(1)证明:DM DA =;(2)如图2,点G 在BE 上,且BDG C ∠=∠,求证:DEG ECF ∆∆∽;(3)在图2中,取CE 上一点H ,使得CFH B ∠=∠,若3BG =,求EH 的长.【解答】(1)证明:如图1所示,//DM EF,∴∠=∠,AMD AFE∠=∠,AFE AAMD A∴∠=∠,∴=.DM DA(其他解法酌情给分)(2)证明:如图2所示,D、E分别是AB、BC的中点,∴,//DE AC∴∠=∠,DEG CBDE A∠=∠,∠=∠,AFE A∴∠=∠,BDE AFEBDG GDE C FEC∴∠+∠=∠+∠,∠=∠,BDG CGDE FEC∴∠=∠,∽.∴∆∆DEG ECF(3)如图3所示,第22页(共23页)BDG C DEB∠=∠=∠,B B∠=∠,BDG BED∴∆∆∽,∴BD BGBE BD=,2BD BG BE∴=,AFE A∠=∠,CFH B∠=∠,180180C A B AFE CFH EFH∴∠=︒-∠-∠=︒-∠-∠=∠,又FEH CEF∠=∠,EFH ECF∴∆∆∽,∴EH EFEF EC=,2EF EH EC∴=,//DE AC,//DM EF,∴四边形DEFM是平行四边形,EF DM DA BD∴===,BG BE EH EC∴=,BE EC=,3EH BG∴==.第23页(共23页)。
四川省绵阳市 中考数学模拟试卷(三)(解析版)

四川省绵阳市中考数学模拟试卷(三)一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一个符合题目要求)1.在体育课的跳远比赛中,以4.00米为标准,若小东跳出了4.22米,可记做+0.22,那么小东跳出了3.85米,记作()A.﹣0.15 B.+0.22 C.+0.15 D.﹣0.222.”造林见林,见林见效”这是退耕还林、造林的基本要求,更是农民的朴实愿望,四川省林业厅副厅长包建华说,退耕还林直补给退耕农户带来实惠,累计兑现政策性补助资金331.92亿元,户均5500元.将331.92亿用科学记数法表示为()A.3.3192×108B.3.3192×109C.3.3192×1010D.3.3192×10113.下列事件中是随机事件的是()A.一星期有7天B.袋中有三个红球,摸出一个球是红球C.字母M、N都轴对称图形D.任意买一张车票,座位刚好靠窗口4.在函数y=中,自变量x的取值范围是()A.x≥﹣2且x≠0 B.x≤2且x≠0 C.x≠0 D.x≤﹣25.如图是一个由5个相同的正方体组成的立体图形,它的三视图是()A. B.C.D.6.已知四边形ABCD,则下列说法中正确的是()A.若AB∥CD,AB=CD,则四边形ABCD是平行四边形B.若AC⊥BD,AC=BD,则四边形ABCD是矩形C.若AC⊥BD,AB=AD,CB=CD则四边形ABCD是菱形D.若AB=BC=CD=AD,则四边形ABCD是正方形7.学校文艺部组织部分文艺积极分子看演出,共购得8张甲票,4张乙票,总计用了112元.已知每张甲票比乙票贵2元,则每张甲票、每张乙票的价格分别是()A.10元和8元B.8元和10元C.12元和10元D.10元和12元8.为了调查某班的学生每天使用零花钱的使用情况,张华随机调查了20名同学,结果如下表:每天使用零花钱(单位:元) 1 2 3 4 5人数 1 3 6 5 5则这20名同学每天使用的零花钱的平均数和中位数分别是()A.3,3 B.3,3.5 C.3.5,3.5 D.3.5,39.如图是一个长方形的铝合金窗框,其长为a(m),高为b(m),装有同样大的塑钢玻璃,当第②块向右拉到与第③块重叠,再把第①块向右拉到与第②块重叠时,用含a与b的式子表示这时窗子的通风面积是()m2.A.B.C.D.10.如图,已知AD∥BC,AC与BD相交于点O,点G是BD的中点,过G作GE∥BC交AC于点E,如果AD=1,BC=3,GE:BC等于()A.1:2 B.1:3 C.1:4 D.2:311.已知二次函数y=x2﹣5x+6,当自变量x取m时,对应的函数值小于0,当自变量x取m﹣1、m+1时,对应的函数值为y1、y2,则y1、y2满足()A.y1>0,y2>0 B.y1<0,y2>0 C.y1<0,y2<0 D.y1>0,y2<012.已知,如图,∠ACB=90°,以AC为直径的⊙O交AB于点D,过点D作⊙O的切线交BC于点E,EF⊥AB于F,连接OE交DC于点P,则下列结论不正确的是()A.OE∥AB B.BC=2DE C.AC•DF=DE•CD D.DE=PD二.填空题(本大题共6小题,每小题3分,共18分)13.小明身高为140cm,比他高20cm的哥哥的身高为cm.14.如图,把一块直角三角板直角顶点放在直尺的一边上,若∠1=25°,则∠2=.15.三角形的两边长分别为8和6,第三边长是一元一次不等式2x﹣1<9的正整数解,则三角形的第三边长是.16.如图所示,如果将矩形纸沿虚线①对折后,沿虚线②剪开,剪出一个直角三角形,展开后得到一个等腰三角形.则展开后三角形的周长是.17.如图,在△ABC中,∠ACB=90°,AC=BC,点P在△ABC内,△AP′C是由△BPC绕着点C旋转得到的,PA=,PB=1,∠BPC=135°.则PC=.18.有依次排列的3个数:3,9,8.对任意相邻的两个数,都用右边的数减去左边的数,所得之差写在这两个数之间,可产生一个新数串:3,6,9,﹣1,8,这称为第一次操作,做第二次同样的操作后也可产生一个新数串:3,3,6,3,9,﹣10,﹣1,9,8.继续依次操作下去,问:从数串3,9,8开始操作第一百次以后所产生的那个新数串的所有数之和是.三.解答题(本大题共7小题,共86分)19.(1)计算:3tan45°+|1﹣|﹣(3.14﹣π)0﹣(2)化简:÷(﹣a﹣2)20.中学生骑电动车上学的现象越来越受到社会的关注.为此某媒体记者小李随机调查了市区若干名中学生家长对这种现象的态度(态度分为:A:无所谓;B:反对;C:赞成)并将调査结果绘制成图①和图②的统计图(不完整)请根据图中提供的信息,解答下列问题:(1)此次抽样调査中.共调査了名中学生家长;(2)将图①补充完整;(3)根据抽样调查结果,请你估计市区80000名中学生家长中有多少名家长持反对态度?21.如图,直角三角形ABC,点A的坐标为(0,2),点B的坐标为(0,﹣2),BC的长为3,反比例函数y=的图象经过点C.(1)求反比例函数与直线AC的解析式;(2)点P是反比例函数图象上的点,若使△OAP的面积恰好等于△ABC的面积,求P点的坐标.22.某商店以每件16元的价格购进一批商品,物价局限定每件商品的利润不得超过20%,则该商家经过两次连续降价(两次降价百分率相等)后,使该商品的利润为20%;(1)若已知该商家商品原来定价为30元,求每次降价的百分率;(2)若每件商品定价为x(x为整数)元,将剩余170件商品全部卖出,商店预期至少盈利340元,则有哪几种定价方案?23.如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.(1)求证:CD为⊙O的切线;(2)求证:∠C=2∠DBE;(3)若EA=AO=2,求图中阴影部分的面积.(结果保留π)24.如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点(A在B点左侧),与y轴交于点C,对称轴为直线x=,OA=2,OD平分∠BOC交抛物线于点D(点D在第一象限);(1)求抛物线的解析式和点D的坐标;(2)点M是抛物线上的动点,在x轴上存在一点N,使得A、D、M、N四个点为顶点的四边形是平行四边形,求出点M的坐标;(3)在抛物线的对称轴上,是否存在一点P,使得△BPD的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.25.已知△ABC,AC=BC,CD⊥AB于点D,点F在BD上,连接CF,AM⊥CF于点M,AM交CD于点E.(1)如图1,当∠ACB=90°时,求证:DE=DF;(2)如图2,当∠ACB=60°时,DE与DF的数量关系是(3)在2的条件若tan∠EAF=,EM=,连接EF,将∠DEF绕点E逆时针旋转,旋转后角的两边交线段CF于N、G两点,交线段BC于P、T两点(如图3),若CN=3FN,求线段GT的长.四川省绵阳市中考数学模拟试卷(三)参考答案与试题解析一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一个符合题目要求)1.在体育课的跳远比赛中,以4.00米为标准,若小东跳出了4.22米,可记做+0.22,那么小东跳出了3.85米,记作()A.﹣0.15 B.+0.22 C.+0.15 D.﹣0.22【考点】正数和负数.【分析】根据高于标准记为正,可得低于标准记为负.【解答】解:∵以4.00米为标准,若小东跳出了4.22米,可记做+0.22,∴小东跳出了3.85米,记作﹣0.15米,故选:A.【点评】本题考查了正数和负数,注意高于标准用正数表示,低于标准用负数表示.2.”造林见林,见林见效”这是退耕还林、造林的基本要求,更是农民的朴实愿望,四川省林业厅副厅长包建华说,退耕还林直补给退耕农户带来实惠,累计兑现政策性补助资金331.92亿元,户均5500元.将331.92亿用科学记数法表示为()A.3.3192×108B.3.3192×109C.3.3192×1010D.3.3192×1011【考点】科学记数法—表示较大的数.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【解答】解:331.92亿=331 9200 0000=3.3192×1010.故选:C.【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n 为整数,表示时关键要正确确定a的值以及n的值.3.下列事件中是随机事件的是()A.一星期有7天B.袋中有三个红球,摸出一个球是红球C.字母M、N都轴对称图形D.任意买一张车票,座位刚好靠窗口【考点】随机事件.【分析】根据必然事件、不可能事件、随机事件的概念可区别各类事件.【解答】解:A、一星期有7天是必然事件,故A错误;B、袋中有三个红球,摸出一个球是红球是必然事件,故B错误;C、字母M是轴对称图形,字母N不是轴对称图形,故C错误;D、任意买一张车票,座位刚好靠窗口是随机事件,故D正确;故选:D.【点评】解决本题需要正确理解必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件.不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.4.在函数y=中,自变量x的取值范围是()A.x≥﹣2且x≠0 B.x≤2且x≠0 C.x≠0 D.x≤﹣2【考点】函数自变量的取值范围.【专题】函数思想.【分析】根据二次根式的性质和分式的意义,被开方数大于或等于0,分母不等于0,可以求出x的范围.【解答】解:根据题意得:x+2≥0且3x≠0,解得:x≥﹣2且x≠0.故选A.【点评】考查了函数自变量的范围,函数自变量的范围一般从三个方面考虑:(1)当函数表达式是整式时,自变量可取全体实数;(2)当函数表达式是分式时,考虑分式的分母不能为0;(3)当函数表达式是二次根式时,被开方数非负.5.如图是一个由5个相同的正方体组成的立体图形,它的三视图是()A. B.C.D.【考点】简单组合体的三视图.【分析】找到从正面、左面、上看所得到的图形即可,注意所有的看到的棱都应表现在视图中.【解答】解:此几何体的主视图有两排,从上往下分别有1,3个正方形;左视图有二列,从左往右分别有2,1个正方形;俯视图有三列,从上往下分别有3,1个正方形,故选:A.【点评】本题考查了三视图的知识,关键是掌握三视图所看的位置.6.已知四边形ABCD,则下列说法中正确的是()A.若AB∥CD,AB=CD,则四边形ABCD是平行四边形B.若AC⊥BD,AC=BD,则四边形ABCD是矩形C.若AC⊥BD,AB=AD,CB=CD则四边形ABCD是菱形D.若AB=BC=CD=AD,则四边形ABCD是正方形【考点】正方形的判定;平行四边形的判定;菱形的判定;矩形的判定.【分析】分别利用平行四边形以及矩形、菱形和正方形的判定方法分别判断得出即可.【解答】解;A、若AB∥CD,AB=CD,则四边形ABCD是平行四边形,故此选项正确;B、若AC⊥BD,AC=BD,无法得到四边形ABCD是矩形,故此选项错误;C、若AC⊥BD,AB=AD,CB=CD,无法得到四边形ABCD是菱形,故此选项错误;D、若AB=BC=CD=AD,无法得到四边形ABCD是正方形,故此选项错误.故选:A.【点评】此题主要考查了平行四边形以及矩形、菱形和正方形的判定方法,正确掌握相关判定定理是解题关键.7.学校文艺部组织部分文艺积极分子看演出,共购得8张甲票,4张乙票,总计用了112元.已知每张甲票比乙票贵2元,则每张甲票、每张乙票的价格分别是()A.10元和8元B.8元和10元C.12元和10元D.10元和12元【考点】二元一次方程组的应用.【专题】计算题.【分析】设每张甲票、每张乙票的价格分别是x元,y元,列方程组得,求解即可.【解答】解:设每张甲票、每张乙票的价格分别是x元,y元,则,解得,答:每张甲票、每张乙票的价格分别是10元,8元.故选A.【点评】本题考查了二元一次方程组的应用,找出等量关系,列出方程组,是解此题的关键.8.为了调查某班的学生每天使用零花钱的使用情况,张华随机调查了20名同学,结果如下表:每天使用零花钱(单位:元) 1 2 3 4 5人数 1 3 6 5 5则这20名同学每天使用的零花钱的平均数和中位数分别是()A.3,3 B.3,3.5 C.3.5,3.5 D.3.5,3【考点】中位数;加权平均数.【分析】根据平均数和中位数的概念求解.【解答】解:这组数据按照从小到大的顺序排列为:1,2,2,2,3,3,3,3,3,3,4,4,4,4,4,5,5,5,5,5,则平均数为:=3.5,中位数为:=3.5.故选C.【点评】本题考查了平均数和中位数的知识:将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.9.如图是一个长方形的铝合金窗框,其长为a(m),高为b(m),装有同样大的塑钢玻璃,当第②块向右拉到与第③块重叠,再把第①块向右拉到与第②块重叠时,用含a与b的式子表示这时窗子的通风面积是()m2.A.B.C.D.【考点】列代数式.【分析】第②块向右拉到与第③块重叠,再把第①块向右拉到与第②块重叠时,第一块和第二块玻璃之间的距离是(﹣)×.窗子的通风面积为①中剩下的部分.【解答】解:[a﹣﹣﹣×(﹣)]×b=ab.故选B.【点评】此题有一定的难度,主要是不能准确的找到窗子的通风部位.应该根据图示找到窗子通风的部位在那里,是那个长方形,其长和宽式多少,都需要求出来,再进行面积计算.10.如图,已知AD∥BC,AC与BD相交于点O,点G是BD的中点,过G作GE∥BC交AC于点E,如果AD=1,BC=3,GE:BC等于()A.1:2 B.1:3 C.1:4 D.2:3【考点】相似三角形的判定与性质.【分析】由AD∥BC,GE∥BC,易证得△AOD∽△COB,△OGE∽△OBC,又由AD=1,BC=3,点G是BD 的中点,根据相似三角形的对应边成比例,易得OG=OD,继而求得答案.【解答】解:∵AD∥BC,∴△AOD∽△COB,∵AD=1,BC=3,∴OD:OB=AD:BC=1:3,∴OD=BD,∵点G是BD的中点,∴DG=BD,∴OD=OG,∵GE∥BC,∴△OGE∽△OBC,∴GE:BC=OG:OB=OD:OB=1:3.故选:B.【点评】此题考查了相似三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.11.已知二次函数y=x2﹣5x+6,当自变量x取m时,对应的函数值小于0,当自变量x取m﹣1、m+1时,对应的函数值为y1、y2,则y1、y2满足()A.y1>0,y2>0 B.y1<0,y2>0 C.y1<0,y2<0 D.y1>0,y2<0【考点】二次函数图象上点的坐标特征.【分析】根据函数的解析式求得函数与x轴的交点坐标,利用自变量x取m时对应的值小于0,确定m ﹣1、m+1的位置,进而确定函数值为y1、y2.【解答】解:令y=x2﹣5x+6=0,解得:x=2或x=3.∵当自变量x取m时对应的值小于0,∴2<m<3,∴m﹣1<2,m+1>3,∴y1>0,y2>0.故选:A.【点评】此题考查了抛物线与x轴的交点和二次函数图象上的点的特征,解题的关键是求得抛物线与横轴的交点坐标.12.已知,如图,∠ACB=90°,以AC为直径的⊙O交AB于点D,过点D作⊙O的切线交BC于点E,EF⊥AB于F,连接OE交DC于点P,则下列结论不正确的是()A.OE∥AB B.BC=2DE C.AC•DF=DE•CD D.DE=PD【考点】切线的性质.【分析】证明BC是⊙O的切线,进而得到P是CD的中点,利用中位线定理求出OE∥AB,据此判断A 正确;证明E是BC的中点,利用∠CDB是直角,据此得到BC=2DE,判断B选项正确;证明△ACD∽△EDF,即可得到AC•DF=DE•CD,判断C选项正确;只有当PE=PD时DE才等于PD,据此判断D选项错误.【解答】解:∵∠ACB=90°,∴BC是⊙O的切线,∵BC是⊙O的切线,∴OE垂直平分CD,∠OEC=∠OED,∴P是CD的中点,∴OP∥AB,∴OE∥AB,A选项正确,∵OE∥AB,O是AC的中点,∴E是BC的中点,∵AC是直径,∴∠ADC=90°,∴CD⊥AB,∴∠CDB=90°,∴BC=2DE,B选项正确;∵EF⊥AB,∴∠DFE=∠ADC=90°,∵DE=CD,BC是⊙O的切线,∴DE是⊙O的切线,∴∠EDF=∠CAD,∴△ACD∽△EDF∴,∴AC•DF=DE•CD,C选项正确.在四边形PDFE中,我们可以证明它是矩形,而不具备证明它是正方形的条件, ∴DE=,只有PE=PD时DE才等于PD,D选项错误,故选D.【点评】本题考查了圆的切线的性质、圆周角定理,相似三角形的判定与性质,切线长性质及三角形的中位线的运用,解答本题的关键是熟练掌握切线的判定定理以及切线的性质,此题有一定的难度.二.填空题(本大题共6小题,每小题3分,共18分)13.小明身高为140cm,比他高20cm的哥哥的身高为160cm.【考点】有理数的加法.【专题】应用题.【分析】根据有理数的加法,即可解答.【解答】解:140+20=160(cm).故答案为:160.【点评】本题考查了有理数的加法,解决本题的关键是熟记有理数加法法则.14.如图,把一块直角三角板直角顶点放在直尺的一边上,若∠1=25°,则∠2=65°.【考点】平行线的性质.【分析】由题意知,∠1+∠3=90°;然后根据“两直线平行,内错角相等”推知∠2=∠3.【解答】解:如图,根据题意,知∠1+∠3=90°.∵∠1=25°,∠3=65°.又∵AB∥CD,∴∠2=∠3=65°;故答案是“65°.【点评】本题考查了平行线的性质.解题时,要注意挖掘出隐含在题中的已知条件∠1+∠3=90°.15.三角形的两边长分别为8和6,第三边长是一元一次不等式2x﹣1<9的正整数解,则三角形的第三边长是3或4.【考点】三角形三边关系;一元一次不等式的整数解.【分析】先求出不等式的解集,再根据x是符合条件的正整数判断出x的可能值,再由三角形的三边关系求出x的值即可.【解答】解:2x﹣1<9,解得:x<5,∵x是它的正整数解,∴x可取1,2,3,4,根据三角形第三边的取值范围,得2<x<14,∴x=3,4.故答案为:3或4.【点评】本题综合考查了求不等式特殊解的方法及三角形的三边关系,正确解不等式,求出解集是解答本题的关键.解不等式应根据不等式的基本性质.16.如图所示,如果将矩形纸沿虚线①对折后,沿虚线②剪开,剪出一个直角三角形,展开后得到一个等腰三角形.则展开后三角形的周长是2+2.【考点】剪纸问题.【专题】压轴题.【分析】严格按照图的示意对折,裁剪后得到的是直角三角形,虚线①为矩形的对称轴,依据对称轴的性质虚线①平分矩形的长,即可得到沿虚线②裁下的直角三角形的短直角边为10÷2﹣4=1,虚线②为斜边,据勾股定理可得虚线②为,据等腰三角形底边的高平分底边的性质可以得到,展开后的等腰三角形的底边为2,故得到等腰三角形的周长.【解答】解:根据题意,三角形的底边为2(10÷2﹣4)=2,腰的平方为32+12=10,因此等腰三角形的腰为,因此等腰三角形的周长为:2+2.答:展开后等腰三角形的周长为2+2.【点评】本题主要考查学生的动手能力和对相关性质的运用能力,只要亲自动手操作,答案就会很容易得出来.17.如图,在△ABC中,∠ACB=90°,AC=BC,点P在△ABC内,△AP′C是由△BPC绕着点C旋转得到的,PA=,PB=1,∠BPC=135°.则PC=.【考点】旋转的性质;勾股定理.【专题】计算题.【分析】根据旋转的性质可以得到∠P′CA=∠PCB,进而可以得到∠P′CP=∠ACB=90°,进而得到等腰直角三角形,求解即可.【解答】解:∵△AP′C是由△BPC绕着点C旋转得到的,∴∠P′CA=∠PCB,CP′=CP,∴∠P′CP=∠ACB=90°,∴△P′CP为等腰直角三角形,可得出∠AP′B=90°,∵PA=,PB=1,∴AP′=1,∴PP′==2,∴PC=,故答案为.【点评】本题考查了旋转的性质及勾股定理的知识,解题的关键是正确的利用旋转的性质得到相等的量.18.有依次排列的3个数:3,9,8.对任意相邻的两个数,都用右边的数减去左边的数,所得之差写在这两个数之间,可产生一个新数串:3,6,9,﹣1,8,这称为第一次操作,做第二次同样的操作后也可产生一个新数串:3,3,6,3,9,﹣10,﹣1,9,8.继续依次操作下去,问:从数串3,9,8开始操作第一百次以后所产生的那个新数串的所有数之和是520.【考点】规律型:数字的变化类.【分析】首先具体地算出每一次操作以后所产生的那个新数串的所有数之和,从中发现规律,进而得出操作第100次以后所产生的那个新数串的所有数之和.【解答】解:设A=3,B=9,C=8,操作第n次以后所产生的那个新数串的所有数之和为S n.n=1时,S1=A+(B﹣A)+B+(C﹣B)+C=B+2C=(A+B+C)+1×(C﹣A);n=2时,S2=A+(B﹣2A)+(B﹣A)+A+B+(C﹣2B)+(C﹣B)+B+C=﹣A+B+3C=(A+B+C)+2×(C﹣A);…故n=100时,S100=(A+B+C)+100×(C﹣A)=﹣99A+B+101C=﹣99×3+9+101×8=520.故答案为:520.【点评】此题主要考查了数字变化类,本题中理解每一次操作的方法是前提,得出每一次操作以后所产生的那个新数串的所有数之和的规律是关键.三.解答题(本大题共7小题,共86分)19.(1)计算:3tan45°+|1﹣|﹣(3.14﹣π)0﹣(2)化简:÷(﹣a﹣2)【考点】分式的混合运算;零指数幂;二次根式的混合运算;特殊角的三角函数值.【分析】(1)根据特殊角的三角函数值,绝对值,零指数次幂以及分母有理化进行计算即可;(2)根据运算顺序,先算括号里面的,再算除法即可.【解答】解:(1)原式=3×1+﹣1﹣1﹣=3﹣2=1;(2)原式=÷=•=﹣=﹣.【点评】本题考查了特殊角的三角函数值,二次根式的混合运算以及分式的混合运算,通分、因式分解和约分是解答分式混合运算的关键.20.中学生骑电动车上学的现象越来越受到社会的关注.为此某媒体记者小李随机调查了市区若干名中学生家长对这种现象的态度(态度分为:A:无所谓;B:反对;C:赞成)并将调査结果绘制成图①和图②的统计图(不完整)请根据图中提供的信息,解答下列问题:(1)此次抽样调査中.共调査了200名中学生家长;(2)将图①补充完整;(3)根据抽样调查结果,请你估计市区80000名中学生家长中有多少名家长持反对态度?【考点】条形统计图;用样本估计总体;扇形统计图.【专题】计算题.【分析】(1)由无所谓的人数除以所占的百分比即可求出学生家长的总数;(2)求出赞成的人数,补全统计图即可;(3)求出反对的人数占得百分比,乘以80000即可得到结果.【解答】解:(1)根据题意得:40÷20%=200(人),则共调查了200名中学生的家长;(2)赞成家长数为200﹣(40+120)=40(人),补全统计图,如图所示:(3)根据题意得:80000×=48000(人),则市区80000名中学生家长中有48000名家长持反对态度.【点评】此题考查了条形统计图,扇形统计图,用样本估计总体,弄清题意是解本题的关键.21.如图,直角三角形ABC,点A的坐标为(0,2),点B的坐标为(0,﹣2),BC的长为3,反比例函数y=的图象经过点C.(1)求反比例函数与直线AC的解析式;(2)点P是反比例函数图象上的点,若使△OAP的面积恰好等于△ABC的面积,求P点的坐标.【考点】反比例函数与一次函数的交点问题.【分析】(1)求出C的坐标,代入反比例函数的解析式,即可求出反比例函数的解析式,设直线AC的解析式是y=ax+b,把A、C的坐标代入即可求出直线AC的解析式;(2)设P的坐标是(x,y),根据三角形面积求出x的值,代入反比例函数的解析式,求出y即可.【解答】解:(1)∵点A的坐标为(0,2),点B的坐标为(0,﹣2),∴AB=4,∵BC的长是3,∴C点的坐标是(3,﹣2),∵反比例函数y=的图象经过点C,∴k=3×(﹣2)=﹣6,∴反比例函数的解析式是y=﹣;设直线AC的解析式是y=ax+b,把A(0,2),C(3,﹣2)代入得:,解得:b=2,k=﹣,即直线AC的解析式是y=﹣x+2;(2)设P的坐标是(x,y),∵△OAP的面积恰好等于△ABC的面积,∴×OA•|x|=×3×4,解得:x=±6,∵P点在反比例函数y=﹣上,∴当x=6时,y=﹣1;当x=﹣6时,y=1;即P点的坐标为(6,﹣1)或(﹣6,1).【点评】本题考查了三角形的面积,用待定系数法求一次函数、反比例函数的解析式的应用,主要考查学生的推理和计算能力,题目比较好,难度适中.22.某商店以每件16元的价格购进一批商品,物价局限定每件商品的利润不得超过20%,则该商家经过两次连续降价(两次降价百分率相等)后,使该商品的利润为20%;(1)若已知该商家商品原来定价为30元,求每次降价的百分率;(2)若每件商品定价为x(x为整数)元,将剩余170件商品全部卖出,商店预期至少盈利340元,则有哪几种定价方案?【考点】一元二次方程的应用.【专题】增长率问题.【分析】(1)设每次降价的百分率为x,根据商家经过两次连续降价(两次降价百分率相等)后,该商品的利润为20%,列出方程,求解即可;(2)若每件商品定价为x(x为整数)元,根据物价局限定每件商品的利润不得超过20%和剩余170件商品全部卖出,商店预期至少盈利340元,列出不等式组,求解即可.【解答】解:(1)设每次降价的百分率为x,根据题意得:30(1﹣x)2=16(1+20%),解得:x1=0.2=20%,x2=1.8(不合题意,舍去),答:每次降价的百分率为20%.(2)若每件商品定价为x(x为整数)元,根据题意得:,解得:18≤x≤,∵x为整数,∴x=18,19,∴共有2种方案,方案①:每件商品定价为18元,方案②:每件商品定价为19元.【点评】此题考查了一元二次方程和一元一次不等式组的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程和不等式组,再求解;注意把不合题意的解舍去.23.如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.(1)求证:CD为⊙O的切线;(2)求证:∠C=2∠DBE;(3)若EA=AO=2,求图中阴影部分的面积.(结果保留π)【考点】切线的判定与性质;扇形面积的计算.【专题】综合题.【分析】(1)连接OD,由BC为圆O的切线,利用切线的性质得到∠ABC为直角,由CD=CB,利用等边对等角得到一对角相等,再由OB=OD,利用等边对等角得到一对角相等,进而得到∠ODC=∠ABC,确定出∠ODC为直角,即可得证;(2)根据图形,利用外角性质及等边对等角得到∠DOE=∠ODB+∠OBD=2∠DBE,由(1)得:OD⊥EC 于点D,可得∠E+∠C=∠E+∠DOE=90°,等量代换即可得证;(3)作OF⊥DB于点F,利用垂径定理得到F为BD中点,连接AD,由EA=AO可得:AD是Rt△ODE 斜边的中线,利用直角三角形斜边上的中线等于斜边的一半得到AD=AE=AO,即三角形AOD为等边三角形,确定出∠DAB=60°,即∠OBD=30°,在直角三角形BOF中,利用30°所对的直角边等于斜边的一半求出OF的长,利用勾股定理求出BFO的长,得到BD的长,得出∠DOB为120°,由扇形BDO面积减去三角形BOD面积求出阴影部分面积即可.【解答】(1)证明:连接OD,∵BC是⊙O的切线,∴∠ABC=90°,∵CD=CB,∴∠CBD=∠CDB,∵OB=OD,∴∠OBD=∠ODB,∴∠ODC=∠ABC=90°,即OD⊥CD,∵点D在⊙O上,∴CD为⊙O的切线;(2)证明:如图,∠DOE=∠ODB+∠OBD=2∠DBE,由(1)得:OD ⊥EC 于点D,∴∠E+∠C=∠E+∠DOE=90°,∴∠C=∠DOE=2∠DBE ;(3)解:作OF ⊥DB 于点F,连接AD,由EA=AO 可得:AD 是Rt △ODE 斜边的中线,∴AD=AO=OD,∴∠DOA=60°,∴∠OBD=30°,又∵OB=AO=2,OF ⊥BD,∴OF=1,BF=, ∴BD=2BF=2,∠BOD=180°﹣∠DOA=120°,∴S 阴影=S 扇形OBD ﹣S △BOD =﹣×2×1=﹣.【点评】此题考查了切线的判定与性质,以及扇形面积的计算,熟练掌握切线的判定与性质是解本题的关键.24.如图,抛物线y=﹣x 2+bx+c 与x 轴交于A 、B 两点(A 在B 点左侧),与y 轴交于点C,对称轴为直线x=,OA=2,OD 平分∠BOC 交抛物线于点D (点D 在第一象限);(1)求抛物线的解析式和点D 的坐标;(2)点M 是抛物线上的动点,在x 轴上存在一点N,使得A 、D 、M 、N 四个点为顶点的四边形是平行四边形,求出点M 的坐标;(3)在抛物线的对称轴上,是否存在一点P,使得△BPD 的周长最小?若存在,请求出点P 的坐标;若不存在,请说明理由.。
2023年山东省泰安市中考数学模拟试卷(三)及答案解析

2023年山东省泰安市中考数学模拟试卷(三)一.选择题(每题4分,本大题共12小题,共48分,在每小题给出的四个选项中,只有一个是正确的,请把正确的选项选出来,每小题选对得4分,选错、不选或选出的答案超过一个,均记零分)1.(4分)下列实数中,最大的数是()A.﹣|﹣4|B.0C.1D.﹣(﹣3)2.(4分)2018年国庆小长假,泰安市旅游再次交出漂亮“成绩单”,全市纳入重点监测的21个旅游景区、旅游大项目、乡村旅游点实现旅游收入近132000000元,将132000000用科学记数法表示为()A.1.32×109B.1.32×108C.1.32×107D.1.32×106 3.(4分)下列运算正确的是()A.a3•a4=a12B.a5÷a﹣3=a2C.(3a4)2=6a8D.(﹣a)5•a=﹣a64.(4分)下列四个图形中,既是轴对称图形又是中心对称图形的是()A.B.C.D.5.(4分)如图,直线a∥b,直线c分别交a、b于点A、C,∠BAC的平分线交直线b于点D,若∠2=50°,则∠1的度数是()A.50°B.60°C.80°D.100°6.(4分)某校对部分参加研学旅行社会实践活动的中学生的年龄(单位:岁)进行统计,结果如表:年龄1212141516人数12231则这些学生年龄的众数和中位数分别是()A.15,14B.15,13C.14,14D.13,147.(4分)如图,点B、C、D在⊙O上,若∠BCD=140°,则∠BOD的度数是()A.40°B.50°C.80°D.90°8.(4分)已知关于x的一元二次方程x2﹣2kx+6=0有两个相等的实数根,则k的值为()A.±2B.±C.2或3D.或9.(4分)函数y=和一次函数y=﹣ax+1(a≠0)在同一平面直角坐标系中的图象可能是()A.B.C.D.10.(4分)如图,⊙O中,AB=AC,∠ACB=75°,BC=1,则阴影部分的面积是()A.1+πB.+πC.+πD.1+π11.(4分)如图,在平面直角坐标系中,反比例函数y=(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N两点.△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是()A.6B.10C.2D.212.(4分)如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD 于点E、F,连接BD、DP,BD与CF相交于点H.给出下列结论:①BE=2AE;②△DFP∽△BPH;③;④DP2=PH•PC;其中正确的是()A.①②③④B.①③④C.②③D.①②④二、填空题(每题4分,本大题共6小题,满分24分只要求填写最后结果,每小题填对得4分)13.(4分)不等式组的解集是.14.(4分)关于x的一元二次方程(m﹣1)x2﹣2x﹣1=0有两个实数根,则实数m的取值范围是.15.(4分)如图是某圆锥的主视图和左视图,则该圆锥的表面积是.16.(4分)如图,一艘海轮位于灯塔P的南偏东45°方向,距离灯塔400海里的A处,它沿正北方向航行一段时间后,到达位于灯塔P的北偏东30°方向上的B处,这时B处与灯塔P的距离为海里.17.(4分)如图,在矩形ABCD中,对角线AC,BD交于点O,过点A作EA⊥CA交DB 的延长线于点E,若AB=3,BC=4,则的值为.18.(4分)在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作第1个正方形A1B1C1C;延长C1B1交x轴于点A2,作第2个正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积是.三、解答题(本大题共7小题,满分78分,解答应写出文字说明、证明过程或演算步骤)19.(8分)先化简,再求值:,其中a=2+.20.(10分)民俗村的开发和建设带动了旅游业的发展,某市有A、B、C、D、E五个民俗旅游村及“其它”景点,该市旅游部门绘制了2018年“五•一”长假期间民俗村旅游情况统计图如下:根据以上信息解答:(1)2018年“五•一”期间,该市五个旅游村及“其它”景点共接待游客万人,扇形统计图中D民俗村所对应的圆心角的度数是,并补全条形统计图;(2)根据近几年到该市旅游人数增长趋势,预计2019年“五•一”节将有70万游客选择该市旅游,请估计有多少万人会选择去E民俗村旅游?(3)甲、乙两个旅行团在A、C、D三个民俗村中,同时选择去同一个民俗村的概率是多少?请用画树状图或列表法加以说明.21.(11分)如图,一次函数y=kx+b与反比例函数y=的图象交于A(2,3),B(﹣3,n)两点.(1)求一次函数与反比例函数的解析式;(2)过点B作BC⊥x轴,垂足为C,连接AC,求△ABC的面积.22.(11分)如图,四边形ABCD中,AC⊥BD交BD于点E,点F,M分别是AB,BC的中点,BN平分∠ABE交AM于点N,AB=AC=BD.连接MF,NF.(1)判断△BMN的形状,并证明你的结论;(2)判断△MFN与△BDC之间的关系,并说明理由.23.(12分)红灯笼,象征着阖家团圆,红红火火,挂灯笼成为我国的一种传统文化.小明在春节前购进甲、乙两种红灯笼,用3120元购进甲灯笼与用4200元购进乙灯笼的数量相同,已知乙灯笼每对进价比甲灯笼每对进价多9元.(1)求甲、乙两种灯笼每对的进价;(2)经市场调查发现,乙灯笼每对售价50元时,每天可售出98对,售价每提高1元,则每天少售出2对:物价部门规定其销售单价不高于每对65元,设乙灯笼每对涨价x元,小明一天通过乙灯笼获得利润y元.①求出y与x之间的函数解析式;②乙种灯笼的销售单价为多少元时,一天获得利润最大?最大利润是多少元?24.(12分)如图1,在平面直角坐标系中,已知抛物线y=ax2+bx﹣5与x轴交于A(﹣1,0),B(5,0)两点,与y轴交于点C.(1)求抛物线的函数表达式;(2)如图2,CE∥x轴与抛物线相交于点E,点H是直线CE下方抛物线上的动点,过点H且与y轴平行的直线与BC,CE分别相交于点F,G,试探究当点H运动到何处时,四边形CHEF的面积最大,求点H的坐标;(3)若点K为抛物线的顶点,点M(4,m)是该抛物线上的一点,在x轴,y轴上分别找点P,Q,使四边形PQKM的周长最小,求出点P,Q的坐标.25.(14分)如图①,在△ABC中,∠BAC=90°,AB=AC,点E在AC上(且不与点A,C重合),在△ABC的外部作△CED,使∠CED=90°,DE=CE,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.(1)请直接写出线段AF,AE的数量关系;(2)将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;(3)在图②的基础上,将△CED绕点C继续逆时针旋转,请判断(2)问中的结论是否发生变化?若不变,结合图③写出证明过程;若变化,请说明理由.2023年山东省泰安市中考数学模拟试卷(三)参考答案与试题解析一.选择题(每题4分,本大题共12小题,共48分,在每小题给出的四个选项中,只有一个是正确的,请把正确的选项选出来,每小题选对得4分,选错、不选或选出的答案超过一个,均记零分)1.【分析】根据任意两个实数都可以比较大小.正实数都大于0,负实数都小于0,正实数大于一切负实数,两个负实数绝对值大的反而小可得答案.【解答】解:﹣|﹣4|=﹣4,﹣(﹣3)=3,3>1>0>﹣4,故选:D.【点评】此题主要考查了实数的比较大小,关键是掌握比较大小的法则.2.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正数;当原数的绝对值<1时,n是负数.【解答】解:132000000=1.32×108;故选:B.【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.3.【分析】根据同底数幂的乘法、同底数幂的除法、积的乘方和幂的乘方进行计算即可.【解答】解:A、a3•a4=a7,故A错误;B、a5÷a﹣3=a8,故B错误;C、(3a4)2=9a8,故C错误;D、(﹣a)5•a=﹣a6,故D正确;故选:D.【点评】本题考查了同底数幂的乘法,同底数幂的除法,积的乘方和幂的乘方,掌握运算法则是解题的关键.4.【分析】根据轴对称图形与中心对称图形的概念求解.【解答】解:A、不是轴对称图形,是中心对称图形,故此选项错误;B、是轴对称图形,也是中心对称图形,故此选项正确;C、是轴对称图形,不是中心对称图形,故此选项错误;D、是轴对称图形,不是中心对称图形,故此选项错误.故选:B.【点评】此题主要考查了中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合.5.【分析】利用平行线的性质求出∠BAD,再根据角平分线的定义,求出∠DAC即可解决问题.【解答】解:∵AB∥CD,∴∠BAD=∠2=50°,∵AD平分∠BAC,∴∠DAC=50°,∴∠1=180°﹣∠BDA﹣∠DAC=80°,故选:C.【点评】本题考查平行线的性质,解题的关键是熟练掌握基本知识,属于中考常考题型.6.【分析】出现次数最多的那个数,称为这组数据的众数;中位数一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求,如果是偶数个则找中间两位数的平均数.【解答】解:15出现的次数最多,15是众数.一共9个学生,按照顺序排列第5个学生年龄是14,所以中位数为14.故选:A.【点评】本题考查了众数及中位数的知识,掌握各部分的概念是解题关键.7.【分析】首先圆上取一点A,连接AB,AD,根据圆的内接四边形的性质,即可得∠BAD+∠BCD=180°,即可求得∠BAD的度数,再根据圆周角的性质,即可求得答案.【解答】解:圆上取一点A,连接AB,AD,∵点A、B,C,D在⊙O上,∠BCD=140°,∴∠BAD=40°,∴∠BOD=80°,故选:C.【点评】此题考查了圆周角的性质与圆的内接四边形的性质.此题比较简单,解题的关键是注意数形结合思想的应用,注意辅助线的作法.8.【分析】利用判别式的意义得到Δ=(﹣2k)2﹣4×6=0,然后解关于k的方程即可.【解答】解:根据题意得Δ=(﹣2k)2﹣4×6=0,解得k=±.故选:B.【点评】本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与Δ=b2﹣4ac 有如下关系:当Δ>0时,方程有两个不相等的实数根;当Δ=0时,方程有两个相等的实数根;当Δ<0时,方程无实数根.9.【分析】根据题目中的函数解析式,利用分类讨论的方法可以判断各个选项中的函数图象是否正确,从而可以解答本题.【解答】解:∵函数y=和一次函数y=﹣ax+1(a≠0),∴当a>0时,函数y=在第一、三象限,一次函数y=﹣ax+1经过一、二、四象限,故选项A、B错误,选项C正确;当a<0时,函数y=在第二、四象限,一次函数y=﹣ax+1经过一、二、三象限,故选项D错误;故选:C.【点评】本题考查反比例函数的图象、一次函数的图象,解答本题的关键是明确题意,利用分类讨论的方法解答.10.【分析】连接OB、OC,先利用同弧所对的圆周角等于所对的圆心角的一半,求出扇形的圆心角为60度,即可求出半径的长1,利用三角形和扇形的面积公式即可求解;【解答】解:作OD⊥BC,则BD=CD,连接OA,OB,OC,∴OD是BC的垂直平分线∴,∴AB=AC,∴A在BC的垂直平分线上,∴A、O、D共线,∵∠ACB=75°,AB=AC,∴∠ABC=∠ACB=75°,∴∠BAC =30°,∴∠BOC =60°,∵OB =OC ,∴△BOC 是等边三角形,∴OA =OB =OC =BC =1,∵AD ⊥BC ,AB =AC ,∴BD =CD ,∴OD =OB =,∴AD =1+,∴S △ABC =BC •AD =,S △BOC =BC •OD =,∴S 阴影=S △ABC +S 扇形BOC ﹣S △BOC =+﹣=,故选:B .【点评】本题主要考查了扇形的面积公式,圆周角定理,垂径定理等,明确S 阴影=S △ABC +S 扇形BOC ﹣S △BOC 是解题的关键.11.【分析】由正方形OABC 的边长是6,得到点M 的横坐标和点N 的纵坐标为6,求得M (6,),N (,6),根据三角形的面积列方程得到M (6,4),N (4,6),作M 关于x 轴的对称点M ′,连接NM ′交x 轴于P ,则NM ′的长=PM +PN 的最小值,根据勾股定理即可得到结论.【解答】解:∵正方形OABC 的边长是6,∴点M 的横坐标和点N 的纵坐标为6,∴M (6,),N (,6),∴BN =6﹣,BM =6﹣,∵△OMN 的面积为10,∴6×6﹣×6×﹣6×﹣×(6﹣)2=10,∴k =24或﹣24(舍去),∴M (6,4),N (4,6),作M关于x轴的对称点M′,连接NM′交x轴于P,则NM′的长=PM+PN的最小值,∵AM=AM′=4,∴BM′=10,BN=2,∴NM′===2,故选:C.【点评】本题考查了反比例函数的系数k的几何意义,轴对称﹣最小距离问题,勾股定理,正方形的性质,正确的作出图形是解题的关键.12.【分析】由正方形的性质和相似三角形的判定与性质,即可得出结论.【解答】解:∵△BPC是等边三角形,∴BP=PC=BC,∠PBC=∠PCB=∠BPC=60°,在正方形ABCD中,∵AB=BC=CD,∠A=∠ADC=∠BCD=90°∴∠ABE=∠DCF=30°,∴BE=2AE;故①正确;∵PC=CD,∠PCD=30°,∴∠PDC=75°,∴∠FDP=15°,∵∠DBA=45°,∴∠PBD=15°,∴∠FDP=∠PBD,∵∠DFP=∠BPC=60°,∴△DFP∽△BPH;故②正确;∵∠DCF=90°﹣60°=30°,∴tan∠DCF==,∵△DFP∽△BPH,∴==,∵BP=CP=CD,∴==;故③错误;∵∠PDH=∠PCD=30°,∠DPH=∠DPC,∴△DPH∽△CPD,∴=,∴DP2=PH•PC,故④正确;故选:D.【点评】本题考查的正方形的性质,等边三角形的性质以及相似三角形的判定和性质,解答此题的关键是熟练掌握性质和定理.二、填空题(每题4分,本大题共6小题,满分24分只要求填写最后结果,每小题填对得4分)13.【分析】先求出两个不等式的解集,再求其公共解.【解答】解:,由①得,x<3,由②得,x≥1,所以不等式组的解集为1≤x<3,故答案为:1≤x<3.【点评】本题主要考查了一元一次不等式组解集的求法,其简便求法就是用口诀求解.求不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到(无解).14.【分析】利用一元二次方程的定义和判别式的意义得到m﹣1≠0且Δ=(﹣2)2﹣4(m ﹣1)×(﹣1)≥0,然后解不等式求出它们的公共部分即可.【解答】解:根据题意得m﹣1≠0且Δ=(﹣2)2﹣4(m﹣1)×(﹣1)≥0.解得m≥0且m≠1.故答案为m≥0且m≠1.【点评】本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与Δ=b2﹣4ac 有如下关系:当Δ>0时,方程有两个不相等的实数根;当Δ=0时,方程有两个相等的实数根;当Δ<0时,方程无实数根.15.【分析】求得圆锥的底面周长以及母线长,即可得到圆锥的侧面积和底面积,从而求得表面积.【解答】解:由题可得,圆锥的底面直径为8,高为3,∴圆锥的底面周长为8π,圆锥的母线长为=5,∴圆锥的侧面积=×8π×5=20π,底面积为42π=16π,∴表面积为20π+16π=36π故答案为:36π.【点评】本题主要考查了由三视图判断几何体以及圆锥的计算,圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.16.【分析】如图作PE⊥AB于E.在Rt△PAE中,求出PE,在Rt△PBE中,根据PB=2PE 即可解决问题.【解答】解:如图作PE⊥AB于E.在Rt△PAE中,∵∠PAE=45°,PA=400海里,∴PE=AE=×400=200海里,在Rt△PBE中,∵∠B=30°,∴PB=2PE=400海里,故答案为:400.【点评】本题考查的是解直角三角形﹣方向角问题,掌握锐角三角函数的定义、方向角的概念是解题的关键.17.【分析】分析题目,作BH⊥OA于H,如图,利用矩形的性质得OA=OC=OB,∠ABC =90°,则根据勾股定理可计算出AC=5,AO=OB=;接下来利用三角形的等面积法,可计算出BH的值,进而利用勾股定理可计算出OH的值;接下来根据相似三角形的判定定理可证明△OBH∽△OEA,最后利用相似三角形的性质可求出的值.【解答】解:作BH⊥OA于H,如图,∵四边形ABCD为矩形,∴∠ABC=90°,OA=OC=OB,在Rt△ABC中,AC===5,∴OB=AO=.∵AB•BC=BH•AC,∴BH==,在Rt△OBH中,OH===.∵EA⊥CA,∴BH∥AE,∴△OBH∽△OEA,∴=,∴===.故答案为:.【点评】此题考查的是相似三角形的判定与性质、矩形的性质、线段垂直平分线的性质,正确作出辅助线是解决此题的关键.18.【分析】先利用勾股定理求出AB=BC=AD,再用三角形相似得出A1B=,A2B2=()2,找出规律A2016B2016=()2016,即可.【解答】解:∵点A的坐标为(1,0),点D的坐标为(0,2),∴OA=1,OD=2,BC=AB=AD=∵正方形ABCD,正方形A1B1C1C,∴∠OAD+∠A1AB=90°,∠ADO+∠OAD=90°,∴∠A1AB=∠ADO,∵∠AOD=∠A1BA=90°,∴△AOD∽△A1BA,∴,∴,∴A1B=,∴A1B1=A1C=A1B+BC=,同理可得,A2B2==()2,同理可得,A3B3=()3,同理可得,A2016B2016=()2016,==[()2016]2=5×()4032,∴S第2016个正方形的面积故答案为5×()4032【点评】此题是正方形的性质题,主要考查正方形的性质,勾股定理,相似三角形的性质和判定,解本题的关键是求出几个正方形的边长,找出规律.三、解答题(本大题共7小题,满分78分,解答应写出文字说明、证明过程或演算步骤)19.【分析】先化简分式,然后将a的值代入即可.【解答】解:原式=[]•=•==,当a=2+时,原式===.【点评】本题考查了分式的化简求值,熟练掌握分式混合运算法则是解题的关键.20.【分析】(1)根据A景点的人数以及百分比进行计算即可得到该市景点共接待游客数,用360°乘以D对应的百分比可得其圆心角度数,总人数乘以B对应百分比求得其人数即可补全条形图;(2)根据样本估计总体的思想解决问题即可;(3)根据甲、乙两个旅行团在A、C、D三个景点中各选择一个景点,画出树状图,根据概率公式进行计算,即可得到同时选择去同一景点的概率.【解答】解:(1)该市五个旅游村及“其它”景点共接待游客15÷30%=50(万人),扇形统计图中D民俗村所对应的圆心角的度数是18%×360°=64.8°,B景点接待游客数为:50×24%=12(万人),补全条形统计图如下:故答案为:50,64.8°;(2)估计选择去E民俗村旅游的人数约为70×=8.4(万人);(3)画树状图可得:∵共有9种可能出现的结果,这些结果出现的可能性相等,其中同时选择去同一个景点的结果有3种,∴同时选择去同一个民俗村的概率是.【点评】本题考查的是条形统计图、扇形统计图、用样本估计总体以及概率的计算的综合应用,读懂统计图、从中获取正确的信息是解题的关键.当有两个元素时,可用树形图列举,也可以列表列举.解题时注意:概率=所求情况数与总情况数之比.21.【分析】(1)把A的坐标代入反比例函数的解析式,求出其解析式,把B的坐标代入反比例函数的解析式,求出B的坐标,把A、B的坐标代入一次函数的解析式,得出方程组,求出方程组的解即可;(2)求出BC=|﹣2|=2,BC边上的高是|﹣3|+2,代入三角形的面积公式求出即可.【解答】解:(1)∵点A(2,3)在y=的图象上,∴m=6,∴反比例函数的解析式为y=,∴n==﹣2,∵点A(2,3),B(﹣3,﹣2)在y=kx+b的图象上,∴∴∴一次函数的解析式为y=x+1.(2)以BC为底,则BC边上的高为3+2=5,S△ABC=×2×5=5,答:△ABC的面积是5.【点评】本题考查了一次函数与反比例函数的交点问题,用待定系数法求一次函数、反比例函数的解析式,三角形的面积的应用,主要培养学生分析问题和解决问题的能力,题型较好,难度适中.22.【分析】(1)根据等腰三角形的性质,可得AM是高线、顶角的角平分线,根据直角三角形的性质,可得∠EAB+∠EBA=90°,根据三角形外角的性质,可得答案;(2)根据三角形中位线的性质,可得MF与AC的关系,根据等量代换,可得MF与BD 的关系,根据等腰直角三角形,可得BM与NM的关系,根据等量代换,可得NM与BC 的关系,根据同角的余角相等,可得∠CBD与∠NMF的关系,根据两边对应成比例且夹角相等的两个三角形相似,可得答案.【解答】(1)答:△BMN是等腰直角三角形.证明:∵AB=AC,点M是BC的中点,∴AM⊥BC,AM平分∠BAC.∵BN平分∠ABE,∠EBN=∠ABN.∵AC⊥BD,∴∠AEB=90°,∴∠EAB+∠EBA=90°,∴∠MNB=∠NAB+∠ABN=(∠BAE+∠ABE)=45°.∴△BMN是等腰直角三角形;(2)答:△MFN∽△BDC.证明:∵点F,M分别是AB,BC的中点,∴FM∥AC,FM=AC.∵AC=BD,∴FM=BD,即.∵△BMN是等腰直角三角形,∴NM=BM=BC,即,∴.∵AM⊥BC,∴∠NMF+∠FMB=90°.∵FM∥AC,∴∠ACB=∠FMB.∵∠CEB=90°,∴∠ACB+∠CBD=90°.∴∠CBD+∠FMB=90°,∴∠NMF=∠CBD.∴△MFN∽△BDC.【点评】本题考查了相似三角形的判定与性质,利用了锐角是45°的直角三角形是等腰直角三角形,两边对应成比例且夹角相等的两个三角形相似.23.【分析】(1)设甲种灯笼单价为x元/对,则乙种灯笼的单价为(x+9)元/对,根据用3120元购进甲灯笼与用4200元购进乙灯笼的数量相同,列分式方程可解;(2)①利用总利润等于每对灯笼的利润乘以卖出的灯笼的实际数量,可以列出函数的解析式;②由函数为开口向下的二次函数,可知有最大值,结合问题的实际意义,可得答案.【解答】解:(1)设甲种灯笼单价为x元/对,则乙种灯笼的单价为(x+9)元/对,由题意得:=,解得x=26,经检验,x=26是原方程的解,且符合题意,∴x+9=26+9=35,答:甲种灯笼单价为26元/对,乙种灯笼的单价为35元/对.(2)①y=(50+x﹣35)(98﹣2x)=﹣2x2+68x+1470,答:y与x之间的函数解析式为:y=﹣2x2+68x+1470.②∵a=﹣2<0,∴函数y有最大值,该二次函数的对称轴为:x=﹣=17,物价部门规定其销售单价不高于每对65元,∴x+50≤65,∴x≤15,∵x<17时,y随x的增大而增大,=2040.∴当x=15时,y最大15+50=65.答:乙种灯笼的销售单价为每对65元时,一天获得利润最大,最大利润是2040元.【点评】本题属于分式方程和二次函数的应用题综合.由于前后步骤有联系,第一问解对,后面才能做对.本题还需要根据问题的实际意义来确定销售单价的取值,本题中等难度.24.【分析】(1)根据待定系数法直接确定出抛物线解析式;(2)先求出直线BC的解析式,进而求出四边形CHEF的面积的函数关系式,即可求出;(3)利用对称性找出点P,Q的位置,进而求出P,Q的坐标.【解答】解:(1)∵点A(﹣1,0),B(5,0)在抛物线y=ax2+bx﹣5上,∴,解得,∴抛物线的表达式为y=x2﹣4x﹣5,(2)设H(t,t2﹣4t﹣5),∵CE∥x轴,∴点E的纵坐标为﹣5,∵E在抛物线上,∴x2﹣4x﹣5=﹣5,∴x=0(舍)或x=4,∴E(4,﹣5),∴CE=4,∵B(5,0),C(0,﹣5),∴直线BC的解析式为y=x﹣5,∴F(t,t﹣5),∴HF=t﹣5﹣(t2﹣4t﹣5)=﹣(t﹣)2+,∵CE∥x轴,HF∥y轴,∴CE⊥HF,=CE•HF=﹣2(t﹣)2+,∴S四边形CHEF∴H(,﹣);(3)如图2,∵K为抛物线的顶点,∴K(2,﹣9),∴K关于y轴的对称点K'(﹣2,﹣9),∵M(4,m)在抛物线上,∴M(4,﹣5),∴点M关于x轴的对称点M'(4,5),∴直线K'M'的解析式为y=x﹣,∴P(,0),Q(0,﹣).【点评】此题是二次函数综合题,主要考查了待定系数法,四边形的面积的计算方法,对称性,解的关键是利用对称性找出点P,Q的位置,是一道中等难度的题目.25.【分析】(1)如图①中,结论:AF=AE,只要证明△AEF是等腰直角三角形即可.(2)如图②中,结论:AF=AE,连接EF,DF交BC于K,先证明△EKF≌△EDA 再证明△AEF是等腰直角三角形即可.(3)如图③中,结论不变,AF=AE,连接EF,延长FD交AC于K,先证明△EDF ≌△ECA,再证明△AEF是等腰直角三角形即可.【解答】解:(1)如图①中,结论:AF=AE.理由:∵四边形ABFD是平行四边形,∴AB=DF,∵AB=AC,∴AC=DF,∵DE=EC,∴AE=EF,∵∠DEC=∠AEF=90°,∴△AEF是等腰直角三角形,∴AF=AE.故答案为AF=AE.(2)如图②中,结论:AF=AE.理由:连接EF,DF交BC于K.∵四边形ABFD是平行四边形,∴AB∥DF,∴∠DKE=∠ABC=45°,∴∠EKF=180°﹣∠DKE=135°,EK=ED,∵∠ADE=180°﹣∠EDC=180°﹣45°=135°,∴∠EKF=∠ADE,∵∠DKC=∠C,∴DK=DC,∵DF=AB=AC,∴KF=AD,在△EKF和△EDA中,,∴△EKF≌△EDA,∴EF=EA,∠KEF=∠AED,∴∠FEA=∠BED=90°,∴△AEF是等腰直角三角形,∴AF=AE.(3)如图③中,结论不变,AF=AE.理由:连接EF,延长FD交AC于K.∵∠EDF=180°﹣∠KDC﹣∠EDC=135°﹣∠KDC,∠ACE=(90°﹣∠KDC)+∠DCE=135°﹣∠KDC,∴∠EDF=∠ACE,∵DF=AB,AB=AC,∴DF=AC在△EDF和△ECA中,,∴△EDF≌△ECA,∴EF=EA,∠FED=∠AEC,∴∠FEA=∠DEC=90°,∴△AEF是等腰直角三角形,∴AF=AE.【点评】本题考查四边形综合题、全等三角形的判定和性质、等腰直角三角形的判定和性质、平行四边形的性质等知识,解题的关键是熟练掌握全等三角形的判定和性质,寻找全等的条件是解题的难点,属于中考常考题型。
2023年四川省绵阳市中考物理模拟试卷(三)

2023年四川省中考物理模拟试卷(三)一、选择题(本题共13小题, 每小题3分,共39分,每个小题只有一个选项最符合题目要求)1.关于图中的声现象,下列分析正确的是A.图甲中敲打鼓面,附近的烛焰跳动,说明声音可以传递能量B.图乙中车间工人佩戴耳罩,是在声源处减弱噪声C.图丙中弹吉他时,增大拨动弦的力度可以增大声音的音调D.图丁中抽出罩内空气,听到钟声音变小,说明发声体振动减弱2.下列对自然现象中所涉及的物态变化、吸放热情况的描述,正确的是( )A.冬天铁丝网上出现霜----凝固、吸热B.深秋草叶上出现露珠-----液化、放热C.屋檐上的冰棱正在消融-----熔化、放热D.食品盒中的干冰变小-----汽化、吸热3.如图所示的光现象,下列说法正确的是( )A.图甲中,蜡烛离小孔越远,屏幕上所成的虚像将离小孔越近,像的大小将变小B.图乙中,雨后晴朗的夜晚,人在月光下行走,人迎着月光走时,亮处是地面,暗处是水.C.图丙中,把纸板F沿ON向后折一-定的角度后,反射光线和入射光线法线仍在同一平面上D.图丁是照相机原理图,当蜡烛燃烧变短时,像也会变短,像变短的速度比蜡烛变短的速度快4.如图中,MN为一-平面镜,a、b、c、d表示一个不透明正方体的四个侧面,其中b面与平面镜平行,e是观察者的眼睛所在位置(位于正方体的正下后方),则通过平面镜能( )A.观察到a、b、c、d四个侧面B.看到a面和d面C.看到a面及部分b面D.看到a面,不能看到b面的任何部位5.某小组利用如图所示的装置进行“探究凸透镜成像规律”实验,已知凸透镜的焦距为10cm,在图示状态下,光屏上承接到清晰的实像(像未画出)。
下列说法正确的是( )A.此时蜡烛的成像特点与照相机的成像特点相同B.将蜡烛移至30.0cm刻度线处,移动光屏可得到等大的实像C.保持透镜位置不动,将蜡烛和光屏位置互换,光屏上成的像不清晰D.在透镜和蜡烛之间放一近视眼镜片,将光屏向左移动可再次呈现清晰的像6.如图所示的电路,开关闭合后,额定电压为220 V的电灯LI不亮,用试电笔分别测试a、b、c、d四点,只有测试d点时氖管不发光,在遵循安全用电原则的前提下,若将与灯L1完全相同且完好的灯L2的两端分别接在其中的两点之间,则下列判断正确的是( )A.灯L2接在ab两点间发光偏亮B.灯L2接在bc两点间正常发光C.灯L2接在cd两点间发光偏暗D.灯L2接在任意两点间均不发光7.在1标准大气压下,利用一燃气热水器对10 kg 20 °C的水进行加热时,完全燃烧了0.105 m3的煤气。
中考语文模拟试题 三(含答案)

2021年初中毕业、升学统一模拟测试(三)语文温馨提示:1、本试卷满分150分,考试时间150分钟。
2、答卷前请在答题卡密封线内填写学校、班级、姓名、考号,请勿遗漏。
3、全卷由试题卷和答题卡两部分组成。
答题时请将答案写在答题卡相应位置上,写在试题卷上无效。
4、考生必须保持答题卡的整洁。
5、考试结束后,上交答题卡。
第一部分积累与运用(30分)1、阅读下面文字,完成各题。
(共4分)古人① 情于山水,很大程度上是因为人世间鲜.有何物能匹敌山之高② 伟岸、海之茫无际涯。
登山③ 海,常让人顿悟天地之阔大、人生之渺小,于是心胸为之豁.然,眼界为之高远。
①依次给上面文字中加点的字注音,全都正确的一项是()(2分)A.xiǎn huōB.xiǎn huòC.xiān huòD.xiān huō②在上面文字横线处填入汉字,全都正确的一项是()(2分)A.①钟②竣③邻B.①衷②峻③临C.①衷②竣③邻D.①钟②峻③临2、下列有关文学、文化常识的表述,不正确的一项是()(2分)A.《诗经》多采用重章叠句的手法,即上下句或上下段的字数、结构基本相同,具有回环往复的表达效果。
B.古人称谓有尊称和谦称的区别,如“尊君”“令堂”是对别人父亲的尊称,“家严”“家君”是对自己父亲的谦称。
C.消息的最大特点是真实、客观、时效性强,它的正文结构通常是按照重要性递减的原则安排的,即所谓“倒金字塔结构”。
D.剧本的主体部分一般是台词,也就是戏剧中人物所说的话,它是推进剧情、刻画人物、表现主题的主要手段。
3、下列关于名著的人物的判断有误的一项是()(2分)A.“他是一个传奇式的人物。
他个子清瘦,中等身材,骨骼小而结实,尽管胡子又长又黑,外表上仍不脱孩子气。
又大又深的眼睛富于热情。
”《红星照耀中国》中所描绘的这个人,就是国民党悬赏8万元要通缉的毛泽东。
B.“这是一个高大身材,长头发,眼球白多黑少的人,看人总像在藐视。
”“其时进来的是一个黑瘦的先生,八字须,戴着眼镜,挟着一叠大大小小的书。
《操作系统》模拟试卷3及参考答案

《操作系统》模拟试卷3及参考答案《操作系统》模拟试卷三一、单项选择题(每小题1分,共 15 分)1.操作系统的主要功能是管理计算机系统中的()。
A. 程序B.数据C.文件D.资源2.一种既有利于短小作业又兼顾到长作业的作业调度算法是( )A.先来先服务B.时间片轮转法C.高响应比优先D.均衡调度法3.操作系统中引入进程概念后并不能够()。
A. 允许一个程序被多个用户调用B.正确描述程序的执行情况C.使处理器与外设之间有效地并行工作D. 提高资源利用率4.以下()属于临界资源。
A.磁盘存储介质B.共用队列结构C.私有变量D.可重入的程序代码5.在下列情况下,会发生引起调度事件并立即产生调度的是()。
A.处理中断的过程中B.进程在操作系统内核程序临界区C. 进程在原子过程中D.正在运行实时任务6.采用资源剥夺的方法可以解除死锁,还可以采用( )的方法解除死锁。
A.执行并行操作B.拒绝分配C.撤消进程D.修改信号量7.用户在程序中试图读某文件的第100个逻辑块,使用操作系统提供的()接口。
A.系统调用B.图形用户接口C.键盘命令D.原语8.若一个程序为多个进程所共享,那么该程序的代码在执行的过程中不能被修改,即程序应是()。
A. 可运行的B.可重入的C.可改变的D.可连接的9.虚拟存储器的容量由计算机的地址结构决定,若CPU的地址为32位,则对于一个进程来说,其最大的虚拟存储空间为()。
A. 2GB. 4GC. 1GD. 8G10.仅有基本地址变换机构的分页存储管理方式中,CPU每次存取一个数据时,要( )访问内存。
A. 1次B.2次C. 3次D. 4次11.MS-DOS采用的外存分配方法是()A.单级索引分配B.隐式链接C.显示连接D.两级索引分配12.UNIX系统对空闲磁盘空间的管理,采用的是()。
A 空闲链表法B 位示图法C成组链接法D.线性检索法13.有能避免“磁臂粘着”的磁盘调度算法是()。
新高考语文模拟试卷3(附答案)

新高考语文模拟试卷3(附答案)一、现代文阅读(35 分)(一)现代文阅读Ⅰ(本题共5 小题,19 分)阅读下面的文字,完成1~5 题。
材料一:在当今数字化时代,虚拟现实(VR)技术正逐渐改变着我们的生活方式和体验。
VR 技术通过创建逼真的虚拟环境,让用户沉浸其中,获得身临其境的感受。
从娱乐领域来看,VR 游戏为玩家带来了全新的游戏体验。
玩家可以在虚拟世界中尽情探索、冒险,感受前所未有的刺激和乐趣。
此外,VR 电影也在逐渐兴起,观众可以坐在家中,通过VR 设备欣赏到仿佛置身于电影院的视听效果。
在教育领域,VR 技术也有着广阔的应用前景。
学生可以通过VR 技术参观历史遗迹、探索自然景观,更加直观地学习知识。
同时,VR 技术还可以用于职业培训,让学员在虚拟环境中进行模拟操作,提高技能水平。
然而,VR 技术的发展也面临着一些挑战。
一方面,VR 设备的价格较高,限制了其普及程度。
另一方面,目前的VR 技术在画面质量、交互性等方面还有待提高。
材料二:人工智能(AI)技术在近年来取得了飞速发展,对各个行业产生了深远的影响。
在医疗领域,AI 技术可以辅助医生进行疾病诊断。
通过对大量医疗数据的分析,AI 系统能够快速准确地识别疾病特征,为医生提供诊断建议。
此外,AI 技术还可以用于医疗影像分析、药物研发等方面。
在交通领域,AI 技术可以实现智能交通管理。
通过对交通流量的实时监测和分析,AI 系统可以优化交通信号控制,提高道路通行效率。
同时,AI 技术还可以用于自动驾驶汽车的研发,为人们的出行带来更大的便利和安全。
但是,AI 技术的发展也带来了一些担忧。
例如,AI 技术可能会导致部分工作岗位的消失,引发就业问题。
此外,AI 技术的安全性也备受关注,一旦AI 系统被黑客攻击,可能会带来严重的后果。
1.下列对材料相关内容的理解和分析,正确的一项是(3 分)A.VR 技术和AI 技术都在各自的领域取得了飞速发展,给人们的生活带来了极大的便利。
有机化学模拟试卷3
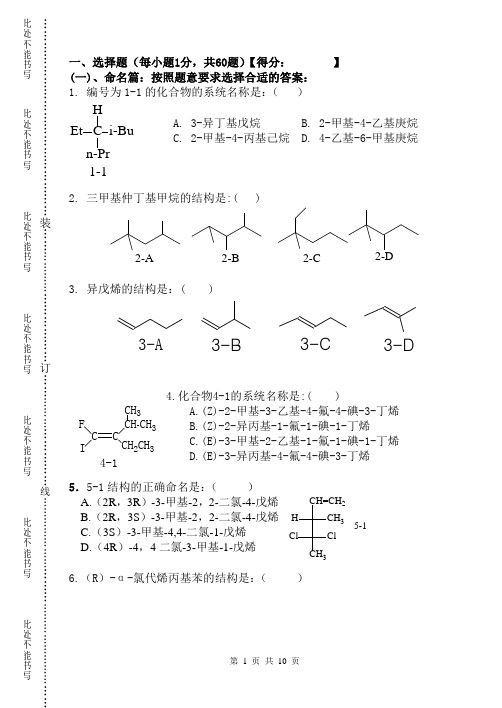
第 1 页 共 10 页……………………………………………装………………………………订…………………………线……………………………………………………此处不能书写此处不能书写此处不能书写 此处不能书写此处不能书写 此处不能书写此处不能书写一、选择题(每小题1分,共60题)【得分: 】 (一)、命名篇:按照题意要求选择合适的答案: 1. 编号为1-1的化合物的系统名称是:( )A. 3-异丁基戊烷B. 2-甲基-4-乙基庚烷C. 2-甲基-4-丙基己烷D. 4-乙基-6-甲基庚烷2. 三甲基仲丁基甲烷的结构是:( )2-A2-B 2-C2-D3. 异戊烯的结构是:( )3-A3-B3-C3-D4.化合物4-1的系统名称是:( )A.(Z)-2-甲基-3-乙基-4-氟-4-碘-3-丁烯B.(Z)-2-异丙基-1-氟-1-碘-1-丁烯C.(E)-3-甲基-2-乙基-1-氟-1-碘-1-丁烯D.(E)-3-异丙基-4-氟-4-碘-3-丁烯5.5-1结构的正确命名是:( )A.(2R ,3R )-3-甲基-2,2-二氯-4-戊烯B.(2R ,3S )-3-甲基-2,2-二氯-4-戊烯C.(3S )-3-甲基-4,4-二氯-1-戊烯D.(4R )-4,4二氯-3-甲基-1-戊烯6.(R )-α-氯代烯丙基苯的结构是:( )C HEt i-Bu n-Pr1-1C CF ICH CH 3CH 32CH 34-1CH 3ClCl CH 3H CH=CH 25-1第2页 共10页ClCH 2CH=CH 2CH 2CH=CHClCH 3CHCH=CH 2ClHPhA B C D7. 5-硝基-2-萘磺酸的结构是:( )NO 2SO 3H SO 3HNO 2NO 2SO 3HNO 2SO 3H7-A7-B7-C7-D8. 8-1结构的命名正确的是:( )A. 2-乙基-4—溴苯胺B. 4-溴-2-乙基苯胺C. 2-氨基-5-溴乙苯D. 3-乙基-4-氨基溴苯 9. 化合物9-1的系统命名为:( )A. 2,2,5-三甲基双环[4.1.0]庚烷B. 2,2,5-三甲基螺[1.4]庚烷C. 3,7,7-三甲基双环[4.1.0]庚烷D. 3,7,7-三甲基螺[1.4]庚烷 10.10-1结构的系统命名是:( )A .反-1-甲基-3-氯环戊烷 B. (E)-1-氯-3-甲基环戊烷 C. 反-1-氯-3-甲基环戊烷 D .(Z )-1-甲基-3-氯环戊烷 11. 甲基苄基乙炔的结构是:( )CH 3CH 3CH 3CH 2CH 2CH 2HCH 3CH 211-A11-B11-C11-D12.化合物12-1的最合适系统命名是:( )A .2-丙炔基-1-己烯 B. 2-丁基-1-戊烯-3-炔 C .4-丁基-4-戊烯-2-炔 D .4-甲叉基-2-辛炔13.1,3-二溴-1,3-环己二烯的结构是:( )NH 2EtBr 8-19-110-112-1第 3 页 共 10 页 ……………………………………………装………………………………订…………………………线……………………………………………………此处不能书写此处不能书写此处不能书写 此处不能书写此处不能书写 此处不能书写此处不能书写BrBrBrBr Br BrBrBr13-A13-C13-D13-B14. 14-1结构的系统命名是:( )A .3-甲基-6-异丁基-3-氯壬烷B .3,8-二甲基 -6-丙基-3-氯壬烷C .2,7-二甲基-4-丙基-7-氯壬烷D .7-甲基-4-异丁基-7-氯壬烷(二)、综合概念篇(根据题意在所给选择项中,选择合适答案): 15.有机化学的定义是:( ) A. 研究化合物的自然科学B. 研究分子和原子结构的自然科学C. 研究含碳化合物的自然科学D. 研究物质变化的自然科学16.多数有机化合物不具备的共性特征的是:( )A .易溶于水 B.容易燃烧 C. 熔沸点较低 D.热稳定差 17. 有机化学发展至今,大约有:( )A. 一千多年B.二百多年C. 一百多年D.超过2千年 18. 开创有机合成历史的第一人是;( )A.拉瓦锡B. 维勒C. 凯库勒D. 贝采里乌斯19.丙二烯的2号碳,也就是中间碳原子的杂化状态是: ( ) A. SP 杂化 B. SP 2杂化 C. SP 3杂化 D.未杂化20.对有机化合物在水中溶解度影响最小的因素是: ( ) A. 范德华引力 B. 氢键 C. 偶极距 D. 分子量 21. 下列化合物的黑H 的酸性顺序自大到小是:( ) a. HC ≡C-H b.H 2C=CH-H c. CH 3CH 2-HA. a >b >cB. c >b >aC. b >a >cD. b >c >a 22.下列物种中,属于Lewis 酸的是:( )A .甲基负离子 B. 甲烷 C. 甲基正离子 D. 碘甲烷 23. 过渡态的概念是指:( )A .中间产物 B. 活性中间体 C. 最稳定的中间状态 D. 反应物转变成产物时的能量最高状态 24. 如下自由基的稳定性顺序是:( ) A. a >c >b B. a >b >ca.CH 2.b. CH 3CH 2.c..Cl14-1C. c>b>aD. b>a>c25.亲电加成机理描述是:( )A. 试剂的正离子部分先反应,而后从底物上再下来一个碎片.B. 试剂的负离子部分先与底物反应,然后正离子部分再加成上去.C. 试剂的正离子部分先与底物反应,然后负离子部分再加成上去.D. 试剂的两个部分同时与底物发生反应.26.烯烃的氢化热可以用来衡量烯烃的稳定性,反过来也可以根据烯烃的稳定性判断氢化热的大小,试判断(E)-2-戊烯(a)、异戊烯(b)和三甲基乙烯(c)的氢化热大小顺序应该是:().A. a>b>cB. c>b>aC. b>c>aD. b>a>c27.与(2R,3S)-2,3-二羟基丁酸是对映体的结构是:()CH3HHO HHOCOOH27-A 27-B 27-C 28.下面有手性的结构是:()COOH COOH ClCl2CClH3CCH3CH328-A 28-B 28-C 28-D 29.如果反应底物是手性结构,下列说法中不正确的是:()A.经由S N1反应得到的产物是外消旋混合物B.经由S N2反应得到的产物通常发生瓦尔登构型反转C.β碳上增加烷基时,有利于S N2发生D.增强试剂的碱性可以提高E2产物的收率30.休克尔规则没有包括如下哪个因素:()A、平面环结构B、单环离域体系C、4n+2个π电子D、单双键相隔31.下列那一项不是E1反应的特征:()A.是正碳离子过程B.是动力学一级反应C.试剂的碱性增大反应速度D.反应过程中有S N1产物生成32.化合物a. CH2=CHCH2Cl b.CH2=CH2Cl c.CH3CH2CH(CH3)Cl发生水解反应,速度排序正确的是:()A、a>b>cB、b>a>cC、c>a>bD、a>c>b第4页共10页第 5 页 共 10 页……………………………………………装………………………………订…………………………线……………………………………………………此处不能书写此处不能书写此处不能书写 此处不能书写此处不能书写 此处不能书写此处不能书写33. 在使用格利雅试剂时,底物和试剂结构中都不能含有一些基团,以免试剂分解,不能按照设计意图反应,但下列基团中,有一种却是可以含有的:(C ) A .-OH B. –COOH C.-OCH 3 D.-NH 2 34. 下列正碳离子的稳定性顺序是:( )CH 3CH 3CH 334-a 34-b 34-cA .a >b >c B. b >a >c C. c >b >a D. a >c >b 35. 下列化合物中没有芳香性的物种是:( )A.+B.- C. D.+36.下列化合物进行硝化反应的速度顺序是:( )CH 3NO 2Cl36-a36-b36-cA .a >b >c B. b >a >c C. c >b >a D. a >c > b 37. 反-1-甲基-3-乙基环己烷最稳定的构象是:( )38. 烯丙基自由基很稳定,它的主要稳定因素是:( ) A .σ-p 超共轭效应 B. π-π共轭效应 C. σ-π超共轭效应 D. p-π共轭效应39.红外谱图中,通常将其分为两大部分,1300CM —1以下称为:( ) A.官能团区 B. 指纹区 C. 氢键区 D. 双键区 40.环烷烃的张力愈大,则:( )A . 能量愈高,分子愈不稳定B . 能量愈高,分子愈稳定C . 能量愈低,分子愈不稳定D . 能量愈低,分子愈稳定 41.下列三个化合物按照E1消去的快慢顺序是:( )CH 3CHCH 3BrNO 2CHCH 3BrCH 3OCHCH 3Br41-a41-b41-cA .a >b >c B. b >a >c C. c >b >a D. c >a > b第6页 共10页Br BrBr Br 46-A 46-B 46-C 46-D 42.下列三个化合物发生S N 2反应的速度顺序是:( )42-b42-cBr Br Br42-aA .a >b >c B. b >a >c C. c >b >a D. c >a >b 43. 一对对映异构体,相互之间物理性质不同的是:( )A .旋光度B .溶解度C .熔点D .沸点 44. 对于H 2O 、NH 3和I -,它们的亲核性顺序是:( )A .H 2O >NH 3>I - B. I ->NH 3>H 2O C. I ->H 2O >NH 3 D. NH 3>I ->H 2O 45. 44题的三个物种,不仅可以做亲核试剂,同时也可以做离去基团,它们做为离去基团的活性顺序是:( )A .H 2O >NH 3>I - B. I ->NH 3>H 2O C. I ->H 2O >NH 3 D. NH 3>I ->H 2O(三)、反应判断选择篇:(根据大题Ⅰ、Ⅱ、Ⅲ、Ⅳ的反应题意,从与括号序号对应的题号中选择合适的答案,完成原题意,每空1分) Ⅰ、46.47.48.49. A. H 2O B.H 2O 2/OH- C.FeCl 3 D. Zn/AcOH4648①②B 2H 649OH 47-A 47-B 47-C 47-DBr BrBrBr48-A 48-B48-C 48-D第7 页共10 页……………………………………………装………………………………订…………………………线……………………………………………………此处不能书写此处不能书写此处不能书写此处不能书写此处不能书写此处不能书写此处不能书写Ⅱ、50.51.52.53.Ⅲ.54.55.CH3CHCH3CH2Br3505152①CO22+5350-A50-B50-C50-DCl Cl51-A51-B51-C51-DClClMgCl MgCl52-A52-B52-C52-DClMgMgClHOOC HOOC53-A53-B53-CCOOHCOOH54CH3HHHBrCH35556CH3HHOHHCH3CH3HHHHOCH3CH3HCH HCH3CH H54-A54-B54-C54-DCH3HHCH2CH3HCH HHCH3CH H55-A55-B55-C55-DCH3HHOSO3HHCH3OOCH3COOH56-A56-B56-C56-D第8页 共10页56. Ⅳ.57.58.59.60.二、反应机理题(5分):【得分: 】试写出甲苯在FeCl 3催化下,发生溴代的反应机理:三、试用简便的化学方法分别鉴别下列两组化合物(10分):【得分: 】⑴ 戊烷 2-戊烯 2,3-二甲基环丙烷 1-丁炔CH 3CH CH 2HC CHCH 3C CH CH 3C C Br 57-A 57-B 57-C 57-D CH 3OH CH 3CH 2Br CH 3I H 2O 58-A 58-B 58-C 58-D CH 3CH 3HH CH 3H 3H CH 3CH 2CH 2CH 3CH 2=CHCH=CH 259-A 59-B59-C 59-D CH 3C NaNH 257CH 3C CCH 3596060-A 60-B 60-C 60-D第 9 页 共 10 页……………………………………………装………………………………订…………………………线……………………………………………………此处不能书写此处不能书写此处不能书写 此处不能书写此处不能书写 此处不能书写此处不能书写⑵ 正溴丁烷 苯 苄基溴 环己烯四、推测结构题:(10分)【 得分: 】A 、B 、C 是三个化学式均为C 4H 6的同分异构体。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
模拟试卷三一、单选题(60题×1分)(1~15题为A1、A2型题,每题只有一个最佳答案)1、下列哪项不属于《医宗金鉴. 正骨心法要旨》对颈骨受伤的分类?()A 打伤B 扭伤C 扑伤D 从高坠下E 坠伤2、失枕的发病与下列哪一项不符?()A 20岁以后的成人发病较多。
B 有季节性,夏秋二季多发。
C 睡眠时枕头过高、过低或过硬。
D 睡眠姿势不当。
E 颈背部遭受风寒侵袭。
3、颈椎病的好发部位是()A 第1~2颈椎关节B 第2~3颈椎关节C 第3~4颈椎关节D 第4~5颈椎关节E 第5~6颈椎关节4、下列哪一项内容与桡侧伸腕肌腱周围炎无关?()A 多见于木工、砖瓦工等工种。
B 起病较快,易反复发作。
C 前臂中下段背桡侧肿胀、疼痛、灼热、压痛,腕部活动受限。
D 作较快的腕关节伸屈旋转动作时,可发出弹响声。
E握拳并作腕关节伸屈时,可感觉到捻发感5、腕管内有哪些肌腱通过?()A 屈指深、浅肌腱B 拇长屈肌腱C 屈指浅肌腱D 屈指深肌腱E 拇长屈肌腱及屈指浅、深肌腱6、肩关节脱位多见于()A 外脱位B 后脱位C 上脱位D 前脱位E 以上都不是7、桡骨下端伸直型骨折复位后,早期应使腕关节固定在()A 背伸桡偏位B 背伸尺偏位C 掌屈桡偏位D 掌屈尺偏位E 以上都不是8、肱骨髁上骨折以何种类型多见?()A 外展型B 内收型C 伸直型D 屈曲型E 以上都不是9、锁骨骨折的好发部位是()A 远端B 近端C 中段D 中内1/3交界处E 中外1/3交界处10、拱桥式、飞燕式功能锻炼常用于()A 颈椎骨折早期B 骶椎骨折早期C 骨盆骨折D 单纯性胸腰椎骨折E 脊椎后关节紊乱11、在进行骨折复位时,下列哪项是正确的()A 原则上将近侧骨折端对准远侧骨折段所指的方向B 原则上将远侧骨折端对准近侧骨折段所指的方向C 应在肢体的中立位进行复位D 应在肢体的功能位进行复位E 原则上应以折顶回旋的手法进行复位12、下列哪项不是骨折的早期并发症()A 感染B 休克C 损伤性骨化D 内脏损伤E 脂肪栓塞13、下列哪种不是导致骨折段移位的因素之一?()A 暴力的大小、作用方向及性质B 伤者的年龄C 搬运和治疗不当D 肌肉的牵拉力E 肢体远侧段的重量14、桡神经损伤后可出现的症状是()A 爪形手 B小指感觉障碍C 腕下垂D 第4、5指屈曲不全E 拇指不能对掌15、夹板固定后肢体指、趾端出现紫绀、麻木剧痛,其原因是()A 神经受压迫B 肌腱受挤压C 骨折移位D 血循环障碍E 筋膜撕裂(16~30题为A3、A4型题,每题有且只有一个正确答案)女,25岁。
自述无明显原因出现右腕部疼痛,握力减弱,右腕部活动时疼痛加重。
按压右侧桡骨茎突时有明显压痛。
16、可能的诊断为()A 右桡骨茎突狭窄性腱鞘炎B 腕部扭挫伤C 腱鞘囊肿D 腕管综合征E 舟状骨骨折17、受累的肌腱()A 拇长展肌和拇长伸肌腱B 桡侧腕长伸肌和桡侧腕短伸肌C拇长展肌和拇短伸肌腱D 拇长伸肌和拇短伸肌E 指伸肌18、首选的治疗方法()A 封闭B 口服非甾体类药物C 针灸或推拿治疗D 小针刀E 手术男,27岁,运动员。
左膝部隐痛、乏力1年,锻炼后加重,休息后减轻,上下楼时疼痛明显。
检查:髌骨两侧偏后部压痛。
19、最可能的诊断()A 右膝半月板损伤B 右髌下脂肪垫损伤C 右膝关节创伤性骨关节炎D 右髌骨软骨软化症E 右膝关节滑膜炎20、本病最常见的阳性体征为()A 浮髌试验B 挺髌试验C 抽屉试验D 侧向试验E 回旋挤压试验21、首选的治疗方法()A 对症处理和加强股四头肌的抗阻力锻炼B 关节内注射醋酸强地松龙C 小针刀治疗D 外侧膝关节囊松解术E 髌骨软骨面钻孔术男性,6岁,胸椎后凸畸形,呼吸、心跳正常,活动不受影响。
22、最适合的辅助检查是()A 胸透B 肺活量测定C 胸椎正侧位片D 心电图E 胸椎CT扫描23、X线片见第T9椎体破坏,椎体压缩成楔形,椎弓根阴影仍清晰可见,最可能的诊断是()A 单纯压缩性骨折B 脊柱肿瘤C 脊柱结核D 化脓性脊柱炎E 先天性脊柱畸形女性,12岁,咳嗽3个月,伴低热,1个月前感觉左髋关节酸痛不适并偶有左膝关节疼痛,查体:跛行,左髋关节活动受限,托马氏征阳性,左膝无肿胀,浮髌试验阴性。
24、该患者应首先进行哪项检查?()A 左髋关节CTB 左髋关节MRIC 血沉D 左髋关节穿刺,生化检查及细菌培养E 胸部平片及左髋关节正侧位片25、胸部平片示左上肺有散在的钙化灶,血沉80mm/1h,这时初步诊断是()A 化脓性髋关节炎B 类风湿性关节炎C 结核性髋关节炎D 创伤性滑膜炎E 退行性关节炎男性,10岁,跌伤致左上臂近端酸痛1个月,无发热,X线示左肱骨近端有一椭圆形透亮区,中心位,骨皮质膨胀变薄,溶骨区呈单房状阴影,无骨膜反应。
26、该患者最可能的诊断是()A 化脓性关节炎B 类风湿性关节炎C 骨囊肿D 骨纤维异常增殖症E 骨软骨瘤27、为进一步明确诊断,下列检查哪项最有价值?()A 血生化B CTC MRID ECTE 穿刺活检28、如已确诊为骨囊肿,下一步最宜采用的治疗是()A 刮除植骨术B 截肢术C 中药治疗D 石膏固定E 放疗男性,65岁,因左髋关节疼痛活动受限1年半。
患者曾于三年前跌伤致左股骨颈骨折,行切开复位内固定术后1年半痊愈并取出内固定。
查体:左髋关节活动明显受限,托马氏征阳性。
X线片示:左股骨头塌陷,头变扁,边缘增生,关节间隙变窄。
29、该患者最可能的诊断是()A 左髋关节结核B 左股骨头骨肿瘤C 左髋关节慢性骨髓炎D 左股骨头缺血性坏死E 左髋关节创伤性关节炎。
30、应采用的最为合适的治疗方法是()A 扶拐行走减轻左髋关节负重B 内服中药辨证治疗C 带血管蒂的骨瓣移植术D 卧床休息,内服补益肝肾的中药治疗E 行左全髋人工关节置换术(31~50题为B1、B2型题,每题有且只有一个正确答案)A 气滞B 气脱C 血瘀D 血虚E 气闭31、痛点固定不移是何证的特点?()32、痛无定处是何证的特点?()33、肿胀疼痛是何证的特点?()34、痛无肿形是何证的特点?()A 肌腱弹跳声B 关节弹响声C 入臼声D 骨擦音E 磨擦音35、关节脱位在整复成功时发出的响声是()36、骨折两断端相互磨擦时发出的响声是()37、屈指肌腱狭窄性腱鞘炎患者,在作伸屈手指检查时听到的弹响声是()38、膝关节半月板损伤时,作膝关节屈伸旋转时听到的弹响声是()A 肘内翻畸形B 肘外翻畸形C 迟发尺神经损伤D 骨折迟缓愈合E 骨化性肌炎39、股骨颈骨折易发生()40、腕舟骨骨折易发生()41、肱骨髁上骨折易发生()A 肌腱损伤B 骨折不愈合C 血管损伤D 骨筋室综合征E 神经损伤42、腕舟骨骨折易造成()43、Colles骨折易造成()A 头下型B 头颈型C 外展型D 内收型44、股骨颈骨折移位过程中在不同阶段有不同的表现,在刚受暴力时,断端表现为()45、股骨颈骨折移位过程中在不同阶段有不同的表现,在暴力持续时,断端表现为()A 横断B 斜型C 蝶型D “Y”型E 不完全性46、直接暴力引起的股骨干骨折多为()47、间接暴力引起的股骨干骨折多为()A 轻度外展旋中位B 内收内旋伸直位C 外展外旋位D 外展旋中位E 伸直中立位48、髋关节后脱位整复后固定位置是()49、髋关节中心性脱位整复后固定位置是()50、髋关节前脱位整复后固定位置是()(51~60题为X型题,每题有2~5个正确答案)51、危亦林在《世医得效方》中记载和叙述的是()A 悬吊复位法治疗脊柱骨折B 过伸复位法治疗屈曲型脊柱骨折C 将踝关节骨折脱位分内翻、外翻两型D 指出麻醉用药用量的依据E 首先记载切开复位治疗胫骨多段骨折52、损伤病机的核心内容是()A 气血与损伤的关系B 肝肾与损伤的关系C 脾胃与损伤的关系D 筋骨与损伤的关系E 津液与损伤的关系53、下列组织哪些属于中医伤科学的范畴?()A 关节囊B 关节软骨C 肌肉D 筋膜E 筋络54、椎间盘由以下几部分组成()A 前纵韧带B 后纵韧带C 纤维环E 软骨板55、建筑工人由高空跌落,容易发生()A 脊柱骨折B 前臂骨折C 下肢骨折D 骨盆骨折E 肱骨外科颈骨折56、肱骨中1/3骨折,近端向外、向前,远端向上移位,他们是由于受何牵拉所致?()A 胸大肌B 三角肌和喙肱肌C 肱三头肌和肱二头肌D 肱肌E 背阔肌57、为了明确肱骨外髁骨折类型和方向,需拍摄()A 正位X线片B 侧位X线片C 轴位X线片D 局部切线位X线片E 斜位X线片58、易发生骨折延迟愈合的骨折是()A 股骨颈头下型骨折B 股骨转子间骨折C 胫骨下1/3骨折D 腕骨腰部骨折E 距骨骨折59、防止骨折畸形愈合的措施是()A 有效的固定B 密切观察C 再移位后及时纠正D 定期摄X线片复查E 绝对卧床60、缺血性肌挛缩早期可出现()A 肢体肿胀B 持续性疼痛麻木C 皮色紫绀,皮温下降D 伤肢远端动脉搏动消失E 肌肉萎缩二、名词解释(5题×2分)1、损伤2、平卧式搬运法3、颈干角4、弹性固定5、内伤三、简答题(5题×4分)1、简答损伤的主要五个分类方法及分类。
2、硬瘫与软瘫的临床表现有何区别?3、简述桡骨远端骨折的固定方法。
4、何谓脱位的早期并发症和晚期并发症,脱位的早期并发症和晚期并发症有哪些?5、良性骨肿瘤的特点是什么?四、病例分析(2题×5分)1、患者男,37岁,驾驶员。
自述3月前长途驾驶后出现腰部疼痛以来,症状持续存在,时轻时重,半月前腰部症状加重,并出现右下肢放射性疼痛和麻木,可放射至右侧大腿后侧、小腿外侧及足背部。
咳嗽、喷嚏及大便时右下肢放射痛及麻木症状加重。
检查:腰部肌肉紧张、僵硬、活动受限,脊柱明显侧弯,L4~5椎间隙棘突右侧有压痛,叩击腰部时,右下肢疼痛症状明显加重,右胫骨前侧皮肤感觉迟钝。
右足第一趾背伸肌力减弱。
试问:诊断、鉴别诊断(列出10种病名即可)及治疗方案(简述)2、患者张某,男性,25岁,农民。
1小时前弯腰立位工作时,边墙倒塌,砸伤右侧腰臀部致右膝跑地,当即觉右臀部疼痛,右下肢不能站立、活动。
查体:右侧臀部皮肤擦伤,轻度肿胀,右臀部膨隆,患肢呈屈曲、内收、内旋畸形,右大转子上移,患肢较健侧短缩,伤侧膝部靠在对侧大腿上。
患肢末端血运、感觉及足趾活动良好。
X线片示右髋关节脱位,股骨头向后上方移位。
请你根据病情,作出相应处理意见,并说明理由。
答案:一、多选题1(B)2(B)3(E)4(D)5(E)6(D)7(D)8(C)9(E)10(D)11(B)12(C)13(B)14(C)15(D)16(A)17(C)18(A)19(D)20(B)21(A)22(C)23(C)24(E)25(C)26(C)27(E)28(A)29(D)30(E)31(C)32(A)33(C)34(A)35(C)36(D)37(A)38(B)39(D)40(D)41(A)42(B)43(A)44(C)45(D)46(A)47(B)48(A)49(D)50(B)51(ACD) 52(A) 53(ABCDE) 54(CDE) 55(ABCDE)56(BC) 57(AB) 58(ACDE) 59(ABCD) 60(ABCD)二、名词解释1、损伤:是指人体受到外界不同因素作用所引起的皮肉、筋骨、脏腑等组织的破坏,及其带来局部和全身不同程度后果者。
