《理论力学》第四章作业答案
理论力学课后答案4

魏 魏 魏
后
泳 泳 泳
ww
涛 涛 涛
m
课
答
四川大学 建筑与环境学院 力学科学与工程系 魏泳涛
案
网
w.
kh
da
xi (2i 1)a cos , yi a sin 轨迹: xi2 yi2 a 2 2 (2i 1)
w.
co
解:以 A1 为对象研究 x a cos , y a sin 同理, Ai (i 2,3,4) 的运动方程为
kh
da
w.
co
我在沙滩上写上你的名字,却被浪花带走了;我在云上写上你的名字,却被风儿带走了;于是我在理论力 学的习题答案上写上我的名字.
4.8 飞轮边缘上一点 M ,随飞轮以匀速 v 10 m s 运动。后因刹车,该点以 at 0.1t m s 2 作减速运动。设轮半径 R 0.4m ,求 M 点在减速运动过程中的运 动方程及 t 2s 时的速度、切向和法向加速度。 解:
魏
at
2 2 v vx vy 2500 4t 2
泳 泳 泳
ww
涛 涛 涛
m
加速度的直角分量 ax 0 , a y 2 切向加速度为
dv 4t dt 2500 4t 2 当 t 0s 时, at 0 ,所以
2 2 an a 2 at2 ax ay at2 2 m s 2
我在沙滩上写上你的名字,却被浪花带走了;我在云上写上你的名字,却被风儿带走了;于是我在理论力 学的习题答案上写上我的名字.
4.1 一动点按 s t 2 6t 1的规律沿直线运动,式中,时间 t 以秒( s )计,坐标 s 以 米( m )计。试求: (1)最初 5s 内的位移; (2)动点改变运动方向的时刻和所在位置; (3)最初 5s 内动点经过的路程; (4) t 5s 时动点的速度和加速度; (5)动点在哪段时间内作加速运动,哪段时间内作减速运动。
理论力学(胡运康)第四章作业答案
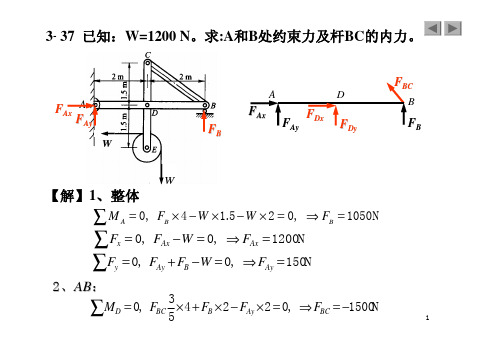
2、AB:
3 M = 0 , F N ∑ D BC × 4 + FB × 2 − FAy × 2 = 0, ⇒ F BC = −1500 5
1
3-39 已知q,M=qa2 。求铰链D受的力;铰链B受的力。
D FDx FDy
qa
C FCy FCx
FDx FDy
FB3
a 3 解: 1、整体 : ∑ M A = 0, FB 3 ⋅ a − qa ⋅ − M = 0, ⇒ FB 3 = qa 2 2 1 M = 0 , F ⋅ a + qa ⋅ a = 0 , ⇒ F = qa 2、DC: ∑ C Dy Dy 2 1 ⇒ FCy = qa ∑ Fy = 0, FDy + FCy − qa = 0, 2
∑ Fy = 0, FAy − 30 + FBC ⋅
3-73 已知M2 、M3 ,AB=d1 、BC=d2 、CD=d3 ,求M1及 A、D处约束力。
FAz FAy
【解】整体:
M3 ⇒ FAy = ∑ M z = 0, M 3 − FAy ⋅ d1 = 0, d1 M2 ⇒ FAz = ∑ M y = 0, M 2 − FAz ⋅ d1 = 0, d1
6
3-53 求桁架中杆BH、CD和GD的内力。
1
FIH 0 FBH
FE
FB 1
FBC
FE
解: FGD = 0 1、整体:
2、1-1面左边:∑ Fy = 0, FE − 60 − FBH
∑M
B
= 0, FE ×15+ 60×10 = 0, ⇒ FE = 26.67kN
1 = 0, ⇒ FBH = −47.1kN 2
∑M
G
理论力学习题答案

理论力学习题答案(总26页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--2第一章 静力学公理和物体的受力分析一、是非判断题在任何情况下,体内任意两点距离保持不变的物体称为刚体。
( ∨ ) 物体在两个力作用下平衡的必要与充分条件是这两个力大小相等、方向相反,沿同一直线。
( × ) 加减平衡力系公理不但适用于刚体,而且也适用于变形体。
( × ) 力的可传性只适用于刚体,不适用于变形体。
( ∨ ) 两点受力的构件都是二力杆。
( × ) 只要作用于刚体上的三个力汇交于一点,该刚体一定平衡。
( × ) 力的平行四边形法则只适用于刚体。
( × ) 凡矢量都可以应用平行四边形法则合成。
( ∨ ) 只要物体平衡,都能应用加减平衡力系公理。
( × ) 凡是平衡力系,它的作用效果都等于零。
( × ) 合力总是比分力大。
( × ) 只要两个力大小相等,方向相同,则它们对物体的作用效果相同。
( × )若物体相对于地面保持静止或匀速直线运动状态,则物体处于平衡。
( ∨ )当软绳受两个等值反向的压力时,可以平衡。
( × )静力学公理中,二力平衡公理和加减平衡力系公理适用于刚体。
( ∨ )静力学公理中,作用力与反作用力公理和力的平行四边形公理适用于任何物体。
( ∨ )凡是两端用铰链连接的直杆都是二力杆。
( × )如图所示三铰拱,受力F ,F 1作用,其中F 作用于铰C 的销子上,则AC 、BC 构件都不是二力构件。
( × )图3二、填空题力对物体的作用效应一般分为 外 效应和 内 效应。
对非自由体的运动所预加的限制条件称为 约束 ;约束力的方向总是与约束所能阻止的物体的运动趋势的方向 相反 ;约束力由 主动 力引起,且随 主动 力的改变而改变。
理论力学习题及答案(全)

第一章静力学基础一、是非题1.力有两种作用效果,即力可以使物体的运动状态发生变化,也可以使物体发生变形。
()2.在理论力学中只研究力的外效应。
()3.两端用光滑铰链连接的构件是二力构件。
()4.作用在一个刚体上的任意两个力成平衡的必要与充分条件是:两个力的作用线相同,大小相等,方向相反。
()5.作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。
()6.三力平衡定理指出:三力汇交于一点,则这三个力必然互相平衡。
()7.平面汇交力系平衡时,力多边形各力应首尾相接,但在作图时力的顺序可以不同。
()8.约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。
()二、选择题1.若作用在A点的两个大小不等的力F1和F2,沿同一直线但方向相反。
则其合力可以表示为。
①F1-F2;②F2-F1;③F1+F2;2.作用在一个刚体上的两个力F A、F B,满足F A=-F B的条件,则该二力可能是。
①作用力和反作用力或一对平衡的力;②一对平衡的力或一个力偶。
③一对平衡的力或一个力和一个力偶;④作用力和反作用力或一个力偶。
3.三力平衡定理是。
①共面不平行的三个力互相平衡必汇交于一点;②共面三力若平衡,必汇交于一点;③三力汇交于一点,则这三个力必互相平衡。
4.已知F1、F2、F3、F4为作用于刚体上的平面共点力系,其力矢关系如图所示为平行四边形,由此。
①力系可合成为一个力偶;②力系可合成为一个力;③力系简化为一个力和一个力偶;④力系的合力为零,力系平衡。
5.在下述原理、法则、定理中,只适用于刚体的有。
①二力平衡原理;②力的平行四边形法则;③加减平衡力系原理;④力的可传性原理;⑤作用与反作用定理。
三、填空题1.二力平衡和作用反作用定律中的两个力,都是等值、反向、共线的,所不同的是。
2.已知力F沿直线AB作用,其中一个分力的作用与AB成30°角,若欲使另一个分力的大小在所有分力中为最小,则此二分力间的夹角为度。
哈尔滨工业大学 第7版 理论力学 第4章 课后习题答案

解 (1)方法 1,如图 4-6b 所示,由已知得
Fxy = F cos 60° , Fz = F cos 30°
F = F cos 60°cos 30°i − F cos 60°sin 30° j − F sin 60°k = 3 i − 1 Fj − 3 Fk 44 2
41
理论力学(第七版)课后题答案 哈工大.高等教育出版社
A
F
β
MA
C
MB
F
10 N
β M θ − 90° C
MB
(a)
(b)
(c)
图 4-11
解 画出 3 个力偶的力偶矩矢如图 4-11b 所示,由力偶矩矢三角形图 4-11c 可见
MC =
M
2 A
+
M
2 B
=
3 0002 + 4 0002 = 5 000 N ⋅ mm
由图 4-11a、图 4-11b 可得
3 = 250 N 13
FRz = 100 − 200 ×
1 = 10.6 N 5
M x = −300 ×
3 × 0.1 − 200 × 1 × 0.3 = −51.8 N ⋅ m
13
5
M y = −100 × 0.20 + 200 ×
2 × 0.1 = −36.6 N ⋅ m 13
M z = 300 ×
z
F45° F3 F3′ B
F2A
E
F1
C
F5
F6
F F4 45°
D
y
K x
M
(a)
(b)
图 4-9
解 (1) 节点 A 为研究对象,受力及坐标如图 4-9b 所示
《理论力学》第四章-力系平衡试题及答案
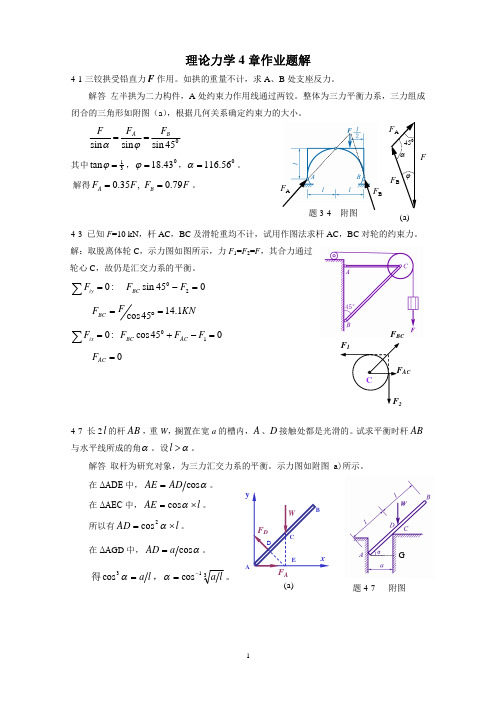
理论力学4章作业题解4-1三铰拱受铅直力F 作用。
如拱的重量不计,求A 、B 处支座反力。
解答 左半拱为二力构件,A 处约束力作用线通过两铰。
整体为三力平衡力系,三力组成闭合的三角形如附图(a ),根据几何关系确定约束力的大小。
45sin sin sin B A F F F ==j a其中31tan =j ,043.18=j ,056.116=a 。
解得F F F F B A 79.0 ,35.0==。
4-3 已知F =10 kN ,杆AC ,BC 及滑轮重均不计,试用作图法求杆AC ,BC 对轮的约束力。
解:取脱离体轮C ,示力图如图所示,力F 1=F 2=F ,其合力通过轮心C ,故仍是汇交力系的平衡。
:0=åiyF 045sin 20=-F F BCKN FF BC 1.1445cos =°=045cos :010=-+=åF F F FAC BC ix0=AC F4-7 长2l 的杆AB ,重W ,搁置在宽a 的槽内,A 、D 接触处都是光滑的。
试求平衡时杆AB 与水平线所成的角a 。
设a >l 。
解答 取杆为研究对象,为三力汇交力系的平衡。
示力图如附图(a)所示。
在ΔADE 中,a cos AD AE =。
在ΔAEC 中,l AE ´=a cos 。
所以有l AD ´=a 2cos 。
在ΔA GD 中,a cos a AD =。
得a =a 3cos ,31cosl a -=a 。
F BCAC题3-4 附图F BF AF BF AFa45j(a)A (a)题4-7 附图G4-9 AB ,AC ,AD 三连杆支撑一重物,如图所示。
已知W=10kN ,AB =4m ,AC =3 m ,且ABEC 在同一水平面内,试求三连杆所受的力。
解:取铰A 研究,示力图如图示,为汇交力系的平衡。
0=åix F : 05430sin =´°+AD AB F F 0=åiy F : 05330sin =´°+AD AC F F 0=åiZF: 030cos =-°W F AD联立求解KNF KNF KN F AD AC AB 5.115.36.4=-=-=4-8 图示结构上作用一水平力F 。
周衍柏《理论力学教程(第三版)》电子教案 3-4章作业解答

2l
mg
B
F
n
y
0 R cos mg
A
1/ 3
Rd MA 0 lmg cos cos i 1 cos 3 d d cos 1 l l
N d
第3.2题图
3.3)两根均质棒AB、BC在B处刚性联结在一起, 且角ABC形成 一直角. 如将此棒的A点用绳系于固定点上, 棒AB和BC的长度分 别为a,b. 则当平衡时, AB和竖直直线所成的角满足下列关系
b2 tan (a 2b)a
3.5)一均质的梯子, 一端置于摩擦系数为1/2的地板上, 另一端 则斜靠在摩擦系数为1/3的高墙上,一人的体重为梯子的三倍, 爬到 梯的顶端时, 梯尚未开始滑动, 则梯与地面的倾角,最小当为若干? 解: 研究对象为梯子, 人在顶端时,梯子与地面的夹角为, 梯子 y 重量p, 人重3p. 平衡时:
x 0 1 y gt 3 cos v0t 2 cos 3 1 2 z v0t gt 2
再积分,并代入初始条件得: 质点再回到地面
3
t 2v0 / g
3 4 8 h 4 v0 y cos and v 2 gh y cos 0 3 g 3 g2
4.10) 质量为m的小环M, 套在半径为a的光滑圆圈上, 并可沿着圆 圈滑动. 如圆圈在水平面内以匀角速绕圈上某点O转动, 试求小 y 环沿圆圈切线方向的运动微分方程. 解: 设坐标系如图, oxy为水平面,它绕z轴转 动,即圆圈为转动参照系 受力分析,重力和约束反力都在z轴方向, 没 有画出. 惯性离心力m2r , 科里奥利力为 FC= -2m×v
3.9)证明对角线长度为d的立方体绕其对角线转动的回转半径为
理论力学(刘又文 彭献)答案第4章
§4.2 思考解析
思考 4-1 已知平面图形 S 的运动方程,试写出 S 上给定点 M 的运动方程, 以及该点的速度和加速度解析表达式。 答:设已知 x A = f1 (t ),
y A = f 2 (t ), ϕ = f3 (t ) 。则 M 点运动方程为
xM = x A + AM cos ϕ = f1 (t ) + AM cos f3 (t ) yM = y A + AM sin ϕ = f 2 (t ) + AM sin f3 (t ) M 点速度和加速度分量分别为
n τ aCv = aO + aC + aC vO vO n τ 其中, aC = Rω 2 , aC = Rα = a0 ,方向与 a0 相反。 vO vO
110
故
n aCv = aC , aCv = Rω 2 = vO
2 v0 R
以 Cv 为基点,M 点的加速度如图 b 所示。 故
n 2 2 aM = (aMC − aCv ) + (aτ ( Rω 2 ) 2 + (2 Rα ) 2 = 2 a0 + MCv ) = v 4 v0 4R2
所以
xM = r cos ω t + AM cos ϕ , yM = r sin ω t − AM sin ϕ
对时间 t 求一阶和二阶导数便得 M 点的速度和加速度坐标分量。
思考 4-4
试求图 a、b、c 中各平面运动刚体的速度瞬心 Cv 。
ω
B
A B
C v
A
ω
(b) (c)
(a)
ω
C
A B
B
A
ω
Cv
vC vB
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
[习题4-4] 一力系由四个力组成,如图4-17所示。
已知F 1=60N,F 2=400N,F 3=500N,F 4=200N,试将该力系向A点简化(图中长度单位为mm)。
解:
方向余弦:
4696.0877
.638300
cos ==
=
∑R
x
F F
α
8553.0877
.63841
.546cos ==
=
∑R
y
F F β
2191.0877
.638140
cos -=-=
=∑R
z
F F
γ
主矢量计算表
主矩计算表
方向余弦:
6790.0831.162564
.110cos 0
-=-=
=
∑M M x
α
7370.0831.162120
cos 0
==
=
∑M M
y
β
0831
.1620
cos 0
==
=
∑M M z
γ
[习题4-6] 起重机如图4-19所示。
已知AD =DB =1m,CD =1.5m,CM =1m;机身与平衡锤E 共重kN W 1001=,重力作用线在平面LMN ,到机身轴线的距离为0.5m;起重量kN W 302=。
求当平面LMN 平行于AB 时,车轮对轨道的压力。
B
N C
N A N
By
R Bz
R Bx
R Ay
R A
T W
D
解:因为起重机平衡,所以:
0)(=∑i AB
F M
05.05.05.121=⨯+⨯+⨯-W W N C
kN kN N C 3.43)(333.435.1/)5.0305.0100(≈=⨯+⨯=
0)(=∑i CD
F M
045.01121=⨯-⨯+⨯-⨯W W N N A B 70=-A B N N (1)
0=∑iz
F
021=--++W W N N N C B A 030100333.43=--++B A N N 667.86=+B A N N ………………(2) (1)+(2)得:
667.1562=A N
kN kN N A 3.78)(334.78≈=
kN kN N N A B 3.8)(333.8334.78667.86667.86≈=-=-=
[习题4-11] 均质杆AB ,重W ,长l ,A 端靠在光滑墙面上并用一绳AC 系住,AC 平行于x轴, B 端用球铰连于水平面上。
求杆A 、B 两端所受的力。
图中长度单位为m 。
解:
0=∑iz
F
0=-W R Bz W R Bz =
0)(=∑i x
F M
060sin 60sin 60cos 2
60sin 60cos 00000=--⋅l R l
W
l R Ay Bz W W W W R R Bz Ay 25.025.05.025.05.0=-=-=
0=∑iy
F
0=+Ay By R R W R R Ay By 25.0-=-=
0)(=∑i AD
F M
060sin 60cos 60cos 60cos 0000=-l R l R Bx By
02321=-Bx By R R W W R R By Bx 144.0)25.0(3
3
33-=-⋅==
0=∑ix
F
0=+Bx A R T W R T Bx A 144.0=-= [习题4-16(a)]
解: ∑∑===
3
1
3
1
i i
i ci
i C A
x
A x ,∑∑===
3
1
3
1
i i
i ci
i C A
y
A y 。
习题2-19(a)
y
x
[习题4-16(e)]
解:建立如图所示的坐标系。
把图形划分为五个规则图形。
)(23312121m A =⨯⨯=
, 3
3,32(1C )(42222m A =⨯= )2
3
,
2(2C )(23312123m A =⨯⨯=
, )3
3,310(3C )(57.1114.321224m A -=⨯⨯-= 314,2(4π
⨯C 即:)425.0,2(4C
)(257
.1866.04866.0257.1310232432234
1
4
1m A
x
A x i i
i ci
i C =-++⨯-⨯+⨯+⨯==
∑∑==
)(912.057
.1866.04866.0425.057.1332323433234
1
4
1m A
y
A y i i
i ci
i
C =-++⨯-⨯+⨯+⨯==
∑∑==。
