自动控制原理-第四章习题集配套答案
自动控制原理参考答案-第4章

d) 与虚轴交点:
特征方程: s3 + 2s2 + (2 + Kg )s + 3Kg = 0
s3
1
2+ Kg
s2
2
3Kg
s1 2 − 0.5Kg
s0
3Kg
当 Kg = 4 时, 2s2 +12 = 0 ⇒ s = ±2.45 j
e) 出射角: βsc = ±180(1+ 2n) − ∑ β + ∑α
s3
1
7
s2
2
Kg −10
s1 12 − 0.5Kg
s0 Kg −10
当 Kg = 24 时, 2s2 +14 = 0 ⇒ s1,2 = ±2.65 j
劳斯表的 s0 行为正 ⇒ Kg > 10 ,即10 < Kg < 24 根轨迹如下图:
题 4-6:已知负反馈控制系统的开环传递函数为
G(s)H(s)
b) 根轨迹趋向: n − m≥ 2 ,则极点-5,-10 之间的根轨迹向右渐进.
c)
渐近线: ⎧⎪⎨ϕk
=
±180(1 + 2
2n)
=
±90o
⎪⎩−σ k = −6.5
d) 分离点与会合点:令 ∂Kg = 0 ∂s
即: 2s3 + 21s2 + 60s +100 = 0 ⇒ s1 = −7.34 ; s2,3 = −1.5794 ± 2.0776j (舍去) 根轨迹如下图:
(4) 稳态速度误差系数是多少?
(5) 系统指标比该点的二阶指标大还是小?如果要求系统有该点二阶指标
的超调量,能否通过改变阻尼线而获得?是增大阻尼比还是减小它?
自动控制原理课后习题第四章答案

G(s)H(s)=
Kr s(s+1)(s+3)
σ根 s=3-K+ω轨r4-3-迹+p4s132ω1-3的+~3ω32分p===s2-离+001K点.p-3r=3:KK~0θrr===012+ωω6021,o=3,=0+±1810.7o
8
jω
1.7
s1
A(s)B'系(s)统=根A'轨(s迹)B(s)
s3 p3
s=sK2±r没=j24有.8.6位×于2K.r根6=×4轨80.迹6=上7,. 舍去。
2
第四章习题课 (4-9)
4-9 已知系统的开环传递函数,(1) 试绘制出
根轨迹图。
G(s)H与(s虚)=轴s交(0点.01s+1K)(系0.统02根s+轨1迹)
jω
70.7
解: GKK(rr=s=)10H5(0s)=ωω2s1,(3=s=0+±17000K.7)r(s+50)
s1
A(s)B'(系s)统=A根'(轨s)迹B(s)
s3 p3
p2
p1
-4
-2
0
((24))ζ阻=尼03.振5s2荡+1响2应s+s的81==K-r0值0.7范+围j1.2
s=s-s10=3=.-80-56.8+50K.7r×=20=s.82-=54×-.631..1155×3.15=3.1
-2.8
450
1080
360
0σ
0σ
第四章习题课 (4-2)
4-2 已知开环传递函数,试用解析法绘制出系
统的根轨迹,并判断点(-2+j0),(0+j1),
国防《自动控制原理》教学资料包 课后习题答案 第四章

第4章课后习题参考答案4-1(a)(b)(c)(d)4-2(1)(2)4-3(1)(2)(j 24.20 ),K=10.14 4-4 (1)(2)(3)4-5(1)0>K (2)2>K 4-6(1)(2) 闭环极点(j 7.597.0±-),K=34.77 4-7 (1)110222-=+++s s s a(2)130202-=+ss a4-8正反馈 负反馈表明K>0对于正反馈系统不稳定,负反馈系统稳定。
4-90.707ξ=,系统开环传递函数为)4(8)(+=s s s G ,系统的单位阶跃响应为)(t h =)452sin(5.012 +--t e t4-10σωj 007.17-93.2-5-10-(1) K=5;(2)不含有衰减振荡分量的K 值范围为86.00<<K 或29>K 。
4-11 系统的开环极点为0和-p ,开环零点为-z 。
由根轨迹的幅角条件, 得π)12()()(+=+∠-∠-+∠q p s s z s 。
将ωσj s +=代入,整理有pz++︒=-+---σωσωσω111tan 180tan tan取上述方程两端的正切,并利用下列关系yx yx y x tan tan 1tan tan )tan( ±=±有p z z +=++-σωωσσω2)(,则zp z z -=++222)(ωσ,这是一个圆的方程,圆心位于(-z ,j 0)处,而半径等于zp z -2(注意,圆心位于开环传递函数的零点上)。
证毕。
4-12(1)分离点-0.465,对应K=0.88;虚轴的交点j 2± (2)88.00<<K ,阶跃响应不出现超调。
4-13(1)(2)70MAX K =4-14负反馈稳定K 值范围为0<K<73.8,正反馈稳定K 值范围为0<K<35,所以确定根轨迹增益K 的范围为0<K<35。
自动控制原理第4章 习题及解析
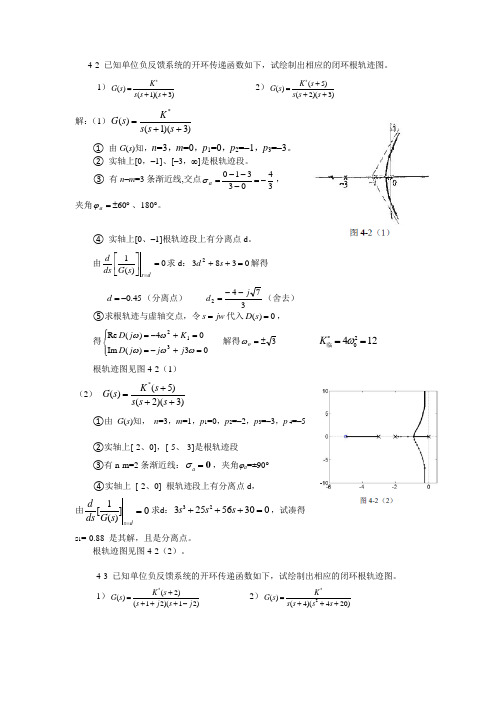
4-2 已知单位负反馈系统的开环传递函数如下,试绘制出相应的闭环根轨迹图。
1)*()(1)(3)K G s s s s =++ 2)*(5)()(2)(3)K s G s s s s +=++解:(1)()(1)(3)*K G s s s s =++① 由G (s )知,n =3,m =0,p 1=0,p 2=–1,p 3=–3。
② 实轴上[0,–1]、[–3,∞]是根轨迹段。
③ 有n –m =3条渐近线,交点3403310-=---=a σ, 夹角︒±=60a ϕ、180°。
④ 实轴上[0、–1]根轨迹段上有分离点d 。
由0)(1=⎥⎦⎤⎢⎣⎡=ds s G ds d 求d :03832=++s d 解得 45.0-=d (分离点) 3742j d --=(舍去) ⑤求根轨迹与虚轴交点,令jw s =代入0)(=s D ,得⎪⎩⎪⎨⎧=+-==+-=03)(Im 04)(Re 312ωωωωωj j j D K j D 解得3±=o ω 20412*K ω==临根轨迹图见图4-2(1)(2) *(5)()(2)(3)K s G s s s s +=++①由 G (s )知, n =3,m =1,p 1=0,p 2=–2,p 3=–3,p 4=–5②实轴上[-2、0],[-5、-3]是根轨迹段 ③有n-m=2条渐近线:0a σ=,夹角ϕa =±90°④实轴上 [-2、0] 根轨迹段上有分离点d , 由1[]0()s dd ds G s ==求d :3232556300s s s +++=,试凑得 s 1=-0.88 是其解,且是分离点。
根轨迹图见图4-2(2)。
4-3 已知单位负反馈系统的开环传递函数如下,试绘制出相应的闭环根轨迹图。
1)*(2)()(12)(12)K s G s s j s j +=+++- 2)*2()(4)(420)K G s s s s s =+++解:(1)*(2)()(12)(12)K s G s s j s j +=+++-根轨迹图见图4-3(1)(2)*2()(4)(420)K G s s s s s =+++① n =4,m =0,p 1=0,p 2=–4,p 3、4=–2±j 4② p 1、p 2连线中点正好是p 3、p 4实部,开环极点分布对称于垂线s=–2,根轨迹也将对称于该垂线。
自动控制原理第二版第四章课后答案

自动控制原理第二版第四章课后答案【篇一:《自动控制原理》第四章习题答案】4-1 系统的开环传递函数为g(s)h(s)?k*(s?1)(s?2)(s?4) 试证明点s1??1?j3在根轨迹上,并求出相应的根轨迹增益k*和开环增益k。
解若点s1在根轨迹上,则点s1应满足相角条件?g(s)h(s)??(2k?1)?,如图解4-1所示。
对于s1= -1+j3,由相角条件?g(s1)h(s1)?0??(?1?j3?1)??(?1?j3?2)??(?1?j3?4)? 0??2??3??6???满足相角条件,因此s1= -1+j3在根轨迹上。
将s1代入幅值条件: g(s1)h(s1?k*?1?1?j3?1??1?j3?2??1?j3?4k8*解出: k=12 ,k=*?324-2 已知开环零、极点如图4-2 所示,试绘制相应的根轨迹。
解根轨如图解4-2所示:4-3 单位反馈系统的开环传递函数如下,试概略绘出系统根轨迹。
⑴ g(s)?ks(0.2s?1)(0.5s?1)k(s?5)s(s?2)(s?3)* ⑵ g(s)?⑶ g(s)?k(s?1)s(2s?1)解⑴ g(s)?ks(0.2s?1)(0.5s?1)=10ks(s?5)(s?2)系统有三个开环极点:p1?0,p2= -2,p3 = -5①实轴上的根轨迹:???,?5?, ??2,0?0?2?57?????a??33②渐近线: ????(2k?1)????,?a?33?③分离点:1d?1d?5?1d?2?0解之得:d1??0.88,d2?3.7863(舍去)。
④与虚轴的交点:特征方程为 d(s)=s3?7s2?10s?10k?0?re[d(j?)]??7?2?10k?0令 ? 3im[d(j?)]????10??0?解得?????k?7。
根轨迹如图解4-3(a)所j)与虚轴的交点(0,?示。
⑵根轨迹绘制如下:①实轴上的根轨迹:??5,?3?, ??2,0?0?2?3?(?5)????0a??2②渐近线: ????(2k?1)????a?22?③分离点: 1d?1d?2?1d?3?1d?5用试探法可得 d??0.886。
自动控制原理简明教程第二版课后答案第四章习题答案

m
n
∑ ∑ θ pi = (2k +1)π +
ϕ − θ z j pi
pi pi
j=1 j=1 ( j≠i)
k = 0,±1,±2,
θ p1 = 1800 θ p2 = 1800 +ϕz1p2 −θ p1p2 −θ = p3p2 1800 + 450 −1350 −
900 = 00 θ p3 = 1800 +ϕz1p3−θ p1p3 −θ p2p3 =1800 − 450 +1350 + 900
(-2+j0)点在根轨迹上,而(0+j1), (-3+j2)点不在根轨迹上。 4-2 设单位反馈控制系统的开环传递函数
G(s) = K (3s +1) s(2s +1)
试用解析法绘出开环增益 K 从零增加到无穷时的闭环根轨迹图。 解:
系统开环传递函数为 G(s) = 3K /2(s +1/3) = K g (s +1/3) s(s +1/ 2) s(s +1/ 2)
mn
∑ ∑ θ pi = (2k +1)π +
ϕ − θ z j pi
pi pi
j=1 j=1
( j≠i)
k = 0,±1,±2,
θ p1 =1800
θ p2 =−900
θ p3 =+90
θ p4 = 00
根轨迹如图所示。
4-9 已知开环传递函数为
12
胡寿松自动控制原理习题解答第四章 电三刘晓峰制作
取分离点为 d1 =−1.7,d2 =−0.29 K *(s + 5)
(3) G(s) = s(s + 2)(s + 3)
自动控制原理第4章课后习题答案

第4章4-1 已知系统的开环传函如下,试绘制系统参数K 从0→∞时系统的根轨迹图,对特殊点要加以简单说明. (1) ()()(4)(1)(2)K s G s H s s s s +=++ (2) ()()2(4)(420)KG s H s s s s s =+++ 解:(1)有3个开环几点,1个开环零点,固有3条根轨迹分别始于0,-1,-2; 1条根轨迹终于-4,另外2条根轨迹趋于无穷远处 实轴上的根轨迹分布在-1~0之间及-4~-2之间 渐近线条数为n-m=3-1=2 渐进线的交点12041312σ++-=-=-渐近线的倾角90θ︒=±分离点22[()()]02152480d G s H s s s s ds =⇒+++= 解得: 12s =- 其它舍去求与虚轴交点:令s j ω=代入特征方程(1)(2)(4)0s s s K s ++++=中得(1)(2)(4)0j j j K j ωωωω++++= 令上式两边实部和虚部分别相等,有226430(2)0 2.83K K K ωωωω⎧=⎧-=⎪⎪⇒⎨⎨+-==±=±⎪⎪⎩⎩绘制系统根轨迹,如图4-1(1)(2)有4个开环几点,无开环零点,有4条根轨迹,分别起始于0,-4, 24j -±终于无穷远处 实轴上的根轨迹分布在-4~0之间; 渐近线条数为n-m=4-0=4 渐进线的交点04242424j j σ++++-=-=-渐近线的倾角45,135θ︒︒=±±分离点22[()()]042472800d G s H s s s s ds=⇒+++=解得: 2s =-由()()1G s H s =得21224(2)4220K=--+--⨯+, K=64绘制系统根轨迹,如图4-1(2)图4-1(1)图4-1(2)4-2 已知系统的开环传函为(2)(3)()()(1)K s s G s H s s s ++=+(1) 试绘制系统参数K 从0→∞时系统的根轨迹图,求取分离点和会和点 (2) 试证明系统的轨迹为圆的一部分解:有2个开环极点,2个开环零点,有2条根轨迹,分别起始于0,-1; 终于-2,-3;实轴上的根轨迹分布在-3~-2之间及-1~0之间分离会和点2221,2,321[()()]02401,12123(2)()()()[()()]0[2(6)4]0203602,18()()[()()]00020,d G s H s s ds KK K s G s H s s s a d G s H s s s a s a dsa a a a s KG s H s sd G s H s s ds a s s =⇒+===-+⨯-++=+=⇒+++=⇒-+≥⇒≤≥===⇒=≤≤=23s ==解得:当10.634s =-时 由()()1G s H s =得(0.6342)(0.6343)10.070.6340.6341K K -+-+=⇒=-⨯-+当2 2.366s =-时 同理 K=13.9 绘制系统根轨迹 如图4-2证明:如果用s j αβ=+代入特征方程1()()0G s H s +=中,并经整理可得到以下方程式:2233()24αβ++=(注:实部虚部相等后消K 可得)显然,这是个圆的方程式,其圆心坐标为3(,0)2-,半径为2图4-24-3 已知系统的开环传函()()(1)(3)KG s H s s s =++(1) 试绘制系统参数K 从0→∞时系统的根轨迹图(2) 为了使系统的阶跃响应呈现衰减振荡形式,试确定K 的范围 解:有2个开环极点,无开环零点,有2条根轨迹,分别起始于-1,-3; 终于无穷远处;实轴上的根轨迹分布-3~-1之间; 渐近线条数2; 渐近线的交点13022σ+-=-=- 渐近线的倾角90θ︒=± 分离会和点[()()]0240d G s H s s ds=⇒+=解:S=-2由()()1G s H s =得1,12123KK ==-+⨯-+绘制系统根轨迹图4-3由图知 当1<K<+∞时系统的响应呈现衰减振荡形式4-4 设负反馈控制系统的开环传函为2(2)()()()K s G s H s s s a +=+试分别确定使系统根轨迹有一个,两个和三个实数分离点的a 值,分别画出图形 解:求分离点2[()()]0[2(6)4]0d G s H s s s a s a ds=⇒+++=解得s=0,或分离点为实数2203602a a a ⇒-+≥⇒≤或18a ≥当a=18时 实数分离点只有s=0 如图4-4(1)当a>18时 实数分离点有三个,分别为1,2,3(6)0,4a s -+=如图4-4(2)当a=2时2()()K G s H s s =分离点[()()]00d G s H s s ds=⇒= 即分离点只有一个s=0 如图4-4(3) 当02a ≤≤分离点有一个s=0 如图4-4(4) 当a<0时 分离点有1230,s s s ===(舍去)如图4-4(5)综上所述:当a=18,0≤a ≤2时,系统有一个分离点 当a >18时,系统有三个实数分离点 当a <0时,系统有两个分离点a=18图4-4(1) a=2图4-4(2)图4-4(3) a=1图4-4(4)图4-4(5)4-65 已知系统的开环传递函数为3(1)(3)()()K S S G S H S S++=(1)绘制系统的根轨迹。
自动控制原理课后习题第四章答案

然后,根据闭环传递函数的定义,闭环传递函数F(s)=G(s)/(1+G(s)H(s))。
解析3
将G(s)H(s)代入闭环传递函数的定义中,得到F(s)=100/((s+1)^2+3)/(1+100/((s+1)^2+4)((s+1)^2+3))。
解析4
化简得到F(s)=100/((s+1)^2+3)(4((s+1)^2+3))=400/(4(s^2+2s+3))。
1)(s + 2)/(s^2 + 3s + 2)。
04
题目四答案
题目内容
• 题目四:已知系统的开环传递函数为 G(s)H(s)=K/(s^2+2s+2),其中K>0,试 求系统的闭环极点和稳定性。
答案解析
闭环极点
根据开环传递函数,我们可以求出闭环传递函数为 G(s)H(s)/(1+G(s)H(s)),然后求出闭环极点。由于开环传递函 数为K/(s^2+2s+2),所以闭环极点为-1±√2i。
标准形式,即 G(s)H(s) = (s + 1)(s + 2)/(s^2 + 3s + 2)。
02
解析二
根据开环传递函数的分子和分母,可以得出系统的开环传递函数为
G(s)H(s) = (s + 1)(s + 2)/(s^2 + 3s + 2)。
03
解析三
根据开环传递函数,可以求出系统的闭环传递函数为 G(s)H(s) = (s +
自动控制原理课后习题第四章 答案
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章 根轨迹分析法习题4-2 单位回馈控制系统的开环传递函数1)(+=s K s G r,试用解析法绘出r K 从零变化到无穷时的死循环根轨迹图,并判断-2, j1, (-3+j2)是否在根轨迹上。
解:1-s 01s 0r=⇒=+=时,K2-s 02s 1r=⇒=+=时,K3-s 03s 2r=⇒=+=时,K……-2 在根轨迹上,(-3+j2),j1不在根轨迹上。
4-3 回馈控制系统的开环传递函数如下,0≥r K ,试画出各系统的根轨迹图。
(2) )4)(1()5.1()(+++=s s s s K s G r (3) 2)1()(+=s s K s G r , 解:(2)1)开环零、极点:p 1=0,p 2=-1,p 3=-4,z=-1.0,n=3,m=1 2)实轴上根轨迹段:(0,-1),(-1.5,-4) 3)根轨迹的渐近线:︒±=±=-+±=-=----=902)12(,75.12)5.1(410)2( ππϕσm n k aa夹角交点条渐近线4)分离点和会合点6.05.1141111-=+=++++d d d d d 试探法求得(3)1)开环零、极点:p 1=0,p 2,3=-1,n=32)实轴上根轨迹段:(0,-1),(-1,-∞) 3)根轨迹的渐近线:±=-+±=-=--=3)12(,323110)3( ππϕσm n k aa夹角交点条渐近线4)分离点和会合点310121-=⇒=++d d d 5)与虚轴交点:223++s s4-5 系统的开环传递函数为)1()2()(++=s s s K s G r ,(1) 画出系统的根轨迹,标出分离点和会合点;(2) 当增益r K 为何值时,复数特征根的实部为-2?求出此根。
解: (1)1)开环零、极点:p 1=0,p 22)实轴上根轨迹段:(0,-13)分离点和会合点.3,586.02111121-=-=⇒+=++d d d d d(2)系统特征方程为02)1(rr2=+++K s K s2j 2322122,1rr±-==-=+-=-s K K a b ,,得:由0123ss s s r2K-r211K rKj,202rr±==⇒=-s K K4-6 单位回馈系统的前向信道函数为)3)(1()(++=s s s K s G r,为使死循环主导极点具有阻尼比5.0=ξ,试确定r K 的值。
解:系统的根轨迹如图在根轨迹图上作射线: β=与根轨迹相交点为s 1和s 2n n j s ωω866.05.01+-=nnj s ωω866.05.02--=则死循环特征方程式可表示为0)()())()((2332233321=--+-+=---nnnns s s s s s s s s s s s ωωωω034r23=+++K s s s 系统特征方程为比较系数,得: ⎪⎩⎪⎨⎧=-=-=-r2332334K s s s nnnnωωωω⎪⎩⎪⎨⎧=-==⇒828.125.375.0r3K s n ω4-7 控制系统的开环传递函数为)4)(2()(++=s s s K s G r(1) 绘出该回馈系统的根轨迹图;(2) 求系统具有阻尼振荡响应的r K 取值范围; (3) 系统稳定的r K 最大为多少?并求等幅震荡的频率;(4) 求使主导极点具有阻尼比5.0=ξ时的r K 值,并求对应该值时, 零极点形式的死循环传递函数。
解:(1)1)开环零、极点:p 1=0,p 2=-22)实轴上根轨迹段:(0,-2),3)根轨迹的渐近线:︒︒±=±=-+±=-=--=180,603)12(,23420)3( ππϕσm n k aa夹角交点条渐近线4)分离点和会合点)(732.4,845.004121121舍-=-=⇒=++++d d d d d分离点对应的08.3155.3155.1845.0r=⨯⨯=K5)与虚轴交点:086r23=+++K s s s(2)系统具有阻尼振荡响应的r K 取值范围是:4808.3r<<K(3)系统稳定的48r<K,等幅振荡频率为22=ω(4)同上题方法可求得: 阻尼比5.0=ξ时j1.1567.0,67.4,3.82,13±-=-==s s K r)15.1j 67.0)(15.1j 67.0)(67.4(3.8)(-++++=Φs s s s4-8单位负反馈系统的开环传递函数为)15.0)(1()(++=s s s K s G r,用根轨迹分析系统的稳定性。
解:1)开环零、极点:p 1=0,p 2=-1,p 3=-2,n=3 2)实轴上根轨迹段:(0,-1),(-23)根轨迹的渐近线:123s ss s r84K-r68 1KrK2j2,48084rr±==⇒=-s K K︒︒±=±=-+±=-=--=180,603)12(,13210)3( ππϕσm n k aa夹角交点条渐近线4)分离点和会合点)(644.1,356.002111121舍-=-=⇒=++++d d d d d5)与虚轴交点:0223r23=+++K s s s所以,系统稳定的rK 取值范围是:30r<<K4-9 单位负反馈系统的开环传递函数为)02.01)(01.01()(s s s K s G r++=(1) 画出系统的根轨迹图;(2) 确定系统临界稳定时的开环增益; (3) 确定与临界阻尼比相应的开环增益。
解:(1))50)(100(5000)(++=s s s Ks G r① 实轴上的根轨迹:[0, -50],[-100,-∞]123s ss s r26K-r2 32 1Kr2Kj,30262,1rr±==⇒=-s K K② 分离点:0100d 150d 1d 1=++++ 求解得87.78d 13.21d 21-=-=,③ 渐近线:o oa a 1806050,,±=ϕ-=σ 根轨迹如图所示。
(2) 系统临界稳定时150750000*==rK K ,(3) 系统临界阻尼比时62.95.48112*==rK K ,4-10 系统的开环传递函数为32)2()(2+++=s s s K s G r ,试绘制系统在∞<<r K 0时的根轨迹,并确定系统临界阻尼时的解:1)开环零、极点:,2j 12,1±-=p2)实轴上根轨迹段:(-2,-∞) 3)分离点和会合点1)( ,22)()( ,32)(2='+='=++=s B s s A s s B s s s A)()()()(s A s B s B s A '=')22)(2(322++=++s s s s s 1=-3.732,s 2=-0.268(舍)此时系统即为临界阻尼情况, 对应的46.5732.1732.22732.2222r=+⨯+=K 4)出射角︒-=︒-︒+︒-=7.1447.5490180θ4-12 系统结构如图所示,试画出回馈系数k 为变数的根轨迹。
解:)110(10)(++=K s s s G 0)110(101)(1=+++=+K s s s G 由 01010s 2=+++⇒s Ks则,系统等效开环传递函数1010)(2++='s s ks s G 1)分离点和会合点1)( ,12)()( ,10)(2='+='=++=s B s s A s s B s s s A )()()()(s A s B s B s A '=')12(102+=++s s s s s 1=-3.16,s 2=3.16(舍)2)与虚轴无交点:010)110(2=+++s k s3)︒-=︒--︒+︒=1.9)1.99(90180θ4-14 系统结构如图所示,闭环根轨迹通过(-0.65+j1.07)点,试绘制r K 从∞→0变化时系统的根轨迹。
-k110+s s1-)(s R )(s Cj3.12),(-0.5︒9.1︒9.1-3.12)(-0.5,-3.16-解:)2)(1()1(10)(1+++=s s s s T K s G 系统特征方程为:0)1(10)2)(1(1=++++s T K s s s 将s=-0.65+j1.07代入上式,可得:667.0,266.01==T K∴G 1 21+d 5所以,与虚轴无交点。
4-16 单位回馈系统的闭环特征方程为04)1(223=++++r r K s K s s 。
试绘制系统的根轨迹,并求闭环出现重根时的r K 值和对应的闭环根。
解:由系统特征方程可得系统等效开环传递函数2)1()4()(++=s s s K s G r12s ss s r.516K+rr1.5 32 1KK+r2K1)根轨迹的渐近线:±-+±==+--=2)12(,124110)2( ππϕσm n k aa夹角交点条渐近线2)与虚轴交点:04)1(223=++++rrK s K s s3)分离点和会合点: 354.041121-=+=++d d d d 求得:分离点对应的04.0646.3646.0646.0354.0r=⨯⨯=K此时特征方程可写为:0)354.0)((23=+-s s s与题目已知系统特征方程对比可得292.13-=s4-17 控制系统结构如图所示,0≥r K ,试画出系统的根轨迹,并分析增益对系统阻尼特性的影响。
解:)1()3)(2()(+++=s s s s K s G r1)分离点和会合点: 31211111-=+++=++d d d d d 求得:123ss s s rrKK 4 21 1+0)1(2=-rK rK42,1j s K r±==⇒j0.354-4-1-22-1此时0718.0366.2366.1366.0634.0r1=⨯⨯=K93.13366.0634.0336.2336.1r2=⨯⨯=K增益对系统阻尼特性的影响:0r>K 时系统都是稳定的;0718.00r<<K 时,系统是过阻尼系统;93.130718.0r<<K 时,系统是欠阻尼系统;93.13r>K 时,系统又变成过阻尼系统。
(注:文档可能无法思考全面,请浏览后下载,供参考。
可复制、编制,期待你的好评与关注!)。
