理论力学第6章
理论力学 第六章

n
FR Fi i 1
汇交力系的合成结果是一合力,合力的大小和方向由各力 的矢量和确定,作用线通过汇交点。
Theoretical Mechanics
返回首页
6.1 汇交力系的简化与平衡
6.1.1 几何法
Theoretical Mechanics
返回首页
6.1 汇交力系的简化与平衡
❖结 论
6.1.1 几何法
平面汇交力系合成的结果是一个合力, 它等于原力系中各力的矢量和,合力的 作用线通过各力的汇交点。
Theoretical Mechanics
返回首页
6.1 汇交力系的简化与平衡
6.1.2 解析法
cos(FR
, i)
FRx FR
,
cos(FR ,
j)
FRy FR
,
cos(FR
, k)
FRz FR
合力作用线过汇交点。
Theoretical Mechanics
返回首页
6.1 汇交力系的简化与平衡
6.1.2 解析法
汇交力系平衡的充分必要条件
汇交力系的合力为零
各力在三个坐标轴上的 投影代数和分别等于零
返回首页
6.3 空间任意力系的简化
6.3.2 力系向一点简化·主矢和主矩
设刚体上作用一任意力系F1、F2、…、Fn。 任选一点O称为力系的简化中心。依据力的平移定理, 将力系中诸力向O点平移。
得到作用于O点的一汇交力系F 1、F 2、…、F n和一力 偶系M1、M2、…、Mn 。
Theoretical Mechanics
n
理论力学6章

1第二篇 运动学运动学研究物体运动的与运动产生原因无关的几何属性。
对刚体而言,运动学是在给定的惯性参考系中,研究刚体相对惯性参考的空间位置变化科学。
第六章 点的运动本章对质点(一种特殊的刚体)在惯性参考系中的位置变化进行分析。
并给出动点,动点的轨迹,动点的速度矢量,动点的加速度矢量等基本概念。
并以不同的几种方试对上述概念进行数学描述。
§6-1 矢量法在地球惯性参考系(体)上任取一定点O 。
对空间中任意一点A ,以O 点为起始点,A 点为末端点作有向值线段,且记A =r则称r A 为A 点相对O 点的位置矢量。
若A 点泛指空间中的一般点,r A 也记为r 。
质点作为仅由孤立物质点构成的刚体,在宏观尺度上,质点在空间所占具的位置可由与质点在空间重叠的几何点的位置矢量r 唯一对应。
一、质点的运动方程和轨迹质点在空间的位置随时间的不同而发生变化,质点在空间位置随时间的变化而导致变化称为质点的运动。
质点运动的数学表述称为质点的运动方程。
在地球惯性参考系(体)中取定O 点时,在任意时刻t ,质点的空间位置矢量唯一确定。
即)(t r r = (6-1)随r =r (t )中时刻t 在其取值区间段的不同取值,质点将在空间占具不同的位置。
参数t 被称为时间参数,或称为时间。
对质点,在时间的取值区间[a ,b ]<<或(a ,b )、[a ,b )、(a ,b ]>>位置矢量时间(参数)变化的函数表达式(矢量表示))(t r r =称为质点在给定的时间取值区间内的运动方程。
在一般的运动学分析中,质点运动方程中的时间参数取值区间总被认为是任意给定了的。
因此通常就称)(t r r =是质点的运动方程。
2当质点的运动方程)(t r r =一但给定,位置矢量在时间参数的取值区间的每一个时间参数取值所确定的位置矢量末端点集合称为质点的运动轨迹。
质点的运动轨迹在三维空间中的几何表示为一条空间曲线。
理论力学第六章-

• (二)理想约束和虚功原理
作用在质点上的力F与质点任一虚位移 δ的r
标积,称为此力在虚位移中的虚功
δ W F F ' δ r
虚功具有功(或能量)的量纲,但没有能 量转化过程与之联系。对于处于平衡状态 的体系,作用在各质点上的力(主动力和 约束力)所做的虚功之和为0
若体系中各个约束力所做的虚功之和等 于零,则这种约束称为理想约束
n
F'
δri
0
i1
◆光滑曲面、曲线、光滑铰链均为理想约 束,受这些约束的质点,约束力恒与相应 的虚位移垂直! ◆如两个质点(研究对象)被不可伸长的 轻绳、或刚性杆连接的约束;两个刚体表 面光滑相互接触,或无滑相互接触的约束, 固定点约束等。
虚功原理:受理想约束的力学系统,保持 平衡的必要条件是作用于该系统的全部主 动力在任意虚位移中的虚功之和为零
s1pqLs1qLqL
称为哈密顿函数(或哈密顿量),是广义坐 标和广义动量的函数。
• (三)虚功原理的广义坐标表述和广义 力
xixi(q 1,q2, ,qs,t)
则质点坐标变量的虚位移与广义坐标虚位 移之间的存在关系
δxi s1qxi δqxti δt
(i1,2, ,3n)
δt 0
代入虚功原理的表达式可得
δW
3n i 1
Fi
s 1
r i r iq ,t 1 ,2 , ,s
ri
dri dt
s
ri
1q
q
ri t
ri q
ri q
d dt q r i s1q 2 riqq t 2q ri
理论力学第六章 点的合成运动 [同济大学]
![理论力学第六章 点的合成运动 [同济大学]](https://img.taocdn.com/s3/m/63fd0a4dbe1e650e53ea9909.png)
解: 从例6-2已知得: 1 =
vr r 3 , 2
ω 4
O
解: 从上例已知得: 1 =
r
M
ω 4
va
A
aaτ =0 ,
3 , 4
aan=2r aen=
ωr 8
x’
2
ac 21vr 2 r
va
30°
3 1 1/ s2 8
2
动点取A,
va v A
ar
dvr d 2 x ' ' d 2 y ' ' d 2 z ' ' 2 r 2 j 2 k dt dt dt dt
dx ' di ' dy ' dj' dz ' dk ' dt dt dt dt dt dt
ar ω vr
a a ae a r ac; ac= 2vr
ve
a n a ae a rn a rτ
矢量
1.瞬时状态; 2.可解两个未知量 (大小,方向)。
例6-5 曲柄滑道机构,OA=01A=r=10cm, =30°,=4, 求: 转到30°时直杆的加速度a。 va vr 动点取A; 绝对:圆周; ve 解:相对:圆周;牵连:直线。 [速度] =
a a ae a r ac; aa a an ae aen ar arn ac;
例6-8 曲柄绕O转动,並通过滑块M带动滑槽绕O′摆动, ’ y 求摆动到30°时的角加速度1。
例6-9 将例6-8滑槽改变为图示牛头刨床机构,MA=2r, 求:刨床刨刀的速度,加速度。
vr
dv e dω dr r ω dt dt dt α r ω v e ω v r ae ω v r
理论力学(第6章)

t 已知:O1A=O2B=18cm,AB=O1O2=2R,R=18cm , 18 t2 求: va , aa s BM
π
加速度合成定理的矢量形式向 直角坐标轴x、y上投影,得:
π aax a a cos 6.67cm / s 2 6 π n n aay ar ae sin 20cm / s 2 6
绝对:大圆周(半径R)
相对:沿OA的直线运动 牵连:定轴转动(绕o轴)
2.速度分析 v a ve 大小 ? 方向 √
ve va 2Rω cos
vr
OM√?√ Nhomakorabeavr ve tan 2 R ω sin ω t
6.3 牵连运动为平移时点的加速度合成定理
点的加速度合成定理:
解:(1) 动点:取顶杆AB的A点 动系:固连在凸轮上。 绝对运动:沿AB竖直方向 的平移。 相对运动:A点沿凸轮边 缘的圆周运动。 牵连运动:动系凸轮沿水 平面向右平移。
已知:
v0
30
2.速度分析
va ve vr
由几何关系可以得到:
3 vB vA v tan 30 v 3
例6-5 平面机构中直杆O1A、O2B平行且等长,分别 绕O1、O2轴转动,直杆的A、B连接半圆形平板,动 点M沿半圆形平板ABD边缘运动,起点为点B。已知 π t, O1A=O2B=18cm,AB=O1O2=2R,R=18cm , 18 t2 。 s BM
求:当 t 3s 时, 动点M的绝对速度 和绝对加速度。
方向竖直向上
例6-2 刨床的急回机构如图所示。曲柄OA的一端 A与滑块用铰链连接。当曲柄OA以匀角速度ω绕固 定轴O转动时,滑块在摇杆O1B上滑动,并带动杆 O1B绕定轴O1摆动。设曲柄长为OA=r,两轴间距 离OO1=l。 B 求: O ① 曲柄在水平位 A 置时摇杆的角 速度 1 。 ② 滑块A对于摇 杆 的相对角 O1 速度
理论力学第6章
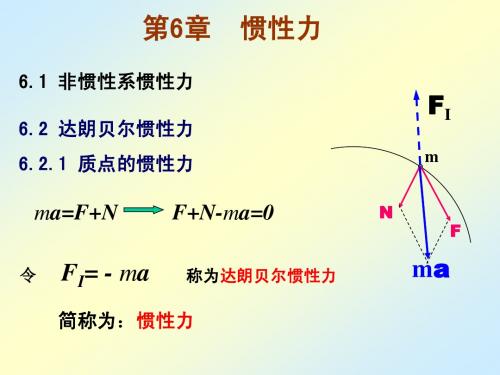
6.1 非惯性系惯性力 6.2 达朗贝尔惯性力
惯性力
FI
m
6.2.1 质点的惯性力
ma=F+N
令
F+N-ma=0
称为达朗贝尔惯性力
N
F
FI= - ma
ma
简称为:惯性力
6.2.2 刚体惯性力系的简化
刚体由无数个质点构成,若对每点去施加惯性力其难度则
不难想象。因此,对于刚体的惯性力系,则应设法将其简化。
2、刚体定轴转动
FIi mi ai mi ri
F mi a mi ri
n Ii n i
2
M Ix M x FIi M x FIit M x FIin
mi ri cos i zi (mi ri 2 sin i zi )
一、惯性力系主矢
FIR FIi mi ai
mi FIi
C
ai aC
对于质量不变的质点系:
m a ma
i i
C
所以,惯性力系的主矢为:
FIR m aC
与质点系的运动形式无关!!!
二、惯性力系主矩及简化结果 1、刚体平移
惯性力系向点O简化.
i
FIi
ri C
O
aC
rC
M IO ri FIi ri (mi aC ) ( mi ri ) aC mrC aC M IC 0 惯性力系向质心简化.
只简化为一个力
FIR maC
平移刚体的惯性力系可以简化为通过质心的惯性力, 其大小等于刚体的质量与加速度的乘积,合力的方向与 加速度方向反向。
由
理论力学第6章

6.1 点的合成运动基本概念
z
x
大梁不动时
y
o
动
点?
定参考系?
z
y x
动参考系? 绝对运动? 相对运动?
牵连运动?
O
6.1 点的合成运动基本概念
动
点?
定参考系 ? 动参考系 ?
绝对运动 ?
相对运动 ?
牵连运动 ?
6.1 点的合成运动基本概念
◆ 运动的相对性 : 物体对于不同的参考系,运动各
va ve v r
注意点: * 牵连运动是刚体(动系)的运动; 牵连速度是动系(刚体)上一 点(该瞬时与动点相重合的点) 的速度。 *速度合成定理适用于任何形式的牵连运动,任意的相对运动。 * v a v r v e 为矢量式,符合平行四边形法则,其 对角线为 va
*矢量
va .vr .ve 满足“6-4=2”即可求两个未知量。
P'1
PP 相对轨迹 2 P 1P 1 牵连点运动轨迹
PP' 绝对位移 PP2 相对位移 P1 P1 牵连点的位移
zP(P1)
A
Dt
A
y
x
O
6.2
点的速度合成定理
B
P2
B
P'
va vr
PP' PP2 va lim v r lim Dt 0 Dt Dt 0 Dt P1 P1 ve lim Dt 0 Dt PP' P1 P1 P1P ' PP' P1 P1 P1P ' lim lim lim Dt 0 Dt Dt 0 Dt Dt 0 Dt
O1
w
O2
j
A
理论力学第六章

由 动能定理 FS
由 动 2 mv c 能 4 对t求导,得 C 3 mvC a定 Fv C 理 2 故 Fr J C α
3
v
m
r
C
F
C
F
Cv
S
Cv
即动量矩定理
6-2 质点系动能定理
d LC dt
v
MC
v
6-2-1 动能定理的三种形式 问题 3 图(a)系统由静平衡位置转动 角, 此时,系统势能以静平衡为“0”,
V 1 2 k( l 2
k
) 2 对吗?为什么?
l 2
l 2
对!弹簧静平衡力与重力在转动时仍平衡, 其功之和为零,可同时不考虑。
k
a
又如图(b)所示:
V 1 2
6-2 质点系动能定理
O
m
k
2
b
6-2-2 动能定理的应用 1. 应用特点 (1)与位形变化有关 (突出空间过程) 已知运动求力,由 T W F
FT
WG GS sin
WF 0 ,
N
S
C
WF 0 ,
T
G
C
FS
FN
WF 2 FS S
S
6-1 功与动能
6-1-1 力的功
2.内力的功
一对内力, FA -FB
d W FA drA FB drB
FA drA drB FA drAB
Cv
求 ,v 问题 2均质轮在OA杆上滚动,已知 m,r,l,ω1求Cr 轮 T 。
T 1 2 m vC
2
1 2
JC
2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
• 例6-4 半径为r的轮子沿地面直线轨道作纯 滚动,转速为ω,转角为φ= ω t。求轮上任 一点M的运动方程、速度、加速度(切向、 法向)。 • 解:初始时,设点M与点O重合。 • 求M点的坐标(运动方程):
OC MC r rt
x OC r sin r (t sin t ) y r r cos r (1 cost )
加速度: a = axi+ ayj+ azk
d 2x ax 2 , dt d2y ay 2 , dt d 2z az 2 , dt
例6-1
• 椭圆规。曲柄OC绕O转动,C与规尺AB铰 接,滑块A和B在滑槽中运动,已知: OC=AC=BC=l,MC=a,φ=ωt。 • 求:M的运动方程、轨迹、速度、加速度。
2
a y y r 2 cost
2 2 a ax ay r 2
dv t 2 a a a ; at r cos dt 2 t 2 2 2 an a at r sin 2
2 2 t 2 n
• 习题6-5 套管A由绕过定滑轮B的绳子牵引 而沿着导轨上升。滑轮中心到导轨等距离 为l,设绳索以速度v0拉下,忽略滑轮尺寸, 求套管A的速度和加速度与x的关系。
• 曲率半径ρ的定义 :
ds s , d
• (2)切向单位矢沿曲线的变化率 • 令:τ(s+Δs)-τ(s)=Δτ
• 显然, Δτ指向曲率中心。
2 sin d 2 lim ds s 0 s 1 lim s 0 s d 1 n ds
作业
• 6-4 • 6-6
• 解:点M的坐标(运动方程):
x(t ) (l a) cos (l a) cost y(t ) (l a) sin (l a) sin t
• 消去t,得轨迹方程:
x 2 y 2 ( ) ( ) 1 la l a
• 速度:
vx (l a) sin t v y (l a) cost
• 求M点的速度:
vx x r ( cost ) r (1 cost ) v y y r sin t v v v
2 x 2 y 2 2
r (1 cost ) sin t 2r sin
t
2
• 求M点的曲线位移: • 方法1
• 解:
s (t ) l 2 x 2 (t )
ds v0 , v x, a x dt
v0
2x x 2 l 2 x 2 (t ) l2 1 2 x 1 l2 2 2 1 x
v x v0 dv a v0 dt
2 2 v0 l 2l 2 (- 3 x) 3 x x
• 3.点的速度
s ds v lim v t 0 t dt
dv a dt
• 点的速度v就是切向速度 。 • 4.点的加速度:
• 动点移动时,速度大小和方向都发生改变。
dv d ds d 2s ds dτ a ( τ) 2 τ dt dt dt dt dt dt
• 加速度:
a x (l a) cost
2
a y (l a) sin t
2
• 例6-2 正弦运动机构,曲柄OM=r,以匀角 速度ω绕O点转动,转角φ= ω t+θ0。滑杆AB 在固定的垂直槽内滑动,滑块M在机构的水 平滑槽内运动,求A、B两点的速度、加速 度。 • 解:点B的运动:
ห้องสมุดไป่ตู้ §6-3 自然法
• 自然法:利用质点轨迹作为曲线坐标系描述 其运动。 • 1. 弧坐标:在轨迹曲线上建立弧坐标。s=s(t) • 2. 自然轴坐标系 • 切线及其单位矢τ:轨迹曲线的切线方向的单 位长度的矢量。 • 主法线单位矢n:由质点所在位置指向曲率 中心的单位长度的矢量。
• 副法线单位矢b:与和构成右手螺旋系的的 单位长度的矢量。 • 密切面:轨迹曲线上两个邻点的切线形成 的平面。 • 法平面:过轨迹曲线某点与切线垂直的平 面。
第六章 点的运动学
• §6-1 矢量法和直角坐标法 • 1. 表示质点运动的矢量法: • 质点的空间位置用矢径r表示,它是时间的 函数, • r = r(t) • 投影式: r = xi+yj+zk • 轨迹:矢径r 端点的连线。
dr r (t t ) r (t ) lim • 速度: v dt t 0 t
• 主法线,n:法平面与密切面的交线。 • 副法线,b:与切线、主法线垂直的线。 • τ ,n,b组成右手螺旋系
• 3. 曲线坐标的一些性质 • (1)曲率中心:曲线上 两个邻点的法线交点。 • 曲率半径:曲线上的一点 到曲率中心的距离。 • 设M和M’是曲线上的两个 邻点,相距△s,切向单 位矢分别τ(s) 为和τ(s+ △ s) ,曲率半径为ρ。
xB r sin(t 0 ) vB x B r cos(t 0 ) aB x B r 2 sin(t 0 )
• 点A的运动:
xA b r sin(t 0 ) v A x A r cos(t 0 ) a A x A r 2 sin(t 0 )
s t 0 0 2
t
2
dt
t
2
dt
ds 2r sin
s 4r (1 cos
t
2 )
dt
t
2
• 轮摆线
x(t ) r (t sin t ) y(t ) r (1 cost )
s(t ) 4r (1 cos
t
2
)
• 求M点的加速度:
a x x r sin t
• 加速度:
dv d r a 2 dt dt
2
• 2. 表示质点运动的 直角坐标法
• 质点的位置坐标是时间的函数: • x=x(t), y=y(t), z=z(t), • 速度: • v = vxi+ vyj+ vzk
dx vx , dt dy vy , dt dz vz , dt
ds v dt s vdt 2r sin
0 t
t
2
dt 4r (1 cos
t
2
)
• 求M点的曲线位移: • 方法2
ds d 2 x d 2 y r 2 2 (1 cost ) 2 r 2 2 sin 2 t dt r 2 2 cost dt r 4 sin 2 r sin
• 切向加速度
d s dv at 2 τ τ dt dt
2
• 法向加速度
ds dτ dτ an v dt dt dt
dτ dτ ds 1 vn dt ds dt an v
2
n
• 全加速度
dv v a τ n at a n dt a a a
