理论力学 第6章
合集下载
理论力学第六章-
• （二）理想约束和虚功原理
作用在质点上的力F与质点任一虚位移 δ的r
标积，称为此力在虚位移中的虚功
δ W F F ' δ r
虚功具有功（或能量）的量纲，但没有能 量转化过程与之联系。对于处于平衡状态 的体系，作用在各质点上的力（主动力和 约束力）所做的虚功之和为0
若体系中各个约束力所做的虚功之和等 于零，则这种约束称为理想约束
n
F'
δri
0
i1
◆光滑曲面、曲线、光滑铰链均为理想约 束，受这些约束的质点，约束力恒与相应 的虚位移垂直! ◆如两个质点（研究对象）被不可伸长的 轻绳、或刚性杆连接的约束；两个刚体表 面光滑相互接触，或无滑相互接触的约束， 固定点约束等。
虚功原理：受理想约束的力学系统，保持 平衡的必要条件是作用于该系统的全部主 动力在任意虚位移中的虚功之和为零
s1pqLs1qLqL
称为哈密顿函数(或哈密顿量)，是广义坐 标和广义动量的函数。
• （三）虚功原理的广义坐标表述和广义 力
xixi(q 1,q2, ,qs,t)
则质点坐标变量的虚位移与广义坐标虚位 移之间的存在关系
δxi s1qxi δqxti δt
(i1,2, ,3n)
δt 0
代入虚功原理的表达式可得
δW
3n i 1
Fi
s 1
r i r iq ,t 1 ,2 , ,s
ri
dri dt
s
ri
1q
q
ri t
ri q
ri q
d dt q r i s1q 2 riqq t 2q ri
理论力学第六章 点的合成运动 [同济大学]
![理论力学第六章 点的合成运动 [同济大学]](https://img.taocdn.com/s3/m/63fd0a4dbe1e650e53ea9909.png)
解： 从例6-2已知得： 1 =
vr r 3 , 2
ω 4
O
解： 从上例已知得： 1 =
r
M
ω 4
va
A
aaτ =0 ，
3 , 4
aan=2r aen=
ωr 8
x’
2
ac 21vr 2 r
va
30°
3 1 1/ s2 8
2
动点取A，
va v A
ar
dvr d 2 x ' ' d 2 y ' ' d 2 z ' ' 2 r 2 j 2 k dt dt dt dt
dx ' di ' dy ' dj' dz ' dk ' dt dt dt dt dt dt
ar ω vr
a a ae a r ac； ac= 2vr
ve
a n a ae a rn a rτ
矢量
1.瞬时状态； 2.可解两个未知量 (大小，方向)。
例6-5 曲柄滑道机构，OA=01A=r=10cm, =30°,=4, 求: 转到30°时直杆的加速度a。 va vr 动点取A； 绝对:圆周； ve 解：相对:圆周；牵连:直线。 [速度] =
a a ae a r ac； aa a an ae aen ar arn ac；
例6-8 曲柄绕O转动，並通过滑块M带动滑槽绕O′摆动， ’ y 求摆动到30°时的角加速度1。
例6-9 将例6-8滑槽改变为图示牛头刨床机构，MA=2r, 求:刨床刨刀的速度，加速度。
vr
dv e dω dr r ω dt dt dt α r ω v e ω v r ae ω v r
理论力学(第6章)
t 已知：O1A=O2B=18cm，AB=O1O2=2R，R=18cm ， 18 t2 求： va , aa s BM
π
加速度合成定理的矢量形式向 直角坐标轴x、y上投影，得：
π aax a a cos 6.67cm / s 2 6 π n n aay ar ae sin 20cm / s 2 6
绝对：大圆周（半径R）
相对：沿OA的直线运动 牵连：定轴转动（绕o轴）
2.速度分析 v a ve 大小 ? 方向 √
ve va 2Rω cos
vr
OM√?√ Nhomakorabeavr ve tan 2 R ω sin ω t
6.3 牵连运动为平移时点的加速度合成定理
点的加速度合成定理：
解：（1） 动点：取顶杆AB的A点 动系：固连在凸轮上。 绝对运动：沿AB竖直方向 的平移。 相对运动：A点沿凸轮边 缘的圆周运动。 牵连运动：动系凸轮沿水 平面向右平移。
已知:
v0
30
2.速度分析
va ve vr
由几何关系可以得到：
3 vB vA v tan 30 v 3
例6-5 平面机构中直杆O1A、O2B平行且等长，分别 绕O1、O2轴转动，直杆的A、B连接半圆形平板，动 点M沿半圆形平板ABD边缘运动，起点为点B。已知 π t， O1A=O2B=18cm，AB=O1O2=2R，R=18cm ， 18 t2 。 s BM
求：当 t 3s 时， 动点M的绝对速度 和绝对加速度。
方向竖直向上
例6-2 刨床的急回机构如图所示。曲柄OA的一端 A与滑块用铰链连接。当曲柄OA以匀角速度ω绕固 定轴O转动时，滑块在摇杆O1B上滑动，并带动杆 O1B绕定轴O1摆动。设曲柄长为OA=r，两轴间距 离OO1=l。 B 求： O ① 曲柄在水平位 A 置时摇杆的角 速度 1 。 ② 滑块A对于摇 杆 的相对角 O1 速度
理论力学第6章
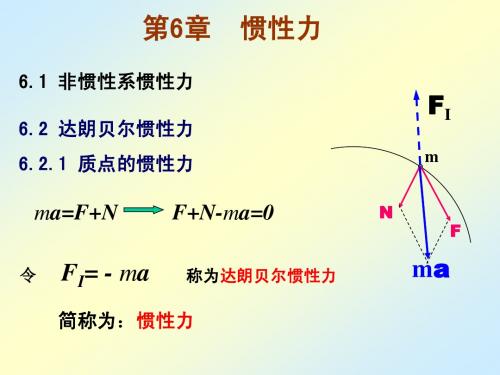
第6章
6.1 非惯性系惯性力 6.2 达朗贝尔惯性力
惯性力
FI
m
6.2.1 质点的惯性力
ma=F+N
令
F+N-ma=0
称为达朗贝尔惯性力
N
F
FI= - ma
ma
简称为：惯性力
6.2.2 刚体惯性力系的简化
刚体由无数个质点构成，若对每点去施加惯性力其难度则
不难想象。因此，对于刚体的惯性力系，则应设法将其简化。
2、刚体定轴转动
FIi mi ai mi ri
F mi a mi ri
n Ii n i
2
M Ix M x FIi M x FIit M x FIin
mi ri cos i zi (mi ri 2 sin i zi )
一、惯性力系主矢
FIR FIi mi ai
mi FIi
C
ai aC
对于质量不变的质点系：
m a ma
i i
C
所以，惯性力系的主矢为：
FIR m aC
与质点系的运动形式无关！！！
二、惯性力系主矩及简化结果 1、刚体平移
惯性力系向点O简化.
i
FIi
ri C
O
aC
rC
M IO ri FIi ri (mi aC ) ( mi ri ) aC mrC aC M IC 0 惯性力系向质心简化.
只简化为一个力
FIR maC
平移刚体的惯性力系可以简化为通过质心的惯性力， 其大小等于刚体的质量与加速度的乘积，合力的方向与 加速度方向反向。
由
6.1 非惯性系惯性力 6.2 达朗贝尔惯性力
惯性力
FI
m
6.2.1 质点的惯性力
ma=F+N
令
F+N-ma=0
称为达朗贝尔惯性力
N
F
FI= - ma
ma
简称为：惯性力
6.2.2 刚体惯性力系的简化
刚体由无数个质点构成，若对每点去施加惯性力其难度则
不难想象。因此，对于刚体的惯性力系，则应设法将其简化。
2、刚体定轴转动
FIi mi ai mi ri
F mi a mi ri
n Ii n i
2
M Ix M x FIi M x FIit M x FIin
mi ri cos i zi (mi ri 2 sin i zi )
一、惯性力系主矢
FIR FIi mi ai
mi FIi
C
ai aC
对于质量不变的质点系：
m a ma
i i
C
所以，惯性力系的主矢为：
FIR m aC
与质点系的运动形式无关！！！
二、惯性力系主矩及简化结果 1、刚体平移
惯性力系向点O简化.
i
FIi
ri C
O
aC
rC
M IO ri FIi ri (mi aC ) ( mi ri ) aC mrC aC M IC 0 惯性力系向质心简化.
只简化为一个力
FIR maC
平移刚体的惯性力系可以简化为通过质心的惯性力， 其大小等于刚体的质量与加速度的乘积，合力的方向与 加速度方向反向。
由
理论力学第6章
6.1 点的合成运动基本概念
z
x
大梁不动时
y
o
动
点？
定参考系？
z
y x
动参考系？ 绝对运动？ 相对运动？
牵连运动？
O
6.1 点的合成运动基本概念
动
点？
定参考系 ？ 动参考系 ？
绝对运动 ？
相对运动 ？
牵连运动 ？
6.1 点的合成运动基本概念
◆ 运动的相对性 ： 物体对于不同的参考系，运动各
va ve v r
注意点： ＊ 牵连运动是刚体(动系)的运动； 牵连速度是动系（刚体）上一 点(该瞬时与动点相重合的点) 的速度。 ＊速度合成定理适用于任何形式的牵连运动，任意的相对运动。 ＊ v a v r v e 为矢量式，符合平行四边形法则，其 对角线为 va
＊矢量
va .vr .ve 满足“6-4=2”即可求两个未知量。
P'1
PP 相对轨迹 2 P 1P 1 牵连点运动轨迹
PP' 绝对位移 PP2 相对位移 P1 P1 牵连点的位移
zP(P1)
A
Dt
A
y
x
O
6.2
点的速度合成定理
B
P2
B
P'
va vr
PP' PP2 va lim v r lim Dt 0 Dt Dt 0 Dt P1 P1 ve lim Dt 0 Dt PP' P1 P1 P1P ' PP' P1 P1 P1P ' lim lim lim Dt 0 Dt Dt 0 Dt Dt 0 Dt
O1
w
O2
j
A
理论力学第六章
2
由 动能定理 FS
由 动 2 mv c 能 4 对t求导，得 C 3 mvC a定 Fv C 理 2 故 Fr J C α
3
v
m
r
C
F
C
F
Cv
S
Cv
即动量矩定理
6-2 质点系动能定理
d LC dt
v
MC
v
6-2-1 动能定理的三种形式 问题 3 图(a)系统由静平衡位置转动 角， 此时，系统势能以静平衡为“0”，
V 1 2 k( l 2
k
) 2 对吗?为什么?
l 2
l 2
对！弹簧静平衡力与重力在转动时仍平衡， 其功之和为零，可同时不考虑。
k
a
又如图(b)所示:
V 1 2
6-2 质点系动能定理
O
m
k
2
b
6-2-2 动能定理的应用 1. 应用特点 (1)与位形变化有关 (突出空间过程) 已知运动求力，由 T W F
FT
WG GS sin
WF 0 ,
N
S
C
WF 0 ,
T
G
C
FS
FN
WF 2 FS S
S
6-1 功与动能
6-1-1 力的功
2.内力的功
一对内力, FA -FB
d W FA drA FB drB
FA drA drB FA drAB
Cv
求 ,v 问题 2均质轮在OA杆上滚动，已知 m,r,l,ω1求Cr 轮 T 。
T 1 2 m vC
2
1 2
JC
2
由 动能定理 FS
由 动 2 mv c 能 4 对t求导，得 C 3 mvC a定 Fv C 理 2 故 Fr J C α
3
v
m
r
C
F
C
F
Cv
S
Cv
即动量矩定理
6-2 质点系动能定理
d LC dt
v
MC
v
6-2-1 动能定理的三种形式 问题 3 图(a)系统由静平衡位置转动 角， 此时，系统势能以静平衡为“0”，
V 1 2 k( l 2
k
) 2 对吗?为什么?
l 2
l 2
对！弹簧静平衡力与重力在转动时仍平衡， 其功之和为零，可同时不考虑。
k
a
又如图(b)所示:
V 1 2
6-2 质点系动能定理
O
m
k
2
b
6-2-2 动能定理的应用 1. 应用特点 (1)与位形变化有关 (突出空间过程) 已知运动求力，由 T W F
FT
WG GS sin
WF 0 ,
N
S
C
WF 0 ,
T
G
C
FS
FN
WF 2 FS S
S
6-1 功与动能
6-1-1 力的功
2.内力的功
一对内力, FA -FB
d W FA drA FB drB
FA drA drB FA drAB
Cv
求 ,v 问题 2均质轮在OA杆上滚动，已知 m,r,l,ω1求Cr 轮 T 。
T 1 2 m vC
2
1 2
JC
2
理论力学课件第6章
lim MM lim MM1 lim M1M
t0 t
t0 t
t0 t
根据点的速度定义，动点 M 在瞬时t 的绝对速度为
va
lim
t 0
MM t
它的方向沿绝对轨迹 MM 的切线。
相对速度
vr
lim
t 0
M1M t
它的方向沿在 M 点处相对轨迹AB 的切线。
牵连速度
ve
lim
t0
MM1 t
同样，它的方向沿曲线 MM1 的切线。 由上述关系，便可得到 va ve vr （6-4）
式（6-4）表示：动点的绝对速度等于动点的牵连速度与相对速度
的矢量和，这就是点的速度合成定理，即动点的绝对速度 va 可由它 的牵连速度 ve 与相对速度vr 构成的平行四边形的对角线来确定，如
图6-3所示。该平行四边形称为速度平行四边形。
度为 ve 。同样由速度合成定理有 va ve vr （b）
现以 aa 表示动点的绝对加速度。根据动点的加速度定义，则动点
的绝对加速度 aa 可写成
aa
lim va va t0 t
（6-5）
将式（a）和式（b）均代入（6-5）式并整理，得到
aa
lim (ve
t 0
vr) (ve t
vr )
本章内容
1 点的合成运动的概念 2 点的速度合成定理
3 牵连运动为平动时点的加速度合成定理 4 牵连运动为定轴转动时点的加速度合成定理
第一节 点的合成运动的概念
引例 图6-1（a）所示的沿直线轨道滚动的车轮，其轮缘上的点 M ， 对于固结在地面上的坐标系来说，其轨迹是旋轮线，但是对于固结在车 厢上的坐标系来说，其轨迹则是一个圆；又如，图6-1（b）所示的等速
理论力学PPT课件第6章 动能定理
碰撞：运动物体在突然受到冲击（包括突然受到约束或 解除约束）时，其运动速度发生急剧变化的现象称为碰撞。
2020年2月10日
36
对接碰撞
2020年2月10日
37
2020年2月10日
38
2020年2月10日
39
2020年2月10日
40
2020年2月10日
？这与碰撞 有关系吗 41
2020年2月10日
47
一、 碰撞的特征和基本假定
1. 碰撞的特征：物体的运动速度或动量在极短的 时间内发生极巨的改变。碰撞时间之短往往以千分 之一秒甚至万分之一秒来度量。因此加速度非常大， 作用力的数值也非常大。
碰撞力（瞬时力）：在碰撞过程中出现的数值 很大的力称为碰撞力；由于其作用时间非常短促， 所以也称为瞬时力。
2R R
2
R2
1 2 kR2
WgA-B W zA zB WR
2020年2月10日
10
4.外力对平面运动刚体的功
dW Fie dri
O ri
ri rc ri
rC
vi vc ω ri
Fn
dri drc d ri
vi
2
3. 柯尼希定理
T
1 2
mvC2
1 2
mi
vi2r
2020年2月10日
15
（1）平移刚体的动能
T
1 2
mvC2
（2）定轴转动刚体的动能
T
1 2
J z 2
（3）平面运动刚体的动能
T＝ 1 2
mvC2
1 2
JC 2
2020年2月10日
36
对接碰撞
2020年2月10日
37
2020年2月10日
38
2020年2月10日
39
2020年2月10日
40
2020年2月10日
？这与碰撞 有关系吗 41
2020年2月10日
47
一、 碰撞的特征和基本假定
1. 碰撞的特征：物体的运动速度或动量在极短的 时间内发生极巨的改变。碰撞时间之短往往以千分 之一秒甚至万分之一秒来度量。因此加速度非常大， 作用力的数值也非常大。
碰撞力（瞬时力）：在碰撞过程中出现的数值 很大的力称为碰撞力；由于其作用时间非常短促， 所以也称为瞬时力。
2R R
2
R2
1 2 kR2
WgA-B W zA zB WR
2020年2月10日
10
4.外力对平面运动刚体的功
dW Fie dri
O ri
ri rc ri
rC
vi vc ω ri
Fn
dri drc d ri
vi
2
3. 柯尼希定理
T
1 2
mvC2
1 2
mi
vi2r
2020年2月10日
15
（1）平移刚体的动能
T
1 2
mvC2
（2）定轴转动刚体的动能
T
1 2
J z 2
（3）平面运动刚体的动能
T＝ 1 2
mvC2
1 2
JC 2
理论力学第六章点的运动学.
d d ds an v v dt ds dt
又 d 1 n dS
an
v2
n an
v2
an是一个沿主法线正方向 的矢量，指向曲率中心 。
法向加速度反映点的速度方向改变的快慢程度。
dv v2 a a a n a a n n n dt
— 与 弧 坐 标 的 正 向 一 致 n — 指 向 曲 线 内 凹 一 侧 b — 与 , n 构 成 右 手 系
b n
[注]：自然坐标系是沿曲 13 线而变动的游动坐标系。
6-3 自然法 3、曲率 (1 / ) ：
定义——曲线切线的转角对弧长 一阶导数的绝对值。表示曲线的 弯曲程度。
一.运动方程、轨迹
矢径是点的单值连续函数，
r xi yj zk
故x,y,z也是时间的单值函数：
x f1 (t ), y f 2 ( t ), z f 3 ( t )
——以直角坐标表示的点的运动方程 上式消去t,即为点的轨迹方程：f ( x , y , z ) 0
6
6-2 直角坐标法
当点M运动时，矢径r随时间而 变化，并且是时间的单值函数：
r r t
—以矢量表示的 点的运动方程
矢端曲线：动点M在运动过程中，矢 径r的末端绘出的一条连续曲线。 ——动点M的运动轨迹
二.点的速度
dr v r dt
方向：沿着矢径r的矢端曲线的切线 方向，且与此点的运动方向一致。
大小：速度矢的模，表明点运动的快慢。
t dv k dt v0 v 0 v ln kt , v v0 e kt v0 v
dx 3、 由 v v0e kt dt
又 d 1 n dS
an
v2
n an
v2
an是一个沿主法线正方向 的矢量，指向曲率中心 。
法向加速度反映点的速度方向改变的快慢程度。
dv v2 a a a n a a n n n dt
— 与 弧 坐 标 的 正 向 一 致 n — 指 向 曲 线 内 凹 一 侧 b — 与 , n 构 成 右 手 系
b n
[注]：自然坐标系是沿曲 13 线而变动的游动坐标系。
6-3 自然法 3、曲率 (1 / ) ：
定义——曲线切线的转角对弧长 一阶导数的绝对值。表示曲线的 弯曲程度。
一.运动方程、轨迹
矢径是点的单值连续函数，
r xi yj zk
故x,y,z也是时间的单值函数：
x f1 (t ), y f 2 ( t ), z f 3 ( t )
——以直角坐标表示的点的运动方程 上式消去t,即为点的轨迹方程：f ( x , y , z ) 0
6
6-2 直角坐标法
当点M运动时，矢径r随时间而 变化，并且是时间的单值函数：
r r t
—以矢量表示的 点的运动方程
矢端曲线：动点M在运动过程中，矢 径r的末端绘出的一条连续曲线。 ——动点M的运动轨迹
二.点的速度
dr v r dt
方向：沿着矢径r的矢端曲线的切线 方向，且与此点的运动方向一致。
大小：速度矢的模，表明点运动的快慢。
t dv k dt v0 v 0 v ln kt , v v0 e kt v0 v
dx 3、 由 v v0e kt dt
理论力学第六章 平衡方程及其应用
第六章 平衡方程及其应用 >> 力偶系的平衡
§6-2 力偶系的平衡 一、平面力偶系的平衡方程 平面力偶系平衡的必要和充分条件是：所有各力偶矩的代数和 等于零，即 M i 0 . 二、空间力偶系的平衡方程
由于空间力偶系可以用一个合力偶来代替，因此，空间力偶系
平衡的必要和充分条件是：该力偶系的合力偶矩等于零，亦即
要使这个刚体平衡，需加一力偶，其力偶矩矢为 -M。
第六章 平衡方程及其应用
§6-3 一般力系的平衡 一、平面一般力系的平衡方程 1. 平面一般力系平衡方程的基本形式
0 MO 0 FR
F
x
0
F
y
0
M
O
(F ) 0
2. 平面一般力系平衡方程的其他形式
（1）二矩式平衡方程
M
FA FB
第六章 平衡方程及其应用 >> 力偶系的平衡 例题6-4 图示（a）所示的三角柱刚体是正方体的一半。在其中三个侧面 各自作用一个力偶。已知力偶（ F1，F1 ）的矩 M 1 20N m ；力偶 （ F2，F2 ）的矩 M 2 20N m ；力偶（ F ，F ）的矩 M 3 20N m 。试 3 3 求合力偶矩矢M。又问使这个刚体平衡，还需要施加怎样一个力偶。
解：根据空间力偶系合成法，先求出力偶
矩矢M。根据三个力偶在空间的作用面不 同，考虑到力偶矩矢是自由矢量，可将力
偶矩矢画在坐标轴上（图 b）。和力偶矩
矢M在三个坐标轴上的投影为
第六章 平衡方程及其应用 >> 力偶系的平衡
M x M 1x M 2 x M 3 x 0
M y M1y M 2 y M 3 y (10 30cos45)N m 11.2 N m
理论力学：第6章 点的合成运动
·1·第6章 点的合成运动6.1 主要内容6.1.1 点的绝对运动、相对运动和牵连运动1．定系和动系若存在两个有相对运动的坐标系，则可指定其中一个为定系，另一个即为动系。
但工程上一般以固定在地面上的坐标系为定系，相对于定系运动着的坐标系称为动系。
2．动点和牵连点动点为研究的对象，牵连点是动点在动系上的重合点，随动点的相对运动而变，是动系上的点，不同瞬时，有不同的牵连点。
3．三种运动的关系动点相对于定系的运动定义为绝对运动；动点相对于动系的运动定义为相对运动；动系相对于定系的运动定义为牵连运动。
本章的主要任务就是建立这三者之间的定量关系，从而用来解决工程实际某些运动分析问题。
6.1.2 点的速度合成定理动点的绝对速度等于它的牵连速度与相对速度的矢量和。
这就是点的速度合成定理。
a e r =+v v v6.1.3 牵连运动为平移时，点的加速度合成定理当牵连运动为平移时，动点的绝对加速度等于牵连加速度与相对加速度的矢量和。
a e r =+a a a6.1.4 牵连运动为转动时，点的加速度合成定理当牵连运动为转动时，动点的绝对加速度等于牵连加速度、相对加速度与科氏加速度的矢量和，这就是牵连运动为转动时点的加速度合成定理。
a e r C =++a a a a其中r C v a ⨯=ω2。
当取平动动系时0=e ω；0=C a 。
6.2 基本要求1．掌握运动合成与分解的基本概念和方法，准确理解本章阐述的若干概念。
2．明确动点与动系的选择原则，能在具体问题中恰当地选择动点与动系，并正确地分析三种运动。
3．熟练掌握点的速度合成定理和牵连运动为平动时的加速度合成定理及其应用。
4．掌握科氏加速度的概念和计算，准确应用牵连运动为转动时的加速度合成定理及其应用。
6.3 重点讨论应用点的合成运动理论解决实际问题时，其关键是正确地选择动点和动系。
选择原则因具体情况不同而略有区别。
常见的问题有三种题型。
1．两个独立运动的物体，研究两者的相对运动。
理论力学第六章
vA vC vD vCA
y
(C)
式中三个未知量，不可解。
C
v
D
vA
B
( 大小 √ (v ) √ (OA ) ？AC AB ) ？ 方向 √ () √ ( OA) √ ( AB) √ (↖) 选取坐标系Cxy，向y x 轴上投影，得
va
ve vC vA vCA
vr
AO杆作定轴转动， AB杆和BC杆作平面运动。
C
v A r
A、B、C点速度方向如图：
vC
B
60
vA
0
O
P点为AB杆瞬心 v A r AB AP 3r 3
其转向为逆时针
vB
A
vB BP AB
3 6r 3r 2 3
P
Q点为BC杆瞬心
va sin 45 vAcos45 vCA
vCA 5 2cm / s 所得为正，说明图中所 设的指向与实际相符 vD vCA vCA AB 0.5rad / s AC 10 2
vA
O
vC
(C)
C
v
D
vCA vA
B
y
例： 如图所示机构中，已知：轮I固定，轮Ⅱ作纯滚动， 其匀角速度为，O1C=L， O1A=3L /4，两轮半径均为r。 试求图示瞬时vA ， AB和 AB.。
vA
零的点称为平面图形在 该瞬时的速度瞬心。
v A AP v A AP vB BP vB BP vC CP vC CP
2、瞬心的求法
（1）当平面图形沿某固定面作纯滚动时，图形上 与固定面的接触点即为图形的瞬心。
《理论力学》06章共75页文档
M x M i x M 3 M 4 c 4 o M 5 5 c s4 o 5 1 s . 1 N 9 m M y M iy M 2 8N 0 m M z M i z M 1 M 4 c 4 o M 5 5 c s4 o 5 1 s . 1 N 9 m
m O (F)
m O (F) 17
例3
已知：手柄ABCD在平面AXY内，
在D处作用一个力 F,l,a,
求：M x F ,M y F ,M zF
解：把力 F 分解如图
M x F F l a cos
M yF Fc lo s
M z F F l a sin
因
力偶矩矢
4.只要保持力偶矩矢不变，力偶可在其作用面内任 意移转，且可以同时改变力偶中力的大小与力偶臂 的长短，对刚体的作用效果不变。
=
=
=
M (F 1 ,F 1 )r B A F 1
5.只要保持力偶矩矢不变，力偶可从其所在平 面移至另一与此平面平行的任一平面，对刚体 的作用效果不变。
(1）大小: 力F与力臂h的乘积，即Fh (2)方向:转动方向 (3)作用面方位：力矩作用面法线方位。
1、矢量积表示式
2、解析表示式
i jk
x y z(yzF zy F )i(zx F xzF )j(xyF yxF )k
F x F y F z
力对点O的矩
在
三个坐标轴上的投影为
[M 0F]xyzF zy F
[M 0F]yzx F xzF
[M 0F]zxy F yxF
3、合力矩定理
理论力学第6章
当刚体绕定轴转动时，刚体内任意一点都作圆 周运动，圆心在轴线上，圆周所在的平面与轴线垂 直，圆周的半径R等于该点到轴线的垂直距离。
设刚体由定平面A绕定轴O转动任一角度j，到达B 位置，其上任一点由O'运动到M。以固定点O'为弧坐 标s的原点，按j角的正向规定弧坐标s的正向，于是
s Rj
动点速度的大小为
当刚体转动时，角j是时间t的单值连续函数，即
j f (t )
这就是刚体绕定轴转动的运动方程。 转角 j 对时间的一阶导数，称为刚体的瞬时角速度， 用w表示: dj w j dt 角速度表征刚体转动的快慢和方向，其单位用rad/s (弧度/秒)表示。 角速度是代数量，从轴的正端向负端看，刚体逆时针 转动时角速度取正值，反之取负值。
ds dj v R Rw dt dt
即：转动刚体内任一点速度的大小等于刚体角速度与 该点到轴线的垂直距离的乘积，它的方向沿圆周的切 线而指向转动的一方。
v Rw
点M的加速度有切向加速度和法向加速度，切向 加速度为：
dv d dw a ( Rw ) R Ra dt dt dt
(1) 在每一瞬时，转动刚体内所有各点的速度和加速 度的大小，分别与这些点到轴线的垂直距离成正比。
(2) 在每一瞬时，刚体内所有各点的加速度a与半径间 的夹角q 都有相同的值。
例 一半径为R=0.2m的圆轮绕定轴O的转动方程 为 j t 2 4t ，单位为弧度。求t=1s时，轮缘上任一点M的 速度和加速度（如图）。如在此轮缘上绕一柔软而不可伸长 的绳子并在绳端悬一物体A，求当t=1s时，物体A的速度和加 速度。 a M v an 解：圆轮在任一瞬时的角速度和角加速度为 R
如果w与a同号，角速度的绝对值增加，刚体作加 速转动，这时点的切向加速度at与速度v的指向相同； 如果w与a异号，刚体作减速转动， at与v的指向相反。 这两种情况如图所示
设刚体由定平面A绕定轴O转动任一角度j，到达B 位置，其上任一点由O'运动到M。以固定点O'为弧坐 标s的原点，按j角的正向规定弧坐标s的正向，于是
s Rj
动点速度的大小为
当刚体转动时，角j是时间t的单值连续函数，即
j f (t )
这就是刚体绕定轴转动的运动方程。 转角 j 对时间的一阶导数，称为刚体的瞬时角速度， 用w表示: dj w j dt 角速度表征刚体转动的快慢和方向，其单位用rad/s (弧度/秒)表示。 角速度是代数量，从轴的正端向负端看，刚体逆时针 转动时角速度取正值，反之取负值。
ds dj v R Rw dt dt
即：转动刚体内任一点速度的大小等于刚体角速度与 该点到轴线的垂直距离的乘积，它的方向沿圆周的切 线而指向转动的一方。
v Rw
点M的加速度有切向加速度和法向加速度，切向 加速度为：
dv d dw a ( Rw ) R Ra dt dt dt
(1) 在每一瞬时，转动刚体内所有各点的速度和加速 度的大小，分别与这些点到轴线的垂直距离成正比。
(2) 在每一瞬时，刚体内所有各点的加速度a与半径间 的夹角q 都有相同的值。
例 一半径为R=0.2m的圆轮绕定轴O的转动方程 为 j t 2 4t ，单位为弧度。求t=1s时，轮缘上任一点M的 速度和加速度（如图）。如在此轮缘上绕一柔软而不可伸长 的绳子并在绳端悬一物体A，求当t=1s时，物体A的速度和加 速度。 a M v an 解：圆轮在任一瞬时的角速度和角加速度为 R
如果w与a同号，角速度的绝对值增加，刚体作加 速转动，这时点的切向加速度at与速度v的指向相同； 如果w与a异号，刚体作减速转动， at与v的指向相反。 这两种情况如图所示
理论力学---第六章
加速度 速度矢端曲线切线
2.直角坐标法
•运动方程
z
k
M ( x, y , z )
x f1 t y f 2 t z f 3 t
r
j
z
x
y
O i
x
轨迹方程
y
f ( x, y, z ) 0
速度
v r xi yj zk
第六章
运动学基础
§6-1 机构运动简图 §6-2 点的运动 §6-3 刚体基本运动
§6-1 机构运动简图 构件与运动副
固定件 支承运动构件的构件 组成机构的各 相对运动实体 – 构件 主动件 驱动力作用的构件 从动件 随主动件运动而运动的构件
机构必须有一个固定件，至少有一个主动件
构件与运动副
高副—通过点、线接触 两构件组成有确定 —运动副 移动副 相对运动的可动联接 低副—通过面接触 转动副
3.弧坐标法
(1)运动方程(沿轨迹的运动规律) (+)
s f (t )
S称为弧坐标
O
(-)
M
s
★自然法适用于描述非自由质点运动
（2）自然轴系
切向单位矢量
主法线单位矢量 副法线单位矢量 •密切面
n
b n
当点M1逐渐趋近于点M时，M1点的切线平移后和M点 的切线所确定的平面趋近于一个极限位置，此极限 位置的平面称为曲线在M点的密切面 。
an a a g cos
2 2
2 2 v0 v0 得 a g cos n
例6-4
列车沿半径为R=800m的圆弧轨道作
匀加速运动。如初速度为零，经过2min后，速度
理论力学第6章 ppt课件
25
作业
• 6-4 • 6-6
ppt课件
26
第六章 点的运动学
• §6-1 矢量法和直角坐标法
• 1. 表示质点运动的矢量法：
• 质点的空间位置用矢径r表示，它是时间的 函数，
•
r = r(t)
• 投影式： r = xi+yj+zk
• 轨迹：矢径r 端点的连线。
ppt课件
1
• 速度：
v dr lim r(t t) r(t)
a dv dt
• 动点移动时，速度大小和方向都发生改变。
a
dv dt
d dt
( ds dt
τ)
d 2s dt 2
τ
ds dt
dτ dt
ppt课件
15
• 切向加速度
at
d 2s dt 2
τ
dv dt
τ
• 法向加速度
an
ds dt
dτ dt
v
dτ dt
dτ dτ ds 1 vn
vy y r sin t
v
vx2
v
2 y
r (1 cost)2 sin2 t
2r sin t
2
ppt课件
19
• 求M点的曲线位移： • 方法1
v ds dt
s
vdt
2r
t
0
sin
t
2
dt
4r (1
cos
t
2
)
ppt课件
20
• 求M点的曲线位移：
理论力学第6章-点的运动
t0 t S j
当t→0时，t 与t′的夹角趋近于直角，即t 趋近
于轨迹在点M的法线，指向曲率中心。若记法线法线的
单位矢量为n，规定它指向曲率中心，则有
密切面：
dt v n dt
副法线
b
M
t
T
切线
n
过点M作 MT 的平行线 MT1 ，
MT和MT1可以确定一个平面。当点 无限趋近点M时，则此平面趋近某
4
49sin2 wt cos2 wt
O
加速度在x轴，y轴上的投影
j
yC
xC
C x
B
ax
=
dvx dt
7Lw2
4
cos wt
w 2 xC
C点的加速度的大小
ay
=
dvy dt
Lw2
4
sin wt
w2 yC
a ax2 ay2 w2
加速度的方向余弦
cos(a, i) ax xC ar
xC2 yC2 w2r
例6-6 曲柄OA绕O轴逆时针方向转动。其转过j角与时间t
的关系为
j
t
4
，若OA=10cm，OO1 =10cm，O1B=24cm，试求
B点运动方程、速度和加速度。
解：建立弧坐标
运动方程 速度 加速度
S O1B 12j 3πt
v dS 3π 9.42 cm/s dt d2S
at dt2 0
v vxi vy j vzk
速度v在三个轴上的投影
vx
=
dx dt
x(t)
vy
=
dy dt
y(t)
vz
=
dz dt
z(t)
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
dt dt2
角加速度表征角速度变化的快慢
代数量：当 ω与 α同号时，转动为加速； 当 与 ω同号α时，转动为减速
匀速转动 ω =常量
匀变速转动
d 0
dt
0 t
α =常量
ω ω0 αt
0
ω0t
1 2
αt
§ 6-3 转动刚体内各点的速度和加速度
转动刚体上任一点作圆周运动（轨迹已知）， 用自然法 点的运动方程
大小： rsin R v
方向： 右手定则
绕定轴转动的刚体上任一 点的速度矢量等于刚体的角 速度矢量与该点矢径的矢量 积
加速度
ar dvr d r rr
ddtr
dt
rr r
drr
dt
dt
r rr r vr
α r α r sin θ ω v ω v
α R
ω 2 R
处于啮合中的两个定轴齿轮的 角速度与两齿轮的齿数成反比（或 与两轮的啮合圆半径成反比）
内啮合
i12
1 2
R2 R1
z2 z1
大轮带动小轮
z1 z2
1 2
i12 1
加速
小轮带动大轮
减速
外啮合 内啮合
2.带轮传动
① 啮合条件
r11 vA vA vB vB r22
② 传动比
齿轮做定轴转动 送料机的杆
运动方程
转角： 单位:弧度(rad)
代数量：逆时针“ + ”， 顺时针“ - ”
f t
刚体绕定轴转动的运动方程
具有一个自由度
角速度和角加速度
角速度： ω d
dt
单位：rad/s
角速度表征刚体转动的快慢和方向
代数量：刚体逆时针转动时为正
角加速度： d d2 & && 单位：rad/s2
方向：tanθ
at an
Rα Rω2
α ω2
v Rω
αR
α2 ω4
tanθ
α ω2
结论： 1.在每一瞬时，转动刚体内所有各点的速度和加 速度的大小，分别与这些点到轴线的垂直距离成 正比。 2.在每一瞬时，刚体内所有各点的加速度与半径 间的夹角都有相同的值。
[例]半径R=0.2m的圆轮绕定轴O的转 动方程 t 2 4t，单位为弧度。求 t=1s时，轮缘上任一点M的速度和加速 度。如在此轮缘上绕一柔软而不可伸长 的绳子并在绳端悬一物体A，求当t=1s 时，物体A的速度和加速度。 解：圆轮在任一瞬时的角速度和角加速度为
r vA
r aB
r dvB dt
r dvA dt
r aA
平动刚体上各点具有相同的速度和加速度
刚体平移→点的运动
刚体平移→点的运动
只要知道其上一点的运动规律、轨迹、速度、加 速度，其他点都相同
例如：
B
A AB杆作平动，A点和B点 运动规律完全相同。
§ 6-2 刚体绕定轴的转动
定义 刚体上(或其扩展部分)两点保持不动，则这种运 动称为刚体绕定轴转动，简称刚体的转动。 特点：转轴是一根固定不动的直线，凡是不在转轴 上的点都在垂直于轴的平面内做圆周运动。圆心位 于转轴上。
角速度矢量和角加速度矢量
角速度矢量
大小：
d
dt
作用线：沿轴线滑动矢量
指向：右手螺旋定则
r
r
k
角加速度矢量
r
dr
d
r k
r
k
dt dt
1.角速度矢量和角加速度 矢量均为滑动矢量。 2.当二者方向相同时，刚 体越转越快；当二者方向 相反时，刚体越转越慢。
绕定轴转动刚体上点的速度和加速度
速度：v r
第六章 刚体的简单运动
第六章 刚体的简单运动
§ 6-1 刚体的平行移动 § 6-2 刚体绕定轴的转动 § 6-3 转动刚体内各点的速度和加速度 § 6-4 轮系的传动比 § 6-5 以矢量表示角运动和角加速度
以矢积表示点的速度和角加速度
目标要求
⑴ 掌握平行移动刚体和定轴转动刚体的运动特 征。
⑵ 正确分析定轴转动刚体的转动方程、角速度 和角加速度及转动刚体内各点的速度和加速度。
ar r rr r vr d rr r vr
dt
15 2
π
75
3
r i
200
r j
r 75k
• 作业： • 习题 6-4 6-6
[例]车细螺纹时，如果车床主轴的转速 n0 300 r/min , 要求主轴在转两圈后立即停车以便很快反转。设停车 过程是匀变速转动，求停车过程中主轴的角加速度。 解：停车前，已知转速，可以求角速度。
⑶ 初步了解用矢积表示点的速度和加速度。
§ 6-1 刚体的平行移动
定义
刚体内任一直线在运动过程中始终平行于初始 位置，这种运动称为平行移动，简称平移。
运动方程 rA rB BA
平动刚体上任意点具有相同的轨迹
速度和加速度
因为 所以
uuur
d AB
0
dt
r vB
r drB dt
r drA dt
a at an
at r —— M点切向加速度 an v ( r) —— M点法向加速度
例6-1
已知：刚体绕定5 sin
πt
r i
5cos
πt
r j
5
3kr。
2
2
求：t =1s时,刚体上点M（0，2，3）的速度矢及
加速度矢。
解：
rrr 10 3i 15 j 10k
s R
速度
v s& R& R
方向：沿圆周的切线而 指向转动的一方
加速度
切向加速度：
at
dv dt
s
Rα
方向：沿切向方向，指向由角加速度的符号决定
法向加速度：an
v2 ρ
1 Rω2
R
Rω2
方向：与速度垂直并指向轴线
加速转动
减速转动
全加速度：α αt2 αn2 R2α2 R2ω4 R α2 ω4
因此轮缘上任一点M的速度和加速度为
因为 上式两边求一阶及二阶导数，则得
因此
§ 6-4 轮系的传动比
1.齿轮传动
外啮合
内啮合
① 啮合条件
R11 vA vB R22
② 传动比
i12
1 2
R2 R1
z2 z1
正号：主动轮与从动轮转向相同 （内啮合）； 负号：转向相反（外啮合）
外啮合
主轴转两圈 主轴转动两圈后停止
负号表示 的转向与主轴转动方向相反，故为减速运动。
例6-3
一矢量 绕a z轴以角速度 ω转动，若 的a大小始终保持不变 求：da
dt
解： 将矢量的端点A看成是绕z轴作定轴转动刚体上的一点 rA a
从而
da dt
drA dt
vA
ω rA
ω
a
i12
1 2
r2 r1
两轮的角速度与其半径成反比
[例]下图是一减速箱，它由四个齿轮组成，其齿 数分别为Z1=10，Z2=60，Z3=12，Z4=70。(a)求减 速箱的总传动比i13；(b)如果n1=3000r/min，求n3。
解：求传动比： 则有：
§ 6-5 以矢量表示角速度和角加速度 以矢积表示点的速度和加速度
角加速度表征角速度变化的快慢
代数量：当 ω与 α同号时，转动为加速； 当 与 ω同号α时，转动为减速
匀速转动 ω =常量
匀变速转动
d 0
dt
0 t
α =常量
ω ω0 αt
0
ω0t
1 2
αt
§ 6-3 转动刚体内各点的速度和加速度
转动刚体上任一点作圆周运动（轨迹已知）， 用自然法 点的运动方程
大小： rsin R v
方向： 右手定则
绕定轴转动的刚体上任一 点的速度矢量等于刚体的角 速度矢量与该点矢径的矢量 积
加速度
ar dvr d r rr
ddtr
dt
rr r
drr
dt
dt
r rr r vr
α r α r sin θ ω v ω v
α R
ω 2 R
处于啮合中的两个定轴齿轮的 角速度与两齿轮的齿数成反比（或 与两轮的啮合圆半径成反比）
内啮合
i12
1 2
R2 R1
z2 z1
大轮带动小轮
z1 z2
1 2
i12 1
加速
小轮带动大轮
减速
外啮合 内啮合
2.带轮传动
① 啮合条件
r11 vA vA vB vB r22
② 传动比
齿轮做定轴转动 送料机的杆
运动方程
转角： 单位:弧度(rad)
代数量：逆时针“ + ”， 顺时针“ - ”
f t
刚体绕定轴转动的运动方程
具有一个自由度
角速度和角加速度
角速度： ω d
dt
单位：rad/s
角速度表征刚体转动的快慢和方向
代数量：刚体逆时针转动时为正
角加速度： d d2 & && 单位：rad/s2
方向：tanθ
at an
Rα Rω2
α ω2
v Rω
αR
α2 ω4
tanθ
α ω2
结论： 1.在每一瞬时，转动刚体内所有各点的速度和加 速度的大小，分别与这些点到轴线的垂直距离成 正比。 2.在每一瞬时，刚体内所有各点的加速度与半径 间的夹角都有相同的值。
[例]半径R=0.2m的圆轮绕定轴O的转 动方程 t 2 4t，单位为弧度。求 t=1s时，轮缘上任一点M的速度和加速 度。如在此轮缘上绕一柔软而不可伸长 的绳子并在绳端悬一物体A，求当t=1s 时，物体A的速度和加速度。 解：圆轮在任一瞬时的角速度和角加速度为
r vA
r aB
r dvB dt
r dvA dt
r aA
平动刚体上各点具有相同的速度和加速度
刚体平移→点的运动
刚体平移→点的运动
只要知道其上一点的运动规律、轨迹、速度、加 速度，其他点都相同
例如：
B
A AB杆作平动，A点和B点 运动规律完全相同。
§ 6-2 刚体绕定轴的转动
定义 刚体上(或其扩展部分)两点保持不动，则这种运 动称为刚体绕定轴转动，简称刚体的转动。 特点：转轴是一根固定不动的直线，凡是不在转轴 上的点都在垂直于轴的平面内做圆周运动。圆心位 于转轴上。
角速度矢量和角加速度矢量
角速度矢量
大小：
d
dt
作用线：沿轴线滑动矢量
指向：右手螺旋定则
r
r
k
角加速度矢量
r
dr
d
r k
r
k
dt dt
1.角速度矢量和角加速度 矢量均为滑动矢量。 2.当二者方向相同时，刚 体越转越快；当二者方向 相反时，刚体越转越慢。
绕定轴转动刚体上点的速度和加速度
速度：v r
第六章 刚体的简单运动
第六章 刚体的简单运动
§ 6-1 刚体的平行移动 § 6-2 刚体绕定轴的转动 § 6-3 转动刚体内各点的速度和加速度 § 6-4 轮系的传动比 § 6-5 以矢量表示角运动和角加速度
以矢积表示点的速度和角加速度
目标要求
⑴ 掌握平行移动刚体和定轴转动刚体的运动特 征。
⑵ 正确分析定轴转动刚体的转动方程、角速度 和角加速度及转动刚体内各点的速度和加速度。
ar r rr r vr d rr r vr
dt
15 2
π
75
3
r i
200
r j
r 75k
• 作业： • 习题 6-4 6-6
[例]车细螺纹时，如果车床主轴的转速 n0 300 r/min , 要求主轴在转两圈后立即停车以便很快反转。设停车 过程是匀变速转动，求停车过程中主轴的角加速度。 解：停车前，已知转速，可以求角速度。
⑶ 初步了解用矢积表示点的速度和加速度。
§ 6-1 刚体的平行移动
定义
刚体内任一直线在运动过程中始终平行于初始 位置，这种运动称为平行移动，简称平移。
运动方程 rA rB BA
平动刚体上任意点具有相同的轨迹
速度和加速度
因为 所以
uuur
d AB
0
dt
r vB
r drB dt
r drA dt
a at an
at r —— M点切向加速度 an v ( r) —— M点法向加速度
例6-1
已知：刚体绕定5 sin
πt
r i
5cos
πt
r j
5
3kr。
2
2
求：t =1s时,刚体上点M（0，2，3）的速度矢及
加速度矢。
解：
rrr 10 3i 15 j 10k
s R
速度
v s& R& R
方向：沿圆周的切线而 指向转动的一方
加速度
切向加速度：
at
dv dt
s
Rα
方向：沿切向方向，指向由角加速度的符号决定
法向加速度：an
v2 ρ
1 Rω2
R
Rω2
方向：与速度垂直并指向轴线
加速转动
减速转动
全加速度：α αt2 αn2 R2α2 R2ω4 R α2 ω4
因此轮缘上任一点M的速度和加速度为
因为 上式两边求一阶及二阶导数，则得
因此
§ 6-4 轮系的传动比
1.齿轮传动
外啮合
内啮合
① 啮合条件
R11 vA vB R22
② 传动比
i12
1 2
R2 R1
z2 z1
正号：主动轮与从动轮转向相同 （内啮合）； 负号：转向相反（外啮合）
外啮合
主轴转两圈 主轴转动两圈后停止
负号表示 的转向与主轴转动方向相反，故为减速运动。
例6-3
一矢量 绕a z轴以角速度 ω转动，若 的a大小始终保持不变 求：da
dt
解： 将矢量的端点A看成是绕z轴作定轴转动刚体上的一点 rA a
从而
da dt
drA dt
vA
ω rA
ω
a
i12
1 2
r2 r1
两轮的角速度与其半径成反比
[例]下图是一减速箱，它由四个齿轮组成，其齿 数分别为Z1=10，Z2=60，Z3=12，Z4=70。(a)求减 速箱的总传动比i13；(b)如果n1=3000r/min，求n3。
解：求传动比： 则有：
§ 6-5 以矢量表示角速度和角加速度 以矢积表示点的速度和加速度