理论力学 第六章作业答案
理论力学简明教程第六章答案

第六章 分析力学滔滔长江东逝水,浪花淘尽英雄。
达朗贝尔,拉格朗日,哈密顿等许多前贤相聚于此“力学论剑”,其“冲击波”使非线性问题也不攻自破。
长江后浪推前浪,你或许在此能够加倍“忘乎因此‘。
微分方程将叱咤风云。
[要点分析与总结]1虚功原理:(平稳时)理想条件下,力学系的平稳条件是各质 点上的主动力所作的虚功之和为零:10ni i i W F r δδ==•=∑用广义坐标来表述:310n ii i x W F q q ααδδ=∂==∂∑ 2达朗贝尔原理(动力学下的虚功原理): 1()0ni i i i i W F m r r δδ==-•=∑〈析〉r δ,W δ均是在时刻未转变(0dt =)时所假想的量,而广义坐标a q 能够是角度,长度或其它的独立的坐标变量。
3拉格朗日方程()d T TQ dt q q ααα∂∂-=∂∂ (1,2,3,,)a s =在保守力下,取拉氏数 L T V =-方程为:()0d L L dt q q αα∂∂-=∂∂ 假设拉氏数中L 不显含广义坐标q β,那么:0Lq β∂=∂ 即 循环积分: Lp const q ββ∂==∂ 4微振动非线性系统在小角度近似下,对拉氏方程的应用 5哈密顿函数与正那么方程 (1) 哈密顿函数1(,,)sH p q t L p q ααα==-+∑式中T Lp q q ααα∂∂==∂∂为广义坐标动量 (2) 正那么方程Hq P Hp q H Lt tαααα∂=∂∂=-∂∂∂=-∂∂ (1,2,3,,)a s =假设哈氏函数H 中不显含广义坐标q β,那么:0Hp q ββ∂=-=∂ 即:循环积分 Tp const q ββ∂==∂ 在稳固条件下(H 中不显含t ),12sp q T ααα==∑那么有能量积分:H T V =+6泊松括号1[,]()sG H G HG H q p p q ααααα=∂∂∂∂=-∂∂∂∂∑ 7哈密顿原理与正那么变换 (1)哈密顿原理保守力系下:210t t Ldt δ=⎰概念:21t t S Ldt =⎰为主函数(3) 正那么变换通过某种变数的变换,找到新的函数*H ,使正那么方程的形式不变(相当于坐标变换)。
理论力学课后习题答案-第6章--刚体的平面运动分析
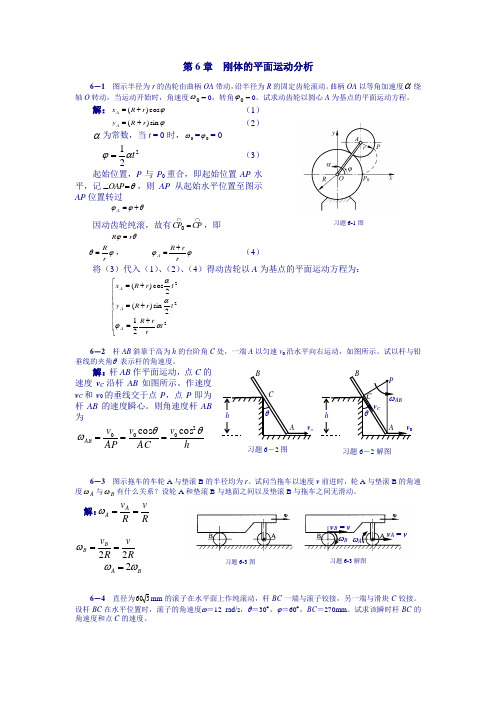
第6章 刚体的平面运动分析6-1 图示半径为r 的齿轮由曲柄OA 带动,沿半径为R 的固定齿轮滚动。
曲柄OA 以等角加速度α绕轴O 转动,当运动开始时,角速度0ω= 0,转角0ϕ= 0。
试求动齿轮以圆心A 为基点的平面运动方程。
解:ϕcos )(r R x A += (1) ϕsin )(r R y A +=(2)α为常数,当t = 0时,0ω=0ϕ= 0 221t αϕ=(3)起始位置,P 与P 0重合,即起始位置AP 水平,记θ=∠OAP ,则AP 从起始水平位置至图示AP 位置转过θϕϕ+=A因动齿轮纯滚,故有⋂⋂=CP CP 0,即 θϕr R = ϕθr R =, ϕϕrr R A += (4)将(3)代入(1)、(2)、(4)得动齿轮以A 为基点的平面运动方程为:⎪⎪⎪⎩⎪⎪⎪⎨⎧+=+=+=222212sin )(2cos )(t r r R t r R y t r R x A A A αϕαα6-2 杆AB 斜靠于高为h 的台阶角C 处,一端A 以匀速v 0沿水平向右运动,如图所示。
试以杆与铅垂线的夹角θ 表示杆的角速度。
解:杆AB 作平面运动,点C 的速度v C 沿杆AB 如图所示。
作速度v C 和v 0的垂线交于点P ,点P 即为杆AB 的速度瞬心。
则角速度杆AB 为6-3 图示拖车的车轮A 与垫滚B 的半径均为r 。
试问当拖车以速度v 前进时,轮A 与垫滚B 的角速度A ω与B ω有什么关系?设轮A 和垫滚B 与地面之间以及垫滚B 与拖车之间无滑动。
解:RvR v A A ==ωR v R v B B 22==ωB A ωω2=6-4 直径为360mm 的滚子在水平面上作纯滚动,杆BC 一端与滚子铰接,另一端与滑块C 铰接。
设杆BC 在水平位置时,滚子的角速度ω=12 rad/s ,θ=30︒,ϕ=60︒,BC =270mm 。
试求该瞬时杆BC 的角速度和点C 的速度。
hv AC v AP v ABθθω2000cos cos ===习题6-1图ABCv 0hθ习题6-2图PωABv CABCv ohθ习题6-2解图习题6-3解图习题6-3图v A = vv B = v ωAωB习题6-6图习题6-6解图解:杆BC 的瞬心在点P ,滚子O 的瞬心在点D BDv B ⋅=ωBPBD BP v B BC ⋅==ωω ︒︒⨯=30sin 27030cos 36012 rad/s 8=PC v BC C ⋅=ωm/s 87.130cos 27.08=︒⨯=6-5 在下列机构中,那些构件做平面运动,画出它们图示位置的速度瞬心。
理论力学习题答案

理论力学习题答案(总26页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--2第一章 静力学公理和物体的受力分析一、是非判断题在任何情况下,体内任意两点距离保持不变的物体称为刚体。
( ∨ ) 物体在两个力作用下平衡的必要与充分条件是这两个力大小相等、方向相反,沿同一直线。
( × ) 加减平衡力系公理不但适用于刚体,而且也适用于变形体。
( × ) 力的可传性只适用于刚体,不适用于变形体。
( ∨ ) 两点受力的构件都是二力杆。
( × ) 只要作用于刚体上的三个力汇交于一点,该刚体一定平衡。
( × ) 力的平行四边形法则只适用于刚体。
( × ) 凡矢量都可以应用平行四边形法则合成。
( ∨ ) 只要物体平衡,都能应用加减平衡力系公理。
( × ) 凡是平衡力系,它的作用效果都等于零。
( × ) 合力总是比分力大。
( × ) 只要两个力大小相等,方向相同,则它们对物体的作用效果相同。
( × )若物体相对于地面保持静止或匀速直线运动状态,则物体处于平衡。
( ∨ )当软绳受两个等值反向的压力时,可以平衡。
( × )静力学公理中,二力平衡公理和加减平衡力系公理适用于刚体。
( ∨ )静力学公理中,作用力与反作用力公理和力的平行四边形公理适用于任何物体。
( ∨ )凡是两端用铰链连接的直杆都是二力杆。
( × )如图所示三铰拱,受力F ,F 1作用,其中F 作用于铰C 的销子上,则AC 、BC 构件都不是二力构件。
( × )图3二、填空题力对物体的作用效应一般分为 外 效应和 内 效应。
对非自由体的运动所预加的限制条件称为 约束 ;约束力的方向总是与约束所能阻止的物体的运动趋势的方向 相反 ;约束力由 主动 力引起,且随 主动 力的改变而改变。
理论力学第6章答案

环 量 为 Γ , 则 根 据 多 连 通 域 的 斯 托 克 斯 定 理 有 : Γ − Γ( 0 , 0 ) =
∫∫ Ω dA = 0 , 即
z
Γ = Γ( 0, 0) = 2πC
6-8
Q圆r = a1 , r = a2是流线 ∴圆r = a1 , r = a2上的流体速度沿切向方向
即 r = a1时,υθ = υ0,υ r = 0;r = a2时,υθ = 0,υr = 0
Ω=
6-9
π (a − a )
2 2 2 1
Γa2 − Γa1
=
0 − 2πa1υ0 2a υ = 2 1 02 2 2 π (a2 − a1 ) a1 − a2
由单连通域的斯托克斯定理可知: Γ k3 = 0 , Γ k4 = ΩA = 2π r
2 0
ω
k2 ,k4 所在为多连通域,由多连通域的斯托克斯定理可知: Γ k1 − Γ a = 0 ,所以
Γ k1 = Γ a = 2π a 2ω Γ k4 = ΩA = 2π r02ω
Γ k2 = Γ AB + Γ Bo + Γ oC + ΓCD + Γ DA = Γ AB + Γ Bo + Γ oC + ΓCD + Γ DA + Γ BC − Γ BC = Γ AB + Γ Bo + Γ oC + ΓCD + Γ DA + Γ BC + ΓCB = (Γ AB + Γ BC + ΓCD + Γ DA ) + (Γ Bo + Γ oC + ΓCB ) 1 2 π a 2ω = 0 + π a 2ω = 4 2
清华理论力学课后答案6

vE 10 = 3 = 5.77 rad/s , CE 3
r3 = r1 + 2r2 ,可得轮 1 的角速度 v r +r (顺时针) ω1 = M = 1 2 ω4 = 12ω4 , r1 r1
轮 1 的转速为 (顺时针). n1 = 12n4 = 10800 r/ min ,
kh da
习题解答
作图示几何关系,图中 v A = v ,解得
解法二:在直角三角形△ACO 中,
sin ϑ =
̇ cosϑ = − R x ̇ ϑ x2 ̇ = v, x = R sin ϑ ,解得 AB 杆的角速度为 其中, x
2 ̇ = − sin ϑ v , ϑ cos ϑ R (负号表示角速度转向与 ϑ 角增大的方向相反,即逆时针)
(d) (e) =
再选定销钉 B 为动点,摇杆为动系,如图(c) ,有
a B = aen + aet + ar + ac
由式(d),(e)得 大小: 方向: 向 BO 轴上投影 解出 ae = aBO − ac ,于是摇杆的角加速度为
τ n
a
n BO
a
n e
+
a
t e
+
a r + ac
?
2 RωO
O1B ⋅ ω 2 O1
其中 ae = aC′ = a A + a 大小: 方向: ? √
t c ′A
答
aB
=
aA
案
+
网
杆的角速度为 ω AB =
vA = 1 rad/s ,而 C 点的牵连速度为 C AB A
t a BA
+
【最新试题库含答案】《理论力学》第六章作业答案

vC?vD?O1A??0.1?5?0.5m/s
nnaC?aD?O1A?2?0.1?52?2.5m/s2
ττaC?aD?O1A??0.1?2?0.2m/s2
6-2如图6-17所示的曲柄滑杆机构中,滑杆BC上有一圆弧形轨道,其半径R=100mm,圆心O1在导杆BC上。曲柄长OA=100mm,以等
解:起重机为研究对象,坐标系如图示,受力为一空间平行力系,平衡方程为:
?
Z?0 N
x
A
?N
C
B
?N
C
?G?P?0
A
?m?m
?N
?0 ?N?0 N
A
?MC?(N
B
?NB)?MD?0
y
?AD?N
B
?DB?G?0.5m?P?4m?0
C
A
?8.33kN N?78.33kN N?43.34kN
6-4水平轴上装有两个凸轮,凸轮上分别作用已知P力=800N和未知力F;如轴
《理论力学》第六章作业答案
:
篇一:理论力学第六章习题
6-1用图示三脚架ABCD和绞车E从矿井中吊起重30kN的30的重物,△ABC
为等边三角形,三脚架的三只脚及绳索DE均与水平面成60o角,不记架重;求当重物被匀速吊起时各叫所受的力。
解:铰链D为研究对象,坐标系如图示,受力分析为一空间汇交力系,O为D
角速度??4rad/s绕O轴转动。设t=0时,??0,求导杆BC的运动规律以及曲柄与水平线的夹角??30?时,导杆BC的速度和加速度。
图6-17
xO1?2OAcos??2Rcos?t?2?0.1?cos4t?0.2cos4tm
?O1??0.8sin4tm/s??30?时x?O1??0.4m/ sx
理论力学(刘又文 彭献)答案第6章

∑ ∑ 二.动能:T = 1 2
mivi2 ,
T
=
1 2
mvC2
+
1 2
mi vr2i
平移刚体: T平移
=
1 2
mvC2
定轴转动刚体: T定转
=
1 2
JOω 2
平面运动对称刚体: T平面
=
1 2
mvC2
+
1 2
JCω 2
FT
C mg
图 6.6
8.如图 6.7 所示,物块 A 质量为 m1 ,杆 AB 质量为
×
1 2
×
G2 g
R2
⋅ω 2
+ G1Rϕ
sinθ
。
对吗?
C
G1
α
R OM
G2
图 6.13
答:不对。此处多计算了重力的功。如果把重力视为外力,则右边不能再有 重力势能,若右边计入重力势能,则左边不再有重力的功。
187
16.如图 6.14 所示,物 A 重为 G1 ,物 B 重为 G2 ,且 G1 > G2 ,不计摩擦。 设由静止开始,A 下降 h 时各速度如图,由动能定理,有
k (δ
2
−
δ
2 S
)
− Gδ
T2 = 0
由机械能守恒,有T1 + V1 = V2 。对吗?
ω
δs δ
I G
II
图 6.16
答:不对。因为在同一问题中,每种势力场的零点位置虽可任取,但一种力 场只能有一个零点。此处重力场和弹性力场分别取了两个不同的零点而导致错 误。
19.如图 6.17 所示,细绳长 l,悬吊重球 M 于 O 点,O1 为铁钉,OO1 = h, 保证 M 能绕过 O1 的最小ϕ 角应使势能满足:
《理论力学》第六章作业答案

《理论力学》第六章作业答案如果不做书中所附的习题,就等于处宝山而空返。
——华罗庚。
1 [习题6-2]半圆形凸轮以匀速s mm v /10=沿水平方向向左运动,活塞杆AB 长l 沿铅直方向运动。
当运动开始时,活塞杆A 端在凸轮的最高点上。
如凸轮的半径mm R 80=,求,求活塞活塞B 的运动方程和速度方程.解:活塞杆AB 作竖向平动。
以凸轮圆心为坐标原点,铅垂向上方向为x 轴的正向,则由图中的几何关系可知,任一时刻,B 点的坐标,即活塞B 的运动方程为:)(64)()(cos 22222cm t l vt R l Rvt R R l R l x B -+=-+=-⋅+=+=ϕ活塞B 的速度方程为:)/(646422122s cm t t t t dt dx v B B --=--==[习题6-4]点M 以匀速率u 在直管OA 内运动,直管OA 又按t ωϕ=规律绕O 转动。
当0=t 时,M 在O 点,求其在任一瞬时的速度及加速度的大小。
解: ut r =,t ωϕ=。
设任一瞬时,M 点的坐标为),(y x M ,则点M 的运动方程为:t ut r x ωϕcos cos ==, tut r y ωϕsin sin ==速度方程为:速度方程为:t t u t u t ut t u t ut dt ddt dxv x ωωωωωωωsin cos )sin (cos )cos (-=⋅-+===t t t u t t u t u v x ωωωωωωcos sin 2sin )(cos 222222⋅-+=t t u t u t ut t u t ut dt ddt dyv y ωωωωωωωcos sin cos sin )sin (+=⋅⋅+===t t t u t t u t u v y ωωωωωωcos sin 2cos )(sin 222222⋅++=2222)(t u u v v y x ω+=+任一瞬时,速度的大小为:22222)(1)(t u t u u v v v y x ωω+=+=+=加速度方程为:)sin cos (t t u t u dt ddt dv a xx ωωω-==]cos sin [)sin (ωωωωωωω⋅⋅+⋅-⋅-⋅=t t u t u t ut t u t u ωωωωcos sin 22--=t t t u t t u t u a x ωωωωωωωcos sin 4cos )(sin 4322222222⋅++=)cos sin (t t u t u dtd dt dv a yy ωωω+==ωωωωωωω⋅-⋅+⋅+⋅⋅=)sin (cos [cos t t u t u t ut t u t u ωωωωsin cos 22⋅-=t t t u t t u t u a y ωωωωωωωcos sin 4sin )(cos 4322222222⋅-+=222222)(4t u u a a y x ωω+=+任一瞬时,速度的大小为:2222222)(4)(4t u t u u a a a y x ωωωω+=+=+=[习题6-14] 电动绞车由带轮Ⅰ和Ⅱ及鼓轮Ⅲ组成如图电动绞车由带轮Ⅰ和Ⅱ及鼓轮Ⅲ组成如图6-426-426-42所示,鼓轮Ⅲ和带轮所示,鼓轮Ⅲ和带轮Ⅱ刚连在同一轴上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
t=5s时,试求飞机在轨迹上的位置M及其速度和加速度。
【解】 因已知飞机沿圆弧轨迹
的运动方程,宜用自然法求解。 O 取M0为弧坐标 s 的原点,s 的 正负方向如图所示。
(-) M0
r
s
当t = 5 s时,飞机的位 置M可由弧坐标确定
s 250t 5t2 1375m
M
(+)
理论力学电子教程
8
C
D
B+s
ω
s
s 2R π sin 2πt
40
O
φ
θ
A R
R
O'
这就是B点的自然形式的运
-s
动方程,所以
E
ds π2
dv π3
v
dt
cos 2πt, 20
a
dt
sin 2πt 10
an
vs
2πt
2
0.1
π4 cos2 40
2πt
理论力学电子教程
v vx2 vy2 vz2
a axi ay j azk
a ax2 ay2 az2
v ds dt
a
dv dt
v2
an
理论力学电子教程
1
飞机在铅直面内从位置M0处以 s=250t+5t2 规律沿
半径r=1500m的圆弧作机动飞行,其中s以m计,t以s计,当
M
(+)
aτ v
飞机的全加速度 a 为
a a2 an2 60.8 m / s2
tan a 0.166, 9.5
an
理论力学电子教程
2 销钉B可沿半径等于R的固定圆弧滑道DE和摆杆的直槽
中滑动,OA=R=0.1m。已知摆杆的转角 π sin 2πt (时间以
【解】 当 t1 0.25 s 时,
1
π 8
rad ,
v1 0 ,
又
a1
π3 10
m/s 2,a1n
0。
可见 , 这时B点的加速度大小
D B1
R
a1=a1τ
A
θ1 a2=a2n Bv2 2
a1 a1
π3 10
m/s 2
且a1沿切线的负向。
E
当
t2
1s
时, 2
0,
v2
2 m/s,
20
又
4
a2
0,a2n
40
m/s2 。
可见,这时点B的加速度大小
a2
a2n
π4 40
m / s2
且 a2 沿半径 B2。
【解】 飞机的速度
v ds 250 10t dt
飞机的切向加速度和法向加速度
a
dv dt
10
an
v2
1 (250 10t)2 1500
代入 t = 5s得
v 300m / s a 10 m / s2, an 60 m / s2
O
r an aθ
(-) M0
s v0
8
s计,以rad计),试求销钉在t1=0.25s和t2=1s时的加速度。
【解】 已知销钉B的轨迹是
圆弧DE,中心在A点,半径
是R。选滑道上O'点作为弧 坐标的原点,并以O'D为正 向。则B点在任一瞬时的弧 坐标
C
D
B+s
s
O
A R
R
O'
-s
s R
E
理论力学电子教程
【解】 由几何关系知 2 , 且 π sin 2πt,则
理论力学电子教程
矢径法
直角坐标法
自然法
运动 方程
r r(t )
x x( t ),y y( t ),z z( t )
s s( t )
速度
v
dr dt
a dv
加
dt
速
d2r
度
dt2
v vxi vy j vzk
vx
dx dt
,vy
dy dt
,vz
dz dt
